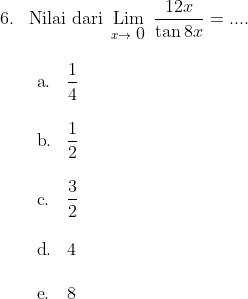
Jawab : c
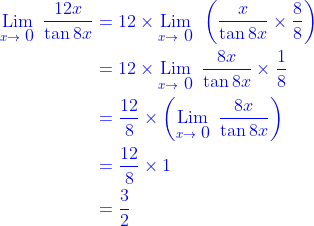
Selanjutnya jika ada soal menentukan nilai limit dan fungsinya berbentuk rasional dengan pembilang atau penyebut berupa sinus atau tangen (kadang keduanya muncul bersamaan yang satu diposisi pembilang dan yang satu diposisi penyebut) semisal bentuk di atas dan masing-masing berpangkat sama, maka kita kemungkinan besar tinggal mengambil koefisien dari masing-masing unsur pembilang dan penyebutnya. Demikian untuk langkah mudahnya dalam menyelesaikan soal yang ada.
Sehingga soal di atas dapat juga diselesaikan dengan cara hematnya:
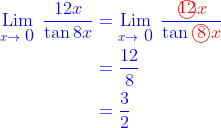
Coba perhatikan soal berikut
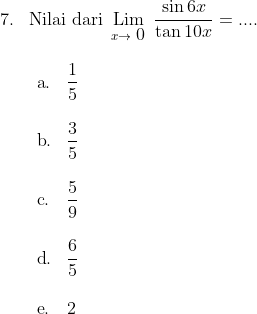
Jawab : b
Walau cukup jelas dan sebagai ulasannya adalah sebagai berikut
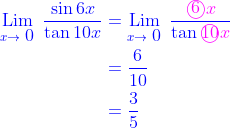
Sebagai tambahan kita berikan contoh pula soal berikut
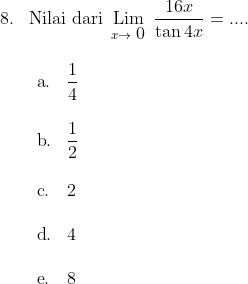
Jawab : d
Cukup jelas bahwa
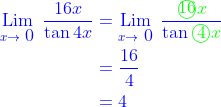
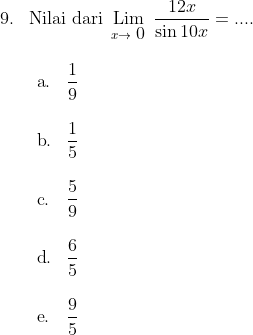
Jawab : d
Cukup jelas
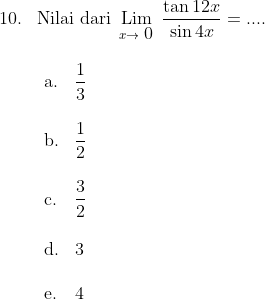
Jawab : d
Jawaban juga sudah cukup jelas