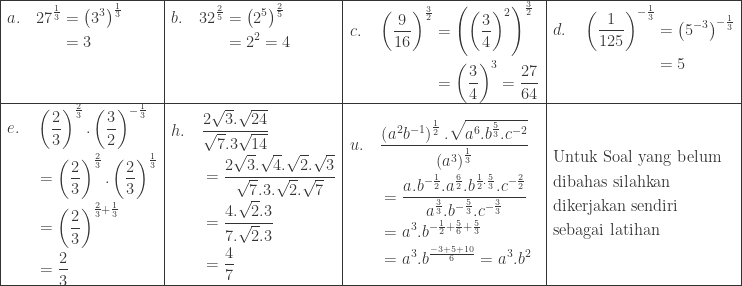Saya pernah lihat soal seperti berikut
Soal tersebut meminta berapa besar tinggi H seperti ilustrasi gambar tersebut di atas dengan x = 8 cm dan y = 6 cm ?
Saya lihat soal ini di try out SMP, wah, mula-mula ada bingungnya juga. Pikir saya, saya mau mengerjakan dengan cara bagaimana? maklum kemampuan saya biasa-biasa aja. Iseng-iseng saya kerjakan soal tersebut dengan bantuan rekayasa diagram kartesius, saya menyebutnya demikianlah.. Saya yakin pembaca yang budiman ada yang gak setuju atau mungkin setuju dengan saya karena terlalu ribet.
Sukur-sukur di antara Anda para pembaca yang budiman ada yang sudi memberikan solusi dengan konsep kesebangunan atau apalah supaya kita tercerahkan.
Ok lanjut aja
Misalkan yang saya maksudkan di atas (bantuan diagram kartesius) seperti berikut:
Selanjutnya kita buat persamaan garisnya yaitu anggap saja garis yang melalui titik $O(0,0)$ adalah $L_{1}$ dan garis yang satunya kita sebut sebagai $L_{2}$.
Karena persamaan garis $L_{1}$ melalui titik $O(0,0)$ dan $(c,b)$, maka persamaan garisnya adalah
$\begin{aligned}\displaystyle \frac{y-0}{b-0}&=\frac{x-0}{c-0}\\ \Leftrightarrow y&=\color{red}\displaystyle \frac{b}{c}x\color{black}\\ \Leftrightarrow x&=\color{blue}\displaystyle \frac{c}{b}y\: \color{black}................(1) \end{aligned}$.
Untuk persamaan garis $L_{2}$ yang melalui titik $(c,0)$ dan $(0,b)$, persamaan garisnya adalah
$\begin{aligned}\frac{(y-0)}{(a-0)}&=\frac{(x-c)}{(0-c)}\\ y&=\color{blue}-\frac{a}{c}(x-c)\: \color{black}................(2) \end{aligned}$.
Dari persamaan 1) dan 2) kita mendapatkan
$\begin{aligned}y&=-\frac{a}{c}(x-c)\\\\ \Leftrightarrow\: \: & y=-\frac{a}{c}(\frac{c}{b}y-c)\\\\ \Leftrightarrow\: \: & y=-\frac{a}{b}y+a\\ \Leftrightarrow\: \: & y+\displaystyle \frac{a}{b}y=a\Leftrightarrow \displaystyle \frac{a+b}{b}y=a\\\\ \therefore &\quad y=\color{red}\frac{ab}{a+b} \end{aligned}$.
Jadi titnggi H adalah sebesar
$\textrm{H}=\displaystyle \frac{xy}{x+y}$.
Sehingga apabila x = 8 cm dan y = 6 cm , maka tinggi H adalah
$\textrm{H}=\displaystyle \frac{8.6}{8+6}=\frac{48}{14}=\frac{24}{7}$.
Sebagai catatannya adalah ternyata harga M tidak muncul dalam formula tersebut , unik memang. Tapi begitulah adanya.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ &(\textbf{OSN SD 2009})\\ &\textrm{Pada gambar berikut, diketahui}\: \: AB=3\: \: cm\\ &\textrm{dan}\: \: CD=4\: \: cm.\: \textrm{Sisi}\: \: AB,EF,\: \textrm{dan}\: \: CD\\ &\textrm{masing-masing tegak lurus}\: \: AC.\: \textrm{Tentukan}\\ &\textrm{panjang}\: \: EF?\\\\ \end{array}$.
$.\qquad\begin{aligned}\textrm{Dengan}&\textrm{rumus di atas akan dengan}\\ \textrm{mudah }&\textrm{kita tentukan panjangnya, yaitu}:\\ \quad EF&=\color{red}\frac{AB\times CD}{AB+CD}\\ &=\displaystyle \frac{3\times 4}{3+4}\\ &=\displaystyle \frac{12}{7}\: \: cm\\\\ \textrm{Jadi,}\: \textrm{ti}&\textrm{nggi}\: \: EF=\color{blue}\displaystyle \frac{12}{7}\: \: \color{black}cm \end{aligned}$.
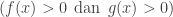
 .
.
![\begin{array}{ll}\\ \fbox{1}.&\textrm{Tentukanlah nilai dari bilangan-bilangan berikut ini}! \end{array}\\ \begin{array}{llllllll}\\ .\quad\quad &a.&27^{\frac{1}{3}}&k.&\left ( \displaystyle \frac{2^{3}.3^{-2}}{2^{-5}.3} \right )^{\displaystyle \frac{1}{2}}&u.&\displaystyle \frac{\left ( a^{2}.b^{-1} \right )^{\frac{1}{2}}\sqrt{a^{6}.b^{\frac{5}{3}}.c^{-2}}}{\left ( a^{3}.b^{-5}.c^{-3} \right )^{\frac{1}{3}}}\\ &b.&32^{^{\frac{2}{5}}}&l.&\displaystyle \frac{\sqrt{2}.\sqrt[3]{8}}{(2)^{\frac{1}{3}}.\sqrt[4]{16^{2}}}&v.&\displaystyle \frac{x^{2}.y^{7}}{x^{3}.y^{5}}\\ &c.&\left ( \displaystyle \frac{9}{16} \right )^{\displaystyle \frac{3}{2}}&m.&\left ( \displaystyle \frac{\sqrt{2}.2\sqrt{6}}{\sqrt{3}.\sqrt[3]{9}} \right )^{\displaystyle \frac{1}{2}}&w.&\left ( \displaystyle \frac{2x^{3}}{y^{2}}:\frac{4x^{6}}{4y^{5}} \right ).\displaystyle \frac{3x^{2}-2y}{3y}\\ &d.&\left ( \displaystyle \frac{1}{125} \right )^{-\frac{1}{3}}&n.&\displaystyle \frac{2.3^{-\frac{1}{2}}-2+3.2^{-\frac{1}{2}}}{2.3^{-\frac{1}{2}}-3.2^{-\frac{1}{2}}}&x.&\left (\sqrt[3]{x^{2}.yz^{3}} \right ).x^{-1}.y^{-2}\\ &e.&\left ( \displaystyle \frac{2}{3} \right )^{\displaystyle \frac{2}{3}}.\left ( \displaystyle \frac{3}{2} \right )^{-\displaystyle \frac{1}{3}}&o.&-3\sqrt{6}+4\sqrt{3}-2\sqrt{81}&y.&\displaystyle \frac{\sqrt{x}.\sqrt{x^{2}y^{3}}.\sqrt{xy^{2}}}{\sqrt[4]{x}.\sqrt[3]{y}}\\ &f.&\left ( \displaystyle \frac{1}{5^{3}} \right )^{-1}.\left ( \displaystyle \frac{1}{5^{2}} \right )^{2}&p.&\sqrt{250}-\sqrt{50}+15\sqrt{2}&z.&\displaystyle \frac{\left ( x^{2} \right )^{3}}{x^{4}}:\left ( \frac{x^{3}}{\left ( x^{3} \right )^{2}} \right )^{-2} \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5C%5C+%5Cfbox%7B1%7D.%26%5Ctextrm%7BTentukanlah+nilai+dari+bilangan-bilangan+berikut+ini%7D%21+%5Cend%7Barray%7D%5C%5C+%5Cbegin%7Barray%7D%7Bllllllll%7D%5C%5C+.%5Cquad%5Cquad+%26a.%2627%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%26k.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B2%5E%7B3%7D.3%5E%7B-2%7D%7D%7B2%5E%7B-5%7D.3%7D+%5Cright+%29%5E%7B%5Cdisplaystyle+%5Cfrac%7B1%7D%7B2%7D%7D%26u.%26%5Cdisplaystyle+%5Cfrac%7B%5Cleft+%28+a%5E%7B2%7D.b%5E%7B-1%7D+%5Cright+%29%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%5Csqrt%7Ba%5E%7B6%7D.b%5E%7B%5Cfrac%7B5%7D%7B3%7D%7D.c%5E%7B-2%7D%7D%7D%7B%5Cleft+%28+a%5E%7B3%7D.b%5E%7B-5%7D.c%5E%7B-3%7D+%5Cright+%29%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D%7D%5C%5C+%26b.%2632%5E%7B%5E%7B%5Cfrac%7B2%7D%7B5%7D%7D%7D%26l.%26%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7B2%7D.%5Csqrt%5B3%5D%7B8%7D%7D%7B%282%29%5E%7B%5Cfrac%7B1%7D%7B3%7D%7D.%5Csqrt%5B4%5D%7B16%5E%7B2%7D%7D%7D%26v.%26%5Cdisplaystyle+%5Cfrac%7Bx%5E%7B2%7D.y%5E%7B7%7D%7D%7Bx%5E%7B3%7D.y%5E%7B5%7D%7D%5C%5C+%26c.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B9%7D%7B16%7D+%5Cright+%29%5E%7B%5Cdisplaystyle+%5Cfrac%7B3%7D%7B2%7D%7D%26m.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7B2%7D.2%5Csqrt%7B6%7D%7D%7B%5Csqrt%7B3%7D.%5Csqrt%5B3%5D%7B9%7D%7D+%5Cright+%29%5E%7B%5Cdisplaystyle+%5Cfrac%7B1%7D%7B2%7D%7D%26w.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B2x%5E%7B3%7D%7D%7By%5E%7B2%7D%7D%3A%5Cfrac%7B4x%5E%7B6%7D%7D%7B4y%5E%7B5%7D%7D+%5Cright+%29.%5Cdisplaystyle+%5Cfrac%7B3x%5E%7B2%7D-2y%7D%7B3y%7D%5C%5C+%26d.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B1%7D%7B125%7D+%5Cright+%29%5E%7B-%5Cfrac%7B1%7D%7B3%7D%7D%26n.%26%5Cdisplaystyle+%5Cfrac%7B2.3%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D-2%2B3.2%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%7D%7B2.3%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D-3.2%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%7D%26x.%26%5Cleft+%28%5Csqrt%5B3%5D%7Bx%5E%7B2%7D.yz%5E%7B3%7D%7D+%5Cright+%29.x%5E%7B-1%7D.y%5E%7B-2%7D%5C%5C+%26e.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B2%7D%7B3%7D+%5Cright+%29%5E%7B%5Cdisplaystyle+%5Cfrac%7B2%7D%7B3%7D%7D.%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B3%7D%7B2%7D+%5Cright+%29%5E%7B-%5Cdisplaystyle+%5Cfrac%7B1%7D%7B3%7D%7D%26o.%26-3%5Csqrt%7B6%7D%2B4%5Csqrt%7B3%7D-2%5Csqrt%7B81%7D%26y.%26%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7Bx%7D.%5Csqrt%7Bx%5E%7B2%7Dy%5E%7B3%7D%7D.%5Csqrt%7Bxy%5E%7B2%7D%7D%7D%7B%5Csqrt%5B4%5D%7Bx%7D.%5Csqrt%5B3%5D%7By%7D%7D%5C%5C+%26f.%26%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B1%7D%7B5%5E%7B3%7D%7D+%5Cright+%29%5E%7B-1%7D.%5Cleft+%28+%5Cdisplaystyle+%5Cfrac%7B1%7D%7B5%5E%7B2%7D%7D+%5Cright+%29%5E%7B2%7D%26p.%26%5Csqrt%7B250%7D-%5Csqrt%7B50%7D%2B15%5Csqrt%7B2%7D%26z.%26%5Cdisplaystyle+%5Cfrac%7B%5Cleft+%28+x%5E%7B2%7D+%5Cright+%29%5E%7B3%7D%7D%7Bx%5E%7B4%7D%7D%3A%5Cleft+%28+%5Cfrac%7Bx%5E%7B3%7D%7D%7B%5Cleft+%28+x%5E%7B3%7D+%5Cright+%29%5E%7B2%7D%7D+%5Cright+%29%5E%7B-2%7D+%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0)
![\begin{array}{llllllll}\\ .\quad\quad&g.&\displaystyle \frac{\sqrt{3}.\sqrt{15}}{\sqrt{5}}\quad\qquad \: \: &q.&\sqrt[2]{75}-\sqrt[4]{27}+\sqrt[3]{128}\\ &h.&\displaystyle \frac{2\sqrt{3}.\sqrt{24}}{\sqrt{7}.3\sqrt{14}}&r.&\displaystyle \frac{5\sqrt{5}+2\sqrt{5}}{5-3\sqrt{5}}\\ &i&\displaystyle \frac{\sqrt{5}.\sqrt[2]{2^{3}}}{2.\sqrt[3]{3}}&s.&\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{\cdots }}}}}}\\ &j.&\displaystyle \frac{\sqrt{3}.\sqrt[3]{2}}{\left ( \frac{4}{9} \right )^{3}.\left ( \frac{2}{3} \right )^{-2}}&t.&\left ( 4^{\frac{1}{2}} \right )^{\frac{1}{2}}\left ( 2^{-2} \right )^{-2}.\sqrt[3]{0,125}.\left ( 0,25 \right ).\displaystyle \frac{1}{2}\sqrt{\frac{1}{2}} \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bllllllll%7D%5C%5C+.%5Cquad%5Cquad%26g.%26%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7B3%7D.%5Csqrt%7B15%7D%7D%7B%5Csqrt%7B5%7D%7D%5Cquad%5Cqquad+%5C%3A+%5C%3A+%26q.%26%5Csqrt%5B2%5D%7B75%7D-%5Csqrt%5B4%5D%7B27%7D%2B%5Csqrt%5B3%5D%7B128%7D%5C%5C+%26h.%26%5Cdisplaystyle+%5Cfrac%7B2%5Csqrt%7B3%7D.%5Csqrt%7B24%7D%7D%7B%5Csqrt%7B7%7D.3%5Csqrt%7B14%7D%7D%26r.%26%5Cdisplaystyle+%5Cfrac%7B5%5Csqrt%7B5%7D%2B2%5Csqrt%7B5%7D%7D%7B5-3%5Csqrt%7B5%7D%7D%5C%5C+%26i%26%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7B5%7D.%5Csqrt%5B2%5D%7B2%5E%7B3%7D%7D%7D%7B2.%5Csqrt%5B3%5D%7B3%7D%7D%26s.%26%5Csqrt%7B2%5Csqrt%7B2%5Csqrt%7B2%5Csqrt%7B2%5Csqrt%7B2%5Csqrt%7B%5Ccdots+%7D%7D%7D%7D%7D%7D%5C%5C+%26j.%26%5Cdisplaystyle+%5Cfrac%7B%5Csqrt%7B3%7D.%5Csqrt%5B3%5D%7B2%7D%7D%7B%5Cleft+%28+%5Cfrac%7B4%7D%7B9%7D+%5Cright+%29%5E%7B3%7D.%5Cleft+%28+%5Cfrac%7B2%7D%7B3%7D+%5Cright+%29%5E%7B-2%7D%7D%26t.%26%5Cleft+%28+4%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D+%5Cright+%29%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%5Cleft+%28+2%5E%7B-2%7D+%5Cright+%29%5E%7B-2%7D.%5Csqrt%5B3%5D%7B0%2C125%7D.%5Cleft+%28+0%2C25+%5Cright+%29.%5Cdisplaystyle+%5Cfrac%7B1%7D%7B2%7D%5Csqrt%7B%5Cfrac%7B1%7D%7B2%7D%7D+%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0)