Lanjutan 3 Soal Persiapan Penilaian Tengah Semester Gasal Kelas XI Pendalaman Matematika (Peminatan)

$\begin{array}{ll}\\ 16.&\textrm{Himpunan penyelesaian dari persamaan}\\ &\cos (x-30)^{\circ}= \displaystyle \frac{1}{2}\sqrt{2} \: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle \left \{ 75^{\circ},285^{\circ} \right \}\\\\ &\textrm{b}.\quad \displaystyle \left \{ 75^{\circ},343^{\circ} \right \}\\\\ &\textrm{c}.\quad \displaystyle \left \{ 75^{\circ},344^{\circ} \right \}\\\\ &\textrm{d}.\quad \displaystyle \color{red}\left \{ 75^{\circ},345^{\circ} \right \}\\\\ &\textrm{e}.\quad \displaystyle \left \{ 75^{\circ},346^{\circ} \right \}\\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ &\begin{aligned} & \cos (x-30)^{\circ}= \displaystyle \frac{1}{2}\sqrt{2} \\ &\cos (x-30)^{\circ}= \cos 45^{\circ}\\ &\Leftrightarrow \: \: x-30^{\circ}=\pm 45^{\circ}+k.360^{\circ}\\ &\Leftrightarrow \quad x =30^{\circ}\pm 45^{\circ}+k.360^{\circ} \\ &k=0\Rightarrow x_{1}=75^{\circ}\: \: (\color{blue}\textrm{mm})\\ &\qquad\textrm{atau}\: \: x_{2}=-15^{\circ}\: \: \color{red}(tm)\\ &k=1\Rightarrow x_{1}=75^{\circ}+360^{\circ} \: \: (\color{red}\textrm{tm})\\ &\qquad \textrm{atau}\: \: \: x_{2}=-15^{\circ}+360^{\circ}=345^{\circ}\: \: \color{blue}(mm) \end{aligned} \\ &\textbf{HP}=\color{red}\color{red}\left \{\displaystyle 75^{\circ},345^{\circ} \right \} \end{array} \end{array}$.

$\begin{array}{ll}\\ 17.&\textrm{Himpunan penyelesaian dari persamaan}\\ &\cos (x-30)^{\circ}= \displaystyle \frac{1}{2}\sqrt{3} \: \: \textrm{untuk}\: \: 0^{\circ}< x< 360^{\circ}\\ &\textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle \left \{ 100^{\circ},330^{\circ} \right \}\\\\ &\textrm{b}.\quad \displaystyle \color{red}\left \{ 30^{\circ},330^{\circ} \right \}\\\\ &\textrm{c}.\quad \displaystyle \left \{ 120^{\circ},300^{\circ} \right \}\\\\ &\textrm{d}.\quad \displaystyle \left \{ 60^{\circ},120^{\circ} \right \}\\\\ &\textrm{e}.\quad \displaystyle \left \{ 50^{\circ},300^{\circ} \right \}\\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ &\begin{aligned} & \cos x^{\circ}= \displaystyle \frac{1}{2}\sqrt{3} \\ &\cos x^{\circ}= \cos 30^{\circ}\\ &\Leftrightarrow \quad x =\pm 30^{\circ}+k.360^{\circ} \\ &k=0\Rightarrow x_{1}=30^{\circ}\: \: (\color{blue}\textrm{mm})\\ &\qquad\textrm{atau}\: \: x_{2}=-30^{\circ}\: \: \color{red}(tm)\\ &k=1\Rightarrow x_{1}=30^{\circ}+360^{\circ}=390^{\circ} \: \: (\color{red}\textrm{tm})\\ &\qquad \textrm{atau}\: \: \: x_{2}=-30^{\circ}+360^{\circ}=330^{\circ}\: \: \color{blue}(mm) \end{aligned} \\ &\textbf{HP}=\color{red}\color{red}\left \{\displaystyle 30^{\circ},330^{\circ} \right \} \end{array} \end{array}$

Lanjutan 2 Soal Persiapan Penilaian Tengah Semester Gasal Kelas XI Pendalaman Matematika (Peminatan)

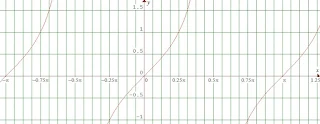
$\begin{array}{ll}\\ 11.&\textrm{Grafik fungsi trigonometri pada gambar}\\ &\textrm{berikut adalah}\: .... \end{array}$.

$.\quad\begin{array}{ll}\\ &\textrm{a}.\quad \displaystyle y=2\sin \left ( x-\displaystyle \frac{1}{2}\pi \right ) \\\\ &\textrm{b}.\quad \displaystyle y=2\sin \left ( \displaystyle \frac{1}{2}\pi -x \right ) \\\\ &\textrm{c}.\quad \displaystyle \color{red}y=2\sin \left ( 2x+\displaystyle \frac{1}{6}\pi \right ) \\\\ &\textrm{d}.\quad \displaystyle y=-2\sin \left ( \displaystyle \frac{1}{2}\pi +x \right ) \\\\ &\textrm{e}.\quad \displaystyle y=-2\sin \left ( \displaystyle \frac{1}{2}\pi -2x \right ) \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Dari grafik tampak jelas bahwa}\\ &\textrm{gambar di atas adalah garfik}\\ &\textrm{fungsi sinus di geser ke}\: \: \textbf{kiri}\\ &\textrm{dengan}\: \: \textbf{amplitudo}\: \: 2\\ &\textrm{dan}\: \: \textbf{periodenya}\: \: 2\pi,\: \textrm{maka}\\ &\textrm{bentuk persamaan}\: \: \textbf{grafik fungsinya}\\ &y=\color{red}2\sin \left ( 2x+k \right )\\ &\textrm{dengan}\: \: +k\: \: \textrm{adalah}\\ &\textbf{besar geseran ke kirinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Grafik fungsi trigonometri pada gambar}\\ &\textrm{berikut adalah}\: .... \end{array}$.

$.\quad\begin{array}{ll}\\ &\textrm{a}.\quad \displaystyle y=-2\sin (3x+45)^{\circ} \\\\ &\textrm{b}.\quad \displaystyle y=-2\sin (3x-15)^{\circ} \\\\ &\textrm{c}.\quad \displaystyle y=-2\sin (3x-45)^{\circ} \\\\ &\textrm{d}.\quad \displaystyle y=2\sin (3x+15)^{\circ} \\\\ &\textrm{e}.\quad \displaystyle \color{red}y=2\sin (3x-45)^{\circ} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Dari grafik tampak jelas bahwa}\\ &\textrm{gambar di atas adalah garfik}\\ &\textrm{fungsi sinus di geser ke}\: \: \textbf{kanan}\\ &\textrm{dengan}\: \: \textbf{amplitudo}\: \: 2\\ &\textrm{dan}\: \: \textbf{periodenya}\: \: \displaystyle \frac{360^{\circ}}{3}=120^{\circ},\: \textrm{maka}\\ &\textrm{bentuk persamaan}\: \: \textbf{grafik fungsinya}\\ &y=\color{red}2\sin 3\left ( x-k \right )\\ &\textrm{dengan}\: \: -k\: \: \textrm{adalah}\\ &\textbf{besar geseran ke kanan}\: \: 15^{\circ}\\ &\textrm{Jadi},\: \: y=\color{red}2\sin 3(x-15)^{\circ}=2\sin (3x-45)^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Grafik fungsi trigonometri pada gambar}\\ &\textrm{berikut adalah}\: .... \end{array}$.

$.\quad\begin{array}{ll}\\ &\textrm{a}.\quad \displaystyle y=-\cos (2x-30)^{\circ} \\\\ &\textrm{b}.\quad \displaystyle y=\sin (2x-60)^{\circ} \\\\ &\textrm{c}.\quad \displaystyle \color{red}y=\cos (2x+30)^{\circ} \\\\ &\textrm{d}.\quad \displaystyle y=\sin (2x-80)^{\circ} \\\\ &\textrm{e}.\quad \displaystyle y=\sin (2x+60)^{\circ} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Dari grafik tampak jelas bahwa}\\ &\textrm{gambar di atas adalah garfik}\\ &\textrm{fungsi cosinus di geser ke}\: \: \textbf{kiri}\\ &\textrm{dengan}\: \: \textbf{amplitudo}\: \: 1\\ &\textrm{dan}\: \: \textbf{periodenya}\: \: \displaystyle \frac{360^{\circ}}{2}=180^{\circ},\: \textrm{maka}\\ &\textrm{bentuk persamaan}\: \: \textbf{grafik fungsinya}\\ &y=\color{red}\cos 2\left ( x+k \right )\\ &\textrm{dengan}\: \: +k\: \: \textrm{adalah}\\ &\textbf{besar geseran ke kiri}\: \: 15^{\circ}\\ &\textrm{Jadi},\: \: y=\color{red}\cos 2(x+15)^{\circ}=\sin (2x+30)^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Himpunan penyelesaian dari persamaan}\\ &\sin x=\sin \displaystyle \frac{2}{10}\pi \: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle \left \{ \displaystyle \frac{22}{10}\pi ,\displaystyle \frac{8}{10}\pi \right \} \\\\ &\textrm{b}.\quad \displaystyle \left \{ \displaystyle \frac{2}{10}\pi ,\displaystyle \frac{28}{10}\pi \right \} \\\\ &\textrm{c}.\quad \displaystyle \color{red}\left \{ \displaystyle \frac{2}{10}\pi ,\displaystyle \frac{8}{10}\pi \right \} \\\\ &\textrm{d}.\quad \displaystyle \left \{ \displaystyle \frac{22}{10}\pi ,\displaystyle \frac{28}{10}\pi \right \} \\\\ &\textrm{e}.\quad \displaystyle \left \{ \displaystyle \frac{12}{10}\pi ,\displaystyle \frac{8}{10}\pi \right \} \\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ &\begin{aligned} & \sin x=\sin \displaystyle \frac{2}{10}\pi \\ &\Leftrightarrow \: \: x_{1}=\displaystyle \frac{2}{10}\pi+k.2\pi \: \: \: \: \color{blue}\textrm{atau}\\ &\Leftrightarrow \quad x_{2} =\left (\pi -\displaystyle \frac{2}{10}\pi \right )+k.2\pi=\displaystyle \frac{8}{10}\pi +k.2\pi \\ &k=0\Rightarrow x_{1}=\displaystyle \frac{2}{10}\pi\: \: (\color{blue}\textrm{mm})\: \: \color{black}\textrm{atau}\\ &\qquad\qquad x_{2}=\displaystyle \frac{8}{10}\pi\: \: (\color{blue}\textrm{mm})\\ &k=1\Rightarrow x_{1,2}=....+2\pi \quad (\color{red}\textrm{tidak memenuhi})\\ \end{aligned} \\ &\textbf{HP}=\color{red}\left \{\displaystyle \frac{2}{10}\pi,\: \displaystyle \frac{8}{10}\pi \right \} \end{array} \end{array}$.

$\begin{array}{ll}\\ 15.&\textrm{Himpunan penyelesaian dari persamaan}\\ &\tan \left ( 2x-\displaystyle \frac{1}{4}\pi \right )=\tan \displaystyle \frac{1}{4}\pi \: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle \left \{ \displaystyle \frac{1}{3}\pi ,\pi ,\displaystyle \frac{5}{3}\pi ,\displaystyle \frac{7}{3}\pi \right \} \\\\ &\textrm{b}.\quad \displaystyle \left \{ \displaystyle \frac{1}{4}\pi ,\displaystyle \frac{3}{5}\pi ,\frac{5}{4}\pi ,\frac{8}{5}\pi \right \} \\\\ &\textrm{c}.\quad \displaystyle \left \{ \displaystyle \frac{1}{4}\pi ,\displaystyle \frac{3}{4}\pi ,\frac{6}{4}\pi ,\displaystyle \frac{7}{4}\pi \right \} \\\\ &\textrm{d}.\quad \displaystyle \left \{ \displaystyle \frac{2}{4}\pi ,\displaystyle \frac{3}{4}\pi ,\pi ,\displaystyle \frac{7}{4}\pi \right \} \\\\ &\textrm{e}.\quad \displaystyle \color{red}\left \{ \displaystyle \frac{1}{4}\pi ,\frac{3}{4}\pi ,\frac{5}{4}\pi ,\displaystyle \frac{7}{4}\pi \right \} \\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ &\begin{aligned} & \tan \left ( 2x-\displaystyle \frac{1}{4}\pi \right )=\tan \displaystyle \frac{1}{4}\pi \\ &\Leftrightarrow \: \: 2x-\displaystyle \frac{1}{4}\pi=\displaystyle \frac{1}{4}\pi+k.\pi\\ &\Leftrightarrow \quad 2x =\displaystyle \frac{2}{4}\pi +k.\pi \\ &\Leftrightarrow \quad x =\displaystyle \frac{1}{4}\pi +k.\frac{\pi}{2} \\ &k=0\Rightarrow x=\displaystyle \frac{1}{4}\pi\: \: (\color{blue}\textrm{mm})\\ &k=1\Rightarrow x=\displaystyle \frac{1}{4}\pi+\frac{\pi}{2}=\displaystyle \frac{3}{4}\pi \: \: (\color{blue}\textrm{mm}) \\ &k=2\Rightarrow x=\displaystyle \frac{1}{4}\pi+\pi =\displaystyle \frac{5}{4}\pi \: \: (\color{blue}\textrm{mm}) \\ &k=3\Rightarrow x=\displaystyle \frac{1}{4}\pi+\frac{3\pi}{2}=\displaystyle \frac{7}{4}\pi \: \: (\color{blue}\textrm{mm}) \\ &k=4\Rightarrow x=\displaystyle \frac{1}{4}\pi+2\pi =\displaystyle \frac{9}{4}\pi \: \: (\color{red}\textrm{tidak memenuhi}) \\ \end{aligned} \\ &\textbf{HP}=\color{red}\color{red}\left \{\displaystyle \frac{1}{4}\pi,\: \displaystyle \frac{3}{4}\pi ,\frac{5}{4}\pi ,\frac{7}{4}\pi \right \} \end{array} \end{array}$

Lanjutan Soal Persiapan Penilaian Tengah Semester Gasal Kelas XI Pendalaman Matematika (Peminatan)

$\begin{array}{ll}\\ 6.&\textrm{Nilai}\: \: x \: \: \textrm{positif terkecil yang memenuhi}\\ &\sin x=-\displaystyle \frac{1}{2}\sqrt{3}\: \: \textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle 30^{\circ} \\\\ &\textrm{b}.\quad \displaystyle 60^{\circ} \\\\ &\textrm{c}.\quad \displaystyle 120^{\circ} \\\\ &\textrm{d}.\quad \color{red}\displaystyle 240^{\circ} \\\\ &\textrm{e}.\quad \displaystyle 300^{\circ} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}\sin x&=-\frac{1}{2}\sqrt{3}\\ \textrm{Gun}&\textrm{akan rumus persamaan}\\ &\textrm{sederhana, yaitu}:\\ \sin x&=-\sin 60^{\circ}\\ &=\sin \left ( 180^{\circ}+60^{\circ} \right )\\ &=\sin 240^{\circ}\\ x&=\color{red}240^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 7.&\textrm{Jika}\: \: \cos x=\displaystyle \frac{2\sqrt{5}}{5} \: \: \textrm{maka nilai}\\ &\cot x\left ( \displaystyle \frac{\pi }{2}-x \right )\: \: \textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \color{red}\displaystyle \frac{1}{2} \\\\ &\textrm{b}.\quad \displaystyle \frac{1}{3} \\\\ &\textrm{c}.\quad \displaystyle \frac{1}{6} \\\\ &\textrm{d}.\quad \displaystyle \frac{1}{7} \\\\ &\textrm{e}.\quad \displaystyle \frac{1}{8} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}\cos x&=\frac{2\sqrt{5}}{5},\: \: \textrm{maka}\\ \sin^{2} x&+\cos ^{2}x=1\\ \sin x&=1-\cos ^{2}x\\ &=\sqrt{1-\cos ^{2}x}=\sqrt{1-\left (\displaystyle \frac{2\sqrt{5}}{5} \right )^{2}}\\ &=\sqrt{1-\displaystyle \frac{20}{25}}=\sqrt{\displaystyle \frac{5}{25}}=\displaystyle \frac{\sqrt{5}}{5}\\ \cot &\left ( \displaystyle \frac{\pi }{2}-x \right )=\tan x,\: \: \textrm{maka}\\ \tan x&=\displaystyle \frac{\sin x}{\cos x}\\ &=\displaystyle \frac{\sqrt{5}}{2\sqrt{5}}\\ &=\color{red}\displaystyle \frac{1}{2} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 8.&\textrm{Periode dari fungsi}\: \: f(x)=-2\cos 3x\: \: \textrm{adalah}\: ....\\\\ &\textrm{a}.\quad 90^{\circ} \\\\ &\textrm{b}.\quad 100^{\circ} \\\\ &\textrm{c}.\quad \color{red}120^{\circ} \\\\ &\textrm{d}.\quad 150^{\circ} \\\\ &\textrm{e}.\quad 180^{\circ} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Periode dari}\: :\: f(x)=-2\cos 3x\\ &\textrm{adalah}\\ &=\displaystyle \frac{360^{\circ}}{3}\\ &=\color{red}120^{\circ}\\ &\\ &\textrm{Ingat bahwa}\\ &f(x)=a\cos bx,\: \: \textrm{maka periodenya}\\ &=\displaystyle \frac{360^{\circ}}{b} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 9.&\textrm{Perhatikanlah grafik berikut} \end{array}$.

$.\quad\begin{array}{ll}\\ &\textrm{Gambar di atas adalah grafik fungsi dari}\\ &\textrm{a}.\quad f(x)=\cos 2x \\\\ &\textrm{b}.\quad f(x)=\cos 3x \\\\ &\textrm{c}.\quad \color{red}f(x)=3\cos x \\\\ &\textrm{d}.\quad f(x)=3\cos 3x \\\\ &\textrm{e}.\quad f(x)=\displaystyle \frac{1}{3}\cos x \\\\ &\textbf{Jawab}:\\ &\textrm{Gambar cukup jelas}\\ &\textrm{dengan periode}\: \: 360^{\circ}\\ &\textrm{gambar dari grafik}\: \: f(x)=\color{red}3\cos x \end{array}$.

$\begin{array}{ll}\\ 10.&\textrm{Nilai dari}\: \: \displaystyle \frac{\sin \displaystyle \frac{3}{4}\pi +\tan \pi +\cos \pi }{\sin \displaystyle \frac{1}{2}\pi +\cos 2\pi -3\cos \displaystyle \frac{1}{3}\pi }=\: ....\\\\ &\textrm{a}.\quad 4 \\\\ &\textrm{b}.\quad 2-\sqrt{2} \\\\ &\textrm{c}.\quad \sqrt{2}-2 \\\\ &\textrm{d}.\quad -4 \\\\ &\textrm{e}.\quad \color{red}-1 \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \frac{\sin \displaystyle \frac{3}{4}\pi +\tan \pi +\cos \pi }{\sin \displaystyle \frac{1}{2}\pi +\cos 2\pi -3\cos \displaystyle \frac{1}{3}\pi }\\ &=\displaystyle \frac{\sin 150^{\circ} +\tan 180^{\circ} +\cos 180^{\circ} }{\sin \displaystyle 90^{\circ} +\cos 360^{\circ} -3\cos \displaystyle 60^{\circ} }\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}+0+(-1)}{1+1-3\left (\displaystyle \frac{1}{2} \right ) }\\ &=\displaystyle \frac{-\displaystyle \frac{1}{2}}{2-\displaystyle \frac{3}{2}}\\ &=-\displaystyle \frac{\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{2}}\\ &=\color{red}-1 \end{aligned} \end{array}$

Soal Persiapan Penilaian Tengah Semester Gasal Kelas XI Pendalaman Matematika (Peminatan)

$\begin{array}{ll}\\ 1.&\textrm{Nilai}\: \: 75^{\circ}\: \: \textrm{jika dinyatakan ke radian}\\ &\textrm{adalah}\: \: ....\: \: \textrm{radian}\\\\ &\textrm{a}.\quad \displaystyle \frac{1}{3}\pi \\\\ &\textrm{b}.\quad \displaystyle \frac{5}{6}\pi \\\\ &\textrm{c}.\quad \displaystyle \color{red}\frac{5}{12}\pi \\\\ &\textrm{d}.\quad \displaystyle \frac{7}{12}\pi \\\\ &\textrm{e}.\quad \displaystyle \frac{9}{12}\pi \\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diketah}&\textrm{ui bahwa}\\ 180^{\circ}&=\pi \: \: \: radian\\ 1^{\circ}&=\displaystyle \frac{\pi }{180}\: \: \: radian\\ 75\times 1^{\circ}&=75\times \displaystyle \frac{\pi }{180}\: \: \: radian\\ 75^{\circ}&=\displaystyle \frac{5}{12}\pi \: \: \: radian \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: \tan \theta =\displaystyle \frac{5}{12}\: \: \textrm{untuk}\: \: 0^{\circ}\leq \theta \leq 90^{\circ}\\ &\textrm{maka}\: \: \cos \theta \: \: \textrm{adalah}\: ....\\\\ &\textrm{a}.\quad \displaystyle \frac{5}{13} \\\\ &\textrm{b}.\quad \displaystyle \color{red}\frac{12}{13} \\\\ &\textrm{c}.\quad \displaystyle \frac{13}{5} \\\\ &\textrm{d}.\quad \displaystyle \frac{13}{12} \\\\ &\textrm{e}.\quad \displaystyle \frac{12}{5} \\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikanlah gambar segitiga berikut} \end{array}$.

$. \qquad\begin{aligned}\textrm{Diketah}&\textrm{ui bahwa}\\ \tan \theta &=\displaystyle \frac{5}{12}\: ,\: \textrm{untuk}\: 0^{\circ}\leq \theta \leq 90^{\circ}\\ &\color{red}\textrm{lihat gambar di atas}\\ &\textrm{dengan dalil Pythagoras akan}\\ &\textrm{didapatkan sisimiringnya}=13\\ \textrm{jadi}&,\: \textrm{nilai dari}\\ \cos \theta &=\displaystyle \frac{12}{13} \end{aligned}$.

$\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar berikut}\\ \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{Panjang BC adalah}\: ....\\ &\textrm{a}.\quad \displaystyle 20\sin 36^{\circ} \\ &\textrm{b}.\quad \displaystyle 20\cos 36^{\circ} \\ &\textrm{c}.\quad \color{red}\displaystyle 20\tan 36^{\circ} \\ &\textrm{d}.\quad \displaystyle 15\\ &\textrm{e}.\quad \displaystyle 16 \\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diketah}&\textrm{ui bahwa}\\ \tan 36^{\circ} &=\displaystyle \frac{BC}{20}\\ \Leftrightarrow &\: \color{red}BC\color{black}=20\tan 36^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Nilai}\: \: \tan 300^{\circ} \: \: \: \textrm{adalah}\: \: ....\\\\ &\textrm{a}.\quad \displaystyle \sqrt{3} \\\\ &\textrm{b}.\quad \displaystyle \frac{1}{3}\sqrt{3} \\\\ &\textrm{c}.\quad \displaystyle -\frac{1}{3}\sqrt{3} \\\\ &\textrm{d}.\quad \displaystyle \frac{1}{2}\sqrt{3} \\\\ &\textrm{e}.\quad \displaystyle \color{red}-\sqrt{3} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}\tan 300^{\circ}&=\tan \left ( 360^{\circ}-60^{\circ} \right )\\ &=-\tan 60^{\circ}\\ &=\color{red}-\sqrt{3}\\ \textbf{catatan}&: \textrm{ingat sudut berelasi} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 5.&\textrm{Nilai}\: \: \tan 60^{\circ}-\sin 120^{\circ}-\tan 210^{\circ} \: \: \: \textrm{adalah}\: \: ....\\\\ &\textrm{a}.\quad \displaystyle \frac{1}{6}\sqrt{6} \\\\ &\textrm{b}.\quad \displaystyle \frac{1}{3}\sqrt{6} \\\\ &\textrm{c}.\quad \displaystyle -\frac{1}{2}\sqrt{6} \\\\ &\textrm{d}.\quad \displaystyle \frac{1}{3}\sqrt{3} \\\\ &\textrm{e}.\quad \displaystyle \color{red}\frac{1}{6}\sqrt{3} \\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\tan 60^{\circ}-\sin 120^{\circ}-\tan 210^{\circ}\\ &=\tan 60^{\circ}-\sin \left ( 180^{\circ}-60^{\circ} \right )-\tan \left ( 180^{\circ}+30^{\circ} \right )\\ &=\tan 60^{\circ}-\sin 60^{\circ}-\tan 30^{\circ}\\ &=\sqrt{3}-\displaystyle \frac{1}{2}\sqrt{3}-\displaystyle \frac{1}{3}\sqrt{3}\\ &=\left (1-\displaystyle \frac{1}{2}-\frac{1}{3} \right )\sqrt{3}\\ &=\displaystyle \color{red}\frac{1}{6}\sqrt{3} \end{aligned} \end{array}$

Grafik Fungsi Trigonometri

Sebelumnya telah diketahui perbandingan trigonometri diberbagai kuadan dan sudut-sudut yang berelasi, selanjutnya dapat digambarkan garfik fungsinya, yaitu : $y =\sin x$, $y =\cos x$, dan $y =\tan x$.

A. Grafik Fungsi Sinus

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\sin b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{360^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{2\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\left | a \right |\\ &\bullet \quad \textrm{nilai minimum}:-\left | a \right |\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

B. Grafik Fungsi Cosinus

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\cos b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{360^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{2\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\left | a \right |\\ &\bullet \quad \textrm{nilai minimum}:-\left | a \right |\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

C. Grafik Fungsi Tangen

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\tan b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{180^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\: \: \color{red}\textit{tidak ada}\\ &\bullet \quad \textrm{nilai minimum}:\: \: \color{red}\textit{tidak ada}\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui fungsi}\: \: f(x)=\displaystyle \frac{4}{5}\sin \left ( 2x-\displaystyle \frac{\pi }{3} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=\displaystyle \frac{4}{5}\sin \left ( 2x-\displaystyle \frac{\pi }{3} \right )\\ &=\displaystyle \frac{4}{5}\sin 2\left ( x-\displaystyle \frac{\pi }{6} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=\displaystyle \frac{4}{5}\sin 2\left ( x-30^{\circ} \right ) \end{aligned}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{360^{\circ}}{2} \right |=180^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \left | \displaystyle \frac{4}{5} \right |=\frac{4}{5}\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: -\left | \displaystyle \frac{4}{5} \right |=-\frac{4}{5}\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 30^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui fungsi}\: \: f(x)=2\cos \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=2\cos \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &=2\cos 2\left ( x-\displaystyle \frac{\pi }{8} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=2\cos 2\left ( x-22,5^{\circ} \right ) \end{aligned} \\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{360^{\circ}}{2} \right |=180^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \left | 2 \right |=2\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: -\left | 2 \right |=-2\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 22,5^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui fungsi}\: \: f(x)=\tan \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=\tan \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &=\tan 2\left ( x-\displaystyle \frac{\pi }{8} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=\tan 2\left ( x-22,5^{\circ} \right ) \end{aligned} \\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{180^{\circ}}{2} \right |=90^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \color{red}\textit{tidak ada}\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: \color{red}\textit{tidak ada}\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 22,5^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.