Grafik Fungsi Trigonometri

Sebelumnya telah diketahui perbandingan trigonometri diberbagai kuadan dan sudut-sudut yang berelasi, selanjutnya dapat digambarkan garfik fungsinya, yaitu : $y =\sin x$, $y =\cos x$, dan $y =\tan x$.

A. Grafik Fungsi Sinus

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\sin b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{360^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{2\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\left | a \right |\\ &\bullet \quad \textrm{nilai minimum}:-\left | a \right |\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

B. Grafik Fungsi Cosinus

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\cos b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{360^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{2\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\left | a \right |\\ &\bullet \quad \textrm{nilai minimum}:-\left | a \right |\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

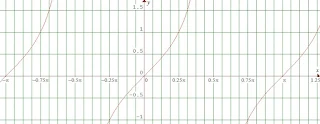
C. Grafik Fungsi Tangen

Berikut ilustrasi grafik fungsi sinus untuk  $-\pi \leq x\leq \pi$.

$\begin{aligned}&\textbf{Bentuk umum}\\ &f(x)=a\tan b\left ( x+c \right )+d\\ &\bullet \quad \textrm{periode}:\displaystyle \frac{180^{\circ}}{b}\: \: \textrm{atau}\: \: \displaystyle \frac{\pi }{\left | b \right |}\\ &\bullet \quad \textrm{nilai maksimum}:\: \: \color{red}\textit{tidak ada}\\ &\bullet \quad \textrm{nilai minimum}:\: \: \color{red}\textit{tidak ada}\\ &\bullet \quad \textrm{geseran grafik ke kiri}:c\\ &\bullet \quad \textrm{geseran grafik ke kanan}:-c\\ &\bullet \quad \textrm{geseran grafik ke atas}:d\\ &\bullet \quad \textrm{geseran grafik ke bawah}:-d\\ \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui fungsi}\: \: f(x)=\displaystyle \frac{4}{5}\sin \left ( 2x-\displaystyle \frac{\pi }{3} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=\displaystyle \frac{4}{5}\sin \left ( 2x-\displaystyle \frac{\pi }{3} \right )\\ &=\displaystyle \frac{4}{5}\sin 2\left ( x-\displaystyle \frac{\pi }{6} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=\displaystyle \frac{4}{5}\sin 2\left ( x-30^{\circ} \right ) \end{aligned}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{360^{\circ}}{2} \right |=180^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \left | \displaystyle \frac{4}{5} \right |=\frac{4}{5}\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: -\left | \displaystyle \frac{4}{5} \right |=-\frac{4}{5}\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 30^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui fungsi}\: \: f(x)=2\cos \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=2\cos \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &=2\cos 2\left ( x-\displaystyle \frac{\pi }{8} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=2\cos 2\left ( x-22,5^{\circ} \right ) \end{aligned} \\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{360^{\circ}}{2} \right |=180^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \left | 2 \right |=2\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: -\left | 2 \right |=-2\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 22,5^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui fungsi}\: \: f(x)=\tan \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \textrm{periode}\\ &\textrm{b}.\quad \textrm{nilai maksimu}\\ &\textrm{c}.\quad \textrm{nilai minimum}\\ &\textrm{d}.\quad \textrm{arah geseran fungsinya}\\ &\textrm{e}.\quad \textrm{gambarlah grafik fungsinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}\\ f(x)&=\tan \left ( 2x-\displaystyle \frac{\pi }{4} \right )\\ &=\tan 2\left ( x-\displaystyle \frac{\pi }{8} \right )\quad \textrm{atau boleh juga}\\ &\quad\qquad\qquad\textrm{dituliskan dengan bentuk}\\ &=\tan 2\left ( x-22,5^{\circ} \right ) \end{aligned} \\ &\begin{aligned}\textrm{a}.\quad&\textrm{Periodenya}:\: \: \left | \displaystyle \frac{180^{\circ}}{2} \right |=90^{\circ}\\ \textrm{b}.\quad&\textrm{Nilai maksimumnya}:\: \: \color{red}\textit{tidak ada}\\ \textrm{c}.\quad&\textrm{Nilai minimumnya}:\: \: \color{red}\textit{tidak ada}\\ \textrm{d}.\quad&\textrm{Arah geserannya ke kanan sejauh}: \: 22,5^{\circ}\\ \textrm{e}.\quad&\textrm{Berikut gambar ilustrasinya} \end{aligned} \end{array}$.