$\begin{array}{|l|l|}\hline \textrm{Pengertian}&\begin{aligned}&\textrm{Suatu fungsi yang berbentuk}\\ &f(x)=ax^{2}+bx+c\\ & a,\: b,\: c,\: \in \mathbb{R},\: a\neq 0 \end{aligned}\\\hline \textrm{Grafik Fungsi}&\textrm{Keterangan}\\\hline \textrm{Titik potong sumbu x}&\textrm{Jika ada}\\\hline &\begin{aligned}&\textrm{untuk titik potong}\\ &\textrm{terhadap sumbu x }\\ &\textrm{Jika y = 0 maka }\\ &ax^{2}+bx+c=0\\ &\textrm{Selanjutnya tinggal}\\ &\textrm{menentukan nilai D}\\ &D=b^{2}-4ac\: \: \textrm{adalah}\\ &\: \: \: \: \: \: \: \: \: \textrm{nilai diskriminan}.\\ &\textrm{Jika} \: D>0\\ &\textrm{maka grafik}\\ &\textrm{memotong sumbu x}\\ &\textrm{di dua tempat berbeda}\\ &\textrm{yaitu di} \: (x_{1},0)\: \textrm{dan}\: (x_{2},0).\\ &\textrm{dan jika D = 0}\\ &\textrm{maka grafik}\\ &\textrm{ hanya menyinggung}\\ &\textrm{sumbu x di satu titik}\\ &\textrm{yaitu di }\: (x_{1},0)\\ &\textrm{dan jika}\: D<0 \\ &\textrm{maka grafik}\\ &\textrm{tidak memotong}\\ &\textrm{atau menyinggung sumbu x} \end{aligned}\\\hline \textrm{Titik potong sumbu y}&\begin{aligned}&\textrm{titik potong terhadap}\\ &\textrm{sumbu y, jika x = 0}\\ &y=f(x)=ax^{2}+bx+c\\ &y=f(0)=a(0)^{2}+b(0)+c\\ &y=c \end{aligned}\\\hline \textrm{Sumbu Simetri (SS)}&x=\displaystyle \frac{-b}{2a}\\\hline \textrm{Titik Puncak}&\left ( \displaystyle \frac{-b}{2a},\displaystyle \frac{D}{-4a} \right )\\\hline \textrm{Posisi grafik}&\textrm{Jika}\: a>0\: \textrm{maka}\\ &\textrm{grafik terbuka ke atas}\\ &\textrm{Dan jika nilai}\: a<0\: \textrm{maka}\\ &\textrm{grafik terbuka ke bawah}\\\hline \end{array}$.
Selanjutnya cara membuat grafik fungsi kudratnya adalah sebagai berikut:
$\begin{array}{|c|c|}\hline \textrm{Jika memotong sumbu}-\textrm{X}&\textrm{Jika menyinggung sumbu}-\textrm{X}\\ \textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan}\: \left ( x_{2},0 \right )&\textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan melalui}\\ \textrm{dan melalui sebuah titik lain}&\textrm{sebuah titik lain} \\\hline &\\ y=f(x)=a\left ( x-x_{1} \right )\left ( x-x_{2} \right )&y=f(x)=a\left ( x-x_{1} \right )^{2}\\ &\\\hline \textrm{Jika grafik fungsi itu melalui}&\textrm{Jika grafik fungsi itu melalui}\\\hline \textrm{Titik puncak}\: \: P\left ( x_{p},y_{p} \right )\: \textrm{dan}&\textrm{tiga buah titik yaitu}\: \left ( x_{1},y_{1} \right )\\ \textrm{sebuah titik lain}&\left ( x_{2},y_{2} \right )\: \: \textrm{dan}\: \: \left ( x_{3},y_{3} \right )\\\hline &\\ y=f(x)=a\left ( x-x_{p} \right )^{2}+y_{p}&y=f(x)=ax^{2}+bx+c\\ &\\\hline \end{array}$.
$\LARGE{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: f\: \: \textrm{adalah fungsi linear dengan}\\ & f(2)-f(-2)=8,\\ & \textrm{maka nilai dari}\: \: f(4)-f(-2)\: \: \textrm{adalah}\: ....\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &f(x)=ax+b\\ &f(2)-f(-2)\\ &=\left (a(2)+b \right )-\left ( a(-2)+b \right )=8\\ &8=2a+2a\\ &8=4a\\ &2=a\\ &f(x)=2x+b,\quad \textrm{dengan}\: \: b\: \: \textrm{konstan}\\ &\textrm{Sehingga nilai}\quad\\ &f(4)-f(-2)=\left (2(4)+b \right )-\left (2(-2)+b \right )\\ &=8+b+4-b\\ &=12 \end{aligned} \end{array}$.
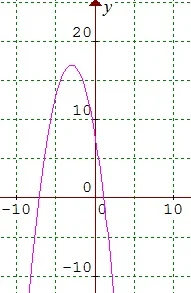
$\begin{array}{ll}\\ 2.&\textrm{Ubahlah}\: \: 8-6x-x^{2}\: \: \textrm{ke dalam bentuk}\\ & a-(x+b)^{2},\: \textrm{selanjutnya tentukan}\\ & \textrm{daerah hasil dari}\: \: f(x)=8-6x-x^{2}\\ & \textrm{untuk}\: \: x\: \: \textrm{bilangan real}\\ &\qquad(\textit{NTU Entrance Examination AO-level})\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|l|}\hline 1.&\textrm{Diketahui}\\\hline &\begin{aligned}\textrm{Misal}\quad\qquad&\\ 8-6x-x^{2}&=f(x)\\ f(x)&=-x^{2}-6x+8\\ &=-\left ( x^{2}+6x-8 \right )\\ &=-\left ( x^{2}+6x+9-17 \right )\\ &=-\left ( (x+3)^{2}-17 \right )\\ &=-(x+3)^{2}+17\\ & \end{aligned}\\\hline 2.&\textrm{Mencari koordinat}\: \: \left ( x_{SS},y_{SS} \right )\\\hline &\begin{aligned}f(x)&=-x^{2}-6x+8\left\{\begin{matrix} a=-1\\ b=-6\\ c=\: \: 8\: \: \end{matrix}\right.\\ \textrm{Maka}&\\ x_{SS}&=\frac{-b}{2a}=\displaystyle \frac{-(-6)}{2(-1)}\\ &=-3\\ y_{SS}&=f(-3)=-\left ( -3+3 \right )^{2}+17=17\\ \therefore &\left ( x_{SS},y_{SS} \right )=(-3,17) \end{aligned}\\\hline 3.&\textrm{Nilai fungsi}\\\hline &\begin{aligned}\textrm{Karena}&\: \: a=-1<0\\ \textrm{maka f}&\textrm{ungsi menghadap}\\ \textbf{ke ba}&\textbf{wah},\: \: \textrm{sehingga}\\ \textrm{daerah}&\: \: \textrm{hasilnya}\: \: \left (R_{f} \right )\\ \textrm{adalah}&:\\ &\left \{ -\infty <y\leq 17 \right \}\\ &\\ &\textrm{Berikut ilustrasinya} \end{aligned}\\\hline \end{array} \end{array}$.
$\begin{array}{ll}\\ 3.&\textrm{Jika}\: \: \alpha \: \: \textrm{dan}\: \: \beta \: \: \textrm{adalah akar-akar dari }\\ &\textrm{persamaan kuadrat}\: \: x^{2}+mx+m=0,\\ &\textrm{maka nilai}\: \: m\: \: \textrm{yang menyebabkan }\\ &\textrm{jumlah kuadrat akar-akar mencapai}\\ &\textrm{minimum adalah}\: ....\\ &\qquad \: \textbf{(UM UNDIP 2014 Mat Das)}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\: \: x^{2}+mx+m=0\\ & \textbf{persamaan kuadrat}\: \textrm{dalam}\: \: x,\\ & \textrm{maka}\\ &x^{2}+mx+m=x^{2}-(\alpha +\beta )x+(\alpha \beta )=0\\ &\begin{cases} \alpha +\beta &=-m \\ & \\ \alpha \beta &=m \end{cases}\\ &\textrm{Selanjutnya}\\ &\alpha ^{2}+\beta ^{2}=\left ( \alpha +\beta \right )^{2}-2\alpha \beta\\ &=(-m)^{2}-2m\: \: \textrm{dan dapat kita tuliskan sebagai}\\ &f(m)=m^{2}-2m\begin{cases} a &=1 \\ b &=-2 \\ c &=0 \end{cases} \\ &\textrm{fungsi kuadrat dalam}\: \: m,\\ &\textrm{sehingga kita perlu mencari titik}\: \: \left ( m_{SS},f\left ( m_{SS} \right ) \right ),\\ & \textrm{tetapi yang kita perlukan}\\ &\textrm{cuma}\: \: m-\textrm{nya saja, yaitu}:\: \: m=m_{SS},\\ &\textrm{dengan}\quad m_{SS}=\displaystyle \frac{-b}{2a}=\frac{-(-2)}{2.1}=1 \end{aligned} \end{array}$.
Link Materi
https://ahmadthohir1098.blogspot.com/2024/11/kumpulan-materi-matematika-ma-sma-kelas.html