CONTOH SOAL 8 LINGKARAN (TERKAIT HUBUNGAN DUA LINGKARAN)

 $\begin{array}{ll}\\ 36.&\textrm{Persamaan lingkaran yang menyinggung}\\ &\textrm{sumbu X serta melalui titik potong}\\ &\textrm{lingkaran}\: \: (x+1)^{2}+(y+2)^{2}=1\: \: \textrm{dan}\\ &x^{2}+y^{2}+3x+3y+4=0\: \: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-4x+2y+4=0\\ &\textrm{b}.\quad x^{2}+y^{2}-4x+2y-4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-4x-2y-4=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}+4x+2y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}+4x+2y-4=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=(x+1)^{2}+(y+2)^{2}=1\\ &\qquad \Leftrightarrow x^{2}+y^{2}+2x+4y+4=0\\ &\bullet \: L_{2}=x^{2}+y^{2}+3x+3y+4=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-x+y=0\Leftrightarrow y=x\\ &\color{blue}\textrm{Dengan cara coba-coba, maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}+2x+4y+4+p(-x+y)=0\\ &\color{blue}\textrm{Untuk}\: \: p=1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4+(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+x+5y+4=0\\ &\color{blue}\textrm{Untuk}\: \: p=-1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+3x+3y+4=0\\ &\color{blue}\textrm{Dan untuk}\: \: p=-2\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-2(-x+y)=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}+4x+2y+4=0 \end{aligned} \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya}  \end{array}$

DAFTAR PUSTAKA

1. Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
2. Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
3. Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
4. Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
5. Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

CONTOH SOAL 7 LINGKARAN (TERKAIT HUBUNGAN DUA LINGKARAN)

 $\begin{array}{ll}\\ 31.&\textrm{Persamaan lingkaran yang melalui titik}\\ &(0,0)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x-8y-11=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-6y-22=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-12x+10y=0\\ &\textrm{b}.\quad x^{2}+y^{2}+8x-10y=0\\ &\textrm{c}.\quad x^{2}+y^{2}-8x+12y=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-8x-10y=0\\ &\textrm{e}.\quad x^{2}+y^{2}+12x-8y=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x-8y-11=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-6y-22=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-2x-2y+11=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (0,0), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x-8y-11 +p(-2x-2y+11)=0\\ &\Leftrightarrow 0^{2}+0^{2}-0-0-11+p(0+11)=0\\ &\Leftrightarrow p=\color{blue}1 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x-8y-11+(-2x-2y+11)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-10y=0  \end{aligned}  \end{array}$.

Berikut ilustrasi gambarnya

$\begin{array}{ll}\\ 32.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (8,4)\: \: \textrm{dan titik potong lingkaran}\: x^{2}+y^{2}=16\\ &\textrm{dan}\: \: x^{2}+y^{2}-4x-4y=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-8x-8y-16=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x+8y+16=0\\ &\textrm{c}.\quad \color{red}x^{2}+y^{2}-8x-8y+16=0\\ &\textrm{d}.\quad x^{2}+y^{2}+8x+8y-16=0\\ &\textrm{e}.\quad x^{2}+y^{2}+8x+8y+16=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-16=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-4y=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=4x+4y-16=0\\ &\Leftrightarrow x+y=4\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (8,4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-16+p(x+y-4)=0\\ &\Leftrightarrow 8^{2}+4^{2}-16+p(8+4-4)=0\\ &\Leftrightarrow -8p=\color{blue}64\color{black}\Leftrightarrow p=\color{blue}-8 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-16-8(x+y-4)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-8y+16=0  \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya}  \end{array}$.

$\begin{array}{ll}\\ 33.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (7,-4)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x+8y-27=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-26x+4y+121=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-36x-2y+121=0\\ &\textrm{b}.\quad x^{2}+y^{2}+24x-4y-222=0\\ &\textrm{c}.\quad 3x^{2}+3y^{2}-18x+2y-121=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-36x+2y+195=0\\ &\textrm{e}.\quad x^{2}+y^{2}+24x+2y+195=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x+8y-27=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-26x+4y+121=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=20x+4y-148=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (7,-4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x+8y-27\\ &\qquad+p(20x+4y-148)=0\\ &\Leftrightarrow 7^{2}+(-4)^{2}-42-32-27\\ &\qquad+p(140-16-148)=0\\ &\Leftrightarrow -24p=\color{blue}36\color{black}\Leftrightarrow p=\color{blue}-\displaystyle \frac{3}{2} \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x+8y-27\\ &\qquad-\displaystyle \frac{3}{2}(20x+4y-148)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-36x+2y+195=0  \end{aligned}  \end{array}$.

Berikut ilustrasi gambarnya

Jika dimensi gambar diperkecil menjadi

$\begin{array}{ll}\\ 34.&\textrm{Persamaan lingkaran yang melalui perpotongan}\\&\textrm{lingkaran}\: \: x^{2}+y^{2}-12x+6y+20=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-16x-14y+64=0\: \: \textrm{serta pusatnya}\\ &\textrm{terletak pada garis}\: \: 8x-3y-19=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-20x-34y+108=0\\ &\textrm{b}.\quad x^{2}+y^{2}-16x+12y+96=0\\ &\textrm{c}.\quad x^{2}+y^{2}-12x+20y+88=0\\ &\textrm{d}.\quad x^{2}+y^{2}+16x-24y+108=0\\ &\textrm{e}.\quad x^{2}+y^{2}+22x-34y+96=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa persamaan lingkaran}:\\ &\bullet \: L_{1}=x^{2}+y^{2}-12x+6y+20=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-16x-14y+64=0\\ &\textrm{Persamaan tali busurnya (garis kuasa)}\\ &\textrm{adalah}:\\ &L_{1}(x,y)-L_{2}(x,y)\\ &=4x+20y-44=0\Leftrightarrow \color{blue}x=11-5y\\ &\textrm{Selanjutnya dengan substitusi }\\ &\begin{aligned}&x^{2}+y^{2}-12x+6y+20=0\\ &\Leftrightarrow (x-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (\color{blue}11-5y\color{black}-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (y-5y)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow 26y^2-44y+9=0 \end{aligned}\\ &\textrm{Sehingga dengan}\: \: \color{red}\textrm{memodifikasi}\\ &\begin{aligned}&26y^2-44y+9=0\\ &\Leftrightarrow 25y^2-44y+y^2+9=0\\ &\quad\textrm{arahkan ke bentuk kuadrat sempurna}\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+8=0\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+17^{2}-17^{2}+8=0\\ &\Leftrightarrow (5y-1)^{2}+(y-17)^{2}-281=0\\ &\quad \textrm{ingat bahwa ada tali busur}\: \: \color{blue}5y=11-x\\ &\Leftrightarrow (\color{blue}11-x\color{black}-1)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow (10-x)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow x^{2}-20x+100+y^{2}-34y+289-281=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-20x-34y+108=0 \end{aligned}  \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$

$\begin{array}{ll}\\ 35.&\textrm{Persamaan lingkaran dengan titik pusat}\\ &\textrm{pada garis}\: \: x+2y-3=0\: \: \textrm{dan melalui}\\ &\textrm{titik potong dua lingkaran}\\ &x^{2}+y^{2}-2x-4y+1=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-2y+4=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-6x+7=0\\ &\textrm{b}.\quad x^{2}+y^{2}-3y+4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-2y+1=0\\ &\textrm{d}.\quad x^{2}+y^{2}-2x-4y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}-3x-2y+7=0\\\\ &\textbf{Jawab}:\\ &\color{blue}\textbf{Alternatif 1}\\ &\textrm{Gunakan cara pembahasan sebagaimana pada}\\ &\textrm{nomor-nomor sebelumnya}\\ &\color{blue}\textbf{Alternatif 2}\\  &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}-2x-4y+1=0,\: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+y^{2}-4x-2y+4=0\\ &\textrm{Persamaan}\: \: \color{red}\textrm{tali busur}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}-2x-4y+1\\ &-(x^{2}+y^{2}-4x-2y+4)=0\\ &\Leftrightarrow 2x-2y-3=0\\ &\textrm{Selanjutnya perlu ditentukan juga}\\&\textrm{Persamaan}\: \: \color{red}\textrm{berkas lingkaran}\: \color{black}\textrm{melalui}\\ &\textrm{titik-titik potong kedua lingkaran}\\ &\textrm{di atas adalah}:\\ &L_{1}+\lambda L_{2}=0\\ &x^{2}+y^{2}-2x-4y+1\\ &\qquad+\lambda \left ( x^{2}+y^{2}-4x-2y+4 \right )=0\\ &\Leftrightarrow (1+\lambda )x^{2}+(1+\lambda )y^{2}-(2+4\lambda )x\\ &\qquad -(4+2\lambda )y+1+4\lambda =0\\ &\textrm{Saat}\: \: \lambda =-1,\: \textrm{maka persamaan berkas}\\ &\textrm{lingkarannya adalah}:\: 2x-2y-3=0\\ &\textrm{Hal ini hasilnya sama persis saat kita}\\ &\textrm{menentukan persamaan}\: \color{red}\textrm{tali busur}\: \color{black}\textrm{di atas}\\ &\textrm{Selanjutnya kita ambil}\\ &L_{2}-(L_{1}+\lambda L_{2})=0\\ &\Leftrightarrow  x^{2}+y^{2}-4x-2y+4-(2x-2y-3)=0\\ &\Leftrightarrow  \color{red}x^{2}+y^{2}-6x+7=0 \end{aligned}  \end{array}$.

Gambar mula-mula

Lingkaran baru yang berpusat di (3,0) 

CONTOH SOAL 6 LINGKARAN (TERKAIT HUBUNGAN DUA LINGKARAN)

 $\begin{array}{ll}\\ 26.&\textrm{Diketahui lingkaran-lingkaran}\\ & x^{2}+y^{2}-2x+3y+k=0\: \: \textrm{dan}\: \\  &x^{2}+y^{2}+8x-6y-7=0\: \: \textrm{saling}\\ &\textrm{berpotongan ortogonal saat}\: \: k=\: ....\\ &\textrm{a}.\quad \color{red}-10\\ &\textrm{b}.\quad -3\\ &\textrm{c}.\quad 1\\ &\textrm{d}.\quad 5\\ &\textrm{e}.\quad 8\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan tabel berikut}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}-2x+3y+k=0&\begin{cases} P_{1} &=\left ( 1,-\displaystyle \frac{3}{2} \right ) \\  r_{1} & = \sqrt{\displaystyle \frac{13-4k}{4}} \end{cases}\\\hline \begin{aligned}L_{2}&\equiv x^{2}+y^{2}+8x-6y-7=0  \end{aligned}&\begin{cases} P_{2} &=\left ( -4,3 \right ) \\  r_{2} & = \sqrt{32} \end{cases}\\\hline \end{array} \\ &\textrm{Syarat dua lingkaran berpotongan ortogonal}\\ &\begin{aligned}&\left (P_{1}P_{2}  \right )^{2}=r_{1}^{2}+r_{2}^{2}\\ &\Leftrightarrow \left ( 1+4 \right )^{2}+\left ( -\displaystyle \frac{3}{2}-3 \right )^{2}=\left ( \sqrt{\displaystyle \frac{13-4k}{4}} \right )^{2}+\sqrt{32}^{2}\\ &\Leftrightarrow \: 25+\displaystyle \frac{81}{4}=\displaystyle \frac{13-4k}{4}+32\\ &\Leftrightarrow \: 100+81=13-4k+128\\ &\Leftrightarrow \: k=-10 \end{aligned} \\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$.

$\begin{array}{ll}\\ 27.&\textrm{Persamaan lingkaran yang berpotongan}\\ &\textrm{lingkaran lain}\: \:  x^{2}+y^{2}+2x+y-11=0\\ &\textrm{secara tegak lurus dan melalui}\: \: (4,3)\: \: \textrm{serta}\\ &\textrm{pusatnya pada}\: \: 9x+4y=37\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-10x+4y+3=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x+10y+6=0\\ &\textrm{c}.\quad x^{2}+y^{2}+4x-8y+7=0\\ &\textrm{d}.\quad x^{2}+y^{2}+6x+y+5=0\\ &\textrm{e}.\quad x^{2}+y^{2}+12x+6y+5=0\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan tabel berikut}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x+y-11=0&\begin{cases} P_{1} &=\left ( -1,-\displaystyle \frac{1}{2} \right ) \\  r_{1} & = \sqrt{\displaystyle \frac{49}{4}}=\displaystyle \frac{7}{2} \end{cases}\\\hline \begin{aligned}L_{2}&\equiv (x-a)^{2}+(y-b)^{2}=r^{2}  \end{aligned}&\begin{cases} P_{2} &=\left ( a,b \right ) \\  r_{2} & = r \end{cases}\\\hline \end{array}\\ &\textrm{Karena berpotongan tegak lurus, maka}\\ &\begin{aligned}&\left (P_{1}P_{2}  \right )^{2}=r_{1}^{2}+r_{2}^{2}\\ &\Leftrightarrow \left ( -1-a \right )^{2}+\left ( -\displaystyle \frac{1}{2}-b \right )^{2}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow a^{2}+2a+1+b^{2}+b+\displaystyle \frac{1}{4}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow \color{blue}a^{2}+b^{2}+2a+b+\displaystyle \frac{5}{4}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow a^{2}+b^{2}+2a+b-11=r^{2}\: .......(1)\\ \end{aligned} \\ &\textrm{Selanjutnya}\\ &\begin{aligned}&\textrm{Lingkaran}\: \: L_{2}\: \: \textrm{melalui titik}\: \: (4,3), \textrm{artinya}\\ &\textrm{bahwa}\: :\: (4-a)^{2}+(3-b)^{2}=r^{2}\\ &\Leftrightarrow a^{2}-8a+16+b^{2}-6b+9=r^{2}\\ &\Leftrightarrow a^{2}+b^{2}-8a-6b+25=r^{2}\: .......(2)\\ &\textrm{Pusat lingkaran}\: \: L_{2}\: \: \textrm{melalui garis}\: \: 9x+4y=37\\ &\textrm{artinya}:\: 9a+4b=37\: ...............(3)\\  \end{aligned}\\ &\begin{aligned}&\textrm{Dengan eliminasi}\: 1\: \&\: 2\: \: \textrm{dapat diperoleh}:\\ &\begin{array}{rll} a^{2}+b^{2}-8a-6b+25&=r^{2}&\\ a^{2}+b^{2}+2a+b-11&=r^{2}&-\\\hline -10a-7b+36&=0&\textrm{atau}\\ 10a+7b&=36&......(4) \end{array}\\ &\textrm{Dari persamaan}\: 3\: \&\: 4\: \: \textrm{dapat diperoleh}:\\ & \end{aligned}\\ &\begin{array}{rll} 10a+7b&=36&(\times 4)\\ 9a+4b&=37&(\times 7)\\\hline 40a+28b&=144&\\ 63a+28b&=259&\\\hline -23a\: \quad\quad&=-115&\\ a&=\displaystyle \frac{-115}{-23}&=5\\ 10(5)+7b&=36&\\ 7b&=-14\\ b&=-2 \end{array}\\ &\textrm{Adapun langkah berikutnya}\\ &\begin{aligned}&L_{2}\equiv (4-a)^{2}+(3-b)^{2}=r^{2}\\ &L_{2}\equiv (4-5)^{2}+(3+2)^{2}=r^{2}\\ &L_{2}\equiv r^{2}=25+1=26\\ &\textrm{Sehingga},\: L_{2}\equiv (x-5)^{2}+(y+2)^{2}=26\\ &\Leftrightarrow x^{2}+y^{2}-10x+4y+25+4-26=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-10x+4y+3=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$.

Jika diperjelas dengan tambahan garis 9x+4y=37

$\begin{array}{ll}\\ 28.&\textrm{Diketahui lingkaran pertama berpusat di}\: \:  (1,2)\\ &\textrm{dan menyinggung garis}\: \: 3x-4y+10=0.\\ &\textrm{Jika ada lingkaran kedua dengan pusat}\: \: (4,6)\\ &\textrm{dan menyinggung lingkaran yang pertama},\\ &\textrm{maka persamaan lingkaran yang kedua}\\ &\textrm{tersebut adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-8x-12y+48=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x-12y+43=0\\ &\textrm{c}.\quad \color{red}x^{2}+y^{2}-8x-12y+36=0\\ &\textrm{d}.\quad x^{2}+y^{2}-8x-12y+27=0\\ &\textrm{e}.\quad x^{2}+y^{2}-8x-12y+16=0\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui bahwa kedua lingkaran saling}\\ &\color{blue}\textrm{bersinggungan di luar},\: \color{black}\textrm{maka}\\ &\begin{aligned}r_{1}+r_{2}&=P_{1}P_{2}\\ &=\sqrt{(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}\\ &=\sqrt{(1-4)^{2}+(2-6)^{2}}\\ &=\sqrt{3^{2}+4^{2}}=\sqrt{5^{2}}=5 \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned}r_{\textrm{pertama}}&=\left |\displaystyle \frac{3(1)-4(2)+10}{\sqrt{3^{2}+4^{2}}}   \right |\\ &=\left | \displaystyle \frac{3-8+10}{\sqrt{5^{2}}} \right |=\left | \displaystyle \frac{5}{5} \right |=\left | 1 \right |=1\\ \textrm{sehingga} &\\ r_{\textrm{kedua}}&=5-r_{\textrm{pertama}}=5-1=4 \end{aligned}\\ &\textrm{maka persamaan lingkaran keduanya adalah}:\\ &\begin{aligned}&(x-4)^{2}+(y-6)^{2}=4^{2}\\ &\Leftrightarrow x^{2}-8x+16+y^{2}-12y+36=16\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-8x-12y+36=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$.

$\begin{array}{ll}\\ 29.&\textrm{Garis kuasa (tali busur sekutu)}\\ &\textrm{dari lingkaran}\\ &L_{1}\equiv x^{2}+y^{2}+6x-4y-12=0\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-12y=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 3x+4y+9=0\\ &\textrm{b}.\quad 3x-4y-8=0\\ &\textrm{c}.\quad 3x-4y+7=0\\ &\textrm{d}.\quad 3x+4y-7=0\\ &\textrm{e}.\quad \color{red}3x+4y-6=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}+6x-4y-12=0,\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-12y=0\\ &\textrm{Persamaan}\: \: \color{red}\textrm{garis kuasa}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}+6x-4y-12\\ &-(x^{2}+y^{2}-12y)=0\\ &\Leftrightarrow 6x+8y-12=0\\ &\Leftrightarrow \color{red}3x+4y-6=0 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 30.&\textrm{Jika dua lingkaran}\\ & x^{2}+y^{2}=9\: \: \textrm{dan}\\ &x^{2}+y^{2}-4y+2y+3=0\: \: \textrm{yang}\\ &\textrm{berpotongan di}\: \: (x_{1},y_{1})\: \: \textrm{dan}\: \: (x_{2},y_{2}),\\ &\textrm{maka nilai}\: \: 5(x_{1}+x_{2})\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}24\\ &\textrm{b}.\quad 26\\ &\textrm{c}.\quad 28\\ &\textrm{d}.\quad 30\\ &\textrm{e}.\quad 32\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}-9=0\: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+y^{2}-4x+2y+3\\ &\textrm{Persamaan}\: \: \color{red}\textrm{garis kuasa}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}-9\\ &-(x^{2}+y^{2}-4y+2y+3)=0\\ &\Leftrightarrow 4x-2y-12=0\\ &\Leftrightarrow 2x-y-6=0\\ &\Leftrightarrow y=6-2x \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned}&x^{2}+y^{2}-9=0\\ &\Leftrightarrow x^{2}+(6-2x)^{2}-9=0\\ &\Leftrightarrow x^{2}+36-24x+4x^{2}-9=0\\ &\Leftrightarrow 5x^{2}-24x+27=0\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{576-540}}{10}\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{36}}{10}=\frac{24\pm 6}{10}\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{36}}{10}=\frac{24\pm 6}{10}\\ &\Leftrightarrow \quad x_{1}=3\: \: \textrm{atau}\: \: x_{2}=1,8\\ &\textrm{maka}\: \: 5(x_{1}+x_{2})=5\left ( 3+1,8 \right )=\color{red}24 \end{aligned} \end{array}$.

CONTOH SOAL 5 LINGKARAN (TERKAIT HUBUNGAN DUA LINGKARAN)

 $\begin{array}{ll}\\ 21.&\textrm{Titik Kuasa dari lingkaran-lingkaran}\\ &\textrm{berikut}\\ &L_{1}\equiv x^{2}+y^{2}+x+y-14=0\\ &L_{2}\equiv x^{2}+y^{2}=13\\ &L_{3}\equiv x^{2}+y^{2}+3x-2y-26=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}(3,-2)\\ &\textrm{b}.\quad (2,-3)\\ &\textrm{c}.\quad (-3,2)\\ &\textrm{d}.\quad (-2,3)\\ &\textrm{e}.\quad (3,2)\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{aligned}&\begin{array}{lrlll} (L_{1})&x^{2}+y^{2}+x+y&=&14\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &x+y&=&1&....(1) \end{array}\\ &\textrm{dan}\\ &\begin{array}{lrlll} (L_{3})&x^{2}+y^{2}+3x-2y&=&26\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &3x-2y&=&13&....(2) \end{array}\\ &\textrm{Selanjutnya kita eliminasi}\: (1)\& (2)\\ &\textrm{dan hasilnya adalah}:\\ &\begin{array}{rrlrl} \color{blue}(2)&3x-2y&=&13\\ \color{blue}(1)&3x+3y&=&3&-\qquad (\times 3)\\\hline &-5y&=&10&\\ &y&=&\color{red}-2&\Rightarrow x=\color{red}3 \end{array}\\ &\textrm{Jadi, titik kuasa ketiganya}: (3,-2) \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$

$\begin{array}{ll}\\ 22.&\textrm{Titik-titik potong dari persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-2)^{2}+y^{2}=10\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-2)^{2}=10\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad (3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{b}.\quad \color{red}(3,3)\: \: \textrm{dan}\: \: (-1,-1)\\ &\textrm{c}.\quad (3,-3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{d}.\quad (-3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{e}.\quad (-3,-3)\: \: \textrm{dan}\: \: (-1,-1)\\\\ &\textbf{Jawab}:\\ &\color{blue}\textrm{Alternatif 1}\\ &\textrm{Dengan substitusi opsi pilihan jawaban}\\ &\textrm{maka akan ketemu jawabannya langsung}\\ &\color{blue}\textrm{Alternatif 2}\\ &\textrm{Dengan eliminasi dan ilustrasi gambar}\\ &\begin{array}{lrlll} (L_{1})&(x-2)^{2}+y^{2}&=&10\\ (L_{2})&x^{2}+(y-2)^{2}&=&10&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-4x&=&6\\ (L_{2})&x^2+y^2-4y&=&6&-\\\hline &-4x+4y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array} \\ &\textrm{Jelas opsi jawaban c, d salah}\\ &\textrm{karena}\: \: y=x,\\ &\textbf{Dengan bantuan ilustrasi, pilihan jawaban}\\ &\textbf{akan tampak dengan jelas}  \end{array}$.

$\begin{array}{ll}\\ 23.&\textrm{Persamaan tali busur persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-3)^{2}+y^{2}=16\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-3)^{2}=16\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad y=-2x\\ &\textrm{b}.\quad y=-x\\ &\textrm{c}.\quad \color{red}y=x\\ &\textrm{d}.\quad y=2x\\ &\textrm{e}.\quad y=\displaystyle \frac{1}{2}x\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{array}{lrlll} (L_{1})&(x-3)^{2}+y^{2}&=&16\\ (L_{2})&x^{2}+(y-3)^{2}&=&16&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-6x&=&9\\ (L_{2})&x^2+y^2-6y&=&9&-\\\hline &-6x+6y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$.

$\begin{array}{ll}\\ 24.&\textrm{Banyaknya garis singgung persekutuan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+2x-6y+9=0\\ &\textrm{dan}\: \:  x^{2}+y^{2}+8x-6y+9=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 0\\ &\textrm{b}.\quad \color{red}1\\ &\textrm{c}.\quad 2\\ &\textrm{d}.\quad 3\\ &\textrm{e}.\quad 4\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x-6y+9=0&\begin{cases} P_{1} &=(-1,3) \\  r_{1} & = 1 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+8x-6y+9=0&\begin{cases} P_{2} &=(-4,3) \\  r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{Perhatikan pula bahwa}\: \: r_{2}-r_{1}=4-1=3\\ &\begin{aligned}&\textrm{Karena}\: \: P_{1}P_{2}=r_{2}-r_{1},\: \textrm{hal ini berarti lingkaran}\\ &L_{1}\: \: \textrm{bersinggungan di dalam dengan lingkaran}\: L_{2}\\ &\textrm{Sehingga kedua lingkaran ini hanya akan }\\ &\textrm{memiliki}\: \: \color{red}\textrm{satu}\: \: \color{black}\textrm{garis singgung persekutuan} \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$.

$\begin{array}{ll}\\ 25.&\textrm{Persamaan lingkaran dengan jari-jari}\: \: 5\\ &\textrm{dan menyinggung lingkaran lain}\\ & x^{2}+y^{2}-2x-4y-20=0\: \: \: \textrm{di titik}\\ &(5,5)\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{b}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{e}.\quad x^{2}+y^{2}-2x-4y-120=0\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahi bahwa}\\ &\begin{aligned}&\begin{array}{rrlll} (L_{1})&(x-a)^2+(y-b)^{2}&=&5^{2}\\ (L_{2})&x^{2}+y^{2}-2x-4y&=&20& \end{array} \\ &\textrm{Titik singgung dua lingkaran}\\ &\textrm{di titik}\: \: (5,5),\: \textrm{artinya}\\ &\begin{pmatrix} 5\\  5 \end{pmatrix}=\displaystyle \frac{\begin{pmatrix} a\\  b \end{pmatrix}+\begin{pmatrix} 1\\  2 \end{pmatrix}}{2}\\ &\Leftrightarrow \begin{pmatrix} 10\\  10 \end{pmatrix}=\begin{pmatrix} a\\  b \end{pmatrix}+\begin{pmatrix} 1\\  2 \end{pmatrix}\\ &\Leftrightarrow \begin{pmatrix} a\\  b \end{pmatrix}=\begin{pmatrix} 10-1\\  10-2 \end{pmatrix}=\begin{pmatrix} 9\\  8 \end{pmatrix} \end{aligned}\\ &\begin{aligned}&\textrm{maka persamaan lingkarannya adalah}:\\ &\Leftrightarrow (x-9)^{2}+(y-8)^{2}=5^{2}\\ &\Leftrightarrow x^{2}+y^{2}-18x-16y+120=0 \end{aligned}\\  &\textbf{Berikut ilustrasi gambarnya}  \end{array}$.

Contoh 5 Soal dan Pembahasan Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 21.&\textrm{Titik Kuasa dari lingkaran-lingkaran}\\ &\textrm{berikut}\\ &L_{1}\equiv x^{2}+y^{2}+x+y-14=0\\ &L_{2}\equiv x^{2}+y^{2}=13\\ &L_{3}\equiv x^{2}+y^{2}+3x-2y-26=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}(3,-2)\\ &\textrm{b}.\quad (2,-3)\\ &\textrm{c}.\quad (-3,2)\\ &\textrm{d}.\quad (-2,3)\\ &\textrm{e}.\quad (3,2)\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{aligned}&\begin{array}{lrlll} (L_{1})&x^{2}+y^{2}+x+y&=&14\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &x+y&=&1&....(1) \end{array}\\ &\textrm{dan}\\ &\begin{array}{lrlll} (L_{3})&x^{2}+y^{2}+3x-2y&=&26\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &3x-2y&=&13&....(2) \end{array}\\ &\textrm{Selanjutnya kita eliminasi}\: (1)\& (2)\\ &\textrm{dan hasilnya adalah}:\\ &\begin{array}{rrlrl} \color{blue}(2)&3x-2y&=&13\\ \color{blue}(1)&3x+3y&=&3&-\qquad (\times 3)\\\hline &-5y&=&10&\\ &y&=&\color{red}-2&\Rightarrow x=\color{red}3 \end{array}\\ &\textrm{Jadi, titik kuasa ketiganya}: (3,-2) \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$

$\begin{array}{ll}\\ 22.&\textrm{Titik-titik potong dari persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-2)^{2}+y^{2}=10\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-2)^{2}=10\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad (3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{b}.\quad \color{red}(3,3)\: \: \textrm{dan}\: \: (-1,-1)\\ &\textrm{c}.\quad (3,-3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{d}.\quad (-3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{e}.\quad (-3,-3)\: \: \textrm{dan}\: \: (-1,-1)\\\\ &\textbf{Jawab}:\\ &\color{blue}\textrm{Alternatif 1}\\ &\textrm{Dengan substitusi opsi pilihan jawaban}\\ &\textrm{maka akan ketemu jawabannya langsung}\\ &\color{blue}\textrm{Alternatif 2}\\ &\textrm{Dengan eliminasi dan ilustrasi gambar}\\ &\begin{array}{lrlll} (L_{1})&(x-2)^{2}+y^{2}&=&10\\ (L_{2})&x^{2}+(y-2)^{2}&=&10&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-4x&=&6\\ (L_{2})&x^2+y^2-4y&=&6&-\\\hline &-4x+4y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array} \\ &\textrm{Jelas opsi jawaban c, d salah}\\ &\textrm{karena}\: \: y=x,\\ &\textbf{Dengan bantuan ilustrasi, pilihan jawaban}\\ &\textbf{akan tampak dengan jelas}  \end{array}$.

$\begin{array}{ll}\\ 23.&\textrm{Persamaan tali busur persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-3)^{2}+y^{2}=16\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-3)^{2}=16\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad y=-2x\\ &\textrm{b}.\quad y=-x\\ &\textrm{c}.\quad \color{red}y=x\\ &\textrm{d}.\quad y=2x\\ &\textrm{e}.\quad y=\displaystyle \frac{1}{2}x\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{array}{lrlll} (L_{1})&(x-3)^{2}+y^{2}&=&16\\ (L_{2})&x^{2}+(y-3)^{2}&=&16&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-6x&=&9\\ (L_{2})&x^2+y^2-6y&=&9&-\\\hline &-6x+6y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$.

$\begin{array}{ll}\\ 24.&\textrm{Banyaknya garis singgung persekutuan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+2x-6y+9=0\\ &\textrm{dan}\: \:  x^{2}+y^{2}+8x-6y+9=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 0\\ &\textrm{b}.\quad \color{red}1\\ &\textrm{c}.\quad 2\\ &\textrm{d}.\quad 3\\ &\textrm{e}.\quad 4\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x-6y+9=0&\begin{cases} P_{1} &=(-1,3) \\  r_{1} & = 1 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+8x-6y+9=0&\begin{cases} P_{2} &=(-4,3) \\  r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{Perhatikan pula bahwa}\: \: r_{2}-r_{1}=4-1=3\\ &\begin{aligned}&\textrm{Karena}\: \: P_{1}P_{2}=r_{2}-r_{1},\: \textrm{hal ini berarti lingkaran}\\ &L_{1}\: \: \textrm{bersinggungan di dalam dengan lingkaran}\: L_{2}\\ &\textrm{Sehingga kedua lingkaran ini hanya akan }\\ &\textrm{memiliki}\: \: \color{red}\textrm{satu}\: \: \color{black}\textrm{garis singgung persekutuan} \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut}  \end{array}$.

$\begin{array}{ll}\\ 25.&\textrm{Persamaan lingkaran dengan jari-jari}\: \: 5\\ &\textrm{dan menyinggung lingkaran lain}\\ & x^{2}+y^{2}-2x-4y-20=0\: \: \: \textrm{di titik}\\ &(5,5)\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{b}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{e}.\quad x^{2}+y^{2}-2x-4y-120=0\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahi bahwa}\\ &\begin{aligned}&\begin{array}{rrlll} (L_{1})&(x-a)^2+(y-b)^{2}&=&5^{2}\\ (L_{2})&x^{2}+y^{2}-2x-4y&=&20& \end{array} \\ &\textrm{Titik singgung dua lingkaran}\\ &\textrm{di titik}\: \: (5,5),\: \textrm{artinya}\\ &\begin{pmatrix} 5\\  5 \end{pmatrix}=\displaystyle \frac{\begin{pmatrix} a\\  b \end{pmatrix}+\begin{pmatrix} 1\\  2 \end{pmatrix}}{2}\\ &\Leftrightarrow \begin{pmatrix} 10\\  10 \end{pmatrix}=\begin{pmatrix} a\\  b \end{pmatrix}+\begin{pmatrix} 1\\  2 \end{pmatrix}\\ &\Leftrightarrow \begin{pmatrix} a\\  b \end{pmatrix}=\begin{pmatrix} 10-1\\  10-2 \end{pmatrix}=\begin{pmatrix} 9\\  8 \end{pmatrix} \end{aligned}\\ &\begin{aligned}&\textrm{maka persamaan lingkarannya adalah}:\\ &\Leftrightarrow (x-9)^{2}+(y-8)^{2}=5^{2}\\ &\Leftrightarrow x^{2}+y^{2}-18x-16y+120=0 \end{aligned}\\  &\textbf{Berikut ilustrasi gambarnya}  \end{array}$.

Hubungan Dua Lingkaran

Hubungan Dua Buah Lingkaran

Coba perhatikan ilustrasi beberapa lingkaran berikut

Sebagai penjelasan dari kondisi di atas adalah:

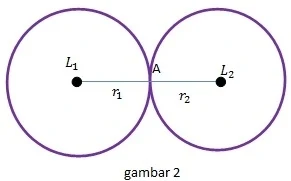
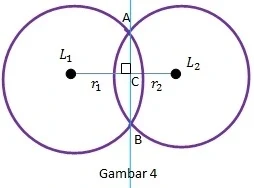
$\begin{array}{|c|c|l|}\hline \textbf{Kedudukan}&\textbf{Ilustrasi}&\qquad\qquad\: \textbf{Keterangan}\\\hline \left | L_{1}L_{2} \right |>r_{1}+r_{2}&\textbf{Gambar 1}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{dan tidak pula bersinggungan}\\ &\textrm{dan saling lepas} \end{aligned}\\\hline \left | L_{1}L_{2} \right |=0&\textbf{Gambar 5}&\textrm{Dikarenakan sepusat}\\\hline \left | L_{1}L_{2} \right |\leq r_{1}+r_{2}&\textbf{Gambar 6}&\textrm{Terletak di dalam lingkaran}\: \: L_{1} \\\hline \left | L_{1}L_{2} \right |=r_{1}+r_{2}&\textbf{Gambar 2}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{tetapi bersinggungan di luar} \end{aligned}\\\hline \left | L_{1}L_{2} \right |=r_{1}-r_{2}&\textbf{Gambar 3}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{tetapi bersinggungan di dalam} \end{aligned}\\\hline \begin{cases} \left | L_{1}L_{2} \right | > r_{1}-r_{2} \\ \left | L_{1}L_{2} \right | < r_{1}+r_{2} \end{cases}&\textbf{Gambar 4}&\begin{aligned}&\textrm{kedua lingkaran berpotongan} \end{aligned}\\\hline \end{array}$.

$\begin{aligned}&\textbf{Kuasa}\\ &\begin{array}{|l|l|}\hline \textrm{Lingkaran}&\textrm{Posisi sebuah titik terhadap lingkaran}\\\hline \begin{aligned}&\textrm{Titik dua}\\ & \textrm{lingkaran} \end{aligned}&\begin{aligned}&\textrm{Tempat kedudukan titik-titik yang memiliki}\\ &\textrm{kuasa yang sama terhadap dua lingkaran} \end{aligned}\\\hline \begin{aligned}&\textrm{Garis tiga}\\ & \textrm{lingkaran} \end{aligned}&\begin{aligned}&\textrm{Tempat kedudukan titik yang memiliki}\\ &\textrm{kuasa yang sama terhadap tiga buah lingkaran} \end{aligned}\\\hline \end{array} \end{aligned}$.

$\begin{aligned}&\textbf{Berkas Lingkaran}\\ &\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\textrm{Posisi}&\qquad\qquad\textrm{Keterangan}\\\hline   \begin{aligned}&\textrm{Berkas}\\ &\textrm{Lingkaran} \end{aligned}&\begin{aligned}&\textrm{Pada garis}\\ &\textrm{busur} \end{aligned}&\begin{aligned}&\textrm{Sejumlah lingkaran yang dapat }\\  &\textrm{dibuat melalui titik-titik potong }\\ &\textrm{kedua lingakaran itu}\end{aligned} \\\hline  \end{array} \end{aligned}$.

$\begin{aligned}&\textbf{Tali Busur Sekutu}\\ &\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\textrm{Posisi}&\qquad\qquad\textrm{Keterangan}\\\hline   \begin{aligned}&\textrm{Tali Busur}\\ &\textrm{Sekutu}\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Kedua}\\ &\textrm{lingkaran}\\ &\textrm{yang}\\ & \textrm{berpotongan} \end{aligned}&\begin{aligned}&\textrm{Ruas garis yang menghubungkan  }\\ &\textrm{titik-titik potong irisan irisan }\\ &\textrm{kedua lingkaran tersebut}\\ & \end{aligned} \\\hline  \end{array}\\ &\bullet \: \: \textrm{Persamaan Tali Busur Sekutunya adalah}:\: \color{blue}L_{1}-L_{2}=0\\ &\bullet \: \: \textrm{Persamaan yang melalui titik potong dan lingkaran (berkas)}\\ &\: \: \quad \textrm{itu adalah}:\: L_{3}=L_{1}+\color{red}p\color{black}(L_{1}-L_{2}),\: \: \textrm{atau}\: \: L_{3}=L_{1}+\color{red}p\color{black}L_{2}\\ &\: \: \quad \textrm{dengan}\: \: \color{red}p\: \: \color{black}\textrm{adalah suatu parameter (suatu patokan nilai)}\\ &\bullet \: \: \textrm{Luas daerah irisan}:\: (\theta _{1}r_{1}^{2}+\theta _{2}r_{2}^{2})-\displaystyle \frac{1}{2}(r_{1}^{2}\sin \theta _{1}+r_{2}^{2}\sin \theta _{2}) \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah kedudukan untuk dua buah lingkaran}\\ & L_{1}\equiv x^{2}+y^{2}-2x-4y+1=0\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-4x-2y-1=0.\\ & \textrm{Jika kedua lingkaran tersebut bersinggungan}\\ &\textrm{atau berpotongan, tentukanlah titik singgung atau potongnya} \\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline L_{1}&L_{2}\\\hline x^{2}+y^{2}-2x-4y+1=0&x^{2}+y^{2}-4x-2y-1=0\\\hline \begin{cases} P_{1} & :\left ( - \displaystyle \frac{1}{2}(-2),-\frac{1}{2}(-4) \right )=(1,2) \\ r &=\sqrt{\displaystyle \frac{1}{4}\left ( (-2)^{2}+(-4^{2}) \right )-1}\\ &=2 \end{cases}&\begin{cases} P_{2} & :\left ( - \displaystyle \frac{1}{2}(-4),-\frac{1}{2}(-2) \right )=(2,1) \\ r &= \sqrt{\displaystyle \frac{1}{4}\left ( (-4)^{2}+(-2^{2}) \right )-(-1)}\\ &=\sqrt{6} \end{cases}\\\hline \end{array}\\ &\begin{aligned}\textrm{Jarak ke}&\textrm{dua pusat lingkarannya adalah}\: \: P_{1}P_{2}\: \: \textrm{yaitu}:\\ P_{1}P_{2}&=\sqrt{(2-1)^{2}+(1-2)^{2}}\\ &=\sqrt{2}\\ \textrm{Karena n}&\textrm{ilai}\: \: P_{1}P_{2}=\sqrt{2}\: \: \textrm{dan nilai}\: \: P_{1}+P_{2}=2+\sqrt{6},\\ \textrm{sehingga}\: &P_{1}P_{2}<P_{1}+P_{2}\: \: \textrm{maka kedua lingkaran }\\ \textrm{itu berpo}&\textrm{tongan} \end{aligned}  \end{array}$.

$.\qquad \begin{aligned}x^{2}+y^{2}-2x-4y+1&=0\: ..................(1)\\ x^{2}+y^{2}-4x-2y-1&=0\: ..................(2)\\ ----------&---\: ^{-}\\ 2x-2y+2&=0\\ y&=x+1\: ........................(3)\\ \textrm{persamaan}\: \: (3)\rightarrow (1)&\\ x^{2}+(x+1)^{2}-2x-&4(x+1)+1=0\\ x^{2}+x^{2}+2x+1-2x&-4x-4+1=0\\ 2x^{2}-4x-2&=0\Leftrightarrow x^{2}-2x-1=0\\ x_{1,2}&=\displaystyle \frac{-(-2)\pm \sqrt{(-2)^{2}-4.1(-1)}}{2}\\ &=\displaystyle \frac{2\pm \sqrt{8}}{2}=\displaystyle \frac{2\pm 2\sqrt{2}}{2}\begin{cases} x_{1} & =1+\sqrt{2}\: .........(4)\: \: \textbf{atau} \\ x_{2} & =1-\sqrt{2}\: .........(5) \end{cases}\\ \textrm{persamaan}\: \: (4)\rightarrow (3)&,\: y_{1}=1+\sqrt{2}+1=2+\sqrt{2}\\ \textrm{persamaan}\: \: (5)\rightarrow (3)&,\: y_{1}=1-\sqrt{2}+1=2-\sqrt{2}\\ \textrm{Sehingga titik poton}&\textrm{gnya ada 2 yaitu}:\\ &\color{red}\begin{cases} \left ( 1+\sqrt{2},2+\sqrt{2} \right )\: \: \textrm{dan} \\ \left ( 1-\sqrt{2},2-\sqrt{2} \right ) \end{cases}& \\\textrm{Berikut ilustrasinya} \end{aligned}$.

$\begin{array}{ll}\\ 2&\textrm{Dari contoh soal no.1, tentukanlah persamaan lingkaran }\\ &\textrm{yang melalui titik potong kedua lingkaran itu serta }\\ &\textrm{melalui titik pusat koordinat}\: \: O(0,0)\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Pada jawaban soal no.1 didapatkan persamaan }\\ &\textbf{tali busur}:L_{1}-L_{2}\equiv x-y+1=0\\ &\textrm{Sehingga persamaan }\\ &\textbf{berkas lingkaran}\textrm{nya adalah}:L_{3}=L_{1}+p\left (L_{1}-L_{2} \right )=0\\ &\, \, \: \qquad \Leftrightarrow L_{3}= \left (x^{2}+y^{2}-2x-4y+1 \right )+p(x-y+1)=0\\ &\textrm{Karena melalui titik asal}\: \: O(0,0),\: \textrm{maka}\\ &\, \, \: \qquad \Leftrightarrow (0+0-0-0+1)+p(0-0+1)=0\Leftrightarrow p=-1\\ &\textrm{Selanjutnya persamaan berkas lingkarannya akan menjadi}\\ &\, \, \: \qquad L_{3}\equiv x^{2}+y^{2}-2x-4y+1 -(x-y+1)=0\\ &\textrm{Jadi},\: L_{3}\equiv x^{2}+y^{2}-3x-3y=0 \\\\ &\textrm{Dan gambar berikut sebagai ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3&\textrm{Diketahuin dua buah lingkaran}\\ & L_{1}\equiv x^{2}+y^{2}-15y+32=0\quad \: \textrm{dan}\\ & L_{2}\equiv x^{2}+y^{2}-18x+2y+32=0\\ &\textrm{Tunjukkan bahwa kedua lingkaran}\\ &\textrm{bersinggungan di luar dan tentukan}\\ &\textrm{titik singgungnya}\\\\ &\textbf{Jawab}:\\ &\color{blue}\textrm{Akan ditunjukkan kedua lingkaran saling}\\ &\textrm{bersinggungan di luar, yaitu:}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}-15y+32=0&\begin{cases} P_{1} &=(0,8) \\  r_{1} & = 4\sqrt{2} \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}-18x+2y+32=0&\begin{cases} P_{2} &=(9,-1) \\  r_{2} & = 5\sqrt{2} \end{cases}\\\hline \end{array}\\ &\textrm{Selanjutnya}\\ &\begin{array}{|l|l|}\hline \textrm{Hitungan jarak kedua pusat}&\textrm{Sebagai bandingan}\\\hline \begin{aligned}&\textrm{Pusat 1 lingkaran}\: P_{1}=(0,8)\\ &\textrm{Pusat 2 lingkaran}\: P_{2}=(9,-1)\\ &\textrm{maka jarak}\: \: \: P_{1}P_{2}\: \: \textrm{adalah}\\ &=\sqrt{(9-0)^{2}+(-1-8)^{2}}\\ &=\sqrt{9^{2}+9^{2}}=\sqrt{2\times 9^{2}}=\color{red}9\sqrt{2} \end{aligned}&\begin{aligned}P_{1}P_{2}&=r_{1}+r_{2}\\&=4\sqrt{2}+5\sqrt{2}\\&=\color{red}9\sqrt{2}\\ &\\ & \end{aligned}\\\hline \end{array}\\ &\color{blue}\textrm{Adapun koordinat titik singgungnya}:\\ &\begin{aligned}\begin{pmatrix} x\\  y \end{pmatrix}&=\displaystyle \frac{5\begin{pmatrix} 0\\ 8 \end{pmatrix}+4\begin{pmatrix} 9\\  -1 \end{pmatrix}}{5+4}=\displaystyle \frac{\begin{pmatrix} 5\times 0+4\times 9\\  5\times 8+4\times (-1) \end{pmatrix}}{9}\\ &=\displaystyle \frac{\begin{pmatrix} 36\\  36 \end{pmatrix}}{9}=\begin{pmatrix} 4\\  4 \end{pmatrix} \end{aligned}\\ &\textrm{Sehingga koordinat titik potongnya adalah}:\: (4,4)\\ &\textbf{Sebagai gambaran perhatikan ilustrasi berikut} \end{array}$.

DAFTAR PUSTAKA

1. Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
2. Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
3. Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
4. Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.