Lanjutan Contoh Soal 6 Distribusi Normal

$\begin{array}{ll}\\ 26.&\textrm{Untuk menguji hipotesis}\\ &\begin{cases} H_{0} &: \mu =16 \\  H_{1} &: \mu >16  \end{cases}\\ &\textrm{Jika dalam penelitian terhadap sampel}\: n=20\\ &\textrm{diperoleh}\: \: \overline{\textrm{x}}=16,9\: \: \textrm{dengan simpangan baku}\\ &\sqrt{2,3},\: \textrm{maka perhitungan nilai statistik ujinya}\\ &\textrm{adalah}\: ....\\  &\textrm{a}.\quad z=-2,65\\ &\textrm{b}.\quad \color{red}t=-2,65\\ &\textrm{c}.\quad z=2,65\\ &\textrm{d}.\quad t=2,65\\ &\textrm{e}.\quad z=2,95\\\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ &\begin{aligned}&\underline{\textrm{Hipotesis (penelitian sampel)}}\\ &\textrm{H}_{0}:\mu =16\\ &\textrm{H}_{0}:\mu >16\\ &\textrm{dengan},\: n=20,\: \overline{\textrm{x}}=16,9,\: s =\sqrt{2,3}=1,52,\\ &\textrm{maka}\\ &\: \textrm{t}\: \: =\left (\displaystyle \frac{\overline{\textrm{x}}-\mu  }{s}  \right )\sqrt{n}=\displaystyle \frac{16,9-16}{1,52}\sqrt{20}\\&\quad =\left (\displaystyle \frac{0,9}{1,52}  \right )\times 4,472=\color{red}2,65 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 27.&\textrm{Pada soal no.26 di atas, jika taraf nyata}\\ &0,01,\: \textrm{maka kesimpulannya adalah}\: ...\\  &\textrm{a}.\quad \color{red}H_{0}\: \: \textrm{ditolak}\\ &\textrm{b}.\quad H_{0}\: \: \textrm{diterima}\\ &\textrm{c}.\quad H_{1}\: \: \textrm{diterima}\\ &\textrm{d}.\quad H_{1}\: \: \textrm{ditolak}\\ &\textrm{e}.\quad \textrm{tidak dapat ditarik kesimpulan}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\textrm{Kasus uji satu pihak}\\ &\begin{aligned}&\underline{\textrm{Hipotesis}}\\ &\textrm{H}_{0}:\mu =16\\ &\textrm{H}_{0}:\mu >16\\ &\textrm{dengan}\: \alpha =0,01=1\%\Rightarrow t_{0,99}=2,54\\ &\textrm{Kriteria pengambilan keputusan}:\\ &\textrm{Tolak}\: \: H_{0}\: \: \textrm{jika}\: \: t\geq  \color{red}2,54 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 28.&\textrm{Seorang petugas}\: \: customer\: service\: \: \textrm{menyatakan}\\ &\textrm{bahwa di dealer A dapat mensevis rata-rata }\\ &\textrm{sebanyak}\: \: 75\: \: \textrm{unit sepeda motor perhari}.\: \textrm{Untuk}\\ & \textrm{mengecek kebenaran pernyataan di atas diambil}\\ &\textrm{sampel beberapa hari secara random sebanyak }\\ &\textrm{20 hari. Dari penelitian ini diperoleh rata-rata}\\ &\textrm{78 unit dengan simpangan bakunya 5. Hasil}\\ &\textrm{perhitungan}\: \: \textrm{z}_{0}-\: \textrm{nya adalah}\:  ....\\ &\textrm{a}.\quad 2,35\\ &\textrm{b}.\quad 2,43\\ &\textrm{c}.\quad 2,55\\ &\textrm{d}.\quad \color{red}2,68\\ &\textrm{e}.\quad 2,75\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ &\begin{aligned}&\textrm{Diketahui data dianggap berdistribusi}\\ &\textrm{normal baku}\: N(0,1)\: \: \textrm{dengan}\\ &\textrm{Rata-rata sampel}=\overline{\textrm{x}}=\color{blue}78\: \: \color{black}\textrm{unit sepeda motor}\\ &\textrm{Rata-rata populasinya yang diuji}=\mu _{0}=75\\ &\textrm{Simpangan bakunya}=\sigma =\color{blue}5\: \: \color{black}\textrm{unit}\\ &\textrm{dengan banyak data sampel}=n=\: \color{blue}20\: \: \color{black}\textrm{hari}\\ &\textrm{Penghitungan nilainya}\: \: z-\textrm{nya}\\ &=\displaystyle \frac{\overline{\textrm{x}}-\mu _{0}}{\displaystyle \frac{\sigma }{\sqrt{n}}}\\ &=\displaystyle \frac{78-75}{\displaystyle \frac{5}{\sqrt{20}}}=\displaystyle \frac{3}{\displaystyle \frac{5}{2\sqrt{5}}}\\ &=\displaystyle \frac{6}{\sqrt{5}}=\frac{6}{2,236}=\color{red}2,683 \end{aligned}  \end{array}$.

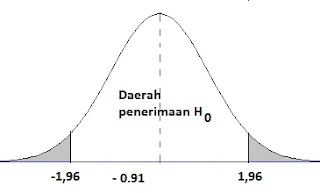
$\begin{array}{ll}\\ 29.&\textrm{Tersiar kabar bahwa harga beras di pasar di}\\ &\textrm{wilayah B adalah}\: \: \textrm{Rp}8.000,00/\textrm{Kg dengan}\\ &\textrm{simpangan baku}\: \: \textrm{Rp}1.500,00.\: \textrm{Berdasar kabar}\\ & \textrm{tersebut dilakukan penelitian dengan mengambil}\\ &\textrm{sampel secara acak sebanyak}\: \: 60\: \: \textrm{kios yang dan}\\ &\textrm{diperoleh rata-rata harga beras}\: \: \textrm{Rp}7.800,00/\textrm{Kg}\\ &\textrm{Jika penghitungan menggunakan tingkat}\\ &\textrm{signifikansi}\: \: 5\%,\: \textrm{maka kesimpulan berikut }\\ &\textrm{yang tepat adalah}\:  ....\\ &\textrm{a}.\quad \textrm{harga beras di pasar lebih dari}\: \: \textrm{Rp}7.800,00/\textrm{Kg}\\ &\textrm{b}.\quad \textrm{harga beras di pasar lebih dari}\: \: \textrm{Rp}8.000,00/\textrm{Kg}\\ &\textrm{c}.\quad \textrm{harga beras di pasar kurang dari}\: \: \textrm{Rp}0.000,00/\textrm{Kg}\\ &\textrm{d}.\quad \textrm{harga beras di pasar}\: \: \textrm{Rp}7.800,00/\textrm{Kg}\\ &\textrm{e}.\quad \color{red}\textrm{harga beras di pasar}\: \: \textrm{Rp}8.000,00/\textrm{Kg}\\\\ &\textbf{Jawab}:\quad \textbf{e}\\&\begin{aligned}&\underline{\textrm{Hipotesis}}\\ &\textrm{Rata-rata harga beras dipasar}\: \: \textrm{Rp}8.000,00/\textrm{Kg}\\ &\textrm{H}_{0}:\mu =8.000\\ &\textrm{H}_{0}:\mu \neq 8.000\\ &\underline{\textrm{Daerah Kritis}}\\ &\textrm{Taraf nyata yang dipilih adalah}=\alpha =0,05=5\%\\ &\displaystyle \frac{\alpha }{2}=2,5\%=0,025\\ &\textrm{z}_{0,025}=1,96\\ &\textrm{maka daerah kritis/penolakannya adalah}\\ &\textrm{z}<-1,96\: \: \textrm{atau}\: \: \textrm{z}>1,96 \end{aligned}  \end{array}$.

$.\: \qquad\begin{aligned}&\underline{\textrm{Nilai Satistik Uji}}\\ &\textrm{Dihitung dengan rumus}:\: \textrm{z}=\displaystyle \frac{\overline{\textrm{x}}-\mu _{0}}{\displaystyle \frac{\sigma }{\sqrt{n}}}\\ &\textrm{z}=\displaystyle \frac{7.800-8.000}{\displaystyle \frac{1.500}{\sqrt{60}}}=-\displaystyle \frac{200\sqrt{60}}{1.500}=-1,03\\ &\underline{\textrm{Keputusan Uji}}\\ &\textrm{Karena nilai}\: \: -1,96<\textrm{z}<1,96,\\ &\textrm{maka}\: \: \textrm{H}_{0}\: \: \color{red}\textrm{diterima}\\ &\underline{\textrm{Kesimpulan}}\\ &\textrm{Rata-rata harga beras dipasar}\: \: \color{red}\textrm{Rp}8.000,00/\textrm{Kg} \end{aligned}$ .

Lanjutan Contoh Soal 5 Distribusi Normal

$\begin{array}{ll}\\ 21.&\textrm{Pada suatu kelas seorang guru matematika}\\ &\textrm{menyatakan bahwa nilai ulangan mapel }\\ & \textrm{yang diampunya tidak kurang dari}\: \:68\\ &\textrm{Untuk menentukan uji tersebut, maka guru}\\ &\textrm{yang bersangkutan memilih 10 anak secara}\\ &\textrm{acak untuk ditanyai nilai hasil ulangannya}\\ &\textrm{Hipotesis}\: \: \textrm{H}_{0}\: \: \textrm{dan}\: \: \textrm{H}_{1}\: \: \textrm{yang tepat dari kondisi}\\ &\textrm{kondisi di atas adalah}\:  ....\\ &\textrm{a}.\quad \begin{matrix} \textrm{H}_{0}:\mu =68\\  \textrm{H}_{1}:\mu \neq 68 \end{matrix}\\ &\textrm{b}.\quad \begin{matrix} \textrm{H}_{0}:\mu =68\\  \textrm{H}_{1}:\mu > 68 \end{matrix}\\ &\textrm{c}.\quad \color{red}\begin{matrix} \textrm{H}_{0}:\mu \geq 68\\  \textrm{H}_{1}:\mu < 68 \end{matrix}\\ &\textrm{d}.\quad \begin{matrix} \textrm{H}_{0}:\mu \leq 68\\  \textrm{H}_{1}:\mu >q 68 \end{matrix}\\ &\textrm{e}.\quad \begin{matrix} \textrm{H}_{0}:\mu >68\\  \textrm{H}_{1}:\mu \neq 68 \end{matrix}\\\\ &\textbf{Jawab}:\quad \textbf{c}\\ &\textrm{Cukup jelas}\\ &\textrm{Dan ini contoh uji satu pihak, yaitu kiri}  \end{array}$.

$\begin{array}{ll}\\ 22.&\textrm{Untuk menguji hipotesis}\\ &\begin{cases} H_{0} &: \mu =800 \\  H_{1} &: \mu \neq 800  \end{cases}\\ &\textrm{Jika dalam penelitian didapatkan}\: \overline{\textrm{x}}=795\\ &\textrm{dan}\: \: n=100\: \: \textrm{serta simpangan baku}\\ &\textrm{populasi}\: \: 55,\: \textrm{maka perhitungan nilai}\\ &\textrm{statistik ujinya adalah}\: ....\\  &\textrm{a}.\quad z=-1,10\\ &\textrm{b}.\quad \color{red}z=-0,91\\ &\textrm{c}.\quad t=-0,91\\ &\textrm{d}.\quad t=0,91\\ &\textrm{e}.\quad z=0,91\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\begin{aligned}&\underline{\textrm{Hipotesis}}\\ &\textrm{H}_{0}:\mu =800\\ &\textrm{H}_{0}:\mu \neq 800\\ &\textrm{dengan},\: n=100,\: \overline{\textrm{x}}=795,\: \sigma =55,\: \textrm{maka}\\ &\: \textrm{z}\: \: =\left (\displaystyle \frac{\overline{\textrm{x}}-\mu  }{\sigma }  \right )\sqrt{n}=\displaystyle \frac{795-800}{55}\sqrt{100}\\&\quad =\left (\displaystyle \frac{-5}{55}  \right )\times 10=\color{red}-0,91 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 23.&\textrm{Pada soal no.22 di atas, jika taraf nyata}\\ &5\%,\: \textrm{maka kesimpulannya adalah}\: ...\\  &\textrm{a}.\quad H_{0}\: \: \textrm{ditolak}\\ &\textrm{b}.\quad \color{red}H_{0}\: \: \textrm{diterima}\\ &\textrm{c}.\quad H_{1}\: \: \textrm{diterima}\\ &\textrm{d}.\quad H_{1}\: \: \textrm{ditolak}\\ &\textrm{e}.\quad \textrm{tidak dapat ditarik kesimpulan}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\textrm{Kasus uji dua pihak}\\ &\begin{aligned}&\underline{\textrm{Hipotesis}}\\ &\textrm{H}_{0}:\mu =800\\ &\textrm{H}_{0}:\mu \neq 800\\ &\textrm{dengan}\: \alpha =5\%=0,05\Rightarrow z_{\frac{1}{2}(1-0,05)}\\ &\quad =z_{0,475}=1,96 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 24.&\textrm{Untuk menguji hipotesis}\\ &\begin{cases} H_{0} &: \mu =20 \\  H_{1} &: \mu <20  \end{cases}\\ &\textrm{Jika dalam penelitian terhadap sampel}\: n=21\\ &\textrm{diperoleh}\: \: \overline{\textrm{x}}=19,8\: \: \textrm{dengan simpangan baku}\\ &0,4,\: \textrm{maka perhitungan nilai statistik ujinya}\\ &\textrm{adalah}\: ....\\  &\textrm{a}.\quad z=-2,29\\ &\textrm{b}.\quad \color{red}t=-2,29\\ &\textrm{c}.\quad z=2,29\\ &\textrm{d}.\quad t=2,29\\ &\textrm{e}.\quad z=2,99\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\begin{aligned}&\underline{\textrm{Hipotesis (penelitian sampel)}}\\ &\textrm{H}_{0}:\mu =20\\ &\textrm{H}_{0}:\mu <20\\ &\textrm{dengan},\: n=21,\: \overline{\textrm{x}}=19,8,\: s =0,4,\: \textrm{maka}\\ &\: \textrm{t}\: \: =\left (\displaystyle \frac{\overline{\textrm{x}}-\mu  }{s}  \right )\sqrt{n}=\displaystyle \frac{19,8-20}{0,4}\sqrt{21}\\&\quad =\left (\displaystyle \frac{-0,2}{0,4}  \right )\times 4,5828=\color{red}-2,29 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 25.&\textrm{Pada soal no.24 di atas, jika taraf nyata}\\ &0,01,\: \textrm{maka kesimpulannya adalah}\: ...\\  &\textrm{a}.\quad H_{0}\: \: \textrm{ditolak}\\ &\textrm{b}.\quad \color{red}H_{0}\: \: \textrm{diterima}\\ &\textrm{c}.\quad H_{1}\: \: \textrm{diterima}\\ &\textrm{d}.\quad H_{1}\: \: \textrm{ditolak}\\ &\textrm{e}.\quad \textrm{tidak dapat ditarik kesimpulan}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\textrm{Kasus uji satu pihak}\\ &\begin{aligned}&\underline{\textrm{Hipotesis}}\\ &\textrm{H}_{0}:\mu =20\\ &\textrm{H}_{0}:\mu < 20\\ &\textrm{dengan}\: \alpha =0,01=1\%\Rightarrow t_{0,99}=2,53\\ &\textrm{Kriteria pengambilan keputusan}:\\ &\textrm{Tolak}\: \: H_{0}\: \: \textrm{jika}\: \: t\leq \color{red}-2,53 \end{aligned} \end{array}$.

Lanjutan Contoh Soal 4 Distribusi Normal

$\begin{array}{ll}\\ 16.&\textrm{Dalam pengujian hipotesis dapat terjadi kesalahan}\\ &\textrm{Jika kita menerima hipotesis yang seharusnya kita}\\ &\textrm{tolak. Kejadian ini merupakan kekeliruan, yaitu}\: ....\\ &\textrm{a}.\quad \textrm{kekeliruan tipe I}\\ &\textrm{b}.\quad \color{red}\textrm{kekeliruan tipe II}\\ &\textrm{c}.\quad \textrm{kekeliruan tipe III}\\ &\textrm{d}.\quad \textrm{kekeliruan sampling}\\ &\textrm{e}.\quad \textrm{kekeliruan non sampling}\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ & \textrm{Cukup jelas} \end{array}$.

$\begin{array}{ll}\\ 17.&\textrm{Pengertian dari taraf signifikansi}\: \: 1\%\: \textrm{adalah}\: ....\\  &\textrm{a}.\quad \textrm{sekitar}\: \: 95\%\: \textrm{kesimpulan benar telah diambil}\\ &\textrm{b}.\quad \textrm{kurang lebih 5 dari 100 kesimpulan yang }\\ &\qquad\textrm{seharusnya hipotesisnya diterima kita tolak}\\ &\textrm{c}.\quad \textrm{kurang lebih 1 dari 100 kesimpulan yang }\\ &\qquad\textrm{seharusnya hipotesisnya ditolak kita terima}\\ &\textrm{d}.\quad \color{red}\textrm{kurang lebih 1 dari 100 kesimpulan yang }\\ &\qquad\color{red}\textrm{seharusnya hipotesisnya diterima kita tolak}\\ &\textrm{e}.\quad \textrm{kurang lebih 5 dari 100 kesimpulan yang }\\ &\qquad\textrm{seharusnya hipotesisnya ditolak kita terima}\\\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ & \textrm{Cukup jelas} \end{array}$.

$\begin{array}{ll}\\ 18.&\textrm{Dalam pengujian hipotesis, penggunaan statistik}\\ &t\: \: \textrm{ketika penghitungan}\: ....\\  &\textrm{a}.\quad \textrm{simpsngsn baku saat sampel tidak diketahui}\\ &\textrm{b}.\quad \textrm{rata-rata sampel tidak diketahui}\\ &\textrm{c}.\quad \color{red}\textrm{simpangan baku populasi tidak diketahui}\\ &\textrm{d}.\quad \textrm{rata-rata populasi tidak diketahui}\\ &\textrm{e}.\quad \textrm{simpangan baku populasi diketahui}\\\\\\ &\textbf{Jawab}:\quad \textbf{c}\\ & \textrm{Cukup jelas} \end{array}$.

$\begin{array}{ll}\\ 19.&\textrm{Penggunaan kriteria pada uji pihak kiri jika}\\ &\textrm{diketahui}\: \: d\: \: \textrm{adalah nilai yang diperoleh dari}\\ &\textrm{daftar distribusi yang bersangkutan dengan}\\ &\textrm{peluang yang ditentukan oleh}\: \: \alpha \: \: \textrm{adalah}\:  ....\\  &\textrm{a}.\quad \textrm{tolak}\: H_{0}\: \textrm{jika nilai statistik uji lebih dari}\\ &\qquad d\: ,\: \textrm{dalam hal lainnya}\: \: H_{0}\: \: \textrm{diterima}\\ &\textrm{b}.\quad \color{red}\textrm{tolak}\: H_{0}\: \textrm{jika nilai statistik uji kurang dari}\\ &\qquad d\: ,\: \textrm{dalam hal lainnya}\: \: H_{0}\: \: \textrm{diterima}\\ &\textrm{c}.\quad \textrm{terima}\: H_{0}\: \textrm{jika nilai statistik uji kurang dari}\\ &\qquad d\: ,\: \textrm{dalam hal lainnya}\: \: H_{0}\: \: \textrm{diterima}\\ &\textrm{d}.\quad \textrm{terima}\: H_{0}\: \textrm{jika nilai statistik uji lebih dari}\\ &\qquad d\: ,\: \textrm{dalam hal lainnya}\: \: H_{0}\: \: \textrm{ditolak}\\ &\textrm{e}.\quad \textrm{terima}\: H_{0}\: \textrm{jika nilai statistik uji lebih dari}\\ &\qquad\textrm{atau sama dengan}\:  d\: ,\: \textrm{dalam hal lainnya}\\ &\qquad H_{0}\: \: \textrm{ditolak}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ & \textrm{Cukup jelas} \end{array}$.

$\begin{array}{ll}\\ 20.&\textrm{Hipotesis nol adalah}\:  ....\\  &\textrm{a}.\quad \textrm{hipotesis yang nilai statistik ujinya}\\ &\qquad \textrm{bernilai nol}\\ &\textrm{b}.\quad \color{red}\textrm{hipotesis yang perumusannys mrngandung}\\ &\qquad \textrm{pengertian yang tidak memiliki perbedaan}\\ &\textrm{c}.\quad \textrm{hipotesis yang perumusannya terkandung}\\ &\qquad \textrm{pengertian yang tidak sama}\\ &\textrm{d}.\quad \textrm{hipotesis yang perumusannya mengandung}\\ &\qquad \textrm{pengertian lebih dari}\\ &\textrm{e}.\quad \textrm{hipotesis yang perumusannya mengandung}\\ &\qquad \textrm{pengertian kurang dari}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ & \textrm{Cukup jelas} \end{array}$.

Lanjutan Contoh Soal 3 Distribusi Normal

$\begin{array}{ll}\\ 11.&\textrm{Perhatikan ilustrasi berikut}\:   ....\\    \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{Jika luas yang diarsir adalah 0,90 dan}\: \: n=21,\\ &\textrm{maka nilai}\: \: t\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad1,32\\ &\textrm{b}.\quad \color{red}1,72\\&\textrm{c}.\quad 2,08\\ &\textrm{d}.\quad 2,09\\ &\textrm{e}.\quad 2,53\\\\ &\textbf{Jawab}:\\ &\textrm{Luas arsiran (distribusi student) adalah}:\\ &=1-0,90=0,10,\: \textrm{karena luas kedua ujung}\\ &\textrm{sama, mulai dari}\: t\: \textrm{ke kanan}=\displaystyle \frac{0,10}{2}=0,05\\ &\textrm{Sehingga luas dari}\: t\: \textrm{ke kiri}=1-0,05=0,95\\ &\textrm{Dari ini diketahui luas arsirannya}=p=\color{red}0,95\\ &\textrm{Dengan}\: dk=n-1=21-1=20,\: \textrm{maka}\\ &t=\color{red}\pm 1,72   \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Misalkan luas dari}\: t\: \textrm{ke kiri}=0,05,\\ &\textrm{dengan}\: \: dk=15.\: \textrm{Nilai}\: \: t\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad -1,76\\ &\textrm{b}.\quad \color{red}-1,75\\&\textrm{c}.\quad -1,74\\ &\textrm{d}.\quad 1,75\\ &\textrm{e}.\quad 1,76\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui dari soal di atas}\\ &\textrm{dari}\: \: t\: \: \textrm{ke kiri}=0,05,\: \textrm{maka}\\ &\textrm{luas arsiran}=p=1-0,05=0,95\\ &t=\color{red}-1,75 \: \: (\textrm{lihat tabel})\end{aligned}   \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Transformasi Z}-score\: \: \textrm{dikaitan dengan}\\ &\textrm{data dimaksudkan agar data}\\ &\textrm{terdistribusi secara}\: ....\\ &\textrm{a}.\quad \textrm{tak normal}\\ &\textrm{b}.\quad \textrm{binomial}\\&\textrm{c}.\quad Chi-square\\ &\textrm{d}.\quad \textrm{Poison}\\ &\textrm{e}.\quad \color{red}\textrm{normal}\\\\ &\textrm{Jawab}:\\ &\begin{aligned} &\color{red}\textrm{Cukup jelas} \end{aligned}   \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Perhatikan ilustrasi berikut}\:   ....\\    \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{Jika kurva normal di atas memiliki simpangan}\\ &\textrm{bakunya}\: \: 12,\: \textrm{maka luar daerah arsiran adalah}\: ....\\ &\textrm{a}.\quad 0,4821\\ &\textrm{b}.\quad 0,4966\\&\textrm{c}.\quad 0,4999\\ &\textrm{d}.\quad \color{red}0,5934\\ &\textrm{e}.\quad 0,6921\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui},\: \mu =60,\sigma =12,\textrm{x}_{1}=50,\textrm{x}_{2}=70\\ &\textrm{dengan nilai}\: \: z=\displaystyle \frac{\textrm{x}-\mu }{\sigma },\: \:\textrm{ maka}\\ &\begin{aligned}\textrm{z}_{1}&=\displaystyle \frac{\textrm{x}_{1}-\mu }{\sigma }=\frac{50-60}{12}=\frac{-10}{12}=-0.83\\ \textrm{z}_{2}&=\displaystyle \frac{\textrm{x}_{2}-\mu }{\sigma }=\frac{70-60}{12}=\frac{10}{12}=0.83 \end{aligned}\\ &\textrm{Luas}=P(-z\leq Z\leq z)=2\times P(0\leq Z\leq z)\\ &\qquad\, \:  =2\times (0,2967)=\color{red}0,5934   \end{array}$.

$\begin{array}{ll}\\ 15.&\textrm{Perhatikan ilustrasi berikut}\:   ....\\    \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{Jika kurva normal di atas memiliki simpangan}\\ &\textrm{bakunya}\: \: 5,\: \textrm{maka luar daerah arsiran adalah}\: ....\\ &\textrm{a}.\quad 0,1585\\ &\textrm{b}.\quad 0,1815\\&\textrm{c}.\quad 0,3413\\ &\textrm{d}.\quad 0,8172\\ &\textrm{e}.\quad \color{red}0,8185\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui},\: \mu =40,\sigma =5,\textrm{x}_{1}=30,\textrm{x}_{2}=45\\ &\textrm{dengan nilai}\: \: z=\displaystyle \frac{\textrm{x}-\mu }{\sigma },\: \:\textrm{ maka}\\ &\begin{aligned}\textrm{z}_{1}&=\displaystyle \frac{\textrm{x}_{1}-\mu }{\sigma }=\frac{30-40}{5}=\frac{-10}{5}=-2\\ \textrm{z}_{2}&=\displaystyle \frac{\textrm{x}_{2}-\mu }{\sigma }=\frac{45-40}{5}=\frac{5}{5}=1 \end{aligned}\\ &\textrm{Luas}=P(z_{1}\leq Z\leq z_{2})= P(0\leq Z\leq z_{1})\\ &\qquad\: \: +P(0\leq Z\leq z_{2})\\ &\qquad\, \:  =P(0\leq Z\leq 2)+P(0\leq Z\leq 1)\\ &\qquad\, \:  =0,3413+0,4772=\color{red}0,8185   \end{array}$.

Distribusi Student (Uji t)

Uji "t"

Dalam pengujian hipotesis kita mengenal 2 rumus pengujian yaitu rumus z (distribusi normal standar) dan rumus t (distribusi student). Rumus z digunakan manakala simpangan baku pada populasi diketahui, sedangkan rumus t digunakan ketika simpangan baku pada populasi tidak diketahui. Ketika simpangan baku setiap populasi jarang diketahui, maka biasanya alternatifnya adalah digunakan simpangan baku sampel dan selanjutnya digunakanlah uji t.

$\begin{aligned}t&=\color{red}\displaystyle \frac{\bar{\textrm{x}}-\mu _{0}}{\frac{s}{\sqrt{n}}}\: \: \color{black}\textrm{atau}\: \:  t=\color{red}\displaystyle \frac{\bar{\textrm{x}}-\mu _{0}}{s}\sqrt{n}\\ &\textrm{Dimana}\\ &t=\textrm{nilai}\: \: t\: \: \textrm{yang dihitung}\\ &\bar{\textrm{x}}=\textrm{rata-rata sampel}\\ &\mu =\textrm{rata-rata populasi}\\ &\qquad \textrm{atau nilai yang dihipotesiskan}\\ &s=\textrm{simpangan baku sampel}\\ &n=\textrm{jumlah anggota sampel}  \end{aligned}$.

Selanjutnya untuk perhitungan simpangan baku s digunakan rumus berikut

$\begin{aligned}s&=\color{red}\sqrt{\displaystyle \frac{\sum (\textrm{x}_{i}-\bar{\textrm{x}})^{2}}{n-1}}\\ &\textrm{Dimana}\\ &\bar{\textrm{x}}=\textrm{rata-rata sampel}\\ &n-1=\textrm{derajat kebebasan}  \end{aligned}$.

Sebagai catatan dalam pemilihan statistik uji dan penghitungan statistik uji

• Jika ukuran sampel  $n\geq 30$, statistik uji yang digunakan adalah z (rumus z di atas), $Z\sim N(0,1)$.
• Jika ukuran sampel  $n< 30$, statistik uji yang digunakan adalah t, dengan derajat kebebasan $dk=n-1$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Sebuah perusahaan X mengatakan bahwa}\\ &\textrm{performance pegawainya rata-rata nilai}\\ &\textrm{skornya adalah}\: 8,5.\: \textrm{Untuk membuktikan}\\ &\textrm{pernyataan tersebut diambillah secara }\\ &\textrm{random 16 orang pegawai untuk dites dan}\\ &\textrm{hasilnya tersaji berikut}\\ &7,8\: \: \: 8,2\: \: \: 8,4\: \: \: 7,8\: \: \: 8,9\: \: \: 9,1\: \: \: 8,5\: \: \: 7,7\\ &8,5\: \: \: 7,9\: \: \: 9,1\: \: \: 7,8\: \: \: 9,2\: \: \: 8,9\: \: \: 8,8\: \: \: 8,3\\ &\textrm{Pada taraf}\: 1\%,\: \textrm{apakah pernyataan}\\ &\textrm{perusahaan tersebut benar}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan rata-rata skor performance}\\ &\textrm{berdistribusi student}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu =8,5\\ &H_{1}:\mu \neq 8,5\\ &\textbf{Daerah kritis}\\ &\textrm{Uji dua pihak/hipotesis dua arah dengan}\: \alpha =1\%\\ &t_{1-\frac{1}{2}(0,01)}=t_{0,995}.\: \textrm{Dengan dk}=16-1=15\\ &\textrm{diperoleh nilai}\: \: t=\color{red}2,95\: \: \color{black}(\textrm{tabel distribusi student})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue}-2,95< t< 2,95\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}t<-2,95\: \: \textrm{atau}\: \:  t> 2,95\\ &\textrm{Berikut disajikan tabel}\: \textbf{distribusi student}\\ &\qquad\qquad \begin{array}{|c|c|c|c|c|}\hline dk&\color{blue}t_{0,995}&t_{0,99}&t_{0,975}&t_{0,95}\\\hline 1&63,66&31,82&12,71&6,31\\\hline 2&9,92&6,96&4,3&2,92\\\hline 3&5,84&4,54&3,18&2,35\\\hline 4&4,6&3,75&2,78&2,13\\\hline 5&4,03&3,36&2,57&2,02\\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline \color{blue}15&\color{red}2,95&2,60&2,13&1,75\\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline 99&\cdots &\cdots &1,99&\cdots \\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline 120&2,62&2,36&1,98&1,66\\\hline \infty &2,56&2,33&1,96&1,645\\\hline \end{array}\\ &\textbf{Nilai statistik uji}\\ &\bar{x}=\displaystyle \frac{7,5+8,2+8,4+\cdots +8,8+8,3}{16},\\ &\quad =8,4125\\ &s=\sqrt{\displaystyle \frac{(7,5-8,4125)^{2}+\cdots +(8,3-8,4125)^{2}}{\color{red}16-1}}\\ &\quad =\sqrt{0,308}=0,555\\ &n=100,\: \: \color{red}t\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{s}\sqrt{n}\\ &\Leftrightarrow \color{red}t\color{black}=\displaystyle \frac{(8,4125-8,5)}{0,555}\sqrt{16}=\color{red}-0,63\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\: -2,95< \color{red}-0,63\color{black}< 2,95\: ,\: H_{0}\: \: \textrm{diterima}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 1}\%\: \: \textrm{rata-rata skor}\\ &\textrm{performan pegawai adalah}\: \: 8,5  \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Sebuah sampel acak 100 catatan kematian}\\ &\textrm{di negara A selama 1 tahun yang kemaren}\\ &\textrm{menunjukkan umur rata-rata 58,8 tahun}\\ &\textrm{dengan simpangan baku 7,8 tahun. Apakah}\\ &\textrm{hal itu menunjukkan bahwa harapan umur}\\ & \textrm{rata-rata sekarang minimal 60 tahun}?\\ &\textrm{Jelaskan pernyataan tersebut dengan tingkat}\\ &\textrm{signifikansi}\: \: 5\%\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan umur rata-rata sekarang}\geq 60\: \: \textrm{tahun}\\ &\textrm{berdistribusi student}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu \geq 60\\ &H_{1}:\mu < 60\\ &\textbf{Daerah kritis}\\ &\textrm{Uji satu pihak/hipotesis pihak kiri dengan}\: \alpha =5\%\\ &t_{1-(0,05)}=t_{0,995}.\: \textrm{Dengan dk}=100-1=99\\ &\textrm{diperoleh nilai}\: \: t=\color{red}2,63\: \: \color{black}(\textrm{tabel distribusi student})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue} t> -2,63\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}t\leq - 2,63\\ &\textbf{Nilai statistik uji}\\ &\mu =58,8,\: s=7,8\: \: \textrm{tahun}\\ &n=100,\: \: \color{red}t\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{s}\sqrt{n}\\ &\Leftrightarrow \color{red}t\color{black}=\displaystyle \frac{(58,8-60)}{7,8}\sqrt{100}=\color{red}-1,54\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\: t\leq  \color{red}-1,54,\: \color{black}H_{0}\: \: \textrm{diterima}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 5}\%\: \: \textrm{umur rata-rata}\\ &\textrm{sekarang minimal}\: \: 60\: \: \textrm{tahun}   \end{aligned} \end{array}$.

DAFTAR PUSTAKA

1. Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
2. Sembiring, S., Zulkifli. M., Marsito, Rusdi. I. 2016. Matematika untuk Siswa SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.
3. Sugiyono. 2013. Statistika untuk Penelitan. Bandung: ALFABETA

Lanjutan Contoh Soal 2 Distribusi Normal

 $\begin{array}{ll}\\ 6.&\textrm{Luas daerah yang diarsir di bawah}\\ &\textrm{kurva normal baku berikut adalah}\:  ....\\ &\textrm{a}.\quad 0,4861\\ &\textrm{b}.\quad \color{red}0,4878\\&\textrm{c}.\quad 0,4881\\ &\textrm{d}.\quad 0,4938\\ &\textrm{e}.\quad 0,4946\\\\   \end{array}$.

$.\qquad\begin{aligned}&\textbf{Jawab}:\\ &\textrm{Perhatikan tabel}\: \color{blue}\textrm{distribusi normal}\:  \color{black}\textrm{berikut}\\&\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline \textrm{z} &0&1&2&3&4&5&6&7&8&9\\\hline \vdots &&&&&&\downarrow &&&&\\ \vdots &&&&&&&&&&\\ 2,2 &&&&&&\color{red}0,4878&&&&\\ \vdots &&&&&&&&&&\\\hline \end{array}\\ &\textrm{Sehingga nilai}\: \: \textrm{z}=2,25\: \: \textrm{luasnya}=0,4878 \end{aligned}$.

$\begin{array}{ll}\\ 7.&\textrm{Luas daerah yang diarsir di bawah}\\ &\textrm{kurva normal baku berikut adalah}\:  ....\\ &\textrm{a}.\quad \color{red}0,1138\\ &\textrm{b}.\quad 0,3810\\&\textrm{c}.\quad 0,3862\\ &\textrm{d}.\quad 0,4948\\ &\textrm{e}.\quad 0,5000\\\\   \end{array}$.

$.\qquad\begin{aligned}&\textbf{Jawab}:\\ &\textrm{Perhatikan tabel}\: \color{blue}\textrm{distribusi normal}\:  \color{black}\textrm{berikut}\\&\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline \textrm{z} &0&1&2&3&4&5&6&7&8&9\\\hline \vdots &&&&&&&\downarrow &&\downarrow&\\ \vdots &&&&&&&&&&\\ 1,1 &&&&&&&\downarrow&&\color{red}0,3810&\\ \vdots &&&&&&&&&&\\ 2,5&&&&&&&\color{red}0,4948&&&\\ \vdots &&&&&&&&&&\\\hline \end{array}\\ &\textrm{Sehingga nilai}\: \: \textrm{z}=1,18\: \: \textrm{luasnya}=0,3810\\ &\textrm{Dan nilai}\: \: \textrm{z}=2,56\: \: \textrm{luasnya}=0,4948\\ &\textrm{maka luas arsiran}\\ &=P(1,18<Z<2,56)\\ &=P(0<Z<2,56)-P(0<Z<1,18)\\ &=0,4948-0,3810\\ &=\color{red}0,1138 \end{aligned}$.

$\begin{array}{ll}\\ 8.&\textrm{Luas daerah yang diarsir pada gambar}\\ &\textrm{di bawah adalah 0,9332, maka nilai}\: \: \textrm{z}=\:  ....\\    \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{a}.\quad 1,05\\ &\textrm{b}.\quad 1,06\\&\textrm{c}.\quad 1,16\\ &\textrm{d}.\quad \color{red}1,50\\ &\textrm{e}.\quad 1,60\\\\ &\textbf{Jawab}:\\ &\textrm{Luas arsiran adalah}\\ &=P(Z<z)=0,9332\\ &=\color{blue}0,5\color{black}+0,4332\\ &=0,5+P(0<Z<z)\\ &\textrm{lihat/konfirmasi ke tabel}\\ &\textrm{z}=\color{red}1,50\\ &\begin{aligned}&\textrm{Perhatikan tabel}\: \color{blue}\textrm{distribusi normal}\:  \color{black}\textrm{berikut}\\&\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline \textrm{z} &0&1&2&3&4&5&6&7&8&9\\\hline \vdots &\downarrow &&&&&&&&&\\ \vdots &&&&&&&&&&\\ 1,5 &\color{red}0,4332&&&&&&&&&\\ \vdots &&&&&&&&&&\\\hline \end{array}\\ &\textrm{Sehingga luasnya}=0,4878,\: \: \textrm{batas z}=1,50  \end{aligned}    \end{array}$.

$\begin{array}{ll}\\ 9.&\textrm{Luas daerah yang diarsir pada gambar}\\ &\textrm{di bawah adalah}=\:  ....\\    \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{a}.\quad 0,9750\\ &\textrm{b}.\quad 0,5000\\&\textrm{c}.\quad 0,4750\\ &\textrm{d}.\quad \color{red}0,0250\\ &\textrm{e}.\quad 0,0200\\\\ &\textbf{Jawab}:\\ &\textrm{Luas arsiran adalah}\\ &=P(0\leq Z\leq \infty )-P(0\leq Z\leq 1,96)\\ &=\color{blue}0,5\color{black}-0,4750\\ &=\color{red}0,0250  \end{array}$.

$\begin{array}{ll}\\ 10.&\textrm{Misalkan tinggi siswa kelas XII berdistribusi}\\ &\textrm{normal dengan rata-rata 167,5 cm dengan}\\ &\textrm{simpangan baku 4,6 cm. Jika jumlah siswa}\\ &\textrm{yang diteliti sebanyak 10.000 siswa, maka }\\ &\textrm{jumlah siswa yang memiliki tinggi lebih}\\ &\textrm{dari 160 cm sebanyak}\: ....\\ &\textrm{a}.\quad 16.300\\ &\textrm{b}.\quad \color{red}9.484\\&\textrm{c}.\quad 5.516\\ &\textrm{d}.\quad 4.484\\ &\textrm{e}.\quad 4.474\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui dari soal di atas}\\ &n=10.000,\: \mu =167,5\: \textrm{cm},\: \sigma =4,6\\ &z=\displaystyle \frac{x-\mu }{\sigma }=\displaystyle \frac{160-167,5}{4,6}=\color{red}-1,63\\ &\begin{aligned}P(X> 160)&=P(Z> -1,63)\\ &=P(0\leq Z\leq 1,63)\\ &\qquad\qquad+P(0\leq Z\leq \infty )\\ &=0,4484+0,5\\ &=0,9484 \end{aligned}\\ &\textrm{Sehingga total siswa yang dimaksud}\\ &\textrm{sebanyak}:0,9484\times 10.000=\color{red}9.484 \end{aligned}   \end{array}$.

Penarikan Kesimpulan

F. Uji Hipotesis

F. 1 Pengertian

Dalam suatu penyelidikan berkaitan suatu permasalahan untuk penarikan suatu kesimpulan diperlukan adanya dugaan atau dalam bahasa matematika dinamakan istilah hipotesis. Hipotesis berasal dari bahasa Yunani Hupo yang berarti sementara dan Thesis yang berarti pernyataan atau dugaan. Sehingga secara bahasa memiliki arti dugaan sementara. Selanjutnya, karena hipotesis ini masih berupa jawaban sementara, maka hipotesis ini harus diuji kebenaranya dan prosesnya dinamakan uji hipotesis. Uji hipotesis yang dibahasa di sini adalah pengujian berkaitan dengan rata-rata  $\mu$ pada sebuah sampel. Jika hasil yang didapatkan dalam penelitian nantinya, jauh berbeda dengan yang diharapkan berdasarkan hipotesis, maka hipotesis ditolak, demikian sebaliknya jika sesuai, maka hipotesis diterima.

F. 2 Jenis-Jenis Hipotesis

Ada dua jenis hipotetsis yaitu:

• Hipotesis nol ($H_{0}$) yang terkandung makna tidak memiliki perbedaan
• Hipotesis alternatif  ($H_{1}$) dengan pengertian terdapat tidak sama atau ada perbedaan.

F. 3 Langkah-Langkah Pengujian Hipotesis.

Berikut prosedur pengujian hipotesis

$.\qquad\quad\color{red}\begin{aligned}&\textrm{Merumuskan}\: H_{0}\: \: \textrm{dan}\: \: H_{1}\\ &\qquad\qquad\color{blue}\Downarrow\\ &\textrm{Menentukan daerah kritis}\\ &(\textrm{taraf signifikansi/kepercayaan})\\ &\qquad\qquad\color{blue}\Downarrow\\ &\textrm{Menentukan nilai statistik uji}\\ &\qquad\qquad\color{blue}\Downarrow\\ &\textrm{Menentukan keputusan uji}\\ &\qquad\qquad\color{blue}\Downarrow\\ &\textrm{Penarikan kesimpulan}  \end{aligned}$.

Sebagai tambahannya, dalam melakukan pengujian hipotesis, ada 2 jenis kekeliruan yang bisa terjadi

• Kekeliruan tipe I, yaitu kita menolak hipotesis yang seharusnya diterima
• Kekeliruan tipe II, yaitu kita menerima hipotesis yang seharusnya kita tolak

$\begin{array}{|l|c|c|}\hline \textrm{Keputusan uji}&H_{0}\: \: \textrm{benar}&H_{0}\: \: \textrm{salah}\\\hline \textrm{Menerima}\: \: H_{0}&\begin{aligned}&\color{red}\textrm{Benar}\\ &(1-\alpha )\end{aligned}&\begin{aligned}&\textrm{Kesalahan}\\ &\textrm{tipe II}\: \: (\beta ) \end{aligned}\\\hline \textrm{Menolak}\: \: H_{0}&\begin{aligned}&\textrm{Kesalahan}\\ &\textrm{tipe I}\: \: (\alpha ) \end{aligned}&\begin{aligned}&\color{blue}\textrm{Benar}\\ &(1-\beta  )\end{aligned}\\\hline \end{array}$.

Untuk meminimalkan kesalahan:

• dalam pengujian hipotesis diinginkan  $\alpha $ (dibaca alfa) dan  $\beta $  (dibaca beta) kecil atau $(1-\beta )$ besar.
• tetapi hal di atas adalah sulit karena jika $\alpha $ makin kecil, maka nilai  $\beta $ semakin besar.
• dari 2 hal tersebut di atas, maka dipilihlah salah satu, dalam hal ini biasanya $\alpha $. dan $\alpha $ yang digunakan bisanya pula adalah 10%, 5%, dan atau 1% tergantung kebutuhgannya dalam bidang apa mau diterapkan. Misal dalam bidang pengobatan diambillah $\alpha $ yang 1%.
• $\alpha $ dalam hal ini selanjutnya disebut taraf signifikansi atau taraf arti atau taraf nyata.

F.4 Bentuk Pengujian Hipotesis

Ada 3 macam, yaitu, uji dua pihak, uji pihak kanan, dan uji pihak kiri.

F. 4. 1 Uji dua Pihak

.

$\begin{array}{|l|l|}\hline \color{red}\textbf{Jika}\: \: \sigma \: \: \textrm{diketahui}&\color{red}\textbf{Jika}\: \: \sigma \: \: \textrm{tidak diketahui}\\\hline \begin{aligned}&\textrm{Untuk menguji pasangan hipotesis}\\ &\qquad \begin{cases} H_{0} & : \mu =\mu _{0} \\ H_{1} & : \mu \neq \mu _{0}  \end{cases}\\ &\textrm{di mana nilai}\: \: z=\left (\displaystyle \frac{\bar{x}-\mu _{0}}{\sigma }  \right )\sqrt{n}\\ &\textrm{Dan untuk}\: \: z\: \: \textrm{berdistribusi normal}\\ &\textrm{baku. Pengambilan kesimpulan}\\ &H_{0}\: \: \textrm{diterima jika}:\\ &-z_{\frac{1}{2}(1-\alpha )}<z<z_{\frac{1}{2}(1-\alpha )}\\ &\textrm{dan daerah ini disebut}\\ &\textbf{daerah tidak nyata}\: \: \textrm{atau}\\ &\textbf{daerah penerimaan}\: \: H_{0} \\ &\\ &\\ &\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Untuk menguji pasangan hipotesis}\\ &\qquad \begin{cases} H_{0} & : \mu =\mu _{0} \\ H_{1} & : \mu \neq \mu _{0}  \end{cases}\\ &\textrm{Gunakan}\: \: \textbf{distribusi student}\\ &\textrm{dengan rumus}\: \: t=\left (\displaystyle \frac{\bar{x}-\mu _{0}}{s }  \right )\sqrt{n}\\ &\textrm{di mana}\: \: s\: \: \textrm{adalah simpangan baku}\\ &\textrm{dan dihitung  dengan rumus}\\ &\qquad\qquad s=\sqrt{\displaystyle \frac{\sum (x_{i}-\bar{x})^{2}}{n-1}}\\ &\textrm{Dan untuk}\: \: t\: \: \textrm{berdsitribusi student}\\ &\textrm{pada pengambilan kesimpulan},\: \: H_{0}\\ &\textrm{diterima jika}:-t_{(1-\frac{1}{2}\alpha )}<t<t_{(1-\frac{1}{2}\alpha )}\\ &\textrm{dan daerah ini disebut}\\ &\textbf{daerah tidak nyata}\: \: \textrm{atau}\\ &\textbf{daerah penerimaan}\: \: H_{0}\\ &\textrm{dengan}\: \: dK=n-1  \end{aligned}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Seorang pengusaha lampu merk X mengatakan}\\ &\textrm{bahwa lampunya memiliki masa pakai rata-rata}\\ &\textrm{900. Untuk menguji pernyataan tersebut, maka}\\ &\textrm{diuji sebanyak 100 lampu dan ternyata rata-rata}\\ &\textrm{masa pakainya 890 jam dengan simpangan baku-}\\ &\textrm{nya 60 jam. Selidikilah dengan tingkat signifikansi}\\ &5\%,\: \textrm{apakah kualitas lampu itu sudah berubah}\\ &\textrm{atau belum}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan masa hidup lampu berdistribusi normal}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu =900\: \: \textrm{jam (masa pakai masih 900 jam)}\\ &H_{1}:\mu \neq 900\: \: \textrm{jam (masa berubah dan)}\neq 900\: \textrm{jam}\\ &\textbf{Daerah kritis}\\ &\textrm{Uji dua pihak/hipotesis dua arah dengan}\: \alpha =5\%\\ &z_{\frac{1}{2}(1-0,05)}=z_{0,475}=1,96\: \: (\textrm{lihat tabel})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue}-1,96< z< 1,96\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}z<-1,96\: \: \textrm{atau}\: \:  z> 1,96\\ &\textbf{Nilai statistik uji}\\ &\bar{x}=890,\: n=100,\: \: \color{red}z\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{\sigma }\sqrt{n}\\ &\Leftrightarrow \color{red}z\color{black}=\displaystyle \frac{(890-900)}{60}\sqrt{100}=\displaystyle \frac{-10\times 10}{60}=\color{red}-1,67\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\: -1,96< \color{red}-1,67\color{black}< 1,96\: ,\: H_{0}\: \: \textrm{diterima}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 5}\%\: \: \textrm{masa pakai lampu}\\ &\textrm{belum berubah dan masih sekitar 900 jam} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Jika pada soal nomor 1 di atas, simpangan baku}\\ &(\sigma )\: \textrm{tidak diketahui, tetapi dari sampel diperoleh}\\ &s=\textrm{55 jam. Selidikilah apakah kualitas lampu itu }\\ &\textrm{sudah berubah atau belum}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan masa hidup lampu berdistribusi student}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu =900\: \: \textrm{jam (masa pakai masih 900 jam)}\\ &H_{1}:\mu \neq 900\: \: \textrm{jam (masa berubah dan)}\neq 900\: \textrm{jam}\\ &\textbf{Daerah kritis}\\ &\textrm{Uji dua pihak/hipotesis dua arah dengan}\: \alpha =5\%\\ &t_{1-\frac{1}{2}(0,05)}=t_{0,975}.\: \textrm{Dengan dk}=100-1=99\\ &\textrm{diperoleh nilai}\: \: t=\color{red}1,99\: \: \color{black}(\textrm{tabel distribusi student})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue}-1,99< t< 1,99\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}t<-1,99\: \: \textrm{atau}\: \:  t> 1,99\\ &\textrm{Berikut disajikan tabel}\: \textbf{distribusi student}\\ &\qquad\qquad \begin{array}{|c|c|c|c|c|}\hline dk&t_{0,995}&t_{0,99}&\color{blue}t_{0,975}&t_{0,95}\\\hline 1&63,66&31,82&12,71&6,31\\\hline 2&9,92&6,96&4,3&2,92\\\hline 3&5,84&4,54&3,18&2,35\\\hline 4&4,6&3,75&2,78&2,13\\\hline 5&4,03&3,36&2,57&2,02\\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline 60&2,66&2,39&2,00&1,67\\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline \color{blue}99&\cdots &\cdots &\color{red}1,99&\cdots \\\hline \vdots &\vdots &\vdots &\vdots &\vdots \\\hline 120&2,62&2,36&1,98&1,66\\\hline \infty &2,56&2,33&1,96&1,645\\\hline \end{array}\\ &\textbf{Nilai statistik uji}\\ &\bar{x}=890,\: s=55\: \textrm{jam},\: n=100,\: \: \color{red}t\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{s}\sqrt{n}\\ &\Leftrightarrow \color{red}t\color{black}=\displaystyle \frac{(890-900)}{55}\sqrt{100}=\displaystyle \frac{-10\times 10}{55}=\color{red}-1,82\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\: -1,99< \color{red}-1,82\color{black}< 1,99\: ,\: H_{0}\: \: \textrm{diterima}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 5}\%\: \: \textrm{masa pakai lampu}\\ &\textrm{belum berubah dan masih sekitar 900 jam}  \end{aligned} \end{array}$.

F. 4. 2 Uji Satu Pihak

a) Uji Pihak Kanan

$\begin{aligned}&\textrm{Jika}\: \: H_{1}:\mu > \mu _{0}\\ &\textrm{Daerah kritis berada di ujung kanan kurva }\end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Seorang petugas menyatakan bahwa pendapatan}\\ &\textrm{penjual mainan X tidak lebih dari}\: \: Rp20.000\\ &\textrm{perhari. Untuk menyangkal pernyataan tersebut}\\ &\textrm{pihak kantor melakukan penelitian terhadap}\\ &\textrm{tingkat pendapatan penjual mainan itu. Pihak}\\ &\textrm{kantor memilih 150 penjual secara acak, ternyata}\\ &\textrm{diperoleh data rata-rata pendapatan mereka}\\ &Rp21.000\: \: \textrm{dengan simpangan baku}\: \: Rp5.000\\ &\textrm{Dengan}\: \: \alpha =5\%\: \: \textrm{cukup beralasankah pernyataan}\\ &\textrm{petugas tersebut}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan pendapatan penjual berdistribusi normal}\\ &\textrm{dengan hasil tidak lebih}\: Rp20.000\: \: \textrm{perhari}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu \leq 20.000\\ &H_{1}:\mu > 20.000\\\ &\textbf{Daerah kritis}\\ &\textrm{Uji satu pihak, daerah kritis kanan dengan}\: \alpha =5\%\\ &z_{0,05}=\color{red}1,64\: \: \color{black}(\textrm{lihat tabel normal baku})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue} z< 1,64\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}z\geq 1,64\\ &\textbf{Nilai statistik uji}\\ &\bar{x}=21.000,\: \mu _{0}=20.000\: \textrm{jam},\: n=150,\\ &\sigma =5.000,\: \textrm{dengan rumus}\: \: \color{red}z\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{\sigma }\sqrt{n}\\ &\Leftrightarrow \color{red}z\color{black}=\displaystyle \frac{(21.000-20.000)}{5000}\sqrt{150}\\ &\qquad =\displaystyle \frac{1.000\times 12,247}{5.000}=\color{red}2,45\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\:  \color{red}2,45\color{black}\geq  1,64\: ,\: H_{0}\: \: \textrm{ditolak}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 5}\%\: \: \textrm{rata-rata pendapatan}\\ &\textrm{penjual lebih dari}\: \: Rp20.000\: \: \textrm{perhari}  \end{aligned} \end{array}$.

b) Uji Pihak Kiri

$\begin{aligned}&\textrm{Jika}\: \: H_{1}:\mu < \mu _{0}\\ &\textrm{Daerah kritis berada di ujung kiri kurva }\end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 2.&\textrm{Seorang petugas menyatakan bahwa pendapatan}\\ &\textrm{penjual mainan X tidak kurang dari}\: \: Rp21.000\\ &\textrm{perhari. Pihak kantor ingin menguji terhadap}\\ &\textrm{tingkat pendapatan penjual mainan itu. Pihak}\\ &\textrm{kantor memilih 150 penjual secara acak, ternyata}\\ &\textrm{diperoleh data rata-rata pendapatan mereka}\\ &Rp20.000\: \: \textrm{dengan simpangan baku}\: \: Rp5.000\\ &\textrm{Dengan}\: \: \alpha =5\%\: \: \textrm{cukup beralasankah pernyataan}\\ &\textrm{petugas tersebut}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan pendapatan penjual berdistribusi normal}\\ &\textrm{dengan hasil tidak kurang dari}\: Rp21.000\: \: \textrm{perhari}\\ &\textbf{Rumusan hipotesis}\: \: H_{0}\: \textrm{dan}\: H_{1}\\ &H_{0}:\mu \geq  21.000\\ &H_{1}:\mu < 21.000\\\ &\textbf{Daerah kritis}\\ &\textrm{Uji satu pihak, daerah kritis kiri dengan}\: \alpha =5\%\\ &z_{0,05}=-\color{red}1,64\: \: \color{black}(\textrm{lihat tabel normal baku})\\ &\bullet \: \: \textrm{Terima}\: \: H_{0},\: \textrm{jika}:\color{blue} z> -1,64\\ &\bullet \: \: \textrm{Tolak}\: \: H_{0},\: \textrm{jika}:\color{blue}z\leq - 1,64\\ &\textbf{Nilai statistik uji}\\ &\bar{x}=20.000,\: \mu _{0}=21.000\: \textrm{jam},\: n=150,\\ &\sigma =5.000,\: \textrm{dengan rumus}\: \: \color{red}z\color{black}=\displaystyle \frac{\bar{x}-\mu _{0}}{\sigma }\sqrt{n}\\ &\Leftrightarrow \color{red}z\color{black}=\displaystyle \frac{(20.000-21.000)}{5000}\sqrt{150}\\ &\qquad =\displaystyle \frac{1.000\times 12,247}{5.000}=\color{red}-2,45\\ &\textbf{Penentuan keputusan uji}\\ &\textrm{Karena}\: :\:  \color{red}-2,45\color{black}\leq -  1,64\: ,\: H_{0}\: \: \textrm{ditolak}\\ &\textbf{Kesimpulan}\\ &\textrm{Dengan taraf nyata 5}\%\: \: \textrm{rata-rata pendapatan}\\ &\textrm{penjual kurang dari}\: \: Rp21.000\: \: \textrm{perhari}  \end{aligned}  \end{array}$.

DAFTAR PUSTAKA

1. Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
2. Noormandiri, B.K. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
3. Sembiring, S., Zulkifli. M., Marsito, Rusdi. I. 2016. Matematika untuk Siswa SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.