Lanjutan Luas Segitiga 2

D. 3 Aturan Sinus

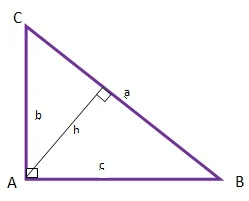
Perhatikan ilustasi berikut

$\Large\begin{array}{|c|}\hline \displaystyle \frac{a}{\sin A}= \frac{b}{\sin B}=\frac{c}{\sin C}=2R\\\hline \end{array}$.

$\begin{aligned}1.\quad a&=b.\displaystyle \frac{\sin \angle A}{\sin \angle B}=c.\displaystyle \frac{\sin \angle A}{\sin \angle C}=2R\sin \angle A\\ 2.\quad b&=c.\displaystyle \frac{\sin \angle B}{\sin \angle C}=a.\displaystyle \frac{\sin \angle B}{\sin \angle A}=2R\sin \angle B\\ 3.\quad c&=a.\displaystyle \frac{\sin \angle C}{\sin \angle A}=b.\displaystyle \frac{\sin \angle C}{\sin \angle B}=2R\sin \angle C \end{aligned}$.

Sehingga luas segitiga dapat dituliskan sebagai berikut:

$\begin{aligned} 1.\quad L\bigtriangleup ABC&=\displaystyle \frac{1}{2}ab\sin \angle C\\ &=\displaystyle \frac{1}{2}a\left ( a.\displaystyle \frac{\sin \angle B}{\sin \angle A} \right )\sin \angle C\\ &=\displaystyle \frac{1}{2}a^{2}\displaystyle \frac{\sin \angle B\sin \angle C}{\sin \angle A}\\ 2.\quad L\bigtriangleup ABC&=\displaystyle \frac{1}{2}bc\sin \angle A\\ &=\displaystyle \frac{1}{2}b\left ( b.\displaystyle \frac{\sin \angle C}{\sin \angle B} \right )\sin \angle A\\ &=\displaystyle \frac{1}{2}b^{2}\displaystyle \frac{\sin \angle B\sin \angle A}{\sin \angle B}\\ 3.\quad L\bigtriangleup ABC&=\displaystyle \frac{1}{2}ac\sin \angle B\\ &=\displaystyle \frac{1}{2}\left ( c.\displaystyle \frac{\sin \angle A}{\sin \angle C} \right )c\sin \angle B\\ &=\displaystyle \frac{1}{2}c^{2}\displaystyle \frac{\sin \angle A\sin \angle B}{\sin \angle C} \end{aligned}$.

D. 4 Luas segitiga sama sisi

$\begin{aligned}L_{\bigtriangleup }ABC&=\displaystyle \frac{1}{2}ab\sin \angle C,\quad a=b=c\\ &\qquad\quad\quad \textrm{dan}\: \: \angle A=\angle B\angle C=60^{\circ}\\ &=\displaystyle \frac{1}{2}a.a\sin 60^{\circ}\\ &=\displaystyle \frac{1}{2}a^{2}\left ( \displaystyle \frac{1}{2}\sqrt{3} \right )\\ &=\color{red}\displaystyle \frac{1}{4}a^{2}\sqrt{3} \end{aligned}$.

D. 5 Lingkaran Luar Segitiga

Perhatikan lagi lingkaran luar segitiga di atas, dari sana kita akan mendapatkan rumus luas segitiga yang dapat kita munculkan harga R nya, yaitu:

$\begin{aligned}1.\quad L\bigtriangleup ABC&=\displaystyle \frac{1}{2}ab\sin \angle C\\ &=\displaystyle \frac{1}{2}(2R\sin \angle A)(2R\sin \angle B)\sin \angle C\\ &=2R^{2}\sin \angle A\sin \angle B\sin \angle C\\ 2.\quad L\bigtriangleup ABC&=\displaystyle \frac{1}{2}ab\sin \angle C\\ &=\displaystyle \frac{1}{2}ab\left ( \displaystyle \frac{c}{2R} \right )\\ &=\color{red}\displaystyle \frac{abc}{4R} \end{aligned}$.

D. 6 Lingkaran dalam segitiga

Perhatikanlah gambar berikut

$\begin{aligned}\textrm{Diketahu}&\textrm{i}\\ L_{\bigtriangleup }AOB&=\displaystyle \frac{1}{2}(AB)(OD)=\color{red}\displaystyle \frac{1}{2}cr\\ L_{\bigtriangleup }AOC&=\displaystyle \frac{1}{2}(AC)(OF)=\color{red}\displaystyle \frac{1}{2}br\\ L_{\bigtriangleup }BOC&=\displaystyle \frac{1}{2}(BC)(OE)=\color{red}\displaystyle \frac{1}{2}ar\\ \textrm{Sehingga}&\\ L_{\bigtriangleup }ABC&=\left [ ABC \right ]\\ &=\color{red}\displaystyle \frac{1}{2}ar+\displaystyle \frac{1}{2}br+\displaystyle \frac{1}{2}cr\\ &=\displaystyle \frac{1}{2}r(a+b+c)\\ &=\displaystyle \frac{1}{2}r(2s)\\ &=rs \end{aligned}$.

D. 7 Lingkaran singgung segitiga

Sebagai ilustrasinya adalah gambar berikut

$\begin{aligned}&\textrm{Diketahui}\\ &DO=EO=FO=r_{a}\\ &\textrm{maka}\\ &1.\quad L_{\bigtriangleup}ABO=\displaystyle \frac{1}{2}(AB)(OD)=\displaystyle \frac{1}{2}cr_{a}\\ &2.\quad L_{\bigtriangleup}ACO=\displaystyle \frac{1}{2}(AC)(OE)=\displaystyle \frac{1}{2}br_{a}\\ &3.\quad L_{\bigtriangleup}BCO=\displaystyle \frac{1}{2}(BC)(OF)=\displaystyle \frac{1}{2}ar_{a} \end{aligned}$.

$\begin{aligned} \textrm{Sehingga}&\\ L_{\bigtriangleup }ABC&=\left [ ABC \right ]\\ &=\left [ ACO \right ]+\left [ ABO \right ]-\left [ BCO \right ]\\ &=\color{red}\displaystyle \frac{1}{2}br_{a}+\displaystyle \frac{1}{2}cr_{a}-\displaystyle \frac{1}{2}ar_{a}\\ &=\displaystyle \frac{1}{2}r_{a}(b+c-a)\\ &=\displaystyle \frac{1}{2}r_{a}(a+b+c-2a)\\ &=\displaystyle \frac{1}{2}r_{a}(2s-2a)\\ &=\color{red}r_{a}(s-a) \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diberikan sembarang}\: \: \bigtriangleup ABC\: .\: \textrm{Jika}\: \: r\\ & \textrm{merupakan jari-jari lingkaran singgung }\\ &\textrm{dalam pada}\: \: \bigtriangleup ABC\: \: \textrm{dan}\: \: r_{a},\: r_{b},\: r_{c}\\ &\textrm{adalah jari-jari singgung luar pad}\: \: \bigtriangleup ABC\\ &\textrm{tunjukkan bahwa}:\: \displaystyle \frac{1}{r_{a}}+\frac{1}{r_{b}}+\frac{1}{r_{c}}=\frac{1}{r}\\\\ &\textbf{Bukti}:\\ &\begin{aligned} \textrm{Diketahu}&\textrm{i}\\ L_{\bigtriangleup }ABC&=\color{red}r_{a}(s-a),\: \color{black}\Rightarrow r_{a}=\displaystyle \frac{\left [ ABC \right ]}{s-a}\\ L_{\bigtriangleup }ABC&=\color{red}r_{b}(s-b),\: \color{black}\Rightarrow r_{b}=\displaystyle \frac{\left [ ABC \right ]}{s-b}\\ L_{\bigtriangleup }ABC&=\color{red}r_{c}(s-c),\: \color{black}\Rightarrow r_{c}=\displaystyle \frac{\left [ ABC \right ]}{s-c}\\ \textrm{maka}\: \quad&\\ \displaystyle \frac{1}{r_{a}}+\frac{1}{r_{b}}&+\frac{1}{r_{c}}\\ &=\displaystyle \frac{1}{\displaystyle \frac{\left [ ABC \right ]}{s-a}}+\displaystyle \frac{1}{\displaystyle \frac{\left [ ABC \right ]}{s-b}}+\displaystyle \frac{1}{\displaystyle \frac{\left [ ABC \right ]}{s-c}}\\ &=\displaystyle \frac{s-a}{\left [ ABC \right ]}+\displaystyle \frac{s-b}{\left [ ABC \right ]}+\displaystyle \frac{s-c}{\left [ ABC \right ]}\\ &=\displaystyle \frac{s-a+s-b+s-c}{\left [ ABC \right ]}\\ &=\displaystyle \frac{3s-(a+b+c)}{\left [ ABC \right ]}\\ &=\displaystyle \frac{3s-2s}{\left [ ABC \right ]}\\ &=\displaystyle \frac{s}{\left [ ABC \right ]}\\ &=\displaystyle \frac{1}{\displaystyle \frac{\left [ ABC \right ]}{s}}\\ &=\color{blue}\displaystyle \frac{1}{r}\qquad \color{black}\blacksquare \end{aligned} \end{array}$.

Lanjutan Luas Segitiga 1

C. Luas Segitiga dengan Integral Tentu

Misalkan suatu garis linear di sekitar  sumbu-X yang tidak sejajar dan sumbu-X itu sendiri yang membatasi suatu daerah di antara keduanya serta dibatasi pula oleh 2 garis yang sejajar dengan sumbu Y yang keduanya tidak berimpit, maka hasil dari proses integral tentu ini akan menghasilkan luas segitiga.

Secara rumus integral tentu untuk model di atas adalah:

$\begin{aligned}&\textrm{Integral Tentu}\\ &=\displaystyle \int_{p}^{q}f(x)dx=\displaystyle \left [ F(x) \right ]_{p}^{q}\\ &=F(x)|_{p}^{q}=F(q)-F(p) \end{aligned}$.

$\begin{aligned}&\textrm{Diketahui}\\ &y=\color{red}m\color{black}x,\quad \textrm{dengan}\: \: m=\displaystyle \frac{b}{a} ,\\ &\textrm{sehingga}\\ &y=\displaystyle \frac{b}{a}x\: \: \textrm{atau}\: \: f(x)=\displaystyle \frac{b}{a}x\\ &\textrm{maka}\\ &L_{area}=\displaystyle \int_{a}^{b}f(x)\: dx\\ &\: \qquad =\displaystyle \int_{a}^{b}\displaystyle \frac{b}{a}x\: dx\\ &\: \qquad =\displaystyle \frac{b}{a}\displaystyle \int_{a}^{b}x\: dx\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}x^{2} \right )\begin{matrix} a\\ |\\ 0 \end{matrix}\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(a)^{2} \right )-\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(0)^{2} \right )\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(a)^{2} \right )-0\\ &\: \qquad =\displaystyle \frac{b\times a^{2}}{2a}\\ &\: \qquad =\displaystyle \frac{a\times b}{2}\\ &\: \qquad =\color{red}\displaystyle \frac{1}{2}\times ab \end{aligned}$.

D. Luas segitiga dengan Trigonometri

D. 1 Segitiga siku-siku

Perhatikan ilustrasi segitiga siku-siku berikut

$\begin{aligned}&1.\quad \sin \angle B=\displaystyle \frac{b}{a}\: \: \: \textrm{dan}\: \: \cos \angle C=\displaystyle \frac{b}{a}\\ &\qquad \textrm{sehingga}\: \: b=a\sin \angle B=a\cos \angle C\\ &2.\quad \sin \angle C=\displaystyle \frac{c}{a}\: \: \: \textrm{dan}\: \: \cos \angle B=\displaystyle \frac{c}{a}\\ &\qquad \textrm{sehingga}\: \: c=a\sin \angle C=a\cos \angle B\\ &3.\quad \tan \angle B=\displaystyle \frac{b}{c}\: \: \: \textrm{dan}\: \: \cot \angle C=\displaystyle \frac{b}{c}\\ &\qquad \textrm{sehingga}\: \: b=c\tan \angle B=c\cot \angle C\\ &4.\quad \tan \angle C=\displaystyle \frac{c}{b}\: \: \: \textrm{dan}\: \: \cot \angle B=\displaystyle \frac{c}{b}\\ &\qquad \textrm{sehingga}\: \: c=b\tan \angle C=b\cot \angle B\\ &5.\quad \sin \angle B=\displaystyle \frac{h}{c}\: \: \: \textrm{dan}\: \: \sin \angle C=\displaystyle \frac{h}{b}\\ &\qquad \textrm{sehingga}\: \: h=c\sin \angle B=b\sin \angle C\\ \end{aligned}$.

Dari fakta-fakta di atas dapat ditunjukkan beberapa rumus segitiga, yaitu:

$\begin{array}{|c|c|l|}\hline 1.&L_{\bigtriangleup }&\displaystyle \frac{1}{2}bc\\\hline &&\begin{aligned}&\displaystyle \frac{1}{2}\left ( a\sin \angle B \right )\left ( a\sin \angle C \right )\\ &=\displaystyle \frac{1}{2}a^{2}\sin \angle B\sin \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}\left ( a\cos \angle C \right )\left ( a\cos \angle B \right )\\ &=\displaystyle \frac{1}{2}a^{2}\cos \angle B\cos \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b)\left ( b\tan \angle C \right )\\ &=\displaystyle \frac{1}{2}b^{2}\tan \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(c\tan \angle B)(c)\\ &=\displaystyle \frac{1}{2}c^{2}\tan \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b)(b\cot \angle B)\\ &=\displaystyle \frac{1}{2}b^{2}\cot \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(c\cot \angle C)(c)\\ &=\displaystyle \frac{1}{2}c^{2}\cot \angle C \end{aligned}\\\hline 2.&L_{\bigtriangleup } &\displaystyle \frac{1}{2}ha\\\hline &&\begin{aligned}&\displaystyle \frac{1}{2}(c\sin \angle B)(a)\\ &=\displaystyle \frac{1}{2}ac\sin \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b\sin \angle C)(a)\\ &=\displaystyle \frac{1}{2}ab\sin \angle C \end{aligned}\\\hline \end{array}$.

D. 2 Segitiga tidak siku-siku

Perhatikan ilustrasi segitiga tidak siku-siku berikut

Jika dari tiap titik sudut ditarik garis tinggi sampai memotong sisi di depannya, misal titik A, maka garis tingginya sebagaimana gambar berikut:

$\begin{aligned}1.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{A}.a\\ &=\displaystyle \frac{1}{2}c\sin \angle B.(a)=\displaystyle \frac{1}{2}ac\sin \angle B\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{A}.a\\ &=\displaystyle \frac{1}{2}b\sin \angle C.(a)=\displaystyle \frac{1}{2}ab\sin \angle C\\ 2.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{B}.b\\ &=\displaystyle \frac{1}{2}c\sin \angle A.(b)=\displaystyle \frac{1}{2}bc\sin \angle A\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{B}.b\\ &=\displaystyle \frac{1}{2}a\sin \angle C.(b)=\displaystyle \frac{1}{2}ab\sin \angle C\\ 3.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{C}.c\\ &=\displaystyle \frac{1}{2}a\sin \angle B.(c)=\displaystyle \frac{1}{2}ac\sin \angle B\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{C}.c\\ &=\displaystyle \frac{1}{2}b\sin \angle A.(c)=\displaystyle \frac{1}{2}bc\sin \angle A \end{aligned}$.

Jika diringkas menjadi

$\begin{aligned}\textbf{Luas}\: \triangle \: ABC&=\frac{1}{2}bc.\sin \angle A\\ &=\frac{1}{2}ac.\sin \angle B\\ &=\frac{1}{2}ab.\sin \angle C \end{aligned}$.