Lanjutan Luas Segitiga 1

C. Luas Segitiga dengan Integral Tentu

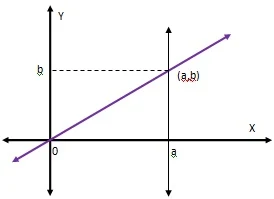
Misalkan suatu garis linear di sekitar  sumbu-X yang tidak sejajar dan sumbu-X itu sendiri yang membatasi suatu daerah di antara keduanya serta dibatasi pula oleh 2 garis yang sejajar dengan sumbu Y yang keduanya tidak berimpit, maka hasil dari proses integral tentu ini akan menghasilkan luas segitiga.

Secara rumus integral tentu untuk model di atas adalah:

$\begin{aligned}&\textrm{Integral Tentu}\\ &=\displaystyle \int_{p}^{q}f(x)dx=\displaystyle \left [ F(x) \right ]_{p}^{q}\\ &=F(x)|_{p}^{q}=F(q)-F(p) \end{aligned}$.

$\begin{aligned}&\textrm{Diketahui}\\ &y=\color{red}m\color{black}x,\quad \textrm{dengan}\: \: m=\displaystyle \frac{b}{a} ,\\ &\textrm{sehingga}\\ &y=\displaystyle \frac{b}{a}x\: \: \textrm{atau}\: \: f(x)=\displaystyle \frac{b}{a}x\\ &\textrm{maka}\\ &L_{area}=\displaystyle \int_{a}^{b}f(x)\: dx\\ &\: \qquad =\displaystyle \int_{a}^{b}\displaystyle \frac{b}{a}x\: dx\\ &\: \qquad =\displaystyle \frac{b}{a}\displaystyle \int_{a}^{b}x\: dx\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}x^{2} \right )\begin{matrix} a\\ |\\ 0 \end{matrix}\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(a)^{2} \right )-\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(0)^{2} \right )\\ &\: \qquad =\displaystyle \frac{b}{a}\left ( \displaystyle \frac{1}{2}(a)^{2} \right )-0\\ &\: \qquad =\displaystyle \frac{b\times a^{2}}{2a}\\ &\: \qquad =\displaystyle \frac{a\times b}{2}\\ &\: \qquad =\color{red}\displaystyle \frac{1}{2}\times ab \end{aligned}$.

D. Luas segitiga dengan Trigonometri

D. 1 Segitiga siku-siku

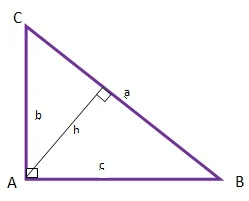
Perhatikan ilustrasi segitiga siku-siku berikut

$\begin{aligned}&1.\quad \sin \angle B=\displaystyle \frac{b}{a}\: \: \: \textrm{dan}\: \: \cos \angle C=\displaystyle \frac{b}{a}\\ &\qquad \textrm{sehingga}\: \: b=a\sin \angle B=a\cos \angle C\\ &2.\quad \sin \angle C=\displaystyle \frac{c}{a}\: \: \: \textrm{dan}\: \: \cos \angle B=\displaystyle \frac{c}{a}\\ &\qquad \textrm{sehingga}\: \: c=a\sin \angle C=a\cos \angle B\\ &3.\quad \tan \angle B=\displaystyle \frac{b}{c}\: \: \: \textrm{dan}\: \: \cot \angle C=\displaystyle \frac{b}{c}\\ &\qquad \textrm{sehingga}\: \: b=c\tan \angle B=c\cot \angle C\\ &4.\quad \tan \angle C=\displaystyle \frac{c}{b}\: \: \: \textrm{dan}\: \: \cot \angle B=\displaystyle \frac{c}{b}\\ &\qquad \textrm{sehingga}\: \: c=b\tan \angle C=b\cot \angle B\\ &5.\quad \sin \angle B=\displaystyle \frac{h}{c}\: \: \: \textrm{dan}\: \: \sin \angle C=\displaystyle \frac{h}{b}\\ &\qquad \textrm{sehingga}\: \: h=c\sin \angle B=b\sin \angle C\\ \end{aligned}$.

Dari fakta-fakta di atas dapat ditunjukkan beberapa rumus segitiga, yaitu:

$\begin{array}{|c|c|l|}\hline 1.&L_{\bigtriangleup }&\displaystyle \frac{1}{2}bc\\\hline &&\begin{aligned}&\displaystyle \frac{1}{2}\left ( a\sin \angle B \right )\left ( a\sin \angle C \right )\\ &=\displaystyle \frac{1}{2}a^{2}\sin \angle B\sin \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}\left ( a\cos \angle C \right )\left ( a\cos \angle B \right )\\ &=\displaystyle \frac{1}{2}a^{2}\cos \angle B\cos \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b)\left ( b\tan \angle C \right )\\ &=\displaystyle \frac{1}{2}b^{2}\tan \angle C \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(c\tan \angle B)(c)\\ &=\displaystyle \frac{1}{2}c^{2}\tan \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b)(b\cot \angle B)\\ &=\displaystyle \frac{1}{2}b^{2}\cot \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(c\cot \angle C)(c)\\ &=\displaystyle \frac{1}{2}c^{2}\cot \angle C \end{aligned}\\\hline 2.&L_{\bigtriangleup } &\displaystyle \frac{1}{2}ha\\\hline &&\begin{aligned}&\displaystyle \frac{1}{2}(c\sin \angle B)(a)\\ &=\displaystyle \frac{1}{2}ac\sin \angle B \end{aligned}\\ &&\begin{aligned}&\displaystyle \frac{1}{2}(b\sin \angle C)(a)\\ &=\displaystyle \frac{1}{2}ab\sin \angle C \end{aligned}\\\hline \end{array}$.

D. 2 Segitiga tidak siku-siku

Perhatikan ilustrasi segitiga tidak siku-siku berikut

Jika dari tiap titik sudut ditarik garis tinggi sampai memotong sisi di depannya, misal titik A, maka garis tingginya sebagaimana gambar berikut:

$\begin{aligned}1.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{A}.a\\ &=\displaystyle \frac{1}{2}c\sin \angle B.(a)=\displaystyle \frac{1}{2}ac\sin \angle B\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{A}.a\\ &=\displaystyle \frac{1}{2}b\sin \angle C.(a)=\displaystyle \frac{1}{2}ab\sin \angle C\\ 2.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{B}.b\\ &=\displaystyle \frac{1}{2}c\sin \angle A.(b)=\displaystyle \frac{1}{2}bc\sin \angle A\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{B}.b\\ &=\displaystyle \frac{1}{2}a\sin \angle C.(b)=\displaystyle \frac{1}{2}ab\sin \angle C\\ 3.\quad L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{C}.c\\ &=\displaystyle \frac{1}{2}a\sin \angle B.(c)=\displaystyle \frac{1}{2}ac\sin \angle B\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}h_{C}.c\\ &=\displaystyle \frac{1}{2}b\sin \angle A.(c)=\displaystyle \frac{1}{2}bc\sin \angle A \end{aligned}$.

Jika diringkas menjadi

$\begin{aligned}\textbf{Luas}\: \triangle \: ABC&=\frac{1}{2}bc.\sin \angle A\\ &=\frac{1}{2}ac.\sin \angle B\\ &=\frac{1}{2}ab.\sin \angle C \end{aligned}$.