Sistem Pertidaksamaan Dua Variabel

Sebelumnya telah diketahui sistem persamaan linear dua variabel, silahkan lihat di sini.

1. Sistem Persamaan Dua Variabel Linear dan Kuadrat

Sebelumnya akan kita singgung dulu fungsi linear dan kuadrat sebagai mana tabel berikut:

Fungsi Linear

$\begin{aligned}&\\ \textrm{Fungsi}&\: \textrm{Linear adalah}:\\ &\textrm{fungsi di aman fungsi yang }\\ &\textrm{hanya memiliki satu variabel}\\ &\textrm{atau peubah dan berpangkat satu}.\\\\ \textrm{Misal},&\: \: \color{red}f:x \mapsto ax+b\\ & \end{aligned}$.

Dalam menentukan persamaan linear/garis lurus adalah:

$\begin{array}{|c|c|}\hline \textrm{Melalui titik}\: \: \left ( x_{1},y_{1} \right )&\textrm{Melalui titik}\: \: \left ( x_{1},y_{1} \right )\\ \textrm{dan bergradien}\: \: m&\textrm{dan}\: \: \left ( x_{2},y_{2} \right )\\\hline y=m\left ( x-x_{1} \right )+y_{1}&\displaystyle \frac{y-y_{1}}{y_{2}-y_{1}}=\displaystyle \frac{x-x_{1}}{x_{2}-x_{1}}\\ &\begin{aligned}\textrm{dengan}:&\\ m&=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \end{aligned}\\\hline \textrm{Sejajar dengan} &\textrm{Tegak lurus dengan}\\ \textrm{garis bergradien}\: \: m_{1}&\textrm{garis bergradien}\: \: m_{1}\\\hline \textrm{Syarat dua garis}&\textrm{Syarat dua garis}\\\hline \textrm{Sejajar}\: \: m_{1}=m_{2}&\textrm{Tegak lurus}\: \: m_{1}\times m_{2}=-1\\\hline y=m_{2}\left ( x-x_{1} \right )+y_{1}&y=-\displaystyle \frac{1}{m_{2}}\left ( x-x_{1} \right )+y_{1}\\\hline \end{array}$

Fungsi Kuadrat

$\begin{array}{|l|l|}\hline \textrm{Pengertian}&\begin{aligned}&\textrm{Suatu fungsi yang berbentuk}\\ &f(x)=ax^{2}+bx+c\\ & a,\: b,\: c,\: \in \mathbb{R},\: a\neq 0 \end{aligned}\\\hline \textrm{Grafik Fungsi}&\textrm{Keterangan}\\\hline \textrm{Titik potong sumbu x}&\textrm{Jika ada}\\\hline &\begin{aligned}&\textrm{untuk titik potong}\\ &\textrm{terhadap sumbu x }\\ &\textrm{Jika y = 0 maka }\\ &ax^{2}+bx+c=0\\ &\textrm{Selanjutnya tinggal}\\ &\textrm{menentukan nilai D}\\ &D=b^{2}-4ac\: \: \textrm{adalah}\\ &\: \: \: \: \: \: \: \: \: \textrm{nilai diskriminan}.\\ &\textrm{Jika} \: D>0\\ &\textrm{maka grafik}\\ &\textrm{memotong sumbu x}\\ &\textrm{di dua tempat berbeda}\\ &\textrm{yaitu di} \: (x_{1},0)\: \textrm{dan}\: (x_{2},0).\\ &\textrm{dan jika D = 0}\\ &\textrm{maka grafik}\\ &\textrm{ hanya menyinggung}\\ &\textrm{sumbu x di satu titik}\\ &\textrm{yaitu di }\: (x_{1},0)\\ &\textrm{dan jika}\: D<0 \\ &\textrm{maka grafik}\\ &\textrm{tidak memotong}\\ &\textrm{atau menyinggung sumbu x} \end{aligned}\\\hline \textrm{Titik potong sumbu y}&\begin{aligned}&\textrm{titik potong terhadap}\\ &\textrm{sumbu y, jika x = 0}\\ &y=f(x)=ax^{2}+bx+c\\ &y=f(0)=a(0)^{2}+b(0)+c\\ &y=c \end{aligned}\\\hline \textrm{Sumbu Simetri (SS)}&x=\displaystyle \frac{-b}{2a}\\\hline \textrm{Titik Puncak}&\left ( \displaystyle \frac{-b}{2a},\displaystyle \frac{D}{-4a} \right )\\\hline \textrm{Posisi grafik}&\textrm{Jika}\: a>0\: \textrm{maka}\\ &\textrm{grafik terbuka ke atas}\\ &\textrm{Dan jika nilai}\: a<0\: \textrm{maka}\\ &\textrm{grafik terbuka ke bawah}\\\hline \end{array}$.

Selanjutnya cara membuat grafik fungsi kudratnya adalah sebagai berikut:

$\begin{array}{|c|c|}\hline \textrm{Jika memotong sumbu}-\textrm{X}&\textrm{Jika menyinggung sumbu}-\textrm{X}\\ \textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan}\: \left ( x_{2},0 \right )&\textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan melalui}\\ \textrm{dan melalui sebuah titik lain}&\textrm{sebuah titik lain} \\\hline &\\ y=f(x)=a\left ( x-x_{1} \right )\left ( x-x_{2} \right )&y=f(x)=a\left ( x-x_{1} \right )^{2}\\ &\\\hline \textrm{Jika grafik fungsi itu melalui}&\textrm{Jika grafik fungsi itu melalui}\\\hline \textrm{Titik puncak}\: \: P\left ( x_{p},y_{p} \right )\: \textrm{dan}&\textrm{tiga buah titik yaitu}\: \left ( x_{1},y_{1} \right )\\ \textrm{sebuah titik lain}&\left ( x_{2},y_{2} \right )\: \: \textrm{dan}\: \: \left ( x_{3},y_{3} \right )\\\hline &\\ y=f(x)=a\left ( x-x_{p} \right )^{2}+y_{p}&y=f(x)=ax^{2}+bx+c\\ &\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: f\: \: \textrm{adalah fungsi linear dengan}\\ & f(2)-f(-2)=8,\\ & \textrm{maka nilai dari}\: \: f(4)-f(-2)\: \: \textrm{adalah}\: ....\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &f(x)=ax+b\\ &f(2)-f(-2)\\ &=\left (a(2)+b \right )-\left ( a(-2)+b \right )=8\\ &8=2a+2a\\ &8=4a\\ &2=a\\ &f(x)=2x+b,\quad \textrm{dengan}\: \: b\: \: \textrm{konstan}\\ &\textrm{Sehingga nilai}\quad\\ &f(4)-f(-2)=\left (2(4)+b \right )-\left (2(-2)+b \right )\\ &=8+b+4-b\\ &=\color{red}12 \end{aligned} \end{array}$.

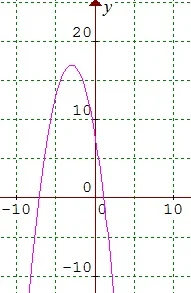
$\begin{array}{ll}\\ 2.&\textrm{Ubahlah}\: \: 8-6x-x^{2}\: \: \textrm{ke dalam bentuk}\\ & a-(x+b)^{2},\: \textrm{selanjutnya tentukan}\\ & \textrm{daerah hasil dari}\: \: f(x)=8-6x-x^{2}\\ & \textrm{untuk}\: \: x\: \: \textrm{bilangan real}\\ &\qquad(\textit{NTU Entrance Examination AO-level})\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|l|}\hline 1.&\color{blue}\textrm{Diketahui}\\\hline &\begin{aligned}\textrm{Misal}\quad\qquad&\\ 8-6x-x^{2}&=f(x)\\ f(x)&=-x^{2}-6x+8\\ &=-\left ( x^{2}+6x-8 \right )\\ &=-\left ( x^{2}+6x+9-17 \right )\\ &=-\left ( (x+3)^{2}-17 \right )\\ &=-(x+3)^{2}+17\\ & \end{aligned}\\\hline 2.&\color{blue}\textrm{Mencari koordinat}\: \: \left ( x_{SS},y_{SS} \right )\\\hline &\begin{aligned}f(x)&=-x^{2}-6x+8\left\{\begin{matrix} a=-1\\ b=-6\\ c=\: \: 8\: \: \end{matrix}\right.\\ \textrm{Maka}&\\ x_{SS}&=\frac{-b}{2a}=\displaystyle \frac{-(-6)}{2(-1)}\\ &=-3\\ y_{SS}&=f(-3)=-\left ( -3+3 \right )^{2}+17=17\\ \therefore &\left ( x_{SS},y_{SS} \right )=(-3,17) \end{aligned}\\\hline 3.&\color{blue}\textrm{Nilai fungsi}\\\hline &\begin{aligned}\textrm{Karena}&\: \: a=-1<0\\ \textrm{maka f}&\textrm{ungsi menghadap}\\ \textbf{ke ba}&\textbf{wah},\: \: \textrm{sehingga}\\ \textrm{daerah}&\: \: \textrm{hasilnya}\: \: \left (R_{f} \right )\\ \textrm{adalah}&:\\ &\left \{ -\infty <y\leq 17 \right \}\\ &\\ &\textrm{Berikut ilustrasinya} \end{aligned}\\\hline \end{array} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Jika}\: \: \alpha \: \: \textrm{dan}\: \: \beta \: \: \textrm{adalah akar-akar dari }\\ &\textrm{persamaan kuadrat}\: \: x^{2}+mx+m=0,\\ &\textrm{maka nilai}\: \: m\: \: \textrm{yang menyebabkan }\\ &\textrm{jumlah kuadrat akar-akar mencapai}\\ &\textrm{minimum adalah}\: ....\\ &\qquad \: \textbf{(UM UNDIP 2014 Mat Das)}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\: \: x^{2}+mx+m=0\\ & \textbf{persamaan kuadrat}\: \textrm{dalam}\: \: x,\\ & \textrm{maka}\\ &x^{2}+mx+m=x^{2}-(\alpha +\beta )x+(\alpha \beta )=0\\ &\begin{cases} \alpha +\beta &=-m \\ & \\ \alpha \beta &=m \end{cases}\\ &\textrm{Selanjutnya}\\ &\alpha ^{2}+\beta ^{2}=\left ( \alpha +\beta \right )^{2}-2\alpha \beta\\ &=(-m)^{2}-2m\: \: \textrm{dan dapat kita tuliskan sebagai}\\ &f(m)=m^{2}-2m\begin{cases} a &=1 \\ b &=-2 \\ c &=0 \end{cases} \\ &\textrm{fungsi kuadrat dalam}\: \: m,\\ &\textrm{sehingga kita perlu mencari titik}\: \: \left ( m_{SS},f\left ( m_{SS} \right ) \right ),\\ & \textrm{tetapi yang kita perlukan}\\ &\textrm{cuma}\: \: m-\textrm{nya saja, yaitu}:\: \: m=m_{SS},\\ &\textrm{dengan}\quad m_{SS}=\displaystyle \frac{-b}{2a}=\frac{-(-2)}{2.1}=1 \end{aligned} \end{array}$.