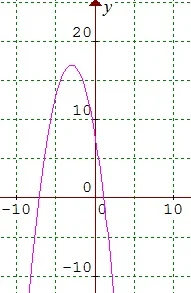
3. Sistem Pertidaksamaan Dua Variabel Kuadrat dan Kuadrat (SPDVKK)
Bentuk Persamaan (SPDVKK)
$\begin{aligned}&\textrm{Bentuk Umum}:\\ &\quad\begin{cases} ax^{2}+by^{2}+cxy+dx+ey+f=0 \\ px^{2}+qy^{2}+rxy+sx+ty+u=0 \end{cases} \end{aligned}$.
Perhatikan tabel berikut
$\begin{array}{|c|l|}\hline 1.&\textrm{Penyelesaian}\\ &y=y\\\hline 2.&\textrm{Proses}:\\ &\begin{aligned}&ax^{2}+bx+c=px^{2}+qx+r\\ &\textrm{dengan}\: \textrm{syarat}\\ &a-p\neq 0\\ &\textrm{diubah kebentuk umum}\\ &Ax^{2}+Bx+C=0\\ &\textrm{dengan}\\ &D=B^{2}-4AC \end{aligned}\\\hline 3.&\textrm{Sebagai Penjelasan}\\ &\begin{aligned} D&> 0\\ &\textrm{SPDVKK mempunyai }\\ &\textrm{2 penyelesaian berbeda}\\ D&=0\\ &\textrm{SPDVKK mempunyai }\\ &\textrm{1 penyelesaian saja}\\ D&< 0\\ &\textrm{SPDVKK tidak }\\ &\textrm{mempunyai penyelesaian} \end{aligned}\\\hline \end{array}$.
Bentuk Pertidaksamaan (SPtDVKK)
$\begin{aligned}&\textrm{Bentuk Umum}:\\ &y\geq ax^{2}+bx+c\\ &y\leq px^{2}+qx+r\\\\ &\underline{\textrm{Catatan}}:\\ &\textrm{Tanda Ketaksamaan bisa diganti}\\ &\textrm{dengan tanda ketaksamaan yang}\\ &\textrm{lainnya} \end{aligned}$
Bentuk Pertidaksamaan dari SPtDVKK adalah wilayah atau daerah dengan menentukan penyelesaian seperti persamaan langkah awalnya kemudian dibuatkan wilayah yang menunjukkan pertidaksamaannya. Wilayah SPtDVKK ini adalah irisan antara wilayah penyelesaian dari pertidaksamaan kuadrat yang pertama dengan wilayah penyelesaian pertidaksamaan kuadrat yang kedua.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Carilah ada/tidaknya penyelesaian }\\ &\textrm{dari SPDVKK berikut ini}.\\\\ &\begin{cases} y=-x^{2} \\ y=x^{2}+2x+1 \end{cases}\\\\ &\textrm{dan sketsalah tafsiran geometrinya}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &\begin{cases} y=-x^{2}\\ y=x^{2}+2x+1 \end{cases}\\ &\textrm{substitusikan}\: \: \: y=-x^{2}\quad \textrm{ke}\quad y=x^{2}+2x+1\\ &\textrm{sehingga diperoleh}\\ &-x^{2}=x^{2}+2x+1\\ &2x^{2}+2x+1=0\\ &\begin{cases} a=2 \\ b=-2 \\ c=1 \end{cases}\\ &\textrm{Karena, nilai}\: \: D=b^{2}-4ac\\ &=(-2)^{2}-4(2)(1)=4-8=-4< 0\\ &\textrm{maka diperoleh keterangan }\\ &\textrm{bahwa kedua parabola tersebut}\\ &\textbf{tidak berpotongan dan tidak bersinggungan} \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 2.&\textrm{Tentukan himpunan penyelesaian }\\ &\textrm{dari SPtDVLK berikut ini}\\ &\begin{cases} y\leq 4-x^{2} \\ y\leq x^{2}-2x-3 \end{cases}\\\\ &\textrm{Jika ada, sketsalah tafsiran geometrinya}\\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ \textbf{a}.&\textrm{Pembuat nol fungsi}\: ,\: \begin{cases} y & =4-x^{2} \\ y & =x^{2}-2x-3 \end{cases},\\ &\textrm{yaitu}:\\ &\textbf{Untuk}:\: \: y=f(x)=4-x^{2}\\ &4-x^{2}=0 \Rightarrow x^{2}=4\Rightarrow x=\pm 2\\ &\textrm{Jadi titik potongnya}:(-2,0)\: \: \textrm{dan}\: \: (2,0)\\ &\textrm{Titik puncak grafik fungsinya}\: \left ( x_{ss},y \right ),\\ &\textrm{yaitu}:\\ &x_{ss}=-\displaystyle \frac{b}{a}\: \: \textrm{atau}\: \: x_{ss}=\displaystyle \frac{x_{1}+x_{2}}{2}\\ &\Rightarrow x_{ss}=\displaystyle \frac{2+(-2)}{2}=\frac{0}{2}=\color{red}0\color{black},\: \: \textrm{maka}\\ &y=f(\color{red}0\color{black})=4-0^{2}=4\\ &\textrm{Jadi, titik puncaknya}:\: (0,4)\\ &\textbf{Dan untuk}:\: \: y=f(x)=x^{2}-2x-3\\ &x^{2}-2x-3=0\Rightarrow (x+1)(x-3)=0\\ &x=-1\: \: \textrm{atau}\: \: x=3\\ &\textrm{Jadi titik potongnya}:(-1,0)\: \: \textrm{dan}\: \: (3,0)\\ &\textrm{Titik puncak grafik fungsinya}\: \left ( x_{ss},y \right ),\\ &\textrm{yaitu}:\\ &x_{ss}=-\displaystyle \frac{b}{a}\: \: \textrm{atau}\: \: x_{ss}=\displaystyle \frac{x_{1}+x_{2}}{2}\\ &\Rightarrow x_{ss}=\displaystyle \frac{(-1)+3}{2}=\frac{2}{2}=\color{red}1\color{black},\: \: \textrm{maka}\\ &y=f(\color{red}1\color{black})=1^{2}-2(1)-3=-4\\ &\textrm{Jadi, titik puncaknya}:\: (0,-4)\\ \textbf{b}.&\textrm{Melakukan uji titik untuk menentukan}\\ &\textrm{wilayah pertidaksamaan, yaitu}:\\ &\textrm{Ambil titik bebas saja, misal kita pilih lagi}\\ &\textrm{titik}\: \: (0,0),\: \textrm{maka}\\ &\begin{aligned}(0,0)&\Rightarrow y\leq 4-x^{2}\\ &0\leq 4-0^{2}\Rightarrow 0\leq 4\: \: \textbf{benar}\\ (0,0)&\Rightarrow y\leq x^{2}-2x-3\: \\ &0\leq 0^{2}-2(0)-3\Rightarrow 0\leq -3\: \: \textbf{salah} \end{aligned}\\ &\textrm{ini berarti wilayah yang di dalamnya}\\ &\textrm{terdapat titik uji}\: \: (0,0)\: \: \textrm{bukan}\\ &\textrm{wilayah penyelesaian kedua pertidaksamaan}\\ &\textrm{tersebut}\\ \textbf{c}.&\textrm{Menggambar wilayah pertidaksamaan}\\ &\textrm{berikut ilustrasi gambarnya}\end{array} \end{array}$.
- Kanginan, M., Akhmad, G., Nurdiansyah, H. 2014. Matematika untuk SMA/MA Kelas X Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
- Yuana, R.A., Indriyastuti. 2017. Matematika untuk Kelas X SMA dan MA Kelompok Mata Pelajaran Wajib. Solo: TIGA SERANGKAI PUSTAKA MANDIRI.