Latihan Soal 3 Persiapan PAS Gasal Matematika Wajib Kelas XII

  

Jika jarak titik A ke C adalah 8 cm, 

maka jarak titik A ke D adalah ... cm

Jawab : b

Pembahasan diserahkan kepada pembaca yang budiman

Jika jarak K ke Q adalah 9 cm,

maka jarak titik K ke L adalah ... cm

Jawab : b

Pembahasan juga diserahkan kepada pembaca yang budiman

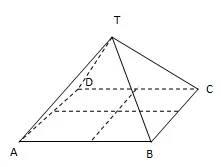
Jika panjang rusuk tegaknya adalah 13 cm, 

serta AB = 8 cm, dan BC = 6 cm, 

maka jarak T ke bidang ABCD (Titik tengah bidang ABCD)

Jawab : e

Pembahasan juga diserahkan kepada pembaca yang budiman

Jika panjang AB = 4 BC = 2 CG = 8 cm,

maka panjang AG adalah ... . cm

Jawab : a

$\begin{aligned}&\textrm{Misalkan}\\ &\textrm{Panjang diagonal sisi}\: \: =s\sqrt{2}=4\: \textrm{cm}\\ &\color{blue}\textbf{Alternatif 1}\\ &s\sqrt{2}=4\\ &\Leftrightarrow s=\displaystyle \frac{4}{\sqrt{2}}\\ &\Leftrightarrow s=\displaystyle \frac{4}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\displaystyle \frac{4}{\sqrt{4}}\sqrt{2}=\displaystyle \frac{4}{2}\sqrt{2}=2\sqrt{2}\\ &\textrm{Jadi, panjang sisinya}\: \: \color{red}2\sqrt{2}\\ &\color{blue}\textbf{Alternatif 2}\\ &\textrm{dikuadratkan kedua ruasnya, yaitu}:\\ &(s\sqrt{2})^{2}=(4)^{2}\Leftrightarrow s^{2}.2=18\\ &\Leftrightarrow s^{2}=\displaystyle \frac{16}{2}=8\\ &\Leftrightarrow s=\sqrt{8}=\sqrt{4.2}=\sqrt{4}.\sqrt{2}=2\sqrt{2}\\ &\textrm{Jadi, panjang sisinya}\: \: \color{red}2\sqrt{2} \end{aligned}$.

$\begin{array}{ll}\\ 26.&\textrm{Perhatikan gambar berikut} \end{array}$.

$\: \qquad \begin{aligned}&\textrm{Pernyataan yang tepat adalah}\: ...\\ &\begin{array}{ll} \textrm{a}.&\textrm{Titik sudut}\: \: H\: \: \textrm{pada rusuk}\: \: AB\\ \textrm{b}.&\textrm{Titik sudut}\: \: C\: \: \textrm{pada rusuk}\: \: BD\\ \textrm{c}.&\textrm{Titik sudut}\: \: A\: \: \textrm{pada rusuk}\: \: DC\\ \textrm{d}.&\textrm{Titik sudut}\: \: D\: \: \textrm{pada rusuk}\: \: BC\\ \textrm{e}.&\color{red}\textrm{Titik sudut}\: \: G\: \: \textrm{pada rusuk}\: \: GF\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\textrm{Cukup jelas bahwa Titik}\: \: G\: \: \textrm{pada ruas}\\ &\textrm{garis}\: \: GF \end{aligned}$.

$\begin{array}{ll}\\ 27.&\textrm{Diketahui kubus dengan rusuk 10}\: \: cm.\\ &\textrm{Titik}\: \: P\: \: \textrm{dan}\: \: Q\: \: \textrm{berturut-turut adalah}\\ &\textrm{titik tengah}\: \: AB\: \: \textrm{dan}\: \: DC.\: \textrm{Titik}\: \: O\\ &\textrm{merupakan perpotongan diagonal bidang}\\ &\textrm{alas}\: \: ABCD.\: \textrm{Pernyataan yang tepat}\\ &\textrm{adalah}\: ....\\ &\begin{array}{ll} \textrm{a}.&\textrm{Titik}\: \: P\: \: \textrm{terletak di luar garis}\: \: AB\\ \textrm{b}.&\textrm{Titik}\: \: P\: \: \textrm{terletak pada}\: \: DC\\ \textrm{c}.&\textrm{Titik}\: \: Q\: \: \textrm{terletak di luar garis}\: \: DC\\ \textrm{d}.&\color{red}\textrm{Titik}\: \: P\: \: \textrm{terletak pada garis}\: \: AB\\ \textrm{e}.&\color{red}\textrm{Titik}\: \: P\: \: \textrm{terletak pada garis}\: \: PQ\\ \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{d,e}\\ &\textrm{ada 2 jawaban yang tepat}\\ &\textrm{perhatikan ilustrasi berikut ini}\\ &\textrm{untuk lebih memahami jawaban di atas} \end{array}$.

$\begin{array}{ll}\\ 28.&\textrm{Pada kubus}\: \: ABCD.EFGH,\: \: ABCD\\ &\textrm{merupakan wakil bidang}\: \: \alpha \: \: \textrm{dan}\: \: BCGF\\ &\textrm{merupakan wakil dari bidang}\: \: \beta .\\ &\textrm{Pernyataan yang kurang tepat adalah}\: ....\\ &\begin{array}{ll} \textrm{a}.&\textrm{Titik}\: \: A\: \: \textrm{terletak pada bidang}\: \: \alpha \: \: \textrm{saja}\\ \textrm{b}.&\textrm{Titik}\: \: D\: \: \textrm{terletak pada bidang}\: \: \alpha \: \: \textrm{saja}\\ \textrm{c}.&\textrm{Titik}\: \: F\: \: \textrm{terletak pada bidang}\: \: \beta \: \: \textrm{saja}\\ \textrm{d}.&\color{red}\textrm{Titik}\: \: B\: \: \textrm{terletak pada bidang}\: \: \alpha \: \: \textrm{saja}\\ \textrm{e}.&\textrm{Titik}\: \: G\: \: \textrm{terletak pada bidang}\: \: \beta \: \: \textrm{saja}\\ \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ &\textrm{Titik}\: \: B\: \: \textrm{terletak pada bidang}\: \: \alpha \: \: \textrm{dan}\: \: \beta \\ &\textrm{sekaligus, perhatikan ilustrasi berikut ini}\\ &\textrm{untuk lebih memahami jawaban di atas} \end{array}$.

$\begin{array}{ll} 29.&\textrm{Diketahui panjang rusuk kubus}\: ABCD.EFGH\\ &\textrm{adalah}\: \: 6\: \: cm\: .\: \textrm{Jarak titik}\: \: E\: \: \textrm{ke bidang}\: \: BDG\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad \sqrt{3}\: \: cm\\ &\textrm{b}.\quad 2\sqrt{3}\: \: cm\\ &\textrm{c}.\quad 3\sqrt{3}\: \: cm\\ &\textrm{d}.\quad \color{red}4\sqrt{3}\: \: cm\\ &\textrm{e}.\quad 6\sqrt{3}\: \: cm\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\textrm{Perhatikanlah ilustrasi berikut ini} \end{array}$.

$.\qquad\begin{aligned}\textrm{Jelas}&\: \textrm{bahwa}\\ &\begin{cases} AB & =BC=CG=QQ'=6\: \: cm\: \: (\color{red}\textrm{dari soal}) \\ AC &=EG =6\sqrt{2}\: \: cm\: \: (\textrm{diagonal sisi kubus}) \\ EQ & =QG= \displaystyle \frac{1}{2}(\textbf{sisi})\sqrt{6}=3\sqrt{6}\: \: cm \end{cases}\\ \textrm{Perh}&\textrm{atikan}\: \: \bigtriangleup EQG\\ &\begin{aligned}&\textrm{Dengan perbandingan luas}\: \: \bigtriangleup EQG=\bigtriangleup EQG\\ &\displaystyle \frac{1}{2}\times QG\times EE'=\displaystyle \frac{1}{2}\times QQ'\times EG\\ &\displaystyle \frac{1}{2}\times \left ( 3\sqrt{6} \right )\times EE'=\displaystyle \frac{1}{2}\times 6\times 6\sqrt{2}\\ &\quad\quad\quad EE'= \displaystyle \frac{\displaystyle \frac{1}{2}\times \left ( 6\sqrt{2} \right )\times 6}{\displaystyle \frac{1}{2}\times \left ( 3\sqrt{6} \right )}\\ &\: \: \: \quad\quad\qquad =\color{blue}4\sqrt{3}\: \: \color{black}cm \end{aligned} \end{aligned}$.

$\begin{array}{ll} 30.&\textrm{Diketahui panjang rusuk kubus}\: ABCD.EFGH\\ &\textrm{adalah}\: \: 8\: \: cm\: .\: \textrm{Jarak titik}\: \: C\: \: \textrm{ke bidang}\: \: BDG\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad 4\sqrt{3}\: \: cm\\ &\textrm{b}.\quad 6\sqrt{3}\: \: cm\\ &\textrm{c}.\quad \color{red}\displaystyle \frac{8}{3}\sqrt{3}\: \: cm\\ &\textrm{d}.\quad 8\sqrt{3}\: \: cm\\ &\textrm{e}.\quad \displaystyle \frac{10}{3}\sqrt{3}\: \: cm\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\textrm{Perhatikanlah ilustrasi} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Jika gambarnya dipartisi lagi di bagian}\\ & \textrm{segitiga} \: \: GCG'\: \: \textrm{maka akan tampak}\\ & \textrm{seperti ilustrasi berikut} \end{aligned}$.

$.\qquad\begin{aligned}\textrm{Jelas}&\: \textrm{bahwa}\\ &\begin{cases} GC & =8\: \: cm\: \: (\color{red}\textrm{dari soal}) \\ BD &=AC =8\sqrt{2}\: \: cm\: \: (\textrm{diagonal sisi kubus}) \\ CG' & = \displaystyle \frac{1}{2}AC=4\sqrt{2}\: \: cm \end{cases}\\ \textrm{maka}&\: \textrm{dengan rumus Pythagoras dapat}\\ \textrm{panja}&\textrm{ng}\: \: GG',\: \textrm{yaitu}:\\ \left ( GG' \right )&^{2}=\left ( G'C \right )^{2}+CG^{2}\\ GG'&=\sqrt{\left ( G'C \right )^{2}+CG^{2}}=\sqrt{\left ( 4\sqrt{2} \right )^{2}+8^{2}}\\ &=\sqrt{32+64}=\sqrt{96}=\sqrt{16.6}=4\sqrt{6}\: \: cm\\ \textrm{Perha}&\textrm{tikan}\: \: \bigtriangleup GCG'\\ &\begin{aligned}&\textrm{Dengan perbandingan luas}\: \: \bigtriangleup GCG'=\bigtriangleup GCG'\\ &\displaystyle \frac{1}{2}\times CC'\times GG'=\displaystyle \frac{1}{2}\times CG'\times CG\\ &\displaystyle \frac{1}{2}\times CC'\times \left ( 4\sqrt{6} \right )=\displaystyle \frac{1}{2}\times \left ( 4\sqrt{2} \right )\times 8\\ &\quad\quad\quad CC'= \displaystyle \frac{\displaystyle \frac{1}{2}\times \left ( 4\sqrt{2} \right )\times 8}{\displaystyle \frac{1}{2}\times \left ( 4\sqrt{6} \right )}\\ &\: \: \: \quad\quad\qquad =\displaystyle \frac{8}{\sqrt{3}}\\ &\: \: \: \quad\quad\qquad =\displaystyle \frac{8}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}\\ &\: \: \: \quad\quad\qquad =\color{blue}\displaystyle \frac{8}{3}\sqrt{3}\: \: \color{black}cm \end{aligned} \end{aligned}$.