Selingan-Luas Segitiga

A. Heron's Formula

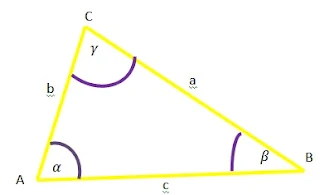
Bukti Luas Segitiga dengan sisi a, b, dan c

$\begin{aligned}& \textrm{Bagaimana membuktikan luas suatu}\\ &\textrm{segitiga jika diketahui sisinya}\: a,b\: \textrm{dan}\: c\\ &\textrm{berupa rumus}\\ &L_{\bigtriangleup }=\left [ ABC \right ]=\sqrt{s(s-a)(s-b)(s-c)}\\ & \textrm{dengan}\\ &\qquad s=\displaystyle \frac{1}{2}(a+b+c) \end{aligned}$.

Berikut akan dipaparkan buktinya

$\begin{aligned}\displaystyle \textrm{L}{\bigtriangleup }\textrm{ABC}&=\frac{1}{2}bc\sin\angle A\\ &=\displaystyle \frac{1}{2}bc\sqrt{\sin ^{2}\angle A}\\ &=\displaystyle \frac{1}{2}\sqrt{b^{2}c^{2}\left ( \sin ^{2}\angle A \right )}\\ &=\displaystyle \frac{1}{2}\sqrt{b^{2}c^{2}\left ( 1-\cos ^{2}\angle A \right )},\\ &\textrm{ingat bahwa};\: \cos \angle A=\frac{b^{2}+c^{2}-a^{2}}{2bc}\\ &=\displaystyle \frac{1}{2}\sqrt{b^{2}c^{2}\left ( 1-\left ( \frac{b^{2}+c^{2}-a^{2}}{2bc} \right )^{2} \right )}\\ &=\displaystyle \frac{1}{2}\sqrt{b^{2}c^{2}-\left ( \frac{b^{2}+c^{2}-a^{2}}{2} \right )^{2}}\\ &=\displaystyle \frac{1}{2}\sqrt{\frac{4b^{2}c^{2}-\left ( b^{2}+c^{2}-a^{2} \right )^{2}}{4}}\\ &=\displaystyle \frac{1}{2}.\frac{1}{2}\sqrt{\left ( 2bc \right )^{2}-\left ( b^{2}+c^{2}-a^{2} \right )^{2}}\\ &=\displaystyle \frac{1}{4}\sqrt{\left ( 2bc+b^{2}+c^{2}-a^{2} \right )\left (2bc-b^{2}-c^{2}+a^{2} \right )}\\ &=\frac{1}{4}\sqrt{\left \{ \left ( b+c \right )^{2}-a^{2} \right \}\left \{ a^{2}-\left ( b-c \right )^{2} \right \}}\\ &=\displaystyle \frac{1}{4}\sqrt{\left ( b+c+a \right )\left ( b+c-a \right )\left ( a+b-c \right )\left ( a-b+c \right )},\\ &\textrm{dengan mengingat bahwa}\: 2s=a+b+c\\ &=\displaystyle \frac{1}{4}\sqrt{(2s)(2s-2a)(2s-2b)(2s-2c)}\\ &=\displaystyle \frac{1}{4}.\sqrt{16.s(s-a)(s-b)(s-c)}\\ &=\displaystyle \frac{1}{4}.4\sqrt{s(s-a)(s-b)(s-c)}\\ \textrm{L}\bigtriangleup \textrm{ABC}&=\sqrt{s(s-a)(s-b)(s-c)}\quad \blacksquare \end{aligned}$.

Rumus di atas lebih dikenal dengan istilah rumus Heron lihat Heron's formula di sini.

Sumber tulisan lagi di antara silahkan kunjungi di sini.

B. Luas segitiga

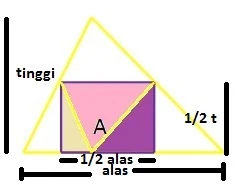
Luas segitiga juga bisa kita dapatkan dengan dengan simulasi berikut

$\begin{aligned}1.\quad &\textrm{Buat suatu segitiga bebas, misal} \end{aligned}$.

$\begin{aligned}2.\quad &\textrm{Perhatikan bahwa luas segitiga sama}\\ &\textrm{dengan luas dua kali persegi panjang}\\ &\textrm{yang terbentuk, perhatikan gambar berikut} \end{aligned}$.

dengan rincian

$\begin{aligned}3.\quad &\textrm{Panjang dari persegi panjang adalah}\\ &\textrm{setengah dari alas segitiga dan lebar }\\ &\textrm{persegi panjang adalah setengah dari}\\ &\textrm{tinggi segitiga} \end{aligned}$.

$.\qquad\begin{aligned} \textrm{Luas}\: &\textrm{segitiga}\\ &=2\times \left ( \textrm{luas persegi panjang} \right )\\ &=2\times \left ( \textrm{panjang}\times \textrm{lebar} \right )\\ &=2\times \left ( \displaystyle \frac{1}{2}a \right )\times \left ( \displaystyle \frac{1}{2}t \right )\\ &=\displaystyle \frac{1}{2}\times a\times t \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui segitiga ABC dengan}\: \: AB=21\: \: cm\\ & AC=10\: \: cm,\: \: \textrm{dan}\: \: BC=17\: \: cm.\: \textrm{Tentukan}\\ &\textrm{segitiga yang ditarik dari titik}\: \: C\\\\ &\textbf{Jawab}:\\ &\textrm{Sebelumnya perhatikan ilustrasi berikut ini} \end{array}$.

$.\: \qquad\begin{aligned}L_{\bigtriangleup }&=\left [ ABC \right ]=\textrm{Luas segitiga}\\ &=\sqrt{s(s-a)(s-b)(s-c)}\\ &\quad \textrm{dengan}\quad s=\displaystyle \frac{1}{2}(a+b+c)\\ &\quad \textrm{sehingga}\: s=\displaystyle \frac{1}{2}(21+10+17)=\color{blue}24\\ \textrm{ma}&\textrm{ka}\\ L_{\bigtriangleup }&=\sqrt{24(24-17)(24-10)(24-21)}\\ &=\sqrt{24(7)(14)(3)}=\sqrt{4.6.7.2.7.3}\\ &=\sqrt{4.49.36}=2.7.6=84\\ L_{\bigtriangleup }&=\displaystyle \frac{1}{2}\left ( \textrm{alas di depan sudut} \right )\times t\\ 84&=\displaystyle \frac{1}{2}.21\times t\\ t&=\color{red}8 \end{aligned}$.

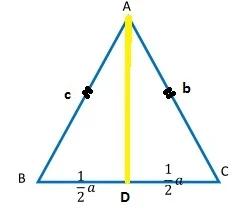
$\begin{array}{ll}\\ 2.&(\textbf{OSK 2008})\textrm{Segitiga sama kaki dengan}\\ & AB=AC\: \: \textrm{dengan keliling}\: \: 32.\: \textrm{Jika panjang}\\ &\textrm{garis tinggi dari titik}\: \: A\: \: \textrm{adalah}\: \: 8,\: \textrm{maka}\\ &\textrm{panjang}\: \: AC\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 9\displaystyle \frac{1}{3}\\ &\textrm{b}.\quad 10\\ &\textrm{c}.\quad 10\displaystyle \frac{2}{3}\\ &\textrm{d}.\quad 11\displaystyle \frac{1}{3}\\ &\textrm{e}.\quad 12\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi gambar berikut ini} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Diketahui bahwa}\: \: AB=AC=x\\ &\textrm{dengan keliling}\: \bigtriangleup ABC=32\\ &\textrm{maka}\\ &\color{blue}x+x+BC=32\\ &\Leftrightarrow BC=32-2x,\: \textrm{sedangkan}\\ &\qquad DC=16-x\\ &\textrm{Diketahui pula garis tinggi dari}\\ &\textrm{titik}\: \: A=8, \\ &\textrm{perhatikan}\: \: \bigtriangleup ADC\\ &\textrm{dengan}\: \: AC^{2}=AD^{2}+DC^{2}\\ &\Leftrightarrow x^{2}=8^{2}+(16-x)^{2}\\ &\Leftrightarrow x^{2}=8^{2}+256-32x+x^{2}\\ &\Leftrightarrow 32x=320\\ &\Leftrightarrow x=\color{red}10 \end{aligned}$.

DAFTRA PUSTAKA

1. Sembiring, S., Sukino. 2020. Super Master KSN Matematika SMA/MA. Bandung: YRAMA WIDYA.
2. Sobel, M.A., Maletsky, E.M. 2004. Mengajar Matematika: Sebuah Buku Sumber Alat Peraga, Aktivitas, dan Strategi untuk Guru Matematika SD, SMP, SMA. ed. ke-3. Alih Bahasa: Suyono. Jakarta: ERLANGGA.