Contoh Soal 1 Program Linear (Matematika Wajib Kelas XI)

$\begin{array}{ll}\\ 1.&\textrm{Daerah yang diarsir berikut adalah himpunan}\\ &\textrm{penyelesaian pertidaksamaan dari}....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&y\geq 0,\: x-2y\geq -2,\: 3x+4y\leq 12\\ \textrm{b}.&y\geq 0,\: x-2y\geq -2,\: 3x+4y\geq 12\\ \textrm{c}.&y\geq 0,\: -2x+y\geq -2,\: 4x+3y\leq 12\\ \textrm{d}.&x\geq 0,\: -2x+y\leq -2,\: 4x+3y\geq 12\\ \textrm{e}.&x\geq 0,\: x-2y\leq -2,\: 3x+4y\leq 12 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\textrm{Cukup jelas. Anda bisa mengecek dengan titik uji} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Daerah yang diarsir berikut adalah himpunan}\\ &\textrm{penyelesaian pertidaksamaan dari}....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&x\geq 0,\: 4x+y\geq 4,\: x+y\leq 2\\ \color{red}\textrm{b}.&x\geq 0,\: 4x+y\leq 4,\: x+y\geq 2\\ \textrm{c}.&x\geq 0,\: 4x+y> 4,\: x+y< 2\\ \textrm{d}.&x\geq 0,\: x+4y> 4,\: x+y< 2\\ \textrm{e}.&x\geq 0,\: x+4y\leq 4,\: x+y\geq 2 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Cukup jelas} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} 2x+y & \leq 24 \\ x+2y &\geq 12 \\ x-y & \geq -2 \end{cases}\\\\ &\textrm{adalah}\: ....\\ & \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} x+2y & \geq 6 \\ 4x+5y &\leq 20 \\ 2x+y & \geq 6 \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \color{red}\textrm{b}.&\textrm{II}\\ \textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} 2x+y & \geq 4 \\ x+y &\geq 3 \\ x-4y & \geq 4 \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

Program Linear Dua Variabel (Matematika Wajib Kelas XI)

$\LARGE\color{blue}\textrm{A. Pendahuluan}$

Untuk menguasai materi ini, materi prasyarat yang harus pembaca kuasai adalah materi tentang persamaan linier dua variabel dan tentunya materi pertidaksamaan linear satu variabel. Materi program linear ini banyak digunakan dalam bidang ekonomi khususnya masalah optimasi.

$\LARGE\color{blue}\textrm{B. Sistem Pertidaksamaan Linear Dua Variabel}$

Sebelumnya perhatikanlah ilustrasi berikut

Bentuk umum yang akan digunakan dalam bahasan ini adalah sebagai berikut

$\color{blue}\begin{aligned}&\begin{cases} ax+by &\geq m \\ ax+by &>m \\ cx+dy &\leq n \\ cx+dy & <n \end{cases}\\\\ &\color{magenta}\textrm{dengan}\\ &a,b,c,d,m,n\: \: \textrm{bilangan riil}\\ &\color{magenta}\textrm{serta}\\ &x,y\: \: \textrm{keduanya adalah peubah bebas/variabel} \end{aligned}$

Sebagai misal 

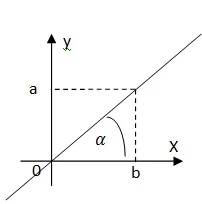
Untuk membantu menentukan pertidaksamaan linear dua variabel di atas tentunya penting juga membuat persamaan garis lurus (linear) sebagai prasyarat untuk membuat pertidaksaan yang dimaksud, yaitu:

$\begin{aligned}&\textrm{Persamaan garis di atas adalah}:\\ &\qquad\qquad\quad ax+by=ab \end{aligned}$

dan jika garisnya berbentuk berikut:

$\begin{aligned}&\textrm{maka persamaan garisnya adalah}:\\ &(1)\qquad ax-by=0,\: \: \textrm{atau}\\ &(2)\qquad y=\left (\tan \alpha \right )x \end{aligned}$

dan jika garisnya berupa ilustrasi berikut

$\begin{aligned}&\textrm{maka persamaan gradien dan garisnya adalah}:\\ &(1)\qquad m=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}},\: \: \textrm{dan}\\ &(2)\qquad y=m\left ( x-x_{1} \right )+y_{1} \end{aligned}$

Dalam program linear terdapat dua hal yang harus diperhatikan yang berkaitan dalam penyelesaian dari masalah optimasi nantinya, yaitu kendala-kendala berupa pertidaksamaan linear dua variabel yang menjadi bahasan utama dan fungsi objektif sebagai fungsi sasarannya untuk mendapatkan dan menentukan mana yang nantinya dinyatakan suatu vektek (titik pojok) sebagai titik maksimum atau minimum.

$\LARGE\color{blue}\textrm{C. Nilai Optimum Fungsi Objektif}$

Bentuk umum dari fungsi objektif ini adalah

$\LARGE\color{magenta}\boxed{f(x,y)=ax+by}$

Fungsi optimum ini akan menunjukkan keoptimumnya mana kala titik-titik pojok disubstitusikan pada fungsi ini sehingga akan didapatkan nilai maksimum atau minimunya. 

Untuk mendapatkan nilai optimum dari fungsi objektif ini dapat digunakan salah satu metode berikut

• metode uji titik pojok
• metode garis selidik

$\LARGE\color{blue}\textrm{D. Langkah Penyelesaian Program Linear}$

$\begin{aligned}(1)\quad&\textrm{Membuat model matematika}.\\ &\color{blue}\textrm{Memodelkan soal ke dalam bahasa matematika}\\ (2)\quad&\textrm{Menyelesaikan sistem pertidaksamaan linear}\\ &\textrm{(dua variabel) dan mengarsir daerah yang}\\ &\color{blue}\textrm{memenuhi pertidaksamaan yang diinginkan} \\ (3)\quad&\textrm{Menentukan titik-titik sudut (verteks / titik ekstrem )}\\ (4)\quad&\textrm{Menentukan penyelesaian Optimasi dari fungsi objektif tersebut}\\ & \textrm{(kadang disebut sebagai fungsi sasaran / tujuan)}\: \: \color{red}f(x,y)=ax+by\\ & \color{blue}\textrm{baik dengan metode uji titik sudut (Verteks / titik ekstrem)}\\ & \color{blue}\textrm{atau garis selidik}. \end{aligned}$

$\LARGE\color{magenta}\fbox{CONTOH SOAL}$

$\begin{array}{ll}\\ &\textrm{Tentukanlah nilai minimum fungsi objektif}\\ & f(x,y)=3x+5y.\: \: \textrm{Jika diketahui}\\ &\textrm{kendala-kendalanya adalah sebagai berikut}:\\ &\begin{cases} 2x+y &\geq 8 \\ 2x+3y &\geq 12 \\ x\geq 0& \\ y\geq 0 & \end{cases}\\\\ &\textbf{Jawab}\\ &\textrm{Mula-mula kita tentukan wilayah kendalanya, yaitu}:\\ &\textrm{kendala 1}:\: \: 2x+y\geq 8,\: \: \textrm{maka garisnya}:2x+y=8\\ &\begin{array}{|c|c|c|}\hline x&0&4\\\hline y&8&0\\\hline (x,y)&(0,8)&(4,0)\\\hline \end{array}\\ &\textrm{kendala 2}:\: \: 2x+3y\geq 12,\: \: \textrm{garisnya}:2x+3y=12\\ &\begin{array}{|c|c|c|}\hline x&0&6\\\hline y&4&0\\\hline (x,y)&(0,4)&(6,0)\\\hline \end{array}\\ &\textrm{kendala 3}:\: \: x\geq 0,\: \: \textrm{garisnya}:x=0\\ &\textrm{yang diarsir wilayah dari sumbu Y ke kanan}\\ &\textrm{kendala y}:\: \: y\geq 0,\: \: \textrm{garisnya}:y=0\\ &\textrm{yang diarsir wilayah dari sumbu X ke atas}\\ &\textrm{Dan titik potong kedua garis di atas, yaitu}:\\ &\begin{array}{|c|c|}\hline 2x+y=8&2x+3y=12\\\hline \textrm{di eliminasi}&\textrm{substitusi}\\\hline \begin{matrix} 2x+y=8\\ 2x+3y=12\\ -------\\ -2y=-4\\ y=2 \end{matrix}&\begin{aligned}&2x+y=8\\ &2x+(2)=8\\ &2x=8-2\\ &x=4-1=3 \end{aligned}\\\hline \color{blue}\begin{aligned}&\qquad\quad\textrm{Jadi}\\ &\textrm{titik potongnya}\\ &\textrm{potongnya adalah} \end{aligned}&\color{red}(3,2)\\\hline \end{array}\\ &\textrm{Langkah berikutnya menentukan vertek dan}\\ &\textrm{menggambar kedalam koordinat Kartesius, yaitu}:\\ \end{array}$

$\color{blue}\begin{aligned}.\quad&\textrm{Langkah berikutnya menentukan}\\ &\textrm{nilai minimumnya, yaitu}: \end{aligned}$

$\begin{array}{|c|c|l|}\hline \textrm{Titik pojok/vertek}&f(x,y)=3x+5y&\textrm{Keterangan}\\\hline (6,0)&3.6+0=18&\color{blue}\textrm{Minimum}\\\hline (3,2)&3.3+5.2=19&\\\hline (0,8)&0+5.8=40&\\\hline \end{array}$

DAFTAR PUSTAKA

1. Muis, A. 2009. Perang Siasat Matematika Dasar. Bantul: KREASI WACANA
2. Tim VisiMath. 2009. 5000Plus Soal Matematika. Jakarta: Cerdas Interaktif

Contoh Soal 5 Induksi Matematika (Matematika Wajib Kelas XI)

$\begin{array}{ll}\\ 21.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &3+6+12+24+...+\left ( 3.2^{n-1} \right )=3.\left ( 2^{n}-1 \right )\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k+1,\: \: \textrm{maka}\\ &\textrm{ruas kiri persamaan tersebut dapat dituliskan}\\ &\textrm{dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&3+6+12+24+...+ 3.2^{k+1} \\ \textrm{b}.&3+6+12+24+...+ 3.2^{k-1} \\ \color{red}\textrm{c}.&3+6+12+24+...+ 3.2^{k-1}+3.2^{k} \\ \textrm{d}.&3+6+12+24+...+ 3.2^{k-1}+3.2^{k+1} \\ \textrm{e}.&3+6+12+24+...+ 3.2^{k}+3.2^{k+1} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}&3+6+12+24+...+ 3.2^{n-1} =3.\left ( 2^{n}-1 \right )\\ &\color{red}3+6+12+24+...+ 3.2^{k-1}+3.2^{k}\color{black}=3.\left ( 2^{k+1}-1 \right ) \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Budhi, W.S. 2018. Bupena Matematika SMA/MA Kelas XI Kelompok Wajib. Jakarta: ERLANGGA.

Contoh Soal 4 Induksi Matematika (Matematika Wajib Kelas XI)

$\begin{array}{ll}\\ 16.&\textrm{Diketahui}\: \: 1+5+9+...+(4n-1)=2n^{2}-n\\ &\textrm{dengan}\: \: n\: \: \textrm{bilangan asli}.\: \textrm{Jika}\: \: m<k\: \: \textrm{dengan}\\ &m,k\: \: \textrm{bilangan asli juga},\: \textrm{maka}\\ &(4m-3)+(4m+1)+...+(4k-3)=....\\ &\begin{array}{llll}\\ \textrm{a}.&(k-m)(2k+2m-2)\\ \color{red}\textrm{b}.&(k-m+1)(2k+2m-3)\\ \textrm{c}.&(k-m+1)(2k-2m+1)\\ \textrm{d}.&(k-m+1)(2k^{2}+2m^{2}-3)\\ \textrm{e}.&(k-m)^{2}(2k-2m+4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}&1+5+9+...+(4m-3)+(4m+1)+...+(4k-3)\\ &=\underset{2k^{2}-k}{\underbrace{1+5+...+(4k-3)}}-\underset{2(m-1)^{2}-(m-1)}{\underbrace{1+5+...+(4(m-1)-3)}}\\ &=2k^{2}-k-\left ( 2(m-1)^{2}-(m-1) \right )\\ &=2k^{2}-k-2(m-1)^{2}+(m-1)\\ &=2k^{2}-k-2\left ( m^{2}-2m+1 \right )+m-1\\ &=2k^{2}-k-2m^{2}+4m-2+m-1\\ &=2k^{2}-k-2m^{2}+5m-3\\ &=(k-m+1)(2k+2m-3) \end{aligned} \end{array}$

$\begin{array}{ll}\\ 17.&\textrm{Diketahui}\: \: 2^{1}+2^{2}+2^{3}+...+2^{n}=2^{n+1}-2\\ &\textrm{dengan}\: \: n\: \: \textrm{bilangan asli}.\: \textrm{Jika}\: \: k\: \: \textrm{bilangan asli},\\ &\textrm{maka}\: \: 2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}=....\\ &\begin{array}{llll}\\ \textrm{a}.&(k-m)(2k+2m-2)\\ \textrm{b}.&(k-m+1)(2k+2m-3)\\ \textrm{c}.&(k-m+1)(2k-2m+1)\\ \color{red}\textrm{d}.&(k-m+1)(2k^{2}+2m^{2}-3)\\ \textrm{e}.&(k-m)^{2}(2k-2m+4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}&2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}\\ &=2^{1}+2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}-2^{1}\\ &=\underset{2^{k+1+1}-2}{\underbrace{2^{1}+2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}}}-2^{1}\\ &=2^{k+2}-2-2\\ &=2^{k+2}-4\\ &=2^{k}.2^{2}-4\\ &=2^{k}\times 4-4\\ &=4\left ( 2^{k}-1 \right ) \end{aligned} \end{array}$

$\begin{array}{ll}\\ 18.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &2+5+10+17+...+\left ( n^{2}+1 \right )=\displaystyle \frac{1}{6}(n+1)\left ( 2n^{2}+n+6 \right )\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k,\: \: \textrm{maka}....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&2+5+10+17+...+\left ( k^{2}+1 \right )\\ &=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{b}.&2+5+10+17+...+\left ( n^{2}+1 \right )\\ &=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{c}.&2+5+10+17+...+\left ( k^{2}+2 \right )\\ &=\displaystyle \frac{1}{6}(k+2)\left ( 2k^{2}+5k+9 \right )\\ \textrm{d}.&\left ( k^{2}+1 \right )=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{e}.&\left ( n^{2}+2 \right )=\displaystyle \frac{1}{6}(n+1)\left ( 2n^{2}+5n+9 \right ) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}&\textrm{Cukup jelas}\\ &\textrm{Tinggal mensubstitusikan dari}\\ &\textrm{tiap}\: \: n\: \: \textrm{diganti}\: \: k \end{aligned} \end{array}$

$\begin{array}{ll}\\ 19.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &12+17+22+...+\left ( 5n+7 \right )=\displaystyle \frac{1}{2}(n+1)(5n+14)\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k,\: \: \textrm{maka benar}\\ &\textrm{untuk}\: \: n=k+1.\: \textrm{Pernyataan ini dapat}\\ &\textrm{dinyatakan dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+14)\\ \textrm{b}.&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+19)\\ \textrm{c}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+1)(5k+19)\\ \textrm{d}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+2)(5k+14)\\ \color{red}\textrm{e}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+2)(5k+19) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+14)\\ &12+17+22+...+\left ( 5(k+1)+7 \right )\\ &\qquad\qquad\qquad\quad=\displaystyle \color{magenta}\frac{1}{2}((k+1)+1)(5(k+1)+14)\\ &12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+2)(5k+19) \end{aligned} \end{array}$

$\begin{array}{ll}\\ 20.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &4+5+6+7+...+(n+3)<5n^{2}\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k+1,\: \: \textrm{maka}\\ &\textrm{pernyataan ini dapat ditulis dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&4+5+6+...+(k+4)<5k^{2}\\ \textrm{b}.&4+5+6+...+(k+3)<5k^{2}\\ \textrm{c}.&4+5+6+...+(k+3)<5(k+1)^{2}\\ \color{red}\textrm{d}.&4+5+6+...+(k+4)<5(k^{2}+2k+1)\\ \textrm{e}.&4+5+6+...+(k+4)<5(k+1)(k-1) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}&4+5+6+...+(n+3)<5n^{2}\\ &\textrm{Saat}\: \: n=k+1,\: \: \textrm{maka}\\ &4+5+6+...+((k+1)+3)<5(k+1)^{2}\\ &=4+5+6+...+(k+4)<5\left ( k^{2}+2k+1 \right ) \end{aligned} \end{array}$

Contoh Soal 3 Induksi Matematika (Matematika Wajib Kelas XI)

 $\begin{array}{ll}\\ 11.&\textrm{Perhatikanlah pernyataan-pernyataan berikut}\\ &(1)\quad \displaystyle \sum_{i=1}^{5}(5i+2)=4\displaystyle \sum_{i=1}^{5}i+10\\ &(2)\quad \displaystyle \sum_{i=1}^{5}(5i^{2}-i)=5\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}i\\ &(3)\quad \displaystyle \sum_{i=1}^{5}(3i-4)=3\displaystyle \sum_{i=1}^{5}i^{2}-4\\ &(4)\quad \displaystyle \sum_{i=1}^{5}(i+7i^{2})=\displaystyle \sum_{i=1}^{5}i-7\sum_{i=1}^{5}i\\ &\textrm{Pernyataan yang tepat ditunjukkan oleh}....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&(1)\: \: \textrm{dan}\: \: (2)\\ \textrm{b}.&(1)\: \: \textrm{dan}\: \: (3)\\ \textrm{c}.&(1)\: \: \textrm{dan}\: \: (4)\\ \textrm{d}.&(2)\: \: \textrm{dan}\: \: (3)\\ \textrm{e}.&(2)\: \: \textrm{dan}\: \: (4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}(1)\quad&\displaystyle \sum_{i=1}^{5}(5i+2)=4\displaystyle \sum_{i=1}^{5}i+\sum_{i=1}^{5}2\\ &=4\displaystyle \sum_{i=1}^{5}i+5\times 2\\ &=4\displaystyle \sum_{i=1}^{5}i+10\\ (2)\quad&\displaystyle \sum_{i=1}^{5}(5i^{2}-i)=5\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}i\\ (3)\quad&\displaystyle \sum_{i=1}^{5}(3i-4)=3\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}4\\ &=3\displaystyle \sum_{i=1}^{5}i^{2}-5\times 4\\ &=3\displaystyle \sum_{i=1}^{5}i^{2}-20\\ (4)\quad&\displaystyle \sum_{i=1}^{5}(i+7i^{2})=\displaystyle \sum_{i=1}^{5}i+7\sum_{i=1}^{5}i \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=1}^{4}i^{2}+\sum_{i=5}^{6}i^{2}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 86\\ \color{red}\textrm{b}.&\displaystyle 91\\ \textrm{c}.&\displaystyle 95\\ \textrm{d}.&\displaystyle 101\\ \textrm{e}.&\displaystyle 105 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}\displaystyle \sum_{i=1}^{4}i^{2}+\sum_{i=5}^{6}i^{2}&=\displaystyle \sum_{i=1}^{6}i^{2}\\ &=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}\\ &=1+4+9+16+25+36\\ &=91 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 13.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=2}^{5}\left ( 4i^{2}-2i \right )\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 144\\ \textrm{b}.&\displaystyle 148\\ \textrm{c}.&\displaystyle 154\\ \textrm{d}.&\displaystyle 164\\ \color{red}\textrm{e}.&\displaystyle 188 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}&\displaystyle \sum_{i=2}^{5}\left ( 4i^{2}-2i \right )\\ &=\left ( 4.2^{2}-2.2 \right )+\left ( 4.3^{2}-2.3 \right )+\left ( 4.4^{2}-2.4 \right )+\left ( 4.5^{2}-2.5 \right )\\ &=12+30+56+90\\ &=188 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 14.&\textrm{Bentuk}\: \: 11^{n}-1\: \: \textrm{dengan}\: \: n\: \: \textrm{bilangan asli}\\ &\textrm{akan habis dibagi oleh}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 7\\ \textrm{b}.&\displaystyle 9\\ \color{red}\textrm{c}.&\displaystyle 10\\ \textrm{d}.&\displaystyle 11\\ \textrm{e}.&\displaystyle 13 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}\textrm{Bentuk}&\: \: 11^{n}-1\\ \textrm{untuk}&\: \: n=1\\ &=11^{1}-1\\ &=10 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 15.&\textrm{Rumus yang tepat untuk pola}\: \: 12,13,14,15,...\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle U_{n}=n+9\\ \textrm{b}.&\displaystyle U_{n}=n+10\\ \color{red}\textrm{c}.&\displaystyle U_{n}=n+11\\ \textrm{d}.&\displaystyle U_{n}=2n+10\\ \textrm{e}.&\displaystyle U_{n}=2n+11 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}\textrm{Bentuk}&\: \: 12,13,14,15,...\\ \textrm{untuk}&\: \: U_{n}=pn+q\\ 12&=p+q\\ 13&=2p+q\\ \textrm{akan}&\: \textrm{didapatkan}\\ &\begin{cases} p & =1 \\ q & =11 \end{cases}\\ \textrm{Sehing}&\textrm{ga}\\ U_{n}&=n+11 \end{aligned} \end{array}$

Contoh Soal 2 Induksi Matematika (Matematika Wajib Kelas XI)

$\begin{array}{ll}\\ 6.&\textrm{Dengan Induksi Matematika untuk}\: \: n\in \mathbb{N}\\ &\textrm{dapat dibuktikan juga bahwa}\: \: 7^{n}-2^{n}\\ &\textrm{akan habis dibagi oleh}\\ &\begin{array}{lllllll}\\ \textrm{a}.&2\\ \textrm{b}.&3\\ \textrm{c}.&4\\ \color{red}\textrm{d}.&5\\ \textrm{e}.&6\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}P(n)&=7^{n}-2^{n}\\ P(1)&=7^{1}-2^{1}\\ &=7-2=5\\ &\textrm{adalah bilangan yang habis dibagi 5} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Diketahui bahwa}\: \: P(n)\: \: \textrm{rumus dari}\\ & 3+6+9+\cdots +3n=\displaystyle \frac{3}{2}n(n+1)\\ &\textrm{maka langkah pertama dengan induksi matematika}\\ &\textrm{dalam pembuktian rumus tersebut adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.&P(n)\: \: \textrm{benar untuk}\: \: n=-1\\ \color{red}\textrm{b}.&P(n)\: \: \textrm{benar untuk}\: \: n=1\\ \textrm{c}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan bulat}\\ \textrm{d}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan rasional}\\ \textrm{d}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan real} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}\textrm{Langkah}&\: \textrm{awal yang harus ditunjukkan adalah}\\ n=1&\: \: \textrm{atau}\: \: P(1)\: \: \textrm{harus benar, yaitu}:\\ P(1)&=3.1(\textit{ruas kiri})=\displaystyle \frac{3}{2}.1.(1+1)(\textit{ruas kanan})=3 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Bila kita hendak membuktikan}\: \: \displaystyle \sum_{i=1}^{n}=\displaystyle \frac{1}{2}n(n+1)\\ &\textrm{dengan induksi matematika}\\ &\textrm{maka untuk langkah}\: \: n=k+1\\ &\textrm{bentuk yang harus ditunjukkan adalah}...\\ &\begin{array}{lll}\\ \textrm{a}.&1+2+3+\cdots +n=\displaystyle \frac{1}{2}n(n+1)\\ \textrm{b}.&1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+1)\\ \textrm{c}.&1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+2)\\ \color{red}\textrm{d}.&1+2+3+\cdots +k+(k+1)=\displaystyle \frac{1}{2}(k+1)(k+2)\\ \textrm{e}.&1+2+3+\cdots +k+(k+1)=\displaystyle \frac{1}{2}(k+2)(k+3)\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}P(n)&=1+2+3+\cdots +n=\displaystyle \frac{1}{2}n(n+1)\\ P(k)&=1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+1)\\ P(k+1)&=1+2+3+\cdots +k+(k+1)\\ &=\underset{\displaystyle \frac{1}{2}k(k+1)}{\underbrace{1+2+3+\cdots +k}}+(k+1)\\ &=\displaystyle \frac{1}{2}k(k+1)+(k+1)=(k+1)\left ( \displaystyle \frac{1}{2}k+1 \right )\\ &=(k+1)\displaystyle \frac{1}{2}(k+2)\\ &=\displaystyle \frac{1}{2}(k+1)(k+2) \end{aligned} \end{array}$

$\begin{array}{ll}\\ 9.&\textrm{Jika}\: \: P(n)=\displaystyle \frac{n-1}{n+3},\: \textrm{maka}\: \: P(k+1)\\ & \textrm{dinyatakan dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle \frac{k-1}{k+3}\\ \textrm{b}.&\displaystyle \frac{k-1}{k+4}\\ \color{red}\textrm{c}.&\displaystyle \frac{k}{k+4}\\ \textrm{d}.&\displaystyle \frac{k+1}{k+4}\\ \textrm{e}.&\displaystyle \frac{k+1}{k+5} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}P(n)=&\displaystyle \frac{n-1}{n+3}\\ P(k+1)&=\displaystyle \frac{k+1-1}{k+1+3}\\ &=\displaystyle \frac{k}{k+4} \end{aligned}\end{array}$

$\begin{array}{ll}\\ 10.&\textrm{Jika}\: \: P(n)=\displaystyle \frac{n^{2}+1}{4},\: \: \textrm{maka}\\ &\textrm{pernyataan untuk}\: \: P(k+1)\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle \frac{k^{2}+2k+1}{4}\\ \color{red}\textrm{b}.&\displaystyle \frac{k^{2}+2k+2}{4}\\ \textrm{c}.&\displaystyle \frac{k^{2}+2k+2}{5}\\ \textrm{d}.&\displaystyle \frac{k^{2}+2k+3}{5}\\ \textrm{e}.&\displaystyle \frac{k^{2}+2k+3}{4} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}P(n)&=\displaystyle \frac{n^{2}+1}{4}\\ P(k+1)&=\displaystyle \frac{(k+1)^{2}+1}{4}\\ &=\displaystyle \frac{k^{2}+2k+2}{4} \end{aligned} \end{array}$

Contoh Soal 1 Induksi Matematika (Matematika Wajib Kelas XI)

$\begin{array}{ll}\\ 1.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=1}^{6}16i\: \: \textrm{adalah}....\\ &\begin{array}{llll}\\ \textrm{a}.&306\\ \textrm{b}.&314\\ \textrm{c}.&326\\ \color{red}\textrm{d}.&336\\ \textrm{e}.&402 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\displaystyle \sum_{i=1}^{6}16i&=16.1+16.2+16.3+16.4+16.5+16.6\\ &=16+32+48+64+80+96\\ &=336 \end{aligned}\end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=2}^{9}i^{2}\: \: \textrm{adalah}....\\ &\begin{array}{llll}\\ \textrm{a}.&274\\ \textrm{b}.&278\\ \textrm{c}.&280\\ \color{red}\textrm{d}.&284\\ \textrm{e}.&286 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\displaystyle \sum_{i=2}^{9}i^{2}&=2^{2}+3^{2}+4^{2}+5^{2}+..+9^{2}\\ &=4+9+16+25+...+81\\ &=284 \end{aligned}\end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Poa bilangan}\: \: 12,14,16,18,20,...,(2n+10).\\ &\textrm{Nilai suku ke-100 adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.&180\\ \textrm{b}.&194\\ \textrm{c}.&198\\ \textrm{d}.&208\\ \color{red}\textrm{e}.&210\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}U_{n}&=2n+10\\ U_{100}&=2\times 100+10\\ &=210 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui bahwa jika}\\ & 31+39+47+\cdots +8n+23=4n^{2}+27n\\ & \textrm{dengan}\: \: k,n\in \mathbb{N}\: \: \textrm{maka}\\ & 31+39+47+\cdots +8n+23+8k+31=....\\ &\begin{array}{lllllll}\\ \textrm{a}.&4k^{2}+27k\\ \textrm{b}.&4k^{2}+35k\\ \color{red}\textrm{c}.&4k^{2}+35k+31\\ \textrm{d}.&4k^{2}+35k+1\\ \textrm{e}.&4k^{2}+35k+54\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}&\underset{4k^{2}+27k}{\underbrace{31+39+47+\cdots +8k+23}}+8k+31\\ &=4k^{2}+27k+8k+31\\ &=4k^{2}+35k+31 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Dengan Induksi Matematika untuk}\: \: n\in \mathbb{N}\\ &\textrm{dapat dibuktikan bahwa}\: \: n(n+1)(n+2)\\ &\textrm{akan habis dibagi oleh}\\ &\begin{array}{lllllll}\\ \textrm{a}.&4\\ \textrm{b}.&5\\ \color{red}\textrm{c}.&6\\ \textrm{d}.&7\\ \textrm{e}.&8\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}P(n)&=n(n+1)(n+2)\\ P(1)&=1(1+1)(1+2)=1.2.3\\ &\textrm{adalah bilangan yang habis dibagi 6} \end{aligned} \end{array}$

Contoh Soal 6 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 26.&\textrm{Jika nilai}\: \: \cot A+\cos A=x\\ &\textrm{dan}\: \: \cot A-\cos A=y,\\ &\textrm{maka nilai}\: \: \left ( x^{2}-y^{2} \right )=\: ....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&4\sqrt{xy}\\ \textrm{b}.&2\sqrt{xy}\\ \textrm{c}.&xy\\ \textrm{d}.&2\\ \textrm{e}.&4 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}\color{magenta}xy&=\left (\cot A+\cos A \right )\left ( \cot A-\cos A \right )\\ &=\cot ^{2}A-\cos ^{2}A\\ &=\displaystyle \frac{\cos^{2}A }{\sin ^{2}A}-\cos ^{2}A\\ &=\displaystyle \frac{\cos^{2}A }{\sin ^{2}A}-\cos ^{2}A\times \frac{\sin ^{2}A}{\sin ^{2}A}\\ &=\displaystyle \frac{\cos ^{2}A}{\sin ^{2}A}\left ( 1-\sin ^{2}A \right )\\ &=\displaystyle \frac{\cos ^{4}A}{\sin ^{2}A}\\ \sqrt{xy}&=\displaystyle \frac{\cos A}{\sin A}\times \cos A\\ \color{black}\textrm{Se}&\color{black}\textrm{lanjutnya}\\ x^{2}-y^{2}&=\left (\cot A+\cos A \right )^{2}-\left ( \cot A-\cos A \right )^{2}\\ (x+y)&(x-y)=(\cot A+\cos A+\cot A-\cos A)\\ &\qquad\times (\cot A+\cos A-(\cot A-\cos A))\\ x^{2}-y^{2}&=2\cot A\times 2\cos A\\ &=4\times \displaystyle \frac{\cos A}{\sin A}\times \cos A\\ &=\color{magenta}4\sqrt{xy} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 27.&\textrm{Jika nilai}\: \: \cos A+\sin A=\sqrt{2}\cos A\\ &\textrm{maka nilai}\: \: \left ( \cos A-\sin A \right )=\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&-\sqrt{2}\cos A\\ \textrm{b}.&-\sqrt{2}\sin A\\ \color{red}\textrm{c}.&\sqrt{2}\sin A\\ \textrm{d}.&\displaystyle \frac{1}{\sqrt{2}}\sec A\\ \textrm{e}.&\displaystyle \frac{1}{\sqrt{2}}\csc A \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}\cos A+\sin A&=\sqrt{2}\cos A\\ \left (\cos A+\sin A \right )^{2}&=\left (\sqrt{2}\cos A \right )^{2}\\ 1+2\sin A\cos A&=2\cos ^{2}A\\ 2\sin A\cos A&=2\cos ^{2}A-1\\ \textrm{maka}&\\ \left (\cos A-\sin A \right )^{2}&=1-2\sin A\cos A\\ &=1-\left ( 2\cos ^{2}A-1 \right )\\ &=2-2\cos ^{2}A\\ &=2\left ( 1-\cos ^{2}A \right )\\ &=2\sin ^{2}A\\ \cos A-\sin A&=\sqrt{2\sin ^{2}A}\\ &=\sin A\sqrt{2}\\ &=\color{magenta}\sqrt{2}.\sin A \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Sembiring, S., Zulkifli, M., Marsito, dan Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU.
2. Sukino. 2016. Matematika untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA

Contoh Soal 5 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 21.&\textrm{Nilai dari}\: \: \displaystyle \frac{1}{\sec ^{2}A}+\frac{1}{\csc ^{2}A}=....\\ &\begin{array}{llll}\\ \textrm{a}.&-\infty \\ \textrm{b}.&\displaystyle -1\\ \textrm{c}.&\displaystyle 0\\ \color{red}\textrm{d}.&\displaystyle 1\\ {e}.&\displaystyle \infty \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}&\displaystyle \frac{1}{\sec ^{2}A}+\frac{1}{\csc ^{2}A}\\ &=\cos ^{2}A+\sin ^{2}=1 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 22.&\textrm{Nilai dari}\: \: \displaystyle \frac{\tan B+\tan C}{\cot B+\cot C}=....\\ &\begin{array}{llll}\\ \textrm{a}.&\cot B\times \cot C \\ \color{red}\textrm{b}.&\displaystyle \tan B\times \tan C\\ \textrm{c}.&\displaystyle \sec B\times \csc C\\ \textrm{d}.&\displaystyle \tan B\times \cot C\\ {e}.&\displaystyle \tan B\times \csc C \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}&\displaystyle \frac{\tan B+\tan C}{\cot B+\cot C}\\ &=\displaystyle \frac{\tan B+\tan C}{\displaystyle \frac{1}{\tan B}+\frac{1}{\tan C}}\\ &=\displaystyle \frac{\tan B+\tan C}{\left ( \displaystyle \frac{\tan B+\tan C}{\tan B\times \tan C} \right )}\\ &=\tan B\times \tan C \end{aligned} \end{array}$

$\begin{array}{ll}\\ 23.&\textrm{Nilai dari}\\ &\displaystyle \frac{\tan A}{\sec A-1}+\frac{\tan A}{\sec A+1}=....\\ &\begin{array}{llll}\\ \textrm{a}.&2\tan A \\ \textrm{b}.&2\cot A\\ \textrm{c}.&\displaystyle 2\sec A\\ \color{red}\textrm{d}.&\displaystyle 2\csc A\\ {e}.&\displaystyle 2\tan A.\sec A \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}&\displaystyle \frac{\tan A}{\sec A-1}+\frac{\tan A}{\sec A+1}\\ &=\tan A\left (\displaystyle \frac{1}{\displaystyle \frac{1}{\cos A}-1}+\frac{1}{\displaystyle \frac{1}{\cos A}+1} \right )\\ &=\displaystyle \frac{\sin A}{\cos A}\left ( \displaystyle \frac{\cos A}{1-\cos A}+\frac{\cos A}{1+\cos A} \right )\\ &=\displaystyle \frac{\sin A}{1-\cos A}+\frac{\sin A}{1+\cos A}\\ &=\displaystyle \frac{\sin A(1+\cos A)+\sin A(1-\cos A)}{(1-\cos A)(1+\cos A)}\\ &=\displaystyle \frac{2\sin A}{1-\cos ^{2}}\\ &=\displaystyle \frac{2\sin A}{\sin ^{2}A}\\ &=\displaystyle \frac{2}{\sin A}\\ &=2\csc A \end{aligned}\\\\ &\textrm{Sebagai catatanya}\\ &\textrm{Anda bisa gunakan cara yang lain} \end{array}$

$\begin{array}{ll}\\ 24.&\textrm{Nilai}\: \: x\: \: \textrm{yang memenuhi persamaan}\\ &\sin \left ( 2x-20^{\circ} \right )=-\cos \left ( 3x+50^{\circ} \right )\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&-30^{\circ}\\ \textrm{b}.&-25^{\circ}\\ \color{red}\textrm{c}.&20^{\circ}\\ \textrm{d}.&25^{\circ}\\ {e}.&30^{\circ} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\begin{aligned}\sin \left ( 2x-20^{\circ} \right )&=-\cos \left ( 3x+50^{\circ} \right )\\ \sin \left ( 20^{\circ}-2x \right )&=\cos \left ( 3x+50^{\circ} \right )\\ \sin A&=\cos B,\: \: \color{black}\textrm{artinya}\\ A+B&=90^{\circ},\: \: \color{magenta}\textrm{maka}\\ \left ( 20^{\circ}-2x \right )+\left ( 3x+50^{\circ} \right )&=90^{\circ}\\ x+70^{\circ}&=90^{\circ}\\ x&=90^{\circ}-70^{\circ}\\ &=20^{\circ} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 25.&\textrm{Nilai}\: \: x\: \: \textrm{yang memenuhi persamaan}\\ &\tan \left ( 2x+60^{\circ} \right )=\cot \left ( 90^{\circ}-3x \right )\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&20^{\circ}\\ \textrm{b}.&30^{\circ}\\ \textrm{c}.&40^{\circ}\\ \textrm{d}.&50^{\circ}\\ \color{red}\textrm{e}.&60^{\circ} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}\tan \left ( 2x+60^{\circ} \right )&=\cot \left ( 90^{\circ}-3x \right )\\ \tan (2x+60^{\circ})&=\tan 3x\\ 2x+60^{\circ}&=3x\\ 2x-3x&=-60^{\circ}\\ -x&=-60^{\circ}\\ x&=60^{\circ} \end{aligned} \end{array}$

Contoh Soal 4 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 16.&\textrm{Jika}\: \: \tan^{2} x +\sec x =5 \: \: \textrm{untuk}\\ &0\leq x\leq \displaystyle \frac{\pi }{2}\: \: \textrm{maka nilai} \: \: \cos x=....\\ &\begin{array}{llll}\\ \textrm{a}.&0\\ \color{red}\textrm{b}.&\displaystyle \frac{1}{2}\\ \textrm{c}.&\displaystyle \frac{1}{3}\\ \textrm{d}.&\displaystyle \frac{1}{\sqrt{2}}\\ \textrm{e}.&\displaystyle \frac{1}{2}\sqrt{3} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}\textrm{Ingat bahwa}&\: \: 0\leq x\leq \displaystyle \frac{\pi }{2}\\ \textrm{berarti sudu}&\textrm{t}\: \: x\: \: \textrm{berada di kuadran I}\\ \textrm{sehingga ak}&\textrm{an menyebabkan nilai}\\ & \color{magenta}\cos x=+\\ \color{black}\textrm{Selanjutnya}&\\ \tan^{2} x +\sec x &=5\\ \sec ^{2}x-1+\sec x&=5\\ \sec ^{2}x+\sec x-6&=0\\ (\sec x+3)(\sec x-2)&=0\\ \sec x=-3\: \: \textrm{atau}&\sec x=2\\ \textrm{untuk}\: \: \sec x&=-3\: \: (\color{red}\textrm{tidak memenuhi})\\ \textrm{untuk}\: \: \sec x&=2\: \: (\color{magenta}\textrm{memenuhi})\\ \color{black}\textrm{Selanjutnya}&\: \color{black}\textrm{lagi}\\ \sec x&=2\\ \displaystyle \frac{1}{\cos x}&=2\\ \cos x&=\color{magenta}\displaystyle \frac{1}{2} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 17.&\textrm{Nilai}\\ &\left ( \sin A+\cos A \right )^{2}+\left ( \sin A-\cos A \right )^{2}=....\\ &\begin{array}{llll}\\ \textrm{a}.&1\\ \color{red}\textrm{b}.&\displaystyle 2\\ \textrm{c}.&\displaystyle 3\\ \textrm{d}.&\displaystyle 3\cos A\\ {e}.&\displaystyle 4\sin A \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}&\left ( \sin A+\cos A \right )^{2}+\left ( \sin A-\cos A \right )^{2}\\ &=\sin ^{2}A+2\sin A\cos A+\cos ^{2}A\\ &\quad +\sin ^{2}A-2\sin A\cos A+\cos ^{2}A\\ &=1+1\\ &=2 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 18.&\textrm{Nilai}\: \: \sqrt{\displaystyle \frac{1+\sin A}{1-\sin A}}=....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\sec A+\tan A\\ \textrm{b}.&\sec ^{2}A+\tan ^{2}A\\ \textrm{c}.&\sec ^{2}A-\tan ^{2}A\\ \textrm{d}.&\tan ^{2}A-\sec ^{2}A\\ {e}.&\sec A\times \tan A \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}&\sqrt{\displaystyle \frac{1+\sin A}{1-\sin A}}\\ &=\sqrt{\displaystyle \frac{1+\sin A}{1-\sin A}\times \frac{1+\sin A}{1+\sin A}}\\ &=\sqrt{\displaystyle \frac{\left ( 1+\sin A \right )^{2}}{1-\sin ^{2}A}}\\ &=\sqrt{\displaystyle \frac{\left ( 1+\sin A \right )^{2}}{\cos ^{2}A}}\\ &=\displaystyle \frac{1+\sin A}{\cos A}\\ &=\displaystyle \frac{1}{\cos A}+\frac{\sin A}{\cos A}\\ &=\sec A+\tan A \end{aligned} \end{array}$

$\begin{array}{ll}\\ 19.&\textrm{Jika}\: \: 0^{\circ}\leq \theta \leqslant 90^{\circ},\: \textrm{maka nilai}\\ &\left ( \displaystyle \frac{5\cos \theta -4}{3-5\sin \theta }-\frac{3+5\sin \theta }{4+5\cos \theta } \right )=....\\ &\begin{array}{llll}\\ \textrm{a}.&-1\\ \color{red}\textrm{b}.&\displaystyle 0\\ \textrm{c}.&\displaystyle \frac{1}{4}\\ \textrm{d}.&\displaystyle \frac{1}{2}\\ {e}.&\displaystyle 1 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}&\left ( \displaystyle \frac{5\cos \theta -4}{3-5\sin \theta }-\frac{3+5\sin \theta }{4+5\cos \theta } \right )\\ &=\left ( \displaystyle \frac{5\cos \theta -4}{3-5\sin \theta }\times \frac{4+5\cos \theta }{4+5\cos \theta } \right )\\ &\qquad-\left ( \displaystyle \frac{3+5\sin \theta }{4+5\cos \theta }\times \frac{3-5\sin \theta }{3-5\sin \theta } \right )\\ &=\displaystyle \frac{25\cos ^{2}-16-\left ( 9-25\sin ^{2}\theta \right )}{(3-5\sin \theta )(4+5\cos \theta )}\\ &=\displaystyle \frac{25\left ( \sin ^{2}\theta +\cos ^{2}\theta \right )-25}{(3-5\sin \theta )(4+5\cos \theta )}\\ &=\displaystyle \frac{0}{(3-5\sin \theta )(4+5\cos \theta )}\\ &=\color{magenta}0 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 20.&\textrm{Nilai}\\ &\left ( 1+\cot \theta -\csc \theta \right )\left ( 1+\tan \theta +\sec \theta \right )=....\\ &\begin{array}{llll}\\ \textrm{a}.&-2\\ \textrm{b}.&\displaystyle -1\\ \textrm{c}.&\displaystyle 0\\ \textrm{d}.&\displaystyle 1\\ \color{red}\textrm{e}.&\displaystyle 2 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}&\left ( 1+\cot \theta -\csc \theta \right )\left ( 1+\tan \theta +\sec \theta \right )\\ &=\left ( 1+\displaystyle \frac{\cos \theta }{\sin \theta } -\frac{1}{\sin \theta } \right )\left ( 1+\frac{\sin \theta }{\cos \theta } +\frac{1}{\cos \theta } \right )\\ &=\left ( \displaystyle \frac{\sin \theta +\cos \theta -1}{\sin \theta } \right )\left ( \displaystyle \frac{\cos \theta +\sin \theta +1}{\cos \theta } \right )\\ &=\displaystyle \frac{\left (\sin \theta +\cos \theta \right )^{2}-1}{\sin \theta \cos \theta }\\ &=\displaystyle \frac{1+2\sin \theta \cos \theta -1}{\sin \theta \cos \theta }\\ &=2 \end{aligned} \end{array}$

Contoh Soal 3 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 11.&\textrm{Himpunan penyelesaian persamaan}\\ &3\cos 2x+5\sin x+1=0\: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 2\pi \\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\left \{ \displaystyle \frac{7}{6}\pi ,\frac{11}{6}\pi \right \}\\ \textrm{b}.&\left \{ \displaystyle \frac{5}{6}\pi ,\frac{11}{6}\pi \right \}\\ \textrm{c}.&\left \{ \displaystyle \frac{1}{6}\pi ,\frac{7}{6}\pi \right \}\\ \textrm{d}.&\left \{ \displaystyle \frac{1}{5}\pi ,\frac{5}{6}\pi \right \}\\ \textrm{e}.&\left \{ \displaystyle \frac{5}{6}\pi ,\frac{7}{6}\pi \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}3\cos 2x+5\sin x+1&=0\\ 3\left ( 1-2\sin ^{2}x \right )+5\sin x+1&=0\\ -6\sin ^{2}+5\sin x+4&=0\\ 6\sin ^{2}x-5\sin x-4&=0\\ \left ( 3\sin x-4 \right )\left ( 2\sin x+1 \right )&=0\\ \sin x=\displaystyle \frac{4}{3}\: \: \textrm{atau}\: \: \sin x&=-\frac{1}{2}\\ \sin x&=\sin 150^{\circ}=\frac{5}{6}\pi \\ x&=\begin{cases} \displaystyle \frac{7}{6}\pi &+k.2\pi \\ \pi -\displaystyle \frac{7}{6}\pi & +k.2\pi \end{cases}\\ \textrm{saat}\: \: k&=0\\ x_{1}&=\displaystyle \frac{7}{6}\pi \\ x_{2}&=-\displaystyle \frac{1}{6}\pi \\ \textrm{saat}\: \: k&=1\\ x_{1}&=\color{red}\displaystyle \frac{7}{6}\pi +2\pi \\ x_{2}&=-\displaystyle \frac{1}{6}\pi +2\pi =\frac{11}{6}\pi \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Himpunan penyelesaian dari}\\ &\sqrt{3}\sin 2x+2\cos ^{2}x=-1\: \: \textrm{untuk}\\ &0^{\circ}\leq x\leq 360^{\circ}\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\left \{ 240^{\circ},300^{\circ} \right \}\\ \textrm{b}.&\left \{ 30^{\circ},60^{\circ} \right \}\\ \textrm{c}.&\left \{ 150^{\circ},315^{\circ} \right \}\\ \color{red}\textrm{d}.&\left \{ 120^{\circ},300^{\circ} \right \}\\ \textrm{e}.&\left \{ 60^{\circ},150^{\circ} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\sqrt{3}\sin 2x+2\cos ^{2}x&=-1\\ \sqrt{3}\sin 2x+1+\cos 2x&=-1\\ \sqrt{3}\sin 2x+\cos 2x&=-2\\ \sqrt{\sqrt{3}^{2}+1^{2}}\cos \left ( 2x-\alpha \right )&=-2\\ a=x=1,\: \: b&=y=\sqrt{3}\\ \alpha &=\arctan \displaystyle \frac{b}{a}=\arctan \frac{\sqrt{3}}{1}\\ \alpha &=60^{\circ}\\ \textrm{maka persamaan akan}&\: \textrm{menjadi}\\ 2\cos \left ( 2x-60^{\circ} \right )&=-2\\ \cos \left ( 2x-60^{\circ} \right )&=-1\\ \cos \left ( 2x-60^{\circ} \right )&=\cos 180^{\circ}\\ \left ( 2x-60^{\circ} \right )&=\pm 180^{\circ}+k.360^{\circ}\\ 2x&=60^{\circ}\pm 180^{\circ}+k.360^{\circ}\\ x&=30^{\circ}\pm 90^{\circ}+k.180^{\circ}\\ \textrm{saat}\: \: k&=0\\ x_{1}&=120^{\circ}\\ x_{2}&=-60^{\circ}\\ \textrm{saat}\: \: k&=1\\ x_{3}&=120^{\circ}+360^{\circ}=....\\ x_{2}&=-60^{\circ}+360^{\circ}=300^{\circ} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 13.&\textrm{Jika}\: \: 3\sin \theta +4\cos \theta =5 \: \: \textrm{maka}\\ &\textrm{nilai dari} \: \: \sin \theta \: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&0,3\\ \color{red}\textrm{b}.&0,60\\ \textrm{c}.&0,75\\ \textrm{d}.&0,80\\ \textrm{e}.&1,20 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}3\sin \theta +4\cos \theta &=5\\ k\cos \left ( \theta -\alpha \right )&=5\\ a=x=4,\: &b=y=3\\ \theta &=\arctan \displaystyle \frac{b}{a}\\ \theta &=\arctan \displaystyle \frac{3}{4}\\ \color{black}\textrm{atau}\: \: &\\ \tan \theta &=\displaystyle \frac{3}{4}\\ \color{black}\textrm{maka}\: \: &\\ \sin \theta &=\displaystyle \frac{3}{\sqrt{3^{2}+4^{2}}}\\ &=\displaystyle \frac{3}{5}\\ &=\color{magenta}0,6 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 14.&\textrm{Jika}\: \: \tan \theta +\sec \theta =x \: \: \textrm{maka}\\ &\textrm{nilai dari} \: \: \tan \theta \: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle \frac{2x}{x^{2}-1}\\ \textrm{b}.&\displaystyle \frac{2x}{x^{2}+1}\\ \textrm{c}.&\displaystyle \frac{x^{2}+1}{2x}\\ \color{red}\textrm{d}.&\displaystyle \frac{x^{2}-1}{2x}\\ \textrm{e}.&\displaystyle \frac{x^{2}-1}{x^{2}+1} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\color{black}\textrm{Langkah}&\: \: 1\\ \tan \theta +\sec \theta &=x\\ \displaystyle \frac{\sin \theta }{\cos \theta } +\frac{1}{\cos \theta }&=x\\ \displaystyle \frac{\sin \theta +1}{\cos \theta }&=x\\ \sin \theta +1&=x\cos \theta ...........1\\ \color{black}\textrm{Langkah}&\: \: 2\\ \left (\tan \theta +\sec \theta \right )^{2}&=x^{2}\\ \tan ^{2}\theta +2\tan \theta \sec \theta +\sec ^{2}\theta &=x^{2}\\ \sec ^{2}\theta -1+2\tan \theta \sec \theta &+\sec ^{2}\theta =x^{2}\\ 2\sec ^{2}\theta +2\tan \theta \sec \theta &=x^{2}+1\\ \displaystyle \frac{2}{\cos ^{2}\theta }+\frac{2\sin \theta }{\cos ^{2}\theta }&=x^{2}+1\\ 1+\sin \theta &=\left (\displaystyle \frac{x^{2}+1}{2} \right )\cos ^{2}\theta.....2\\ \color{black}\textrm{Langkah}&\: \: 3\\ \left (\displaystyle \frac{x^{2}+1}{2} \right )\cos ^{2}&=x\cos \theta \\ \cos \theta &=\displaystyle \frac{2x}{x^{2}+1}\\ \textrm{maka}\: \: &(\color{magenta}\textbf{dengan sisi segitiga})\\ \tan \theta =\displaystyle \frac{\sqrt{\left ( x^{2}+1 \right )^{2}-(2x)^{2}}}{2x}&=\displaystyle \frac{\sqrt{x^{4}+2x^{2}+1-4x^{2}}}{2x}\\ \tan \theta &=\displaystyle \frac{\sqrt{x^{4}-2x^{2}+1}}{2x}\\ &=\displaystyle \frac{\sqrt{\left ( x^{2}-1 \right )^{2}}}{2x}\\ &=\displaystyle \frac{x^{2}-1}{2x} \end{aligned} \end{array}$

$\begin{aligned}.\: \: \qquad \textbf{Sehingga}&\: \textbf{dari kasus di atas didapatkan}\\ \color{magenta}\sin \theta &=\displaystyle \frac{x^{2}-1}{x^{2}+1}\\ \color{magenta}\cos \theta &=\displaystyle \frac{2x}{x^{2}+1}\\ \color{magenta}\tan \theta &=\displaystyle \frac{x^{2}-1}{2x} \end{aligned}$

$\begin{array}{ll}\\ 15.&\textrm{Jika}\: \: \sec x +\tan x =\displaystyle \frac{3}{2} \: \: \textrm{untuk}\\ &0\leq x\leq \displaystyle \frac{\pi }{2}\: \: \textrm{maka nilai} \: \: \sin x=....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\displaystyle \frac{5}{13}\\ \textrm{b}.&\displaystyle \frac{12}{13}\\ \textrm{c}.&\displaystyle 1\\ \textrm{d}.&\displaystyle \frac{2}{13}\\ \textrm{e}.&\displaystyle \frac{5}{12} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}\sec x +\tan x &=\displaystyle \frac{3}{2}\\ \textrm{ingat saat}&\: \color{black}\textrm{mengerjakan soal no}.14\\ \sec \theta +\tan \theta &=x\\ \sin \theta &=\displaystyle \frac{x^{2}-1}{x^{2}+1},\: \: \color{black}\textrm{maka}\\ \sin x&=\color{magenta}\displaystyle \frac{\left ( \displaystyle \frac{3}{2} \right )^{2}-1}{\left (\displaystyle \frac{3}{2} \right )^{2}+1}\\ &=\displaystyle \frac{\displaystyle \frac{9}{4}-1}{\displaystyle \frac{9}{4}+1}\\ &=\frac{\displaystyle \frac{5}{4}}{\displaystyle \frac{13}{4}}\\ &=\color{magenta}\displaystyle \frac{5}{13} \end{aligned} \end{array}$

Contoh Soal 2 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 6.&\textrm{Bentuk}\: \: \sqrt{3}\cos x-\sin x\: \: \textrm{untuk}\: \: 0\leq x\leq 2\pi ,\\ &\textrm{dapat dinyatakan sebagai}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&2\cos \left ( x+\displaystyle \frac{\pi }{6} \right )\\ \textrm{b}.&2\cos \left ( x+\displaystyle \frac{7\pi }{6} \right ) \\ \color{red}\textrm{c}.&2\cos \left ( x-\displaystyle \frac{11\pi }{6} \right )\\ \textrm{d}.&2\cos \left ( x-\displaystyle \frac{7\pi }{6} \right )\\ \textrm{e}.&2\cos \left ( x-\displaystyle \frac{\pi }{6} \right ) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textrm{c}\\ &\color{blue}\begin{aligned}\sqrt{3}\cos x-\sin x&=k\cos (x-\alpha )\\ (1)\qquad & (a,b)=\begin{cases} a &=\sqrt{3} \\ b &=-1 \end{cases}\\ \textrm{maka}\: &\textrm{titik ada dikadran IV}\\ (2)\: \quad k&=\sqrt{a^{2}+b^{2}}\\ &=\sqrt{\sqrt{3}^{2}+(-1)^{2}}\\ &=\sqrt{4}=2\\ (3)\quad \alpha &=\arctan \frac{b}{a}=\arctan \left (\frac{-1}{\sqrt{3}} \right )=-30^{\circ}\\ &=\left ( 360^{\circ}-30^{\circ} \right )=330^{\circ}=\displaystyle \frac{11}{6}\pi \\ \textrm{sehingga}&\\ \sqrt{3}\cos x-\sin x&=2\cos \left ( x-\displaystyle \frac{11}{6}\pi \right )\\ \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Nilai-nilai}\: \: x\: \: \textrm{yang terletak pada}\: \: 0\leq x\leq 2\pi ,\\ &\textrm{yang memenuhi persamaan}\: \: \sqrt{3}\cos x+\sin x=\sqrt{2}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&75^{\circ}\: \: \textrm{atau}\: \: 285^{\circ}\\ \color{red}\textrm{b}.&75^{\circ}\: \: \textrm{atau}\: \: 345^{\circ}\\ \textrm{c}.&15^{\circ}\: \: \textrm{atau}\: \: 285^{\circ}\\ \textrm{d}.&15^{\circ}\: \: \textrm{atau}\: \: 345^{\circ}\\ \textrm{e}.&15^{\circ}\: \: \textrm{atau}\: \: 75^{\circ} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textrm{b}\\ &\color{blue}\begin{aligned}\sqrt{3}\cos x+\sin x&=\sqrt{2}\\ \sqrt{\sqrt{3}^{2}+1^{2}}&\left ( \cos \left ( \alpha -\arctan \displaystyle \frac{1}{\sqrt{3}} \right ) \right )=\sqrt{2}\\ 2\cos \left ( x-30^{\circ} \right )&=\sqrt{2}\\ \cos \left ( x-30^{\circ} \right )&=\displaystyle \frac{\sqrt{2}}{2}=\frac{1}{2}\sqrt{2}\\ \cos \left ( x-30^{\circ} \right )&=\cos 45^{\circ}\\ \left ( x-30^{\circ} \right )&=\pm 45^{\circ}+k.360^{\circ}\\ x&=30^{\circ}\pm 45^{\circ}+k.360^{\circ}\\ \textrm{saat}\: \: k&=0\\ x_{1}&=75^{\circ}\\ x_{2}&=\color{red}-15^{\circ}\\ \textrm{saat}\: \: k&=1\\ x_{3}&=75^{\circ}+360^{\circ}=\color{red}435^{\circ}\\ x_{4}&=-15^{\circ}+360^{\circ}=345^{\circ} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Diketahui fungsi trigonometri}\: \: f(x)=\displaystyle \frac{1}{2}\sin 3x\\ &\textrm{perhatikanlah pernyataan-pernyataan berikut}\\ &(1)\quad \textrm{hasil dari}\: \: f(0)+f\left ( \displaystyle \frac{\pi }{6} \right )=1\\ &(2)\quad \textrm{hasil dari}\: \: f\left ( \displaystyle \frac{\pi }{6} \right )+f\left ( \displaystyle \frac{\pi }{3} \right )=\displaystyle \frac{1}{2}\\ &(3)\quad \textrm{hasil dari}\: \: f\left ( \displaystyle \frac{\pi }{6} \right )-f\left ( \displaystyle \frac{\pi }{3} \right )=\displaystyle \frac{1}{2}\\ &(4)\quad \textrm{hasil dari}\: \: f\left ( \displaystyle \frac{\pi }{3} \right )-f\left ( \displaystyle \frac{\pi }{6} \right )=1\\ &\textrm{Pernyataan yang tepat adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&(1)\: \: \textrm{dan}\: \: (2)\\ \textrm{b}.&(1)\: \: \textrm{dan}\: \: (3)\\ \textrm{c}.&(1)\: \: \textrm{dan}\: \: (4)\\ \color{red}\textrm{d}.&(2)\: \: \textrm{dan}\: \: (3)\\ \textrm{e}.&(3)\: \: \textrm{dan}\: \: (4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textrm{d}\\ &\color{blue}\begin{aligned}\textrm{Diketahui}&\\ f(x)&=\displaystyle \frac{1}{2}\sin 3x\\ \textrm{maka}\qquad&\\ f(0)&=\displaystyle \frac{1}{2}\sin 3(0^{\circ})=0\\ f\left ( \displaystyle \frac{\pi }{3} \right )&=\displaystyle \frac{1}{2}\sin 3\left ( \displaystyle \frac{\pi }{3} \right )=0\\ f\left ( \displaystyle \frac{\pi }{6} \right )&=\displaystyle \frac{1}{2}\sin 3\left ( \displaystyle \frac{\pi }{6} \right )=\displaystyle \frac{1}{2}\\ \end{aligned} \end{array}$

$\begin{array}{ll}\\ 9.&\textrm{Himpunan penyelesaian dari}\: \: \sin x-\sqrt{3}\cos x=-1\\ &\textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\left \{ 0^{\circ},120^{\circ} \right \}\\ \textrm{b}.&\left \{ 90^{\circ},330^{\circ} \right \}\\ \textrm{c}.&\left \{ 60^{\circ},180^{\circ} \right \}\\ \textrm{d}.&\left \{ 90^{\circ},120^{\circ} \right \}\\ \color{red}\textrm{e}.&\left \{ 30^{\circ},270^{\circ} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\begin{aligned}\sin x-\sqrt{3}\cos x&=-1\\ \sqrt{1^{2}+\left ( -\sqrt{3} \right )^{2}}\cos \left ( x-\alpha \right )&=-1\\ a&=x=-\sqrt{3},\: \: b=y=1\\ &\textbf{kuadran II}\\ \alpha &=\arctan \left ( \displaystyle \frac{1}{-\sqrt{3}} \right )=-30^{\circ}\\ &=180^{\circ}-30^{\circ}=150^{\circ}\\ \textrm{maka persamaan akan}&\: \textrm{menjadi}\\ 2\cos \left ( x-150^{\circ} \right )&=-1\\ \cos \left ( x-150^{\circ} \right )&=\displaystyle \frac{-1}{2}\\ \cos \left ( x-150^{\circ} \right )&=\cos 120^{\circ}\\ \left ( x-150^{\circ} \right )&=\pm 120^{\circ}+k.360^{\circ}\\ x&=150^{\circ}\pm 120^{\circ}+k.360^{\circ}\\ \textrm{saat}\: \: &k=0\\ x_{1}&=270^{\circ}\\ x_{2}&=30^{\circ}\\ \textrm{saat}\: \: &k=1\\ x_{3}&=270^{\circ}+360^{\circ}=....\\ x_{4}&=30^{\circ}+360^{\circ}=.... \end{aligned} \end{array}$

$\begin{array}{ll}\\ 10.&\textrm{Nilai}\: \: \tan x\: \: \textrm{yang memenuhi persamaan}\\ &\cos 2x+7\cos x-3=0\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\sqrt{3}\\ \textrm{b}.&\displaystyle \frac{1}{2}\sqrt{3}\\ \textrm{c}.&\displaystyle \frac{1}{3}\sqrt{3}\\ \textrm{d}.&\displaystyle \frac{1}{2}\\ \textrm{e}.&\displaystyle \frac{1}{5}\sqrt{5} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}\cos 2x+7\cos x-3&=0\\ 2\cos ^{2}x-1+7\cos x-3&=0\\ 2\cos ^{2}x+7\cos x-4&=0\\ \left ( \cos x+4 \right )\left (2 \cos -1 \right )&=0\\ \color{red}\cos x=-4\: \: \color{black}\textrm{atau}\: \: \color{magenta}\cos x&=\displaystyle \frac{1}{2}=\cos 60^{\circ}\\ x&=60^{\circ},\\ \textrm{maka}&\\ \tan 60^{\circ}&=\sqrt{3}\\\\ \textrm{ dan ingat bahwa}&\: \: \cos x=-4\: \: \color{red}\textrm{tidak memenuhi} \end{aligned} \end{array}$

Contoh Soal 1 Persamaan Trigonometri (Matematika Peminatan Kelas XI)

$\begin{array}{ll}\\ 1.&\textrm{Himpunan penyelesaian dari}\\ &\sin 2x=\displaystyle \frac{1}{2}\sqrt{3}\: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\left \{ 30^{\circ},210^{\circ} \right \}\\ \textrm{b}.&\left \{ 60^{\circ},240^{\circ} \right \}\\ \textrm{c}.&\left \{ 30^{\circ},60^{\circ},210^{\circ} \right \}\\ \color{red}\textrm{d}.&\left \{ 30^{\circ},60^{\circ},210^{\circ},240^{\circ} \right \}\\ \textrm{e}.&\left \{ 30^{\circ},60^{\circ},210^{\circ},240^{\circ},270^{\circ} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\sin 2x&=\displaystyle \frac{1}{2}\sqrt{3}\\ \sin 2x&=\sin 60^{\circ}\\ 2x&=\begin{cases} 60^{\circ} & +k.360^{\circ} \\ \left ( 180^{\circ}-60^{\circ} \right ) & +k.360^{\circ} \end{cases}\\ x&=\begin{cases} 30^{\circ} & +k.180^{\circ}\\ 60^{\circ} & +k.180^{\circ} \end{cases}\\ \textrm{saat}&\: \: k=0\\ x&=\begin{cases} 30^{\circ} & \\ 60^{\circ} & \end{cases}\\ \textrm{saat}&\: \: k=1\\ x&=\begin{cases} 30^{\circ} & +1.180^{\circ}=210^{\circ}\\ 60^{\circ} & +1.180^{\circ}=240^{\circ} \end{cases}\\ \textrm{saat}&\: \: k=2\\ x&=\begin{cases} 30^{\circ} & +2.180^{\circ}=\color{red}390^{\circ}\\ 60^{\circ} & +2.180^{\circ}=\color{red}420^{\circ} \end{cases}\\ \color{red}\textrm{kedua}&\color{red}\textrm{nnya tidak memenuhi} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Himpunan penyelesaian dari}\\ &\tan 2x-\sqrt{3}=0\: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\left \{ 15^{\circ},105^{\circ},195^{\circ},285^{\circ} \right \}\\ \color{red}\textrm{b}.&\left \{ 30^{\circ},120^{\circ},210^{\circ},300^{\circ} \right \}\\ \textrm{c}.&\left \{ 45^{\circ},135^{\circ},225^{\circ},315^{\circ} \right \}\\ \textrm{d}.&\left \{ 15^{\circ},105^{\circ},195^{\circ},285^{\circ} \right \}\\ \textrm{e}.&\left \{ 15^{\circ},30^{\circ},45^{\circ},60^{\circ},75^{\circ} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\begin{aligned}\tan 2x&-\sqrt{3}=0\\ \tan 2x&=\sqrt{3}\\ \tan 2x&=\tan 60^{\circ}\\ 2x&=60+k.180^{\circ}\\ x&=30^{\circ}+k.90^{\circ}\\ \textrm{saat}&\: \: k=0\\ x&=30^{\circ}\\ \textrm{saat}&\: \: k=1\\ x&=30^{\circ}+90^{\circ}=120^{\circ}\\ \textrm{saat}&\: \: k=2\\ x&=30^{\circ}+180^{\circ}=210^{\circ}\\ \textrm{saat}&\: \: k=3\\ x&=30^{\circ}+270^{\circ}=300^{\circ}\\ \textrm{saat}&\: \: k=4\\ x&=30^{\circ}+360^{\circ}=\color{red}390^{\circ}\\ \color{red}\textrm{tidak}&\: \color{red}\textrm{memenuhi} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Himpunan penyelesaian dari}\\ &\cos 3x=-\displaystyle \frac{1}{2}\sqrt{3}\: \: \textrm{untuk}\: \: 0^{\circ}\leq x\leq 180^{\circ}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\left \{ 40^{\circ},80^{\circ} \right \}\\ \textrm{b}.&\left \{ 50^{\circ},70^{\circ} \right \}\\ \textrm{c}.&\left \{ 40^{\circ},70^{\circ},80^{\circ} \right \}\\ \color{red}\textrm{d}.&\left \{ 50^{\circ},70^{\circ},170^{\circ} \right \}\\ \textrm{e}.&\left \{ 50^{\circ},80^{\circ},170^{\circ} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\begin{aligned}\cos 3x&=-\displaystyle \frac{1}{2}\sqrt{3}\\ \cos 3x&=-\cos 30^{\circ}\\ \cos 3x&=\cos \left (180^{\circ}-30^{\circ} \right )=\cos 150^{\circ}\\ 3x&=\pm 150^{\circ}+k.360^{\circ}\\ x&=\pm 50^{\circ}+k.120^{\circ}\\ \textrm{saat}&\: \: k=0\\ x&=\pm 50^{\circ}\: \rightarrow x=50^{\circ}\: \: (\textrm{mm})\\ \textrm{saat}&\: \: k=1\\ x&=\pm 50^{\circ}+120^{\circ}=\begin{cases} 170^{\circ} & (\textrm{mm}) \\ 70^{\circ} & (\textrm{mm}) \end{cases} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Nilai}\: \: x\: \: \textrm{yang memenuhi persamaan}\\ &2\cos ^{2}x+\cos x-1=0\: \: \textrm{untuk}\: \: 0\leq x\leq \pi \\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\displaystyle \frac{1}{3}\pi \: \: \textrm{dan}\: \: \pi \\ \textrm{b}.&\displaystyle \frac{1}{3}\pi \: \: \textrm{dan}\: \: \frac{2}{3}\pi \\ \textrm{c}.&\displaystyle \frac{1}{3}\pi \: \: \textrm{dan}\: \: \frac{3}{4}\pi \\ \textrm{d}.&\displaystyle \frac{1}{4}\pi \: \: \textrm{dan}\: \: \frac{3}{4}\pi \\ \textrm{e}.&\displaystyle \frac{1}{4}\pi \: \: \textrm{dan}\: \: \frac{2}{3}\pi \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}2\cos ^{2}x+\cos x-1&=0\\ \left (2\cos x-1 \right )\left (\cos x+1 \right )&=0\\ \cos x=\displaystyle \frac{1}{2}\: \: \color{magenta}\textrm{atau}\: \: &\cos x=-1\\ \cos x=\cos 60^{\circ}=\cos \frac{1}{3}\pi \: \: &\\ \color{magenta}\textrm{atau}\: \: \cos x&=\cos 180^{\circ}=\cos \pi \\ \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Untuk}\: \: x\: \: \textrm{yang memenuhi persamaan}\\ &\tan ^{2}x-\tan x-6=0\: \: \textrm{pada}\: \: 0\leq x\leq \pi ,\\ &\textrm{maka himpunan nilai}\: \: \sin x\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\left \{ \displaystyle \frac{3\sqrt{10}}{10},\frac{2\sqrt{5}}{5} \right \}\\ \textrm{b}.&\left \{ \displaystyle \frac{3\sqrt{10}}{10},-\frac{2\sqrt{5}}{5} \right \} \\ \textrm{c}.&\left \{ -\displaystyle \frac{3\sqrt{10}}{10},\frac{2\sqrt{5}}{5} \right \} \\ \textrm{d}.&\left \{ \displaystyle \frac{\sqrt{10}}{10},\frac{\sqrt{5}}{5} \right \} \\ \textrm{e}.&\left \{ \displaystyle \frac{\sqrt{10}}{10},\frac{2\sqrt{5}}{5} \right \} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\begin{aligned}\tan ^{2}x-\tan x-6&=0\\ \left (\tan x-3 \right )\left (\tan x+2 \right )&=0\\ \tan x=3\: \: \textrm{atau}\: \: &\tan x=-2\\ \tan x=\displaystyle \frac{3}{1}\: \: \textrm{atau}\: \: &\tan x=\frac{-2}{1}\\ \sin x=\displaystyle \frac{3}{\sqrt{1^{2}+3^{2}}}\: \: \textrm{atau}\: \: &\sin x=\frac{2}{\sqrt{1^{2}+2^{2}}}\\ \sin x=\displaystyle \frac{3}{\sqrt{10}}\: \: \textrm{atau}\: \: &\sin x=\frac{2}{\sqrt{5}}\\ \sin x=\displaystyle \frac{3}{10}\sqrt{10}\: \: \textrm{atau}\: \: &\sin x=\frac{2}{5}\sqrt{5} \end{aligned} \end{array}$