Program Linear Dua Variabel (Matematika Wajib Kelas XI)

$\LARGE\color{blue}\textrm{A. Pendahuluan}$

Untuk menguasai materi ini, materi prasyarat yang harus pembaca kuasai adalah materi tentang persamaan linier dua variabel dan tentunya materi pertidaksamaan linear satu variabel. Materi program linear ini banyak digunakan dalam bidang ekonomi khususnya masalah optimasi.

$\LARGE\color{blue}\textrm{B. Sistem Pertidaksamaan Linear Dua Variabel}$

Sebelumnya perhatikanlah ilustrasi berikut

Bentuk umum yang akan digunakan dalam bahasan ini adalah sebagai berikut

$\color{blue}\begin{aligned}&\begin{cases} ax+by &\geq m \\ ax+by &>m \\ cx+dy &\leq n \\ cx+dy & <n \end{cases}\\\\ &\color{magenta}\textrm{dengan}\\ &a,b,c,d,m,n\: \: \textrm{bilangan riil}\\ &\color{magenta}\textrm{serta}\\ &x,y\: \: \textrm{keduanya adalah peubah bebas/variabel} \end{aligned}$

Sebagai misal 

Untuk membantu menentukan pertidaksamaan linear dua variabel di atas tentunya penting juga membuat persamaan garis lurus (linear) sebagai prasyarat untuk membuat pertidaksaan yang dimaksud, yaitu:

$\begin{aligned}&\textrm{Persamaan garis di atas adalah}:\\ &\qquad\qquad\quad ax+by=ab \end{aligned}$

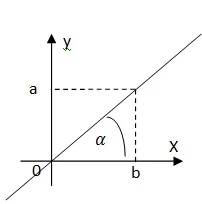
dan jika garisnya berbentuk berikut:

$\begin{aligned}&\textrm{maka persamaan garisnya adalah}:\\ &(1)\qquad ax-by=0,\: \: \textrm{atau}\\ &(2)\qquad y=\left (\tan \alpha \right )x \end{aligned}$

dan jika garisnya berupa ilustrasi berikut

$\begin{aligned}&\textrm{maka persamaan gradien dan garisnya adalah}:\\ &(1)\qquad m=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}},\: \: \textrm{dan}\\ &(2)\qquad y=m\left ( x-x_{1} \right )+y_{1} \end{aligned}$

Dalam program linear terdapat dua hal yang harus diperhatikan yang berkaitan dalam penyelesaian dari masalah optimasi nantinya, yaitu kendala-kendala berupa pertidaksamaan linear dua variabel yang menjadi bahasan utama dan fungsi objektif sebagai fungsi sasarannya untuk mendapatkan dan menentukan mana yang nantinya dinyatakan suatu vektek (titik pojok) sebagai titik maksimum atau minimum.

$\LARGE\color{blue}\textrm{C. Nilai Optimum Fungsi Objektif}$

Bentuk umum dari fungsi objektif ini adalah

$\LARGE\color{magenta}\boxed{f(x,y)=ax+by}$

Fungsi optimum ini akan menunjukkan keoptimumnya mana kala titik-titik pojok disubstitusikan pada fungsi ini sehingga akan didapatkan nilai maksimum atau minimunya. 

Untuk mendapatkan nilai optimum dari fungsi objektif ini dapat digunakan salah satu metode berikut

• metode uji titik pojok
• metode garis selidik

$\LARGE\color{blue}\textrm{D. Langkah Penyelesaian Program Linear}$

$\begin{aligned}(1)\quad&\textrm{Membuat model matematika}.\\ &\color{blue}\textrm{Memodelkan soal ke dalam bahasa matematika}\\ (2)\quad&\textrm{Menyelesaikan sistem pertidaksamaan linear}\\ &\textrm{(dua variabel) dan mengarsir daerah yang}\\ &\color{blue}\textrm{memenuhi pertidaksamaan yang diinginkan} \\ (3)\quad&\textrm{Menentukan titik-titik sudut (verteks / titik ekstrem )}\\ (4)\quad&\textrm{Menentukan penyelesaian Optimasi dari fungsi objektif tersebut}\\ & \textrm{(kadang disebut sebagai fungsi sasaran / tujuan)}\: \: \color{red}f(x,y)=ax+by\\ & \color{blue}\textrm{baik dengan metode uji titik sudut (Verteks / titik ekstrem)}\\ & \color{blue}\textrm{atau garis selidik}. \end{aligned}$

$\LARGE\color{magenta}\fbox{CONTOH SOAL}$

$\begin{array}{ll}\\ &\textrm{Tentukanlah nilai minimum fungsi objektif}\\ & f(x,y)=3x+5y.\: \: \textrm{Jika diketahui}\\ &\textrm{kendala-kendalanya adalah sebagai berikut}:\\ &\begin{cases} 2x+y &\geq 8 \\ 2x+3y &\geq 12 \\ x\geq 0& \\ y\geq 0 & \end{cases}\\\\ &\textbf{Jawab}\\ &\textrm{Mula-mula kita tentukan wilayah kendalanya, yaitu}:\\ &\textrm{kendala 1}:\: \: 2x+y\geq 8,\: \: \textrm{maka garisnya}:2x+y=8\\ &\begin{array}{|c|c|c|}\hline x&0&4\\\hline y&8&0\\\hline (x,y)&(0,8)&(4,0)\\\hline \end{array}\\ &\textrm{kendala 2}:\: \: 2x+3y\geq 12,\: \: \textrm{garisnya}:2x+3y=12\\ &\begin{array}{|c|c|c|}\hline x&0&6\\\hline y&4&0\\\hline (x,y)&(0,4)&(6,0)\\\hline \end{array}\\ &\textrm{kendala 3}:\: \: x\geq 0,\: \: \textrm{garisnya}:x=0\\ &\textrm{yang diarsir wilayah dari sumbu Y ke kanan}\\ &\textrm{kendala y}:\: \: y\geq 0,\: \: \textrm{garisnya}:y=0\\ &\textrm{yang diarsir wilayah dari sumbu X ke atas}\\ &\textrm{Dan titik potong kedua garis di atas, yaitu}:\\ &\begin{array}{|c|c|}\hline 2x+y=8&2x+3y=12\\\hline \textrm{di eliminasi}&\textrm{substitusi}\\\hline \begin{matrix} 2x+y=8\\ 2x+3y=12\\ -------\\ -2y=-4\\ y=2 \end{matrix}&\begin{aligned}&2x+y=8\\ &2x+(2)=8\\ &2x=8-2\\ &x=4-1=3 \end{aligned}\\\hline \color{blue}\begin{aligned}&\qquad\quad\textrm{Jadi}\\ &\textrm{titik potongnya}\\ &\textrm{potongnya adalah} \end{aligned}&\color{red}(3,2)\\\hline \end{array}\\ &\textrm{Langkah berikutnya menentukan vertek dan}\\ &\textrm{menggambar kedalam koordinat Kartesius, yaitu}:\\ \end{array}$

$\color{blue}\begin{aligned}.\quad&\textrm{Langkah berikutnya menentukan}\\ &\textrm{nilai minimumnya, yaitu}: \end{aligned}$

$\begin{array}{|c|c|l|}\hline \textrm{Titik pojok/vertek}&f(x,y)=3x+5y&\textrm{Keterangan}\\\hline (6,0)&3.6+0=18&\color{blue}\textrm{Minimum}\\\hline (3,2)&3.3+5.2=19&\\\hline (0,8)&0+5.8=40&\\\hline \end{array}$

DAFTAR PUSTAKA

1. Muis, A. 2009. Perang Siasat Matematika Dasar. Bantul: KREASI WACANA
2. Tim VisiMath. 2009. 5000Plus Soal Matematika. Jakarta: Cerdas Interaktif