Mengenal laju perubahan untuk nilai suatu fungsi
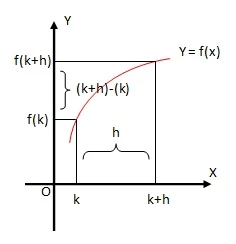
Perhatikanlah ilustrasi gambar berikut
Misalkan diketahui fungsi  terdefinisi untuk semua harga x di sekitar
terdefinisi untuk semua harga x di sekitar 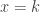 . Jika
. Jika 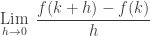 ada, maka bentuk
ada, maka bentuk 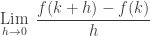 disebut turunan dari fungsi
disebut turunan dari fungsi  saat
saat 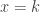 .
.
B. Notasi
- Notasi turunan fungsi dilambangkan dengan
dengan
.
- Lambang
dibaca f aksen k desebut turunan atau derivatif untuk fungsi
terhadap
saat
.
- Jika limitnya ada, dapat dikatakan fungsi
diferensiabel(dapat didiferebsialkan) saat
dan bentuk limitnya selanjutna dilambangkan dengan
.
- Misalkan fungsi
memiliki turunan
. Jika
tidak terdefinisi maka
tidak diferensiabel di
.
Tidak ada komentar:
Posting Komentar
Informasi