Lanjutan Materi Distribusi Peluang Kontinu (Matematika Peminatan Kelas XII)

 $\color{blue}\begin{aligned}\textrm{C. 2}.\quad&\textrm{Distribusi Peluang Kontinue} \end{aligned}$

Jika pada distribusi peluang diskrit nilai  x diperjelas lagi menjadi nilai eksak atau kontinue, maka distribusi peluangnya akan berubah menjadi distribusi peluang kontinu.

Luas seluruh daerah di dalam kurva memiliki luas 1. Luas daerah pada wilayah yang diarsi (warna kuning) yang terletak antara X=a  dan X=b dapat dinyatakan dengan :  $P(a\leq X\leq b)=\displaystyle \int_{a}^{b}f(x)\: \: dx$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Fungsi peluang lama bicara seorang}\\ &\textrm{operator sebagai berikut}\\ &f(x)=\begin{cases} kx &\textrm{untuk}\: \: 0\leq k\leq 5 \\ k(10-x)&\textrm{untuk}\: \: 5\leq k\leq 10\\ \qquad 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{Nilai}\: \: k\\ &\textrm{b}.\quad \textrm{Peluang operator telpon berbicara}\\ &\qquad \textrm{lebih dari 8 menit}\\ &\qquad \textrm{Peluang operator telpon berbicara}\\ &\qquad \textrm{2 sampai 4 menit}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Karena}\: \: f(x)\: \: \textrm{adalah fungsi peluang, maka}\\ &\displaystyle \int_{0}^{5}kx\: dx+\int_{5}^{10}k(10-x)\: dx=1\\ &\Leftrightarrow \left [ \displaystyle \frac{1}{2}kx^{2} \right ]_{0}^{5}+\left [ 10kx-\displaystyle \frac{1}{2}kx^{2} \right ]_{5}^{10}=1\\ &\Leftrightarrow \displaystyle \frac{1}{2}k(5^{2}-0^{2})+\left ( 10k(10-5)-\displaystyle \frac{1}{2}k(10^{2}-5^{2}) \right )=1\\ &\Leftrightarrow \displaystyle \frac{1}{2}k(25)+10k(5)-\displaystyle \frac{1}{2}k(100-25)=1\\ &\Leftrightarrow \displaystyle \frac{25}{2}k+50k-\displaystyle \frac{75}{2}k=1\\ &\Leftrightarrow 50k-25k=1\\ &\Leftrightarrow 25k=1\\ &\Leftrightarrow k=\color{red}\displaystyle \frac{1}{25}\\ \textrm{b}.\quad&\textrm{Misalkan saja}\\ &X=\textrm{lama operator telpon bicara}\\ &\textrm{Peluang operator berbicara lebih}\\ &\textrm{dari 8 menit}=P(X>8),\\ &P(X>8)=P(8<X\leq 10)\\ &\quad\qquad =\displaystyle \int_{8}^{10}k(10-x)\: dx\\ &\quad\qquad =\displaystyle \int_{8}^{10}\frac{1}{25}(10-x)\: dx\\ &\quad\qquad =\displaystyle \frac{1}{25}\left [ 10x-\displaystyle \frac{1}{2}x^{2} \right ]_{8}^{10}\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 10(10-8)-\displaystyle \frac{1}{2}(10^{2}-8^{2}) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 10.(2)-\displaystyle \frac{1}{2}(100-64) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 20-\displaystyle \frac{1}{2}(36) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}(20-18)\\ &\quad\qquad =\displaystyle \frac{1}{25}(2)=\color{red}\frac{2}{25}=0,08\\ \textrm{c}.\quad&\textrm{Peluang operator telpon berbicara}\\ &P(2\leq X\leq 4)\\ &=\displaystyle \int_{2}^{4}kx\: dx\\ &=\displaystyle \int_{2}^{4}\displaystyle \frac{1}{25}x\: dx\\ &=\displaystyle \frac{1}{25}\left [ \displaystyle \frac{1}{2}x^{2} \right ]_{2}^{4}\\ &=\displaystyle \frac{1}{25}\times \frac{1}{2}(4^{2}-2^{2})\\ &=\displaystyle \frac{1}{50}(16-4)\\ &=\color{red}\displaystyle \frac{12}{50}=0,24 \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Kurnia, N., dkk. 2018. Jelajah Matematika SMA Kelas XII Peminatan MIPA. Bogor: YUDHISTIRA.
2. Tasari. Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.

Contoh Soal Distribusi Binomial (2)

$\color{blue}\textbf{Contoh Variabel Acak}$

$\begin{array}{ll}\\ 6.&\textrm{Sebuah uang logam ditos sebanyak 3 kali}\\ &\textrm{Jika}\: \: X\: \: \textrm{sebagai variabel acak dari kejadian}\\ &\textrm{munculnya sisi angka (A), maka peluang}\\ &\textrm{a. kejadian terjadi muncul 0 angka}\\ &\textrm{b. kejadian terjadi muncul 1 angka}\\ &\textrm{c. kejadian terjadi muncul 2 angka}\\ &\textrm{d. kejadian terjadi muncul 3 angka}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{aligned} \color{blue}\textrm{Mula}\: \, &\color{red}(1)\quad (2)\quad (3)\quad \color{blue}\textbf{Ruang sampel}\\ \textbf{Mulai}&\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (A,A,A)\\ G\rightarrow (A,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (A,G,A)\\ G\rightarrow (A,G,G) \end{matrix}\right. \end{matrix}\right.\\ G\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (G,A,A)\\ G\rightarrow (G,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (G,G,A)\\ G\rightarrow (G,G,G) \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. \end{aligned}\\ &\begin{aligned}P(X=0)&=P((G,G,G))\\ &=\displaystyle \frac{n(X=0)}{n(S)}\\ &=\color{red}\displaystyle \frac{1}{8}\\ P(X=1)&=P((G,G,A),(G,A,G),(A,G,G))\\ &=\displaystyle \frac{n(X=1)}{n(S)}\\ &=\color{red}\displaystyle \frac{3}{8}\\ P(X=2)&=P((G,A,A),(A,G,A),(A,A,G))\\ &=\displaystyle \frac{n(X=2)}{n(S)}\\ &=\color{red}\displaystyle \frac{3}{8}\\ P(X=3)&=P((A,A,A))\\ &=\displaystyle \frac{n(X=3)}{n(S)}\\ &=\color{red}\displaystyle \frac{1}{8} \end{aligned} \end{array}$

Contoh Soal Distribusi Binomial (1)

$\color{blue}\textbf{Contoh Peluang dan Kombinasi}$

$\begin{array}{ll}\\ 1.&\textrm{Seorang melempar sebuah dadu dengan enam muka}\\ &\textrm{Tentukukanlah}\\ &\textrm{a}.\quad \textrm{ruang sampel}\\ &\textrm{b}.\quad \textrm{peluang muncul mata dadu ganjil}\\ &\textrm{c}.\quad \textrm{peluang muncul mata dadu genap}\\ &\textrm{d}.\quad \textrm{peluang muncul mata dadu angka prima}\\ &\textrm{e}.\quad \textrm{peluang muncul mata dadu kurang dari 6}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Mata}&\: \textrm{dadu ada 6, yaitu}:\color{red}1,2,3,4,5,\: \& \: 6\\ \textrm{a}.\quad&\textrm{Raung sampel}\\ &S=\color{red}\left \{ 1,2,3,4,5,6 \right \}\: \color{black}\Rightarrow n(S)=6\\ \textrm{b}.\quad&\textrm{peluang}\: \color{red}\textrm{muncul mata dadu ganjil}\color{black}(J)\\ &\textrm{Mata dadu ganjil}:1,3,5\: \Rightarrow n(J)=3\\ &\textrm{Peluangnya}=\displaystyle \frac{n(J)}{n(S)}=\frac{3}{6}=\frac{1}{2}\\ \textrm{c}.\quad&\textrm{peluang}\: \color{red}\textrm{muncul mata dadu ganap}\color{black}(P)\\ &\textrm{Mata dadu ganap}:2,4,6\: \Rightarrow n(P)=3\\ &\textrm{Peluangnya}=\displaystyle \frac{n(P)}{n(S)}=\frac{3}{6}=\frac{1}{2}\\ \textrm{d}.\quad&\textrm{peluang}\: \color{red}\textrm{muncul mata dadu angka prima}\color{black}(R)\\ &\textrm{Mata dadu angka prima}:2,3,5\: \Rightarrow n(R)=3\\ &\textrm{Peluangnya}=\displaystyle \frac{n(R)}{n(S)}=\frac{3}{6}=\frac{1}{2}\\ \textrm{e}.\quad&\textrm{peluang}\: \color{red}\textrm{muncul mata dadu kurang dari 6}\color{black}(Z)\\ &\textrm{Mata dadu kurang dari 6}:1,2,3,4,5\: \Rightarrow n(Z)=5\\ &\textrm{Peluangnya}=\displaystyle \frac{n(Z)}{n(S)}=\frac{5}{6} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Andi akan mengambil 4 buah bola dari}\\ &\textrm{10 warna yang berbeda. Berapakah banyak}\\ &\textrm{kombinasi warna yang berbeda yang diambil}\\ &\textrm{oleh Andi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}n=10&\: \: \textrm{dan}\: \: r=4\\ C(n,r)&=\displaystyle \frac{n!}{r!(n-r)!}\\ C(10,4)&=\displaystyle \frac{10!}{4!(10-4)!}\\ &=\displaystyle \frac{10!}{4!\times 6!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6!}{(4\times 3\times 2\times 1)\times 6!}\\ &=420\: \: \textrm{kombinasi warna bola berbeda} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Dua kantong berisi bola merah dan biru}\\ &\textrm{Kantong I memuat 4 bola merah dan }\\ &\textrm{6 bola biru. Sedangkan kantong II memuat}\\ &\textrm{5 bola merah dan 3 bola biru. Jika pada}\\ &\textrm{masing-masing kantong diambil 2 bola}\\ &\textrm{sekaligus, maka peluang terambilnya}\\ &\textrm{1 bola merah dan 1 bola biru pada kantong}\\ &\textrm{I serta 2 bola biru pada kantong II}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Kejadian di atas adalah kejadian saling}\\ &\textrm{bebas karena tidak saling mempengaruhi}\\ &\begin{aligned}\textrm{Misal}&\: X=\textrm{kejadian terambil}\: 1M,1B\\ \bullet \quad&\color{red}\textrm{pada kantong I}\\ P(X)&=\displaystyle \frac{C(4,1)\times C(6,1)}{C(10,2)}\\ &=\displaystyle \frac{4\times 6}{\displaystyle \frac{10\times 9}{2}}=\frac{8}{15}\\ \textrm{Misal}&\: Y=\textrm{kejadian terambil}\: 2B\\ \bullet \quad&\color{red}\textrm{pada kantong II}\\ P(Y)&=\displaystyle \frac{C(3,2)}{C(8,2)}\\ &=\displaystyle \frac{3}{\displaystyle \frac{8\times 7}{2}}=\frac{3}{28}\\ \color{magenta}\textrm{maka}&\: \textrm{peluang dari}\: \: X\: \: \textrm{dan}\: \: Y\\ P(X\cap Y)&=P(X)\times P(Y)\\ &=\displaystyle \frac{8}{15}\times \frac{3}{28}\\ &=\displaystyle \frac{2}{35} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Berapa banyak cara dapat memilih untuk}\\ &\textrm{3 perwakilan dari 10 anggota suatu}\\ &\textrm{kelompok, jika}\\ &\textrm{a. tanpa perlakuan khusus}\\ &\textrm{b. salah seorang harus terpilih}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Dengan tanpa perlakuan}\\ &\textrm{memilih 3 orang dari 10 orang adalah}:\\ &C(10,3)=\displaystyle \frac{10!}{3!(10-3)!}=\frac{10!}{3!\times 7!}=\color{blue}120\\ \textrm{b}.\quad&\textrm{Dengan perlakuan 1 orang terpilih}\\ &\color{red}(\textrm{1 orang ini artinya tidak perlu diperhitungkan})\\ &\textrm{memilih 2 orang dari 9 orang adalah}:\\ &C(9,2)=\displaystyle \frac{9!}{2!(9-2)!}=\frac{9!}{2!\times 8!}=\color{blue}36 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Berapa banyak cara dapat memilih 2 buku}\\ &\textrm{matematika dan 3 buku fisika serta 4 buku}\\ &\textrm{ekonomi pada suatu lemari buku yang}\\ &\textrm{di dalamnya terdapat 10 buku matematika,}\\ &\textrm{11 buku fisika dan 12 buku ekonomi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Banyak}&\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,2)\times C(11,3)\times C(12,4)\\ &=\displaystyle \frac{10!}{2!\times 8!}\times \frac{11!}{3!\times 8!}\times \frac{12!}{4!\times 8!}\\ &=\displaystyle \frac{10\times 9}{1\times 2}\times \frac{11\times 10\times 9}{1\times 2\times 3}\times \frac{12\times 11\times 10\times 9}{1\times 2\times 3\times 4}\\ &=\color{red}3675375 \end{aligned} \end{array}$

Lanjutan Materi Distribusi Peluang Diskrit (Matematika Peminatan Kelas XII)

$\color{blue}\begin{aligned}\textrm{C. 1}.\quad&\textrm{Distribusi Peluang Diskrit} \end{aligned}$

$\begin{aligned} &\textrm{Misalkan}\: \: X\: \: \textrm{adalah variabel acak diskrit}\\ &\textrm{dari nilai}\: :\: \: x_{1},\: x_{2},\: x_{3},\: x_{4},\: \cdots \: ,\: x_{k},\: \textrm{dan}\\ &P\: \textrm{adalah seluruh nilai peluang untuk}\: :\\ &p_{1},\: p_{2},\: p_{3},\: p_{4},\: \cdots \: ,p_{k}, \textrm{maka nilai untuk}\\ &\color{blue}p_{1}+ p_{2}+ p_{3}+ p_{4}+ \cdots +p_{k}=1\\ &\textbf{dan}\\ &\textrm{Fungsi}\: \: f(x) =P(X=x)\: \: \textrm{yang mempunyai}\\ &\textrm{nilai}\: \: p_{1},\: p_{2},\: p_{3},\: p_{4},\: \cdots \: ,p_{k},\: \textrm{pada variabel}\\ &X=x_{1},\: x_{2},\: x_{3},\: x_{4},\: \cdots \: ,\: x_{k},\: \textrm{disebut fungsi}\\ &\textrm{kepekatan peluang dari variabel acak}\: \: X.\\ &\textrm{Selanjutnya jika kita gambar grafik}\: \: f(x)\\ &\textrm{terhadap}\: \: x,\: \textrm{maka kita akan grafik yang}\\ &\textrm{dinamakan dengan}\: \: \color{red}\textbf{grafik peluang} \end{aligned}$

Suatu fungsi  $f(x)=P(X=x)$  disebut fungsi peluang (probabilitas) dari  $X$, jika memenuhi syarat-syarat:

$\color{blue}\begin{matrix} (\textrm{i})\quad f(x)\geq 0\: \: \: \textrm{untuk semua}\: \: x\qquad\qquad\qquad\qquad\qquad\qquad\: \:  \\\\ (\textrm{ii})\quad \sum_{i=1}^{n}f\left ( x_{i} \right )=\color{red}f(x_{1})+f(x_{2})+f(x_{3})+...+f(x_{n})=\color{black}1 \end{matrix}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Pada percobaan melempar 3 koin identik}\\ &\textrm{sekaligus bersama-sama. Variabel acak}\\ &\textrm{dalam hal ini pada kejadian muncul sisi}\\ &\textrm{gambar, tentukan}\\ &\textrm{a}.\: \: \textrm{distribusi peluangnya}\\ &\textrm{b}.\: \: \textrm{tabel fungsi peluangnya}\\ &\textrm{c}.\: \: \textrm{grafik fungsi peluangnya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui dari soal}\: \: \color{red}\textrm{variabel acak}\\ &\textrm{pada kejadian di atas adalah munculnya}\\ &\textrm{sisi gambar pada pelemparan 3 koin}\\ &\textrm{maka} \end{aligned}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya}\\ &\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline \textrm{Sampel}&AAA&AA\color{red}G&A\color{red}G\color{black}A&A\color{red}GG&\color{red}G\color{black}AA&\color{red}G\color{black}A\color{red}G&\color{red}GG\color{black}A&\color{red}GGG\\\hline \textrm{Muncul}\: \color{red}(G)&0&1&1&2&1&2&2&3\\\hline \end{array}\\ \textrm{b}.\quad&\textrm{Tabel fungsi peluangnya}\\ &x=\textrm{muncul kejadian sisi gambar}\: \: \color{red}(G)\\ &\begin{array}{|c|c|c|c|c|c|}\hline x&0&1&2&3&\color{red}\textrm{Jumlah}\\\hline f(x)&\displaystyle \frac{1}{8}&\displaystyle \frac{3}{8}&\displaystyle \frac{3}{8}&\displaystyle \frac{1}{8}&\color{red}1\\\hline \end{array}\\ \textrm{c}.\quad&\textrm{Grafik fungsi peluangnya adalah}\\ & \end{aligned} \end{array}$

 

$\begin{array}{ll}\\ 2.&\textrm{Pada sebuah kotak terdapat 2 kelereng}\\ &\textrm{biru dan 4 kelereng merah. Tiga kereng}\\ &\textrm{diambil secara acak. Tentukanlah distribusi}\\ &\textrm{peluang}\: \: \color{red}x\: \: \color{black}\textrm{jika}\: \: \color{red}x\: \: \color{black}\textrm{menyatakan banyaknya}\\ &\textrm{terambilnya bola biru}\\\\ &\textbf{Jawab}:\\ &\begin{array}{|l|c|}\hline \qquad\qquad\textrm{Nama}&\textrm{Perhitungan}\\\hline \textrm{Banyak}&\\ \textrm{titik sampel}&\begin{aligned}C_{3}^{6}&=\displaystyle \frac{6!}{3!(6-3)!}=20 \end{aligned}\\\hline \textrm{Banyak cara}&\\ \textrm{mendapatkan bola biru}&C_{x}^{2}\\\hline \textrm{Banyak cara}&\\ \textrm{mendapatkan bola merah}&C_{3-x}^{4}\\\hline \end{array} \end{array}$

$.\quad \: \begin{array}{|l|l|}\hline \color{red}\textrm{Distribusi peluang}&\qquad\quad\color{red}\textrm{Perhitungan}\\\hline P(X=x)=f(x)&f(x)=\displaystyle \frac{\displaystyle C_{x}^{2}.C_{3-x}^{4}}{\displaystyle C_{3}^{6}},\\ \textrm{untuk}&\begin{aligned}x&=0,1,2 \end{aligned}\\\hline x=0\Rightarrow P(x=0)&f(x)=\displaystyle \frac{\displaystyle C_{0}^{2}.C_{3-0}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{0}^{2}.C_{3}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{0!2!}\times \frac{4!}{3!1!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2\\\hline x=1\Rightarrow P(x=1)&f(x)=\displaystyle \frac{\displaystyle C_{1}^{2}.C_{3-1}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{1}^{2}.C_{2}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{1!1!}\times \frac{4!}{2!2!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!2!6!}=0,6\\\hline x=2\Rightarrow P(x=2)&f(x)=\displaystyle \frac{\displaystyle C_{2}^{2}.C_{3-2}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{2}^{2}.C_{1}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{2!0!}\times \frac{4!}{1!3!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2\\\hline \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tunjukkan bahwa fungsi}\: \: P(x)=\displaystyle \frac{x+2}{12}\\ &\textrm{untuk}\: \: x=1,2,\: \textrm{dan}\: \: 3\: \: \textrm{merupakan fungsi}\\ &\textrm{peluang}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Perhatik}&\textrm{an bahwa}\\ \bullet \quad P(1)&=\displaystyle \frac{1+2}{12}=\frac{3}{12}=\frac{1}{4}\\ \bullet \quad P(2)&=\displaystyle \frac{2+2}{12}=\frac{4}{12}=\frac{1}{3} \\ \bullet \quad P(3)&=\displaystyle \frac{5+2}{12}=\frac{5}{12} \\ \textrm{Sehing}&\textrm{ga}\: \: \displaystyle \sum_{i=1}^{3}P(i)=\displaystyle \frac{3}{12}+\frac{4}{12}+\frac{5}{12}=\color{red}\frac{12}{12}=1\\ &\begin{cases} (\textrm{i}) & \textrm{Peluangnya berada}\: \: \color{red}0\leq P(i)\leq 1 \\ (\textrm{ii}) & \textrm{dan nilai totolnya}=\displaystyle \color{red}\sum_{i=1}^{3}P(i)=1 \end{cases}\\ \textrm{Jadi},\: &\textrm{fungsi}\: \: P(x)=\displaystyle \frac{x+2}{12}\: \: \textrm{untuk}\: \: x=1,2,\: \textrm{dan}\: \: 3\\ &\textbf{merupakan fungsi peluang} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui fungsi peluang adalah}\: \: P(x)=\displaystyle \frac{\color{red}m}{x+1}\\ &\textrm{untuk}\: \: x=0,1,2,\: \textrm{dan}\: \: 3\: .\: \textrm{Tentukanlah}\\ &\textrm{a}.\: \: \textrm{nilai}\: \: \color{red}m\\ &\textrm{b}.\: \: \textrm{nilai}\: \: \color{red}P(x\leq 2)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\displaystyle \sum_{i=0}^{3}P(i)=\color{blue}1\\ &\Leftrightarrow \displaystyle \frac{\color{red}m}{0+1}+\frac{\color{red}m}{1+1}+\frac{\color{red}m}{2+1}+\frac{\color{red}m}{3+1}=1\\ &\Leftrightarrow \color{red}m\color{black}+\displaystyle \frac{\color{red}m}{2}+\frac{\color{red}m}{3}+\frac{\color{red}m}{4}=1\\ &\Leftrightarrow \left (\displaystyle \frac{12+6+4+3}{12} \right )\color{red}m\color{black}=1\\ &\Leftrightarrow \color{red}m\color{black}=\displaystyle \frac{12}{25}\\ \textrm{b}.\quad&P(x\leq 2)=P(x=0)+P(x=1)+P(x=2)\\ &\Leftrightarrow \color{red}m\color{black}+\displaystyle \frac{\color{red}m}{2}+\frac{\color{red}m}{3}=1\\ &\Leftrightarrow \left ( \displaystyle \frac{6+3+2}{6} \right )\color{red}m\color{black}=\displaystyle \frac{11}{6}\color{red}m\\ &\Leftrightarrow \quad =\displaystyle \frac{11}{6}\left ( \displaystyle \frac{12}{25} \right )=\frac{22}{25} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Diketahui fungsi}\: \: f(x)=\begin{cases} \displaystyle \frac{x}{6} &\textrm{untuk}\: \: x=1,2,3 \\\\ 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{adalah suatu fungsi peluang/probabilitas}\\ &\textrm{dari pubah/variabel acak}\: \: X.\: \: \textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{distribusi peluangnya untuk}\: \: X\\ &\textrm{b}.\quad P(X=2),\: P(X< 3),\: \textrm{dan}\: P(X\geq 2)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya adalah}:\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline X=x&1&2&3&4&5&\cdots &\textrm{Jumlah}\\\hline P(X=x)&\displaystyle \frac{1}{6}&\displaystyle \frac{2}{6}&\displaystyle \frac{3}{6}&\color{red}0&\color{red}0&\color{red}0&\color{blue}1\\\hline \end{array}\\ \textrm{b}.\quad &\textrm{Karena}\: \: f(x)=\begin{cases} \color{red}\displaystyle \frac{x}{6} &\textrm{untuk}\: \: x=1,2,3 \\\\ 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{maka}\\ &\bullet P(X=2)=\color{red}\displaystyle \frac{2}{6}\\ &\bullet P(X<3)=P(X=1)+P(X=2)\\ &\: \quad\qquad \qquad =\displaystyle \frac{1}{6}+\frac{2}{6}\\ &\: \quad\qquad \qquad =\displaystyle \frac{3}{6}=\color{red}\frac{1}{2}\\ &\bullet P(X\geq 2)=P(X=2)+P(X=3)\\ &\: \quad\qquad \qquad =\displaystyle \frac{2}{6}+\frac{3}{6}\\ &\: \quad\qquad \qquad =\color{red}\displaystyle \frac{5}{6} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 6.&\textrm{Diketahui fungsi peluang variabel}\: \: X\\ &f(x)=\begin{cases} \displaystyle \frac{x+2}{14} &\textrm{untuk}\: \: x=0,1,2,\: \: \textrm{dan}\: \: 3 \\\\ \quad 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{bahwa}\: \: X\: \: \textrm{merupakan variabel acak diskrit}\\ &\textrm{b}.\quad P(X=4),\: F(2),\: P(1<X\leq 3),\\ &\qquad \textrm{dan}\: P(X\geq 1)\: \: \textrm{serta}\: \: P(\left |X-2 \right |\leq 1)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya adalah}:\\ &\begin{array}{|c|c|c|c|c|c|c}\hline X=x&0&1&2&3&\textrm{Jumlah}\\\hline P(X=x)&\displaystyle \frac{2}{14}&\displaystyle \frac{3}{14}&\displaystyle \frac{4}{14}&\displaystyle \frac{5}{14}&1\\\hline \end{array} \\ &\textrm{Karena}\: \: \displaystyle \sum_{x=0}^{3}f(x)=1,\: \textrm{serta}\\ &0\leq \displaystyle \frac{2}{14},\: \frac{3}{14},\: \frac{4}{14},\: \frac{5}{14}<1.\: \textrm{Sehingga syarat}\\ &0\leq f(x)<1\: \: \textrm{dan}\: \: \sum f(x)=1\: \: \: \color{red}\textbf{terpenuhi}\\ &\textrm{Jadi, terbukti}\: \: X\: \: \textrm{adalah variabel acak diskrit}\\ \textrm{b}.\quad&\bullet P(X=4)=f(4)=\color{red}0\\ &\bullet F(2)=P(X\leq 2)\\ &\quad\qquad=P(X=0)+P(X=1)+P(X=2)\\ &\quad\qquad=f(0)+f(1)+f(2)\\ &\quad\qquad=\displaystyle \frac{2}{14}+\frac{3}{14}+\frac{4}{14}=\color{red}\frac{9}{14}\\ &\bullet P(1<X\leq 3)=P(X=2)+P(X=3)\\ &\quad\qquad =f(2)+f(3)=\displaystyle \frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{9}{14}\\ &\bullet P(X\geq 1)=f(1)+f(2)+f(3)\\ &\quad\qquad =\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{12}{14}\\ &\bullet P(\left | X-2 \right |\leq 1)=P(-1\leq X-2\leq 1)\\ &\quad\qquad =P(1\leq X\leq 3)\\ &\quad\qquad =f(1)+f(2)+f(3)\\ &\quad\qquad =\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{12}{14} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Distribusipeluang acak X disajikan dalam tabel berikut}\\ &\begin{array}{|c|c|c|c|}\hline x&2&3&4\\\hline f(x)&\displaystyle \frac{1}{8}&k+\displaystyle \frac{1}{8}&2k\\\hline \end{array}\\ &\textrm{Jika X merupakan variabel acak diskret, tentukanlah}\\ &\textrm{a}.\quad \textrm{nilai \textit{k}}\\ &\textrm{b}.\quad \textrm{nilai}\: \: \textrm{P}(\textrm{X}\geq 3)-\textrm{F}(3)\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad \sum f(x)&=f(2)+f(3)+f(4)=1\\ \Leftrightarrow \quad &\displaystyle \frac{1}{8}+k+\frac{1}{8}+2k=1\\ \Leftrightarrow \quad &3k=1-\displaystyle \frac{2}{8}=\frac{6}{8}\\ \Leftrightarrow \quad &k=\displaystyle \frac{2}{8}=\color{red}\frac{1}{4}\\ \textrm{b}.\quad \textrm{P}(\textrm{X}\, \geq 3&)-\textrm{F}(3)=\textrm{P}(\textrm{X}\geq 3)-\textrm{P}(\textrm{X}\leq 3)\\ &=f(3)+f(4)-\left ( f(2)+f(3) \right )\\ &=f(4)-f(2)\\ &=2\left ( \displaystyle \frac{1}{4} \right )-\frac{1}{8}\\ &=\displaystyle \frac{4}{8}-\frac{1}{8}=\color{red}\frac{3}{8} \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Noormandiri. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
2. Kurnia, N., dkk. 2018. Jelajah Matematika SMA Kelas XII Peminatan MIPA. Bogor: YUDHISTIRA.

Distribusi Binomial (Matematika Peminatan kelas XII)

$\color{blue}\textrm{A. Pendahuluan}$

$\begin{aligned}&\left\{\begin{matrix} (1)\: \textrm{Review}\begin{cases} \textrm{Peluang} \begin{cases} \textrm{Populasi} \\ \textrm{Sampel}\begin{cases} \textrm{Acak} \\ \textrm{Bukan Acak}.\quad \end{cases} \end{cases} \\ \textrm{Kombiasi} & \end{cases}\\ (2)\: \textrm{Variabel Acak}\begin{cases} \textrm{Diskrit} & .\qquad\qquad\qquad\qquad \\ \textrm{Kontinue} & \end{cases}\\ (3)\: \textrm{Distribusi}\begin{cases} \textrm{Distribusi Peluang Variabel Acak} & \\ \textrm{Fungsi Distribusi Kumulatif} & \\ \textrm{Variabel Acak Binomial}&\\ \textrm{Distribusi Binomial} \end{cases}\\ \end{matrix}\right. \end{aligned}$

$\color{blue}\textrm{Penjelasan}$

$\begin{array}{|c|l|l|}\hline \textrm{No}&\quad\textrm{Istilah}&\qquad\qquad\qquad\textrm{Penjelasan}\\\hline 1&\textrm{Statistika}&\textrm{Ilmu tentang pengumpulan, pengolahan},\\ &&\textrm{penganalisaan serta penarikan kesimpulan}\\ &&\textrm{data. Selanjutnya akan dibagi dua yaitu}\\ &&\color{blue}\textrm{deskriptif dan inferensia}\\\hline 2&\textrm{Statistik}&\color{red}\textrm{Kumpulan data/ukuran sampel}\\\hline 3&\textrm{Parameter}&\textrm{Ukuran populasi}\\\hline 4&\textrm{Populasi}&\color{blue}\textrm{Keseluruhan/semua anggota objek/data}\\\hline 5&\textrm{Sampel}&\color{blue}\textrm{Subjek/Objek yang mewakili populasi}\\\hline 6&\textrm{Sesus}&\textrm{Penelitian seluruh data (populasi)}\\\hline 7&\textrm{Tekik}&\textrm{Cara pengambilan data terbatas pada}\\ &\textrm{Sampling}&\textrm{sebagian saja dari populasi yang diteliti}\\\hline \end{array}$

$\color{blue}\textrm{lanjutan}$

$\begin{array}{|l|l|l|}\hline \textrm{No}&\textrm{Istilah}&\qquad\qquad\qquad\textrm{Penjelasan}\\\hline 8&\textrm{Cara}&\color{blue}\textrm{atau radom}.\: \textrm{yaitu setiap elemen populasi}\\ &\textrm{Acak}&\textrm{memiliki kesempatan yang yang sama}\\ &&\textrm{sehingga bersifat objektif}\\\hline 9&\textrm{Ruang}&\textrm{Himpunan dari semua hasil yang mungkin}\\ &\textrm{Sampel}&\textrm{dari sebuah percobaan}\\\hline 10&\textrm{Variabel}&\textrm{Suatu fungsi (aturan) yang memetakan }\\ &\textrm{Acak}&\textrm{setiap anggota ruang sampel dengan}\\ &(\textrm{VA})&\textrm{sebuah bilangan riil. Biasanya dinotasikan}\\ &&\textrm{dengan huruf besar, sedangkan nilai}\\ &&\textrm{variabel acaknya dinotasikan dengan}\\ &&\textrm{huruf kecil}\\\hline 11&(\textrm{VA})&\textrm{Jika VA tersebut memiliki sejumlah nilai}\\ &\textrm{Diskrit}&\textrm{yang dapat dihitung(berupa bilangan}\\ &&\textrm{bulat positif)}\\\hline 12&\textrm{VA}&\textrm{Sebaliknya yaitu berupa bilangan yang}\\ &\textrm{Kontinu}&\textrm{tidak bulat}\\\hline \end{array}$

$\color{red}\textrm{Sebagai contoh}$

$\begin{aligned}\textbf{a}\quad&\color{blue}\textrm{Variabel Acak Diskrit (Bilangan bulat positif)}\\ &\bullet \: \: \textrm{Jumlah siswa kelas XII MIA MA FUTUHIYAH}\\ &\: \, \quad \textrm{JEKETRO GUBUG}\\ &\bullet \: \: \textrm{Jumlah guru laki-laki di MA FUTUHIYAH}\\ &\: \, \quad \textrm{JEKETRO GUBUG}\\ &\bullet \: \: \textrm{Jumlah guru dan siswa di MA FUTUHIYAH}\\ &\: \, \quad \textrm{JEKETRO GUBUG yang tidak terpapar}\\ &\: \, \quad \textrm{COVID-19}\\ &\bullet \: \: \textrm{Jumlah motor yang terjual dalam sebulan}\\ \textbf{b}\quad&\color{magenta}\textrm{Variabel Acak Kontinu (Bukan bilangan bulat)}\\ &\bullet \: \: \textrm{Jumlah miyak yang tumpah di suatu lantai}\\ &\bullet \: \: \textrm{Ketinggian permukaan air di sebuah waduk}\\ \end{aligned}$

$\color{blue}\textrm{B. Variabel Acak}$

$\begin{array}{|c|l|l|}\hline \textrm{No}&\quad\textrm{Istilah}&\qquad\qquad\qquad\textrm{Definisi}\\\hline 13&\textrm{Variabel}&\textrm{Suatu variabel}\: \: X\: \: \textrm{adalah variabel acak jika}\\ &\textrm{Acak}&\textrm{nilai-nilai yang dimiliki oleh}\: \: X\: \: \textrm{merupakan}\\ &&\textrm{suatu kemungkinan atau peristiwa acak}.\\ &&\color{blue}\textrm{Selanjutnya variabel acak dibedakan}\\ &&\color{blue}\textrm{menjadi dua, yaitu variabel acak diskrit dan}\\ &&\color{blue}\textrm{variabel acak kontinu sebagaimana pada}\\ &&\color{blue}\textrm{penjelasan sebelumnya di atas}\\\hline \end{array}$

$\color{blue}\textrm{C. Distribusi Peluang}$

$\begin{array}{|c|l|l|}\hline \textrm{No}&\quad\textrm{Istilah}&\qquad\qquad\qquad\textrm{Definisi}\\\hline 14&\textrm{Distribusi}&\textrm{Sebuah daftar yang berisi seluruh hasil}\\ &\textrm{Peluang}&\textrm{yang mungkin dari suatu percobaan dan}\\ &(\textrm{Probabilitas})&\textrm{probabilitas yang berkaitan dengan setiap}\\ &&\textrm{hasil tersebut}.\\ &&\color{red}\textrm{Nilai probabilitas berada di antara 0 dan 1}\\ &&\color{blue}\textrm{Jumlah dari seluruh probabilitas hasil harus}\\ &&\color{blue}\textrm{harus sama dengan 1}\\\hline \end{array}$

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Sebuah koin dilempar sebanyak tiga kali}\\ &\textrm{a}.\quad \textrm{tentukan semua titik sampelnya}\\ &\textrm{b}.\quad \textrm{tentukan peluang mendapatkan tepat}\\ &\qquad \textrm{dua gambar}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\: \: \: &\textrm{Sebuah koin hanya memiliki dua muka,}\\ &\textrm{yaitu muka gambar (G) dan muka angka (A)}\\ &\textrm{sehingga setiap pelemparan hanya memiliki}\\ &\textrm{dua kemungkinan, yaitu muncul sisi A atau G}\\ &\textrm{maka ruang sampelnya adalah}:\\ &\begin{aligned} \color{blue}\textrm{Mula}\: \, &(1)\quad (2)\quad (3)\quad \color{blue}\textbf{Ruang sampel}\\ \textbf{Mulai}&\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (A,A,A)\\ G\rightarrow (A,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (A,G,A)\\ G\rightarrow (A,G,G) \end{matrix}\right. \end{matrix}\right.\\ G\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (G,A,A)\\ G\rightarrow (G,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (G,G,A)\\ G\rightarrow (G,G,G) \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. \end{aligned} \\ &\textrm{Jadi, banyaknya ruang sampel adalah }\color{red}8 \end{aligned}\\ &\begin{aligned}\textrm{b}.\: \: \: &\textrm{Dari ruang sampel yang tepat}\\ &\textrm{ada 2 sisi gambar : AGG,GAG,GGA}\\ &\textrm{sehingga peluangnya}=\displaystyle \frac{3}{\textrm{total ruang sampel}}=\color{red}\frac{3}{8} \end{aligned} \end{array}$

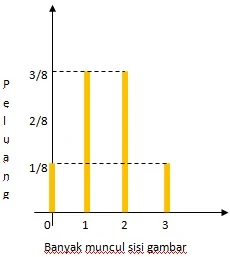
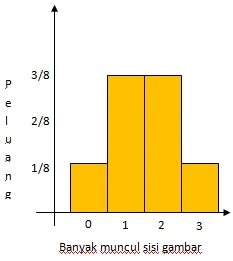
$\begin{array}{ll}\\ 2.&\textrm{Misalkan}\: \: X\: \: \textrm{menyatakan sisi angka (A)}\\ &\textrm{pada soal No.1 di atas, tentukanlah nilai}\\ &X\: \: \textrm{yang mungkin}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Perhatikanlah ilustrasi berikut}\\ &\begin{aligned} \color{blue}\textrm{Mula}\: \, &(1)\quad (2)\quad (3)\quad \color{blue}\textbf{Ruang sampel}\quad \textbf{Nilai}\\ \textbf{Mulai}&\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow \color{magenta}(A,A,A)\rightarrow \rightarrow \rightarrow X=3\\ G\rightarrow (A,A,G)\rightarrow \rightarrow \rightarrow X=2 \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (A,G,A)\rightarrow \rightarrow \rightarrow X=2\\ G\rightarrow (A,G,G)\rightarrow \rightarrow \rightarrow X=1 \end{matrix}\right. \end{matrix}\right.\\ G\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (G,A,A)\rightarrow \rightarrow \rightarrow X=2\\ G\rightarrow (G,A,G)\rightarrow \rightarrow \rightarrow X=1 \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (G,G,A)\rightarrow \rightarrow \rightarrow X=1\\ G\rightarrow \color{red}(G,G,G)\rightarrow \rightarrow \rightarrow X=0 \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. \end{aligned}\\ &\textrm{Jadi, nilai}\: \: X\: \: \textrm{yang mungkin}=\color{red}0,1,2,\: \color{black}\textrm{atau}\: \color{red}3 \end{aligned} \end{array}$

Perhatikanlah contoh pada No.2 di atas, nilai  X  ternyata tidak memiliki nilai tunggal. Karena  X  tidak memiliki nilai tunggal, maka  X  selanjutnya disebut dengan variabel. Dan variabel seperti ini yang nilainya ditentukan oleh percobaan sehingga akan mendapatkan beberapa kemungkinan selanjutnya disebut dengan variabel acak. Sehingga  X  pada No.2 di atas adalah salah satu contoh untuk variabel acak.