PAS MATEMATIKA BLOG

Vektor di Ruang

$A. Vektor Di Ruang$

Perhatikanlah ilustrasi gambar berikut

\begin{array}{cc} Nama & R^{3} \\ Vektor Satuan & Ruang (Bidang XYZ) \\ {\hat{e}}_{\bar{a}} = \frac{\bar{a}}{| \bar{a} |} & {\begin{cases} i = & vektor satuan \\ yang searah sumbu X \\ j = & Vektor satuan \\ yang searah sumbu Y \\ k = & Vektor satuan \\ searah sumbu Z \end{cases} \\ Vektor nol & \vec{O} = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}) \\ Vektor posisi & \vec{O P} = \vec{p} = (\begin{matrix} p_{1} \\ p_{2} \\ p_{3} \end{matrix}) = p_{1} \bar{i} + p_{2} \bar{j} + p_{3} \bar{j} \\ Besar Vektor & \vec{O P} = \sqrt{p_{1}^{2} + p_{2}^{2} + p_{3}^{2}} \end{array}

B. Operasi Vektor

1. Sifat-Sifat Aljabar Vektor

\begin{array}{lll} 1. & Komutatif penjumlahan & \vec{a} + \vec{b} = \vec{b} + \vec{a} \\ 2. & Asosiatif penjumlahan & (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \\ 3. & Elemen Identitas & \vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a} \\ 4. & Invers Penjumlahan & \vec{a} + (- \vec{a}) = (- \vec{a}) + \vec{a} = \vec{0} \\ 5. & Perkalian dengan skalar & k (l \vec{a}) = (k l) \vec{a} \\ k (\vec{a} + \vec{b}) = k \vec{a} + k \vec{b} \\ k (\vec{a} - \vec{b}) = k \vec{a} - k \vec{b} \\ 6. & \begin{aligned} Jika A, B, dan C segaris \\ (Kolinear) \end{aligned} & {\begin{cases} \vec{A B} = k \vec{B C} \\ \vec{A C} = k \vec{A B} \\ d l l \end{cases} \end{array}

\begin{array}{cc} Vektor & Contoh \\ \vec{z} = a \vec{i} + b \vec{j} + c \vec{k} & \begin{aligned} diketahui \vec{p} = \vec{i} - 2 \vec{j} + 2 \vec{k} \\ maka pangjang vektor \vec{p} adalah \\ | \vec{p} | = \sqrt{1^{2} + (- 2)^{2} + 2^{2}} \\ = \sqrt{1 + 4 + 4} = \sqrt{9} = 3 \end{aligned} \\ \begin{aligned} Vektor satuan dari \vec{p} adalah \\ {\vec{e}}_{\vec{p}} = \frac{\vec{p}}{| \vec{p} |} = \frac{(\begin{array}{c} 1 \\ - 2 \\ 2 \end{array})}{3} \\ = \frac{1}{3} (\begin{array}{c} 1 \\ - 2 \\ 2 \end{array}) = (\begin{array}{c} \frac{1}{3} \\ - \frac{2}{3} \\ \frac{2}{3} \end{array}) \end{aligned} \end{array}

CONTOH SOAL

\begin{array}{ll} 1. & Diketahui vektor-vektor \vec{a} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \\ \vec{b} = (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}), dan \vec{c} = (\begin{array}{c} 7 \\ 0 \\ 4 \end{array}), \\ tentukanlah hasil dari \\ a . \vec{a} + \vec{b} \\ b . 6 \vec{a} + 2 \vec{b} \\ c . 2 \vec{a} - \vec{b} + \vec{c} \\ d . \frac{1}{2} \vec{c} - \vec{a} + \frac{3}{4} \vec{b} \\ Jawab : \\ \begin{aligned} a & \vec{a} + \vec{b} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) + (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}) \\ = (\begin{array}{c} 2 + (- 3) \\ 1 + (- 5) \\ (- 4) + 2 \end{array}) \\ = (\begin{array}{c} 2 - 3 \\ 1 - 5 \\ - 4 + 2 \end{array}) = (\begin{array}{c} - 1 \\ - 4 \\ - 2 \end{array}) \\ b . & 6 \vec{a} + 2 \vec{b} = 6 (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) + 2 (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}) \\ = (\begin{array}{c} 18 - 6 \\ 6 - 10 \\ - 24 + 4 \end{array}) = (\begin{array}{c} 12 \\ - 4 \\ - 20 \end{array}) \\ c . & 2 \vec{a} - \vec{b} + \vec{c} \\ 2 (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) - (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}) + (\begin{array}{c} 7 \\ 0 \\ 4 \end{array}) \\ = (\begin{array}{c} 4 + 3 + 7 \\ 2 + 5 + 0 \\ - 8 - 2 + 4 \end{array}) = (\begin{array}{c} 17 \\ 7 \\ - 6 \end{array}) \\ d . & \frac{1}{2} \vec{c} - \vec{a} + \frac{3}{4} \vec{b} = \dots \end{aligned} \end{array}

\begin{array}{ll} 2. & Diketahui vektor-vektor \vec{a} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \\ tentukanlah | \vec{a} | \\ Jawab : \\ \begin{aligned} | \vec{a} | & = \sqrt{2^{2} + 1^{2} + (- 4)^{2}} \\ = \sqrt{4 + 1 + 16} \\ = \sqrt{21} \end{aligned} \end{array}

2. Perkalian Skalar Dua Vektor

Konsep perkalian skalar dua buah vektor di ruang sama persis dengan konsep di bidang, yaitu:

\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ

Misalkan diketahui

\begin{aligned} \vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}), \vec{b} = (\begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array}), maka \\ \vec{a} \cdot \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) \cdot (\begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array}) \\ = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} \end{aligned}

CONTOH SOAL

\begin{array}{ll} 1. & Diketahui vektor-vektor \vec{a} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \\ \vec{b} = (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}), dan \vec{c} = (\begin{array}{c} 7 \\ 0 \\ 4 \end{array}), \\ tentukanlah hasil dari \\ a . \vec{a} \cdot \vec{b} \\ b . \vec{a} \cdot \vec{c} \\ c . \vec{b} \cdot \vec{c} \\ Jawab : \\ \begin{aligned} a & \vec{a} \cdot \vec{b} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \cdot (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}) \\ = (2) (- 3) + (1) (- 5) + (- 4) (2) \\ = - 6 - 5 - 8 = - 19 \\ b & \vec{a} \cdot \vec{c} = (\begin{array}{c} 2 \\ 1 \\ - 4 \end{array}) \cdot (\begin{array}{c} 7 \\ 0 \\ 4 \end{array}) \\ = (2) (7) + (1) (0) + (- 4) (4) \\ = 14 + 0 - 16 = - 2 \\ c & \vec{b} \cdot \vec{c} = (\begin{array}{c} - 3 \\ - 5 \\ 2 \end{array}) \cdot (\begin{array}{c} 7 \\ 0 \\ 4 \end{array}) \\ = (- 3) (7) + (- 5) (0) + (2) (4) \\ = - 21 + 0 + 8 = - 13 \end{aligned} \end{array}

\begin{array}{ll} 2. & Tentukanlah nilai t jika \\ \vec{p} = 3 \bar{i} + t \bar{j} + \bar{k} dan \vec{p} \cdot \vec{p} = 13 \\ Jawab : \\ \begin{aligned} \vec{p} \cdot \vec{p} = 13 \\ \vec{p} \cdot \vec{p} = | \vec{p} | | \vec{p} | \cos 0^{\circ} = 13, \\ ingat bahwa ∠ (\vec{p}, \vec{p}) = 0^{\circ} \\ dan nilai \cos 0^{\circ} = 1, \\ maka \\ \vec{p} \cdot \vec{p} = {| \vec{p} |}^{2} .1 = 13 \Leftrightarrow {| \vec{p} |}^{2} = 13 \\ \Leftrightarrow {(\sqrt{3^{2} + t^{2} + 1^{2}})}^{2} = 13 \\ \Leftrightarrow 3^{2} + t^{2} + 1^{2} = 13 \\ \Leftrightarrow 9 + t^{2} + 1 = 13 \\ \Leftrightarrow t^{2} = 13 - 9 - 1 = 10 \\ \Leftrightarrow t^{2} = 3 \\ \Leftrightarrow t = \pm \sqrt{3} \end{aligned} \end{array}

\begin{array}{ll} 3. & Diketahui \vec{p} = (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) dan \vec{q} = (\begin{array}{c} 4 \\ - 1 \\ t \end{array}) \\ Jika \vec{p} tegak lurus \vec{q} maka \\ tentukanlah nilai t \\ Jawab : \\ \begin{aligned} Diketahui bahwa \\ \vec{p} = (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) dan \vec{q} = (\begin{array}{c} 4 \\ - 1 \\ t \end{array}) \\ dengan \vec{p} dan \vec{q} tegak lurus \\ artinya ∠ (\vec{p}, \vec{q}) = 90^{\circ} . Sehingga \\ nilai \cos 90^{\circ} = 0 \\ maka \\ \vec{p} \cdot \vec{q} = | \vec{p} | | \vec{q} | \cos θ \\ \vec{p} \cdot \vec{q} = | \vec{p} | | \vec{q} | \cdot 0 = 0 \\ \Leftrightarrow (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) \cdot (\begin{array}{c} 4 \\ - 1 \\ t \end{array}) = 0 \\ \Leftrightarrow (- 2) (4) + (1) (- 1) + (3) (t) = 0 \\ \Leftrightarrow - 8 - 1 + 3 t = 0 \\ \Leftrightarrow 3 t = 9 \\ \Leftrightarrow t = 3 \end{aligned} \end{array}

DAFTAR PUSTAKA

Yuana, R.A., Indriyastuti. 2017. Persektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan Matematika dan Ilmu Alam. Solo: PT TIGA SERANGKAI MANDIRI.

Polinom

$A. Pendahuluan$

Polinom disebut juga suku banyak. Polinom atau suku banyak adalah suatu bentuk variabel yang berpangkat/berderajat.

Secara definisi suku banyak (polinomial) dalam $x$ berderajat $n$ adalah:

Suatu bentuk

$a_{n} x^{n} + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + . . . + a_{2} x^{2} + a_{1} x^{1} + a_{0}$

dengan $n$ bilangan cacah serta $a_{0}, a_{1}, a_{2}, . . ., a_{n}$ koefisien dari suku $x$ dan $a_{n} \neq 0$ dengan $a_{0}$ sebagai suku tetap (konstan)nya.

Selanjutnya perhatikanlah tabel berikut!

$\begin{array}{ll} \begin{aligned} a_{n} & adalah koefisien dari x^{n} \\ a_{n - 1} & adalah koefisien dari x^{n - 1} \\ a_{n - 2} & adalah koefisien dari x^{n - 2} \\ ⋮ \\ a_{2} & adalah koefisien dari x^{2} \\ a_{1} & adalah koefisien dari x^{1} \\ a_{0} & adalah konstanta \\ (suku tetap) \end{aligned} & \begin{aligned} a_{n} & \neq 0 \\ n : & bilangan cacah, \\ : & adalah derajat (pangkat) \\ tertinggi dalam suku \\ banyak tersebut \end{aligned} \end{array}$

$CONTOH SOAL 1$

$\begin{aligned} 1. & Polinom 2 x^{3} - 6 x^{2} + 2020 dapat dinyatakan \\ dengan 2 x^{3} - 6 x^{2} + 0 x^{1} + 2020 x^{0} \\ Polinom tersebut memiliki suku tetap 2020 \\ 2. & Polinom 5 x^{4} - 8 x^{3} + 6 x - 2021 dapat dinyatakan \\ dengan 5 x^{4} - 8 x^{3} + 0 x^{2} + 6 x^{1} - 2021 x^{0} \\ Polinom tersebut memiliki suku tetap - 2021 \\ 3. & Polinom x^{4} - 2 x^{3} + 3 x^{2} - 2 \sqrt{x} + 1 tidak dapat \\ dinamakan polinom, sebab ada variabel dari x \\ yang berderajat bukan bilangan cacah \\ 4. & Sedangkan polinom 5 - x + (2 - x) (1 + x + x^{2}) \\ adalah bentuk polinom, karena dapat dinayatakan \\ dengan - x^{3} + x^{2} + 7 \end{aligned}$

$B. Nilai Polinom$

Polinom atau suku banyak yang berderajat $n$ yang selanjutnya dinyatakan dengan

$f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + . . . + a_{1} x^{1} + a_{0}$

Berkaitan dengan kebutuhan penentuan nilai ini, dapat ditentukan dengan dua cara:

$a. Substitusi$

$\begin{aligned} Nilai suku banyak f (x) berderajat \\ n saat x = k adalah f (k) . \\ Jika f (k) = 0 maka x = k akar dari f (x), \\ dan (x - k) faktor dari f (x) \end{aligned}$

$CONTOH SOAL 2$

Jika suatu polinom dinyatakan dengan $f (x)$ , maka nilai polinom itu untuk $x = 3$ adalah $f (3)$ .

Misalkan diketahui

$\begin{aligned} 1. f (x) & = x^{3} - 1 \\ mak & a \\ f (1) & = 1^{3} - 1 = 1 - 1 = 0 \\ f (3) & = 3^{3} - 1 = 27 - 1 = 26 \\ f (- 4) & = (- 4)^{2} - 1 = - 64 - 1 = - 65 \end{aligned}$

$\begin{array}{ll} 2. & Diketahui h (x) = 2 x^{3} + 5 x^{2} - 12 x - 6 \\ Tentukanlah nilai untuk h (- 2), h (- 1), \\ h (0), h (1), dan h (2) \\ Jawab : \\ \begin{array}{ccl} x = k & h (k) & Nilai \\ x = - 2 & h (- 2) & \begin{aligned} h (- 2) & = 2 (- 2)^{3} + 5 (- 2)^{2} - 12 (- 2) - 6 \\ = - 16 + 20 + 24 - 6 \\ = 22 \end{aligned} \\ x = - 1 & h (- 1) & \begin{aligned} h (- 1) & = 2 (- 1)^{3} + 5 (- 1)^{2} - 12 (- 1) - 6 \\ = - 2 + 5 + 12 - 6 \\ = 9 \end{aligned} \\ x = 0 & h (0) & \begin{aligned} h (0) & = 2 (0)^{3} + 5 (0)^{2} - 12 (0) - 6 \\ = - 6 \end{aligned} \\ x = 1 & h (1) & \begin{aligned} h (1) & = 2 (1)^{3} + 5 (1)^{2} - 12 (1) - 6 \\ = 2 + 5 - 12 - 6 \\ = - 11 \end{aligned} \\ x = 2 & h (2) & \begin{aligned} h (2) & = 2 (2)^{3} + 5 (2)^{2} - 12 (2) - 6 \\ = 16 + 20 - 24 - 6 \\ = 6 \end{aligned} \end{array} \end{array}$

$\begin{array}{ll} 3. & Diketahui p (x) = x - 2019 \\ dan q (x) = x^{2019} + 1. Tentukanlah \\ nilai untuk p (q (2)) dan q (p (2)) \\ Jawab : \\ Yang dibahas yang bagian p (q (2)) \\ q (2) = 2^{2019} + 1, maka nilai \\ \begin{aligned} p (q (2)) & = (2^{2019} + 1) - 2019 \\ = 2^{2019} - 2018 \end{aligned} \\ Untuk yang q (p (2)) adalah \\ p (2) = \dots, maka nilai \\ \begin{aligned} q (p (2)) & =∵ \dots^{2019} + 1 \\ = \dots \end{aligned} \end{array}$

$b. Horner/Sintetik$

Nilai suatu polinom dapat ditentukan dengan pembagian sintesis Horner

Misalkan:

$\begin{aligned} f (x) & = a x^{3} + b x^{2} + c x + d saat akan dibagi \\ x = h, maka pembagian Horner itu : \end{aligned}$

Perhatikan bahwa proses ke bawah adalah berup proses penjumlahan.

Proses di atas akan sama saat kita mensubstitusikan

x = h

ke dalam

f (x)

, yaitu:

\begin{aligned} f (x) & = a x^{3} + b x^{2} + c x + d saat \\ x = h, maka \\ f (h) & = a h^{3} + b h^{2} + c h + d \\ Cukup JELAS bukan ? \end{aligned}

$CONTOH SOAL 3$

$\begin{array}{l} Tentukanlah nilai dari f (4) jika \\ diketahui f (x) = x^{3} - x - 5 \\ Jawab : \\ \begin{aligned} (1) . & Cara substitusi langsung \\ f (x) = x^{3} - x - 5 \\ f (4) = 4^{3} - 4 - 5 \\ = 64 - 9 = 55 \\ (2) . & Cara Horner \\ Karena f (x) = x^{3} - x - 5 \\ dan koefisiennya yang akan \\ adalah : \\ a_{3} = 1, a_{2} = 0, a_{1} = - 1, & a_{0} = - 5 \\ maka bagan pembagian Hornernya \\ \begin{array}{llllllllllll} x = 4 & 1 & 0 & - 1 & - 5 \\ 4 & 16 & 60 & + \\ 1 & 4 & 15 & 55 \end{array} \end{aligned} \end{array}$

Lanjutan Contoh Soal 6 Distribusi Normal

$\begin{array}{ll} 26. & Untuk menguji hipotesis \\ {\begin{cases} H_{0} & : μ = 16 \\ H_{1} & : μ > 16 \end{cases} \\ Jika dalam penelitian terhadap sampel n = 20 \\ diperoleh \overset{―}{x} = 16, 9 dengan simpangan baku \\ \sqrt{2, 3}, maka perhitungan nilai statistik ujinya \\ adalah . . . . \\ a . z = - 2, 65 \\ b . t = - 2, 65 \\ c . z = 2, 65 \\ d . t = 2, 65 \\ e . z = 2, 95 \\ Jawab : d \\ \begin{aligned} \underset{―}{Hipotesis (penelitian sampel)} \\ H_{0} : μ = 16 \\ H_{0} : μ > 16 \\ dengan, n = 20, \overset{―}{x} = 16, 9, s = \sqrt{2, 3} = 1, 52, \\ maka \\ t = (\frac{\overset{―}{x} - μ}{s}) \sqrt{n} = \frac{16, 9 - 16}{1, 52} \sqrt{20} \\ = (\frac{0, 9}{1, 52}) \times 4, 472 = 2, 65 \end{aligned} \end{array}$ .

$\begin{array}{ll} 27. & Pada soal no.26 di atas, jika taraf nyata \\ 0, 01, maka kesimpulannya adalah . . . \\ a . H_{0} ditolak \\ b . H_{0} diterima \\ c . H_{1} diterima \\ d . H_{1} ditolak \\ e . tidak dapat ditarik kesimpulan \\ Jawab : b \\ Kasus uji satu pihak \\ \begin{aligned} \underset{―}{Hipotesis} \\ H_{0} : μ = 16 \\ H_{0} : μ > 16 \\ dengan α = 0, 01 = 1 % \Rightarrow t_{0, 99} = 2, 54 \\ Kriteria pengambilan keputusan : \\ Tolak H_{0} jika t \geq 2, 54 \end{aligned} \end{array}$ .

$\begin{array}{ll} 28. & Seorang petugas c u s t o m e r s e r v i c e menyatakan \\ bahwa di dealer A dapat mensevis rata-rata \\ sebanyak 75 unit sepeda motor perhari . Untuk \\ mengecek kebenaran pernyataan di atas diambil \\ sampel beberapa hari secara random sebanyak \\ 20 hari. Dari penelitian ini diperoleh rata-rata \\ 78 unit dengan simpangan bakunya 5. Hasil \\ perhitungan z_{0} - nya adalah . . . . \\ a . 2, 35 \\ b . 2, 43 \\ c . 2, 55 \\ d . 2, 68 \\ e . 2, 75 \\ Jawab : d \\ \begin{aligned} Diketahui data dianggap berdistribusi \\ normal baku N (0, 1) dengan \\ Rata-rata sampel = \overset{―}{x} = 78 unit sepeda motor \\ Rata-rata populasinya yang diuji = μ_{0} = 75 \\ Simpangan bakunya = σ = 5 unit \\ dengan banyak data sampel = n = 20 hari \\ Penghitungan nilainya z - nya \\ = \frac{\overset{―}{x} - μ_{0}}{\frac{σ}{\sqrt{n}}} \\ = \frac{78 - 75}{\frac{5}{\sqrt{20}}} = \frac{3}{\frac{5}{2 \sqrt{5}}} \\ = \frac{6}{\sqrt{5}} = \frac{6}{2, 236} = 2, 683 \end{aligned} \end{array}$ .

$\begin{array}{ll} 29. & Tersiar kabar bahwa harga beras di pasar di \\ wilayah B adalah Rp 8.000, 00 / Kg dengan \\ simpangan baku Rp 1.500, 00. Berdasar kabar \\ tersebut dilakukan penelitian dengan mengambil \\ sampel secara acak sebanyak 60 kios yang dan \\ diperoleh rata-rata harga beras Rp 7.800, 00 / Kg \\ Jika penghitungan menggunakan tingkat \\ signifikansi 5 %, maka kesimpulan berikut \\ yang tepat adalah . . . . \\ a . harga beras di pasar lebih dari Rp 7.800, 00 / Kg \\ b . harga beras di pasar lebih dari Rp 8.000, 00 / Kg \\ c . harga beras di pasar kurang dari Rp 0.000, 00 / Kg \\ d . harga beras di pasar Rp 7.800, 00 / Kg \\ e . harga beras di pasar Rp 8.000, 00 / Kg \\ Jawab : e \\ \begin{aligned} \underset{―}{Hipotesis} \\ Rata-rata harga beras dipasar Rp 8.000, 00 / Kg \\ H_{0} : μ = 8.000 \\ H_{0} : μ \neq 8.000 \\ \underset{―}{Daerah Kritis} \\ Taraf nyata yang dipilih adalah = α = 0, 05 = 5 % \\ \frac{α}{2} = 2, 5 % = 0, 025 \\ z_{0, 025} = 1, 96 \\ maka daerah kritis/penolakannya adalah \\ z < - 1, 96 atau z > 1, 96 \end{aligned} \end{array}$ .

$. \begin{aligned} \underset{―}{Nilai Satistik Uji} \\ Dihitung dengan rumus : z = \frac{\overset{―}{x} - μ_{0}}{\frac{σ}{\sqrt{n}}} \\ z = \frac{7.800 - 8.000}{\frac{1.500}{\sqrt{60}}} = - \frac{200 \sqrt{60}}{1.500} = - 1, 03 \\ \underset{―}{Keputusan Uji} \\ Karena nilai - 1, 96 < z < 1, 96, \\ maka H_{0} diterima \\ \underset{―}{Kesimpulan} \\ Rata-rata harga beras dipasar Rp 8.000, 00 / Kg \end{aligned}$ .

Lanjutan Contoh Soal 5 Distribusi Normal

$\begin{array}{ll} 21. & Pada suatu kelas seorang guru matematika \\ menyatakan bahwa nilai ulangan mapel \\ yang diampunya tidak kurang dari 68 \\ Untuk menentukan uji tersebut, maka guru \\ yang bersangkutan memilih 10 anak secara \\ acak untuk ditanyai nilai hasil ulangannya \\ Hipotesis H_{0} dan H_{1} yang tepat dari kondisi \\ kondisi di atas adalah . . . . \\ a . \begin{array}{c} H_{0} : μ = 68 \\ H_{1} : μ \neq 68 \end{array} \\ b . \begin{array}{c} H_{0} : μ = 68 \\ H_{1} : μ > 68 \end{array} \\ c . \begin{array}{c} H_{0} : μ \geq 68 \\ H_{1} : μ < 68 \end{array} \\ d . \begin{array}{c} H_{0} : μ \leq 68 \\ H_{1} : μ > q 68 \end{array} \\ e . \begin{array}{c} H_{0} : μ > 68 \\ H_{1} : μ \neq 68 \end{array} \\ Jawab : c \\ Cukup jelas \\ Dan ini contoh uji satu pihak, yaitu kiri \end{array}$ .

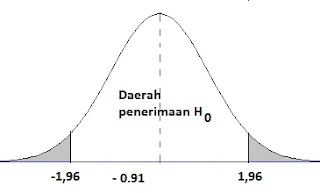
$\begin{array}{ll} 22. & Untuk menguji hipotesis \\ {\begin{cases} H_{0} & : μ = 800 \\ H_{1} & : μ \neq 800 \end{cases} \\ Jika dalam penelitian didapatkan \overset{―}{x} = 795 \\ dan n = 100 serta simpangan baku \\ populasi 55, maka perhitungan nilai \\ statistik ujinya adalah . . . . \\ a . z = - 1, 10 \\ b . z = - 0, 91 \\ c . t = - 0, 91 \\ d . t = 0, 91 \\ e . z = 0, 91 \\ Jawab : b \\ \begin{aligned} \underset{―}{Hipotesis} \\ H_{0} : μ = 800 \\ H_{0} : μ \neq 800 \\ dengan, n = 100, \overset{―}{x} = 795, σ = 55, maka \\ z = (\frac{\overset{―}{x} - μ}{σ}) \sqrt{n} = \frac{795 - 800}{55} \sqrt{100} \\ = (\frac{- 5}{55}) \times 10 = - 0, 91 \end{aligned} \end{array}$ .

$\begin{array}{ll} 23. & Pada soal no.22 di atas, jika taraf nyata \\ 5 %, maka kesimpulannya adalah . . . \\ a . H_{0} ditolak \\ b . H_{0} diterima \\ c . H_{1} diterima \\ d . H_{1} ditolak \\ e . tidak dapat ditarik kesimpulan \\ Jawab : b \\ Kasus uji dua pihak \\ \begin{aligned} \underset{―}{Hipotesis} \\ H_{0} : μ = 800 \\ H_{0} : μ \neq 800 \\ dengan α = 5 % = 0, 05 \Rightarrow z_{\frac{1}{2} (1 - 0, 05)} \\ = z_{0, 475} = 1, 96 \end{aligned} \end{array}$ .

$\begin{array}{ll} 24. & Untuk menguji hipotesis \\ {\begin{cases} H_{0} & : μ = 20 \\ H_{1} & : μ < 20 \end{cases} \\ Jika dalam penelitian terhadap sampel n = 21 \\ diperoleh \overset{―}{x} = 19, 8 dengan simpangan baku \\ 0, 4, maka perhitungan nilai statistik ujinya \\ adalah . . . . \\ a . z = - 2, 29 \\ b . t = - 2, 29 \\ c . z = 2, 29 \\ d . t = 2, 29 \\ e . z = 2, 99 \\ Jawab : b \\ \begin{aligned} \underset{―}{Hipotesis (penelitian sampel)} \\ H_{0} : μ = 20 \\ H_{0} : μ < 20 \\ dengan, n = 21, \overset{―}{x} = 19, 8, s = 0, 4, maka \\ t = (\frac{\overset{―}{x} - μ}{s}) \sqrt{n} = \frac{19, 8 - 20}{0, 4} \sqrt{21} \\ = (\frac{- 0, 2}{0, 4}) \times 4, 5828 = - 2, 29 \end{aligned} \end{array}$ .

$\begin{array}{ll} 25. & Pada soal no.24 di atas, jika taraf nyata \\ 0, 01, maka kesimpulannya adalah . . . \\ a . H_{0} ditolak \\ b . H_{0} diterima \\ c . H_{1} diterima \\ d . H_{1} ditolak \\ e . tidak dapat ditarik kesimpulan \\ Jawab : b \\ Kasus uji satu pihak \\ \begin{aligned} \underset{―}{Hipotesis} \\ H_{0} : μ = 20 \\ H_{0} : μ < 20 \\ dengan α = 0, 01 = 1 % \Rightarrow t_{0, 99} = 2, 53 \\ Kriteria pengambilan keputusan : \\ Tolak H_{0} jika t \leq - 2, 53 \end{aligned} \end{array}$ .

Lanjutan Contoh Soal 4 Distribusi Normal

$\begin{array}{ll} 16. & Dalam pengujian hipotesis dapat terjadi kesalahan \\ Jika kita menerima hipotesis yang seharusnya kita \\ tolak. Kejadian ini merupakan kekeliruan, yaitu . . . . \\ a . kekeliruan tipe I \\ b . kekeliruan tipe II \\ c . kekeliruan tipe III \\ d . kekeliruan sampling \\ e . kekeliruan non sampling \\ Jawab : b \\ Cukup jelas \end{array}$ .

$\begin{array}{ll} 17. & Pengertian dari taraf signifikansi 1 % adalah . . . . \\ a . sekitar 95 % kesimpulan benar telah diambil \\ b . kurang lebih 5 dari 100 kesimpulan yang \\ seharusnya hipotesisnya diterima kita tolak \\ c . kurang lebih 1 dari 100 kesimpulan yang \\ seharusnya hipotesisnya ditolak kita terima \\ d . kurang lebih 1 dari 100 kesimpulan yang \\ seharusnya hipotesisnya diterima kita tolak \\ e . kurang lebih 5 dari 100 kesimpulan yang \\ seharusnya hipotesisnya ditolak kita terima \\ Jawab : d \\ Cukup jelas \end{array}$ .

$\begin{array}{ll} 18. & Dalam pengujian hipotesis, penggunaan statistik \\ t ketika penghitungan . . . . \\ a . simpsngsn baku saat sampel tidak diketahui \\ b . rata-rata sampel tidak diketahui \\ c . simpangan baku populasi tidak diketahui \\ d . rata-rata populasi tidak diketahui \\ e . simpangan baku populasi diketahui \\ Jawab : c \\ Cukup jelas \end{array}$ .

$\begin{array}{ll} 19. & Penggunaan kriteria pada uji pihak kiri jika \\ diketahui d adalah nilai yang diperoleh dari \\ daftar distribusi yang bersangkutan dengan \\ peluang yang ditentukan oleh α adalah . . . . \\ a . tolak H_{0} jika nilai statistik uji lebih dari \\ d, dalam hal lainnya H_{0} diterima \\ b . tolak H_{0} jika nilai statistik uji kurang dari \\ d, dalam hal lainnya H_{0} diterima \\ c . terima H_{0} jika nilai statistik uji kurang dari \\ d, dalam hal lainnya H_{0} diterima \\ d . terima H_{0} jika nilai statistik uji lebih dari \\ d, dalam hal lainnya H_{0} ditolak \\ e . terima H_{0} jika nilai statistik uji lebih dari \\ atau sama dengan d, dalam hal lainnya \\ H_{0} ditolak \\ Jawab : b \\ Cukup jelas \end{array}$ .

$\begin{array}{ll} 20. & Hipotesis nol adalah . . . . \\ a . hipotesis yang nilai statistik ujinya \\ bernilai nol \\ b . hipotesis yang perumusannys mrngandung \\ pengertian yang tidak memiliki perbedaan \\ c . hipotesis yang perumusannya terkandung \\ pengertian yang tidak sama \\ d . hipotesis yang perumusannya mengandung \\ pengertian lebih dari \\ e . hipotesis yang perumusannya mengandung \\ pengertian kurang dari \\ Jawab : b \\ Cukup jelas \end{array}$ .

Lanjutan Contoh Soal 3 Distribusi Normal

$\begin{array}{ll} 11. & Perhatikan ilustrasi berikut . . . . \end{array}$ .

$. \begin{array}{ll} Jika luas yang diarsir adalah 0,90 dan n = 21, \\ maka nilai t adalah . . . . \\ a . 1, 32 \\ b . 1, 72 \\ c . 2, 08 \\ d . 2, 09 \\ e . 2, 53 \\ Jawab : \\ Luas arsiran (distribusi student) adalah : \\ = 1 - 0, 90 = 0, 10, karena luas kedua ujung \\ sama, mulai dari t ke kanan = \frac{0, 10}{2} = 0, 05 \\ Sehingga luas dari t ke kiri = 1 - 0, 05 = 0, 95 \\ Dari ini diketahui luas arsirannya = p = 0, 95 \\ Dengan d k = n - 1 = 21 - 1 = 20, maka \\ t = \pm 1, 72 \end{array}$ .

$\begin{array}{ll} 12. & Misalkan luas dari t ke kiri = 0, 05, \\ dengan d k = 15. Nilai t adalah . . . . \\ a . - 1, 76 \\ b . - 1, 75 \\ c . - 1, 74 \\ d . 1, 75 \\ e . 1, 76 \\ Jawab : \\ \begin{aligned} Diketahui dari soal di atas \\ dari t ke kiri = 0, 05, maka \\ luas arsiran = p = 1 - 0, 05 = 0, 95 \\ t = - 1, 75 (lihat tabel) \end{aligned} \end{array}$ .

$\begin{array}{ll} 13. & Transformasi Z - s c o r e dikaitan dengan \\ data dimaksudkan agar data \\ terdistribusi secara . . . . \\ a . tak normal \\ b . binomial \\ c . C h i - s q u a r e \\ d . Poison \\ e . normal \\ Jawab : \\ \begin{aligned} Cukup jelas \end{aligned} \end{array}$ .

$\begin{array}{ll} 14. & Perhatikan ilustrasi berikut . . . . \end{array}$ .

$. \begin{array}{ll} Jika kurva normal di atas memiliki simpangan \\ bakunya 12, maka luar daerah arsiran adalah . . . . \\ a . 0, 4821 \\ b . 0, 4966 \\ c . 0, 4999 \\ d . 0, 5934 \\ e . 0, 6921 \\ Jawab : \\ Diketahui, μ = 60, σ = 12, x_{1} = 50, x_{2} = 70 \\ dengan nilai z = \frac{x - μ}{σ}, maka \\ \begin{aligned} z_{1} & = \frac{x_{1} - μ}{σ} = \frac{50 - 60}{12} = \frac{- 10}{12} = - 0.83 \\ z_{2} & = \frac{x_{2} - μ}{σ} = \frac{70 - 60}{12} = \frac{10}{12} = 0.83 \end{aligned} \\ Luas = P (- z \leq Z \leq z) = 2 \times P (0 \leq Z \leq z) \\ = 2 \times (0, 2967) = 0, 5934 \end{array}$ .

$\begin{array}{ll} 15. & Perhatikan ilustrasi berikut . . . . \end{array}$ .

$. \begin{array}{ll} Jika kurva normal di atas memiliki simpangan \\ bakunya 5, maka luar daerah arsiran adalah . . . . \\ a . 0, 1585 \\ b . 0, 1815 \\ c . 0, 3413 \\ d . 0, 8172 \\ e . 0, 8185 \\ Jawab : \\ Diketahui, μ = 40, σ = 5, x_{1} = 30, x_{2} = 45 \\ dengan nilai z = \frac{x - μ}{σ}, maka \\ \begin{aligned} z_{1} & = \frac{x_{1} - μ}{σ} = \frac{30 - 40}{5} = \frac{- 10}{5} = - 2 \\ z_{2} & = \frac{x_{2} - μ}{σ} = \frac{45 - 40}{5} = \frac{5}{5} = 1 \end{aligned} \\ Luas = P (z_{1} \leq Z \leq z_{2}) = P (0 \leq Z \leq z_{1}) \\ + P (0 \leq Z \leq z_{2}) \\ = P (0 \leq Z \leq 2) + P (0 \leq Z \leq 1) \\ = 0, 3413 + 0, 4772 = 0, 8185 \end{array}$ .

Distribusi Student (Uji t)

Uji "t"

Dalam pengujian hipotesis kita mengenal 2 rumus pengujian yaitu rumus z (distribusi normal standar) dan rumus t (distribusi student). Rumus z digunakan manakala simpangan baku pada populasi diketahui, sedangkan rumus t digunakan ketika simpangan baku pada populasi tidak diketahui. Ketika simpangan baku setiap populasi jarang diketahui, maka biasanya alternatifnya adalah digunakan simpangan baku sampel dan selanjutnya digunakanlah uji t.

$\begin{aligned} t & = \frac{\bar{x} - μ_{0}}{\frac{s}{\sqrt{n}}} atau t = \frac{\bar{x} - μ_{0}}{s} \sqrt{n} \\ Dimana \\ t = nilai t yang dihitung \\ \bar{x} = rata-rata sampel \\ μ = rata-rata populasi \\ atau nilai yang dihipotesiskan \\ s = simpangan baku sampel \\ n = jumlah anggota sampel \end{aligned}$ .

Selanjutnya untuk perhitungan simpangan baku s digunakan rumus berikut

$\begin{aligned} s & = \sqrt{\frac{\sum (x_{i} - \bar{x})^{2}}{n - 1}} \\ Dimana \\ \bar{x} = rata-rata sampel \\ n - 1 = derajat kebebasan \end{aligned}$ .

Sebagai catatan dalam pemilihan statistik uji dan penghitungan statistik uji

Jika ukuran sampel $n \geq 30$ , statistik uji yang digunakan adalah z (rumus z di atas), $Z \sim N (0, 1)$ .
Jika ukuran sampel $n < 30$ , statistik uji yang digunakan adalah t, dengan derajat kebebasan $d k = n - 1$ .

$CONTOH SOAL$ .

$\begin{array}{ll} 1. & Sebuah perusahaan X mengatakan bahwa \\ performance pegawainya rata-rata nilai \\ skornya adalah 8, 5. Untuk membuktikan \\ pernyataan tersebut diambillah secara \\ random 16 orang pegawai untuk dites dan \\ hasilnya tersaji berikut \\ 7, 8 8, 2 8, 4 7, 8 8, 9 9, 1 8, 5 7, 7 \\ 8, 5 7, 9 9, 1 7, 8 9, 2 8, 9 8, 8 8, 3 \\ Pada taraf 1 %, apakah pernyataan \\ perusahaan tersebut benar \\ Jawab : \\ \begin{aligned} Misalkan rata-rata skor performance \\ berdistribusi student \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ = 8, 5 \\ H_{1} : μ \neq 8, 5 \\ Daerah kritis \\ Uji dua pihak/hipotesis dua arah dengan α = 1 % \\ t_{1 - \frac{1}{2} (0, 01)} = t_{0, 995} . Dengan dk = 16 - 1 = 15 \\ diperoleh nilai t = 2, 95 (tabel distribusi student) \\ ∙ Terima H_{0}, jika : - 2, 95 < t < 2, 95 \\ ∙ Tolak H_{0}, jika : t < - 2, 95 atau t > 2, 95 \\ Berikut disajikan tabel distribusi student \\ \begin{array}{ccccc} d k & t_{0, 995} & t_{0, 99} & t_{0, 975} & t_{0, 95} \\ 1 & 63, 66 & 31, 82 & 12, 71 & 6, 31 \\ 2 & 9, 92 & 6, 96 & 4, 3 & 2, 92 \\ 3 & 5, 84 & 4, 54 & 3, 18 & 2, 35 \\ 4 & 4, 6 & 3, 75 & 2, 78 & 2, 13 \\ 5 & 4, 03 & 3, 36 & 2, 57 & 2, 02 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 15 & 2, 95 & 2, 60 & 2, 13 & 1, 75 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 99 & \dots & \dots & 1, 99 & \dots \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 120 & 2, 62 & 2, 36 & 1, 98 & 1, 66 \\ \infty & 2, 56 & 2, 33 & 1, 96 & 1, 645 \end{array} \\ Nilai statistik uji \\ \bar{x} = \frac{7, 5 + 8, 2 + 8, 4 + \dots + 8, 8 + 8, 3}{16}, \\ = 8, 4125 \\ s = \sqrt{\frac{(7, 5 - 8, 4125)^{2} + \dots + (8, 3 - 8, 4125)^{2}}{16 - 1}} \\ = \sqrt{0, 308} = 0, 555 \\ n = 100, t = \frac{\bar{x} - μ_{0}}{s} \sqrt{n} \\ \Leftrightarrow t = \frac{(8, 4125 - 8, 5)}{0, 555} \sqrt{16} = - 0, 63 \\ Penentuan keputusan uji \\ Karena : - 2, 95 < - 0, 63 < 2, 95, H_{0} diterima \\ Kesimpulan \\ Dengan taraf nyata 1 % rata-rata skor \\ performan pegawai adalah 8, 5 \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Sebuah sampel acak 100 catatan kematian \\ di negara A selama 1 tahun yang kemaren \\ menunjukkan umur rata-rata 58,8 tahun \\ dengan simpangan baku 7,8 tahun. Apakah \\ hal itu menunjukkan bahwa harapan umur \\ rata-rata sekarang minimal 60 tahun ? \\ Jelaskan pernyataan tersebut dengan tingkat \\ signifikansi 5 % \\ Jawab : \\ \begin{aligned} Misalkan umur rata-rata sekarang \geq 60 tahun \\ berdistribusi student \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ \geq 60 \\ H_{1} : μ < 60 \\ Daerah kritis \\ Uji satu pihak/hipotesis pihak kiri dengan α = 5 % \\ t_{1 - (0, 05)} = t_{0, 995} . Dengan dk = 100 - 1 = 99 \\ diperoleh nilai t = 2, 63 (tabel distribusi student) \\ ∙ Terima H_{0}, jika : t > - 2, 63 \\ ∙ Tolak H_{0}, jika : t \leq - 2, 63 \\ Nilai statistik uji \\ μ = 58, 8, s = 7, 8 tahun \\ n = 100, t = \frac{\bar{x} - μ_{0}}{s} \sqrt{n} \\ \Leftrightarrow t = \frac{(58, 8 - 60)}{7, 8} \sqrt{100} = - 1, 54 \\ Penentuan keputusan uji \\ Karena : t \leq - 1, 54, H_{0} diterima \\ Kesimpulan \\ Dengan taraf nyata 5 % umur rata-rata \\ sekarang minimal 60 tahun \end{aligned} \end{array}$ .

DAFTAR PUSTAKA

Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
Sembiring, S., Zulkifli. M., Marsito, Rusdi. I. 2016. Matematika untuk Siswa SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.
Sugiyono. 2013. Statistika untuk Penelitan. Bandung: ALFABETA

Lanjutan Contoh Soal 2 Distribusi Normal

$\begin{array}{ll} 6. & Luas daerah yang diarsir di bawah \\ kurva normal baku berikut adalah . . . . \\ a . 0, 4861 \\ b . 0, 4878 \\ c . 0, 4881 \\ d . 0, 4938 \\ e . 0, 4946 \end{array}$ .

. \begin{aligned} Jawab : \\ Perhatikan tabel distribusi normal berikut \\ \begin{array}{ccccccccccc} z & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ ⋮ & ↓ \\ ⋮ \\ 2, 2 & 0, 4878 \\ ⋮ \end{array} \\ Sehingga nilai z = 2, 25 luasnya = 0, 4878 \end{aligned}

\begin{array}{ll} 7. & Luas daerah yang diarsir di bawah \\ kurva normal baku berikut adalah . . . . \\ a . 0, 1138 \\ b . 0, 3810 \\ c . 0, 3862 \\ d . 0, 4948 \\ e . 0, 5000 \end{array}

. \begin{aligned} Jawab : \\ Perhatikan tabel distribusi normal berikut \\ \begin{array}{ccccccccccc} z & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ ⋮ & ↓ & ↓ \\ ⋮ \\ 1, 1 & ↓ & 0, 3810 \\ ⋮ \\ 2, 5 & 0, 4948 \\ ⋮ \end{array} \\ Sehingga nilai z = 1, 18 luasnya = 0, 3810 \\ Dan nilai z = 2, 56 luasnya = 0, 4948 \\ maka luas arsiran \\ = P (1, 18 < Z < 2, 56) \\ = P (0 < Z < 2, 56) - P (0 < Z < 1, 18) \\ = 0, 4948 - 0, 3810 \\ = 0, 1138 \end{aligned}

\begin{array}{ll} 8. & Luas daerah yang diarsir pada gambar \\ di bawah adalah 0,9332, maka nilai z = . . . . \end{array}

. \begin{array}{ll} a . 1, 05 \\ b . 1, 06 \\ c . 1, 16 \\ d . 1, 50 \\ e . 1, 60 \\ Jawab : \\ Luas arsiran adalah \\ = P (Z < z) = 0, 9332 \\ = 0, 5 + 0, 4332 \\ = 0, 5 + P (0 < Z < z) \\ lihat/konfirmasi ke tabel \\ z = 1, 50 \\ \begin{aligned} Perhatikan tabel distribusi normal berikut \\ \begin{array}{ccccccccccc} z & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ ⋮ & ↓ \\ ⋮ \\ 1, 5 & 0, 4332 \\ ⋮ \end{array} \\ Sehingga luasnya = 0, 4878, batas z = 1, 50 \end{aligned} \end{array}

\begin{array}{ll} 9. & Luas daerah yang diarsir pada gambar \\ di bawah adalah = . . . . \end{array}

. \begin{array}{ll} a . 0, 9750 \\ b . 0, 5000 \\ c . 0, 4750 \\ d . 0, 0250 \\ e . 0, 0200 \\ Jawab : \\ Luas arsiran adalah \\ = P (0 \leq Z \leq \infty) - P (0 \leq Z \leq 1, 96) \\ = 0, 5 - 0, 4750 \\ = 0, 0250 \end{array}

\begin{array}{ll} 10. & Misalkan tinggi siswa kelas XII berdistribusi \\ normal dengan rata-rata 167,5 cm dengan \\ simpangan baku 4,6 cm. Jika jumlah siswa \\ yang diteliti sebanyak 10.000 siswa, maka \\ jumlah siswa yang memiliki tinggi lebih \\ dari 160 cm sebanyak . . . . \\ a . 16.300 \\ b . 9.484 \\ c . 5.516 \\ d . 4.484 \\ e . 4.474 \\ Jawab : \\ \begin{aligned} Diketahui dari soal di atas \\ n = 10.000, μ = 167, 5 cm, σ = 4, 6 \\ z = \frac{x - μ}{σ} = \frac{160 - 167, 5}{4, 6} = - 1, 63 \\ \begin{aligned} P (X > 160) & = P (Z > - 1, 63) \\ = P (0 \leq Z \leq 1, 63) \\ + P (0 \leq Z \leq \infty) \\ = 0, 4484 + 0, 5 \\ = 0, 9484 \end{aligned} \\ Sehingga total siswa yang dimaksud \\ sebanyak : 0, 9484 \times 10.000 = 9.484 \end{aligned} \end{array}

Penarikan Kesimpulan

F. Uji Hipotesis

F. 1 Pengertian

Dalam suatu penyelidikan berkaitan suatu permasalahan untuk penarikan suatu kesimpulan diperlukan adanya dugaan atau dalam bahasa matematika dinamakan istilah hipotesis. Hipotesis berasal dari bahasa Yunani Hupo yang berarti sementara dan Thesis yang berarti pernyataan atau dugaan. Sehingga secara bahasa memiliki arti dugaan sementara. Selanjutnya, karena hipotesis ini masih berupa jawaban sementara, maka hipotesis ini harus diuji kebenaranya dan prosesnya dinamakan uji hipotesis. Uji hipotesis yang dibahasa di sini adalah pengujian berkaitan dengan rata-rata $μ$ pada sebuah sampel. Jika hasil yang didapatkan dalam penelitian nantinya, jauh berbeda dengan yang diharapkan berdasarkan hipotesis, maka hipotesis ditolak, demikian sebaliknya jika sesuai, maka hipotesis diterima.

F. 2 Jenis-Jenis Hipotesis

Ada dua jenis hipotetsis yaitu:

Hipotesis nol ( $H_{0}$ ) yang terkandung makna tidak memiliki perbedaan
Hipotesis alternatif ( $H_{1}$ ) dengan pengertian terdapat tidak sama atau ada perbedaan.

F. 3 Langkah-Langkah Pengujian Hipotesis.

Berikut prosedur pengujian hipotesis

$. \begin{aligned} Merumuskan H_{0} dan H_{1} \\ ⇓ \\ Menentukan daerah kritis \\ (taraf signifikansi/kepercayaan) \\ ⇓ \\ Menentukan nilai statistik uji \\ ⇓ \\ Menentukan keputusan uji \\ ⇓ \\ Penarikan kesimpulan \end{aligned}$ .

Sebagai tambahannya, dalam melakukan pengujian hipotesis, ada 2 jenis kekeliruan yang bisa terjadi

Kekeliruan tipe I, yaitu kita menolak hipotesis yang seharusnya diterima
Kekeliruan tipe II, yaitu kita menerima hipotesis yang seharusnya kita tolak

\begin{array}{lcc} Keputusan uji & H_{0} benar & H_{0} salah \\ Menerima H_{0} & \begin{aligned} Benar \\ (1 - α) \end{aligned} & \begin{aligned} Kesalahan \\ tipe II (β) \end{aligned} \\ Menolak H_{0} & \begin{aligned} Kesalahan \\ tipe I (α) \end{aligned} & \begin{aligned} Benar \\ (1 - β) \end{aligned} \end{array}

Untuk meminimalkan kesalahan:

dalam pengujian hipotesis diinginkan $α$ (dibaca alfa) dan $β$ (dibaca beta) kecil atau $(1 - β)$ besar.
tetapi hal di atas adalah sulit karena jika $α$ makin kecil, maka nilai $β$ semakin besar.
dari 2 hal tersebut di atas, maka dipilihlah salah satu, dalam hal ini biasanya $α$ . dan $α$ yang digunakan bisanya pula adalah 10%, 5%, dan atau 1% tergantung kebutuhgannya dalam bidang apa mau diterapkan. Misal dalam bidang pengobatan diambillah $α$ yang 1%.
$α$ dalam hal ini selanjutnya disebut taraf signifikansi atau taraf arti atau taraf nyata.

F.4 Bentuk Pengujian Hipotesis

Ada 3 macam, yaitu, uji dua pihak, uji pihak kanan, dan uji pihak kiri.

F. 4. 1 Uji dua Pihak

\begin{array}{ll} Jika σ diketahui & Jika σ tidak diketahui \\ \begin{aligned} Untuk menguji pasangan hipotesis \\ {\begin{cases} H_{0} & : μ = μ_{0} \\ H_{1} & : μ \neq μ_{0} \end{cases} \\ di mana nilai z = (\frac{\bar{x} - μ_{0}}{σ}) \sqrt{n} \\ Dan untuk z berdistribusi normal \\ baku. Pengambilan kesimpulan \\ H_{0} diterima jika : \\ - z_{\frac{1}{2} (1 - α)} < z < z_{\frac{1}{2} (1 - α)} \\ dan daerah ini disebut \\ daerah tidak nyata atau \\ daerah penerimaan H_{0} \end{aligned} & \begin{aligned} Untuk menguji pasangan hipotesis \\ {\begin{cases} H_{0} & : μ = μ_{0} \\ H_{1} & : μ \neq μ_{0} \end{cases} \\ Gunakan distribusi student \\ dengan rumus t = (\frac{\bar{x} - μ_{0}}{s}) \sqrt{n} \\ di mana s adalah simpangan baku \\ dan dihitung  dengan rumus \\ s = \sqrt{\frac{\sum (x_{i} - \bar{x})^{2}}{n - 1}} \\ Dan untuk t berdsitribusi student \\ pada pengambilan kesimpulan, H_{0} \\ diterima jika : - t_{(1 - \frac{1}{2} α)} < t < t_{(1 - \frac{1}{2} α)} \\ dan daerah ini disebut \\ daerah tidak nyata atau \\ daerah penerimaan H_{0} \\ dengan d K = n - 1 \end{aligned} \end{array}

$CONTOH SOAL$ .

$\begin{array}{ll} 1. & Seorang pengusaha lampu merk X mengatakan \\ bahwa lampunya memiliki masa pakai rata-rata \\ 900. Untuk menguji pernyataan tersebut, maka \\ diuji sebanyak 100 lampu dan ternyata rata-rata \\ masa pakainya 890 jam dengan simpangan baku- \\ nya 60 jam. Selidikilah dengan tingkat signifikansi \\ 5 %, apakah kualitas lampu itu sudah berubah \\ atau belum \\ Jawab : \\ \begin{aligned} Misalkan masa hidup lampu berdistribusi normal \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ = 900 jam (masa pakai masih 900 jam) \\ H_{1} : μ \neq 900 jam (masa berubah dan) \neq 900 jam \\ Daerah kritis \\ Uji dua pihak/hipotesis dua arah dengan α = 5 % \\ z_{\frac{1}{2} (1 - 0, 05)} = z_{0, 475} = 1, 96 (lihat tabel) \\ ∙ Terima H_{0}, jika : - 1, 96 < z < 1, 96 \\ ∙ Tolak H_{0}, jika : z < - 1, 96 atau z > 1, 96 \\ Nilai statistik uji \\ \bar{x} = 890, n = 100, z = \frac{\bar{x} - μ_{0}}{σ} \sqrt{n} \\ \Leftrightarrow z = \frac{(890 - 900)}{60} \sqrt{100} = \frac{- 10 \times 10}{60} = - 1, 67 \\ Penentuan keputusan uji \\ Karena : - 1, 96 < - 1, 67 < 1, 96, H_{0} diterima \\ Kesimpulan \\ Dengan taraf nyata 5 % masa pakai lampu \\ belum berubah dan masih sekitar 900 jam \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Jika pada soal nomor 1 di atas, simpangan baku \\ (σ) tidak diketahui, tetapi dari sampel diperoleh \\ s = 55 jam. Selidikilah apakah kualitas lampu itu \\ sudah berubah atau belum \\ Jawab : \\ \begin{aligned} Misalkan masa hidup lampu berdistribusi student \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ = 900 jam (masa pakai masih 900 jam) \\ H_{1} : μ \neq 900 jam (masa berubah dan) \neq 900 jam \\ Daerah kritis \\ Uji dua pihak/hipotesis dua arah dengan α = 5 % \\ t_{1 - \frac{1}{2} (0, 05)} = t_{0, 975} . Dengan dk = 100 - 1 = 99 \\ diperoleh nilai t = 1, 99 (tabel distribusi student) \\ ∙ Terima H_{0}, jika : - 1, 99 < t < 1, 99 \\ ∙ Tolak H_{0}, jika : t < - 1, 99 atau t > 1, 99 \\ Berikut disajikan tabel distribusi student \\ \begin{array}{ccccc} d k & t_{0, 995} & t_{0, 99} & t_{0, 975} & t_{0, 95} \\ 1 & 63, 66 & 31, 82 & 12, 71 & 6, 31 \\ 2 & 9, 92 & 6, 96 & 4, 3 & 2, 92 \\ 3 & 5, 84 & 4, 54 & 3, 18 & 2, 35 \\ 4 & 4, 6 & 3, 75 & 2, 78 & 2, 13 \\ 5 & 4, 03 & 3, 36 & 2, 57 & 2, 02 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 60 & 2, 66 & 2, 39 & 2, 00 & 1, 67 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 99 & \dots & \dots & 1, 99 & \dots \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 120 & 2, 62 & 2, 36 & 1, 98 & 1, 66 \\ \infty & 2, 56 & 2, 33 & 1, 96 & 1, 645 \end{array} \\ Nilai statistik uji \\ \bar{x} = 890, s = 55 jam, n = 100, t = \frac{\bar{x} - μ_{0}}{s} \sqrt{n} \\ \Leftrightarrow t = \frac{(890 - 900)}{55} \sqrt{100} = \frac{- 10 \times 10}{55} = - 1, 82 \\ Penentuan keputusan uji \\ Karena : - 1, 99 < - 1, 82 < 1, 99, H_{0} diterima \\ Kesimpulan \\ Dengan taraf nyata 5 % masa pakai lampu \\ belum berubah dan masih sekitar 900 jam \end{aligned} \end{array}$ .

F. 4. 2 Uji Satu Pihak

a) Uji Pihak Kanan

\begin{aligned} Jika H_{1} : μ > μ_{0} \\ Daerah kritis berada di ujung kanan kurva \end{aligned}

CONTOH SOAL

\begin{array}{ll} 1. & Seorang petugas menyatakan bahwa pendapatan \\ penjual mainan X tidak lebih dari R p 20.000 \\ perhari. Untuk menyangkal pernyataan tersebut \\ pihak kantor melakukan penelitian terhadap \\ tingkat pendapatan penjual mainan itu. Pihak \\ kantor memilih 150 penjual secara acak, ternyata \\ diperoleh data rata-rata pendapatan mereka \\ R p 21.000 dengan simpangan baku R p 5.000 \\ Dengan α = 5 % cukup beralasankah pernyataan \\ petugas tersebut \\ Jawab : \\ \begin{aligned} Misalkan pendapatan penjual berdistribusi normal \\ dengan hasil tidak lebih R p 20.000 perhari \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ \leq 20.000 \\ H_{1} : μ > 20.000 \\ Daerah kritis \\ Uji satu pihak, daerah kritis kanan dengan α = 5 % \\ z_{0, 05} = 1, 64 (lihat tabel normal baku) \\ ∙ Terima H_{0}, jika : z < 1, 64 \\ ∙ Tolak H_{0}, jika : z \geq 1, 64 \\ Nilai statistik uji \\ \bar{x} = 21.000, μ_{0} = 20.000 jam, n = 150, \\ σ = 5.000, dengan rumus z = \frac{\bar{x} - μ_{0}}{σ} \sqrt{n} \\ \Leftrightarrow z = \frac{(21.000 - 20.000)}{5000} \sqrt{150} \\ = \frac{1.000 \times 12, 247}{5.000} = 2, 45 \\ Penentuan keputusan uji \\ Karena : 2, 45 \geq 1, 64, H_{0} ditolak \\ Kesimpulan \\ Dengan taraf nyata 5 % rata-rata pendapatan \\ penjual lebih dari R p 20.000 perhari \end{aligned} \end{array}

b) Uji Pihak Kiri

\begin{aligned} Jika H_{1} : μ < μ_{0} \\ Daerah kritis berada di ujung kiri kurva \end{aligned}

CONTOH SOAL

\begin{array}{ll} 2. & Seorang petugas menyatakan bahwa pendapatan \\ penjual mainan X tidak kurang dari R p 21.000 \\ perhari. Pihak kantor ingin menguji terhadap \\ tingkat pendapatan penjual mainan itu. Pihak \\ kantor memilih 150 penjual secara acak, ternyata \\ diperoleh data rata-rata pendapatan mereka \\ R p 20.000 dengan simpangan baku R p 5.000 \\ Dengan α = 5 % cukup beralasankah pernyataan \\ petugas tersebut \\ Jawab : \\ \begin{aligned} Misalkan pendapatan penjual berdistribusi normal \\ dengan hasil tidak kurang dari R p 21.000 perhari \\ Rumusan hipotesis H_{0} dan H_{1} \\ H_{0} : μ \geq 21.000 \\ H_{1} : μ < 21.000 \\ Daerah kritis \\ Uji satu pihak, daerah kritis kiri dengan α = 5 % \\ z_{0, 05} = - 1, 64 (lihat tabel normal baku) \\ ∙ Terima H_{0}, jika : z > - 1, 64 \\ ∙ Tolak H_{0}, jika : z \leq - 1, 64 \\ Nilai statistik uji \\ \bar{x} = 20.000, μ_{0} = 21.000 jam, n = 150, \\ σ = 5.000, dengan rumus z = \frac{\bar{x} - μ_{0}}{σ} \sqrt{n} \\ \Leftrightarrow z = \frac{(20.000 - 21.000)}{5000} \sqrt{150} \\ = \frac{1.000 \times 12, 247}{5.000} = - 2, 45 \\ Penentuan keputusan uji \\ Karena : - 2, 45 \leq - 1, 64, H_{0} ditolak \\ Kesimpulan \\ Dengan taraf nyata 5 % rata-rata pendapatan \\ penjual kurang dari R p 21.000 perhari \end{aligned} \end{array}

DAFTAR PUSTAKA

Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
Noormandiri, B.K. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
Sembiring, S., Zulkifli. M., Marsito, Rusdi. I. 2016. Matematika untuk Siswa SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.

Contoh Soal Distribusi Normal

$\begin{array}{ll} 1. & Fungsi distribusi normal variabel acak X \\ dengan μ = 8 dan σ = 2 adalah . . . . \\ a . f (x) = \frac{1}{\sqrt{2 π}} e^{.^{- \frac{(x - 8)^{2}}{2}}} \\ b . f (x) = \frac{1}{\sqrt{2 π}} e^{.^{- \frac{(x - 8)^{2}}{4}}} \\ c . f (x) = \frac{1}{\sqrt{2 π}} e^{.^{- \frac{(x - 8)^{2}}{2}}} \\ d . f (x) = \frac{1}{\sqrt{8 π}} e^{.^{- \frac{(x - 8)^{2}}{4}}} \\ e . f (x) = \frac{1}{\sqrt{8 π}} e^{.^{- \frac{(x - 8)^{2}}{8}}} \\ Jawab : e \\ \begin{aligned} f (x) & = \frac{1}{σ \sqrt{2 π}} e^{.^{- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}}}, dengan {\begin{array}{c} μ = 8 \\ σ = 2 \end{array} \\ = \frac{1}{2 \sqrt{2 π}} e^{.^{- \frac{1}{2} {(\frac{x - 8}{2})}^{2}}} \\ = \frac{1}{\sqrt{8 π}} e^{.^{- \frac{(x - 8)^{2}}{8}}} \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Jika variabel acak Z berdistribusi normal \\ N (0, 1), nilai P (Z < 2) adalah . . . . \\ a . \int_{0}^{2} \frac{1}{\sqrt{2 π}} e^{.^{- \frac{1}{2} z^{2}}} d z \\ b . \int_{2}^{\infty} \frac{1}{\sqrt{2 π}} e^{.^{- \frac{1}{2} z^{2}}} d z \\ c . \int_{- \infty}^{2} \frac{1}{\sqrt{2 π}} e^{.^{- \frac{1}{2} z^{2}}} d z \\ d . \int_{0}^{2} \frac{1}{σ \sqrt{2 π}} e^{.^{- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}}} d z \\ e . \int_{0}^{2} \frac{1}{σ \sqrt{2 π}} e^{.^{- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}}} d z \\ Jawab : c \\ \begin{aligned} P (Z < 2), Z \sim N (0, 1) \\ = P (- \infty < Z < 0) + P (0 < Z < 2) \\ = \int_{- \infty}^{2} \frac{1}{\sqrt{2 π}} e^{.^{- \frac{1}{2} z^{2}}} d z \end{aligned} \end{array}$ .

$\begin{array}{ll} 3. & Jika luas daerah di bawah kurva \\ berdistribusi normal pada interval Z > z \\ adalah L, nilai P (- z < Z < z) adalah . . . . \\ a . 0, 5 + L \\ b . 0, 5 - L \\ c . 1 - L \\ d . 1 - 2 L \\ e . 2 L \\ Jawab : d \\ \begin{aligned} P & (- z < Z < z) \\ = 0, 5 - L + 0, 5 - L \\ = 1 - 2 L \\ Berikut ilustrasi kurva beserta luasnya \end{aligned} \end{array}$ .

$\begin{array}{ll} 4. & Diketahui X \sim N (20, 4) dan Z \sim N (0, 1) \\ Jika P (0 < Z < 1) = 0, 3413, maka nilai \\ P (X < 24) adalah . . . . \\ a . 0, 1587 \\ b . 0, 3174 \\ c . 0, 3413 \\ d . 0, 6826 \\ e . 0, 8413 \\ Jawab : e \\ \begin{aligned} Diketahui bahwa X \sim N (20, 4) {\begin{cases} μ & = 20 \\ σ & = 4 \end{cases} \\ Dan diketahui pula P (0 < Z < 1) = 0, 3413 \\ Jika Z \sim N (0, 1), maka untuk P (X < 24) \\ transformasi x = 24 menjadi \\ z = \frac{x - μ}{σ} = \frac{24 - 20}{4} = \frac{4}{4} = 1 \\ Selanjutnya \\ \begin{aligned} P (X < 24) & = P (Z < 1) \\ = 0, 5 + P (0 < Z < 1) \\ = 0, 5 + 0, 3413 \\ = 0, 8413 \end{aligned} \end{aligned} \end{array}$ .

$\begin{array}{ll} 5. & Nilai kuartil atas dari data \\ berdistribusi normal baku = q \\ Pernyataan berikut yang tepat adalah . . . . \\ a . Luas daerah pada (Z < q) = 0, 25 \\ b . Luas daerah pada (Z > q) = 0, 25 \\ c . Luas daerah pada (0 < Z < q) = 0, 25 \\ d . Luas daerah pada (Z < - 0, 25) = q \\ e . Luas daerah pada (0 < Z < 0, 25) = q \\ Jawab : a \\ Pembahasan diserahkan kepada pembaca \\ yang budiman \end{array}$ .

Lanjutan 2 Distribusi Normal

D. Menentukan nilai k (batas interval)

Penentuan batas ini adalah kebalikan dari pencarian nilai luasan di bawah kurva

$CONTOH SOAL$ .

$\begin{array}{ll} 1. & Dengan bantuan tabel distribusi normal \\ tentukan nilai k pada P (Z \leq k) = 0, 9834 \\ Jawab : \\ \begin{aligned} P (Z \leq k) & = P (Z \leq 0) + P (0 \leq Z \leq k) \\ = 0, 9834 > 0, 5 \\ 0, 9834 & = 0, 5 + P (0 \leq Z \leq k) \\ P (0 \leq Z \leq k) & = 0, 9834 - 0, 5 = 0, 4834 \\ = P (0 \leq Z \leq 2, 13) \\ ∴ k & = 2, 13 \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Dengan bantuan tabel distribusi normal \\ tentukan nilai k pada P (Z \geq k) = 0, 3669 \\ Jawab : \\ \begin{aligned} P (0 \leq Z \leq \infty) & = P (0 \leq Z \leq k) + P (k \leq Z \leq \infty) \\ 0, 5 & = P (0 \leq Z \leq k) + 0, 3669 \\ P (0 \leq Z \leq k) & = 0, 5 - 0, 3669 = 0, 1331 \\ = P (0 \leq Z \leq 0, 34) \\ ∴ k & = 0, 34 \end{aligned} \end{array}$ .

$\begin{array}{ll} 3. & Dengan tabel distribusi normal, tentukan \\ nilai k pada P (- k \leq Z \leq k) = 0, 9854 \\ Jawab : \\ \begin{aligned} P (- k \leq Z \leq k) & = P (- k \leq Z \leq 0) + P (0 \leq Z \leq k) \\ = 2 \times P (0 \leq Z \leq k) \\ 0, 9854 & = 2 \times P (0 \leq Z \leq k) \\ P (0 \leq Z \leq k) & = \frac{0, 9854}{2} = 0, 4972 \\ = P (0 \leq Z \leq 2, 77) \\ ∴ k & = 2, 77 \end{aligned} \end{array}$ .

E. Pendekatan distribusi binomial dengan distribusi normal

Pada kasus distribusi binomial (distribusi Bernoulli) terdapat jumlah sampel yang besar, misalkan untuk $n = 60$ , maka penghitungan dengan menggunakan metode ini akan memakan waktu yang lama. Penghitungan yang lebih ringkas dengan tingkat ketelitian hasil yang baik adalah dapat kita gunakan penghitungan dengan distribusi normal (distibusi Gauss) dengan syarat $N p \geq 5$ dan $N (1 - p) \geq 5$ .

$\begin{array}{ccll} Notasi & Dibaca & Istilah & Rumus \\ μ & mu & rata-rata & μ = N p \\ σ^{2} & Variansi & σ^{2} = N p q \\ σ & sigma & simpangan baku & σ = \sqrt{N p q} \end{array}$ .

Dengan

$\begin{aligned} Dengan rumus distribusi binomial \\ P (X = x) = b (x; n; p) \\ = \frac{n!}{x! . (n - x)!} . p^{x} . q^{n - x} = (\begin{array}{c} n \\ x \end{array}) . . p^{x} . q^{n - x} \\ Dengan rumus distribusi normal \\ nilai Z - score, untuk x adalah : Z = \frac{x - μ}{σ} \end{aligned}$ .

$CONTOH SOAL$ .

$\begin{array}{ll} 1. & Dari 64 kali percobaan melempar sebuah \\ uang logam peubah acak X menyatakan \\ banyak kemunculan sisi angka, tentukan \\ a . mean \\ b . standar deviasi atau simpangan baku \\ Jawab : \\ \begin{aligned} Misal p = peluang kejadian muncul angka \\ p = \frac{1}{2}, maka q = 1 - p = 1 - \frac{1}{2} = \frac{1}{2} \\ dengan N = 64 \\ maka \\ a . μ = N . p = 64 \times \frac{1}{2} = 32 \\ b . σ = \sqrt{N . p . q} = \sqrt{64 \times \frac{1}{2} \times \frac{1}{2}} = \sqrt{16} \\ = 4 \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Tentukan probabilitas perolehan 5 sisi angka \\ pada pelemparan sebuah uang logam sebanyak \\ 12 kali \\ Jawab : \\ \begin{aligned} Dengan rumus distribusi binomial \\ Diketahui n = 12, x = 5, dan p = \frac{1}{2}, q = 1 - p \\ P (X = x) = b (x; n; p) \\ = \frac{n!}{x! . (n - x)!} . p^{x} . q^{n - x} = (\begin{array}{c} n \\ x \end{array}) . . p^{x} . q^{n - x} \\ P (x = 5) = b (5; 12; \frac{1}{2}) \\ = (\begin{array}{c} 12 \\ 5 \end{array}) . {(\frac{1}{2})}^{5} . {(1 - \frac{1}{2})}^{12 - 5} \\ = \frac{12!}{5! .7!} . {(\frac{1}{2})}^{12} \\ = \frac{792}{4048} = 0, 1934 (Pembulatan 4D) \end{aligned} \\ \begin{aligned} Dengan rumus distribusi normal \\ μ = n . p = 12. (\frac{1}{2}) = 6 \\ σ = \sqrt{n p q} = \sqrt{12. (\frac{1}{2}) (1 - \frac{1}{2})} = \sqrt{3} \\ = 1, 7321 \\ nilai Z - score, untuk x di antara \\ 4, 5 dan 5, 5 \\ Z_{1} = \frac{x_{1} - μ}{σ} = \frac{4, 5 - 6}{1, 7321} = - 0, 87 \\ \Rightarrow P (Z = 0, 87) = 0, 3078 \\ Z_{2} = \frac{x_{2} - μ}{σ} = \frac{5, 5 - 6}{1, 7321} = - 0, 29 \\ \Rightarrow P (Z = 0, 29) = 0, 1141 \\ Luasan 4, 5 hingga 5, 5 \\ = 0, 3078 - 0, 1141 = 0, 1937 \end{aligned} \\ Perbedaan selisihnya adalah \\ = 0, 1937 - 0, 1934 = 0, 0003 \end{array}$ .

$\begin{array}{ll} 3. & Pada soal nomor 1 di atas, carilah probabilitas \\ mendapatakan 2 sisi angka dan probabilitas \\ mendapatkan sisi angka kurang dari 50 \\ Jawab : \\ \begin{aligned} ∙ untuk x = 2, n = 64, dan p = \frac{1}{2}, q = 1 - p \\ P (X = x) = b (x; n; p) \\ = \frac{n!}{x! . (n - x)!} . p^{x} . q^{n - x} = (\begin{array}{c} n \\ x \end{array}) . . p^{x} . q^{n - x} \\ maka P (X = 2) = P (x = 2) \\ P (x = 2) = (\begin{array}{c} 64 \\ 2 \end{array}) {(\frac{1}{2})}^{2} {(\frac{1}{2})}^{64 - 2} \\ = \frac{64 \times 63}{2} \times {(\frac{1}{2})}^{64} = \frac{4032}{2^{65}} \\ Alternatif 1 \\ ∙ P (X < 50) = P (x = 0) + P (x = 1) \\ + P (x = 2) + P (x = 3) + . . . + P (x = 49) \end{aligned} \\ \begin{aligned} Alternatif 2 \\ Diketahui μ = 32, σ = 4, dan x = 50 \\ z = \frac{x - μ}{σ} = \frac{50 - 32}{4} = \frac{18}{4} = 4, 5 \\ maka nilai \\ P (x < 50) = P (z < 4, 5) \\ = P (z \leq 0) + P (0 \leq z < 4, 5) \\ = 0, 5 + 0, 4999 \\ = 0, 9999 \end{aligned} \end{array}$ .

DAFTAR PUSTAKA

Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
Noormandiri, B.K. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
Sari, B.-------. Pendekatan Binomial untuk Kasus Distribusi Normal. pada https://dosen.yai.ac.id/v5/dokumen/materi/030013/103_20211207093237_Pertemuan%2010_Pendekatan%20Binomial%20Untuk%20Kasus%20Distribusi%20Normal.pdf

PAS MATEMATIKA BLOG

Lanjutan Materi Polinom

Lanjutan Vektor di Ruang

Vektor di Ruang

Polinom

Lanjutan Contoh Soal 6 Distribusi Normal

Lanjutan Contoh Soal 5 Distribusi Normal

Lanjutan Contoh Soal 4 Distribusi Normal

Lanjutan Contoh Soal 3 Distribusi Normal

Distribusi Student (Uji t)

Lanjutan Contoh Soal 2 Distribusi Normal

Penarikan Kesimpulan

Contoh Soal Distribusi Normal

Lanjutan 2 Distribusi Normal