PAS MATEMATIKA BLOG

Contoh Soal 8 Materi Hubungan Dua Lingkaran

$\begin{array}{ll} 36. & Persamaan lingkaran yang menyinggung \\ sumbu X serta melalui titik potong \\ lingkaran (x + 1)^{2} + (y + 2)^{2} = 1 dan \\ x^{2} + y^{2} + 3 x + 3 y + 4 = 0 adalah . . . . \\ a . x^{2} + y^{2} - 4 x + 2 y + 4 = 0 \\ b . x^{2} + y^{2} - 4 x + 2 y - 4 = 0 \\ c . x^{2} + y^{2} - 4 x - 2 y - 4 = 0 \\ d . x^{2} + y^{2} + 4 x + 2 y + 4 = 0 \\ e . x^{2} + y^{2} + 4 x + 2 y - 4 = 0 \\ Jawab : \\ \begin{aligned} Diketahui bahwa : L_{3} = L_{1} + p (L_{1} - L_{2}) = 0 \\ dengan \\ ∙ L_{1} = (x + 1)^{2} + (y + 2)^{2} = 1 \\ \Leftrightarrow x^{2} + y^{2} + 2 x + 4 y + 4 = 0 \\ ∙ L_{2} = x^{2} + y^{2} + 3 x + 3 y + 4 = 0 \\ Untuk L_{1} - L_{2} = - x + y = 0 \Leftrightarrow y = x \\ Dengan cara coba-coba, maka \\ \begin{aligned} L_{3} & = L_{1} + p (L_{1} - L_{2}) = 0 \\ = x^{2} + y^{2} + 2 x + 4 y + 4 + p (- x + y) = 0 \\ Untuk p = 1 \\ \Leftrightarrow x^{2} + y^{2} + 2 x + 4 y + 4 + (- x + y) = 0 \\ \Leftrightarrow x^{2} + y^{2} + x + 5 y + 4 = 0 \\ Untuk p = - 1 \\ \Leftrightarrow x^{2} + y^{2} + 2 x + 4 y + 4 - (- x + y) = 0 \\ \Leftrightarrow x^{2} + y^{2} + 3 x + 3 y + 4 = 0 \\ Dan untuk p = - 2 \\ \Leftrightarrow x^{2} + y^{2} + 2 x + 4 y + 4 - 2 (- x + y) = 0 \\ \Leftrightarrow x^{2} + y^{2} + 4 x + 2 y + 4 = 0 \end{aligned} \end{aligned} \\ Berikut ilustrasi gambarnyanya \end{array}$

DAFTAR PUSTAKA

Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Contoh Soal 7 Materi Hubungan Dua Lingkaran

$\begin{array}{ll} 31. & Persamaan lingkaran yang melalui titik \\ (0, 0) dan titik potong kedua lingkaran \\ x^{2} + y^{2} - 6 x - 8 y - 11 = 0 dan \\ x^{2} + y^{2} - 4 x - 6 y - 22 = 0 adalah . . . . \\ a . x^{2} + y^{2} - 12 x + 10 y = 0 \\ b . x^{2} + y^{2} + 8 x - 10 y = 0 \\ c . x^{2} + y^{2} - 8 x + 12 y = 0 \\ d . x^{2} + y^{2} - 8 x - 10 y = 0 \\ e . x^{2} + y^{2} + 12 x - 8 y = 0 \\ Jawab : \\ \begin{aligned} Diketahui bahwa : L_{3} = L_{1} + p (L_{1} - L_{2}) = 0 \\ dengan \\ ∙ L_{1} = x^{2} + y^{2} - 6 x - 8 y - 11 = 0 \\ ∙ L_{2} = x^{2} + y^{2} - 4 x - 6 y - 22 = 0 \\ Untuk L_{1} - L_{2} = - 2 x - 2 y + 11 = 0 \\ Karena L_{3} melalui (0, 0), maka \\ \begin{aligned} L_{3} & = L_{1} + p (L_{1} - L_{2}) = 0 \\ = x^{2} + y^{2} - 6 x - 8 y - 11 + p (- 2 x - 2 y + 11) = 0 \\ \Leftrightarrow 0^{2} + 0^{2} - 0 - 0 - 11 + p (0 + 11) = 0 \\ \Leftrightarrow p = 1 \end{aligned} \\ Sehingga \\ L_{3} = x^{2} + y^{2} - 6 x - 8 y - 11 + (- 2 x - 2 y + 11) = 0 \\ \Leftrightarrow L_{3} = x^{2} + y^{2} - 8 x - 10 y = 0 \end{aligned} \end{array}$ .

Berikut ilustrasi gambarnya

$\begin{array}{ll} 32. & Persamaan lingkaran yang melalui titik \\ (8, 4) dan titik potong lingkaran x^{2} + y^{2} = 16 \\ dan x^{2} + y^{2} - 4 x - 4 y = 0 adalah . . . . \\ a . x^{2} + y^{2} - 8 x - 8 y - 16 = 0 \\ b . x^{2} + y^{2} - 8 x + 8 y + 16 = 0 \\ c . x^{2} + y^{2} - 8 x - 8 y + 16 = 0 \\ d . x^{2} + y^{2} + 8 x + 8 y - 16 = 0 \\ e . x^{2} + y^{2} + 8 x + 8 y + 16 = 0 \\ Jawab : \\ \begin{aligned} Diketahui bahwa : L_{3} = L_{1} + p (L_{1} - L_{2}) = 0 \\ dengan \\ ∙ L_{1} = x^{2} + y^{2} - 16 = 0 \\ ∙ L_{2} = x^{2} + y^{2} - 4 x - 4 y = 0 \\ Untuk L_{1} - L_{2} = 4 x + 4 y - 16 = 0 \\ \Leftrightarrow x + y = 4 \\ Karena L_{3} melalui (8, 4), maka \\ \begin{aligned} L_{3} & = L_{1} + p (L_{1} - L_{2}) = 0 \\ = x^{2} + y^{2} - 16 + p (x + y - 4) = 0 \\ \Leftrightarrow 8^{2} + 4^{2} - 16 + p (8 + 4 - 4) = 0 \\ \Leftrightarrow - 8 p = 64 \Leftrightarrow p = - 8 \end{aligned} \\ Sehingga \\ L_{3} = x^{2} + y^{2} - 16 - 8 (x + y - 4) = 0 \\ \Leftrightarrow L_{3} = x^{2} + y^{2} - 8 x - 8 y + 16 = 0 \end{aligned} \\ Berikut ilustrasi gambarnyanya \end{array}$ .

$\begin{array}{ll} 33. & Persamaan lingkaran yang melalui titik \\ (7, - 4) dan titik potong kedua lingkaran \\ x^{2} + y^{2} - 6 x + 8 y - 27 = 0 dan \\ x^{2} + y^{2} - 26 x + 4 y + 121 = 0 adalah . . . . \\ a . x^{2} + y^{2} - 36 x - 2 y + 121 = 0 \\ b . x^{2} + y^{2} + 24 x - 4 y - 222 = 0 \\ c . 3 x^{2} + 3 y^{2} - 18 x + 2 y - 121 = 0 \\ d . x^{2} + y^{2} - 36 x + 2 y + 195 = 0 \\ e . x^{2} + y^{2} + 24 x + 2 y + 195 = 0 \\ Jawab : \\ \begin{aligned} Diketahui bahwa : L_{3} = L_{1} + p (L_{1} - L_{2}) = 0 \\ dengan \\ ∙ L_{1} = x^{2} + y^{2} - 6 x + 8 y - 27 = 0 \\ ∙ L_{2} = x^{2} + y^{2} - 26 x + 4 y + 121 = 0 \\ Untuk L_{1} - L_{2} = 20 x + 4 y - 148 = 0 \\ Karena L_{3} melalui (7, - 4), maka \\ \begin{aligned} L_{3} & = L_{1} + p (L_{1} - L_{2}) = 0 \\ = x^{2} + y^{2} - 6 x + 8 y - 27 \\ + p (20 x + 4 y - 148) = 0 \\ \Leftrightarrow 7^{2} + (- 4)^{2} - 42 - 32 - 27 \\ + p (140 - 16 - 148) = 0 \\ \Leftrightarrow - 24 p = 36 \Leftrightarrow p = - \frac{3}{2} \end{aligned} \\ Sehingga \\ L_{3} = x^{2} + y^{2} - 6 x + 8 y - 27 \\ - \frac{3}{2} (20 x + 4 y - 148) = 0 \\ \Leftrightarrow L_{3} = x^{2} + y^{2} - 36 x + 2 y + 195 = 0 \end{aligned} \end{array}$ .

Berikut ilustrasi gambarnya

Jika dimensi gambar diperkecil menjadi

$\begin{array}{ll} 34. & Persamaan lingkaran yang melalui perpotongan \\ lingkaran x^{2} + y^{2} - 12 x + 6 y + 20 = 0 dan \\ x^{2} + y^{2} - 16 x - 14 y + 64 = 0 serta pusatnya \\ terletak pada garis 8 x - 3 y - 19 = 0 adalah . . . . \\ a . x^{2} + y^{2} - 20 x - 34 y + 108 = 0 \\ b . x^{2} + y^{2} - 16 x + 12 y + 96 = 0 \\ c . x^{2} + y^{2} - 12 x + 20 y + 88 = 0 \\ d . x^{2} + y^{2} + 16 x - 24 y + 108 = 0 \\ e . x^{2} + y^{2} + 22 x - 34 y + 96 = 0 \\ Jawab : \\ \begin{aligned} Diketahui bahwa persamaan lingkaran : \\ ∙ L_{1} = x^{2} + y^{2} - 12 x + 6 y + 20 = 0 \\ ∙ L_{2} = x^{2} + y^{2} - 16 x - 14 y + 64 = 0 \\ Persamaan tali busurnya (garis kuasa) \\ adalah : \\ L_{1} (x, y) - L_{2} (x, y) \\ = 4 x + 20 y - 44 = 0 \Leftrightarrow x = 11 - 5 y \\ Selanjutnya dengan substitusi \\ \begin{aligned} x^{2} + y^{2} - 12 x + 6 y + 20 = 0 \\ \Leftrightarrow (x - 6)^{2} + (y + 3)^{2} = 25 \\ \Leftrightarrow (11 - 5 y - 6)^{2} + (y + 3)^{2} = 25 \\ \Leftrightarrow (y - 5 y)^{2} + (y + 3)^{2} = 25 \\ \Leftrightarrow 26 y^{2} - 44 y + 9 = 0 \end{aligned} \\ Sehingga dengan memodifikasi \\ \begin{aligned} 26 y^{2} - 44 y + 9 = 0 \\ \Leftrightarrow 25 y^{2} - 44 y + y^{2} + 9 = 0 \\ arahkan ke bentuk kuadrat sempurna \\ \Leftrightarrow 25 y^{2} - 10 y + 1 + y^{2} - 34 y + 8 = 0 \\ \Leftrightarrow 25 y^{2} - 10 y + 1 + y^{2} - 34 y + 17^{2} - 17^{2} + 8 = 0 \\ \Leftrightarrow (5 y - 1)^{2} + (y - 17)^{2} - 281 = 0 \\ ingat bahwa ada tali busur 5 y = 11 - x \\ \Leftrightarrow (11 - x - 1)^{2} + (y - 17)^{2} - 281 = 0 \\ \Leftrightarrow (10 - x)^{2} + (y - 17)^{2} - 281 = 0 \\ \Leftrightarrow x^{2} - 20 x + 100 + y^{2} - 34 y + 289 - 281 = 0 \\ \Leftrightarrow x^{2} + y^{2} - 20 x - 34 y + 108 = 0 \end{aligned} \end{aligned} \\ Berikut ilustrasi gambarnya \end{array}$

$\begin{array}{ll} 35. & Persamaan lingkaran dengan titik pusat \\ pada garis x + 2 y - 3 = 0 dan melalui \\ titik potong dua lingkaran \\ x^{2} + y^{2} - 2 x - 4 y + 1 = 0 dan \\ x^{2} + y^{2} - 4 x - 2 y + 4 = 0 adalah . . . . \\ a . x^{2} + y^{2} - 6 x + 7 = 0 \\ b . x^{2} + y^{2} - 3 y + 4 = 0 \\ c . x^{2} + y^{2} - 2 x - 2 y + 1 = 0 \\ d . x^{2} + y^{2} - 2 x - 4 y + 4 = 0 \\ e . x^{2} + y^{2} - 3 x - 2 y + 7 = 0 \\ Jawab : \\ Alternatif 1 \\ Gunakan cara pembahasan sebagaimana pada \\ nomor-nomor sebelumnya \\ Alternatif 2 \\ \begin{aligned} Diketahui \\ L_{1} \equiv x^{2} + y^{2} - 2 x - 4 y + 1 = 0, dan \\ L_{2} \equiv x^{2} + y^{2} - 4 x - 2 y + 4 = 0 \\ Persamaan tali busur dari kedua \\ lingkaran tersebut adalah : \\ L_{1} (x, y) - L_{2} (x, y) = 0 \\ \Leftrightarrow x^{2} + y^{2} - 2 x - 4 y + 1 \\ - (x^{2} + y^{2} - 4 x - 2 y + 4) = 0 \\ \Leftrightarrow 2 x - 2 y - 3 = 0 \\ Selanjutnya perlu ditentukan juga \\ Persamaan berkas lingkaran melalui \\ titik-titik potong kedua lingkaran \\ di atas adalah : \\ L_{1} + λ L_{2} = 0 \\ x^{2} + y^{2} - 2 x - 4 y + 1 \\ + λ (x^{2} + y^{2} - 4 x - 2 y + 4) = 0 \\ \Leftrightarrow (1 + λ) x^{2} + (1 + λ) y^{2} - (2 + 4 λ) x \\ - (4 + 2 λ) y + 1 + 4 λ = 0 \\ Saat λ = - 1, maka persamaan berkas \\ lingkarannya adalah : 2 x - 2 y - 3 = 0 \\ Hal ini hasilnya sama persis saat kita \\ menentukan persamaan tali busur di atas \\ Selanjutnya kita ambil \\ L_{2} - (L_{1} + λ L_{2}) = 0 \\ \Leftrightarrow x^{2} + y^{2} - 4 x - 2 y + 4 - (2 x - 2 y - 3) = 0 \\ \Leftrightarrow x^{2} + y^{2} - 6 x + 7 = 0 \end{aligned} \end{array}$ .

Gambar mula-mula

Lingkaran baru yang berpusat di (3,0)

Contoh Soal 6 Materi Hubungan Dua Lingkaran

$\begin{array}{ll} 26. & Diketahui lingkaran-lingkaran \\ x^{2} + y^{2} - 2 x + 3 y + k = 0 dan \\ x^{2} + y^{2} + 8 x - 6 y - 7 = 0 saling \\ berpotongan ortogonal saat k = . . . . \\ a . - 10 \\ b . - 3 \\ c . 1 \\ d . 5 \\ e . 8 \\ Jawab : \\ Perhatikan tabel berikut \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} - 2 x + 3 y + k = 0 & {\begin{cases} P_{1} & = (1, - \frac{3}{2}) \\ r_{1} & = \sqrt{\frac{13 - 4 k}{4}} \end{cases} \\ \begin{aligned} L_{2} & \equiv x^{2} + y^{2} + 8 x - 6 y - 7 = 0 \end{aligned} & {\begin{cases} P_{2} & = (- 4, 3) \\ r_{2} & = \sqrt{32} \end{cases} \end{array} \\ Syarat dua lingkaran berpotongan ortogonal \\ \begin{aligned} {(P_{1} P_{2})}^{2} = r_{1}^{2} + r_{2}^{2} \\ \Leftrightarrow {(1 + 4)}^{2} + {(- \frac{3}{2} - 3)}^{2} = {(\sqrt{\frac{13 - 4 k}{4}})}^{2} + {\sqrt{32}}^{2} \\ \Leftrightarrow 25 + \frac{81}{4} = \frac{13 - 4 k}{4} + 32 \\ \Leftrightarrow 100 + 81 = 13 - 4 k + 128 \\ \Leftrightarrow k = - 10 \end{aligned} \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}$ .

$\begin{array}{ll} 27. & Persamaan lingkaran yang berpotongan \\ lingkaran lain x^{2} + y^{2} + 2 x + y - 11 = 0 \\ secara tegak lurus dan melalui (4, 3) serta \\ pusatnya pada 9 x + 4 y = 37 adalah . . . . \\ a . x^{2} + y^{2} - 10 x + 4 y + 3 = 0 \\ b . x^{2} + y^{2} - 8 x + 10 y + 6 = 0 \\ c . x^{2} + y^{2} + 4 x - 8 y + 7 = 0 \\ d . x^{2} + y^{2} + 6 x + y + 5 = 0 \\ e . x^{2} + y^{2} + 12 x + 6 y + 5 = 0 \\ Jawab : \\ Perhatikan tabel berikut \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} + 2 x + y - 11 = 0 & {\begin{cases} P_{1} & = (- 1, - \frac{1}{2}) \\ r_{1} & = \sqrt{\frac{49}{4}} = \frac{7}{2} \end{cases} \\ \begin{aligned} L_{2} & \equiv (x - a)^{2} + (y - b)^{2} = r^{2} \end{aligned} & {\begin{cases} P_{2} & = (a, b) \\ r_{2} & = r \end{cases} \end{array} \\ Karena berpotongan tegak lurus, maka \\ \begin{aligned} {(P_{1} P_{2})}^{2} = r_{1}^{2} + r_{2}^{2} \\ \Leftrightarrow {(- 1 - a)}^{2} + {(- \frac{1}{2} - b)}^{2} = \frac{49}{4} + r^{2} \\ \Leftrightarrow a^{2} + 2 a + 1 + b^{2} + b + \frac{1}{4} = \frac{49}{4} + r^{2} \\ \Leftrightarrow a^{2} + b^{2} + 2 a + b + \frac{5}{4} = \frac{49}{4} + r^{2} \\ \Leftrightarrow a^{2} + b^{2} + 2 a + b - 11 = r^{2} . . . . . . . (1) \end{aligned} \\ Selanjutnya \\ \begin{aligned} Lingkaran L_{2} melalui titik (4, 3), artinya \\ bahwa : (4 - a)^{2} + (3 - b)^{2} = r^{2} \\ \Leftrightarrow a^{2} - 8 a + 16 + b^{2} - 6 b + 9 = r^{2} \\ \Leftrightarrow a^{2} + b^{2} - 8 a - 6 b + 25 = r^{2} . . . . . . . (2) \\ Pusat lingkaran L_{2} melalui garis 9 x + 4 y = 37 \\ artinya : 9 a + 4 b = 37 . . . . . . . . . . . . . . . (3) \end{aligned} \\ \begin{aligned} Dengan eliminasi 1 & 2 dapat diperoleh : \\ \begin{aligned} a^{2} + b^{2} - 8 a - 6 b + 25 & = r^{2} \\ a^{2} + b^{2} + 2 a + b - 11 & = r^{2} & - \\ - 10 a - 7 b + 36 & = 0 & atau \\ 10 a + 7 b & = 36 & . . . . . . (4) \end{aligned} \\ Dari persamaan 3 & 4 dapat diperoleh : \end{aligned} \\ \begin{aligned} 10 a + 7 b & = 36 & (\times 4) \\ 9 a + 4 b & = 37 & (\times 7) \\ 40 a + 28 b & = 144 \\ 63 a + 28 b & = 259 \\ - 23 a & = - 115 \\ a & = \frac{- 115}{- 23} & = 5 \\ 10 (5) + 7 b & = 36 \\ 7 b & = - 14 \\ b & = - 2 \end{aligned} \\ Adapun langkah berikutnya \\ \begin{aligned} L_{2} \equiv (4 - a)^{2} + (3 - b)^{2} = r^{2} \\ L_{2} \equiv (4 - 5)^{2} + (3 + 2)^{2} = r^{2} \\ L_{2} \equiv r^{2} = 25 + 1 = 26 \\ Sehingga, L_{2} \equiv (x - 5)^{2} + (y + 2)^{2} = 26 \\ \Leftrightarrow x^{2} + y^{2} - 10 x + 4 y + 25 + 4 - 26 = 0 \\ \Leftrightarrow x^{2} + y^{2} - 10 x + 4 y + 3 = 0 \end{aligned} \\ Berikut ilustrasi gambarnya \end{array}$ .

Jika diperjelas dengan tambahan garis 9x+4y=37

$\begin{array}{ll} 28. & Diketahui lingkaran pertama berpusat di (1, 2) \\ dan menyinggung garis 3 x - 4 y + 10 = 0. \\ Jika ada lingkaran kedua dengan pusat (4, 6) \\ dan menyinggung lingkaran yang pertama, \\ maka persamaan lingkaran yang kedua \\ tersebut adalah . . . . \\ a . x^{2} + y^{2} - 8 x - 12 y + 48 = 0 \\ b . x^{2} + y^{2} - 8 x - 12 y + 43 = 0 \\ c . x^{2} + y^{2} - 8 x - 12 y + 36 = 0 \\ d . x^{2} + y^{2} - 8 x - 12 y + 27 = 0 \\ e . x^{2} + y^{2} - 8 x - 12 y + 16 = 0 \\ Jawab : \\ Diketahui bahwa kedua lingkaran saling \\ bersinggungan di luar, maka \\ \begin{aligned} r_{1} + r_{2} & = P_{1} P_{2} \\ = \sqrt{(y_{2} - y_{1})^{2} + (x_{2} - x_{1})^{2}} \\ = \sqrt{(1 - 4)^{2} + (2 - 6)^{2}} \\ = \sqrt{3^{2} + 4^{2}} = \sqrt{5^{2}} = 5 \end{aligned} \\ Selanjutnya \\ \begin{aligned} r_{pertama} & = | \frac{3 (1) - 4 (2) + 10}{\sqrt{3^{2} + 4^{2}}} | \\ = | \frac{3 - 8 + 10}{\sqrt{5^{2}}} | = | \frac{5}{5} | = | 1 | = 1 \\ sehingga \\ r_{kedua} & = 5 - r_{pertama} = 5 - 1 = 4 \end{aligned} \\ maka persamaan lingkaran keduanya adalah : \\ \begin{aligned} (x - 4)^{2} + (y - 6)^{2} = 4^{2} \\ \Leftrightarrow x^{2} - 8 x + 16 + y^{2} - 12 y + 36 = 16 \\ \Leftrightarrow x^{2} + y^{2} - 8 x - 12 y + 36 = 0 \end{aligned} \\ Berikut ilustrasi gambarnya \end{array}$ .

$\begin{array}{ll} 29. & Garis kuasa (tali busur sekutu) \\ dari lingkaran \\ L_{1} \equiv x^{2} + y^{2} + 6 x - 4 y - 12 = 0 \\ dan L_{2} \equiv x^{2} + y^{2} - 12 y = 0 adalah . . . . \\ a . 3 x + 4 y + 9 = 0 \\ b . 3 x - 4 y - 8 = 0 \\ c . 3 x - 4 y + 7 = 0 \\ d . 3 x + 4 y - 7 = 0 \\ e . 3 x + 4 y - 6 = 0 \\ Jawab : \\ \begin{aligned} Diketahui \\ L_{1} \equiv x^{2} + y^{2} + 6 x - 4 y - 12 = 0, \\ dan L_{2} \equiv x^{2} + y^{2} - 12 y = 0 \\ Persamaan garis kuasa dari kedua \\ lingkaran tersebut adalah : \\ L_{1} (x, y) - L_{2} (x, y) = 0 \\ \Leftrightarrow x^{2} + y^{2} + 6 x - 4 y - 12 \\ - (x^{2} + y^{2} - 12 y) = 0 \\ \Leftrightarrow 6 x + 8 y - 12 = 0 \\ \Leftrightarrow 3 x + 4 y - 6 = 0 \end{aligned} \end{array}$ .

$\begin{array}{ll} 30. & Jika dua lingkaran \\ x^{2} + y^{2} = 9 dan \\ x^{2} + y^{2} - 4 y + 2 y + 3 = 0 yang \\ berpotongan di (x_{1}, y_{1}) dan (x_{2}, y_{2}), \\ maka nilai 5 (x_{1} + x_{2}) adalah . . . . \\ a . 24 \\ b . 26 \\ c . 28 \\ d . 30 \\ e . 32 \\ Jawab : \\ \begin{aligned} Diketahui \\ L_{1} \equiv x^{2} + y^{2} - 9 = 0 dan \\ L_{2} \equiv x^{2} + y^{2} - 4 x + 2 y + 3 \\ Persamaan garis kuasa dari kedua \\ lingkaran tersebut adalah : \\ L_{1} (x, y) - L_{2} (x, y) = 0 \\ \Leftrightarrow x^{2} + y^{2} - 9 \\ - (x^{2} + y^{2} - 4 y + 2 y + 3) = 0 \\ \Leftrightarrow 4 x - 2 y - 12 = 0 \\ \Leftrightarrow 2 x - y - 6 = 0 \\ \Leftrightarrow y = 6 - 2 x \end{aligned} \\ Selanjutnya \\ \begin{aligned} x^{2} + y^{2} - 9 = 0 \\ \Leftrightarrow x^{2} + (6 - 2 x)^{2} - 9 = 0 \\ \Leftrightarrow x^{2} + 36 - 24 x + 4 x^{2} - 9 = 0 \\ \Leftrightarrow 5 x^{2} - 24 x + 27 = 0 \\ \Leftrightarrow x_{1, 2} = \frac{24 \pm \sqrt{576 - 540}}{10} \\ \Leftrightarrow x_{1, 2} = \frac{24 \pm \sqrt{36}}{10} = \frac{24 \pm 6}{10} \\ \Leftrightarrow x_{1, 2} = \frac{24 \pm \sqrt{36}}{10} = \frac{24 \pm 6}{10} \\ \Leftrightarrow x_{1} = 3 atau x_{2} = 1, 8 \\ maka 5 (x_{1} + x_{2}) = 5 (3 + 1, 8) = 24 \end{aligned} \end{array}$ .

Contoh Soal 5 Materi Hubungan Dua Lingkaran

$\begin{array}{ll} 21. & Titik Kuasa dari lingkaran-lingkaran \\ berikut \\ L_{1} \equiv x^{2} + y^{2} + x + y - 14 = 0 \\ L_{2} \equiv x^{2} + y^{2} = 13 \\ L_{3} \equiv x^{2} + y^{2} + 3 x - 2 y - 26 = 0 adalah . . . . \\ a . (3, - 2) \\ b . (2, - 3) \\ c . (- 3, 2) \\ d . (- 2, 3) \\ e . (3, 2) \\ Jawab : \\ Dengan eliminasi, kita mendapatkan \\ \begin{aligned} \begin{array}{lrlll} (L_{1}) & x^{2} + y^{2} + x + y & = & 14 \\ (L_{2}) & x^{2} + y^{2} & = & 13 & - \\ x + y & = & 1 & . . . . (1) \end{array} \\ dan \\ \begin{array}{lrlll} (L_{3}) & x^{2} + y^{2} + 3 x - 2 y & = & 26 \\ (L_{2}) & x^{2} + y^{2} & = & 13 & - \\ 3 x - 2 y & = & 13 & . . . . (2) \end{array} \\ Selanjutnya kita eliminasi (1) & (2) \\ dan hasilnya adalah : \\ \begin{array}{rrlrl} (2) & 3 x - 2 y & = & 13 \\ (1) & 3 x + 3 y & = & 3 & - (\times 3) \\ - 5 y & = & 10 \\ y & = & - 2 & \Rightarrow x = 3 \end{array} \\ Jadi, titik kuasa ketiganya : (3, - 2) \end{aligned} \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}$

\begin{array}{ll} 22. & Titik-titik potong dari persekutuan dua \\ lingkaran L_{1} \equiv (x - 2)^{2} + y^{2} = 10 dan \\ L_{2} \equiv x^{2} + (y - 2)^{2} = 10 adalah . . . . \\ a . (3, 3) dan (1, 1) \\ b . (3, 3) dan (- 1, - 1) \\ c . (3, - 3) dan (1, 1) \\ d . (- 3, 3) dan (1, 1) \\ e . (- 3, - 3) dan (- 1, - 1) \\ Jawab : \\ Alternatif 1 \\ Dengan substitusi opsi pilihan jawaban \\ maka akan ketemu jawabannya langsung \\ Alternatif 2 \\ Dengan eliminasi dan ilustrasi gambar \\ \begin{array}{lrlll} (L_{1}) & (x - 2)^{2} + y^{2} & = & 10 \\ (L_{2}) & x^{2} + (y - 2)^{2} & = & 10 \\ menjadi \\ (L_{1}) & x^{2} + y^{2} - 4 x & = & 6 \\ (L_{2}) & x^{2} + y^{2} - 4 y & = & 6 & - \\ - 4 x + 4 y & = & 0 \\ maka hasilnya \\ y & = & x \end{array} \\ Jelas opsi jawaban c, d salah \\ karena y = x, \\ Dengan bantuan ilustrasi, pilihan jawaban \\ akan tampak dengan jelas \end{array}

\begin{array}{ll} 23. & Persamaan tali busur persekutuan dua \\ lingkaran L_{1} \equiv (x - 3)^{2} + y^{2} = 16 dan \\ L_{2} \equiv x^{2} + (y - 3)^{2} = 16 adalah . . . . \\ a . y = - 2 x \\ b . y = - x \\ c . y = x \\ d . y = 2 x \\ e . y = \frac{1}{2} x \\ Jawab : \\ Dengan eliminasi, kita mendapatkan \\ \begin{array}{lrlll} (L_{1}) & (x - 3)^{2} + y^{2} & = & 16 \\ (L_{2}) & x^{2} + (y - 3)^{2} & = & 16 \\ menjadi \\ (L_{1}) & x^{2} + y^{2} - 6 x & = & 9 \\ (L_{2}) & x^{2} + y^{2} - 6 y & = & 9 & - \\ - 6 x + 6 y & = & 0 \\ maka hasilnya \\ y & = & x \end{array} \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}

\begin{array}{ll} 24. & Banyaknya garis singgung persekutuan \\ lingkaran-lingkaran x^{2} + y^{2} + 2 x - 6 y + 9 = 0 \\ dan x^{2} + y^{2} + 8 x - 6 y + 9 = 0 adalah . . . . \\ a . 0 \\ b . 1 \\ c . 2 \\ d . 3 \\ e . 4 \\ Jawab : \\ Perhatikan bahwa \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} + 2 x - 6 y + 9 = 0 & {\begin{cases} P_{1} & = (- 1, 3) \\ r_{1} & = 1 \end{cases} \\ L_{2} \equiv x^{2} + y^{2} + 8 x - 6 y + 9 = 0 & {\begin{cases} P_{2} & = (- 4, 3) \\ r_{2} & = 4 \end{cases} \end{array} \\ Perhatikan pula bahwa r_{2} - r_{1} = 4 - 1 = 3 \\ \begin{aligned} Karena P_{1} P_{2} = r_{2} - r_{1}, hal ini berarti lingkaran \\ L_{1} bersinggungan di dalam dengan lingkaran L_{2} \\ Sehingga kedua lingkaran ini hanya akan \\ memiliki satu garis singgung persekutuan \end{aligned} \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}

$\begin{array}{ll} 25. & Persamaan lingkaran dengan jari-jari 5 \\ dan menyinggung lingkaran lain \\ x^{2} + y^{2} - 2 x - 4 y - 20 = 0 di titik \\ (5, 5) adalah . . . . \\ a . x^{2} + y^{2} - 2 x - 4 y - 120 = 0 \\ b . x^{2} + y^{2} - 2 x - 4 y - 120 = 0 \\ c . x^{2} + y^{2} - 2 x - 4 y - 120 = 0 \\ d . x^{2} + y^{2} - 2 x - 4 y - 120 = 0 \\ e . x^{2} + y^{2} - 2 x - 4 y - 120 = 0 \\ Jawab : \\ Diketahi bahwa \\ \begin{aligned} \begin{array}{rrlll} (L_{1}) & (x - a)^{2} + (y - b)^{2} & = & 5^{2} \\ (L_{2}) & x^{2} + y^{2} - 2 x - 4 y & = & 20 \end{array} \\ Titik singgung dua lingkaran \\ di titik (5, 5), artinya \\ (\begin{array}{c} 5 \\ 5 \end{array}) = \frac{(\begin{array}{c} a \\ b \end{array}) + (\begin{array}{c} 1 \\ 2 \end{array})}{2} \\ \Leftrightarrow (\begin{array}{c} 10 \\ 10 \end{array}) = (\begin{array}{c} a \\ b \end{array}) + (\begin{array}{c} 1 \\ 2 \end{array}) \\ \Leftrightarrow (\begin{array}{c} a \\ b \end{array}) = (\begin{array}{c} 10 - 1 \\ 10 - 2 \end{array}) = (\begin{array}{c} 9 \\ 8 \end{array}) \end{aligned} \\ \begin{aligned} maka persamaan lingkarannya adalah : \\ \Leftrightarrow (x - 9)^{2} + (y - 8)^{2} = 5^{2} \\ \Leftrightarrow x^{2} + y^{2} - 18 x - 16 y + 120 = 0 \end{aligned} \\ Berikut ilustrasi gambarnya \end{array}$ .

Contoh Soal 4 Materi Lingkaran dan Hubungan Dua Lingkaran

$\begin{array}{ll} 16. & Salah satu garis singgung yang bersudut 120^{\circ} \\ terhadap sumbu x positif terhadap lingkaran \\ dengan ujung diameter titik (7, 6) dan (1, - 2) \\ adalah . . . . \\ a . y = - x \sqrt{3} + 4 \sqrt{3} + 12 \\ b . y = - x \sqrt{3} - 4 \sqrt{3} + 8 \\ c . y = - x \sqrt{3} + 4 \sqrt{3} - 4 \\ d . y = - x \sqrt{3} - 4 \sqrt{3} - 8 \\ e . y = - x \sqrt{3} + 4 \sqrt{3} + 22 \\ Jawab : \\ \begin{array}{cc} Pusat Lingkaran & Gradien Garis Singgung \\ \begin{aligned} (a, b) \\ = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}) \\ = (\frac{7 + 1}{2}, \frac{6 + (- 2)}{2}) \\ = (4, 2) \end{aligned} & \begin{aligned} m & = \tan 120^{\circ} \\ = - \tan (180^{\circ} - 60^{\circ}) \\ = - \tan 60^{\circ} \\ = - \sqrt{3} \end{aligned} \\ Jari-jari & Garis Singgung \\ \begin{aligned} r & = jarak titik \\ singgung ke pusat \\ = \sqrt{(7 - 4)^{2} + (6 - 2)^{2}} \\ = \sqrt{3^{2} + 4^{2}} \\ = \sqrt{25} \\ = 5 \end{aligned} & \begin{aligned} (y - b) = m (x - a) \pm r \sqrt{1 + m^{2}} \\ \Leftrightarrow (y - 2) = - \sqrt{3} (x - 4) \pm 5 \sqrt{1 + (- \sqrt{3})^{2}} \\ \Leftrightarrow y - 2 = - \sqrt{3} x + 4 \sqrt{3} \pm 5 \sqrt{1 + 4} \\ \Leftrightarrow y = - \sqrt{3} x + 4 \sqrt{3} + 2 \pm 10 \\ \Leftrightarrow y = {\begin{cases} - \sqrt{3} x + 4 \sqrt{3} + 2 + 10 \\ - \sqrt{3} x + 4 \sqrt{3} + 2 - 10 \end{cases} \\ \Leftrightarrow y = {\begin{cases} - \sqrt{3} x + 4 \sqrt{3} + 12 \\ - \sqrt{3} x + 4 \sqrt{3} - 8 \end{cases} \end{aligned} \end{array} \\ Berikut ilustrasi gambarnya \end{array}$ .

Dengan ilustrasi tambahan

\begin{array}{ll} 17. & Salah satu garis singgung lingkaran \\ x^{2} + y^{2} = 10 yang ditarik dari \\ titik (4, 2) adalah . . . . \\ a . x + 3 y = 10 \\ b . x - 3 y = 10 \\ c . - x - 3 y = 10 \\ d . 2 x + y = 10 \\ e . x + 2 y = 10 \\ Jawab : \\ \begin{array}{cc} \begin{aligned} Garis Singgung \\ di titik \\ (x_{1}, y_{1}) = (4, 2) \end{aligned} & \begin{aligned} Tahapan menentukan \\ harga m \end{aligned} \\ \begin{aligned} y - y_{1} = m (x - x_{1}) \\ y - 2 = m (x - 4) \\ y = m x - 4 m + 2 \end{aligned} & \begin{aligned} x^{2} + y^{2} = 10 \\ x^{2} + {(m x - 4 m + 2)}^{2} = 10 \\ x^{2} + m^{2} x^{2} + 16 m^{2} + 4 - 8 m^{2} x + 4 m x - 16 m = 10 \\ x^{2} + m^{2} x^{2} + 16 m^{2} - 8 m^{2} x + 4 m x - 16 m - 6 = 0 \\ (1 + m^{2}) x^{2} + (4 m - 8 m^{2}) x + 16 m^{2} - 16 m - 6 = 0 \\ {\begin{cases} a & = 1 + m^{2} \\ b & = 4 m - 8 m^{2} \\ c & = 16 m^{2} - 16 m - 6 \end{cases} \end{aligned} \end{array} \\ \begin{aligned} Syarat menyinggung D = 0 \\ b^{2} - 4 a c = 0 \\ {(4 m - 8 m^{2})}^{2} - 4 (1 + m^{2}) (16 m^{2} - 16 m - 6) = 0 \\ 16 m^{2} - 64 m^{3} + 64 m^{4} - 64 m^{2} + 64 m + 24 - 64 m^{4} + 64 m^{3} + 24 m^{2} = 0 \\ - 24 m^{2} + 64 m + 24 = 0 \\ - 3 m^{2} + 8 m + 3 = 0 \\ (m - 3) (3 m + 1) = 0 \\ m = 3 atau m = - \frac{1}{3} \\ m = {\begin{cases} 3 & \Rightarrow y = 3 x - 10 \\ \Rightarrow 3 x - y = 10 \\ - \frac{1}{3} & \Rightarrow y = - \frac{1}{3} x + \frac{4}{3} + 2 \\ \Rightarrow x + 3 y = 10 \end{cases} \end{aligned} \end{array}

. \begin{aligned} Berikut ilustrasi gambarnya \end{aligned}

\begin{array}{ll} 18. & Diketahui persamaan lingkaran x^{2} + y^{2} = r^{2} \\ dan sebuah titik di luar lingkaran M (a, b) \\ Posisi garis a x + b y = r^{2} adalah . . . . \\ a . menyinggung lingkaran \\ b . memotong lingkaran di dua titik \\ c . melalui titik pusat lingkaran \\ d . tidak memotong lingkaran \\ e . tidak ada yang benar \\ Jawab : \\ Diketahui bahwa \\ ∙ L \equiv x^{2} + y^{2} = r^{2} \\ ∙ M (a, b) di luar lingkaran L \\ Selanjutnya perhatikan penjelasan berikut \\ \begin{aligned} Karena M (a, b) di luar lingkaran L, maka \\ maka salah satu dari a atau b atau keduanya \\ akan lebih besar nilanya dari pada r . \\ Misalkan kita pilih a > r \\ Ambil posisi saat memotong sumbu - X, y = 0 \\ \begin{aligned} Untuk lingkaran x^{2} + y^{2} = r^{2} \\ ∙ y = 0 \Rightarrow x^{2} + 0^{2} = r^{2} \Rightarrow x = | r | \\ Untuk garis a x + b y = r^{2} \\ ∙ y = 0 \Rightarrow a x = r^{2} \Rightarrow x = \frac{r^{2}}{a} \\ Dari sini tampak posisi x = | r | > \frac{r^{2}}{a} \geq 0 \end{aligned} \\ Sehingga kesimpulannya adalah : \\ garis tersebut akan selalu memotong lingkaran \end{aligned} \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}

\begin{array}{ll} 19. & Dua lingkaran dengan persamaan \\ lingkaran-lingkaran x^{2} + y^{2} + 6 x - 8 y + 21 = 0 \\ dan x^{2} + y^{2} + 10 x - 8 y + 25 = 0 adalah . . . . \\ a . berpotongan di luar titik \\ b . tidak berpotongan atau bersinggungan \\ c . bersinggungan luar \\ d . bersinggungan dalam \\ e . sepusat \\ Jawab : \\ Perhatikan bahwa \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} + 6 x - 8 y + 21 = 0 & {\begin{cases} P_{1} & = (- 3, 4) \\ r_{1} & = 2 \end{cases} \\ L_{2} \equiv x^{2} + y^{2} + 10 x - 8 y + 25 = 0 & {\begin{cases} P_{2} & = (- 5, 4) \\ r_{2} & = 4 \end{cases} \end{array} \\ dan \\ \begin{array}{cc} Jarak kedua pusat & Jumlah/selisih jari-jari \\ \begin{aligned} (P_{1} P_{2}) \\ = \sqrt{(- 3 + 5)^{2} + (4 - 4)^{2}} \\ = \sqrt{2^{2} + 0^{2}} = \sqrt{4} = 2 \end{aligned} & \begin{array}{r} {\begin{cases} r_{1} + r_{2} & = 2 + 4 = 6 \\ | r_{1} - r_{2} | & = | 2 - 4 | = 2 \end{cases} \end{array} \end{array} \\ Karena nilai P_{1} P_{2} = | r_{1} - r_{2} | = 2 \\ hal ini menunjukkan keduanya bersinggungan \\ di dalam \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}

\begin{array}{ll} 20. & Dua lingkaran dengan persamaan \\ lingkaran-lingkaran x^{2} + y^{2} + 2 x - 6 y + 9 = 0 \\ dan x^{2} + y^{2} + 8 x - 6 y + 9 = 0 adalah . . . . \\ a . berpotongan \\ b . bersinggungan di dalam \\ c . bersinggungan luar \\ d . tidak berpotongan \\ e . sepusat \\ Jawab : \\ Perhatikan bahwa \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} + 2 x - 6 y + 9 = 0 & {\begin{cases} P_{1} & = (- 1, 3) \\ r_{1} & = 1 \end{cases} \\ L_{2} \equiv x^{2} + y^{2} + 8 x - 6 y + 9 = 0 & {\begin{cases} P_{2} & = (- 4, 3) \\ r_{2} & = 4 \end{cases} \end{array} \\ dan \\ \begin{array}{cc} Jarak kedua pusat & Jumlah/selisih jari-jari \\ \begin{aligned} (P_{1} P_{2}) \\ = \sqrt{(- 1 + 4)^{2} + (3 - 3)^{2}} \\ = \sqrt{3^{2} + 0^{2}} = \sqrt{9} = 3 \end{aligned} & \begin{array}{r} {\begin{cases} r_{1} + r_{2} & = 1 + 4 = 5 \\ | r_{1} - r_{2} | & = | 1 - 4 | = 3 \end{cases} \end{array} \end{array} \\ Karena nilai P_{1} P_{2} = | r_{1} - r_{2} | = 3 \\ hal ini menunjukkan keduanya bersinggungan \\ di dalam \\ Sebagai ilustrasi perhatikan gambar berikut \end{array}

DAFTAR PUSTAKA

Budi, W. S. 2010. Bahan Ajar Persiapan Menuju Olimpiade Sain Nasional/Internasional Matematika 3. Jakarta: ZAMRUD KEMALA.
Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Contoh Soal 3 Materi Lingkaran

$\begin{array}{ll} 11. & Lingkaran x^{2} + y^{2} + 2 a x + 2 b y + c = 0 \\ menyinggung sumbu Y jika c = . . . . \\ A . a b \\ B . a b^{2} \\ C . a^{2} b \\ D . a^{2} \\ E . b^{2} \\ Jawab : \\ Alternatif 1 \\ \begin{aligned} x^{2} + y^{2} + 2 a x + 2 b y + c = 0 \\ x = 0 \Rightarrow 0^{2} + y^{2} + 2 a .0 + 2 b y + c = 0 \\ y^{2} + 2 b y + c = 0 {\begin{cases} a & = 1 \\ b & = 2 b \\ c & = c \end{cases} \\ Syarat menyinggung adalah : \\ D = b^{2} - 4 a c = 0 \\ \Leftrightarrow (2 b)^{2} - 4.1 . c = 0 \\ \Leftrightarrow 4 c = 4 b^{2} \\ \Leftrightarrow c = b^{2} \end{aligned} \\ Alternatif 2 \\ \begin{aligned} x^{2} + y^{2} + 2 a x + 2 b y + c = 0 \\ \Leftrightarrow x^{2} + 2 a x + a^{2} + y^{2} + 2 b y + b^{2} + c - a^{2} - b^{2} = 0 \\ \Leftrightarrow (x + a)^{2} + (y + b)^{2} = a^{2} + b^{2} - c \\ Karena menyinggung sumbu-Y, maka R = a \\ Sehingga R^{2} = a^{2} + b^{2} - c = a^{2} \\ \Leftrightarrow b^{2} - c = 0 \\ \Leftrightarrow b^{2} = c \\ \Leftrightarrow c = b^{2} \end{aligned} \end{array}$ .

$\begin{array}{ll} 12. & Diketahui pusat lingkaran L terletak dikuadran \\ I dan berada di sepanjang garis y = 2 x . Jika \\ lingkaran L menyinggung sumbu Y di titik \\ (0, 6), maka persamaan lingkaran L adalah . . . . \\ A . x^{2} + y^{2} - 3 x - 6 y = 0 \\ B . x^{2} + y^{2} + 6 x + 12 y - 108 = 0 \\ C . x^{2} + y^{2} + 12 x + 6 y - 72 = 0 \\ D . x^{2} + y^{2} - 12 x - 6 y = 0 \\ E . x^{2} + y^{2} - 6 x - 12 y + 36 = 0 \\ Jawab : \\ \begin{aligned} (x - a)^{2} + (y - b)^{2} = r^{2}, \\ menyinggung titik (0, 6) \\ berarti pusat lingkaran L juga terletak \\ pada garis y = 6. Hal ini menunjukkan bahwa \\ pusat lingkaran L berpusat di (x, 2 x) = (\frac{y}{2}, y), \\ dengan y = 6. Dari informasi di atas, \\ didapatlah pusat lingkaran berada di titik (3, 6) . \\ Sehingga persamaan lingkarannya adalah : \\ (x - 3)^{2} + (y - 6)^{2} = 3^{2} ingat r = absis x = 3 \\ \Leftrightarrow (x - 3)^{2} + (y - 6)^{2} = x^{2} - 6 x + 9 + y^{2} + 12 x + 36 = 9 \\ \Leftrightarrow x^{2} + y^{2} - 6 x + 12 y + 36 = 0 \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}$ .

\begin{array}{ll} 13. & Persamaan garis singgung lingkaran \\ x^{2} + y^{2} + 8 x - 3 y - 24 = 0, di titik \\ (2, 4) adalah . . . . \\ A . 12 x - 5 y - 44 = 0 \\ B . 12 x + 5 y - 44 = 0 \\ C . 12 x - y - 50 = 0 \\ D . 12 x + y - 50 = 0 \\ E . 12 x + y + 50 = 0 \\ Jawab : \\ \begin{aligned} x^{2} + y^{2} + 8 x - 3 y - 24 \\ \Leftrightarrow x^{2} + 8 x + 16 + y^{2} - 3 y + \frac{9}{4} - 24 = 16 + \frac{9}{4} \\ \Leftrightarrow (x + 4)^{2} + (y - \frac{3}{2})^{2} = 16 + \frac{9}{4} + 24 = 42 \frac{1}{4} \\ Persamaan garis singgung lingkar an lingkaran \\ di titik (x_{1}, y_{1}) adalah : \\ (x_{1} + 4) (x + 4) + (y_{1} - \frac{3}{2}) (y - \frac{3}{2}) = 42 \frac{1}{4}, \\ untuk (x_{1}, y_{1}) = (2, 4), maka \\ (2 + 4) (x + 4) + (4 - \frac{3}{2}) (y - \frac{3}{2}) = \frac{169}{4} \\ \Leftrightarrow 6 (x + 4) + \frac{5}{2} (y - \frac{3}{2}) = \frac{169}{4} \\ \Leftrightarrow 24 (x + 4) + 5 (2 y - 3) = 169 \\ \Leftrightarrow 24 x + 96 + 10 y - 15 = 169 \\ \Leftrightarrow 24 x + 10 y = 169 - 96 + 15 = 88 \\ \Leftrightarrow 12 x + 5 y - 44 = 0 \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}

\begin{array}{ll} 14. & Sebuah garis singgung g menyinggung \\ lingkaran yang berpusat di (- 2, 5) dan \\ berjari-jari 2 \sqrt{10} di titk (4, 3), maka \\ persamaan garis singgung g adalah . . . . \\ A . y = 3 x + 9 \\ B . y = 3 x - 9 \\ C . y = - 3 x + 9 \\ D . y = - 3 x - 9 \\ E . y = 3 x + 21 \\ Jawab : \\ \begin{aligned} (x - a)^{2} + (y - b)^{2} = r^{2} \\ {\begin{cases} Pusat & = (- 2, 5) \\ r & = 2 \sqrt{10} \end{cases} \\ maka persamaan lingkarannya : \\ (x + 2)^{2} + (y - 5)^{2} = (2 \sqrt{10})^{2} \\ \Leftrightarrow (x_{1} + 2) (x + 2) + (y_{1} - 5) (y - 5) = 40, \\ menyingung garis g di (4, 3) \\ (4 + 2) (x + 2) + (3 - 5) (y - 5) = 40 \\ \Leftrightarrow 6 x + 12 - 2 y + 10 = 40 \\ \Leftrightarrow 6 x - 2 y = 40 - 12 - 10 \\ \Leftrightarrow 3 x - y = 9 \\ \Leftrightarrow - y = - 3 x + 9 \\ \Leftrightarrow y = 3 x - 9 \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}

\begin{array}{ll} 15. & Suatu lingkaran dengan titik pusatnya terletak \\ pada kurva y = \sqrt{x} dan melalui titik asal O (0, 0) . \\ Jika diketahui absis titik pusat lingkaran tersebut \\ adalah a, maka persamaan garis singgung \\ lingkaran yang melalui titik O tersebut adalah . . . . \\ A . y = - x \\ B . y = - x \sqrt{a} \\ C . y = - a x \\ D . y = - 2 x \sqrt{2} \\ E . y = - 2 a x \\ Jawab : \\ \begin{array}{lcl} \begin{aligned} Pusat \\ lingkaran \end{aligned} & \begin{aligned} Gradien garis singgung \\ yang tegak lurus dengan \\ garis yang melalui titik \\ pusat lingkaran yang \\ bergradien m_{L} \end{aligned} & \begin{aligned} Persamaan garis \\ singgung yang \\ melalui titik asal \\ O (0, 0) \end{aligned} \\ \begin{aligned} (a, b) \\ = (a, \sqrt{a}) \end{aligned} & \begin{aligned} m . m_{1} = - 1 \\ m . \frac{y}{x} = - 1 \\ m = - \frac{x}{y} = - \frac{a}{\sqrt{a}} \\ = - \sqrt{a} \end{aligned} & \begin{aligned} y & = m x, \\ karena melalui \\ titik asal \\ y & = - \sqrt{a} x, \\ y & = - x \sqrt{a} \end{aligned} \end{array} \end{array}

Contoh Soal 2 Materi Lingkaran

$\begin{array}{ll} 6. & Diketahui lingkaran x^{2} + y^{2} + 4 x + k y - 12 = 0 \\ melalui titik (- 2, 8) maka jari-jari lingkaran \\ tersebut adalah . . . . \\ A . 1 \\ B . 5 \\ C . 6 \\ D . 12 \\ E . 25 \\ Jawab : \\ \begin{aligned} Diketahui ingkaran berpusat di (- 2, - \frac{1}{2} k), \\ yaitu : \\ x^{2} + y^{2} + 4 x + k y - 12 = 0 \\ melalui (- 2, 8) berarti \\ (- 2)^{2} + 8^{2} + 4 (- 2) + k .8 - 12 = 0 \\ 4 + 64 - 8 - 12 + 8 k = 0 \\ 48 + 8 k = 0 \\ k = - 6 \\ Sehingga r = \sqrt{\frac{4^{2}}{4} + \frac{(- 6)^{2}}{4} - (- 12)} \\ = \sqrt{4 + 9 + 12} = \sqrt{25} = 5 \end{aligned} \end{array}$ .

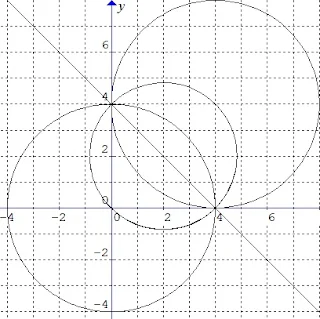
$\begin{array}{ll} 7. & Persmaan lingkaran x^{2} + y^{2} + p x + 8 y + 9 = 0 \\ menyinggung sumbu X. Pusat lingkaran tersebut \\ adalah . . . . \\ A . (6, - 4) \\ B . (6, 6) \\ C . (3, - 4) \\ D . (- 6, - 4) \\ E . (3, 4) \\ Jawab : \\ \begin{aligned} Lingkaran x^{2} + y^{2} + p x + 8 y + 9 = 0 \\ maka, \\ x^{2} + p x + y^{2} + 8 y + 9 = 0 \\ {(x + \frac{1}{2} p)}^{2} - \frac{1}{4} p^{2} + (y + 4)^{2} - 16 + 9 = 0 \\ \Leftrightarrow {(x + \frac{1}{2} p)}^{2} + (y + 4)^{2} = 7 + \frac{1}{4} p^{2} \\ karena menyinggung sumbu-X, R = b = 4, \\ sehingga \\ 7 + \frac{1}{4} p^{2} = 4^{2} \\ \Leftrightarrow \frac{1}{4} p^{2} = 16 - 7 = 9 \Leftrightarrow p^{2} = 36 \Leftrightarrow p = \pm 6 \\ p = - 6 \Rightarrow x^{2} + y^{2} - 6 x + 8 y + 9 = 0 \\ \Rightarrow pusatnya adalah (- \frac{A}{2}, - \frac{B}{2}) = (3, - 4) \\ p = 6 \Rightarrow x^{2} + y^{2} + 6 x + 8 y + 9 = 0 \\ \Rightarrow pusatnya adalah (- \frac{A}{2}, - \frac{B}{2}) = (- 3, - 4) \\ dan berikut ilustrasi gambarnya \end{aligned} \end{array}$ .

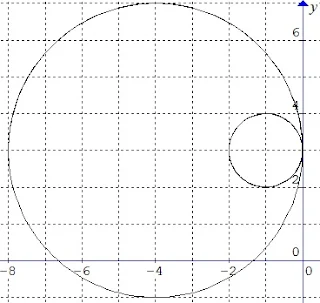
\begin{array}{ll} 8. & Titik-titik berikut yang posisinya berada di luar \\ lingkaran x^{2} + y^{2} - 2 x + 8 y - 32 = 0 adalah . . . . \\ A . (0, 0) \\ B . (- 6, - 4) \\ C . (- 3, 2) \\ D . (3, 1) \\ E . (4, 1) \\ Jawab : \\ \begin{aligned} \begin{array}{cclc} Opsi & Titik & Lingkaran & Keterangan \\ A & (0, 0) & 0^{2} + 0^{2} - 2.0 + 8.0 - 32 = - 32 & dalam \\ B & (- 6, - 4) & (- 6)^{2} + (- 4)^{2} - 2 (- 6) + 8 (- 4) - 32 = 0 & pada \\ C & (- 3, 2) & (- 3)^{2} + (2)^{2} - 2 (- 3) + 8 (2) - 32 = 3 & di luar \\ D & (3, 1) & 3^{2} + 1^{2} - 2.3 + 8.1 - 32 = - 20 & dalam \\ E & (4, 1) & 4^{2} + 1^{2} - 2.4 + 8.1 - 32 = - 15 & dalam \end{array} \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}

\begin{array}{ll} 9. & Diketahui garis x - 2 y = 5 memotong lingkaran \\ x^{2} + y^{2} - 4 y + 8 y + 10 = 0 di titik A dan B . \\ Panjang ruas garis AB adalah . . . . \\ A . 4 \sqrt{2} \\ B . 2 \sqrt{5} \\ C . \sqrt{10} \\ D . 5 \\ E . 4 \\ Jawab : \\ \begin{aligned} \begin{aligned} Perhatikanlah bahwa garis x - 2 y = 5 \\ memotong lingkaran \\ x^{2} + y^{2} - 4 x + 8 y + 10 = 0, \\ maka garis x = 2 y + 5 disubstitusikan ke \\ lingkaran tersebut, yaitu : \\ (2 y + 5)^{2} + y^{2} - 4 (2 y + 5) + 8 y + 10 = 0 \\ 4 y^{2} + 20 y + 25 + y^{2} - 8 y - 20 + 8 y + 10 = 0 \\ 5 y^{2} + 20 y + 15 = 0 \\ y^{2} + 4 y + 3 = 0 \\ (y + 1) (y + 3) = 0 \\ y = - 1 \lor y = - 3 \\ untuk nilai \\ y = - 3 \Rightarrow x = 2 (- 3) + 5 = - 1, A (- 1, - 3) \\ y = - 1 \Rightarrow x = 2 (- 1) + 5 = 3, B (3, - 1) \\ maka, AB = \sqrt{(3 - (- 1))^{2} + (- 1 - (- 3))^{2}} \\ = \sqrt{4^{2} + 2^{2}} \\ = \sqrt{16 + 4} \\ = \sqrt{20} \\ = 2 \sqrt{5} \end{aligned} \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}

\begin{array}{ll} 10. & Kekhususan persamaan lingkaran \\ x^{2} + y^{2} - 6 x - 6 y + 6 = 0 adalah . . . . \\ A . menyinggung sumbu X \\ B . menyinggung sumbu Y \\ C . berpusat di O (0, 0) \\ D . titik pusatnya terletak pada x - y = 0 \\ E . berjari-jari 3 \\ Jawab : \\ \begin{aligned} Diketahui persamaan lingkaran \\ x^{2} + y^{2} - 6 x - 6 y + 6 = 0 \\ x^{2} - 6 x + 9 + y^{2} - 6 y + 9 + 6 = 9 + 9 \\ (x - 3)^{2} + (y - 3)^{2} = 18 - 6 \\ (x - 3)^{2} + (y - 3)^{2} = 12 \\ (x - 3)^{2} + (y - 3)^{2} = {(2 \sqrt{3})}^{2} \\ lingkaran ini {\begin{cases} Pusat & = (3, 3) \\ Jari-jari & = 2 \sqrt{3} \end{cases} \\ \begin{array}{clc} Opsi & Pernyataan & Keterangan \\ A & menyinggung sumbu X & tidak tepat \\ B & menyinggung sumbu Y & tidak tepat \\ C & berpusat di O (0, 0) & tidak tepat \\ D & titik pusatnya terletak pada garis x - y = 0 & tepat \\ E & berjari-jari 3 & tidak tepat \end{array} \\ Berikut ilustrasi gambarnya \end{aligned} \end{array}

Contoh Soal 1 Materi Lingkaran

$\begin{array}{ll} 1. & Jari-jari lingkaran dengan persamaan x^{2} + y^{2} = 48 \\ adalah . . . . \\ A . 3 \sqrt{5} \\ B . 4 \sqrt{3} \\ C . 5 \sqrt{2} \\ D . 6 \sqrt{3} \\ E . 7 \\ Jawab : \\ \begin{aligned} r^{2} & = 48 \\ r & = \sqrt{48} \\ = \sqrt{16.3} \\ = 4 \sqrt{3} \end{aligned} \end{array}$ .

$\begin{array}{ll} 2. & Titik pusat lingkaran (x - 7)^{2} + (y + 9)^{2} = 48 \\ adalah . . . . \\ A . (- 7, - 9) \\ B . (- 7, 9) \\ C . (7, - 9) \\ D . (7, 6) \\ E . (15, 48) \\ Jawab : \\ \begin{aligned} Jelas bahwa (a, b) & = (- 6, 9) \end{aligned} \end{array}$ .

$\begin{array}{ll} 3. & Persamaan lingkaran yang berpusat di P (- 2, 5) \\ dan melalui titik T (3, 4) adalah . . . . \\ A . (x + 2)^{2} + (y - 5)^{2} = 26 \\ B . (x - 3)^{2} + (y + 5)^{2} = 36 \\ C . (x + 2)^{2} + (y - 5)^{2} = 82 \\ D . (x - 3)^{2} + (y + 5)^{2} = 82 \\ E . (x + 2)^{2} + (y + 5)^{2} = 82 \\ Jawab : \\ \begin{aligned} Persamaan Lingkaran Berpusat di (a, b) \\ adalah : (x - a)^{2} + (y - b)^{2} = r^{2} \\ \begin{array}{lll} Pusat di P (- 2, 5) & Melalui Titik T (3, 4) \\ \begin{aligned} (x - a)^{2} + (y - b)^{2} & = r^{2} \\ (x + 2)^{2} + (y - 5)^{2} & = r^{2} \end{aligned} & \begin{aligned} (x - a)^{2} + (y - b)^{2} & = r^{2} \\ (3 + 2)^{2} + (4 - 5)^{2} & = r^{2} \\ 5^{2} + (- 1)^{2} & = r^{2} \\ 26 & = r^{2} \end{aligned} \\ \begin{aligned} Sehinga persamaan \\ lingkarannya \end{aligned} & \begin{aligned} adalah : \\ (x + 2)^{2} + (y - 5)^{2} = r^{2} = 26 \\ (x + 2)^{2} + (y - 5)^{2} = 26 \end{aligned} \end{array} \end{aligned} \end{array}$ .

$\begin{array}{ll} 4. & Koordinat titik pusat dan jari-jari lingkaran x^{2} + y^{2} - 4 x + 6 y + 4 = 0 adalah . . . . \\ A . (- 3, 2) dan 3 \\ B . (3, - 2) dan 3 \\ C . (- 2, - 3) dan 3 \\ D . (2, - 3) dan 3 \\ E . (2, 3) dan 3 \\ Jawab : \\ Alterntif 1 \\ \begin{array}{ll} Persamaan Lingkaran Berpusat di (a, b) dan berjari-jari r adalah \\ \begin{aligned} (x - a)^{2} + (y - b)^{2} & = r^{2} \\ x^{2} + y^{2} - 4 x + 6 y + 4 & = 0 \\ x^{2} - 4 x + y^{2} + 6 y + 4 & = 0 \\ x^{2} - 4 x + 4 - 4 + y^{2} + 6 y + 9 - 9 + 4 & = 0 \\ (x - 2)^{2} - 4 + (y + 3)^{2} - 9 + 4 & = 0 \\ (x - 2)^{2} + (y + 3)^{2} & = 4 + 9 - 4 \\ (x - 2)^{2} + (y + 3)^{2} & = 9 \\ (x - 2)^{2} + (y - (- 3))^{2} & = 3^{2} {\begin{cases} Pusat & = (2, - 3) \\ dan \\ r & = 3 \end{cases} \end{aligned} \end{array} \\ Alterntif 2 \\ \begin{aligned} Diketahui & persamaan lingkaran : x^{2} + y^{2} - 4 x + 6 y + 4 = 0 {\begin{cases} A & = - 4 \\ B & = 6 \\ C & = 4 \end{cases} \\ x^{2} + y^{2} + A x + B y + C = 0 \\ {\begin{cases} Pusat & = (- \frac{1}{2} A, - \frac{1}{2} B) = (- \frac{1}{2} \dots, - \frac{1}{2} \dots) = (\dots, \dots) \\ Jari-jari & = \sqrt{\frac{1}{4} A^{2} + \frac{1}{4} B^{2} - C} = \sqrt{\frac{1}{4} \dots^{2} + \frac{1}{4} \dots^{2} - \dots} = \sqrt{\dots} \end{cases} \end{aligned} \end{array}$ .

$\begin{array}{ll} 5. & Suatu lingkaran x^{2} + y^{2} - 4 x + 2 y + p = 0 \\ berjari-jari 3, maka nilai p adalah . . . . \\ A . - 1 \\ B . - 2 \\ C . - 3 \\ D . - 4 \\ E . - 5 \\ Jawab : \\ \begin{aligned} r = \sqrt{\frac{A^{2}}{4} + \frac{B^{2}}{4} - C} & = 3 \\ \sqrt{\frac{(- 4)^{2}}{4} + \frac{2^{2}}{4} - p} & = 3 \\ \frac{16}{4} + \frac{4}{4} - p & = 9 \\ 4 + 1 - p & = 9 \\ - p & = 9 - 5 \\ p & = - 4 \end{aligned} \end{array}$ .

Hubungan Dua Lingkaran (Lanjutan)

Hubungan Dua Buah Lingkaran

Coba perhatikan ilustrasi beberapa lingkaran berikut

Sebagai penjelasan dari kondisi di atas adalah:

\begin{array}{ccl} Kedudukan & Ilustrasi & Keterangan \\ | L_{1} L_{2} | > r_{1} + r_{2} & Gambar 1 & \begin{aligned} kedua lingkaran tidak berpotongan \\ dan tidak pula bersinggungan \\ dan saling lepas \end{aligned} \\ | L_{1} L_{2} | = 0 & Gambar 5 & Dikarenakan sepusat \\ | L_{1} L_{2} | \leq r_{1} + r_{2} & Gambar 6 & Terletak di dalam lingkaran L_{1} \\ | L_{1} L_{2} | = r_{1} + r_{2} & Gambar 2 & \begin{aligned} kedua lingkaran tidak berpotongan \\ tetapi bersinggungan di luar \end{aligned} \\ | L_{1} L_{2} | = r_{1} - r_{2} & Gambar 3 & \begin{aligned} kedua lingkaran tidak berpotongan \\ tetapi bersinggungan di dalam \end{aligned} \\ {\begin{cases} | L_{1} L_{2} | > r_{1} - r_{2} \\ | L_{1} L_{2} | < r_{1} + r_{2} \end{cases} & Gambar 4 & \begin{aligned} kedua lingkaran berpotongan \end{aligned} \end{array}

\begin{aligned} Kuasa \\ \begin{array}{ll} Lingkaran & Posisi sebuah titik terhadap lingkaran \\ \begin{aligned} Titik dua \\ lingkaran \end{aligned} & \begin{aligned} Tempat kedudukan titik-titik yang memiliki \\ kuasa yang sama terhadap dua lingkaran \end{aligned} \\ \begin{aligned} Garis tiga \\ lingkaran \end{aligned} & \begin{aligned} Tempat kedudukan titik yang memiliki \\ kuasa yang sama terhadap tiga buah lingkaran \end{aligned} \end{array} \end{aligned}

\begin{aligned} Berkas Lingkaran \\ \begin{array}{lll} Istilah & Posisi & Keterangan \\ \begin{aligned} Berkas \\ Lingkaran \end{aligned} & \begin{aligned} Pada garis \\ busur \end{aligned} & \begin{aligned} Sejumlah lingkaran yang dapat \\ dibuat melalui titik-titik potong \\ kedua lingakaran itu \end{aligned} \end{array} \end{aligned}

\begin{aligned} Tali Busur Sekutu \\ \begin{array}{lll} Istilah & Posisi & Keterangan \\ \begin{aligned} Tali Busur \\ Sekutu \end{aligned} & \begin{aligned} Kedua \\ lingkaran \\ yang \\ berpotongan \end{aligned} & \begin{aligned} Ruas garis yang menghubungkan \\ titik-titik potong irisan irisan \\ kedua lingkaran tersebut \end{aligned} \end{array} \\ ∙ Persamaan Tali Busur Sekutunya adalah : L_{1} - L_{2} = 0 \\ ∙ Persamaan yang melalui titik potong dan lingkaran (berkas) \\ itu adalah : L_{3} = L_{1} + p (L_{1} - L_{2}), atau L_{3} = L_{1} + p L_{2} \\ dengan p adalah suatu parameter (suatu patokan nilai) \\ ∙ Luas daerah irisan : (θ_{1} r_{1}^{2} + θ_{2} r_{2}^{2}) - \frac{1}{2} (r_{1}^{2} \sin θ_{1} + r_{2}^{2} \sin θ_{2}) \end{aligned}

CONTOH SOAL

\begin{array}{ll} 1. & Tentukanlah kedudukan untuk dua buah lingkaran \\ L_{1} \equiv x^{2} + y^{2} - 2 x - 4 y + 1 = 0 \\ dan L_{2} \equiv x^{2} + y^{2} - 4 x - 2 y - 1 = 0. \\ Jika kedua lingkaran tersebut bersinggungan \\ atau berpotongan, tentukanlah titik singgung atau potongnya \\ Jawab : \\ \begin{array}{cc} L_{1} & L_{2} \\ x^{2} + y^{2} - 2 x - 4 y + 1 = 0 & x^{2} + y^{2} - 4 x - 2 y - 1 = 0 \\ {\begin{cases} P_{1} & : (- \frac{1}{2} (- 2), - \frac{1}{2} (- 4)) = (1, 2) \\ r & = \sqrt{\frac{1}{4} ((- 2)^{2} + (- 4^{2})) - 1} \\ = 2 \end{cases} & {\begin{cases} P_{2} & : (- \frac{1}{2} (- 4), - \frac{1}{2} (- 2)) = (2, 1) \\ r & = \sqrt{\frac{1}{4} ((- 4)^{2} + (- 2^{2})) - (- 1)} \\ = \sqrt{6} \end{cases} \end{array} \\ \begin{aligned} Jarak ke & dua pusat lingkarannya adalah P_{1} P_{2} yaitu : \\ P_{1} P_{2} & = \sqrt{(2 - 1)^{2} + (1 - 2)^{2}} \\ = \sqrt{2} \\ Karena n & ilai P_{1} P_{2} = \sqrt{2} dan nilai P_{1} + P_{2} = 2 + \sqrt{6}, \\ sehingga & P_{1} P_{2} < P_{1} + P_{2} maka kedua lingkaran \\ itu berpo & tongan \end{aligned} \end{array}

. \begin{aligned} x^{2} + y^{2} - 2 x - 4 y + 1 & = 0 . . . . . . . . . . . . . . . . . . (1) \\ x^{2} + y^{2} - 4 x - 2 y - 1 & = 0 . . . . . . . . . . . . . . . . . . (2) \\ - - - - - - - - - - & - - -^{-} \\ 2 x - 2 y + 2 & = 0 \\ y & = x + 1 . . . . . . . . . . . . . . . . . . . . . . . . (3) \\ persamaan (3) \to (1) \\ x^{2} + (x + 1)^{2} - 2 x - & 4 (x + 1) + 1 = 0 \\ x^{2} + x^{2} + 2 x + 1 - 2 x & - 4 x - 4 + 1 = 0 \\ 2 x^{2} - 4 x - 2 & = 0 \Leftrightarrow x^{2} - 2 x - 1 = 0 \\ x_{1, 2} & = \frac{- (- 2) \pm \sqrt{(- 2)^{2} - 4.1 (- 1)}}{2} \\ = \frac{2 \pm \sqrt{8}}{2} = \frac{2 \pm 2 \sqrt{2}}{2} {\begin{cases} x_{1} & = 1 + \sqrt{2} . . . . . . . . . (4) atau \\ x_{2} & = 1 - \sqrt{2} . . . . . . . . . (5) \end{cases} \\ persamaan (4) \to (3) & , y_{1} = 1 + \sqrt{2} + 1 = 2 + \sqrt{2} \\ persamaan (5) \to (3) & , y_{1} = 1 - \sqrt{2} + 1 = 2 - \sqrt{2} \\ Sehingga titik poton & gnya ada 2 yaitu : \\ {\begin{cases} (1 + \sqrt{2}, 2 + \sqrt{2}) dan \\ (1 - \sqrt{2}, 2 - \sqrt{2}) \end{cases} \\ Berikut ilustrasinya \end{aligned}

\begin{array}{ll} 2 & Dari contoh soal no.1, tentukanlah persamaan lingkaran \\ yang melalui titik potong kedua lingkaran itu serta \\ melalui titik pusat koordinat O (0, 0) \\ Jawab : \\ \begin{aligned} Pada jawaban soal no.1 didapatkan persamaan \\ tali busur : L_{1} - L_{2} \equiv x - y + 1 = 0 \\ Sehingga persamaan \\ berkas lingkaran nya adalah : L_{3} = L_{1} + p (L_{1} - L_{2}) = 0 \\ \Leftrightarrow L_{3} = (x^{2} + y^{2} - 2 x - 4 y + 1) + p (x - y + 1) = 0 \\ Karena melalui titik asal O (0, 0), maka \\ \Leftrightarrow (0 + 0 - 0 - 0 + 1) + p (0 - 0 + 1) = 0 \Leftrightarrow p = - 1 \\ Selanjutnya persamaan berkas lingkarannya akan menjadi \\ L_{3} \equiv x^{2} + y^{2} - 2 x - 4 y + 1 - (x - y + 1) = 0 \\ Jadi, L_{3} \equiv x^{2} + y^{2} - 3 x - 3 y = 0 \\ Dan gambar berikut sebagai ilustrasinya \end{aligned} \end{array}

\begin{array}{ll} 3 & Diketahuin dua buah lingkaran \\ L_{1} \equiv x^{2} + y^{2} - 15 y + 32 = 0 dan \\ L_{2} \equiv x^{2} + y^{2} - 18 x + 2 y + 32 = 0 \\ Tunjukkan bahwa kedua lingkaran \\ bersinggungan di luar dan tentukan \\ titik singgungnya \\ Jawab : \\ Akan ditunjukkan kedua lingkaran saling \\ bersinggungan di luar, yaitu: \\ \begin{array}{lll} Lingakaran & Pusat/r \\ L_{1} \equiv x^{2} + y^{2} - 15 y + 32 = 0 & {\begin{cases} P_{1} & = (0, 8) \\ r_{1} & = 4 \sqrt{2} \end{cases} \\ L_{2} \equiv x^{2} + y^{2} - 18 x + 2 y + 32 = 0 & {\begin{cases} P_{2} & = (9, - 1) \\ r_{2} & = 5 \sqrt{2} \end{cases} \end{array} \\ Selanjutnya \\ \begin{array}{ll} Hitungan jarak kedua pusat & Sebagai bandingan \\ \begin{aligned} Pusat 1 lingkaran P_{1} = (0, 8) \\ Pusat 2 lingkaran P_{2} = (9, - 1) \\ maka jarak P_{1} P_{2} adalah \\ = \sqrt{(9 - 0)^{2} + (- 1 - 8)^{2}} \\ = \sqrt{9^{2} + 9^{2}} = \sqrt{2 \times 9^{2}} = 9 \sqrt{2} \end{aligned} & \begin{aligned} P_{1} P_{2} & = r_{1} + r_{2} \\ = 4 \sqrt{2} + 5 \sqrt{2} \\ = 9 \sqrt{2} \end{aligned} \end{array} \\ Adapun koordinat titik singgungnya : \\ \begin{aligned} (\begin{array}{c} x \\ y \end{array}) & = \frac{5 (\begin{array}{c} 0 \\ 8 \end{array}) + 4 (\begin{array}{c} 9 \\ - 1 \end{array})}{5 + 4} = \frac{(\begin{array}{c} 5 \times 0 + 4 \times 9 \\ 5 \times 8 + 4 \times (- 1) \end{array})}{9} \\ = \frac{(\begin{array}{c} 36 \\ 36 \end{array})}{9} = (\begin{array}{c} 4 \\ 4 \end{array}) \end{aligned} \\ Sehingga koordinat titik potongnya adalah : (4, 4) \\ Sebagai gambaran perhatikan ilustrasi berikut \end{array}

DAFTAR PUSTAKA

Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Persamaan Garis Singgung Lingkaran dengan Gradien m (Lanjutan)

D. Garis Singgung dengan Gradien m

Perhatikan ilustrasi berikut

Jika ada 2 garis yang saling sejajar dan keduanya atau salah satunya menyinggung lingkaran dengan kondisi garis singgungnya hanya diketahui garadiennya saja tanpa diketahui persamaannya, maka bagaimana kita menentukan persamaanya garis singgung tersebut?

Coba perhatikan lagi ilustrasi gambar di atas dengan tambahan beberapa keterangan

Berikut uraiannya

\begin{aligned} Misalkan diketahui \\ ∙ Persamaan lingkarannya : x^{2} + y^{2} = r^{2} \\ ∙ Persamaan garisnya : y = m x + c \\ Jika kita substitusikan persamaan garis \\ ke persamaan lingkaran, maka hasilnya \\ x^{2} + (m x + c)^{2} = r^{2} \\ \Leftrightarrow x^{2} + m^{2} x^{2} + 2 m c x + c^{2} - r^{2} = 0 \\ \Leftrightarrow (1 + m^{2}) x^{2} + 2 m c k + c^{2} - r^{2} = 0 \\ Syarat garis menyinggung lingkaran, D = 0 \\ D = b^{2} - 4 a c = 0 \\ \Leftrightarrow (2 m c)^{2} - 4 (1 + m^{2}) (c^{2} - r^{2}) = 0 \\ \Leftrightarrow 4 m^{2} c^{2} - 4 (c^{2} + m^{2} c^{2} - r^{2} - m^{2} r^{2}) = 0 \\ \Leftrightarrow m^{2} c^{2} - c^{2} - m^{2} c^{2} + r^{2} + m^{2} r^{2} = 0 \\ \Leftrightarrow c^{2} = r^{2} + m^{2} r^{2} = r^{2} (1 + m^{2}) \\ \Leftrightarrow c = \pm r \sqrt{1 + m^{2}} \\ Sehingga persamaan garis singgungnya \\ berubah menjadi bentuk \\ y = m x + c \\ \Leftrightarrow y = m x \pm r \sqrt{1 + m^{2}} \end{aligned}

Catatan:

Untuk lingkaran berpusat di (a,b), maka persamaan garis singgungnya adalah:

(y - b) = m (x - a) \pm r \sqrt{1 + m^{2}}

CONTOH SOAL

\begin{array}{ll} 1. & Tentukan persamaan garis singgung \\ lingkaran yang bergradien m = \frac{3}{4} dan \\ persamaan lingkaran singgungnya \\ x^{2} + y^{2} = 25 \\ Jawab : \\ \begin{aligned} Diketahui lingkaran {\begin{cases} x^{2} + y^{2} & = 25 \\ r & = 5 \end{cases} \\ maka persamaan garis singgung lingkarannya \\ y = m x \pm r \sqrt{1 + m^{2}} \\ \Leftrightarrow y = \frac{3}{4} x \pm 5 \sqrt{1 + {(\frac{3}{4})}^{2}} = \frac{3}{4} x \pm 5 \sqrt{1 + \frac{9}{16}} \\ \Leftrightarrow y = \frac{3}{4} x \pm 5 \sqrt{\frac{25}{16}} = \frac{3}{4} x \pm \frac{25}{4} \\ \Leftrightarrow 4 y = 3 x \pm 25 \\ \Leftrightarrow 3 x - 4 y \pm 25 = 0 \\ Jadi, persamaan garis singgungnya adalah \\ 3 x - 4 y + 25 = 0 dan 3 x - 4 y - 25 = 0 \end{aligned} \end{array}

\begin{array}{ll} 2. & Tentukan persamaan garis singgung \\ lingkaran yang bergradien - \frac{4}{3} dengan \\ persamaan lingkaran singgungnya \\ (x - 1)^{2} + (y - 2)^{2} = 25 \\ Jawab : \\ \begin{aligned} Diketahui lingkaran {\begin{cases} (x - 1)^{2} + (y - 2)^{2} & = 25 \\ r & = 5 \end{cases} \\ Persamaan garis singgungnya adalah : \\ y - b = m (x - a) \pm r \sqrt{1 + m^{2}} \\ \Leftrightarrow y - 2 = - \frac{4}{3} (x - 1) \pm 5 \sqrt{1 + {(- \frac{4}{3})}^{2}} \\ \Leftrightarrow y - 2 = - \frac{4}{3} (x - 1) \pm 5 \sqrt{1 + \frac{16}{9}} \\ \Leftrightarrow y - 2 = - \frac{4}{3} (x - 1) \pm 5 \sqrt{\frac{25}{9}} \\ \Leftrightarrow y - 2 = - \frac{4}{3} (x - 1) \pm \frac{25}{3} \\ \Leftrightarrow 3 y - 6 = - 4 x + 4 \pm 25 \\ \Leftrightarrow 4 x + 3 y - 10 \pm 25 = 0 \\ Jadi, persamaan garis singgungnya adalah \\ 4 x + 3 y + 15 = 0 dan 4 x + 3 y - 35 = 0 \end{aligned} \end{array}

\begin{array}{ll} 3. & Tentukan persamaan garis singgung yang \\ sejajar dengan garis y = 2 x + 5 pada \\ lingkaran x^{2} + y^{2} = 16 \\ Jawab : \\ \begin{aligned} Diketahui lingkaran L : x^{2} + y^{2} = 16 \\ dengan pusat (0, 0) dan r = \sqrt{16} = 4 \\ Sedangkan garis singgung yang sejajar \\ dengan y = 2 x + 5 mempunyai gradien 2, \\ yaitu sama dengan gradien garis y = 2 x + 5 \\ Persamaan garis singgung bergradien m \\ y = m x \pm r \sqrt{1 + m^{2}} \\ \Leftrightarrow y = 2 x \pm 4 \sqrt{1 + 2^{2}} \\ \Leftrightarrow y = 2 x \pm 4 \sqrt{5} \end{aligned} \end{array}

\begin{array}{ll} 4. & Tentukan persamaan garis singgung yang \\ tegak lurus dengan garis x + 2 y - 4 = 0 \\ pada lingkaran (x - 4)^{2} + (y - 2)^{2} = 25 \\ Jawab : \\ \begin{aligned} Diketahui garis x + 2 y - 4 = 0 dengan gradien \\ 2 y = - x + 4 \Rightarrow y = - \frac{1}{2} x + 2 \Rightarrow m_{1} = - \frac{1}{2} \\ tegak lurus dengan garis yang menyinggung \\ lingkaran. Misalkan garis singgung yang \\ menyinggung lingkaran tersebut adalah \\ bergradien m_{2}, maka syarat dua garis \\ berpotongan saling tegak lurus adalah \\ m_{1} \times m_{2} = - 1 \Leftrightarrow m_{2} = - \frac{1}{m_{1}} = - \frac{1}{(- \frac{1}{2})} \\ \Leftrightarrow m_{2} = 2. \end{aligned} \\ \begin{aligned} Dan diketahui pula lingkaran \\ (x - 4)^{2} + (y - 2)^{2} = 25 \\ pusatnya (4, 2), dan r = 5 \\ maka PGSL-nya ini adalah \\ y = m_{2} (x - a) + b \pm r \sqrt{1 + m_{2}^{2}} \\ = 2 (x - 4) + 2 \pm 5 \sqrt{1 + 2^{2}} \\ = 2 x - 8 + 2 \pm 5 \sqrt{1 + 4} \\ = 2 x - 6 \pm 5 \sqrt{5} \end{aligned} \end{array}

DAFTAR PUSTAKA

Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.