Lanjutan 4 Materi Geometri Ruang (Dimensi Tiga)

C. Menentukan Besar dan Nilai Sudut dalam Dimensi Tiga

C. 1 Sudut antara Garis dengan Bidang

Secara definisi jika garis $g$ menembus bidang $\alpha$ secara tidak tegak lurus, maka sudut antara garis $g$ dan bidang $\alpha$ adalah sudut lancip yang dibentuk oleh garis $g$ dan proyeksi garis $g$ pada bidang $\alpha$.

Perhatikanlah ilustrasi berikut

Pada bidang di atas 

$\begin{aligned}\angle (g,\alpha )&=\angle (g,g')=\theta\\ \theta &=\textrm{sudut antara garis}\: \: g\: \: \textrm{dan bidang}\: \: \alpha.\\ \theta &=\textrm{huruf yunani kuno dan baca}\: \: Theta \end{aligned}$.

Selanjutnya beberapa singkatan akan digunakan dalam pembicaraan geometri dimensi tiga, yaitu:

$\begin{aligned}\textrm{Titik}\: \: (a,b)&=\textrm{titik potong garis} \: \: a\: \: \textrm{dan garis}\: \: b\\ \textrm{Titik}\: \: (g,\alpha )&=\textrm{titik tembus garis}\: \: g\: \: \textrm{terhadap}\\ &\: \: \quad \textrm{bidang}\: \: \alpha\\ \textrm{garis}\: (\alpha ,\beta )&=\textrm{garis potong antara bidang}\: \: \alpha\: \: \textrm{dan}\\ &\: \: \quad \textrm{bidang}\: \: \beta\\ \textrm{Bidang}\: \: (A&BC)=\textrm{bidang melalui titik A, B, C}\\ \textrm{Bidang}\: \: (g,&A)=\textrm{bidang yang dilalui garis}\: \: g\: \: \textrm{dan}\\ &\: \: \quad \textrm{titik A}\\ \textrm{Bidang}\: \: (g,&h)=\textrm{bidang melalui garis}\: \: g\: \: \textrm{dan}\: \: h \end{aligned}$.

C. 2 Sudut antara Bidang dengan Bidang

Sudut antara bidang dua yang berpotongan adalah sudut yang terbentuk oleh dua garis pada masing-masing bidang tersebut di mana setiap garis itu tegak lurus pada garis potong kedua bidang tersebut di satu titik.

$\begin{aligned}\textrm{garis}\: (\alpha ,\beta )&=\textrm{garis potong antara bidang}\: \: \alpha\: \: \textrm{dan}\\ &\: \: \quad \textrm{bidang}\: \: \beta\\ \textrm{Garis TQ}\: \: \: &\textrm{pada bidang}\: \: \alpha\: \: \textrm{dengan}\: \: \textrm{TQ}\perp \textrm{garis}\: (\alpha ,\beta )\\ &\textrm{dan garis}\: \: \textrm{ST}\: \: \textrm{pada bidang}\: \: \beta \: \: j\textrm{uga}\\ &\textrm{ST}\perp \textrm{garis}\: (\alpha ,\beta )\\ \angle QST\: \: \textrm{ad}&\textrm{alah}\: \: \: \textbf{sudut tumpuan}\\ \textrm{Bidang}\: \: \: \gamma &\: \: \textrm{adalah}\: \: \: \textbf{bidang tumpuan}\\ &(\textrm{bidang yang memuat sudut tumpuan}) \end{aligned}$.

Sudut tumpuan sebuah sudut bidang dua menunjukkan besar kecilnya sudut bidang dua itu dan sudut bidang dua itu lancip, siku-siku, atau tumpul jika  sudut tumpuannya lancip, siku-siku, atau tumpul.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 14.&\textrm{Pada kubus ABCD.EFGH dengan panjang rusuk}\\ &12\: \: cm,\: \textrm{titik M adalah perpotongan diagonal}\\ &\textrm{bidang alas. Tentukanlah besar sudut antara}\\ &\textrm{garis MH dan bidang ADHE}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi kubus ABCD.EFGH berikut} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Lihat}\: \: \bigtriangleup \textrm{HM}'\textrm{M},\: \textrm{dengan}\: \: \angle \textrm{HM}'\textrm{M}=90^{\circ}\\ &\textrm{dengan}\: \: \textrm{M}'\: =\: \textrm{proyeksi titik M ke bidang ADHE}\\ &\textrm{Sudut antara garis MH dan bidang ADHE}\\ &\textrm{adalah}\: \: \angle \textrm{M}'\textrm{HM}\\ &(\textrm{bidang ADHE di wakili oleh garis HM}')\\ &\textrm{Sehingga}\\ &\begin{aligned} \sin \angle \textrm{M}'\textrm{HM}&=\displaystyle \frac{\textrm{MM}'}{\textrm{HM}}\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}(sisi)}{\displaystyle \frac{1}{2}(sisi)\sqrt{6}}\\ &=\displaystyle \frac{1}{\sqrt{6}}=\displaystyle \frac{1}{\sqrt{6}}\times\frac{\sqrt{6}}{\sqrt{6}}=\displaystyle \frac{1}{6}\sqrt{6}\\ \angle \textrm{M}'\textrm{HM}&=\arcsin \left ( \displaystyle \frac{1}{6}\sqrt{6} \right )\\ &\approx \color{blue}24,1^{\circ} \end{aligned}\\ &\textrm{Jadi},\: \: \angle \textrm{M}'\textrm{HM}\approx 24,1^{\circ} \end{aligned}$.

$\begin{array}{ll}\\ 15.&\textrm{Pada kubus ABCD.EFGH dengan panjang rusuk}\\ &10\: \: cm.\: \: \textrm{Tentukanlah besar sudut yang terbentuk}\\ &\textrm{antara garis BH dan bidang ADHE}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi kubus ABCD.EFGH berikut} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Lihat}\: \: \bigtriangleup \textrm{HBA},\: \textrm{dengan}\: \: \angle \textrm{HAB}=90^{\circ}\\ &\textrm{dengan}\: \: \textrm{A}\: =\: \textrm{proyeksi titik B ke bidang ADHE}\\ &\textrm{Sudut antara garis BH dan bidang ADHE}\\ &\textrm{adalah}\: \: \angle \textrm{AHB}\\ &(\textrm{bidang ADHE di wakili oleh garis AH})\\ &\textrm{Sehingga}\\ &\begin{aligned} \tan \angle \textrm{AHB}&=\displaystyle \frac{\textrm{AB}}{\textrm{HA}}\\ &=\displaystyle \frac{\displaystyle \textrm{sisi}}{\textrm{diagonal sisi}}\\ &=\displaystyle \frac{(sisi)}{\displaystyle (sisi)\sqrt{2}}=\displaystyle \frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}=\displaystyle \frac{1}{2}\sqrt{2}\\ \angle \textrm{AHB}&=\arctan \left ( \displaystyle \frac{1}{2}\sqrt{2} \right )\\ &\approx \color{blue}35,26^{\circ} \end{aligned}\\ &\textrm{Jadi},\: \: \angle \textrm{AHB}\approx 35,26^{\circ} \end{aligned}$.

DAFTAR PUSTAKA

1. Rasiman. 2000. Diktat Geometri. Semarang: IKIP Semarang
2. Tampomas, H. 1999. Seribu Pena Matematika SMU Kelas 3. Jakarta: ERLANGGA.

Lanjutan 3 Materi Geometri Ruang (Dimensi Tiga)

B. 3 Kedudukan Garis Terhadap Garis dalam Ruang

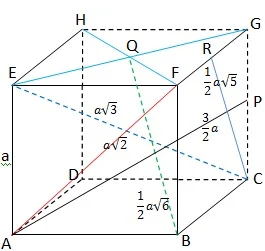
Pada bangun sebuah kubus di mana bangun ruang ini dibatasi oleh tiga pasang bidang persegi. Setiap daerah persegi membatasi kubus yang disebut sebagai sisi kubus. Setiap dua sisi yang tidak sejajar  akan saling berpotongan pada sebuah garis yang disebut rusuk, yaitu AB, BC, AE, dan lain-lainnya. Perhatikan ilustrasi kubus ABCD.EFGH berikut

Sehingga sebuah kubus memiliki 12 rusuk yang sama panjang. Jika Anda perhatikan susunan dan struktur dari rusuk-rusk kubus kubus di atas, maka 12 di atas dapat dibagi menjadi 3 kelompok, yaitu:

• kelompok pertama : AB, DC, HG, dan EF
• kelompok kedua : AD, BC, FG, dan EH
• kelompok ketiga : AE, BF, CG, dan DH

Selanjutnya Anda juga dapat menemukan atau melihat bahwa setiap tiga rusuk bertemu di suatu titik yang selanjutnya disebut titik sudut kubus. Sebuah kubus memiliki 8 titik sudut. Terdapat pasangan-pasangan titik sudut yang tidak terletak pada sebuah bidang sisi, yaitu titik A dengan G, B dengan H, C dengan E, serta D dengan F, pasangan titik yang demikian disebut dengan pasangan titik yang berhadapan.

Ruas garis yang menghubungkan dua buah titik yang berhadapan disebut diagonal ruang kubus. Karena terdapat empat pasang titik berhadapan, maka terdapat 4 buah diagonal ruang, yaitu: AB, BH, CE, dan DF. Selain itu juga karena sisi kubus ada 6 buah dan masing-masing memiliki dua diagonal, sehingga terdapat 12 diagonal sisi, yaitu: AC, BD, AF, BE, EG, FH, AH, DE, BG, dan CF.

Anda juga dapat menemukan pasangan rusuk yang sejajar tetapi tidak terletak pada sebuah bidang sisi, misalnya AB dengan HG, dan lain-lainnya. Dari sana Anda akan menemukan 6 pasang rusuk yang yang berhadapan. Bidang yang melalui dua rusuk yang berhadapan disebut bidang diagonal. Sehingga dalam sebuah kubus terdapat 6 buah bidang diagonal.

Perhatikan letak rusuk AB dan DH, kedua rusuk itu tidak terletak pada sebuah bidang, maka dikatakan AB dan DH dua rusuk saling bersilangan demikian juga garis yang lain dengan kondisi semisal. Selain itu hubungan dua garis adalah saling sejajar dan saling tegak lurus.

B. 4 Kedudukan Garis terhadap Bidang yang Sejajar

Jarak anatar suatu garis  $g$  dan bidang  $\alpha$ yang saling sejajar adalah jarak antara sebarang titik A pada  $g$  dengan bidang  $\alpha$. Jika proyeksi titik A pada garis $g$ ke bidang $\alpha$ yang saling sejajar adalah A', maka AA' adalah jarak antara garis  $g$  dan bidang  $\alpha$ yang saling sejajar.

Berikut ilustrasinya

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 9.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk 8 cm}\\ &\textrm{Tentukanlah jarak titik A ke bidang} \\ &\textrm{a}\quad \textrm{BCGF}\\ &\textrm{b}\quad \textrm{BCHE}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut ini} \end{array}$

$.\qquad\begin{aligned}\textrm{a}.\quad \textrm{titik}&\: A\: \textrm{ke}\: \textrm{BCGF}=\textrm{A}\: \textrm{ke}\: \textrm{B}=\textrm{AB}=8\: \: cm\\ \textrm{b}.\quad \textrm{titik}&\: \textrm{A}\: \textrm{ke}\: \textrm{BCHE}=A\: \textrm{ke tengah-tengan}\: \textrm{BE}\\ &=\displaystyle \frac{1}{2}\textrm{diagonal sisi kubus}=\displaystyle \frac{1}{2}\left ( 8\sqrt{2} \right )\\ &=4\sqrt{2}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 10.&\textrm{Pada kubus ABCD.EFGH dengan panjang rusuk}\\ &6\: \: cm,\: \textrm{titik S dan R berturut turut adalah pusat}\\ &\textrm{bidang EFGH dan ABCD. Tentukanlah jarak}\\ &\textrm{antara garis RF dan DS}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi kubus ABCD.EFGH berikut} \end{array}$.

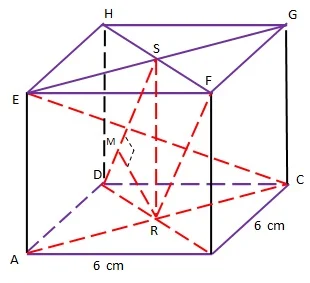
$.\qquad\begin{aligned}&\textrm{Diketahui bahwa}:\\ &BD=6\sqrt{2}\: \: cm\: (\color{red}\textrm{diagonal sisi kubus}\color{black})\\ &RD=\displaystyle \frac{1}{2}BD=\displaystyle \frac{1}{2}\left ( 6\sqrt{2} \right )=3\sqrt{2}\: \: cm\\ &DS=\displaystyle \frac{1}{2}(sisi)\sqrt{6}=\displaystyle \frac{1}{2}(6)\sqrt{6}=3\sqrt{6}\: \: cm\\ &\textrm{Langkah selanjutnya}\\ &\begin{aligned}\left [ DSR \right ]&=\left [ DSR \right ]\\ \displaystyle \frac{1}{2}\times DS\times RM&=\displaystyle \frac{1}{2}\times DR\times RS\\ \color{red}RM&=\displaystyle \frac{\displaystyle \frac{1}{2}\times DR\times RS}{\displaystyle \frac{1}{2}\times DS}\\ &=\displaystyle \frac{DR\times RS}{DS}\\ &=\displaystyle \frac{3\sqrt{2}\times 6}{3\sqrt{6}}\\ &=\displaystyle \frac{18\sqrt{2}}{3\sqrt{6}}\times \frac{\sqrt{6}}{\sqrt{6}}\\ &=\displaystyle \frac{18\sqrt{12}}{18}=\sqrt{12}=\sqrt{4.3}\\ &=\color{blue}2\sqrt{3}\: \: \color{black}cm \end{aligned}\\ \\ \textrm{Jadi},\: &\textrm{jarak garis RF ke DS}=2\sqrt{3}\: \: m \end{aligned}$

B. 5 Kedudukan antara Dua Bidang yang Sejajar

Jarak antara dua bidang $\alpha$ dan $\beta$ yang saling sejajar adalah sama dengan jarak antara sebarang titik A pada bidang  $\alpha$  dan A' pada bidang  $\beta$  dengan A' adalah proyeksi titik A pada bidang  $\beta$.

Berikut ilustrasinya

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 11.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk 8 cm}\\ &\textrm{Tentukanlah jarak bidang ABCD ke bidang} \\ &\textrm{a}\quad \textrm{BCGF}\\ &\textrm{b}\quad \textrm{EFGH}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad \textrm{bidang}&\: \textrm{ABCD}\: \textrm{ke}\: \textrm{BCGF}=\color{red}\textrm{tidak terdefinisi}\\ \color{blue}\textrm{alasan}&:\: \: \textbf{karena saling tegak lurus}\\ \textrm{b}.\quad \textrm{bidang}&\: \textrm{ABCD}\: \textrm{ke}\: \textrm{EFGH}=A\: \textrm{ke }\: \textrm{E}=8\: \: cm\\ \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Pada kubus ABCD.EFGH dengan panjang rusuk}\\ &8\: \: cm,\: \textrm{titik P, Q, R, dan S berturut turut berada}\\ &\textrm{di pertengahan rusuk BC, CG, DH, dan AD.}\\ &\textrm{Tentukanlah jarak antara bidang ABGH dan}\\ &\textrm{bidang PQRS}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi kubus ABCD.EFGH berikut} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Diketahui bahwa}:\\ &BP=\displaystyle \frac{1}{2}BC=\displaystyle \frac{1}{2}8=4\: \: cm\: (\color{red}\textrm{rusuk kubus}\color{black})\\ &\sin \angle PBP'=\displaystyle \frac{PP'}{BP}\Leftrightarrow PP'=BP\times \sin \angle PBP'\\ &\qquad\qquad \quad =4\times \sin 45^{\circ}=4\times \displaystyle \frac{1}{2}\sqrt{2}=2\sqrt{2}\: \: cm\\ &DS=\displaystyle \frac{1}{2}(sisi)\sqrt{6}=\displaystyle \frac{1}{2}(6)\sqrt{6}=3\sqrt{6}\: \: cm\\ &\textrm{Jadi, jarak bidang ABGH ke PQRS adalah}\: \: 2\sqrt{2}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 13.&\textrm{Pada sebuah kubus ABCD.EFGH, tunjukkan}\\ &\textrm{bahwa bidang AFH sejajar dengan bidang BDG}\\\\ &\textrm{Bukti}:\\ &\textrm{Perhatikan ilustrasi kubus ABCD.EFGH berikut} \end{array}$

$.\qquad\begin{aligned}&\textrm{Untuk menunjukkan bidang AFH dan BDG}\\ &\textrm{itu sejajar, maka harus ditunjukkan bahwa}\\ &\textrm{kedua bidang itu masing-masing memuat}\\ &\textrm{dua garis berpotongan yang sepasang-sepasang}.\\ &\textrm{Bidang ADHE}\: //\: \textrm{bidang BCGF},\: \textrm{sedang bidang}\\ &\textrm{ABGH memotong kedua bidang yang sejajar itu}\\ &\textrm{berupa garis AH dan BG, maka AH}\: //\: \textrm{BG}.\\ &\textrm{Demikian pula bidang ABCD dan EFGH yang}\\ &\textrm{dipotong oleh bidang BDHF, masing-masing}\\ &\textrm{berupa garis BD dan FH, maka BD}\: // \textrm{FH}\\ &\textrm{Berdasarkan fakta di atas, yaitu}:\\ &\textrm{garis AH}\: //\: \textrm{BG dan BD}\: //\: \textrm{FH, maka sudah}\\ &\textrm{cukup menunjukkan bahwa}\: \: \textrm{bidang AFH}\\ &\textrm{bidang BDG sejajar}\: \: \: \: \: \blacksquare \end{aligned}$.

DAFTAR PUSTAKA

1. Rasiman. 2000. Diktat Geometri. Semarang: IKIP Semarang
2. Tampomas, H. 1999. Seribu Pena Matematika SMU Kelas 3. Jakarta: ERLANGGA.

Lanjutan 2 Materi Geometri Ruang (Dimensi Tiga)

 $\color{blue}\textrm{B. 3. Kedudukan Titik terhadap Bidang}$.

Perhatikan kubus ABCD.EFGH berikut

Pandang titik A terhadap bidang EFGH. Tampak bahwa titik A terletak tidak pada bidang EFGH termasuk juga titik-titik yang lain yang tidak terletak pada bidang EFGH tersebut yaitu: titik B, C, dan D. Walaupun demikian pada kubus ABCD.EFGH tersebut terdapat beberapa titik yang terletak pada bidang EFGH, yaitu: titik E, F, G, G, dan P. Selanjutnya hubungan kedudukan suatu titik terhadap bidang dapat kita tuliskan sebagaimana dalam tabel berikut:

$\begin{array}{|c|l|l|}\hline \textrm{No}&\: \: \, \textrm{Kedudukan}&\: \quad\qquad\textrm{Keterangan}\\\hline 1.&\textrm{pada bidang}&\textrm{titik terletak pada bidang}\\\hline 2.&\textrm{di luar bidang}&\textrm{titik berada di luar bidang}\\\hline \end{array}$

Sebagai tambahan penjelasan perhatikan pula gambar limas D.ABC berikut

Pada limas D.ABC di atas terlihat jelas bagwa titik D terletak di luar bidan ABC, tetapi titik A atau titik B ataupun titik C, semuanya terletak pada bidang ABC pada bangun limas D.ABC di atas.

Selanjutnya dalam penentuan jarak antar titik dengan suatu bidang adalah panjang ruas garis secara tegak lurus yang menghungkan titik tersebut dengan bidang yang dimaksud.

Sebagai ilustrasi adalah gambar berikut

Pada ilsutrasi gambar di atas jarak titik A ke bidang V adalah sepanjang ruas garis AB yang mana ruas garis AB tegak lurus dengan bidang V.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 7.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk 8 cm}.\\ &\textrm{Tentukanlah jarak titik C ke bidang BDG}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah ilustrasi} \end{array}$.

Jika gambarnya dipartisi lagi di bagian segitiga GCG' maka akan tampak seperti ilustrasi berikut

$.\qquad\begin{aligned}\textrm{Jelas}&\: \textrm{bahwa}\\ &\begin{cases} GC & =8\: \: cm\: \: (\color{red}\textrm{dari soal}) \\ BD &=AC =8\sqrt{2}\: \: cm\: \: (\textrm{diagonal sisi kubus}) \\ CG' & = \displaystyle \frac{1}{2}AC=4\sqrt{2}\: \: cm \end{cases}\\ \textrm{maka}&\: \textrm{dengan rumus Pythagoras dapat}\\ \textrm{panja}&\textrm{ng}\: \: GG',\: \textrm{yaitu}:\\ \left ( GG' \right )&^{2}=\left ( G'C \right )^{2}+CG^{2}\\ GG'&=\sqrt{\left ( G'C \right )^{2}+CG^{2}}=\sqrt{\left ( 4\sqrt{2} \right )^{2}+8^{2}}\\ &=\sqrt{32+64}=\sqrt{96}=\sqrt{16.6}=4\sqrt{6}\: \: cm\\ \textrm{Perha}&\textrm{tikan}\: \: \bigtriangleup GCG'\\ &\begin{aligned}&\textrm{Dengan perbandingan luas}\: \: \bigtriangleup GCG'=\bigtriangleup GCG'\\ &\displaystyle \frac{1}{2}\times CC'\times GG'=\displaystyle \frac{1}{2}\times CG'\times CG\\ &\displaystyle \frac{1}{2}\times CC'\times \left ( 4\sqrt{6} \right )=\displaystyle \frac{1}{2}\times \left ( 4\sqrt{2} \right )\times 8\\ &\quad\quad\quad CC'= \displaystyle \frac{\displaystyle \frac{1}{2}\times \left ( 4\sqrt{2} \right )\times 8}{\displaystyle \frac{1}{2}\times \left ( 4\sqrt{6} \right )}\\ &\: \: \: \quad\quad\qquad =\displaystyle \frac{8}{\sqrt{3}}\\ &\: \: \: \quad\quad\qquad =\displaystyle \frac{8}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}\\ &\: \: \: \quad\quad\qquad =\color{blue}\displaystyle \frac{8}{3}\sqrt{3}\: \: \color{black}cm \end{aligned} \end{aligned}$.

$\begin{array}{ll}\\ 8.&\textrm{Diketahui rusuk kubus ABCD.EFGH adalah 6 cm}\\ &\textrm{Tentukanlah jarak titik E ke bidang BDG}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah ilustrasi berikut ini} \end{array}$.

$.\qquad\begin{aligned}\textrm{Jelas}&\: \textrm{bahwa}\\ &\begin{cases} AB & =BC=CG=QQ'=6\: \: cm\: \: (\color{red}\textrm{dari soal}) \\ AC &=EG =6\sqrt{2}\: \: cm\: \: (\textrm{diagonal sisi kubus}) \\ EQ & =QG= \displaystyle \frac{1}{2}(\textbf{sisi})\sqrt{6}=3\sqrt{6}\: \: cm \end{cases}\\ \textrm{Perh}&\textrm{atikan}\: \: \bigtriangleup EQG\\ &\begin{aligned}&\textrm{Dengan perbandingan luas}\: \: \bigtriangleup EQG=\bigtriangleup EQG\\ &\displaystyle \frac{1}{2}\times QG\times EE'=\displaystyle \frac{1}{2}\times QQ'\times EG\\ &\displaystyle \frac{1}{2}\times \left ( 3\sqrt{6} \right )\times EE'=\displaystyle \frac{1}{2}\times 6\times 6\sqrt{2}\\ &\quad\quad\quad EE'= \displaystyle \frac{\displaystyle \frac{1}{2}\times \left ( 6\sqrt{2} \right )\times 6}{\displaystyle \frac{1}{2}\times \left ( 3\sqrt{6} \right )}\\ &\: \: \: \quad\quad\qquad =4\sqrt{3}\: \: \color{black}cm \end{aligned} \end{aligned}$

Lanjutan Materi Geometri Ruang (Dimensi Tiga)

 $\color{blue}\textrm{B. 2. Kedudukan Titik terhadap Garis}$.

$\begin{array}{|c|l|l|}\hline \textrm{No}&\: \textrm{Kedudukan}&\quad\qquad\textrm{Keterangan}\\\hline 1.&\textrm{pada garis}&\textrm{titik berimpit pada garis}\\\hline 2.&\textrm{di luar garis}&\textrm{titik berada di luar garis}\\\hline \end{array}$.

Pada contoh kubus ABCD.EFGH di atas adalah :

• terletak pada garis : Titik A terletak pada tiga garis yaitu ruas garis AB, AD, dan AE
• terletak di luar garis : Titik A di luar rus garis BC, CD, BF, CG, DH, EF, ED, FG, dan GH.

Secara definisi jarak antara suatu titik dengan garis adalah panjang ruas garis yang ditarik dari titik tersebut ke garis tersebut secara tegak lurus.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 4.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk}.\\ &\textrm{10 cm. Tentukanlah jarak titik F ke garis AC}\\\\ &\color{purple}\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar kubus berikut} \end{array}$.

$.\qquad \textrm{perhatikan pula gambar kedua berikut}$

$.\qquad\begin{aligned}\textrm{Tampak}&\: \textrm{bahwa jakak titik F ke garis AC}\\ \textrm{adalah s}&\textrm{ama dengan jarak titik F ke P}\\ \textrm{dengan}\: \, \, &\textrm{panjang rusuk 10}\: cm,\: \textrm{yaitu}:\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 1}\\ \textrm{Dengan}\: \, &\textrm{memandang segitiga BFP kita}\\ \textrm{gunakan}&\: \textrm{rumus Pythagoras, yaitu}:\\ PF^{2}&=PB^{2}+BF^{2}\\ PF&=\sqrt{PB^{2}+BF^{2}}\\ &=\sqrt{\left (5\sqrt{2} \right )^{2}+10^{2}}\\ &\color{red}\textrm{ingat}\: \: \color{black}\textrm{PB setengah diagonal sisi}\\ &=\sqrt{50+100}=\sqrt{150}=\sqrt{25.6}\\ &=5\sqrt{6}\: \: cm\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 2}\\ \textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \textrm{Luas}\: \bigtriangleup \: &\textrm{PBF}=\textrm{Luas}\: \bigtriangleup \: \textrm{PBF, atau}\\ \left [ PBF \right ]&=\left [ PBF \right ]\\ &\color{red}\textrm{karena}\: \color{black}\bigtriangleup \textrm{PBF segitiga sama sisi}\\ &\textrm{maka AC=CF=FA=}10\sqrt{2}\: \: \textrm{dan ketiga}\\ &\textrm{sudutnya masing-masing}\: 60^{\circ}\\ \displaystyle \frac{1}{2}\times AC&\times FP=\displaystyle \frac{1}{2}\times AF\times FC\times \sin \angle AFC\\ \displaystyle \frac{1}{2}\times AC&\times FP=\displaystyle \frac{1}{2}\times AC\times AC\times \sin \angle AFC\\ FP&=AC\times \sin \angle AFC=10\sqrt{2}\times \sin 60^{\circ}\\ &=10\sqrt{2}\times \left ( \displaystyle \frac{1}{2}\sqrt{3} \right )=5\sqrt{6}\: \: cm\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 3}\\ \textrm{Perhatik}&\textrm{an gambar berikut} \end{aligned}$.

$.\qquad\begin{aligned}\textrm{Tampak}&\: \textrm{bahwa jakak titik F ke garis AC}\\ \textrm{seperti}\: \: &\textrm{jarak titik B ke Q}\: =\displaystyle \frac{1}{2}a\sqrt{6}\\ \textrm{maka}\: \textrm{P}&\textrm{F}=BQ=\displaystyle \frac{1}{2}a\sqrt{6}\\ PF&=\displaystyle \frac{1}{2}(\textrm{sisi})\sqrt{6}\\ &=\displaystyle \frac{1}{2}(10)\sqrt{6}\\ &=5\sqrt{6}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 5.&\textrm{Diketahui limas beraturan T.ABCD. Panjang}\\ &\textrm{rusuk alasnya 8 cm dan panjang rusuk tegaknya}\\ &\textrm{12 cm. Tentukanlah jarak B ke TD}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar limas beraturan T.ABCD}\\ &\textrm{berikut} \end{array}$.

$.\qquad \textrm{perhatikan pula gambar kedua berikut}$

$.\qquad\begin{aligned}\textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \textrm{Luas}\: \bigtriangleup \: &\textrm{TBD}=\textrm{Luas}\: \bigtriangleup \: \textrm{TBD atau}\\ \left [ TBD \right ]&=\left [ TBD \right ]\\ &\color{red}\textrm{karena}\: \color{black}\bigtriangleup \textrm{TBD segitiga sama kaki}\\ &\textrm{maka TB=TD=}\: 12\: \: cm\: \textrm{dan BD}\\ &\textrm{adalah diagonal sisi alas} =8\sqrt{2}\: \: cm\\ &\textrm{dengan menghitung tinggi}\: \bigtriangleup TBD\\ &\textrm{dengan alas TD dengan tinggi ditarik dari}\\ &\textrm{B ke arak rusuk TD, maka akan ketemu}\\ &\textrm{jarak titik B ke garis TD}.\\ &\textrm{Berikut perhitungannya}\\ \displaystyle \frac{1}{2}\times TD&\times Tinggi=\displaystyle \frac{1}{2}\times TP\times DB\\ \displaystyle \frac{1}{2}\times TD&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ TB^{2}-PB^{2}} \right )\times DB\\ \displaystyle \frac{1}{2}\times 12&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ 12^{2}-\left ( 4\sqrt{2} \right )^{2}} \right )\times 8\sqrt{2}\\ &\color{red}\textrm{ingat bahwa}\: \: \color{black}PB=\displaystyle \frac{1}{2}BD\\ Tinggi&=\displaystyle \frac{\displaystyle \frac{1}{2}\times \left (\sqrt{ 12^{2}-\left ( 4\sqrt{2} \right )^{2}} \right )\times 8\sqrt{2}}{6}\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}\times \sqrt{144-32}\times 8\sqrt{2}}{6}\\ &=\displaystyle \frac{ \sqrt{112}\times 4\sqrt{2}}{6}\\ &=\displaystyle \frac{\sqrt{16\times 7}\times 4\sqrt{2}}{6}\\ &=\displaystyle \frac{4\sqrt{7}\times 2\sqrt{2}}{3}\\ &=\displaystyle \frac{8}{3}\sqrt{7.2}\\ &=\displaystyle \frac{8}{3}\sqrt{14}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 6.&\textrm{Diketahui limas beraturan T.ABCD. Panjang}\\ &\textrm{rusuk alasnya}\: \: 5\sqrt{2}\: \: cm\: \: \textrm{dan panjang rusuk}\\ &\textrm{tegaknya 13 cm. Tentukanlah jarak A ke TC}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar limas beraturan T.ABCD}\\ &\textrm{berikut} \end{array}$.

$.\qquad\begin{aligned}\textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \left [ TAC \right ]&=\left [ TAC \right ]\\ \textrm{dengan}&\: \textrm{proses pengerjaaan sama semisal}\\ \textrm{no.5 di}&\textrm{ atas, maka} \\ &\begin{aligned}\displaystyle \frac{1}{2}\times TC&\times Tinggi=\displaystyle \frac{1}{2}\times TT'\times AC\\ \displaystyle \frac{1}{2}\times TC&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ TA^{2}-AT'^{2}} \right )\times AC\\ \displaystyle \frac{1}{2}\times 13&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ 13^{2}-\left ( \displaystyle \frac{10}{2} \right )^{2}} \right )\times 10\\ 13&\times Tinggi=12\times 10\\ &Tinggi=\displaystyle \frac{120}{13} \end{aligned} \end{aligned}$

Contoh Soal Bangun Ruang Dimensi Tiga (Matematika Wajib Kelas XII)

 

Sebagai tambahan penjelasan berikut diilustrasikan panjang beberapa unsur dalam kubus

dan