Lanjutan Materi Geometri Ruang (Dimensi Tiga)

 $\color{blue}\textrm{B. 2. Kedudukan Titik terhadap Garis}$.

$\begin{array}{|c|l|l|}\hline \textrm{No}&\: \textrm{Kedudukan}&\quad\qquad\textrm{Keterangan}\\\hline 1.&\textrm{pada garis}&\textrm{titik berimpit pada garis}\\\hline 2.&\textrm{di luar garis}&\textrm{titik berada di luar garis}\\\hline \end{array}$.

Pada contoh kubus ABCD.EFGH di atas adalah :

• terletak pada garis : Titik A terletak pada tiga garis yaitu ruas garis AB, AD, dan AE
• terletak di luar garis : Titik A di luar rus garis BC, CD, BF, CG, DH, EF, ED, FG, dan GH.

Secara definisi jarak antara suatu titik dengan garis adalah panjang ruas garis yang ditarik dari titik tersebut ke garis tersebut secara tegak lurus.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 4.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk}.\\ &\textrm{10 cm. Tentukanlah jarak titik F ke garis AC}\\\\ &\color{purple}\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar kubus berikut} \end{array}$.

$.\qquad \textrm{perhatikan pula gambar kedua berikut}$

$.\qquad\begin{aligned}\textrm{Tampak}&\: \textrm{bahwa jakak titik F ke garis AC}\\ \textrm{adalah s}&\textrm{ama dengan jarak titik F ke P}\\ \textrm{dengan}\: \, \, &\textrm{panjang rusuk 10}\: cm,\: \textrm{yaitu}:\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 1}\\ \textrm{Dengan}\: \, &\textrm{memandang segitiga BFP kita}\\ \textrm{gunakan}&\: \textrm{rumus Pythagoras, yaitu}:\\ PF^{2}&=PB^{2}+BF^{2}\\ PF&=\sqrt{PB^{2}+BF^{2}}\\ &=\sqrt{\left (5\sqrt{2} \right )^{2}+10^{2}}\\ &\color{red}\textrm{ingat}\: \: \color{black}\textrm{PB setengah diagonal sisi}\\ &=\sqrt{50+100}=\sqrt{150}=\sqrt{25.6}\\ &=5\sqrt{6}\: \: cm\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 2}\\ \textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \textrm{Luas}\: \bigtriangleup \: &\textrm{PBF}=\textrm{Luas}\: \bigtriangleup \: \textrm{PBF, atau}\\ \left [ PBF \right ]&=\left [ PBF \right ]\\ &\color{red}\textrm{karena}\: \color{black}\bigtriangleup \textrm{PBF segitiga sama sisi}\\ &\textrm{maka AC=CF=FA=}10\sqrt{2}\: \: \textrm{dan ketiga}\\ &\textrm{sudutnya masing-masing}\: 60^{\circ}\\ \displaystyle \frac{1}{2}\times AC&\times FP=\displaystyle \frac{1}{2}\times AF\times FC\times \sin \angle AFC\\ \displaystyle \frac{1}{2}\times AC&\times FP=\displaystyle \frac{1}{2}\times AC\times AC\times \sin \angle AFC\\ FP&=AC\times \sin \angle AFC=10\sqrt{2}\times \sin 60^{\circ}\\ &=10\sqrt{2}\times \left ( \displaystyle \frac{1}{2}\sqrt{3} \right )=5\sqrt{6}\: \: cm\\ \color{blue}\textrm{Alternat}&\color{blue}\textrm{if 3}\\ \textrm{Perhatik}&\textrm{an gambar berikut} \end{aligned}$.

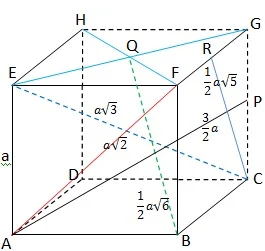
$.\qquad\begin{aligned}\textrm{Tampak}&\: \textrm{bahwa jakak titik F ke garis AC}\\ \textrm{seperti}\: \: &\textrm{jarak titik B ke Q}\: =\displaystyle \frac{1}{2}a\sqrt{6}\\ \textrm{maka}\: \textrm{P}&\textrm{F}=BQ=\displaystyle \frac{1}{2}a\sqrt{6}\\ PF&=\displaystyle \frac{1}{2}(\textrm{sisi})\sqrt{6}\\ &=\displaystyle \frac{1}{2}(10)\sqrt{6}\\ &=5\sqrt{6}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 5.&\textrm{Diketahui limas beraturan T.ABCD. Panjang}\\ &\textrm{rusuk alasnya 8 cm dan panjang rusuk tegaknya}\\ &\textrm{12 cm. Tentukanlah jarak B ke TD}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar limas beraturan T.ABCD}\\ &\textrm{berikut} \end{array}$.

$.\qquad \textrm{perhatikan pula gambar kedua berikut}$

$.\qquad\begin{aligned}\textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \textrm{Luas}\: \bigtriangleup \: &\textrm{TBD}=\textrm{Luas}\: \bigtriangleup \: \textrm{TBD atau}\\ \left [ TBD \right ]&=\left [ TBD \right ]\\ &\color{red}\textrm{karena}\: \color{black}\bigtriangleup \textrm{TBD segitiga sama kaki}\\ &\textrm{maka TB=TD=}\: 12\: \: cm\: \textrm{dan BD}\\ &\textrm{adalah diagonal sisi alas} =8\sqrt{2}\: \: cm\\ &\textrm{dengan menghitung tinggi}\: \bigtriangleup TBD\\ &\textrm{dengan alas TD dengan tinggi ditarik dari}\\ &\textrm{B ke arak rusuk TD, maka akan ketemu}\\ &\textrm{jarak titik B ke garis TD}.\\ &\textrm{Berikut perhitungannya}\\ \displaystyle \frac{1}{2}\times TD&\times Tinggi=\displaystyle \frac{1}{2}\times TP\times DB\\ \displaystyle \frac{1}{2}\times TD&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ TB^{2}-PB^{2}} \right )\times DB\\ \displaystyle \frac{1}{2}\times 12&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ 12^{2}-\left ( 4\sqrt{2} \right )^{2}} \right )\times 8\sqrt{2}\\ &\color{red}\textrm{ingat bahwa}\: \: \color{black}PB=\displaystyle \frac{1}{2}BD\\ Tinggi&=\displaystyle \frac{\displaystyle \frac{1}{2}\times \left (\sqrt{ 12^{2}-\left ( 4\sqrt{2} \right )^{2}} \right )\times 8\sqrt{2}}{6}\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}\times \sqrt{144-32}\times 8\sqrt{2}}{6}\\ &=\displaystyle \frac{ \sqrt{112}\times 4\sqrt{2}}{6}\\ &=\displaystyle \frac{\sqrt{16\times 7}\times 4\sqrt{2}}{6}\\ &=\displaystyle \frac{4\sqrt{7}\times 2\sqrt{2}}{3}\\ &=\displaystyle \frac{8}{3}\sqrt{7.2}\\ &=\displaystyle \frac{8}{3}\sqrt{14}\: \: cm \end{aligned}$.

$\begin{array}{ll}\\ 6.&\textrm{Diketahui limas beraturan T.ABCD. Panjang}\\ &\textrm{rusuk alasnya}\: \: 5\sqrt{2}\: \: cm\: \: \textrm{dan panjang rusuk}\\ &\textrm{tegaknya 13 cm. Tentukanlah jarak A ke TC}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar limas beraturan T.ABCD}\\ &\textrm{berikut} \end{array}$.

$.\qquad\begin{aligned}\textrm{Gunaka}&\textrm{n rumus luas segitiga, yaitu}:\\ \left [ TAC \right ]&=\left [ TAC \right ]\\ \textrm{dengan}&\: \textrm{proses pengerjaaan sama semisal}\\ \textrm{no.5 di}&\textrm{ atas, maka} \\ &\begin{aligned}\displaystyle \frac{1}{2}\times TC&\times Tinggi=\displaystyle \frac{1}{2}\times TT'\times AC\\ \displaystyle \frac{1}{2}\times TC&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ TA^{2}-AT'^{2}} \right )\times AC\\ \displaystyle \frac{1}{2}\times 13&\times Tinggi=\displaystyle \frac{1}{2}\times \left (\sqrt{ 13^{2}-\left ( \displaystyle \frac{10}{2} \right )^{2}} \right )\times 10\\ 13&\times Tinggi=12\times 10\\ &Tinggi=\displaystyle \frac{120}{13} \end{aligned} \end{aligned}$