Geometri Ruang (Dimensi Tiga)

 $\color{blue}\textrm{A. Kedudukan Titik, Garis, dan Bidang}$

Perhatikanlah gambar bangunan gedung MA Futuhiyah Jeketro (gambar diambil sekitar awal tahun 2020) berikut

Jika tiang-tiang yang ada pada gambar di atas diasumsikan sebagai garis lurus dan tembok atau lantai atau pun halaman madrasah diasumsikan sebagai luasan maka dari kedua hal tersebut kita dapat melihat kedudukan antara garis dengan garis atau antara garis dengan bidang yang akhirnya mendasari bagaimana hubungan sebuah titik dengan titik yang lain yang tidak berimpit.

Dan perhatikanlah pula gambar kubus ABCD.EFGH berikut ini

Semakin jelas bahwa kedudukan 3 unsur utama yaitu titik, garis an bidang sangat dominan dalam pembahasan selanjutnya

Selanjutnya tempat kedudukan dalam hal ini akan terbagi dalam beberapa bagian dalam bangun ruang dimensi tiga yang lebih detil yaitu:

• hubungan titik dengan titik
• hubungan titik dengan garis 
• hubungan titik dengan bidang 
• hubungan garis dengan garis
• hubungan garis dengan bidang, dan
• hubungan bidang dengan bidang

$\color{blue}\textrm{B. Menghitung Jarak}$.

$\color{blue}\textrm{B.1 Kedudukan Suatu Titik Terhadap Titik Lain}$.

Jarak antara suatu titik dengan dengan suatu titik yang lain adalah panjang garis yang menghubungkan kedua titik itu

Selanjutnya untuk menentukan jarak antara titik beberapa pemecahan masalah dibutuihkan dalil Pythagoras.

Perhatikanlah ilustrasi gambar kubus ABCD.EFGH berikut ini yang telah disertakan jaraknya berbantuan dalil Pythagoras

Pada ilustrasi gambar di atas sudah dimunculkan jarak antar titik di antaranya sebagai berikut

$\begin{array}{|c|c|l|}\hline \textrm{No}&\textrm{Kedudukan}&\: \: \quad\textrm{Besar jarak}\\\hline 1&\textrm{A ke B}&\textrm{AB}=\textrm{AE}=a\\\hline 2&\textrm{A ke C}&\textrm{AC}=\textrm{AF}=a\sqrt{2}\\\hline 3&\textrm{A ke G}&\textrm{AG}=\textrm{CE}=a\sqrt{3}\\\hline 4&\textrm{A ke Q}&\textrm{AQ}=\textrm{BQ}=\displaystyle \frac{1}{2}a\sqrt{6}\\\hline 5&\textrm{A ke P}&\textrm{AP}=\textrm{EP}=\displaystyle \frac{3}{2}a\\\hline 6&\textrm{C ke R}&\textrm{CR}=\textrm{BR}=\displaystyle \frac{1}{2}a\sqrt{5}\\\hline \end{array}$.

$\color{blue}\textrm{B. 1. 1 Penamaan Bangun Ruang}$.

perhatikanlah gambar kubus di atas. Penamaan bangun ruang model kubus itu dinamakan dengan istilah kubus ABCD.EFGH atau  $\displaystyle \frac{\textrm{EFGH}}{\textrm{ABCD}}$. Dan penulisan ABCD posisi di depan atau di bawah menunjukkan posisi bidang alas dan EFGH dituliskan setelah ABCD atau EFGH posisi di atas menunjukkan bahwa bidang EFGH adalah bidang atas. Urutan penyebutan titik pada bangun ruang itupun harus mengikuti arah putar jarum jam atau sebaliknya, sebagi misal pada bidang alas kubus tidak boleh disebutkan bidang ABDC tetapi ditulis dengan arah putar berkebalikan arah putar jarum jam yaitu ABCD. Jika Bagian alas dituliskan menggunakan kebalikan arah putar jarum jam, maka bidang alasnyapun mengikuti dengan diikuti peletakaan tanda titik yang menunjukkan perbedaan posisi bidangnya, sehingga bangun ruang kubus biasa disebutkan dengan istilah ABCD.EFGH. Hal penamaan tersebut akan berlaku pula pada bangun ruang seperti: Balok, Prisma dan semacamnya. Khusus untuk Limas penamaan di awali dengan posisi puncaknya terlebih dahulu sebagai contoh limas D.ABC berikut

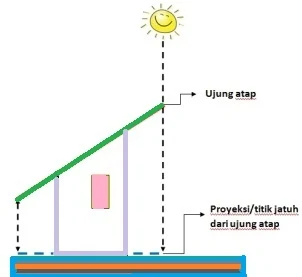
$\color{blue}\textrm{B. 1. 2  Proyeksi Titik}$.

Perhatikanlah ilustrasi berikut

Ilustrasi di atas adalah suasana ketika tengah hari dan posisi matahari tepat di atas sehingga posisi matahari tepat memebentuk sudut $90^{\circ}$ terhadap permukaan bumi, maka bayangan benda akan tepat tegak lurus sebagaimana ilustrasi di atas. 

Ilustrasi di atas adalah sebagai gambaran proyeksi suatu benda pada benda lain. Proyeksi adalah bayangan yang terbentuk dari suatu bangun pada bidang datar dengan arah bayangan dengan bidang datar tersebut sebagai bidang proyeksi membentuk sudut $90^{\circ}$ jika dilukiskan.  

$\color{purple}\textrm{a. Proyeksi titik pada garis}$.

$\color{purple}\textrm{b. Proyeksi titik pada bidang}$.

$\color{purple}\textrm{c. Proyeksi garis pada bidang}$.

$\color{blue}\textrm{B. 1. 3  Alat Bantu Hitung Bangun Ruang}$.

$\color{purple}\textrm{a. Luas bangun datar beraturan}$.

$\begin{array}{|c|l|l|}\hline \textrm{No}&\textrm{Bangun Datar}&\qquad\qquad\textrm{Luas}\\\hline 1&\textrm{Segitiga}&\begin{aligned}&\displaystyle \frac{\textrm{alas}\times \textrm{tinggi}}{2}\\ &\color{red}\textrm{atau}\\ &\sqrt{s(s-a)(s-b)(s-c)}\\ &\textrm{dengan}\\ &s\: \: \textrm{adalah keliling segitiga}\\ &\color{yellow}\textrm{atau}\\ &s=a+b+c\\ &\color{purple}\textrm{atau}\\ &\left [ ABC \right ]=\displaystyle \frac{1}{2}ab\sin \angle C\\ &\left [ ABC \right ]=\displaystyle \frac{1}{2}ac\sin \angle B\\ &\left [ ABC \right ]=\displaystyle \frac{1}{2}bc\sin \angle A\\ &\color{purple}\textrm{dengan}\\ &\left [ ABC \right ]=\textrm{luas segitiga ABC} \end{aligned}\\\hline 2&\textrm{Persegi}&\begin{aligned}&\textrm{sisi}\times \textrm{sisi}\\ &\color{red}\textrm{atau}\\ &\displaystyle \frac{\textrm{diagonal 1}\times \textrm{diagonal 2}}{2} \end{aligned}\\\hline 3&\textrm{Persegi panjang}&\textrm{panjang}\times \textrm{lebar}\\\hline 4&\textrm{Belah ketupat}&\displaystyle \frac{\textrm{diagonal 1}\times \textrm{diagonal 2}}{2}\\\hline 5&\textrm{Layang-Layang}&\displaystyle \frac{\textrm{diagonal 1}\times \textrm{diagonal 2}}{2}\\\hline 6&\textrm{Trapesium}&\displaystyle \frac{\textrm{jumlah sisi sejajar}\times \textrm{tinggi}}{2}\\\hline 7&\textrm{Lingkaran}&\begin{aligned}&\pi \times \textrm{jari-jari}^{2}\\ &\color{red}\textrm{atau}\\ &\displaystyle \frac{1}{4}\times \pi \times \textrm{diagonal}^{2} \end{aligned}\\\hline \end{array}$

$\color{purple}\textrm{b. Dalil Pythagoras untuk segitiga siku-siku}$.

$\begin{array}{c|c}\\ \begin{aligned}&\textrm{Dalil/rumus Pythagoras}\\ &a^{2}+b^{2} =c^{2}\\ &\color{red}\textrm{atau}\\ &c=\sqrt{a^{2}+b^{2}} \end{aligned}&\begin{aligned}&\sin \angle ACB=\displaystyle \frac{a}{c}\\ &\cos \angle ACB=\displaystyle \frac{b}{c}\\ &\tan \angle ACB=\displaystyle \frac{a}{b}=\displaystyle \frac{\sin \angle ACB}{\cos \angle ACB}\\ &\csc \angle ACB=\displaystyle \frac{c}{a}\\ &\sec \angle ACB=\displaystyle \frac{c}{b}\\ &\cot \angle ACB=\displaystyle \frac{b}{a}=\displaystyle \frac{\cos \angle ACB}{\sin \angle ACB} \end{aligned} \end{array}$

$\color{purple}\textrm{c. Identitas trigonometri pada segitiga siku-siku}$.

$\begin{aligned}&\textrm{Dalil/rumus Pythagoras}\\ &a^{2}+b^{2} =c^{2}\\ &\textrm{Perhatikan lagi gambar di poin c di atas}\\ &\begin{array}{|c|l|}\hline 1.&\textrm{Rumus saat dibagi dengan}\: \: c^{2}\\ &\displaystyle \frac{a^{2}}{c^{2}}+\displaystyle \frac{b^{2}}{c^{2}}=\displaystyle \frac{c^{2}}{c^{2}}\Leftrightarrow \color{red}\displaystyle \frac{a^{2}}{c^{2}}+\displaystyle \frac{b^{2}}{c^{2}}=1\\&\\ &\textrm{menjadi}\: \: \: \left ( \displaystyle \frac{a}{c} \right )^{2}+\left ( \displaystyle \frac{b}{c} \right )^{2}=1\\ &\color{blue}\sin ^{2}\angle ACB+\cos ^{2}\angle ACB=1\\\hline 2&\textrm{Rumus saat dibagi dengan}\: \: b^{2}\\ &\displaystyle \frac{a^{2}}{b^{2}}+\displaystyle \frac{b^{2}}{b^{2}}=\displaystyle \frac{c^{2}}{b^{2}}\Leftrightarrow \color{red}\displaystyle \frac{a^{2}}{b^{2}}+1=\displaystyle \frac{c^{2}}{b^{2}}\\&\\ &\textrm{menjadi}\: \: \: \left ( \displaystyle \frac{a}{b} \right )^{2}+1=\left ( \displaystyle \frac{c}{b} \right )^{2}\\ &\color{blue}\tan ^{2}\angle ACB+1=\sec ^{2}\angle ACB\\\hline 3&\textrm{Rumus saat dibagi dengan}\: \: a^{2}\\ &\displaystyle \frac{a^{2}}{a^{2}}+\displaystyle \frac{b^{2}}{a^{2}}=\displaystyle \frac{c^{2}}{a^{2}}\Leftrightarrow \color{red}1+\displaystyle \frac{b^{2}}{a^{2}}=\displaystyle \frac{c^{2}}{a^{2}}\\&\\ &\textrm{menjadi}\: \: \: 1+\left ( \displaystyle \frac{b}{a} \right )^{2}=\left ( \displaystyle \frac{c}{a} \right )^{2}\\ &\color{blue}1+\cot ^{2}\angle ACB=\csc ^{2}\angle ACB\\\hline \end{array} \end{aligned}$

$\color{purple}\textrm{d. Tabel trigonometri nilai sudut istimewa}$.

$\begin{array}{|c|c|c|c|c|c|c|}\hline \alpha &0^{\circ}&30&45^{\circ}&60^{\circ}&90^{\circ}&180^{\circ}\\\hline \sin \alpha &0&\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}\sqrt{2}&\displaystyle \frac{1}{2}\sqrt{3}&1&0\\\hline \cos \alpha &1&\displaystyle \frac{1}{2}\sqrt{3}&\displaystyle \frac{1}{2}\sqrt{2}&\displaystyle \frac{1}{2}&0&-1\\\hline \tan \alpha &0&\displaystyle \frac{1}{3}\sqrt{3}&1&\sqrt{3}&\color{red}\textrm{TD}&0\\\hline \end{array}$.

$\color{purple}\textrm{e. Aturan sinus pada segitiga sebarang}$.

$\displaystyle \frac{BC}{\sin \angle A}=\displaystyle \frac{AC}{\sin \angle B}=\displaystyle \frac{AB}{\sin \angle C}$

$\color{purple}\textrm{f. Aturan cosinus pada segitiga sebarang}$.

Perhatikanlah gmabar pada poin e di atas, aturan cosinusnya adalah:

$\begin{aligned}\bullet \: \: &\cos \angle A=\displaystyle \frac{b^{2}+c^{2}-a^{2}}{2bc}\\ \bullet \: \: &\cos \angle B=\displaystyle \frac{a^{2}+c^{2}-a^{2}}{2ac}\\ \bullet \: \: &\cos \angle C=\displaystyle \frac{a^{2}+b^{2}-a^{2}}{2ab} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

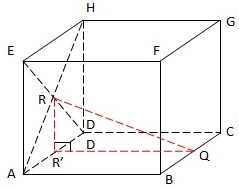
$\begin{array}{ll}\\ 1.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk 8 cm}.\\ &\textrm{Jika titik P, Q dan R berturut-turut terletak pada}\\ &\textrm{pertengahan garis AB, BC, dan bidang ADHE,}\\ &\textrm{tentukanlah jarak antara}\\ &\textrm{a}.\quad \textrm{titik P ke titik R}\\ &\textrm{b}.\quad\textrm{titik Q ke titik R}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar kubus berikut} \end{array}$.

$.\qquad\begin{aligned}\textrm{a}.\: \: \: \textrm{PR}&=...(\textrm{gunakan rumus Pythagoras}\\ &\textrm{pada segitiga PAR, yaitu}:)\\ \textrm{PR}^{2}&=\textrm{PA}^{2}+\textrm{AR}^{2}\\ &\bullet \: \: \textrm{dengan PA}=\displaystyle \frac{1}{2}sisi=\frac{1}{2}.8=4\: cm\\ &\bullet \: \: \textrm{AR}=\displaystyle \frac{1}{2}.\textrm{diagonal sisi kubus}=\frac{1}{2}\left ( 8\sqrt{2} \right )=4\sqrt{2}\\ \textrm{seh}&\textrm{ingga panjang PR dapat dihitung, yaitu:}\\ \textrm{PR}^{2}&=\textrm{PA}^{2}+\textrm{AR}^{2}\\ \textrm{PR}&=\sqrt{\textrm{PA}^{2}+\textrm{AR}^{2}}\\ &=\sqrt{4^{2}+\left ( 4\sqrt{2} \right )^{2}}=\sqrt{16+16.2}=\sqrt{48}=\sqrt{16.3}\\ &=4\sqrt{3}\, \: cm\\ \textrm{b}\: \: \: \textrm{QR}&=.....\\ &\textrm{perhatikanlah gambar berikut} \end{aligned}$.

$.\: \: \: \qquad\begin{aligned}\textrm{QR}&=...(\textrm{gunakan rumus Pythagoras}\\ &\textrm{pada segitiga qR'R, yaitu}:)\\ \textrm{QR}^{2}&=\textrm{(QR')}^{2}+\textrm{(R'R)}^{2}\\ &\bullet \: \: \textrm{dengan QR'}=sisi\: \: kubus=8\: cm\\ &\bullet \: \: \textrm{R'R}=\displaystyle \frac{1}{2}.\textrm{sisi kubus}=\frac{1}{2}\left ( 8 \right )=4\: cm\\ \textrm{seh}&\textrm{ingga panjang QR dapat dihitung, yaitu:}\\ \textrm{QR}^{2}&=\textrm{(QR')}^{2}+\textrm{(R'R)}^{2}\\ \textrm{QR}&=\sqrt{\textrm{(QR')}^{2}+\textrm{(R'R)}^{2}}\\ &=\sqrt{8^{2}+\left ( 4 \right )^{2}}=\sqrt{64+16}=\sqrt{80}=\sqrt{16.5}\\ &=4\sqrt{5}\, \: cm\\ \end{aligned}$.

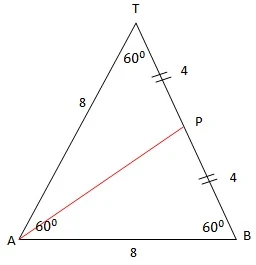
$\begin{array}{ll}\\ 2.&\textrm{Diketahui limas beraturan T.ABCD dengan }.\\ &\textrm{panjang semua rusuknya adalah sama yaitu }\\ &\textrm{8 cm. Jika titik P terletak pada pada rusuk }\\ &\textrm{tegak TB, tentukanlah jarak titik A ke titik P}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar kubus berikut} \end{array}$.

Kita gambarkan posisi titik P yang berada di rusuk tegak TB, yaitu

Selanjutnya gambar kita partisi lagi supaya kita lebih fokus menjadi

Tampak bahwa dengan memandang sebuah segitiga ABP dalam segitiga besar ABT kita akan dengan mudah menentukan jarak titik A ke titik P dengan aturan cosinus.

Perhatikanlah gambar berikut

$\begin{aligned}\color{blue}\textrm{Aturan}&\: \: \color{blue}\textrm{Cosinus}:\\ \cos \angle B&=\displaystyle \frac{AB^{2}+BP^{2}-AP^{2}}{2.AB.AP}\\ \cos 60^{\circ}&=\displaystyle \frac{8^{2}+4^{2}-x^{2}}{2.8.4}\\ \displaystyle \frac{1}{2}&=\displaystyle \frac{64+16-x^{2}}{64}\\ 32&=80-x^{2}\\ x^{2}&=80-32\\ x&=\sqrt{80-32}=\sqrt{48}=\sqrt{16.3}\\ &=4\sqrt{3}\: \: cm \end{aligned}$.

Jadi, jarak titik A ke titik P adalah sebesar  $4\sqrt{3}$   cm.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui kubus ABCD.EFGH dengan rusuk}\: a\: cm.\\ &\textrm{Jika titik P merupakan proyeksi titik C pada}\\ &\textrm{bidang AFH, tentukanlah jarak dari titik A }\\ &\textrm{ke titik S}\\\\ &\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar kubus berikut} \end{array}$.

$.\qquad\begin{aligned}\textrm{Diket}&\textrm{hui bahwa}:\\ \textrm{proye}&\textrm{ksi titik C pada bidang AFH adalah S}\\ \textrm{Ketik}&\textrm{a dilukiskan tampak sebagaimana ilustrasi}\\ \textrm{gamb}&\textrm{ar di atas. Dan diketahui pula, masih terkait}\\ \textrm{pemb}&\textrm{ahasan materi ini beberapa komponen ruas}\\ \textrm{garis}\: &\textrm{telah diketahui panjangnya, yaitu}:\\ \bullet \: \, AP&=PC=\displaystyle \frac{1}{2}a\sqrt{6}\: \: cm\\ \bullet \: \, AC&=a\sqrt{2}\: \: cm\\ \bullet \: \, PQ&=a\: \: cm\\ \bullet \: \, CS&=\: ...\: \: cm\quad (\textrm{belum diketahui, demikian pula})\\ \bullet \: \, AS&=\: ...\: \: cm\quad (\textrm{juga belum diketahui}) \end{aligned}$.

$.\qquad\begin{aligned}\textrm{Pandang}&\textrm{lah}\: \: \bigtriangleup APC\\ \textrm{dengan}\: \: \: &\textrm{menghitung luas}\: \: \bigtriangleup APC,\: \textrm{kita akan}\\ \textrm{menentu}&\textrm{kan jarak titik C ke S, yaitu}:\\ \left [ APC \right ]&=\left [ APC \right ]\\ \displaystyle \frac{alas\times t}{2}&=\displaystyle \frac{alas\times t}{2}\Leftrightarrow \color{red}alas\times t=alas\times t\\ \textrm{misalka}&\textrm{n}\: \: \color{blue}t_{CS}\: \: \color{black}\textrm{adalah jarak titik C ke S}\\ alas_{AP}\times &\color{blue}t_{CS}\color{black}=alas_{AC}\times t_{PQ}\\ \color{blue}t_{CS}&\color{black}=\displaystyle \frac{alas_{AC}\times t_{PQ}}{alas_{AP}}\\ \color{blue}t_{CS}&\color{black}=\displaystyle \frac{AC\times PQ}{AP}\\ &=\displaystyle \frac{a\sqrt{2}\times a}{\displaystyle \frac{1}{2}a\sqrt{6}}=\frac{2a}{\sqrt{3}}\\ &=\displaystyle \frac{2a}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{2a}{3}\sqrt{3}\: \: cm\\ \textrm{Jelas jug}&\textrm{a bahwa}:\: \textrm{AP}\perp \textrm{CS},\: \textrm{maka}\: \: \bigtriangleup ASC\\ \textrm{siku-siku}&\: \textrm{karena semua ini efek proyeksi, akibatnya}\\ \textrm{berlaku}\: \: &\textrm{rumus Pythagoras, yaitu}:\\ \color{blue}AC^{2}&\color{black}=AS^{2}+SC^{2}\\ \color{black}AS^{2}&=\color{blue}AC^{2}\color{black}-SC^{2}\\ \color{black}AS&=\sqrt{\color{blue}AC^{2}\color{black}-SC^{2}}\\ &=\sqrt{\left ( a\sqrt{2} \right )^{2}-\left ( \displaystyle \frac{2a}{\sqrt{3}} \right )^{2}}\\ &=\sqrt{2a^{2}-\displaystyle \frac{4a^{2}}{3}}\\ &=\sqrt{\displaystyle \frac{6a^{2}-4a^{2}}{3}}=\sqrt{\displaystyle \frac{2a^{2}}{3}}\\ &=\sqrt{\displaystyle \frac{2a^{2}}{3}\times \frac{3}{3}}=\frac{a}{3}\sqrt{6}\: \: cm \end{aligned}$

DAFTAR PUSTAKA

1. Sharma, S.N., dkk. 2017. Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta: YUDHISTIRA.
2. Thohir, Ahmad. 2020. Geometri Ruang. http:https://ahmadthohir1089.wordpress.com/2020/07/25/geometri-ruang-xii-matematika-wajib/