Lanjutan : Fungsi Eksponensial

1. Pengertian Fungsi Eksponen

Sebuah fungsi adalah relasi khusus dengan aturan tertentu. Fungsi adalah sebuah pemetaan yang memetakan setiap anggota domoain dengan tepat satu anggota kodomain. Jika suatu himpunan A sebagai domain yang setiap anggota himpunannya dipetakan ke tepat satu anggota himpunan B sebagai kodomain selanjutnya disebut fungsi dari himpunan A ke B atau  $f:A\rightarrow B$.

Perhatikanlah gambar berikut

Pada gambar di atas terlihat jelas bahwa setiap bilangan riil  $x$ dipetakan dengan tepat ke bilangan riil  $y$. Sehingga fungsi $f$  memtakan  $x\in A$  ke  $y$  atau  $f:x\rightarrow y$ dan aturan dari fungsi  $f$ ini sendiri ini biasanya sering dituliskan dalam notasi  $y=f(x)$. Selanjutnya untuk ilustrasi fungsi eksponensial adalah sebagai berikut:

Tampak jelas bahwa  $y\in B$  adalah  $y=f(x)=k.a^{x}$,  dengan  $k$ konstanta,  $x$ sebagai variabel bebas, serta  $a$ adalah bilangan basis atau bilangan pokok, dengan  $a>0$  dan   $a\neq 1$.

2. Garfik Fungsi Eksponen

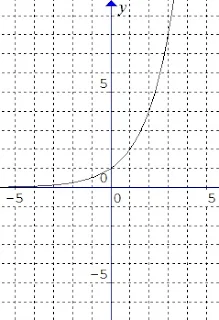
a. Grafik fungsi eksponen  $y=f(x)=k.a^{x}$, dengan  $a>1$  dan   $x\in \mathbb{R}$.

Perhatikan ilustrasi berikut

a. Grafik fungsi eksponen  $y=f(x)=k.a^{x}$, dengan  $0<a<1$,  $a\in \mathbb{Q}$  dan   $x\in \mathbb{R}$.

Ilustrasi lain dari garfik fungsi eksponen adalah sebagai berikut

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Lengkapilah tabel berikut}\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline \color{blue}\textrm{fungsi}&-3&-2&-1&\: 0\: &\: 1\: &\: 2\: &\: 3\: &\: 4\: \\\hline f(x)=2^{x}&&&&&&&&\\\hline f(x)=2^{-x}&&&&&&&&\\\hline f(x)=3^{x}&&&&&&&&\\\hline f(x)=3^{-x}&&&&&&&&\\\hline \end{array}\\\\ &\textbf{Jawab}\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline \color{blue}\textrm{fungsi}&-3&-2&-1&0 &1&2&3&4\\\hline f(x)=2^{x}&\displaystyle \frac{1}{8}&\displaystyle \frac{1}{4}&\displaystyle \frac{1}{2}&1&2&4&8&16\\\hline f(x)=2^{-x}&8&4&2&1&\displaystyle \frac{1}{2}&\displaystyle \frac{1}{4}&\displaystyle \frac{1}{8}&\displaystyle \frac{1}{16}\\\hline f(x)=3^{x}&\displaystyle \frac{1}{27}&\displaystyle \frac{1}{9}&\displaystyle \frac{1}{3}&1&3&9&27&81\\\hline f(x)=3^{-x}&27&9&3&1&\displaystyle \frac{1}{3}&\displaystyle \frac{1}{9}&\displaystyle \frac{1}{27}&\displaystyle \frac{1}{81}\\\hline \end{array} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Gambarlah grafik fungsi eksponen berikut}\\ &\textrm{a}.\quad f(x)=3^{x+1}\\ &\textrm{b}.\quad f(x)=3^{x}+1\\\\ &\textbf{Jawab}\\ &\textrm{a. Untuk fungsi}\: \: f(x)=3^{x+1}\: \: \textrm{sebagai berikut}:\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \color{blue}\textrm{fungsi/titik}&-\infty &\cdots &-3&-2&-1&0 &1&2&3&\cdots &\infty \\\hline f(x)=3^{x}&0&\cdots &\displaystyle \frac{1}{27}&\displaystyle \frac{1}{9}&\displaystyle \frac{1}{3}&1&3&9&27&\cdots &\textrm{TD}\\\hline f(x)=3^{x+1}&0&\cdots &\displaystyle \frac{1}{9}&\displaystyle \frac{1}{3}&1&3&9&27&81&\cdots &\textrm{TD}\\\hline \left ( x,f(x) \right )&(-\infty ,0)&\cdots &\left (-3,\displaystyle \frac{1}{9} \right )&\left (-2,\displaystyle \frac{1}{3} \right )&(-1,1)&(0,3)&(1,9)&(2,27)&(3,81)&\cdots &\\\hline \end{array}\\ &\textrm{b. Dan untuk fungsi}\: \: f(x)=3^{x}+1\: \: \textrm{sebagai berikut}:\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \color{blue}\textrm{fungsi/titik}&-\infty &\cdots &-3&-2&-1&0 &1&2&3&\cdots &\infty \\\hline f(x)=3^{x}&0&\cdots &\displaystyle \frac{1}{27}&\displaystyle \frac{1}{9}&\displaystyle \frac{1}{3}&1&3&9&27&\cdots &\textrm{TD}\\\hline f(x)=3^{x}+1&1&\cdots &1\displaystyle \frac{1}{27}&1\displaystyle \frac{1}{9}&1\displaystyle \frac{1}{3}&2&4&10&28&\cdots &\textrm{TD}\\\hline \left (x,f(x) \right )&\left (-\infty ,1 \right )&\cdots &\left (-3,1\displaystyle \frac{1}{27} \right )&\left (-2,1\displaystyle \frac{1}{9} \right )&\left (-1,1\displaystyle \frac{1}{3} \right )&(0,2)&(1,4)&(2,10)&(3,28)&\cdots &\\\hline \end{array} \end{array}$

.