PAS MATEMATIKA BLOG

Contoh Soal 1 Materi Integral Tentu Fungsi Aljabar

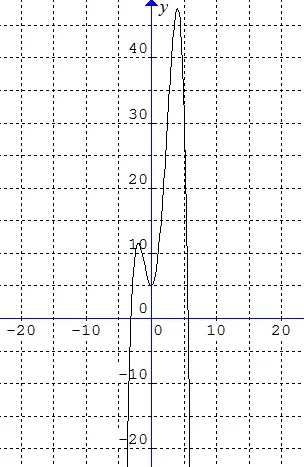
$\begin{array}{ll}\\ 1.&\textbf{(UAN 2014)}\\ &\textrm{Hasil}\: \: \displaystyle \int_{-1}^{2}\left ( x^{3}+3x^{2}+4x+5 \right )\: dx=\: ....\\ &\begin{array}{lll} \textrm{a}.&33\displaystyle \frac{1}{4}\\ \textrm{b}.&\color{red}33\displaystyle \frac{3}{4}\\ \textrm{c}.&32\displaystyle \frac{1}{4}\\ \textrm{d}.&31\displaystyle \frac{3}{4}\\ \textrm{e}.&23\displaystyle \frac{3}{4} \end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\int_{-1}^{2}\left ( x^{3}+3x^{2}+4x+5 \right )\: dx\\ &=\displaystyle \frac{x^{4}}{4}+x^{3}+2x^{2}+5x\: |_{-1}^{2}\\ &=\left (\displaystyle \frac{2^{4}}{4}+2^{3}+2.2^{2}+5.2 \right )\\ &\quad -\left ( \frac{\left ( -1 \right )^{4}}{4}+\left ( -1 \right )^{3}+2.\left ( -1 \right )^{2}+5\left ( -1 \right ) \right )\\ &=\color{red}33\frac{3}{4} \end{aligned} \end{array}$.

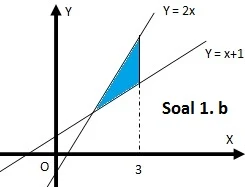
$\begin{array}{ll}\\ 2.&\textbf{(UAN 2003)}\\ &\textrm{Jika}\: f(x)=\left ( x-2 \right )^{2}-4\: \: \textrm{dan}\: \: g(x)=-f(x),\\ &\textrm{maka luas daerah yang di batasi kurva }\\ &f\: \: \textrm{dan}\: \: g\: \: \textrm{adalah}\: ....\\ &\begin{array}{lll} \textrm{a}.&10\displaystyle \frac{2}{3}\: \: \textrm{satuan luas}\\ \textrm{b}.&\color{red}21\displaystyle \frac{1}{3}\: \: \textrm{satuan luas}\\ \textrm{c}.&22\displaystyle \frac{2}{3}\: \: \textrm{satuan luas}\\ \textrm{d}.&42\displaystyle \frac{2}{3}\: \: \textrm{satuan luas}\\ \textrm{e}.&45\displaystyle \frac{1}{3}\: \: \textrm{satuan luas} \end{array}\\\\ &\textbf{Jawab}:\\ & \end{array}$.

$.\qquad\begin{aligned}&\color{blue}\textrm{Alternatif 1}\\ &\begin{aligned}&\displaystyle \int_{0}^{4}\left ( g(x)-f(x) \right )\: \: dx\\ &=\displaystyle \int_{0}^{4}\left ( 4x-x^{2} \right )-\left ( x^{2}-4x \right )\: \: dx\\ &=\displaystyle \int_{0}^{4}\left ( 8x-2x^{2} \right )\: \: dx\\ &=\displaystyle \left [4x^{2}-\frac{2}{3}x^{3} \right ]_{0}^{4}\\ &=\displaystyle \left ( 4.4^{2}-\frac{2}{3}.4^{3} \right )-\left ( 4.0^{2}-\frac{2}{3}.0^{3} \right )\\ &=\displaystyle \left ( 64-\frac{2}{3}.64 \right )-0\\ &=\displaystyle \frac{64}{3}=\color{red}21\frac{1}{3}\: \: \color{black}\textrm{satuan luas} \end{aligned}\\ &\color{blue}\textrm{Alternatif 2}\\ &\textrm{Dengan menggunakan rumus}\: \: L=\displaystyle \frac{D\sqrt{D}}{6a^{2}}\\ &\begin{array}{|l|}\hline \begin{aligned}&f(x)=g(x)\\ &f(x)=-f(x),\quad\textrm{ingat}\: \: g(x)= -f(x)\\ &2f(x)=0,\quad\color{blue}\textrm{tidak boleh disederhanakan},\\ &2\times \left (\left ( x-2 \right )^{2}-4 \right )=0,\quad \color{blue}\textrm{karena akan }\\ &2\times \left ( x^{2}-4x \right )=0\quad \color{blue}\textrm{mempengaruhi hasil }\\ &2x^{2}-8x=0,\qquad\quad \color{blue}\textrm{akhir}\\ &\begin{cases} a=2,\: b=-8 & c=0 \\ D=b^{2}-4ac, & D=\left ( -8 \right )^{2}-4(2)(0)=64 \end{cases}\\ &L_{\: \textbf{daerah}}=\displaystyle \frac{\textbf{D}\sqrt{\textbf{D}}}{6\textbf{a}^{2}}\\ &\quad\qquad=\displaystyle \frac{64\sqrt{64}}{6(2)^{2}}\\ &\quad\qquad=\displaystyle \frac{64\times 8}{6\times 4}\\ &\quad\qquad=\displaystyle \frac{64}{3}\\ &\quad\qquad=\color{red}21\displaystyle \frac{1}{3} \end{aligned}\\\hline\end{array} \end{aligned}$.

$\begin{array}{ll}\\ 3.&\textbf{(UAN 2014)}\\ &\textrm{Luas daerah yang diarsir pada gambar }\\ &\textrm{dapat dinyatakan dengan rumus} \end{array}$.

$.\: \quad\begin{array}{ll}\\ &\begin{array}{lll} \textrm{a}.&\displaystyle \int_{0}^{4}4x\: dx-\int_{2}^{4}\left ( 2x-4 \right )\: dx\\ \textrm{b}.&\displaystyle \int_{0}^{4}4x\: dx - \int_{2}^{4}\left ( 2x+4 \right )\: dx\\ \textrm{c}.&\color{red}\displaystyle \int_{0}^{4}2\sqrt{2}\: dx - \int_{2}^{4}\left ( 2x-4 \right )\: dx\\ \textrm{d}.&\displaystyle \int_{0}^{4}2\sqrt{2}\: dx - \int_{2}^{4}\left ( 4-2x \right )\: dx\\ \textrm{e}.&\displaystyle \int_{0}^{4}2\sqrt{x}\: dx - \int_{2}^{4}\left ( 4+2x \right )\: dx \end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}&\textrm{Luas}_{\color{blue}\textrm{arsiran}}=\displaystyle \int_{0}^{4}y_{1}\: dx-\int_{2}^{4}y_{2}\: dx\\ &=\displaystyle \int_{0}^{4}\sqrt{4x}\: dx-\int_{2}^{4}\left ( 2x-4 \right )\: dx\\ & =\displaystyle \int_{0}^{4}2\sqrt{x}\: dx-\int_{2}^{4}\left ( 2x-4 \right )\: dx. \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 4.&\textbf{(UAN 2014)}\\ &\textrm{Volume benda putar yang terbentuk dari daerah}\\ &\textrm{yang dikuadran I yang dibatasi oleh kurva}\\ &x=2\sqrt{3}y^{2}\: ,\: \textrm{sumbu Y , dan lingkaran}\: x^{2}+y^{2}=1,\\ &\textrm{diputar mengelilingi sumbu Y adalah}\: ....\\ &\begin{array}{lll} \textrm{a}.&\displaystyle \frac{4}{60}\pi \: \: \textrm{satuan volum}\\ \textrm{b}.&\color{red}\displaystyle \frac{17}{60}\pi \: \: \textrm{satuan volum}\\ \textrm{c}.&\displaystyle \frac{23}{60}\pi \: \: \textrm{satuan volum}\\ \textrm{d}.&\displaystyle \frac{44}{60}\pi \: \: \textrm{satuan volum}\\ \textrm{e}.&\displaystyle \frac{112}{60}\pi \: \: \textrm{satuan volum} \end{array}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \end{array}$.

$.\: \quad\begin{aligned}&\textrm{Volumenya jika diputar mengelilingi Sumbu }\\ &\textrm{Y adalah}:\\ & V=\pi \displaystyle \int_{0}^{\frac{1}{2}}x_{1}^{2}\: dy+\pi \int_{\frac{1}{2}}^{1}x_{2}^{2}\: dy\\ &\Leftrightarrow \: \: V=\pi \int_{0}^{\frac{1}{2}}\left ( 2\sqrt{3}y^{2} \right )^{2}\: dy+\pi \int_{\frac{1}{2}}^{1}\left ( 1-y^{2} \right )\: dy\\ &\Leftrightarrow \: \: V=\frac{12}{5}y^{5}\pi |_{0}^{\frac{1}{2}}+\left ( y-\frac{1}{3}y^{3} \right )\pi |_{\frac{1}{2}}^{1}\\ &\Leftrightarrow \: \: V=\pi \left ( \frac{12}{5}\times \frac{1}{32}+\left ( 1-\frac{1}{3} \right )-\left ( \frac{1}{2}-\frac{1}{3}\times \frac{1}{8} \right ) \right )\\ &\Leftrightarrow \: \: V=\color{red}\frac{17}{60}\pi.\end{aligned}$.

$\begin{array}{ll}\\ 5.&\textrm{Jika}\: \displaystyle \frac{d}{dx}g(x)=f(x)\: \: \textrm{di mana} \: f(x)\\ &\textrm{kontinu dari a sampai b, }\\ &\textrm{maka}\: \displaystyle \int_{a}^{b}f(x).g(x)\: dx\\ &\begin{array}{ll}\\ \textrm{a}.\quad 0\\ \textrm{b}.\quad f(b)-f(a)\\ \textrm{c}.\quad g(b)-g(a)\\ \textrm{d}.\quad \displaystyle \frac{\left [ f(b) \right ]^{2}-\left [ f(a) \right ]^{2}}{2}\\ \textrm{e}.\quad \color{red}\displaystyle \frac{\left [ g(b) \right ]^{2}-\left [ g(a) \right ]^{2}}{2}\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int_{a}^{b} f(x).g(x)\: dx\\ &=\displaystyle \int_{a}^{b} g(x).f(x)\: dx\\ &=\displaystyle \int_{a}^{b} g(x).\displaystyle \frac{d\left ( g(x) \right )}{dx}\: dx,\\ &\quad \textrm{ingat bahwa}\quad \displaystyle \frac{d}{dx}g(x)=f(x),\\ &\quad\textrm{f(x) kontinu dari a sampai b}\\ &=\displaystyle \int_{a}^{b} g(x)\: d\left ( g(x) \right )\\ &=\left [\displaystyle \frac{\left ( g(x) \right )^{2}}{2} \right ]_{a}^{b}\\ &=\displaystyle \frac{\left [ g(b) \right ]^{2}-\left [ g(a) \right ]^{2}}{2} \end{aligned} \end{array}$.

Penggunaan Integral Tentu Fungsi Aljabar

A. Luas

Menghitung luas yang dibatasi oleh sebuah kurva dan sumbu X kita dapat menggunakan bantuan integral tentuk sebagaimana uraian sebelumnya

Perhatikan ilustrasi gambar berikut

$\begin{array}{|c|c|}\hline \textrm{Di Atas Sumbu X}&\textrm{Di Bawah Sumbu X}\\\hline &-\displaystyle \int_{a}^{b}f(x)\: \: dx\\ \displaystyle \int_{a}^{b}f(x)\: \: dx&atau\\ &\displaystyle \int_{b}^{a}f(x)\: \: dx\\\hline \end{array}$.

B. Volume Benda Putar

Adapun untuk volume diformulasikan dengan integral tentu berikut

$\boxed{V=\pi \displaystyle \int_{a}^{b}\left ( f(x) \right )^{2}\: \: dx=\pi \displaystyle \int_{a}^{b}y^{2}\: \: dx}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah luas daerah bidang berikut dan }\\ &\textrm{tentukan pula volumenya seandainya bidang }\\ &\textrm{yang diarsir tersebut diputar terhadap sumbu X} \end{array}$.

$.\qquad\begin{aligned}&\begin{aligned}L_{\textrm{Arsiran}}&=\displaystyle \int_{1}^{3}2x\: dx\\ &=\displaystyle \left [ x^{2} \right ]_{1}^{3}\\ &=\left ( 3 \right )^{2}-\left ( 1 \right )^{2}\\ &=9-1\\ &=\color{red}8\quad \color{black}\textbf{satuan luas} \end{aligned}\\&\begin{aligned}V_{\textrm{Benda putar}}&=\pi \displaystyle \int_{1}^{3}\left ( y \right )^{2}\: dx\\ &=\pi \displaystyle \int_{1}^{3}\left ( 2x \right )^{2}\: dx\\ &=\pi \displaystyle \int_{1}^{3}4x^{2}\: dx\\ &=\pi \left [ \displaystyle \frac{4x^{3}}{3} \right ]_{1}^{3}\\ &=\pi \left ( \displaystyle \frac{4\times 3^{3}}{3} \right )-\pi \left ( \displaystyle \frac{4\times 1^{3}}{3} \right )\\ &=36\pi -\displaystyle \frac{4}{3}\pi \\ &=\color{red}34\displaystyle \frac{2}{3}\pi \quad \color{black}\textbf{satuan volum} \end{aligned} \end{aligned}$.

\begin{array}{ll}\\ 2.&\textrm{Diketahui parabola}\: \: f_{1}(x)=a_{1}x^{2}+b_{1}x+c_{1}\\ &\textrm{dan}\: \: f_{2}(x)=a_{2}x^{2}+b_{2}x+c_{2}.\\ &\textrm{Titik potong kedua parabola tersebut }\\ &\textrm{dapat cari dengan}\\ &\\ &f_{1}(x)=f_{2}(x)\\ &\Leftrightarrow \: \: a_{1}x^{2}+b_{1}x+c_{1}=a_{2}x^{2}+b_{2}x+c_{2}\\ & \Leftrightarrow \: ax^{2}+bx+c=0.\\ &\\ &\textrm{Jika kedua parabola berpotongan di dua}\\ &\textrm{titik, tunjukkan bahwa luas daerah antara}\\ &\textrm{kedua parabola tersebut dapat }\\ &\textrm{dinyatakan dengan}\: \: \: \displaystyle \textbf{L}=\frac{\textbf{D}\sqrt{\textbf{D}}}{\textbf{6a}^{\textbf{2}}}\\\\ &\textbf{Bukti}:\\ &ax^{2}+bx+c=0\: \begin{cases} &x_{1}=\displaystyle \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \\ & \\ &x_{2}=\displaystyle \frac{-b- \sqrt{b^{2}-4ac}}{2a} \end{cases}\\ &\begin{aligned}L&=\displaystyle \int_{\frac{-b- \sqrt{b^{2}-4ac}}{2a}}^{\frac{-b+ \sqrt{b^{2}-4ac}}{2a}}\: \left ( ax^{2}+bx+c \right )\: \: dx=\left [ \displaystyle \frac{ax^{3}}{3}+\frac{bx^{2}}{2}+cx \right ]_{\frac{-b- \sqrt{b^{2}-4ac}}{2a}}^{\frac{-b+ \sqrt{b^{2}-4ac}}{2a}}\\ &=\left [ \displaystyle \frac{a}{3}\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right )^{3}+\displaystyle \frac{b}{2}\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right )^{2}+c\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right ) \right ]\\ &\quad -\left [ \displaystyle \frac{a}{3}\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right )^{3}+\displaystyle \frac{b}{2}\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right )^{2}+c\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right ) \right ]\\ &=\displaystyle \frac{a}{24a^{3}}\left [ \left ( \sqrt{D}^{3}-3\sqrt{D}^{2}b+3\sqrt{D}b^{2}-b^{3} \right )+\left ( \sqrt{D}^{3}+3\sqrt{D}^{2}b+3\sqrt{D}b^{2}+b^{3} \right ) \right ]\\ &\quad +\displaystyle \frac{b}{8a^{2}}\left [ \left ( b^{2}-2b\sqrt{D}+\sqrt{D}^{2} \right )-\left ( b^{2}+2b\sqrt{D}+\sqrt{D}^{2} \right ) \right ]+\displaystyle \frac{c}{2a}\left [ \left ( -b+\sqrt{D} \right )-\left ( -b-\sqrt{D} \right ) \right ]\\ &=\displaystyle \frac{1}{24a^{2}}\left [ 2\sqrt{D}^{3}+6\sqrt{D}b^{2} \right ]+\displaystyle \frac{b}{8a^{2}}\left [ -4b\sqrt{D} \right ]+\displaystyle \frac{c}{2a}\left [ 2\sqrt{D} \right ]\\ &=\displaystyle \frac{\sqrt{D}^{3}}{12a^{2}}+\frac{b^{2}\sqrt{D}}{4a^{2}}-\frac{b^{2}\sqrt{D}}{2a^{2}}+\frac{c\sqrt{D}}{a}=\displaystyle \frac{D\sqrt{D}}{12a^{2}}+\frac{b^{2}\sqrt{D}}{4a^{2}}-\frac{b^{2}\sqrt{D}}{2a^{2}}+\frac{c\sqrt{D}}{a}\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}} \left (D+3b^{2}-6b^{2}+12ac \right )\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}}\left [ \left ( b^{2}-4ac \right )-3b^{2}+12ac \right ]\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}}\left [ -2b^{2}+8ac \right ]\\ &=-\displaystyle \frac{\sqrt{D}}{6a^{2}}\left [ b^{2}-4ac \right ]=-\frac{\sqrt{D}}{6a^{2}}\left [ D \right ]\\ &=-\frac{D\sqrt{D}}{6a^{2}},\quad \textbf{luas tidak mungkin negatif}\\ &=\displaystyle \frac{D\sqrt{D}}{6a^{2}}\quad \blacksquare \end{aligned} \end{array}.

$\begin{array}{ll}\\ 3.&\textrm{Tentukan volume benda putar yang terbentuk, }\\ &\textrm{jika suatu daerah yang dibatasi oleh kurva}\\ &y^{2}=x\: \: \textrm{dan}\: \: y=x\: \textrm{diputar mengelilingi sumbu X} \\\end{array}$.

$.\: \quad\begin{aligned}&\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \end{aligned}$.

$.\: \quad\begin{aligned}&\textbf{Menentukan batas}\\ &\begin{array}{|r|l|}\hline \begin{aligned}y&=y\\ x^{2}&=x\\ x^{2}-x&=0\\ x\left ( x-1 \right )&=0\\ x=0\: \: \textrm{atau}\: \: x&=1\\ &\\ &\\ & \end{aligned}&\begin{aligned}V&=\pi \displaystyle \int_{a}^{b}\left ( y_{1}^{2}-y_{2}^{2} \right )\: \: dx\\ &=\pi \displaystyle \int_{0}^{1}\left ( x-x^{2} \right )\: \: dx\\ &=\pi \left [ \displaystyle \frac{1}{2}x^{2}-\frac{1}{3}x^{3} \right ]_{0}^{1}\\ &=\pi \left [ \displaystyle \frac{1}{2}-\frac{1}{3} \right ]\\ V&=\displaystyle \frac{1}{6}\pi \end{aligned} \\\hline \end{array}\\ &\textbf{Keterangan lanjutan}\\ &\begin{aligned}&\textnormal{Perhatikan bahwa;}\\&y^{2}=x\Rightarrow y=\sqrt{x},\: \textrm{dianggap sebagai}\: \: y_{1}\\ &\textnormal{Sehingga}\: y_{1}-\textrm{nya adalah}\: \: \sqrt{x}\\ &\textnormal{dan}\: \: y=x\: \: \textrm{dianggap sebagai}\: \: y_{2}\\ &\left ( y_{1}^{2}-y_{2}^{2} \right )=\left ( \left ( \sqrt{x} \right )^{2}-\left ( x \right )^{2} \right )=x-x^{2}\end{aligned}\\ &\textrm{Jadi, volume dari benda putar tersebut}\\ &\textrm{dalam satuan volum adalah}\: \: \color{red}\displaystyle \frac{1}{6}\pi \end{aligned}$.

$\begin{array}{ll}\\ 4.&\textrm{Tentukan volume benda putar yang terbentuk,}\\ &\textrm{jika suatu daerah yang dibatasi oleh kurva} \\ &y=2x\: ,\: y=x,\: x=1,\: \textrm{dan}\: \: x=3\\ &\textrm{diputar mengelilingi sumbu X}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi gambar berikut} \end{array}$.

$.\: \quad\begin{aligned}&\textrm{Langkah-Langkah penyelesaiannya adalah:}\\ &\begin{array}{|c|c|}\hline \textrm{Batas}&\textrm{Menentukan Volumenya}\\\hline x=1\: \: \textrm{dan}\: \: x=3&\begin{aligned}V&=\displaystyle \pi \int_{a}^{b}\left ( f^{2}(x)-g^{2}(x) \right )\: \: dx\\ &=\displaystyle \pi \int_{1}^{3}\left ( \left ( 2x \right )^{2}-\left ( x \right )^{2} \right )\: \: dx\\ &=\displaystyle \pi \int_{1}^{3}3x^{2}\: \: dx\\ &=\displaystyle \pi \left [ x^{3} \right ]_{1}^{3}\\ &=\displaystyle \pi \left ( 3^{3} \right )-\pi \left ( 1^{3} \right )\\ &=27\pi -1\pi \\ V&=26\pi\: \textbf{Satuan Volum} \end{aligned}\\\hline \end{array} \end{aligned}$.

$\begin{array}{ll}\\ 5.&\textrm{Tentukan volume daerah yang dibatasi}\\ &\textrm{oleh lingkaran}\: \: x^{2}+y^{2}=4\: ,\: \textrm{selang}\\ &-2\leq x\leq 2\: \: \textrm{dan}\: \: \textrm{diputar mengelilingi}\\ &\textrm{sumbu X}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \\\end{array}$.

$.\: \quad\begin{aligned}&\textrm{Langkah-Langkah penyelesaiannya adalah:}\\ &\begin{array}{|c|c|}\hline \textrm{Batas}&\textrm{Menentukan Volumenya}\\\hline x=-2\: \: \textrm{sampai}\: \: x=2&\begin{aligned}V&=\displaystyle \pi \int_{a}^{b}y^{2}\: \: dx\\ &=\displaystyle \pi \int_{-2}^{2}\left ( 4-x^{2} \right )\: \: dx\\ &=\displaystyle \pi \left [ 4x-\displaystyle \frac{x^{3}}{3} \right ]_{-2}^{2} \\ &=\displaystyle \pi \left ( 8-\displaystyle \frac{8}{3} \right )-\pi \left ( -8+\displaystyle \frac{8}{3} \right )\\ &=\displaystyle \pi \left ( 8+8-\frac{8}{3}-\frac{8}{3} \right )\\ V&=\displaystyle \frac{32}{3}\pi\: \: \textbf{Satuan Volum} \end{aligned}\\\hline \end{array} \end{aligned}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah luas daerah yang diarsir berikut} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tunjukkan bahwa luas ellips}\: \: \displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\\ &\textrm{adalah}\: \: \pi ab \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah volume benda putar yang terjadi}\\ &\textrm{jika daerah dari hasil putar tersebut mengelilingi }\\ &\textrm{sumbu X serta dibatasi oleh}\\ &\begin{array}{ll} \textrm{a}.\quad y=x+3,\: \textrm{sumbu x, garis x = 2, dan x = 4}\\ \textrm{b}.\quad \displaystyle y=\frac{1}{2}x+2,\: \textrm{sumbu x, garis x = 0, dan x = 4}\\ \textrm{c}.\quad \displaystyle y=\sqrt{x+2} ,\: \textrm{sumbu x, garis x = 2, dan x = 4}\\ \textrm{d}.\quad y=4-2x,\: \textrm{sumbu x, garis x = 0, dan x = 4}\\ \textrm{e}.\quad \displaystyle x^{2}+y^{2}=16,\: \textrm{dan sumbu X} \end{array} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Tentukanlah volume benda putar yang}\\ &\textrm{terjadi jika daerah dari hasil putar tersebut }\\ &\textrm{mengelilingi sumbu X serta dibatasi oleh}\\ &\begin{array}{ll} \textrm{a}.\quad y=2x-x^{2},\: \textrm{dan}\: \: y=0\\ \textrm{b}.\quad \displaystyle y^{2}=x,\: \textrm{dan}\: \: y=2\\ \textrm{c}.\quad \displaystyle y=x^{2} ,\: \textrm{dan}\: \: y=-x^{2}+4\\ \textrm{d}.\quad y=7-2x^{2},\: \textrm{dan}\: \: y=x^{2}+4\\ \textrm{e}.\quad \displaystyle y=x^{2},\: \textrm{dan}\: \: y^{2}=x \end{array} \end{array}$.

DAFTAR PUSTAKA

Kuntarti, Sulistiyono, Kurnianingsih, S. 2007. Matematika SMA dan MA untuk Kelas XII Semester 1 Program IPA Standar ISI 2006. Jakarta: ESIS.

Inetgral Tentu Fungsi Aljabar

A. Integral Tentu

Sebelumnya sudah dibahasa mengenai integral tak tentu, di mana integral ini memiliki ciri selalu ada nilai konstantanya. Hal ini menunjukkan bahwa ada nilai yang belum terukur dengan jelas. Jika nantinya pada integral sudah ditentukan batas bawah dan batas atasnya, sehingga tidak akan diperlukan lagi nilai konstantanya. Adapun rumus formulasi dari integral tentu adalah sebagai berikut:

$\displaystyle \int_{a}^{b}f(x)\: dx=\left [ F(x) \right ]_{a}^{b}=F(x)|_{a}^{b}=F(b)-F(a)$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{aligned}1.\quad &\int_{1}^{3}\left ( 2x-1 \right )\: dx\\ &=\left [ x^{2}-x \right ]_{1}^{3}\\ &=(9-3)-(1-1)=6\\ 2.\quad &\int_{0}^{5}\left | x-1 \right |+\left | x-2 \right |\: dx\\ &=\frac{1}{2}(x-1)\left | x-1 \right ||_{0}^{5}\: +\frac{1}{2}(x-2)\left | x-2 \right ||_{0}^{5}\\ &=\left ( \frac{1}{2}.4.4+\frac{1}{2}.3.3 \right )-\left ( \frac{1}{2}.-1.1+\frac{1}{2}.-2.2 \right )\\ &=8+4\frac{1}{2}+\frac{1}{2}+2=15 \end{aligned}$.

Anda dapat mengecek jawaban di atas dengan melmperhatikan gambar kemudian menyelesaikannya dengan prinsip segitiga, persegi, dan atau persegipanjang.

B. Sifat-Sifat Integral Tentu

$\begin{aligned}1.\quad&\int_{a}^{b}f(x)\: dx=-\int_{b}^{a}f(x)\: dx\\ 2.\quad&\displaystyle \int_{a}^{b}k.f(x)\: dx=k\int_{a}^{b}f(x)\: dx\\ 3.\quad&\displaystyle \int_{a}^{b}\left ( f(x)\pm g(x) \right )\: dx\\ &=\displaystyle \int_{a}^{b}f(x)\: dx\: \pm\int_{a}^{b}g(x) \: dx\\ 4.\quad &\displaystyle \int_{a}^{b}f(x)\: dx\\ &=\displaystyle \int_{a}^{c}f(x)\: dx+\int_{c}^{b}f(x)\: dx\: ,\: \: dengan\: \: a<c<b\\ 5.\quad &\displaystyle \int_{a}^{a}f(x)\: dx=0 \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Hitunglah hasil dari integral}\: \: \displaystyle \int_{1}^{3}\left ( 2y+1 \right )\: dy\\ \\\\&\textbf{Jawab}:\\ &\begin{aligned}\int_{1}^{3}\left ( 2y+1 \right )\: dy&=y^{2}+y\: |_{1}^{3}\\ &=\left ( 3^{2}+3 \right )-\left ( 1^{2}+1 \right )\\ &=12-2\\ &=10 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Hitunglah hasil dari integral}\: \: \displaystyle \int_{-1}^{1}x^{3}-1\: dx\\\\&\textbf{Jawab}:\\ &\begin{aligned}\int_{-1}^{1}&\left ( x^{3}-1 \right )\: dx\\ &=-(\displaystyle \frac{1}{4}x^{4}-x|_{-1}^{1})\\ &=-\left ( \displaystyle \frac{1}{4}.\left ( 1 \right )^{4}-1 \right )+\left ( \displaystyle \frac{1}{4}.\left ( -1 \right )^{4}-\left ( -1 \right ) \right )\\ &=-\left ( \displaystyle \frac{1}{4}-1 \right )+\left ( \displaystyle \frac{1}{4}+1 \right )\\ &=2 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Hitunglah hasil dari integral}\: \: \displaystyle \int_{-2}^{1}\left ( x+3 \right )^{2}\: dx\\\\&\textbf{Jawab}:\\ &\begin{aligned}\int_{-2}^{1}&\left ( x+3 \right )^{2}\: dx\\ &=\displaystyle \frac{1}{3}x^{2}+3x^{2}+9x|_{-2}^{1}\\ &=\left ( \displaystyle \frac{1}{3}.\left ( 1 \right )^{3}+3.1^{2}+9.1 \right )-\left ( \displaystyle \frac{1}{3}.\left ( -2 \right )^{3}+3.(-2)^{2}+9.(-2) \right )\\ &=\left ( \displaystyle \frac{1}{3}+12\right )-\left ( -\displaystyle \frac{8}{3}+12-18 \right )\\ &=\displaystyle \frac{9}{3}+18=3+18=21 \end{aligned} \end{array}$ .

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ &\textrm{Hitunglah nilai tiap integral berikut ini}\\ &\begin{array}{lllll}\\ 1.&\displaystyle \int_{0}^{3}2x\: dx&10.&\displaystyle \int_{1}^{2}\sqrt{x^{5}}\: dx\\ 2.&\displaystyle \int_{2}^{3}2x^{2}\: dx&11.&\displaystyle \int_{1}^{2}\displaystyle \frac{1}{x^{2}}\: dx\\ 3.&\displaystyle \int_{3}^{7}\displaystyle \frac{1}{2}x^{3}\: dx&12.&\displaystyle \int_{4}^{9}3\sqrt{x}\: dx\\ 4.&\displaystyle \int_{0}^{3}\left ( x^{2}+2x-1 \right )\: dx&\displaystyle \\ 5.&\displaystyle \int_{0}^{3}\left ( x+3 \right )^{2}\: dx&\\ 6.&\displaystyle \displaystyle \int_{-1}^{2}\left ( x+2 \right )\left ( x-1 \right )\: dx&\\ 7.&\displaystyle \int_{1}^{3}\left ( t+t^{2}-3t^{3} \right )\: dt&\\ 8.&\displaystyle \int_{1}^{4}\left ( \displaystyle \frac{x^{4}-x^{3}+\sqrt{x}-1}{x^{2}} \right )\: dx&\\ 9.&\displaystyle \int_{4}^{6}\left ( \sqrt{t}+t^{2}-\sqrt[3]{t^{2}} \right )\: dt \end{array} \end{array}$.

Contoh Soal 4 Materi Integral Tak Tentu Fungsi Aljabar

$\begin{array}{ll}\\ 16.&\textbf{(UN 2015 Matematika IPA)}\\ &\textrm{Hasil}\: \: \displaystyle \int 6x\left ( 1-x^{2} \right )^{4}\: \: dx\: \: \textrm{adalah ....}\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle \frac{3}{5}\left ( 1+x^{2} \right )^{5}+C\\\\ \textrm{b}.\quad \displaystyle \frac{2}{5}\left ( 1+x^{2} \right )^{5}+C\\\\ \textrm{c}.\quad \displaystyle -\frac{1}{5}\left ( 1-x^{2} \right )^{5}+C\\\\ \textrm{d}.\quad -\displaystyle \frac{2}{5}\left ( 1-x^{2} \right )^{5}+C\\\\ \textrm{e}.\quad \color{red}-\displaystyle \frac{3}{5}\left ( 1-x^{2} \right )^{5}+C\end{array}\\\\&\textbf{Jawab}:\\&\color{blue}\textrm{Alternatif 1}\\ &\textrm{Dengan integral substitusi}\\ &\begin{array}{l}\\ \begin{aligned}\displaystyle &\int 6x\left ( 1-x^{2} \right )^{4}\: dx\\ &=\int \left ( 1-x^{2} \right )^{4}.6x\: dx\\ &\begin{cases} u& =1-x^{2} \\ & \\ du& =-2x\: \: \: dx\quad \Rightarrow \quad -3\: dx=6x\: dx \end{cases}\\ &\displaystyle \int u^{4}.\left ( -3\: du \right )\\ &=-3\displaystyle \int u^{4}\: du\\ &=-\displaystyle \frac{3}{5}u^{5}+C\\ &=-\displaystyle \frac{3}{5}\left ( 1-x^{2} \right )^{5}+C \end{aligned} \end{array}\\ &\color{blue}\textrm{Alternatif 2}\\ &\begin{aligned} &\displaystyle \int \left ( 1-x^{2} \right )^{4}\: 6x\: dx\\ &=\int \left ( 1-x^{2} \right )^{2}.(-3).\left ( -2x\: dx \right )\\ &=-3\displaystyle \int \left ( 1-x^{2} \right )^{4}.\: \left ( -2x\: dx \right )\\ &=-3\displaystyle \int \left ( 1-x^{2} \right )^{4}\: .d\left ( 1-x^{2} \right )\\ &=-3\left [ \displaystyle \frac{\left ( 1-x^{2} \right )^{5}}{5} \right ]+C\\ &=-\displaystyle \frac{3}{5}\left ( 1-x^{2} \right )^{5}+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 17.&\begin{aligned}\displaystyle &\int \frac{dx}{2022x+2023}=\: ....\end{aligned}\\ &\begin{array}{ll}\\ \textrm{a}.\quad \ln \left | 2022x+2023 \right |+C\\ &\\ \textrm{b}.\quad \displaystyle \frac{1}{2021}\ln \left | 2022x+2023 \right |+C\\ &\\ \textrm{c}.\quad \color{red}\displaystyle \frac{1}{2022}\ln \left | 2022x+2023 \right |+C\\ &\\ \textrm{d}.\quad \displaystyle \frac{1}{2023}\ln \left | 2022x+2023 \right |+C\\ &\\ \textrm{e}.\quad \displaystyle \frac{2022}{2023}\ln \left | 2022x+2023 \right |+C \end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}&\displaystyle \int \frac{dx}{2022x+2023}\\ &\textrm{Misalkan}\\ &u=2022x+2023\\ &\Leftrightarrow du=2022\: dx\Leftrightarrow \displaystyle \frac{1}{2022}\: du=\: dx\\ &\textrm{Sehingga}\\ &=\displaystyle \int \frac{1}{u}.\left ( \frac{1}{2022}\: du \right )=\displaystyle \frac{1}{2022}\int \frac{1}{u}\: du\\ &=\displaystyle \frac{1}{2022}\ln \left | 2022x+2023 \right |+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 18.&\textrm{Diketahui}\: \: \displaystyle \frac{d}{dx}f(x)=3\sqrt{x}\: \: \textrm{jika} \: f(4)=19,\\ &\textrm{ maka}\: \: f(1)=....\\ &\begin{array}{ll}\\ \textrm{a}.\quad 2\\ \textrm{b}.\quad 3\\ \textrm{c}.\quad 4\\ \textrm{d}.\quad \color{red}5\\ \textrm{e}.\quad 6\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Perlu diingat bahwa}\: \: \displaystyle \frac{d}{dx}f(x)=h(x)\\ &\Leftrightarrow d(f(x))=h(x)\: dx\\ &\Leftrightarrow \displaystyle \int d(f(x))=\displaystyle \int h(x)\: dx\\ &\textrm{Perhatikan kasus di pada soal di atas}\\ &\displaystyle \frac{d}{dx}f(x)=3\sqrt{x}\Leftrightarrow d\left ( f(x) \right )=3\sqrt{x}\: dx\\ &\Leftrightarrow \displaystyle \int d\left ( f(x) \right )=\int 3\sqrt{x}\: dx=\int 3x^{.^{\frac{1}{2}}}\: dx\\&\Leftrightarrow f(x)=2x^{.^{\frac{3}{2}}}+C=2x\sqrt{x}+C \end{aligned}\\&\begin{aligned}&\textrm{Karena diketahui}\\ &f(4)=19,\: \: \textrm{maka}\\ &\Leftrightarrow 2(4)(\sqrt{4})+C=19\\ &\Leftrightarrow 16+C=19\\ &\Leftrightarrow C=3\\ &\textrm{Sehingga}\quad f(x)=2x\sqrt{x}+3\\ &\textrm{maka}\quad f(1)=2.1.\sqrt{1}+3=2+3=5 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 19.&\begin{aligned}\displaystyle &-\int \frac{dx}{x^{2}+3x+2}\: \: dx=\: .... \end{aligned}\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle \ln \left | \displaystyle \frac{x+1}{x+2} \right |+C\\ &\\ \textrm{b}.\quad \color{red}\displaystyle \ln \left | \displaystyle \frac{x+2}{x+1} \right |+C\\ &\\ \textrm{c}.\quad \displaystyle \ln \left | x^{2}+3x+2 \right |+C\\ &\\ \textrm{d}.\quad \arctan 2\left ( \displaystyle x+\frac{3}{2} \right )+C\\ &\\ \textrm{e}.\quad -\displaystyle \arctan 2\left (\displaystyle x+ \frac{3}{2}\right )+C \end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}\displaystyle -\int \frac{dx}{x^{2}+3x+2}&=-\displaystyle \int \frac{1}{\left ( x+1 \right )\left ( x+2 \right )}\: dx\\ &=-\displaystyle \int \left ( \displaystyle \frac{1}{x+1}-\displaystyle \frac{1}{x+2} \right )\: dx\\ &=-\displaystyle \int \frac{1}{x+1}\: dx+\displaystyle \int \frac{1}{x+2}\: dx\\ &=\displaystyle \int \frac{1}{x+2}\: dx-\displaystyle \int \frac{1}{x+1}\: dx\\ &=\displaystyle \ln \left | x+2 \right |-\displaystyle \ln \left | x+1 \right |+C\\ &=\displaystyle \ln \left | \displaystyle \frac{x+2}{x+1} \right |+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 20.&\textrm{Tentukanah integral berikut}?\\ &\textrm{a}.\quad \int dt\\&\textrm{b}.\quad \int 4\: dw\\ &\textrm{c}.\quad \int \left ( x^{3}+5 \right )\: dx\\ &\textrm{d}.\quad \int \left ( x^{\frac{3}{2}}-2\sqrt{x}+1 \right )dx\\ &\textrm{e}.\quad \int \left ( 5x^{\frac{3}{2}}-2x+3x^{-\frac{1}{3}} \right )dx\\\\ &\textbf{Jawab}:\\ &\begin{array}{l}\\ \begin{aligned}\textrm{a}.\quad \int dt=t+c \end{aligned}\\ \begin{aligned}\textrm{b}.\quad \int 4\: dw=4w+C \end{aligned}\\ \begin{aligned}\textrm{c}.\quad \int (x^{3}+5)\: dx&=\displaystyle \frac{1}{3+1}x^{3+1}+5x+C\\ &=\displaystyle \frac{1}{4}x^{4}+5x+C \end{aligned} \end{array}\\ &\begin{aligned}\textrm{d}.\quad &\int (x^{\frac{3}{2}}+2\sqrt{x}+1)\: dx\\ &=\int \left (x^{\frac{3}{2}}+2x^{\frac{1}{2}}+1 \right )\: dx\\ &=\displaystyle \frac{1}{\displaystyle \frac{3}{2}+1}x^{\frac{3}{2}+1}+\frac{2}{\displaystyle \frac{1}{2}+1}x^{\frac{1}{2}+1} +x+C\\ &=\displaystyle \frac{1}{\displaystyle \frac{5}{2}}x^{\frac{5}{2}}+\frac{2}{\displaystyle \frac{3}{2}}x^{\frac{3}{2}}+x+C\\ &=\frac{2}{5}x^{\frac{5}{2}}+\frac{4}{3}x^{\frac{3}{2}}+x+C\\ &\quad \textrm{atau dapat juga kita menyatakan dengan}\\ &=\frac{2}{5}x^{2\frac{1}{2}}+\frac{4}{3}x^{1\frac{1}{2}}+x+C\\ &=\frac{2}{5}x^{2}\sqrt{x}+\frac{4}{3}x\sqrt{x}+x+C \end{aligned} \\ &\begin{aligned}\textrm{e}.\quad &\int \left ( 5x^{\frac{3}{2}}-2x+3x^{-\frac{1}{3}} \right )dx\\ &=.....\\ &\quad \textrm{silahkan dicoba sendiri sebagai latihan}\end{aligned} \end{array}$.

Contoh Soal 3 Materi Integral Tak Tentu Fungsi Aljabar

$\begin{array}{ll}\\ 11.&\displaystyle \int d\left ( 2x \right )=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle x+C\\ \textrm{b}.\quad \color{red}\displaystyle 2x+C\\ \textrm{c}.\quad \displaystyle 3x+C\\ \textrm{d}.\quad \displaystyle 4x+C\\ \textrm{e}.\quad \displaystyle 5x+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int d\left ( 2x \right )=\int 2\: \: dx=2x+C. \end{array}$.

$\begin{array}{ll}\\ 12.&\displaystyle \int 5\: \: d\left ( 2x \right )=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle 5+C\\ \textrm{b}.\quad \displaystyle \frac{5}{2}x+C\\ \textrm{c}.\quad \displaystyle 5x+C\\ \textrm{d}.\quad \color{red}\displaystyle 10x+C\\ \textrm{e}.\quad \displaystyle 25x+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int 5\: \: d\left ( 2x \right )=\int5. 2\: \: dx=\int 10\: dx=10x+C. \end{array}$.

$\begin{array}{ll}\\ 13.&\displaystyle \int 6x\: \: d\left ( 3x \right )=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle 18x^{2}+C\\ \textrm{b}.\quad \color{red}\displaystyle 9x^{2}+C\\ \textrm{c}.\quad \displaystyle 5x^{2}+C\\ \textrm{d}.\quad \displaystyle 3x^{2}+C\\ \textrm{e}.\quad \displaystyle 2x^{2}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int 6x\: \: d\left ( 3x \right )=\int 6x. 3\: \: dx=\int 18x\: dx\\ &=\displaystyle \frac{18x^{2}}{2}+C=9x^{2}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 14.&\displaystyle \int \left ( 8x^{3}-2x \right )\: \: d\left ( -2x \right )=\: ....\\&\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle -16x^{4}+4x^{2}+C\\ \textrm{b}.\quad \displaystyle 16x^{4}-4x^{2}+C\\ \textrm{c}.\quad \displaystyle -4x^{4}-2x^{2}+C\\ \textrm{d}.\quad \color{red}\displaystyle -4x^{4}+2x^{2}+C\\ \textrm{e}.\quad \displaystyle 4x^{4}-2x^{2}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int \left (8x^{3}-2x \right )\: \: d\left ( -2x \right )\\ &=\int \left ( 8x^{3}-2x \right ).\left (-2\: \: dx \right )\\&=\int \left (-16x^{3}+4x \right )\: dx\\ &=\displaystyle -\frac{16x^{4}}{4}+\frac{4x^{2}}{2}+C\\ &=\displaystyle -4x^{4}+2x^{2}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 15.&\displaystyle \int \left ( x+3 \right )\: \: d\left ( 2x+6 \right )=\: ....\\&\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle 4x^{2}+24x+C\\ \textrm{b}.\quad \displaystyle 2x^{2}+12x+C\\ \textrm{c}.\quad \color{red}\displaystyle x^{2}+6x+C\\ \textrm{d}.\quad \displaystyle 4x^{2}+C\\ \textrm{e}.\quad \displaystyle x^{2}+C\end{array}\\\\ &\textrm{Jawab}:\\ &\begin{array}{|c|c|}\hline \color{blue}\textrm{Pertama}&\color{red}\textrm{Kedua}\\\hline \begin{aligned}&\displaystyle \int \left ( x+3 \right )\: d\left ( 2x+6 \right )\\ &=\displaystyle \frac{1}{2}\int \left ( 2x+6 \right )\: d\left ( 2x+6 \right )\\ &=\displaystyle \frac{1}{2}\left [ \frac{1}{2}\left ( 2x+6 \right )^{2} \right ]+C\\ &=\displaystyle \frac{1}{4}\left ( 4x^{2}+24x+36 \right )+C\\ &=\displaystyle \frac{4x^{2}}{4}+\frac{24x}{4}+\frac{36}{4}+C\\ &=x^{2}+6x+\underset{C}{\underbrace{9+C}}\\ &=x^{2}+6x+C \end{aligned}&\begin{aligned}&\displaystyle \int \left ( x+3 \right )\: d\left ( 2x+6 \right )\\ &=\int \left ( x+3 \right ).\left ( 2\: dx \right )\\ &=\int \left ( 2x+6 \right )\: dx\\ &=\displaystyle \frac{2x^{2}}{2}+6x+C\\ &=x^{2}+6x+C\\ &\\ &\\ & \end{aligned}\\\hline \end{array} \end{array}$ .

Contoh Soal 2 Materi Integral Tak Tentu Fungsi Aljabar

$\begin{array}{ll}\\ 6.&\displaystyle \int x^{3}\sqrt{x}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \color{red}\displaystyle \frac{2}{9}x^{4}\sqrt{x}+C\\ \textrm{b}.\quad \displaystyle \frac{9}{2}x^{4}\sqrt{x}+C\\ \textrm{c}.\quad \displaystyle \frac{1}{9}x^{4}\sqrt{x}+C\\ \textrm{d}.\quad \displaystyle 9x^{4}\sqrt{x}+C\\ \textrm{e}.\quad \displaystyle x^{4}\sqrt{x}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int x^{3}\sqrt{x}\: dx=\int x^{3}.x^{\frac{1}{2}}\: dx\\ &=\int x^{3\frac{1}{2}}\: dx=\int x^\frac{7}{2}\: dx=\displaystyle \frac{x^{\frac{7}{2}+1}}{\displaystyle \frac{7}{2}+1}+C\\ &=\displaystyle \frac{x^{\frac{9}{2}}}{\displaystyle \frac{9}{2}}+C=\displaystyle \frac{2}{9}x^{4\frac{1}{2}}+C=\displaystyle \frac{2}{9}x^{4}\sqrt{x}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 7.&\displaystyle \int x\sqrt{x\sqrt[3]{x^{2}}}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle \frac{17}{6}x^{2}\sqrt{x\sqrt[3]{x^{2}}}+C\\ \textrm{b}.\quad \color{red}\displaystyle \frac{6}{17}x^{2}\sqrt{x\sqrt[3]{x^{2}}}+C\\ \textrm{c}.\quad \displaystyle x^{2}\sqrt{x\sqrt[3]{x^{2}}}+C\\ \textrm{d}.\quad \displaystyle \frac{6}{17}x\sqrt{x\sqrt[3]{x^{2}}}+C\\ \textrm{e}.\quad \displaystyle \frac{1}{2}x\sqrt{x\sqrt[3]{x^{2}}}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int x\sqrt{x\sqrt[3]{x^{2}}}\: dx\\&=\displaystyle \int x\left ( x.x^{\frac{2}{3}} \right )^{\frac{1}{2}}\: dx\\ &=\displaystyle \int x^{1+\frac{1}{2}+\frac{2}{6}}\: dx\\ &=\displaystyle \int x^{\frac{11}{6}}\: dx=\displaystyle \frac{x^{\frac{11}{6}+1}}{\displaystyle \frac{11}{6}+1}+C\\ &=\displaystyle \frac{x^{\frac{17}{6}}}{\displaystyle \frac{17}{6}}+C=\displaystyle \frac{6}{17}x^{2}.x^{\frac{5}{6}}+C\\ &=\displaystyle \frac{6}{17}x^{2}\left ( x.x^{\frac{2}{3}} \right )^{\frac{1}{2}}+C\\&=\displaystyle \frac{6}{17}x^{2}\sqrt{x\sqrt[3]{x^{2}}}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 8.&\displaystyle \int x^{2}\sqrt{x^{2}\sqrt[3]{x^{3}}}\: dx=\: ....\\&\begin{array}{ll}\\ \textbf{a}.\quad \displaystyle x^{3}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\\ \textbf{b}.\quad \displaystyle \frac{27}{6}x^{3}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\\ \textbf{c}.\quad \color{red}\displaystyle \frac{6}{27}x^{3}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\\ \textbf{d}.\quad \displaystyle \frac{6}{21}x^{2}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\\ \textbf{e}.\quad \displaystyle \frac{6}{21}x^{3}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}&\displaystyle \int x^{2}\sqrt{x^{2}\sqrt[3]{x^{3}}}\: dx=\int x^{2}\left ( x^{2}.x^{1} \right )^{\frac{1}{2}}\: dx\\ &=\int x^{2+\frac{2}{2}+\frac{1}{2}}\: dx=\int x^{\frac{7}{2}}\: dx=\displaystyle \frac{x^{\frac{7}{2}+1}}{\displaystyle \frac{7}{2}+1}+C\\ &=\displaystyle \frac{x^{\frac{9}{2}}}{\displaystyle \frac{9}{2}}+C\\ &=\displaystyle \frac{2}{9}x^{\frac{9}{2}}+C\\ &=\displaystyle \frac{2.3}{9.3}x^{3}.x^{\frac{3}{2}}+C\\ &=\displaystyle \frac{6}{27}x^{3}\left ( x^{3} \right )^{\frac{1}{2}}+C\\ &=\displaystyle \frac{6}{27}x^{3}\sqrt{x^{2}.x}+C\\ &=\displaystyle \frac{6}{27}x^{3}\sqrt{x^{2}\sqrt[3]{x^{3}}}+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 9.&\displaystyle \int x^{3}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle \frac{1}{4}x^{4}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}+C\\ \textrm{b}.\quad \color{red}\displaystyle \frac{6}{23}x^{4}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}+C\\ \textrm{c}.\quad \displaystyle \frac{23}{6}x^{4}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}+C\\ \textrm{d}.\quad \displaystyle \frac{23}{6}x^{3}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}+C\\ \textrm{e}.\quad \displaystyle \frac{3}{4}x^{3}\sqrt{\displaystyle \frac{1}{x}\sqrt[3]{x^{2}}}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int x^{3}\sqrt{\frac{1}{x}\sqrt[3]{x^{2}}}\: dx=\int x^{3}\left ( x^{-1}.x^{\frac{2}{3}} \right )^{\frac{1}{2}}\: dx\\ &=\int x^{3-\frac{1}{2}+\frac{1}{3}}\: dx=\int x^{\frac{17}{6}}\: dx\\ &=\displaystyle \frac{x^{\frac{17}{6}+1}}{\displaystyle \frac{17}{6}+1}+C=\displaystyle \frac{x^{\frac{23}{6}}}{\displaystyle \frac{23}{6}}+C\\ &=\displaystyle \frac{6}{23}x^{\frac{24-1}{6}}+C\\ &=\displaystyle \frac{6}{23}x^{4}.x^{-\frac{1}{6}}+C\\ &=\displaystyle \frac{6}{23}x^{4}.\left ( x^{-\frac{1}{3}} \right )^{\frac{1}{2}}+C\\ &=\displaystyle \frac{6}{23}x^{4}\sqrt{x^{-1+\frac{2}{3}}}+C\\ &=\displaystyle \frac{6}{23}x^{4}\sqrt{\frac{1}{x}\sqrt[3]{x^{2}}}+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 10.&\displaystyle \int x\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle x^{2}\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\\\\ \textrm{b}.\quad \displaystyle \frac{13}{8}x^{2}\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\\\\ \textrm{c}.\quad \color{red}\displaystyle \frac{8}{13}x^{2}\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\\\\ \textrm{d}.\quad \displaystyle \frac{1}{2}x^{2}\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\\\\ \textrm{e}.\quad \displaystyle \frac{8}{5}x^{2}\sqrt{\displaystyle \frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int x\sqrt{\frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}\: \: dx\\&=\int x\left ( x^{-1}\left ( x\left ( x^{-1} \right )^{\frac{1}{2}} \right )^{\frac{1}{2}} \right )^{\frac{1}{2}} \: dx\\ &=\int x\left ( x^{-\frac{1}{2}}.x^{\frac{1}{4}}.x^{-\frac{1}{8}} \right )\: dx\\ &=\int x^{1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}}\: dx=\int x^{\frac{5}{8}}\: dx\\ &=\displaystyle \frac{x^{\frac{5}{8}+1}}{\displaystyle \frac{5}{8}+1}+C\\ &=\displaystyle \frac{x^{\frac{13}{8}}}{\displaystyle \frac{13}{8}}+C\\ &=\displaystyle \frac{8}{13}x^{\frac{16-3}{8}}+C\\ &=\displaystyle \frac{8}{13}x^{2}.x^{-\frac{3}{8}}+C\\ &=\displaystyle \frac{8}{13}x^{2}\sqrt{x^{-\frac{3}{4}}}+C\\ &=\displaystyle \frac{8}{13}x^{2}\sqrt{x^{-1+\frac{1}{4}}}+C\\ &=\displaystyle \frac{8}{13}x^{2}\sqrt{\frac{1}{x}.\left ( x^{\frac{1}{2}} \right )^{\frac{1}{2}}}+C\\ &=\displaystyle \frac{8}{13}x^{2}\sqrt{\frac{1}{x}\sqrt{x^{1-\frac{1}{2}}}}+C\\ &=\displaystyle \frac{8}{13}x^{2}\sqrt{\frac{1}{x}\sqrt{x\sqrt{\frac{1}{x}}}}+C\end{aligned} \end{array}$

Contoh Soal 1 Materi Integral Tak Tentu Fungsi Aljabar

$\begin{array}{ll}\\ 1.&\displaystyle \int x^{2}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \color{red}\displaystyle \frac{1}{3}x^{3}+C\\ \textrm{b}.\quad \displaystyle \frac{1}{4}x^{6}+C\\ \textrm{c}.\quad \displaystyle \frac{1}{3}x^{6}+C\\ \textrm{d}.\quad \displaystyle \frac{1}{6}x^{3}+C\\ \textrm{e}.\quad \displaystyle \frac{2}{3}x^{3}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int x^{2}\: dx=\displaystyle \frac{x^{2+1}}{2+1}+C= \displaystyle \frac{1}{3}x^{3}+C \end{array}$

$\begin{array}{ll}\\ 2.&\displaystyle \int x^{-2}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle -2x^{-1}+C\\ \textrm{b}.\quad \color{red}\displaystyle -x^{-1}+C\\ \textrm{c}.\quad \displaystyle -\frac{1}{2}x^{-2}+C\\ \textrm{d}.\quad \displaystyle -\frac{1}{3}x^{-3}+C\\ \textrm{e}.\quad \displaystyle -3x^{-3}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int x^{-2}\: dx=\displaystyle \frac{x^{-2+1}}{-2+1}+C= \displaystyle \frac{1}{-1}x^{-1}+C=-x^{-1}+C \end{array}$.

$\begin{array}{ll}\\ 3.&\displaystyle \int x^{.^{\frac{1}{3}}}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \color{red}\displaystyle \frac{3}{4}x^{\frac{4}{3}}+C\\ \textrm{b}.\quad \displaystyle x^{\frac{4}{3}}+C\\ \textrm{c}.\quad \displaystyle \frac{3}{4}x^{\frac{2}{3}}+C\\ \textrm{d}.\quad \displaystyle x^{-\frac{2}{3}}+C\\ \textrm{e}.\quad \displaystyle \frac{3}{4}x^{-\frac{2}{3}}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int x^{.^{\frac{1}{3}}}\: dx=\displaystyle \frac{x^{\frac{1}{3}+1}}{\displaystyle \frac{1}{3}+1}+C= \displaystyle \frac{1}{\displaystyle \frac{4}{3}}x^{.^{\frac{4}{3}}}+C=\displaystyle \frac{3}{4}x^{.^{\frac{4}{3}}}+C. \end{array}$.

$\begin{array}{ll}\\ 4.&\displaystyle \int \frac{1}{x^{3}}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \color{red}\displaystyle -\frac{1}{2x^{2}}+C\\ \textrm{b}.\quad \displaystyle -\frac{2}{x^{2}}+C\\ \textrm{c}.\quad \displaystyle \frac{1}{3x^{4}}+C\\ \textrm{d}.\quad \displaystyle \frac{3}{x^{4}}+C\\ \textrm{e}.\quad \displaystyle -\frac{1}{4x^{3}}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \int \frac{1}{x^{3}}\: dx=\int x^{-3}\: dx\\ &=\displaystyle \frac{x^{-3+1}}{-3+1}+C=\frac{x^{-2}}{-2}+C=-\frac{1}{2x^{2}}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 5.&\displaystyle \int \frac{1}{3}x^{3}\: dx=\: ....\\ &\begin{array}{ll}\\ \textrm{a}.\quad \displaystyle \frac{1}{3}x^{4}+C\\ \textrm{b}.\quad \displaystyle \frac{1}{4}x^{4}+C\\ \textrm{c}.\quad \displaystyle x^{4}+C\\ \textrm{d}.\quad \color{red}\displaystyle \frac{1}{12}x^{4}+C\\ \textrm{e}.\quad \displaystyle \frac{4}{3}x^{4}+C\end{array}\\\\ &\textbf{Jawab}:\\ &\displaystyle \int \frac{1}{3}x^{3}\: dx=\displaystyle \frac{1}{3}.\frac{x^{3+1}}{3+1}+C= \displaystyle \frac{1}{12}x^{4}+C \end{array}$.

Penggunaan Integral Tak Tentu

Penggunaan integral tak tentu ini dapat digunakan dalam menentukan suatu fungsi jika turunan dari fungsi tersebut diberikan. Selain itu untuk menentukan posisi, kecepatan, percepatan suatu benda pada waktu tertentu.

$\begin{aligned}&\textrm{Misalkan}\\ &\bullet \quad s\: \: \textrm{adalah menunjukkan posisi}\\ &\bullet \quad v\: \: \textrm{adalah menunjukkan kecepatan}\\ &\bullet \quad a\: \: \textrm{adalah menunjukkan percepatan}\\ &\bullet \quad t\: \: \textrm{adalah menunjukkan waktu}\\\\ &\textbf{Perhatikan hubungan berikut}\\ &v=\displaystyle \frac{ds}{dt}\Leftrightarrow ds=v\: dt\\ &\Leftrightarrow \displaystyle \int ds =\int v\: dt\\ &\Leftrightarrow \: \: \quad s=\displaystyle \int v\: dt\\\\ &\textbf{Demikian juga hubungan berikut}\\ &a=\displaystyle \frac{dv}{dt}\Leftrightarrow dv=a\: dt\\ &\Leftrightarrow \displaystyle \int dv =\int a\: dt\\ &\Leftrightarrow \: \: \quad v=\displaystyle \int a\: dt \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukan}\: \: y,\: \textrm{Jika}\: \: \displaystyle \frac{dy}{dx}=2022x\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\\ &\displaystyle \frac{dy}{dx}=2022x\Leftrightarrow dy=2022x\: dx\\ &\Leftrightarrow \displaystyle \int dy=\int 2022x\: dx\\ &\Leftrightarrow y=\displaystyle \frac{2022}{2}x^{2}+C\\ &\Leftrightarrow y=1011x^{2}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui fungsi turunan pertama kurva}\\ &\textrm{adalah}\: \: \displaystyle \frac{dy}{dx}=2x-2\: .\: \textrm{Jika kurva melalui}\\ &\textrm{titik}\: \: (3,2)\: ,\: \textrm{tentukan persamaan dari kurva}\\ &\textrm{tersebut}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}\\ &\displaystyle \frac{dy}{dx}=2x-2\\ &\Leftrightarrow dy=(2x-2)\: dx\\ &\Leftrightarrow \displaystyle \int dy=\int (2x-2)\: dx\\ &\Leftrightarrow \quad y=x^{2}-2x+C\\ &\textrm{Karena kurva melalui}\: \: (3,2),\: \textrm{maka}\\ &(2)=(3)^{2}-2(3)+C\Leftrightarrow 2=3+C\\ &\Leftrightarrow C=-1\\ &\textrm{Jadi},\: y=x^{2}-2x-1\: \: \textrm{atau}\\ &\qquad f(x)=x^{2}-2x-1 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui bahwa}\: \: f''(x)=x^{2}.\: \textrm{Jika}\: \: f'(0)=6\\ &\textrm{dan}\: \: f(0)=3\: ,\: \textrm{tentukanlah}\: \: f(x)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}\\ &\displaystyle f''(x)=x^{2}\\ &\Leftrightarrow \displaystyle \int f''(x)\: dx=\displaystyle \int x^{2}\: dx\\ &\Leftrightarrow \displaystyle f'(x)=\displaystyle \frac{1}{3}x^{3}+C\\ &\textrm{Karena}\: \: f'(x)=6,\: \textrm{maka}\\ &f'(x)=\displaystyle \frac{1}{3}x^{3}+C\Leftrightarrow 6=\displaystyle \frac{1}{3}(0)^{3}+C\\ &\Leftrightarrow C=6\\ &\textrm{Sehingga}\: \: f'(x)=\displaystyle \frac{1}{3}x^{3}+6\\ &\textrm{Selanjutnya}\: \: \displaystyle \int f'(x)\: dx=\displaystyle \int \displaystyle \frac{1}{3}x^{3}+6\: dx\\ &f(x)=\displaystyle \frac{1}{12}x^{4}+6x+C\\ &\textrm{Dan juga karena}\: \: f(0)=3,\: \textrm{maka}\\ &f(0)=\displaystyle \frac{1}{12}(0)^{4}+6(0)+C=3\\ &C=3, \: \textrm{sehingga diperoleh}\\ &f(x)=\displaystyle \frac{1}{12}x^{4}+6x+3\\ &\textrm{Jadi},\: f(x)=\color{red}\displaystyle \frac{1}{12}x^{4}+6x+3 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Diketahui}\: f'\left ( x \right )=6x^{2}-2x+6\: \textrm{dan}\\ & \textrm{nilai}\: \textrm{fungsi}\: f\left ( 2 \right )=-7.\: \textrm{Tentukanlah}\\ &\textrm{rumus}\: \textrm{fungsi}\: \textrm{tersebut}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}f\left ( x \right )&=\int f'\left ( x \right )\: dx\\ &=\int \left ( 6x^{2}-2x+6 \right )\: dx\\ &=2x^{3}-x^{2}+6x+C \end{aligned}\\\\ &\textrm{Karena}\: f\left ( 2 \right )=-7,\: \textrm{maka}\\\\ &\begin{aligned}f\left ( 2 \right )&=2.2^{3}-2^{2}+6.2+C\\ \Leftrightarrow -7&=16-4+12+C\\ \Leftrightarrow C&=-31 \end{aligned}\\\\ &\textrm{Jadi},\: f\left ( x \right )=2x^{3}-x^{2}+6x-31 \end{array}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukan}\: \: f(x),\: \textrm{Jika diketahui}\\ &\textrm{a}.\quad f'(x)=12x^{3}\: \: \textrm{dan}\: \: f(1)=8\\ &\textrm{b}.\quad f'(x)=x^{2}-2x+3\: \: \textrm{dan}\: \: f(3)=9\\ &\textrm{c}.\quad f''(x)=2,\: \: f'(2)=2\: \: \textrm{dan}\: \: f(2)=10\\ &\textrm{d}.\quad f''(x)=x^{2},\: \: f'(0)=6\: \: \textrm{dan}\: \: f(0)=3 \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan persamaan kurva}\: \: f(x)\\ &\textrm{disetiap titik}\: \: (x,y)\: \: \textrm{yang memenuhi}\\ &\textrm{syarat berikut}\\ &\textrm{a}.\quad \displaystyle \frac{dy}{dx}=4x+1\: \: \textrm{dan kurva melalui}\: \: (0,2)\\ &\textrm{b}.\quad \displaystyle \frac{dy}{dx}=\displaystyle \frac{1}{x^{2}}+3\: \: \textrm{dan kurva melalui}\: \: (1,4) \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui}\: \: 2x-y=3\: \: \textrm{merupakan garis}\\ &\textrm{kurva di titik}\: \: (1,-1)\: .\: \textrm{Jika di tiap titik}\\ &\textrm{pada kurva berlaku}\: \: \displaystyle y''=2x^{2}-3x+1\\ &\textrm{tentukan persamaan kurva tersebut} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Diketahui kecepatan sebuah sepeda}\\ &\textrm{diformulasian dengan}\: \: \displaystyle \frac{ds}{dt}=3t^{2}+4t-1\\ &\textrm{Jika}\: \: s\: \: \textrm{menyatakan jarak yang ditempuh}\\ &\textrm{dalam satuan meter}\: ,\: t\: \textrm{menyatakan waktu}\\ &\textrm{dengan}\: \: s=5\: \: \textrm{untuk}\: \: t=2,\: \textrm{tentukanlah}\\ &\textrm{jarak yang ditempuh pengendara dalam}\\ &\textrm{waktu 5 menit} \end{array}$.

Teknik Pengintegralan (Bagian 2)

2. Integral Parsial

2. 1 Integral Parsial

Jika teknik pada no.1 pada pembahasan sebelumnya tidak dapat digunakan, maka kemungkinan adalah dengan menggunakan teknik yang satunya ini, yaitu teknik integral parsial. Adapun untuk teknik integral ini diformulasikan dengan bentuk rumus

$\displaystyle \int u\: dv=uv-\displaystyle \int v\: du$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Perhatian kembali soal berikut}\\ &\displaystyle \int x\sqrt{x-1}\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\color{blue}\textrm{Alternatif 1}\\ &\textrm{Misalkan}\qquad u=x-1\\ &du=1\quad dx\: \Leftrightarrow \: du=dx \end{aligned}\\ &\textrm{Dengan integral substitusi}\\ &\begin{aligned} &\displaystyle \int x\sqrt{x-1}\: dx\\&=\int \left ( x-1+1 \right )\sqrt{x-1}\: dx\\ &=\int \left ( \underset{u}{\underbrace{\left (x-1 \right )}}+1 \right )\sqrt{\underset{u}{\underbrace{x-1}}}\: dx \\ &=\int \left ( u+1 \right )\sqrt{u}\: du\\ &=\int \left (u\sqrt{u}+\sqrt{u}\: \right )\: du\\ &=\int \left (u^{\frac{3}{2}}+u^{\frac{1}{2}} \right )\: du\\ &=\displaystyle \frac{1}{\left ( \frac{3}{2}+1 \right )}u^{\left (\frac{3}{2}+1 \right )}+\displaystyle \frac{1}{\left (\frac{1}{2}+1 \right )}u^{\left (\frac{1}{2}+1 \right )}+C\\ &=\displaystyle \frac{2}{5}\left ( x-1 \right )^{\frac{5}{2}}+\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}+C\\\\ &\color{blue}\textrm{Alternatif 2}\\ &\begin{array}{ll}\\ \displaystyle \int x\sqrt{x-1}\: dx=\int \underset{\displaystyle \underset{u}{\mid }}{x}.\underset{\displaystyle \underset{dv}{\mid }}{\underbrace{\sqrt{x-1}\: dx}}&\\ \begin{matrix} u=x &&& dv=\sqrt{x-1}\: dx\\ du=dx &&& \displaystyle \int dv=\int \sqrt{x-1}\: dx\\ &&&v=\int \left ( x-1 \right )^{\frac{1}{2}}\: dx\\ &&&v=\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}\\ \end{matrix} \end{array}\\ &\textrm{Dengan integral parsial}\\&\begin{aligned}&\displaystyle \int x\sqrt{x-1}\: dx\\ &=\int \underset{\displaystyle \underset{u}{\mid }}{x}.\underset{\displaystyle \underset{dv}{\mid }}{\underbrace{\sqrt{x-1}\: dx}}= u.v-\int v.du\\ &=x.\left ( \displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}} \right )-\int \left ( \displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}} \right )dx\\ &=\displaystyle \frac{2x}{3}\left ( x-1 \right )^{\frac{3}{2}}-\displaystyle \frac{2}{3}\times \frac{2}{5}\left ( x-1 \right )^{\frac{5}{2}}+C\\ &=\displaystyle \frac{2x}{3}\left ( x-1 \right )^{\frac{3}{2}}-\displaystyle \frac{4}{15}\left ( x-1 \right )^{\frac{5}{2}}+C \end{aligned} \\\end{aligned} \end{array}$.

$\begin{aligned}&\textrm{Perhatikan bahwa}\\ &\begin{array}{|c|c|}\hline \textrm{Hasil dengan Substitusi}&\textrm{Hasil dengan Integral Parsial}\\\hline \displaystyle \frac{2}{5}\left ( x-1 \right )^{\frac{5}{2}}+\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}+C&\displaystyle \frac{2x}{3}\left ( x-1 \right )^{\frac{3}{2}}-\displaystyle \frac{4}{15}\left ( x-1 \right )^{\frac{5}{2}}+C\\\hline \end{array}\\ &\textrm{Jika kita sejajarkan dengan ruas }\\ &\textrm{yang berbeda, maka}\\ &\begin{aligned}\displaystyle \frac{2}{5}\left ( x-1 \right )^{\frac{5}{2}}+\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}+C&=\displaystyle \frac{2x}{3}\left ( x-1 \right )^{\frac{3}{2}}-\displaystyle \frac{4}{15}\left ( x-1 \right )^{\frac{5}{2}}+C\\ \displaystyle \frac{2}{5}\left ( x-1 \right )\left ( x-1 \right )^{\frac{3}{2}}+\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}&=\displaystyle \frac{2x}{3}\left ( x-1 \right )^{\frac{3}{2}}-\displaystyle \frac{4}{15}\left ( x-1 \right )\left ( x-1 \right )^{\frac{3}{2}}\\ \left ( \displaystyle \frac{2}{5}\left ( x-1 \right )+\frac{2}{3} \right )\left ( x-1 \right )^{\frac{3}{2}}&=\left ( \displaystyle \frac{2x}{3}-\frac{4}{15}\left ( x-1 \right ) \right )\left ( x-1 \right )^{\frac{3}{2}}\\ \displaystyle \frac{2x}{5}-\frac{2}{5}+\frac{2}{3}&=\displaystyle \frac{2x}{3}-\frac{4x}{15}+\frac{4}{15}\\ \displaystyle \frac{2x}{5}+\frac{4}{15}&=\displaystyle \frac{2x}{5}+\frac{4}{15}\\ \textrm{ruas kiri}\: &=\: \textrm{ruas kanan} \end{aligned} \end{aligned}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah integral dari}\: \: \int (x+2)\: dx\\ &\textrm{dengan cara}\\ &\textrm{a})\quad \textrm{substitusi}\\ &\textrm{b})\quad \textrm{parsial}\\\\&\textbf{Jawab}:\\ &\begin{aligned}&\textbf{Cara substitusi}\\ &\int (x+2)\: dx=........?\\ &\textrm{Misalkan}\: \: m=x+2\\ &\qquad\qquad \, dm=dx\\ &\textrm{maka},\\ &\int (x+2)\: dx=\int \underset{\begin{matrix} |\\ \textbf{m} \end{matrix}}{\underbrace{(x+2)}}.\underset{\begin{matrix} |\\ \textbf{dm} \end{matrix}}{\underbrace{dx}}\\ &=\frac{1}{2}m^{2}+C=\frac{1}{2}(x+2)^{2}+C\\ &=\frac{1}{2}\left ( x^{2}+4x+4 \right )+C=\frac{1}{2}x^{2}+2x+\underset{\begin{matrix} |\\ \textbf{C} \end{matrix}}{\underbrace{2+C}}\\ &=\frac{1}{2}x^{2}+2x+C \end{aligned}\\\\ &\begin{aligned}&\textbf{Cara parsial}\\ &\int (x+2)\: dx=\int \underset{\begin{matrix} |\\ \textbf{u} \end{matrix}}{\underbrace{1}}.\underset{\begin{matrix} |\\ \textbf{dv} \end{matrix}}{\underbrace{(x+2)\: dx}}\\ &\left\{\begin{matrix} u=1\quad \rightarrow \quad du=0\qquad\qquad\qquad\qquad\qquad \\ \\ v=\underset{\begin{matrix} |\\ =\frac{1}{2}x^{2}+2x+C \end{matrix}}{\int dv} \leftarrow dv=(x+2)dx \end{matrix}\right.\\ &=\textbf{u.v}-\int \textbf{v.du}\\ &=1.\left (\frac{1}{2}x^{2}+2x+C \right )-\int \left (\frac{1}{2}x^{2}+2x+C \right ).0\\ &=\frac{1}{2}x^{2}+2x+C \end{aligned} \end{array}$.

2. 2 Aturan Tanzalin

Sumber Referensi

$\begin{aligned}&\textrm{Tentukanlah hasil integral berikut}\\ &\displaystyle \int 2x^{2}(x-4)^{2}dx\\\\ &\textbf{Jawab}:\\ &\textrm{Bentuk}\: \: \displaystyle \int 2x^{2}(x-4)^{2}dx\: \: \textrm{dianggap sebagai}\\ &\color{red}\displaystyle \int u\: dv\: \: \color{black}\textrm{dengan}\: \: \color{red}u\: \: \color{black}\textrm{adalah bagian yang mudah}\\ &\textrm{kita diferensialkan, maka}\: \: u\: \: \textrm{kita pilihkan}\\ &\textrm{yaitu}\: \: u=\color{red}2x^{2}\\ &\textrm{Selanjutnya dengan}\: \: \textbf{aturan Tanzalin}\\ &\textrm{sebagai berikut} \end{aligned}$.

$\begin{array}{|c|c|}\hline \textrm{Diderensialkan}&\textrm{Diintegralkan}\\\hline \begin{aligned}&+\: \color{red}2x^{2}\\ &-\: \color{blue}4x\\ &+\: \color{magenta}4\\ &-\: 0\\ & \end{aligned}&\begin{aligned}&(x-4)^{4}\\ &\color{red}\displaystyle \frac{1}{5}(x-4)^{5}\\ &\color{blue}\displaystyle \frac{1}{30}(x-4)^{6}\\ &\color{magenta}\displaystyle \frac{1}{210}(x-4)^{7} \end{aligned}\\\hline \end{array}$.

Hasil dari integral teknik ini adalah:

$\begin{aligned}&\displaystyle \int 2x^{2}(x-4)^{4}\: dx\\ &=(+2x^{2})\left ( \displaystyle \frac{1}{5}(x-4)^{5} \right )+(-4x)\left ( \displaystyle \frac{1}{30}\left ( x-4 \right )^{6} \right )\\ &\quad +(+4)\left ( \displaystyle \frac{1}{210}(x-4)^{7} \right )+C\\ &=\displaystyle \frac{2}{5}x^{2}(x-4)^{5}-\displaystyle \frac{2}{15}x(x-4)^{6}+\displaystyle \frac{2}{105}(x-4)^{7}+C \end{aligned}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{aligned}&\textrm{1. Selesaikan soal berikut ini}\\ &\begin{array}{llllll}\\ &\textrm{a}.&\displaystyle \int \displaystyle x^{2}\sqrt{x+7}\: \: dx&\textrm{d}.&\displaystyle \int -(2x^{2}+1)\sqrt{3-x}\: \: dx\\ &\textrm{b}.&\displaystyle \int 2x^{2}\sqrt{3-x}\: \: dx&\textrm{e}.&\displaystyle \int x^{5}(2x+1)^{6}\: dx\\ &\textrm{c}.&\displaystyle \int 3x^{2}\sqrt{2x+1}\: dx&\textrm{f}.&\displaystyle \int \displaystyle \frac{2x^{6}}{\sqrt[3]{3x-1}}\: \: dx \end{array} \end{aligned}$ .

$\begin{aligned}&\textrm{2. Selesaikan soal berikut dengan Metode Tanzalin}\\ &\begin{array}{llllll}\\ &\textrm{a}.&\displaystyle \int -(2x^{2}+1)\sqrt{3-x}\: \: dx\\ &\textrm{b}.&\displaystyle \int x^{5}(2x+1)^{6}\: dx\\ &\textrm{c}.&\displaystyle \int \displaystyle \frac{2x^{6}}{\sqrt[3]{3x-1}}\: \: dx\\ &\textrm{d}.&\displaystyle \int \displaystyle 3(x-2)^{4}.\sqrt[3]{x}\: \: dx\\ &\textrm{e}.&\displaystyle \int \displaystyle \frac{(x^{4}-3)}{\sqrt{1-x}}\: \: dx\\ &\textrm{f}.&\displaystyle \int \displaystyle x^{3}\sqrt{1-2x}\: \: dx \end{array} \end{aligned}$.

DAFTAR PUSTAKA

Kuntarti, Sulistiyono dan Kurnianingsih, S. 2007. Matematika SMA dan MA untuk Kelas XII Semester 1 Probram IPA Standar ISI 2006. Jakarta: ESIS
Sharma, S.N., dkk. 2017. Jelajah Matematika SMA Kelas XI Program Wajib. Jakarta: YUDHISTIRA.
Tung, K.Y. 2012. Pintar Matematika SMA Kelas XII IPA untuk Olimpiade dan Pengayaan Pelajaran. Yogyakarta: ANDI.

Teknik Pengintegralan (Bagian 1)

1. Integral Substitusi

Ada beberapa bentuk integral yang terkadang pengintegralannya membutuhkan teknik tertentu. Di antara bentuk tertentu itu adalah dengan substitusi, yaitu:

$\displaystyle \int u^{n}.u'\: dx=\displaystyle \int u^{n}\: du=\displaystyle \frac{1}{n+1}u^{n+1}+C$ .

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \left ( x^{2}+3 \right )^{20}2x\: dx\\\\ &\textbf{Jawab}:\\ &\textrm{Misalkan}\\ &\left\{\begin{matrix} u & = & x^{2} &+&3&,&\textrm{maka} \\ du &= &2x & dx \end{matrix}\right.\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned}&\int \left ( x^{2}+3 \right )^{20}2x\: dx=\int u^{20}\: du\\ &=\frac{1}{21}u^{21}+C=\frac{1}{21}\left ( x^{2}+3 \right )^{21}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \left ( x^{4}-x^{2} \right )^{5}\left ( 16x^{3}-8x \right )dx\\\\ &\textbf{Jawab}:\\ &\textrm{Misalkan}\\ &\left\{\begin{matrix} u & = & x^{4} & - & x^{2}&,&\textrm{maka}\\ du & = & 4x^{3} & - &2x&dx \\ 4du & = & 16x^{3} & - & 8x&dx \end{matrix}\right.\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned}&\displaystyle \int u^{5}.4du=\frac{4}{6}u^{6}+C\\ &=\displaystyle \frac{2}{3}\left ( x^{4}-x^{2} \right )^{6}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \frac{x+2}{x^{2}+4x+4}dx\\\\ &\textbf{Jawab}:\\ &\textrm{Misalkan}\\ &\left\{\begin{matrix} u & = & x^{2} & + & 4x&+&4&,&\textrm{maka}\\ du & = & 2x & + &4&dx \\ \frac{1}{2}du & = & x & + & 2&dx \end{matrix}\right.\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned}&\displaystyle \int \frac{1}{u}.\frac{1}{2}du=\displaystyle \frac{1}{2}\int \frac{1}{u}du\\ &=\displaystyle \frac{1}{2}\ln u+C=\frac{1}{2}\ln \left ( x^{2}+4x+4 \right )+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \frac{e^{3y}}{\left ( 1-2e^{3y} \right )^{2}}dy\\\\ &\textbf{Jawab}:\\ &\textrm{Misalkan}\\ &\left\{\begin{matrix} u & = & 1 & - & 2e^{3y}& ,&\textrm{maka}\\ du & =&- & 6e^{3y} &dy &, \\ -\frac{1}{6}du & = & e^{3y} & dy \end{matrix}\right.\\ &\textrm{sehingga dengan integral substitusi}\\&\begin{aligned}&\displaystyle \int -\frac{1}{6}\frac{1}{u^{2}}du=-\frac{1}{6}\int \frac{du}{u^{2}}\\ &=-\displaystyle \frac{1}{6}\left ( -1 \right )\left ( u^{-1} \right )+C\\ &=\displaystyle \frac{1}{6u}+C\\ &=\displaystyle \frac{1}{6}.\frac{1}{1-2e^{3y}}+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 5.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int 12x\left ( x^{2}+3 \right )^{5}\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Misalkan}\\ u&=x^{2}+3\\ du&=2x\qquad dx \end{aligned}\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned} &\displaystyle \int 12x\left ( x^{2}+3 \right )^{5}\: dx\\ &=\int \left ( x^{2}+3 \right )^{5}.6.2x\: dx\\ &=6\int \underset{u^{5}}{\underbrace{\left ( x^{2}+3 \right )^{5}}}.\underset{du}{\underbrace{2x\: dx}}\\ &=6\int u^{5}\: du\\ &=6.\displaystyle \frac{u^{5+1}}{5+1}+C\\ &=u^{6}+C\\ &=\left ( x^{2}+3 \right )^{6}+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 6.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int x\sqrt{x-1}\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan}\qquad u=x-1\\ &du=1\quad dx\: \Leftrightarrow \: du=dx \end{aligned}\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned} &\displaystyle \int x\sqrt{x-1}\: dx\\&=\int \left ( x-1+1 \right )\sqrt{x-1}\: dx\\ &=\int \left ( \underset{u}{\underbrace{\left (x-1 \right )}}+1 \right )\sqrt{\underset{u}{\underbrace{x-1}}}\: dx \\ &=\int \left ( u+1 \right )\sqrt{u}\: du\\ &=\int \left (u\sqrt{u}+\sqrt{u}\: \right )\: du\\ &=\int \left (u^{\frac{3}{2}}+u^{\frac{1}{2}} \right )\: du\\ &=\displaystyle \frac{1}{\left ( \frac{3}{2}+1 \right )}u^{\left (\frac{3}{2}+1 \right )}+\displaystyle \frac{1}{\left (\frac{1}{2}+1 \right )}u^{\left (\frac{1}{2}+1 \right )}+C\\ &=\displaystyle \frac{2}{5}\left ( x-1 \right )^{\frac{5}{2}}+\displaystyle \frac{2}{3}\left ( x-1 \right )^{\frac{3}{2}}+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 7.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \displaystyle \frac{x^{5}}{x^{6}+a}\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan}\\ &u=x^{6}+a\\ &\Leftrightarrow du=6x^{5}\quad dx\\ &\Leftrightarrow \displaystyle \frac{1}{6}du=x^{5}\quad dx \end{aligned}\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned} &\int \displaystyle \frac{x^{5}}{x^{6}+a}\: dx\\ &=\int \displaystyle \frac{1}{x^{6}+a}.x^{5}\: dx\\ &=\int \displaystyle \frac{1}{\underset{u}{\underbrace{x^{6}+a}}}.\underset{\frac{1}{6}du}{\underbrace{x^{5}\: dx}}\\ &=\displaystyle \frac{1}{6}\int \frac{1}{u}\: du\\ &=\displaystyle \frac{1}{6}\ln \left | u \right |+C\\ &=\displaystyle \frac{1}{6}\ln \left | x^{6}+a \right |+C\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 8.&\textrm{Selesaikan integral berikut}\\ &\displaystyle \int \displaystyle \left ( x^{2}+1 \right )\left ( x^{3}+3x+2 \right )^{5}\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan}\\ &u=x^{3}+3x+2\\ &\Leftrightarrow du=\left (3x^{2}+3 \right ) dx\\ &\Leftrightarrow du=3\left ( x^{2}+1 \right )dx\\ &\Leftrightarrow \displaystyle \frac{1}{3}du=\left ( x^{2}+1 \right )\: dx \end{aligned}\\ &\textrm{sehingga dengan integral substitusi}\\ &\begin{aligned} \int &\left ( x^{2}+1 \right )\left ( x^{3}+3x+2 \right )^{5}\: dx\\&=\int \left ( x^{3}+3x+2 \right )^{5}.\left ( x^{2}+1 \right )\: dx\\ &=\int \underset{u^{5}}{\underbrace{\left ( x^{3}+3x+2 \right )^{5}}}.\underset{\frac{1}{3}du}{\underbrace{\left ( x^{2}+1 \right )\: dx}}\\ &=\displaystyle \frac{1}{3}\int u^{5}\: du\\ &=\displaystyle \frac{1}{3}.\displaystyle \frac{u^{5+1}}{5+1}+C\\ &=\displaystyle \frac{1}{18}.u^{6}+C\\ &=\displaystyle \frac{1}{18}\left ( x^{3}+3x+2 \right )^{6}+C\end{aligned} \end{array}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{aligned}&\textrm{Selesaikan soal berikut ini}\\ &\begin{array}{llllll}\\ &\textrm{a}.&\displaystyle \int \displaystyle \frac{4x^{6}+3x^{5}-8}{x^{5}}\: \: dx&\textrm{f}.&\displaystyle \int \displaystyle \frac{\left ( \sqrt{x}+4 \right )^{3}}{\sqrt{x}}\: \: dx\\ &\textrm{b}.&\displaystyle \int \displaystyle \frac{x^{2}}{\sqrt{4-x^{3}}}\: \: dx&\textrm{g}.&\displaystyle \int \displaystyle \frac{x+3}{\sqrt[5]{\left ( x^{2}+6x-1 \right )^{2}}}\: dx\\ &\textrm{c}.&\displaystyle \int x^{3}\left ( x^{4}+10 \right )^{.^{-\frac{2}{3}}}\: dx&\textrm{h}.&\displaystyle \int x^{5}\sqrt{x^{6}+1}\: \: dx \end{array} \end{aligned}$.

DAFTAR PUSTAKA

Kuntarti, Sulistiyono dan Kurnianingsih, S. 2007. Matematika SMA dan MA untuk Kelas XII Semester 1 Probram IPA Standar ISI 2006. Jakarta: ESIS
Sharma, S.N., dkk. 2017. Jelajah Matematika SMA Kelas XI Program Wajib. Jakarta: YUDHISTIRA.
Tung, K.Y. 2012. Pintar Matematika SMA Kelas XII IPA untuk Olimpiade dan Pengayaan Pelajaran. Yogyakarta: ANDI.

Integral Fungsi Aljabar

A. Pengertian

Pengintegralan dari suatu fungsi $f(x)$ berbentuk $\int f(x)dx$ dapat disebut sebagai integral tak tentu dari fungsi $f(x)$ dan jika $F(x)$ adalah anti turunan dari $f(x)$, maka $F(x)dx=F(x)+C$.

$\begin{aligned}&\textrm{Dengan}\\ &\begin{aligned}F(x)&= \textrm{fungsi integral dari}\: \: f(x)\\ f(x)&=\textrm{fungsi yang diintegralkan}\\ C&=\textbf{Konstanta} \end{aligned} \end{aligned}$.

B. Rumus Dasar Integral tak Tentu Fungsi Ajabar

Berikut rumus dasar yang perlu diingat

$\begin{aligned}\bullet \: \: \: &\int dx=x+C\\ \bullet \: \: \: &\int k.\left ( \displaystyle f(x) \right )dx=k\int f(x)dx\\ \bullet \: \: \: &\int \left (f(x)\pm g(x) \right )dx=\int f(x)dx+\int g(x)dx\\ \bullet \: \: \: &\int ax^{n}dx=\displaystyle \frac{a}{n+1}x^{n+1}+C \end{aligned}$.

Sebagai rumus-rumus integral yang lain adalah sebagai berikut

$\begin{array}{ll}\\ \bullet &\displaystyle \int a\: x^{n} dx=\frac{a}{n+1}.x^{n+1}+C, \: \textrm{dengan}\: \: n\neq -1\\ \bullet &\displaystyle \int a\: dx=ax+C\\ \bullet &\displaystyle \int \frac{1}{x}\: dx=\int x^{-1}\: dx=\ln x+C\\ \bullet &\displaystyle \int \left | x \right |\: dx=\frac{1}{2}x\left | x \right |+C\\ \bullet &\displaystyle \int \ln x\: dx=x\ln x-x+C\\ \bullet &\displaystyle \int e^{x}\: dx=e^{x}+C\\ \bullet &\displaystyle \int a^{x}\: dx=\frac{a^{x}}{\ln a}+C\\ \bullet &\displaystyle \int e^{ax}\: dx=\frac{1}{a}.e^{ax}+C\\ \bullet &\displaystyle \int (x^{m}+x^{n}+...+x^{p})\: dx\\ &\qquad =\displaystyle \int x^{m}\: dx+\int x^{n}\: dx+...+\int x^{p}\: d \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int x^{5}\: dx\\ &\textrm{b}.\quad \displaystyle \int 2022x^{5}\: dx\\ &\textrm{c}.\quad \displaystyle \int \displaystyle \frac{1}{x^{2022}}\: dx\\ &\textrm{d}.\quad \displaystyle \int 2022y\: dy\\ &\textrm{e}.\quad \displaystyle \int e^{2022x}\: dx\\ &\textrm{f}.\quad \displaystyle \int 2022^{x}\: dx\\\\ &\textbf{Jawab}:\\ &\textrm{a}.\quad \displaystyle \int x^{5}\: dx=\frac{1}{5+1}.x^{5+1}+C=\frac{1}{6}.x^{6}+C\\ &\textrm{b}.\quad \displaystyle \int 2022x^{5}\: dx=\frac{2022}{5+1}.x^{5+1}+C=337x^{6}+C\\ &\textrm{c}.\quad \displaystyle \int \frac{1}{x^{2022}}\: dx=\int x^{-2022}\: dx\\ &\qquad=\displaystyle \frac{1}{-2022+1}.x^{-2022+1}+C=-\frac{1}{2021}.x^{-2021}+C\\ &\qquad =-\displaystyle \frac{1}{2021x^{2021}}+C\\ &\textrm{d}.\quad \displaystyle \int 2022y\: dy=\frac{2022}{1+1}y^{1+1}+C=1011y^{2}+C\\ &\textrm{e}.\quad \displaystyle \int e^{2022x}\: dx=\frac{1}{2022}.e^{2022x}+C\\ &\textrm{f}.\quad \displaystyle \int 2022^{x}\: dx=\frac{2022^{x}}{\ln 2022}+C \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int \left ( 3x^{2}-x+2-\frac{1}{x}+ \frac{3}{x^{2}}\right )dx\\ &\textrm{b}.\quad \displaystyle \int \left ( x^{2}-2xy+y^{2} \right )dx\\ &\textrm{c}.\quad \displaystyle \int \left | x-1 \right |\: +\left | x-2 \right |\: dx\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad \displaystyle &\int \left ( 3x^{2}-x+2-\frac{1}{x}+ \frac{3}{x^{2}}\right )dx\\ &=\displaystyle \int 3x^{2}\: dx-\int x\: dx+2\int dx-\int \frac{1}{x}\: dx+3\int \frac{1}{x^{2}}\: dx\\ &=\displaystyle \frac{3}{2+1}x^{2+1}-\frac{1}{1+1}x^{1+1}+2x-\ln x\: +3\left ( \frac{1}{-2+1}x^{-2+1} \right )+C\\ &=\displaystyle \frac{2}{3}x^{3}-\frac{1}{2}x^{2}+2x-\ln x\: -\frac{3}{x}+C \end{aligned}\\&\begin{aligned}\textrm{b}.\quad \displaystyle &\int \left ( x^{2}-2xy+y^{2} \right )dx\\ &=\displaystyle \int x^{2}\: dx-2y\int x\: dx+y^{2}\int dx\\ &=\displaystyle \frac{1}{2+1}x^{2+1}-\frac{2y}{1+1}x^{1+1}+y^{2}.x+C\\ &=\displaystyle \frac{1}{3}x^{3}-x^{2}y+xy^{2}+C \end{aligned}\\ &\begin{aligned}\textrm{c}.\quad \displaystyle &\int \left | x-1 \right |\: +\left | x-2 \right |\: dx\\ &=\displaystyle \frac{(x-1)}{2}\left | x-1 \right |\: +\frac{(x-2)}{2}\left | x-2 \right |+C \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int 2x^{.^{\frac{2}{3}}}dx\\ &\textrm{b}.\quad \displaystyle \int \frac{1}{3}\sqrt[4]{x^{3}}\: dx\\ &\textrm{c}.\quad \displaystyle \int \displaystyle \frac{x^{4}-4x^{3}}{x^{2}}\: dx\\\\ &\textbf{Jawab}:\\ &\textrm{a}.\quad \displaystyle \int 2x^{.^{\frac{2}{3}}}dx=\displaystyle \frac{2}{\displaystyle \frac{2}{3}+1}x^{.^{\frac{2}{3}+1}}+C=\displaystyle \frac{6}{5}x^{.^{\frac{5}{3}}}+C\\ &\textrm{b}.\quad \displaystyle \int \frac{1}{3}\sqrt[4]{x^{3}}\: dx=\displaystyle \frac{1}{3}x^{.^{\frac{3}{4}}}\: dx=\left (\displaystyle \frac{1}{3} \right ).\displaystyle \frac{1}{\displaystyle \frac{3}{4}+1}x^{.^{\frac{3}{4}+1}}+C\\ &\qquad =\left ( \displaystyle \frac{1}{3} \right )\displaystyle \frac{4}{7}x^{.^{\frac{7}{4}}}+C=\displaystyle \frac{4}{21}x^{.^{\frac{7}{4}}}+C\\ &\textrm{c}.\quad \displaystyle \int \displaystyle \frac{x^{4}-4x^{3}}{x^{2}}\: dx=\int x^{2}-4x\: dx\\ &\qquad =\displaystyle \frac{1}{2+1}x^{2+1}-\displaystyle \frac{4}{1+1}x^{1+1}+C\\ &\qquad =\displaystyle \frac{1}{3}x^{3}-2x^{2}+C \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int \displaystyle \frac{\sqrt{x}(6x^{2}-2x)}{x}dx\\ &\textrm{b}.\quad \displaystyle \int (12x^{2}-4x)(2x+1)\: dx\\\\ &\textbf{Jawab}:\\ &\textrm{a}.\quad \displaystyle \int \displaystyle \frac{\sqrt{x}(6x^{2}-2x)}{x}dx=\displaystyle \int \displaystyle \frac{x^{.^{\frac{1}{2}}}(6x^{2}-2x)}{x}dx\\ &\qquad =\displaystyle \int \displaystyle \frac{6x^{.^{\frac{5}{2}}}-2x^{.^{\frac{3}{2}}}}{x}dx=\displaystyle \int 6x^{.^{\frac{3}{2}}}-2x^{.^{\frac{1}{2}}}dx\\ &\qquad =\displaystyle \frac{6}{\displaystyle \frac{3}{2}+1}x^{.^{\frac{3}{2}+1}}-\frac{2}{\displaystyle \frac{1}{2}+1}x^{.^{\frac{1}{2}+1}}+C\\ &\qquad =\displaystyle \frac{12}{5}x^{.^{\frac{5}{2}}}-\displaystyle \frac{4}{3}x^{.^{\frac{3}{2}}}+C=\displaystyle \frac{12}{5}x^{2}\sqrt{x}-\displaystyle \frac{4}{3}x\sqrt{x}+C\\ &\textrm{b}.\quad \displaystyle \int (12x^{2}-4x)(2x+1)\: dx\\ &\qquad =\displaystyle \int (24x^{3}+4x^{2}-4x)dx\\ &\qquad =\displaystyle \frac{24}{3+1}x^{3+1}+\frac{4}{2+1}x^{2+1}-\frac{4}{1+1}x^{1+1}\: dx\\ &\qquad =6x^{4}+\displaystyle \frac{4}{3}x^{3}-2x^{2}+C \end{array}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int 2022\: dx\\ &\textrm{b}.\quad \displaystyle \int \frac{dx}{2022}\\ &\textrm{c}.\quad \displaystyle \int 2022x\: dx\\ &\textrm{d}.\quad \displaystyle \int -2022x^{2}\: dx\\ &\textrm{e}.\quad \displaystyle \int \left ( x+2022 \right )dx\\ &\textrm{f}.\quad \displaystyle \int \left (-2022x^{3}+2023x^{2}-2024 \right )dx\\ &\textrm{g}.\quad \displaystyle \int x\sqrt{x}\: dx\\ &\textrm{h}.\quad \displaystyle \int \sqrt{x\sqrt[3]{x\sqrt[4]{x\sqrt[5]{x\sqrt[6]{x}}}}}\: dx\\ &\textrm{i}.\quad \displaystyle \int \frac{2022}{\sqrt[3]{x^{2}}}\: dx\\ &\textrm{j}.\quad \displaystyle \int \frac{2022x}{\sqrt[3]{x^{5}}}\: dx\\ &\textrm{k}.\quad \displaystyle \int \left (2022-2020t+t^{2} \right )dt\\ &\textrm{l}.\quad \displaystyle \int \left (\frac{3}{t^{3}} +\frac{2}{t^{2}} +2022\right )dt\\ &\textrm{m}.\quad \displaystyle \int \left (\sqrt{t} +\frac{1}{2\sqrt{t}} \right )dt\\ &\textrm{n}.\quad \displaystyle \int \left (ay^{4} +by^{2} \right )dy\\ &\textrm{o}.\quad \displaystyle \int \left (4ax^{3}+3bx^{2}+2cx+1 \right )dx\\ &\textrm{p}.\quad \displaystyle \int \frac{x^{2}+2022}{x^{2}}\: dx\\ &\textrm{q}.\quad \displaystyle \int \left (e ^{x}+e^{-x} \right )dx\\ &\textrm{r}.\quad \displaystyle \int e^{2023x}dx\\ &\textrm{s}.\quad \displaystyle \int \frac{dx}{e^{2023x}}dx\\ &\textrm{t}.\quad \displaystyle \int \left ( \sqrt{10^{x}} \right )dx \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int (2022x-2202)dx\\ &\textrm{b}.\quad \displaystyle \int (x^{2}-2x-8) dx\\ &\textrm{c}.\quad \displaystyle \int \sqrt{2x}\: dx\\ &\textrm{d}.\quad \displaystyle \int x^{2}(x+2)(x-1)\: dx \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int 3x\left ( 2x-\displaystyle \frac{1}{x} \right )dx\\ &\textrm{b}.\quad \displaystyle \int \displaystyle \frac{(x^{2}-4)}{x^{2}} dx\\ &\textrm{c}.\quad \displaystyle \int \left ( 2x-\displaystyle \frac{1}{x^{2}} \right )^{2}\: dx\\ &\textrm{d}.\quad \displaystyle \int x^{2}\left ( \displaystyle \frac{(x+4)(x-3)}{x} \right )\: dx \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Selesaikan integral berikut}\\ &\textrm{a}.\quad \displaystyle \int \displaystyle \frac{2x^{3}-3x}{\sqrt{x}}dx\\ &\textrm{b}.\quad \displaystyle \int \displaystyle \frac{2}{\sqrt{x}}\left ( 1-\sqrt{x^{2}} \right )^{2} dx\\ &\textrm{c}.\quad \displaystyle \int x^{2}\left ( \sqrt{x}+\displaystyle \frac{1}{\sqrt{x}} \right )^{2}\: dx\\ &\textrm{d}.\quad \displaystyle \int \displaystyle \frac{x^{2}\left ( 2+\sqrt[3]{x^{4}} \right )^{2}}{\sqrt{x}}\: dx \end{array}$.

DAFTAR PUSTAKA

Kuntarti, Sulistiyono dan Kurnianingsih, S. 2007. Matematika SMA dan MA untuk Kelas XII Semester 1 Probram IPA Standar ISI 2006. Jakarta: ESIS
Sharma, S.N., dkk. 2017. Jelajah Matematika SMA Kelas XI Program Wajib. Jakarta: YUDHISTIRA.
Tung, K.Y. 2012. Pintar Matematika SMA Kelas XII IPA untuk Olimpiade dan Pengayaan Pelajaran. Yogyakarta: ANDI.

Contoh Soal 4 Turunan Fungsi Aljabar

$\begin{array}{ll}\\ 16.&\textrm{Jika grafik fungsi}\: \: f(x)=5+15x+9x^{2}+x^{3}\\ &\textrm{naik untuk}\: \: x\: \: \textrm{yang memenuhi}....\\ &\begin{array}{lll}\\ \textrm{a}.\quad x< 1\: \: \textrm{atau}\: \: x> 5 &\textrm{d}.\quad \color{red}x< -5\: \: \textrm{atau}\: \: x> -1 \\ \textrm{b}.\quad -\displaystyle 1< x< 5 \quad &\textrm{e}.\quad -5< x< 1\\ \textrm{c}.\quad \displaystyle -5< x< -1 \quad \end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &f(x)=x^{3}+9x^{2}+15x+5.\\ &\textrm{Dikatakan fungsi}\: \: f\: \: \textrm{naik, maka}\\ &{f}\, '(x)> 0\\ &\Leftrightarrow 3x^{2}+18x+15> 0,\quad \textrm{tiap ruas dibagi 3}\\ &\Leftrightarrow x^{2}+6x+5> 0\\ &\Leftrightarrow (x+1)(x+5)> 0 \end{aligned}\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.

$\begin{array}{ll}\\ 17.&\textrm{Sebuah bola dilempar ke atas secara vertikal.}\\ &\textrm{Jika lintasan bola pada saat}\: \: t\: \: \textrm{detik adalah}\\ &h(t)=-\displaystyle \frac{1}{4}t^{4}+\frac{2}{3}t^{3}+4t^{2}+5\: \: \textrm{m},\\ &\textrm{maka tinggi maksimum yang} \\ &\textrm{dicapai oleh bola tersebut adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle \frac{67}{3} &&\textrm{d}.\quad \displaystyle \frac{133}{3} \\\\ \textrm{b}.\quad \displaystyle \frac{123}{3} \quad &\textrm{c}.\quad \displaystyle \frac{128}{3} \quad &\textrm{e}.\quad \color{red}\displaystyle \frac{143}{3} \end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}\textrm{Perh}&\textrm{atikan bahwa lintasan bola saat dilempar }\\ \textrm{verti}&\textrm{kal dituliskan dengan fungsi}\\ h(t)&=-\displaystyle \frac{1}{4}t^{4}+\frac{2}{3}t^{3}+4t^{2}+5.\\ \textrm{mak}&\textrm{a tinggi maksimum akan dicapai bola }\\ \textrm{saat}&\: \: \: {h}\, '(t)=0,\\ \textrm{Sela}&\textrm{njutnya},\\ {h}\, '(t)&=0\\ -t^{3}+&2t^{2}+8t=0\\ -t(t^{2}&-2t-8)=0\\ t(t-&4)(t+2)=0\begin{cases} t & =0 \\ t & =4 \\ t & =-2 \end{cases}\\ \textrm{kita}&\: \textrm{ambil yang bernilai positif untuk }\\ &t\: \: \textrm{yaitu}\: \: t=4.\\ t=4&\rightarrow h(4)=-\displaystyle \frac{1}{4}(4)^{4}+\frac{2}{3}(4)^{3}+4(4)^{2}+5\\ h(4)&=-64+\displaystyle \frac{128}{3}+64+5\\ &=\displaystyle \frac{143}{3}\: \: m \end{aligned}\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.

Contoh Soal 3 Turunan Fungsi Aljabar

$\begin{array}{ll}\\ 11.&\textrm{Jika}\: \: \: f(x)=\displaystyle (x^{2}+2)\sqrt{x^{2}+x+3}\\&\textrm{maka}\: \: {f}\, '(2)=.... \\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle 18 &&\textrm{d}.\quad 13 \\\\ \textrm{b}.\quad \displaystyle \color{red}17 \quad &\textrm{c}.\quad \displaystyle 15 \quad &\textrm{e}.\quad 12 \end{array}\\\\ &\textbf{Jawab}:\\&\begin{aligned}f(x)&=\displaystyle (x^{2}+2)\sqrt{x^{2}+x+3} \\ {f}\, '(x)&=(2x)\sqrt{x^{2}+x+3}\\ &+(x^{2}+2).\displaystyle \frac{1}{2}\left ( x^{2}+x+3 \right )^{^{-\frac{1}{2}}}.\left ( 2x+1 \right ) \\ &=2x\sqrt{x^{2}+x+3}+\displaystyle \frac{(x^{2}+2)(2x+1)}{2\sqrt{x^{2}+x+3}} \\ {f}\, '(2)&=2(2)\sqrt{(2)^{2}+(2)+3}+\displaystyle \frac{((2)^{2}+2)(2(2)+1)}{2\sqrt{(2)^{2}+(2)+3}} \\ &=4\sqrt{9}+\displaystyle \frac{6.5}{2\sqrt{9}} \\ &=4.3+\displaystyle \frac{6.5}{2.3}\\ &=12+5\\ &=17 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Jika rusuk suatu kubus bertambah panjang }\\ &\textrm{dengan laju 7}\: \: cm/detik\: , \: \textrm{maka laju}\\ &\textrm{bertambahnya volume pada saat rusuk }\\ &\textrm{panjangnya 15}\: \: cm\: \: \textrm{adalah}.... \\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle 675 \: \: \: \: cm^{3}/detik &\textrm{d}.\quad \color{red}4725 \: \: \: \: cm^{3}/detik \\ \textrm{b}.\quad \displaystyle 1575 \: \: \: \: cm^{3}/detik \quad &\textrm{e}.\quad 23625 \: \: \: \: cm^{3}/detik\\ \textrm{c}.\quad \displaystyle 3375 \: \: \: \: cm^{3}/detik \quad \end{array}\\\\&\textbf{Jawab}:\\&\begin{aligned}\textrm{Laju }&\textrm{pertambahan volumenya}:\\ &\begin{cases} \bullet \: \: \: \frac{\mathrm{d} s}{\mathrm{d} t} & = 7\: \: cm/detik\\ \bullet \: \: \: V & =s^{3} \rightarrow \textrm{d}V=3s^{2}\: \: \textrm{d}s\: \: \: \textrm{atau}\\ \, \: \: \: \: \frac{\mathrm{d} V}{\mathrm{d} s} & =3s^{2}\: \: cm^{3}/cm\rightarrow s=15\: \: cm \end{cases}\\ \frac{\mathrm{d} V}{\mathrm{d} t}&=\frac{\mathrm{d} V}{\mathrm{d} t}\\ &=\frac{\mathrm{d} V}{\mathrm{d} s}\times \frac{\mathrm{d} s}{\mathrm{d} t}\\ &=3s^{2} \: \: \: \: cm^{3}/cm \times 7\: \: \: \: cm/detik \\ &=3(15)^{2}\times 7\: \: \: \: cm^{3}/detik\\ &=4725\: \: \: \: cm^{3}/detik \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{persamaan garis singgung di}\: \: x=1\\ &\textrm{pada kurva}\: \: y=x^{3}-3x^{2}+1\: \: \textrm{adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}y=-3x+2&\textrm{d}.\quad y=3x-2\\ \textrm{b}.\quad y=-3x+4\quad &\textrm{e}.\quad y=-3x+3\\ \textrm{c}.\quad y=3x-4\quad \end{array}\\\\ &\textbf{Jawab}:\\ &\begin{array}{|l|}\hline \textrm{Titik singgung di}\: \: x=1\\\hline \begin{aligned} y&=x^{3}-3x^{2}+1\\ y&=(1)^{3}-3(1)^{2}+1\\ &=1-3+1\\ &=-1\\ &\textrm{titik}\: (a,b)=(1,-1) \end{aligned}\\\hline \textrm{Gradien garis singgung di}\: \: x=1\\\hline \begin{aligned} {y}\, '=m\, _{_{x=1}}&=3x^{2}-6x\\ &=3(1)^{2}-6(1)\\ &=3-6\\ &=-3 \end{aligned}\\\hline \textrm{Persamaan garis singgung}\\\hline \begin{aligned}y&=m(x-a)+b\\ &=-3(x-1)+(-1)\\ &=-3x+3-1\\ &=-3x+2\end{aligned}\\\hline \end{array}\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Suatu kurva}\: \: y=x^{3}+2ax^{2}+b\\ &\textrm{Sebuah garis}\: \: y=-9x-2\: \: \textrm{menyinggung}\\ &\textrm{kurva di titik dengan} \: \: x=1,\\ &\textrm{maka nilai}\: \: a \: \: \textrm{adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}-3&&\textrm{d}.\quad 3\\ \textrm{b}.\quad -\displaystyle \frac{1}{3} \quad &\textrm{c}.\quad \displaystyle \frac{1}{3} \quad &\textrm{e}.\quad 8 \end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Gradien garis singgung}\\ &y\: _{_{_{di\: \: x=1}}}\begin{cases} y & =x^{3}+2ax^{2}+b \\ &\rightarrow m={y}\, '=\color{blue}3x^{2}+4ax\\\\ y & =-9x-2 \rightarrow m=y'= \color{blue}-9 \end{cases}\\ &\textrm{Sehingga}\:, \\ &m=m={y}\, '\\ &-9=3x^{2}+4ax\\ &-9=3(1)^{2}+4a(1)\\ &-9=3+4a\\ &-4a=3+9\\ &a=\displaystyle \frac{12}{-4}\\ &=-3\\ & \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 15.&\textrm{Jika grafik fungsi}\: \: f(x)=x^{3}+ax^{2}+bx+c\\ &\textrm{hanya turun untuk interval}\: \: -1< x< 5\, ,\\ &\textrm{maka nilai}\: \: a+b \: \: \textrm{adalah}....\\&\begin{array}{lll}\\ \textrm{a}.\quad \color{red}-21&&\textrm{d}.\quad 21\\ \textrm{b}.\quad -\displaystyle 9 \quad &\textrm{c}.\quad \displaystyle 9 \quad &\textrm{e}.\quad 24 \end{array}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &f(x)=x^{3}+ax^{2}+bx+c\\ &\textrm{grafik fungsi turun}\: \: \textrm{berarti}:\: \: \: {f}\, '(x)< 0\\ &{f}\, '(x)< 0\\ &\Leftrightarrow 3x^{2}+2ax+b< 0\\ &\Leftrightarrow (x+1)(x-5)< 0 \\ &\textrm{ini maksud pada interval}\\ &-1< x< 5\: \: \: \textrm{pada soal}\\ &x^{2}-4x-5< 0\\ &\textrm{dikalikan dengan 3 supaya terjadi persamaan}\\ &3x^{2}-3.4x-3.5=3x^{2}+2ax+b< 0\\ &3x^{2}+2(-6)x+(-15)=3x^{2}+2ax+b< 0\\ &\begin{cases} a & =-6 \\ b & = -15 \end{cases}\\ &\textrm{Sehingga}\: ,\\ &a+b=-6+(-15)=-21 \end{aligned} \end{array}$.