A. Luas
Menghitung luas yang dibatasi oleh sebuah kurva dan sumbu X kita dapat menggunakan bantuan integral tentuk sebagaimana uraian sebelumnya
Perhatikan ilustrasi gambar berikut
$\begin{array}{|c|c|}\hline \textrm{Di Atas Sumbu X}&\textrm{Di Bawah Sumbu X}\\\hline &-\displaystyle \int_{a}^{b}f(x)\: \: dx\\ \displaystyle \int_{a}^{b}f(x)\: \: dx&atau\\ &\displaystyle \int_{b}^{a}f(x)\: \: dx\\\hline \end{array}$.
B. Volume Benda Putar
Adapun untuk volume diformulasikan dengan integral tentu berikut
$\boxed{V=\pi \displaystyle \int_{a}^{b}\left ( f(x) \right )^{2}\: \: dx=\pi \displaystyle \int_{a}^{b}y^{2}\: \: dx}$.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah luas daerah bidang berikut dan }\\ &\textrm{tentukan pula volumenya seandainya bidang }\\ &\textrm{yang diarsir tersebut diputar terhadap sumbu X} \end{array}$.
\begin{array}{ll}\\ 2.&\textrm{Diketahui parabola}\: \: f_{1}(x)=a_{1}x^{2}+b_{1}x+c_{1}\\ &\textrm{dan}\: \: f_{2}(x)=a_{2}x^{2}+b_{2}x+c_{2}.\\ &\textrm{Titik potong kedua parabola tersebut }\\ &\textrm{dapat cari dengan}\\ &\\ &f_{1}(x)=f_{2}(x)\\ &\Leftrightarrow \: \: a_{1}x^{2}+b_{1}x+c_{1}=a_{2}x^{2}+b_{2}x+c_{2}\\ & \Leftrightarrow \: ax^{2}+bx+c=0.\\ &\\ &\textrm{Jika kedua parabola berpotongan di dua}\\ &\textrm{titik, tunjukkan bahwa luas daerah antara}\\ &\textrm{kedua parabola tersebut dapat }\\ &\textrm{dinyatakan dengan}\: \: \: \displaystyle \textbf{L}=\frac{\textbf{D}\sqrt{\textbf{D}}}{\textbf{6a}^{\textbf{2}}}\\\\ &\textbf{Bukti}:\\ &ax^{2}+bx+c=0\: \begin{cases} &x_{1}=\displaystyle \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \\ & \\ &x_{2}=\displaystyle \frac{-b- \sqrt{b^{2}-4ac}}{2a} \end{cases}\\ &\begin{aligned}L&=\displaystyle \int_{\frac{-b- \sqrt{b^{2}-4ac}}{2a}}^{\frac{-b+ \sqrt{b^{2}-4ac}}{2a}}\: \left ( ax^{2}+bx+c \right )\: \: dx=\left [ \displaystyle \frac{ax^{3}}{3}+\frac{bx^{2}}{2}+cx \right ]_{\frac{-b- \sqrt{b^{2}-4ac}}{2a}}^{\frac{-b+ \sqrt{b^{2}-4ac}}{2a}}\\ &=\left [ \displaystyle \frac{a}{3}\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right )^{3}+\displaystyle \frac{b}{2}\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right )^{2}+c\left ( \frac{-b+ \sqrt{b^{2}-4ac}}{2a} \right ) \right ]\\ &\quad -\left [ \displaystyle \frac{a}{3}\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right )^{3}+\displaystyle \frac{b}{2}\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right )^{2}+c\left ( \frac{-b- \sqrt{b^{2}-4ac}}{2a} \right ) \right ]\\ &=\displaystyle \frac{a}{24a^{3}}\left [ \left ( \sqrt{D}^{3}-3\sqrt{D}^{2}b+3\sqrt{D}b^{2}-b^{3} \right )+\left ( \sqrt{D}^{3}+3\sqrt{D}^{2}b+3\sqrt{D}b^{2}+b^{3} \right ) \right ]\\ &\quad +\displaystyle \frac{b}{8a^{2}}\left [ \left ( b^{2}-2b\sqrt{D}+\sqrt{D}^{2} \right )-\left ( b^{2}+2b\sqrt{D}+\sqrt{D}^{2} \right ) \right ]+\displaystyle \frac{c}{2a}\left [ \left ( -b+\sqrt{D} \right )-\left ( -b-\sqrt{D} \right ) \right ]\\ &=\displaystyle \frac{1}{24a^{2}}\left [ 2\sqrt{D}^{3}+6\sqrt{D}b^{2} \right ]+\displaystyle \frac{b}{8a^{2}}\left [ -4b\sqrt{D} \right ]+\displaystyle \frac{c}{2a}\left [ 2\sqrt{D} \right ]\\ &=\displaystyle \frac{\sqrt{D}^{3}}{12a^{2}}+\frac{b^{2}\sqrt{D}}{4a^{2}}-\frac{b^{2}\sqrt{D}}{2a^{2}}+\frac{c\sqrt{D}}{a}=\displaystyle \frac{D\sqrt{D}}{12a^{2}}+\frac{b^{2}\sqrt{D}}{4a^{2}}-\frac{b^{2}\sqrt{D}}{2a^{2}}+\frac{c\sqrt{D}}{a}\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}} \left (D+3b^{2}-6b^{2}+12ac \right )\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}}\left [ \left ( b^{2}-4ac \right )-3b^{2}+12ac \right ]\\ &=\displaystyle \frac{\sqrt{D}}{12a^{2}}\left [ -2b^{2}+8ac \right ]\\ &=-\displaystyle \frac{\sqrt{D}}{6a^{2}}\left [ b^{2}-4ac \right ]=-\frac{\sqrt{D}}{6a^{2}}\left [ D \right ]\\ &=-\frac{D\sqrt{D}}{6a^{2}},\quad \textbf{luas tidak mungkin negatif}\\ &=\displaystyle \frac{D\sqrt{D}}{6a^{2}}\quad \blacksquare \end{aligned} \end{array}.
$.\: \quad\begin{aligned}&\textrm{Langkah-Langkah penyelesaiannya adalah:}\\ &\begin{array}{|c|c|}\hline \textrm{Batas}&\textrm{Menentukan Volumenya}\\\hline x=-2\: \: \textrm{sampai}\: \: x=2&\begin{aligned}V&=\displaystyle \pi \int_{a}^{b}y^{2}\: \: dx\\ &=\displaystyle \pi \int_{-2}^{2}\left ( 4-x^{2} \right )\: \: dx\\ &=\displaystyle \pi \left [ 4x-\displaystyle \frac{x^{3}}{3} \right ]_{-2}^{2} \\ &=\displaystyle \pi \left ( 8-\displaystyle \frac{8}{3} \right )-\pi \left ( -8+\displaystyle \frac{8}{3} \right )\\ &=\displaystyle \pi \left ( 8+8-\frac{8}{3}-\frac{8}{3} \right )\\ V&=\displaystyle \frac{32}{3}\pi\: \: \textbf{Satuan Volum} \end{aligned}\\\hline \end{array} \end{aligned}$.
$\begin{array}{ll}\\ 3.&\textrm{Tentukan volume benda putar yang terbentuk, }\\ &\textrm{jika suatu daerah yang dibatasi oleh kurva}\\ &y^{2}=x\: \: \textrm{dan}\: \: y=x\: \textrm{diputar mengelilingi sumbu X} \\\end{array}$.
$.\: \quad\begin{aligned}&\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \end{aligned}$.
$.\: \quad\begin{aligned}&\textbf{Menentukan batas}\\ &\begin{array}{|r|l|}\hline \begin{aligned}y&=y\\ x^{2}&=x\\ x^{2}-x&=0\\ x\left ( x-1 \right )&=0\\ x=0\: \: \textrm{atau}\: \: x&=1\\ &\\ &\\ & \end{aligned}&\begin{aligned}V&=\pi \displaystyle \int_{a}^{b}\left ( y_{1}^{2}-y_{2}^{2} \right )\: \: dx\\ &=\pi \displaystyle \int_{0}^{1}\left ( x-x^{2} \right )\: \: dx\\ &=\pi \left [ \displaystyle \frac{1}{2}x^{2}-\frac{1}{3}x^{3} \right ]_{0}^{1}\\ &=\pi \left [ \displaystyle \frac{1}{2}-\frac{1}{3} \right ]\\ V&=\displaystyle \frac{1}{6}\pi \end{aligned} \\\hline \end{array}\\ &\textbf{Keterangan lanjutan}\\ &\begin{aligned}&\textnormal{Perhatikan bahwa;}\\&y^{2}=x\Rightarrow y=\sqrt{x},\: \textrm{dianggap sebagai}\: \: y_{1}\\ &\textnormal{Sehingga}\: y_{1}-\textrm{nya adalah}\: \: \sqrt{x}\\ &\textnormal{dan}\: \: y=x\: \: \textrm{dianggap sebagai}\: \: y_{2}\\ &\left ( y_{1}^{2}-y_{2}^{2} \right )=\left ( \left ( \sqrt{x} \right )^{2}-\left ( x \right )^{2} \right )=x-x^{2}\end{aligned}\\ &\textrm{Jadi, volume dari benda putar tersebut}\\ &\textrm{dalam satuan volum adalah}\: \: \color{red}\displaystyle \frac{1}{6}\pi \end{aligned}$.
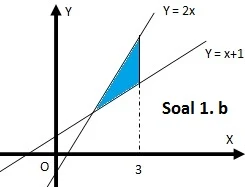
$\begin{array}{ll}\\ 4.&\textrm{Tentukan volume benda putar yang terbentuk,}\\ &\textrm{jika suatu daerah yang dibatasi oleh kurva} \\ &y=2x\: ,\: y=x,\: x=1,\: \textrm{dan}\: \: x=3\\ &\textrm{diputar mengelilingi sumbu X}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi gambar berikut} \end{array}$.
$.\: \quad\begin{aligned}&\textrm{Langkah-Langkah penyelesaiannya adalah:}\\ &\begin{array}{|c|c|}\hline \textrm{Batas}&\textrm{Menentukan Volumenya}\\\hline x=1\: \: \textrm{dan}\: \: x=3&\begin{aligned}V&=\displaystyle \pi \int_{a}^{b}\left ( f^{2}(x)-g^{2}(x) \right )\: \: dx\\ &=\displaystyle \pi \int_{1}^{3}\left ( \left ( 2x \right )^{2}-\left ( x \right )^{2} \right )\: \: dx\\ &=\displaystyle \pi \int_{1}^{3}3x^{2}\: \: dx\\ &=\displaystyle \pi \left [ x^{3} \right ]_{1}^{3}\\ &=\displaystyle \pi \left ( 3^{3} \right )-\pi \left ( 1^{3} \right )\\ &=27\pi -1\pi \\ V&=26\pi\: \textbf{Satuan Volum} \end{aligned}\\\hline \end{array} \end{aligned}$.
$\begin{array}{ll}\\ 5.&\textrm{Tentukan volume daerah yang dibatasi}\\ &\textrm{oleh lingkaran}\: \: x^{2}+y^{2}=4\: ,\: \textrm{selang}\\ &-2\leq x\leq 2\: \: \textrm{dan}\: \: \textrm{diputar mengelilingi}\\ &\textrm{sumbu X}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \\\end{array}$.
$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah luas daerah yang diarsir berikut} \end{array}$.
$\begin{array}{ll}\\ 2.&\textrm{Tunjukkan bahwa luas ellips}\: \: \displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\\ &\textrm{adalah}\: \: \pi ab \end{array}$.
$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah volume benda putar yang terjadi}\\ &\textrm{jika daerah dari hasil putar tersebut mengelilingi }\\ &\textrm{sumbu X serta dibatasi oleh}\\ &\begin{array}{ll} \textrm{a}.\quad y=x+3,\: \textrm{sumbu x, garis x = 2, dan x = 4}\\ \textrm{b}.\quad \displaystyle y=\frac{1}{2}x+2,\: \textrm{sumbu x, garis x = 0, dan x = 4}\\ \textrm{c}.\quad \displaystyle y=\sqrt{x+2} ,\: \textrm{sumbu x, garis x = 2, dan x = 4}\\ \textrm{d}.\quad y=4-2x,\: \textrm{sumbu x, garis x = 0, dan x = 4}\\ \textrm{e}.\quad \displaystyle x^{2}+y^{2}=16,\: \textrm{dan sumbu X} \end{array} \end{array}$.
$\begin{array}{ll}\\ 4.&\textrm{Tentukanlah volume benda putar yang}\\ &\textrm{terjadi jika daerah dari hasil putar tersebut }\\ &\textrm{mengelilingi sumbu X serta dibatasi oleh}\\ &\begin{array}{ll} \textrm{a}.\quad y=2x-x^{2},\: \textrm{dan}\: \: y=0\\ \textrm{b}.\quad \displaystyle y^{2}=x,\: \textrm{dan}\: \: y=2\\ \textrm{c}.\quad \displaystyle y=x^{2} ,\: \textrm{dan}\: \: y=-x^{2}+4\\ \textrm{d}.\quad y=7-2x^{2},\: \textrm{dan}\: \: y=x^{2}+4\\ \textrm{e}.\quad \displaystyle y=x^{2},\: \textrm{dan}\: \: y^{2}=x \end{array} \end{array}$.
DAFTAR PUSTAKA
- Kuntarti, Sulistiyono, Kurnianingsih, S. 2007. Matematika SMA dan MA untuk Kelas XII Semester 1 Program IPA Standar ISI 2006. Jakarta: ESIS.
Tidak ada komentar:
Posting Komentar
Informasi