Penggunaan Turunan Fungsi (Lanjutan Materi Turunan Fungsi Aljabar)

 Penggunaan Turunan Fungsi Aljabar ini nantinya terdapat di antaranya pada:

• Persamaan garis singgung
• Fungsi naik dan fungsi turun
• Menggambar grafik fungsi aljabar
• Maksimum dan minimum fungsi
• Teorema L'Hopital (dibaca : Lopital)
• Titik Stasioner/Titik kritis/Titik Ekstrim (titik maksmum, titik minimum, dan titik belok)
• Kecepatan dan percepatan

Perhatikanlah tabel berikut

$\begin{array}{|c|l|l|}\hline \textrm{No}&\quad\textrm{Turunan Pertama}&\qquad\textrm{Turunan Pertama}\\\hline 1.&\textrm{Gradien garis singgung}&\begin{aligned}m&={f}\, '(x)\\&=\underset{h\rightarrow 0}{\textrm{Lim}}=\displaystyle \frac{f(x+h)-f(x)}{h}\end{aligned}\\\hline 2.&\textrm{Fungsi naik dan turun}&y=f(x)\begin{cases} {f}'(x)> 0, & \\ \text{ fungsi naik }&\\\\ {f}'(x)< 0, &\\ \text{ fungsi turun }& \end{cases}\\\hline 3.&\textrm{Jarak, kec, percepatan}&y=s(t)\begin{cases} s(t) & \text{ jarak} \\ {s}\, '(t) & \text{ kecepatan } \\ {s}\, ''(t) & \text{ percepatan}\end{cases}\\\hline4.\textrm{a}&\textrm{Stasioner}&\begin{aligned}\textrm{Maksimum}:&\\ \rightarrow {f}&\, ''(k)< 0\\ \textrm{titik mak}&\: \left ( k, f(k)\right ) \end{aligned}\\\hline 4.\textrm{b}&\textrm{Stasioner}&\begin{aligned}\textrm{Minimum}:&\\ \rightarrow {f}&\, ''(k) > 0\\ \textrm{titik min}&\: \left ( k, f(k)\right ) \end{aligned}\\\hline 4.\textrm{c}&\begin{aligned}&\textrm{Syarat stasioner}\\ &f'(x)=0,\: \: \rightarrow x\\ &\textrm{dengan}\quad x=k \end{aligned}&\begin{aligned}\textrm{Belok}:&\\ \rightarrow {f}&\, ''(k)= 0\\ \textrm{titik belok}&\: \left ( k, f(k)\right ) \end{aligned}\\\hline5.&\begin{aligned}&\textrm{Limit fungsi}\\ &\textrm{bentuk tak tentu}\end{aligned}&\begin{aligned}&\textrm{Aturan L'Hopital}\\ &\\ &\underset{x\rightarrow h}{\textrm{Lim}}\: \: \displaystyle \frac{f(x)}{g(x)}=\underset{x\rightarrow h}{\textrm{Lim}}\: \: \displaystyle \frac{{f}\, '(x)}{g\,'(x)}\\ &\\ &\textrm{untuk hasil limit}\\ &\textrm{bentuk}\: \: \frac{0}{0}\: \: \textrm{atau}\: \: \frac{\infty }{\infty }\end{aligned}\\\hline\textrm{No}&\textrm{Turunan Kedua}&\textrm{Turunan Kedua}\\\hline6.&f''=\displaystyle \frac{d^{2}y}{dx^{2}}&\begin{aligned}\bullet \quad &\textrm{Belok}\\ \bullet \quad &\textrm{Percepatan}\\ \bullet \quad &\textrm{Maksimum}\\ \bullet \quad &\textrm{Minimum}\end{aligned}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

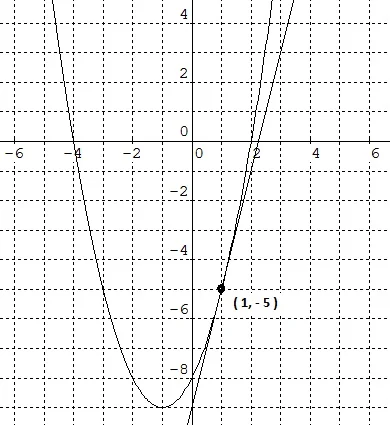
$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah persamaan garis singgung }\\ &\textrm{pada kurva}\: \: y=x^{2}+2x-8\: \: \textrm{di titik yang}\\ &\textrm{berabsis}\: \: 1\\\\&\textbf{Jawab}:\\&\begin{aligned}&\textrm{Diketahui},\: \textrm{persamaan sebuah kurva adalah:}\\ &y=\color{blue}x^{2}+2x-8\\ & \end{aligned}\\ &\begin{array}{|c|c|}\hline  \textrm{Titik singgung}&\textrm{Gradien}\: ,\: x=1\\\hline \begin{aligned}\textrm{absis}\: \: x&=1,\\ \textrm{maka}\: \: y&=(1)^{2}+2(1)-8\\ &=1+2-8\\ &=-5\\ &\\ \textrm{di titik}&\: \: (a,b)=(1,-5)\end{aligned}&\begin{aligned}\displaystyle \frac{dy}{dx}=m&=2x+2\\ &=2(1)+2\\ &=4\\ &\\ & \end{aligned}\\\hline \textrm{Persamaan garis singgung}&\textrm{Kesimpulan}\\\hline\begin{aligned}y&=m(x-a)+b\\ &=4(x-1)+(-5)\\ &=4x-4-5\\ &=4x-9\end{aligned}&\begin{aligned}&\textrm{Sehingga},\: \textrm{PGS adalah:}\\ &y=\color{red}4x-9\qquad \color{black}\textbf{atau}\qquad\\ &\color{red}y-4x+9=0\\ & \end{aligned} \\\hline  \end{array}\\ &\begin{aligned}&\textrm{Jadi},\: \textrm{persamaan garis singgungnya adalah:}\\ &y=\color{red}4x-9\qquad \color{black}\textbf{atau}\qquad  \color{red}y-4x+9=0\\\\ &\textrm{Dan berikut ilustrasi gambarnya} \end{aligned}  \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah interval di mana kurva }\\ &\textrm{fungsi}\: \: f(x)=x^{3}+3x^{2}-9x+5\\ &\textrm{a}.\quad \textrm{naik}\\ &\textrm{b}.\quad \textrm{turun}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui fungsi}\\f(x)&=x^{3}+3x^{2}-9x+5\\ {f}\, '(x)&=3x^{2}+6x-9\\ &=3(x+3)(x-1)\\ & \end{aligned}\\ &\begin{array}{|l|l|}\hline  \qquad\textrm{naik}\: ;\: \: {f}\, '(x)> 0&\quad\textrm{turun}\: ;\: \: {f}\, '(x)< 0\\\hline \begin{aligned}&\\ &3(x+3)(x-1)> 0\\ & \end{aligned}&\begin{aligned}&\\ &3(x+3)(x-1) < 0\\ & \end{aligned}\\\hline \begin{aligned}&\\ \textrm{naik}\: ,&\: x< -3\: \: \textrm{atau}\: \: x> 1\\ & \end{aligned}&\begin{aligned}&\\ \textrm{turun}\: ,&\: -3< x< 1\\ & \end{aligned}\\\hline \end{array} \end{array}$ .

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah nilai stasioner fungsi}\\ & f(x)=x^{3}+3x^{2}-9x+5 \: \: \textrm{dan }\\ &\textrm{tentukan pula jenisnya}\\\\&\textbf{Jawab}:\\&\begin{aligned}&\textrm{Diketahu fungsi}\\&f(x)=x^{3}+3x^{2}-9x+5\\ &\color{blue}\textrm{Syarat stasioner}\: \: \color{black}f'(x)=0,\: \: \textrm{maka}\\ &{f}\, '(x)=3x^{2}+6x-9=0\\ &\qquad 0=3(x+3)(x-1)\\ &\: \: \: \qquad x=-3\: \: \textrm{atau}\: \: x=1\\ &\color{blue}\textrm{Dan untuk nilai dan titik stasionernya}: \\ &f(-3)=(-3)^{3}+3(-3)^{2}-9(-3)+5=32\\ &\rightarrow \left ( -3,32 \right )\: \color{red}\textrm{adalah titik balik maksimum}\\\\ &f(1)=(1)^{3}+3(1)^{2}-9(1)+5=0\\ &\rightarrow \left ( 1,0 \right )\: \color{red}\textrm{adalah titik balik minimum}\\\\ &\textrm{Dan berikut ilustrasi gambarnya}\\ &\textrm{untuk soal no.2 dan 3} \end{aligned}  \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Masih sama dengan soal seperti pada  }\\ &\textrm{No. sebelumnya yaitu fungsi}\\ &f(x)=x^3+3x^2-9x+5\: .\\ & \textrm{Tentukanlah koordinat titik beloknya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned} f(x)&=x^3+3x^2-9x+5\\ {f}\, '(x)&=3x^{2}+6x-9\\ {f}\, ''(x)&=6x+6\\ \textrm{Proses}\: &\textrm{mencari titik beloknya}\\ {f}\, ''(x)&=0\\ 6x+6&=0\\ 6x&=-6\\ x&=-1\\ & \end{aligned} \\ &\begin{array}{|c|c|c|c|l|}\hline  \textrm{Interval}&f(x)&{f}\, '(x)&{f}\, ''(x)&\: \: \qquad \textrm{Keterangan}\\\hline x< -1&&&-&\textrm{grafik cekung ke bawah}\\\hline x= -1&16&-12&0&\textrm{grafik memiliki titik belok}\\\hline x > -1&&&+&\textrm{grafik cekung ke atas}\\\hline \end{array} \\ &\textrm{Koordinat titik beloknya}: \: (-1,16)\\\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.