Perbandingan Trigonometri Sudut dalam Segitiga Siku-Siku

B. Perbandingan Trigonometri Suatu Sudut

B. 1 Perbandingan Trigonometri pada Segitiha Siku-Siku

Perhatikanlah ilustrasi  dari segitiga ABC siku-siku di C berikut

$\begin{matrix} \sin \alpha =\displaystyle \frac{BC}{AB}\qquad\Leftrightarrow\quad \csc \alpha =\displaystyle \frac{AB}{BC}=\color{red}\displaystyle \frac{1}{\sin \alpha }\\\\ \cos \alpha =\displaystyle \frac{AC}{AB}\qquad\Leftrightarrow \quad \sec \alpha =\displaystyle \frac{AB}{AC}=\color{red}\displaystyle \frac{1}{\cos \alpha }\\\\ \tan \alpha =\displaystyle \frac{BC}{AC}\qquad\Leftrightarrow \quad \cot \alpha =\displaystyle \frac{AC}{BC}=\color{red}\displaystyle \frac{1}{\tan \alpha }  \end{matrix}$.

B. 2 Perbandingan Trigonometri untuk Sudut Istimewa.

$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline \alpha ^{0}&0^{0}&30^{0}&45^{0}&60^{0}&90^{0}&180^{0}&270^{0}&360^{0}\\\hline \sin \alpha ^{0}&0&\color{red}\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}\sqrt{2}&\displaystyle \frac{1}{2}\sqrt{3}&1&0&-1&0\\\hline \cos \alpha ^{0}&1&\displaystyle \frac{1}{2}\sqrt{3}&\displaystyle \frac{1}{2}\sqrt{2}&\color{red}\displaystyle \frac{1}{2}&0&-1&0&1\\\hline \tan \alpha ^{0}&0&\displaystyle \frac{1}{3}\sqrt{3}&1&\sqrt{3}&TD&0&TD&0\\\hline \end{array}$.

B. 3. Tripel Pythagoras pada Segitiga Siku-Siku

$\begin{array}{|c|c|c|c|}\hline a&b&c=\sqrt{a^{2}+b^{2}}&\color{red}\textrm{Tripel}\\\hline 3&4&5&(3,4,5)\\\hline 5&12&13&(5,12,13)\\\hline 7&24&25&(7,24,25)\\\hline 8&15&17&(8,15,17)\\\hline 9&40&41&(9,40,41)\\\hline 11&60&61&(11,60,61)\\\hline 12&35&37&(12,35,37)\\\hline 15&112&113&(15,112,113)\\\hline 16&63&65&(16,63,65)\\\hline 17&144&145&(17,144,145)\\\hline 19&180&181&(19,180,181)\\\hline 20&21&29&(20,21,29)\\\hline 21&220&221&(21,220,221)\\\hline 29&420&421&(29,420,421)\\\hline 30&224&226&(30,224,226)\\\hline 31&480&481&(31,480,481)\\\hline 33&544&545&(33,544,545)\\\hline 35&612&613&(35,612,613)\\\hline 37&684&685&(37,684,685)\\\hline 39&760&761&(39,760,761)\\\hline 41&840&841&(41,840,841)\\\hline 43&924&925&(43,924,925)\\\hline 45&1012&1013&(45,1012,1013)\\\hline 47&1104&1105&(47,1104,1105)\\\hline 48&55&73&(48,55,73)\\\hline 49&1200&1201&(49,1200,1201)\\\hline 51&1300&1301&(51,1300,1301)\\\hline 60&63&87&(60,63,87)\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah nilai perbandingan}\: \:  \color{red}\sin \alpha \\ & \color{red}\cos \alpha , \tan \alpha  \: \: \color{black}\textrm{untuk segitiga berikut} \end{array}$.

$.\: \qquad\begin{aligned}&\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Untuk sisi miringnya adalah}\\ &\begin{aligned}\textrm{Sisi  miring}&=\sqrt{3^{2}+4^{2}}\\ &=\sqrt{9+16}\\ &=\sqrt{25}\\ &=5 \end{aligned}\\ &\textrm{Sehingga}\\ &\color{red}\sin \alpha =\displaystyle \frac{3}{5},\: \: \:  \cos \alpha =\frac{4}{5}\: \:  \color{black}\textrm{dan}\: \color{red}\tan \alpha =\frac{3}{4}\\ &\textrm{Dengan langkah sama}\\ \end{aligned}\\&\begin{aligned}\textrm{b}.\quad&\textrm{Untuk sisi miringnya adalah}\\&\begin{aligned}\textrm{Sisi  miring}&=\sqrt{5^{2}+12^{2}}\\&=\sqrt{25+144}\\&=\sqrt{169}\\ &=13 \end{aligned}\\ &\textrm{Sehingga}\\ &\color{red}\sin \alpha =\frac{12}{13}\: \:  \cos \alpha =\frac{5}{13}\: \:  \color{black}\textrm{dan}\: \color{red}\tan \alpha =\frac{12}{5}. \end{aligned}  \end{aligned}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah nilai dari}\\ &\begin{array}{llll} \textrm{a}.&\left ( \tan 30^{0}+\sin 30^{0} \right )\cos 30^{0}\\ \textrm{b}.&\left ( \tan 60^{0} \right )^{2}+4\left ( \sin 60^{0} \right )^{2}\\ \textrm{c}.&\tan 60^{0}-\sin 60^{0}-\tan 30^{0}\\ \textrm{d}.&\displaystyle \frac{1+\sin 30^{0}}{\sin 30^{0}}+\frac{\cos 30^{0}}{1+\sin 30^{0}}\\ \textrm{e}.&\displaystyle \frac{2\tan 30^{0}}{1+\tan ^{2}30^{0}} \end{array}\\\\ &\textbf{Jawab}:\\ \end{array}$.

$.\: \qquad\begin{array}{|l|l|}\hline \begin{array}{llll} \textrm{a}.&\left ( \tan 30^{0}+\sin 30^{0} \right )\cos 30^{0}\\ &=\displaystyle \left ( \frac{1}{3}\sqrt{3}+\frac{1}{2} \right ).\frac{1}{2}\sqrt{3}\\ &=\displaystyle \frac{1}{2}+\frac{1}{4}\sqrt{3} \end{array}&\begin{array}{llll} \textrm{b}.&\left ( \tan 60^{0} \right )^{2}+4\left ( \sin 60^{0} \right )^{2}\\ &\displaystyle =\left ( \sqrt{3} \right )^{2}+4\left ( \frac{1}{2}\sqrt{3} \right )^{2}\\ &\displaystyle =3+3\\ &=6 \end{array}\\\hline \begin{array}{llll} \textrm{c}.&\tan 60^{0}-\sin 60^{0}-\tan 30^{0}\\ &=\displaystyle \sqrt{3}-\frac{1}{2}\sqrt{3}-\frac{1}{3}\sqrt{3}\\ &=\displaystyle \sqrt{3}-\frac{5}{6}\sqrt{3}\\&=\displaystyle \frac{1}{6}\sqrt{3} \end{array}&\begin{array}{llll} \textrm{d}.&\displaystyle \frac{1+\sin 30^{0}}{\sin 30^{0}}+\frac{\cos 30^{0}}{1+\sin 30^{0}}\\ &=\displaystyle \frac{1+\frac{1}{2}}{\frac{1}{2}}+\frac{\frac{1}{2}\sqrt{3}}{1+\frac{1}{2}}\\ &=\displaystyle 3+\frac{1}{3}\sqrt{3} \end{array}.\\\hline \begin{array}{llll} \textrm{e}.&\displaystyle \frac{2\tan 30^{0}}{1+\tan ^{2}30^{0}}\\ &=\displaystyle \frac{2\times \frac{1}{3}\sqrt{3}}{1+\left ( \frac{1}{3}\sqrt{3} \right )^{2}}\\ &=\displaystyle \frac{\frac{2}{3}\sqrt{3}}{1+\frac{1}{3}}\\ &=\displaystyle \frac{\frac{2}{3}\sqrt{3}}{\frac{4}{3}}\\ &=\displaystyle \frac{1}{2}\sqrt{3} \end{array}.&\\\hline \end{array}$.

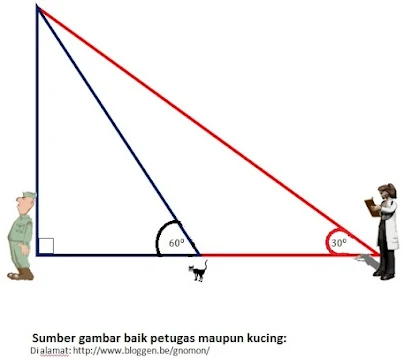
$\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah ilustrasi berikut}\\ \end{array}$

$.\: \qquad\begin{aligned}&\textrm{Jika Jarak antara kucing seorang pencatat}\\ &\textrm{dan kucing adalah 100 m, maka jarak}\\ &\textrm{Pencatat tersebut dengan seorang tentara}\\ &\textrm{sebagaimana gambar tersebut di atas adalah}?\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan gambar di atas dengan diberikan}\\ &\textrm{tambahan keterangan sebagai berikut} \end{aligned}$.

$.\: \qquad\begin{aligned}&\textrm{Ditanya berpakah  panjang jarak } \left ( x+100 \right ) ?\\ &\begin{aligned}\quad&\textrm{Pilih}\: :\qquad  \color{blue}y=y\\ &\Leftrightarrow x.\tan 60^{0}=\left ( x+100 \right ).\tan 30^{0}\\ &\Leftrightarrow x.\sqrt{3}=\left ( x+100 \right )\frac{1}{3}\sqrt{3}\\ &\Leftrightarrow 3x=x+100\\ &\Leftrightarrow 2x=100\\ &\Leftrightarrow x=50 \end{aligned}\\ &\textrm{Jadi}\: \:   x+100=50+100=\color{red}150 \: \: \color{black}\textrm{meter}. \end{aligned}$.

$\begin{array}{ll}\\ 4. &\textrm{Tentukanlah perbandingan trigonometri}\\ &\quad  \angle XOA\: \:   \textrm{jika}\: \:  A(3,5)\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \end{array}$.

$\: \qquad\begin{aligned}&\textrm{Dengan memandang ilustrasi gambar di atas}\\ &\textrm{kita mendapatkan}\: \:   \triangle OAA',\: \:  \textrm{dengan menggunakan}\\ &\textrm{teorema pythagoras kita mendapatkan}\\ &\begin{aligned}OA^{2}&=\left ( OA' \right )^{2}+\left ( AA' \right )^{2}\\ &=3^{2}+5^{2}\\ &=9+25\\ &=34\\ OA&=\sqrt{34} \end{aligned}.\\ &\textrm{Sehingga akan didapatkan}\\ &\begin{array}{llll} \textrm{a}.&\displaystyle \sin A'OA=\frac{5}{\sqrt{34}}=\frac{5}{34}\sqrt{34}\\ \textrm{b}.&\displaystyle \cos A'OA=\frac{3}{\sqrt{34}}=\frac{3}{34}\sqrt{34}\\ \textrm{c}.&\displaystyle \tan A'OA=\frac{5}{3} \end{array}. \end{aligned}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah nilai dari}\\ &\begin{array}{llll} \textrm{a}.&\left ( \tan 60^{0}+\sin 45^{0} \right )\cos 0^{0}\\ \textrm{b}.&\left ( \tan 30^{0} \right )^{2}+4\left ( \sin 30^{0} \right )^{2}\\ \textrm{c}.&\tan 60^{0}+\sin 60^{0}+\tan 30^{0}\\ \textrm{d}.&\displaystyle \frac{1+\sin 45^{0}}{\sin 30^{0}}+\frac{\cos 30^{0}}{1+\sin 45^{0}}\\ \textrm{e}.&\displaystyle \frac{2\tan 60^{0}}{1+\tan ^{2}60^{0}} \end{array} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan nilai perbandingan trigonometrinya}\\ &\textrm{dari gambar segitiga berikut} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui}\: \: \tan \alpha =0,75.\: \: \textrm{Tentukan nilai}\\ &\textrm{perbandingan trigonometri berikut}\\ &\begin{array}{llll} \textrm{a}.&\sin \alpha \\ \textrm{b}.&\cos \alpha \\ \textrm{c}.&\csc \alpha \\ \textrm{d}.&\sec \alpha \\ \textrm{e}.&\cot \alpha \\ \textrm{f}.&\sin^{2} \alpha+\cos ^{2}\alpha  \\ \end{array} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Jika}\: \: 1-\cos \beta  =\displaystyle \frac{9}{25(1+\cos \beta )}\: \: \textrm{Tentukan}\\ &\textrm{nilai dari}\: \: \: \tan \beta  \end{array}$.

DAFTAR PUSTAKA

1. Kurnianingsih, S., Kuntarti, Sulistiyono. 2007. Matematika SMA dan MA untuk Kelas X Semester 2 Standar Isi 2006. Jakarta: ESIS.
2. Marwanta, dkk. 2013. Matematika SMA Kelas X. Jakarta: YUDHISTIRA.
3. Yuana. R.A., Indriyastuti. 2017. Persepktif Matematika untuk Kelas X SMA dan MA Kelompok Matematika Wajib. Solo: TIGA SERANGKAI PUSTAKA MANDIRI.