Fungsi Trigonometri dan Grafiknya

F. Fungsi Trigonometri dan Grafiknya

F. 1 Fungsi Trigonometri

Perhatikan ilustrasi berikut ini

Dengan

$\begin{array}{c|c}\\ \begin{aligned}&\textrm{Dalil/rumus Pythagoras}\\ &a^{2}+b^{2} =c^{2}\\ &\color{red}\textrm{atau}\\ &c=\sqrt{a^{2}+b^{2}} \end{aligned}&\begin{aligned}&\sin \angle ACB=\displaystyle \frac{a}{c}\\ &\cos \angle ACB=\displaystyle \frac{b}{c}\\ &\tan \angle ACB=\displaystyle \frac{a}{b}=\displaystyle \frac{\sin \angle ACB}{\cos \angle ACB} \end{aligned} \end{array}$.

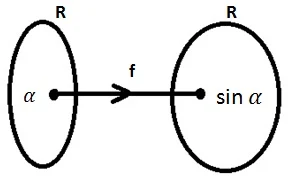
Adapun gambar dari fungsi atau pemetaan trigonometrinya dari setiap sudut $\alpha $ ke salah satu nilai dari $\sin \alpha$ , $\cos \alpha$, maupun $\tan \alpha$  dalam wilayah bilangan real adalah  sebagaimana ilustrasi berikut:

$\begin{aligned}&\textrm{Misalkan}\: \: A\: \: \textrm{dan}\: \: B\: \: \textrm{dua himpunan}\\ &\textrm{Suatu relasi}\: \: F\subseteq A\times B\: \: \textrm{disebut fungsi jika}\\ &\textrm{setiap}\: a\in A,\: \textrm{maka hanya ada tepat satu}\: \: b\in B\\ &\textrm{dengan}\: \: (a,b)\in F.\\ &\textrm{Fungsi}\: \: F\: \: \textrm{disebut dengan fungsi dari}\: \: A\: \: \textrm{ke}\: \: B\\ &\textrm{Selanjutnya}\: \: A\: \: \textrm{dinamakan}\: \: \textbf{Domain}\: \: \textrm{atau}\\ &\textrm{daerah asal atau juga daerah definisi fungsi}\\ &\textrm{dan}\: \: B\: \: \textrm{disebut}\: \: \textbf{Kodomain}\\ &\textrm{Himpunan}\: \: \left \{ b\in B|(a,b)\in F \right \}\: \textrm{selanjutnya disebut}\\ &\textrm{sebagai}\: \: \textbf{nilai fungsi}\\ &\textrm{Jika}\: \: (a,b)\in F,\: \: \textrm{maka dapat tuliskan dengan}\\ &b=F(a),\: \: \textrm{yaitu nilai fungsi}\: \: F\: \: \textrm{di titik}\: \: a\\\\ &\textrm{Perhatikan tabel berikut}\\ &\begin{array}{|c|l|c|}\hline \textrm{No}&\: \: \quad\color{red}\textrm{Gambar}&\color{red}\textrm{Fungsi}\: \left ( f:\mathbb{R}\Rightarrow \mathbb{R} \right )\\\hline 1&\textrm{Fungsi Sinus}&\begin{aligned}&f:\alpha \Rightarrow \sin \alpha  \end{aligned}\\\hline 2&\textrm{Fungsi Cosinus}&\begin{aligned}&f:\alpha \Rightarrow \cos \alpha  \end{aligned}\\\hline 3&\textrm{Fungsi Tangen}&\begin{aligned}&f:\alpha \Rightarrow \tan \alpha  \end{aligned}\\\hline \end{array}  \end{aligned}$.

$\begin{aligned}&\textrm{Jangan lupa, sebagai pengingat kita untuk}\\ &\textrm{nilai sudut istimewanya adalah sebagai berikut}:\\ &\begin{array}{|c|c|c|c|c|c|c|}\hline \alpha &0^{\circ}&30&45^{\circ}&60^{\circ}&90^{\circ}&180^{\circ}\\\hline \sin \alpha &0&\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}\sqrt{2}&\displaystyle \frac{1}{2}\sqrt{3}&1&0\\\hline \cos \alpha &1&\displaystyle \frac{1}{2}\sqrt{3}&\displaystyle \frac{1}{2}\sqrt{2}&\displaystyle \frac{1}{2}&0&-1\\\hline \tan \alpha &0&\displaystyle \frac{1}{3}\sqrt{3}&1&\sqrt{3}&\color{red}\textrm{TD}&0\\\hline \end{array} \end{aligned}$.

$\LARGE\colorbox{yellow}{ CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Jika diketahui}\: \: f(x)=\sin 2x,\: \: \textrm{tentukan nilai}\\ &\textrm{a}.\quad f(60^{\circ})\\ &\textrm{b}.\quad f\left ( \displaystyle \frac{1}{3}\pi  \right )\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&f(60^{\circ})=\sin 2\left ( 60^{\circ} \right )=\sin 120^{\circ}\\ &\: \: \: \qquad =\sin \left ( 180^{\circ}-60^{\circ} \right )=\sin 60^{\circ}=\displaystyle \frac{1}{2}\sqrt{3}\\ \textrm{b}.\quad&f\left ( \displaystyle \frac{1}{3}\pi  \right )=\sin 2\left ( \displaystyle \frac{1}{3}\pi  \right )=\sin \left ( \displaystyle \frac{2}{3}\pi  \right )\\ &\: \: \qquad\quad =\sin \left ( \displaystyle \frac{2}{3}(180^{\circ}) \right )=\sin 120^{\circ}=\displaystyle \frac{1}{2}\sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Jika diketahui}\: \: f(x)=\sin x,\: \: \textrm{tentukan harga}\\ &x\: \: \textrm{jika diketahui}\: (\: x\: \: \textrm{sudut lancip})\\ &\textrm{a}.\quad f(x)=\displaystyle \frac{1}{2}\\ &\textrm{b}.\quad f(x)=\displaystyle \frac{1}{4}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&f(x)=\displaystyle \frac{1}{2}=\sin x\Rightarrow x=30^{\circ}\\ \textrm{b}.\quad&f(x)=\displaystyle \frac{1}{4}=\sin x\Rightarrow x=\color{red}\sin ^{-1}\left ( \displaystyle \frac{1}{4} \right )\\ &\textrm{hal ini dikarenakan}\: \: \displaystyle \frac{1}{4}\: \: \textrm{bukanlah}\\ &\textrm{nilai dari salah satu sudut istimewa}\\ &\textrm{untuk fungsi}\: \: \textbf{sinus} \end{aligned} \end{array}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Jika diketahui}\: \: f(x)=\cos 2x,\: \: \textrm{tentukan nilai}\\  &\textrm{a}.\quad f(60^{\circ})\\ &\textrm{b}.\quad f\left ( \displaystyle \frac{1}{3}\pi  \right )\end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Jika diketahui}\: \: f(x)=\tan x,\: \: \textrm{tentukan nilai}\\  &\textrm{a}.\quad f(60^{\circ})\\ &\textrm{b}.\quad f\left ( \displaystyle \frac{1}{3}\pi  \right )\end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Jika diketahui}\: \: f(x)=\cos x,\: \: \textrm{tentukan harga}\\ &x\: \: \textrm{jika diketahui}\: (\: x\: \: \textrm{sudut lancip})\\ &\textrm{a}.\quad f(x)=\displaystyle \frac{1}{2}\\ &\textrm{b}.\quad f(x)=\displaystyle \frac{1}{4} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Jika diketahui}\: \: f(x)=\tan x,\: \: \textrm{tentukan harga}\\ &x\: \: \textrm{jika diketahui}\: (\: x\: \: \textrm{sudut lancip})\\ &\textrm{a}.\quad f(x)=\displaystyle \frac{1}{3}\sqrt{3}\\ &\textrm{b}.\quad f(x)=\displaystyle \frac{1}{6}\sqrt{3} \end{array}$

DAFTAR PUSTAKA

1. Budhi, W.S. 2014. Bupena Matematika SMA/MA Kelas X Kelompok Wajib. Jakarta: ERLANGGA.
2. Yuana, R.A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Mata Pelajaran Wajib. Solo: TIGA SERANGKAI PUSTAKA MANDIRI.