$\begin{array}{ll}\\ 16.&\textrm{Salah satu garis singgung yang bersudut}\: \: 120^{\circ}\\ &\textrm{terhadap sumbu x positif terhadap lingkaran}\\ &\textrm{dengan ujung diameter titik}\: \: (7,6)\: \textrm{dan}\: \: (1,-2)\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}y=-x\sqrt{3}+4\sqrt{3}+12\\ &\textrm{b}.\quad y=-x\sqrt{3}-4\sqrt{3}+8\\ &\textrm{c}.\quad y=-x\sqrt{3}+4\sqrt{3}-4\\ &\textrm{d}.\quad y=-x\sqrt{3}-4\sqrt{3}-8\\ &\textrm{e}.\quad y=-x\sqrt{3}+4\sqrt{3}+22\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline \textrm{Pusat Lingkaran}&\textrm{Gradien Garis Singgung}\\\hline \begin{aligned}&(a,b)\\ &=\left ( \displaystyle \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )\\ &=\left ( \displaystyle \frac{7+1}{2},\frac{6+(-2)}{2} \right )\\ &=(4,2) \end{aligned}&\begin{aligned}m&=\tan 120^{\circ}\\ &=-\tan \left ( 180^{\circ}-60^{\circ} \right )\\ &=-\tan 60^{\circ}\\ &=-\sqrt{3}\\ &\\ \end{aligned} \\\hline \textrm{Jari-jari}&\textrm{Garis Singgung}\\\hline \begin{aligned}r&=\textrm{jarak titik}\\ &\: \: \: \: \: \, \textrm{singgung ke pusat}\\ &=\sqrt{(7-4)^{2}+(6-2)^{2}}\\ &=\sqrt{3^{2}+4^{2}}\\ &=\sqrt{25}\\ &=5\\ &\\ &\\ & \end{aligned}&\begin{aligned} &(y-b)=m(x-a)\pm r\sqrt{1+m^{2}}\\ &\Leftrightarrow (y-2)=-\sqrt{3}(x-4)\pm 5\sqrt{1+(-\sqrt{3})^{2}}\\ &\Leftrightarrow y-2=-\sqrt{3}x+4\sqrt{3}\pm 5\sqrt{1+4}\\ &\Leftrightarrow y=-\sqrt{3}x+4\sqrt{3}+2\pm 10\\ &\Leftrightarrow y=\begin{cases} -\sqrt{3}x+4\sqrt{3}+2+ 10 \\ -\sqrt{3}x+4\sqrt{3}+2- 10 \end{cases}\\ &\Leftrightarrow y=\begin{cases} \color{red}-\sqrt{3}x+4\sqrt{3}+12 & \\ -\sqrt{3}x+4\sqrt{3}-8 & \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.

Dengan ilustrasi tambahan

$\begin{array}{ll}\\ 17.&\textrm{Salah satu garis singgung lingkaran}\\\ & x^{2}+y^{2}=10\: \: \textrm{yang ditarik dari}\\ &\textrm{titik}\: \: (4,2)\: \: \textrm{adalah}....\\ &\textrm{a}.\quad \color{red}x+3y=10\\ &\textrm{b}.\quad x-3y=10\\ &\textrm{c}.\quad -x-3y=10\\ &\textrm{d}.\quad 2x+y=10\\ &\textrm{e}.\quad x+2y=10\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline \begin{aligned}&\textrm{Garis Singgung}\\ &\quad\quad \textrm{di titik}\\ &(x_{1},y_{1})=(4,2) \end{aligned}&\begin{aligned}&\textrm{Tahapan menentukan}\\ &\quad\qquad \textrm{harga}\: \: m\\ & \end{aligned}\\\hline \begin{aligned}&y-y_{1}=m(x-x_{1})\\ &y-2=m(x-4)\\ &y=mx-4m+2\\ &\\ &\\ &\\ & \end{aligned}&\begin{aligned}&x^{2}+y^{2}=10\\ &x^{2}+\left ( mx-4m+2 \right )^{2}=10\\ &x^{2}+m^{2}x^{2}+16m^{2}+4-8m^{2}x+4mx-16m=10\\ &x^{2}+m^{2}x^{2}+16m^{2}-8m^{2}x+4mx-16m-6=0\\ &(1+m^{2})x^{2}+(4m-8m^{2})x+16m^{2}-16m-6=0\\ &\begin{cases} a & =1+m^{2} \\ b & =4m-8m^{2} \\ c & =16m^{2}-16m-6 \end{cases} \end{aligned}\\\hline \end{array}\\ &\begin{aligned}&\textrm{Syarat menyinggung}\: \: D=0\\ &b^{2}-4ac=0\\ &\left ( 4m-8m^{2} \right )^{2}-4\left ( 1+m^{2} \right )\left ( 16m^{2}-16m-6 \right )=0\\ &16m^{2}-64m^{3}+64m^{4}-64m^{2}+64m+24-64m^{4}+64m^{3}+24m^{2}=0\\ &-24m^{2}+64m+24=0\\ &-3m^{2}+8m+3=0\\ &(m-3)(3m+1)=0\\ &m=3\: \: \textrm{atau}\: \: m=-\displaystyle \frac{1}{3}\\ &m=\begin{cases} 3 & \Rightarrow y=3x-10\\ &\Rightarrow 3x-y=10\\ -\displaystyle \frac{1}{3} & \Rightarrow y=-\displaystyle \frac{1}{3}x+\frac{4}{3}+2\\ &\Rightarrow \color{red}x+3y=10 \end{cases} \end{aligned} \end{array}$.
$.\qquad\begin{aligned}&\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned}$

$\begin{array}{ll}\\ 18.&\textrm{Diketahui persamaan lingkaran}\: \: x^{2}+y^{2}=r^{2}\\ &\textrm{dan sebuah titik di luar lingkaran}\: \: M(a,b)\\ &\textrm{Posisi garis}\: \: ax+by=r^{2}\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{menyinggung lingkaran}\\ &\textrm{b}.\quad \color{red}\textrm{memotong lingkaran di dua titik}\\ &\textrm{c}.\quad \textrm{melalui titik pusat lingkaran}\\ &\textrm{d}.\quad \textrm{tidak memotong lingkaran}\\ &\textrm{e}.\quad \textrm{tidak ada yang benar}\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\\ &\bullet \quad L\equiv x^{2}+y^{2}=r^{2}\\ &\bullet \quad M(a,b)\: \: \textrm{di luar lingkaran}\: \: L\\ &\color{purple}\textrm{Selanjutnya perhatikan penjelasan berikut}\\ &\begin{aligned}&\textrm{Karena}\: M(a,b)\: \textrm{di luar lingkaran}\: L,\: \textrm{maka}\\ &\textrm{maka salah satu dari}\: \: a\: \: \textrm{atau}\: \: b\: \: \textrm{atau keduanya}\\ &\textrm{akan lebih besar nilanya dari pada}\: \: r.\\ &\textrm{Misalkan kita pilih}\: \: a>r\\ &\color{blue}\textrm{Ambil posisi saat memotong sumbu}-X,\: \color{black}y=0\\ &\begin{aligned}&\textrm{Untuk lingkaran}\: \: x^{2}+y^{2}=r^{2}\\ &\bullet \quad y=0\Rightarrow x^{2}+0^{2}=r^{2}\Rightarrow x=\left | r \right |\\ &\textrm{Untuk garis}\: \: ax+by=r^{2}\\ &\bullet \quad y=0\Rightarrow ax=r^{2}\Rightarrow x=\displaystyle \frac{r^{2}}{a}\\ &\textrm{Dari sini tampak posisi}\: \: x=\color{red}\left | r \right |> \displaystyle \frac{r^{2}}{a}\geq 0 \end{aligned}\\ &\textrm{Sehingga kesimpulannya adalah}:\\ &\color{red}\textrm{garis tersebut akan selalu memotong lingkaran} \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

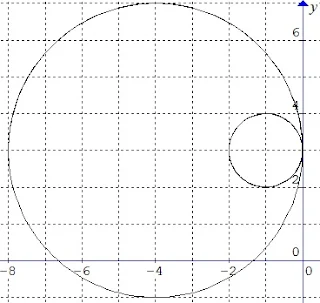
$\begin{array}{ll}\\ 19.&\textrm{Dua lingkaran dengan persamaan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+6x-8y+21=0\\ &\textrm{dan}\: \: x^{2}+y^{2}+10x-8y+25=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{berpotongan di luar titik}\\ &\textrm{b}.\quad \textrm{tidak berpotongan atau bersinggungan}\\ &\textrm{c}.\quad \textrm{bersinggungan luar}\\ &\textrm{d}.\quad \color{red}\textrm{bersinggungan dalam}\\ &\textrm{e}.\quad \textrm{sepusat}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+6x-8y+21=0&\begin{cases} P_{1} &=(-3,4) \\ r_{1} & = 2 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+10x-8y+25=0&\begin{cases} P_{2} &=(-5,4) \\ r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{dan}\\ &\begin{array}{|c|c|}\hline \textrm{Jarak kedua pusat}&\textrm{Jumlah/selisih jari-jari}\\\hline \begin{aligned}&\left (P_{1}P_{2} \right )\\ &=\sqrt{(-3+5)^{2}+(4-4)^{2}}\\ &=\sqrt{2^{2}+0^{2}}=\sqrt{4}=2 \end{aligned}&\begin{aligned}\begin{cases} r_{1}+r_{2} & =2+4=6 \\ \left |r_{1}-r_{2} \right | & =\left | 2-4 \right |=2 \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Karena nilai}\: \: \color{red}P_{1}P_{2}\color{black}=\color{red}\left |r_{1}-r_{2} \right |\color{black}=\color{red}2\\ &\textrm{hal ini menunjukkan keduanya bersinggungan}\\ &\color{blue}\textrm{di dalam}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$ .

$\begin{array}{ll}\\ 20.&\textrm{Dua lingkaran dengan persamaan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+2x-6y+9=0\\ &\textrm{dan}\: \: x^{2}+y^{2}+8x-6y+9=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{berpotongan}\\ &\textrm{b}.\quad \color{red}\textrm{bersinggungan di dalam}\\ &\textrm{c}.\quad \textrm{bersinggungan luar}\\ &\textrm{d}.\quad \textrm{tidak berpotongan}\\ &\textrm{e}.\quad \textrm{sepusat}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x-6y+9=0&\begin{cases} P_{1} &=(-1,3) \\ r_{1} & = 1 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+8x-6y+9=0&\begin{cases} P_{2} &=(-4,3) \\ r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{dan}\\ &\begin{array}{|c|c|}\hline \textrm{Jarak kedua pusat}&\textrm{Jumlah/selisih jari-jari}\\\hline \begin{aligned}&\left (P_{1}P_{2} \right )\\ &=\sqrt{(-1+4)^{2}+(3-3)^{2}}\\ &=\sqrt{3^{2}+0^{2}}=\sqrt{9}=3 \end{aligned}&\begin{aligned}\begin{cases} r_{1}+r_{2} & =1+4=5 \\ \left |r_{1}-r_{2} \right | & =\left | 1-4 \right |=3 \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Karena nilai}\: \: \color{red}P_{1}P_{2}\color{black}=\color{red}\left |r_{1}-r_{2} \right |\color{black}=\color{red}3\\ &\textrm{hal ini menunjukkan keduanya bersinggungan}\\ &\color{blue}\textrm{di dalam}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.
DAFTAR PUSTAKA
- Budi, W. S. 2010. Bahan Ajar Persiapan Menuju Olimpiade Sain Nasional/Internasional Matematika 3. Jakarta: ZAMRUD KEMALA.
- Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
- Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
- Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
- Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
- Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.






Tidak ada komentar:
Posting Komentar
Informasi