PAS MATEMATIKA BLOG

Metode statistika banyak dijumpai dalam kehidupan kita sehari-hari. Pernyataan-pernyataan berikut terkait dengan statistika:rRata-rata nilai ulangan matematika siswa kelas XI SMA Ceria adalah 7,8; Jenis mobil yang banyak dibeli masyarakat triwulan tahun 2024 ini adalah jenis MPV, dan lain-lain.

B. Statitik dan Statistika

B. 1 Pengertian Statistika dan Statistik

Statistika adalah ilmu yang mempelajari metode-metode ilmiah terkait pengumpulan data, pengorganisasian dat, penyajian data, pengolahan data, serta interpretasi dan penarikan kesimpulan. Metode yang berkaitan dengan pengumpulan, pengorganisasian, penyajian serta pengolahan data disebut statistika deskriptif, sedangkan metode yang berkaitan dengan pengujian hipotesis, penarikan kesimpulan, pendugaan dan lain-lainnya yang semisal disebut statistika inferensia.

Dalam kehidupan sehari-hari kita sering melihat atau membaca berbagai macam laporan baik dalam bentuk angka maupun diagram. Laporan dalam bentuk diagram atau angka ini selanjutnya diamakan statistik.

B. 2 Populasi dan Sampel

Misalkan suatu hari tertentu seorang karyawan dari sebuah pabrik lampu ingin mengetahui berapa persen produksi lampu yang mengalami cacat produksi. Untuk keperluan tersebut tentunya karyawan tersebut tidak akan mengecek seluruh lampu yang telah diproduksi tersebut, tetapi cukup mengambil secara acak/random untuk diteliti. Dalam hal ini bagian dari total produksi yang diambil secara acak tadi disebut sebagai sampel dari keselurhan produksi lampu tadi yang selanjutnya disebut sebagai contoh populasi.

C. Penyajian Data

Data yang telah dikumpulkan semuanya dapat disajikan dalam bentuk daftar atau tabel. Untuk data yang besar biasanya akan disusun dalam suatu daftar atau tabel yang disebut daftar distriusi frekuensi atau daftar sebaran frekuensi. Adapun dafar distribusi dapat dibedakan menjadi dua macam, yaitu daftar distribusi frekuensi tunggal dan satunya daftar distribusi frekuensi berkelompok.

D. Ukuran Pemusatan Data

D.1 Data Tunggal

$\begin{array}{|c|l|}\hline 1.& \textrm{Mean}\quad \left ( \overline{X} \right )\\\hline &\begin{aligned}\overline{x}&=\displaystyle \frac{x_{1}+x_{2}+x_{3}+\cdots +x_{n}}{n} \end{aligned}\\\hline 2.&\textrm{Median}\quad \left ( M_{e} \right )\\\hline &\begin{aligned}&\textrm{Nilai datum tengah}\\ &\begin{aligned}M_{e}&=x_{\textrm{ganjil}}=x_{\frac{n+1}{2}}\\ M_{e}&=x_{\textrm{genap}}=\displaystyle \frac{1}{2}\left ( x_{\frac{1}{2}}+x_{\frac{1}{2}+1} \right ) \end{aligned} \end{aligned}\\\hline 3.&\textrm{Modus}\quad \left ( M_{o} \right )\\\hline &\textrm{Datum dengan frekuensi terbesar}\\\hline \end{array}$.

$\LARGE\colorbox{magenta}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukan rata-rata dari}\: \: 75,60,62,87,83,65\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\overline{x}&=\displaystyle \frac{75+60+62+87+83+65}{6}\\ &=\frac{432}{6}=72 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui nilai rata-rata 10 siswa adalah }\: \: 7,0\\ &\textrm{Jika ditambah sejumlah siswa dengan nilai 8,}\\ &\textrm{nilai rata-ratanya menjadi}\: 7\displaystyle \frac{1}{3}.\: \textrm{Berapakah }\\ &\textrm{banyak siswa yang ditambahkan}?\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\overline{x}_{baru}&=\displaystyle \frac{\overline{x}_{lama}\times 10+8\times n}{10+n}\\ 7\displaystyle \frac{1}{3}&=\displaystyle \frac{7\times 10+8\times n}{10+n}\\ \displaystyle \frac{22}{3}&=\displaystyle \frac{70+8n}{10+n}\\ &\begin{aligned}\Leftrightarrow \quad &220+22n=210+24n\\ \Leftrightarrow \quad &22n-24n=210-220\\ \Leftrightarrow \quad &-2n=-10\\ \Leftrightarrow \quad &n=\displaystyle \frac{-10}{-2}=5 \end{aligned}\\ &\textrm{Jadi, banyak siswa yang ditambahkan sebanyak 5 orang} \end{aligned} \end{array}$

D. 2 Data Berkelompok

$\begin{array}{|c|l|}\hline 1.& \textrm{Mean}\quad \left ( \overline{X} \right )\\\hline &\begin{aligned}\overline{x}&=\displaystyle \frac{\displaystyle \sum_{i=1}^{n}f_{i}x_{i}}{\displaystyle \sum_{i=1}^{n}f_{i}}\quad \textbf{atau}\quad \overline{X}=\overline{x}_{s}+\displaystyle \frac{\displaystyle \sum_{i=1}^{n}d_{i}x_{i}}{\displaystyle \sum_{i=1}^{n}f_{i}} \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ \overline{x}&=\textrm{rataan sementara}\\ x_{i}&=\textrm{titik tengah interval kelas ke}-i\\ d_{i}&=x_{i}-\overline{x}_{s}\\ f_{i}&=\textrm{frekuensi kelas ke}-i \end{aligned}\\\hline \end{array}$.

$\begin{array}{|c|l|}\hline 2.& \textrm{Median}\quad \left ( M_{e}=Q_{2} \right )\\\hline &\begin{aligned}M_{e}&=L_{2}+c\left ( \displaystyle \frac{\displaystyle \frac{1}{2}n-F_{2}}{f_{3}} \right ) \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ L_{2}&=\textrm{tepi bawah kelas kuartil tengah}\: \left (Q_{2} \right )\\ n&=\textrm{ukuran data=total datum=total frekuensi}\\ f_{2}&=\textrm{frekuensi pada kelas kuartil tengah}\: \left (Q_{2} \right )\\ F_{2}&=\textrm{frekuensi kumulatif sebelum kelas kuartil tengah}\\ c&=\textrm{panjang kelas} \end{aligned}\\\hline \end{array}$.

$\begin{array}{|c|l|}\hline 3.& \textrm{Modus}\quad \left ( M_{o} \right )\\\hline &\begin{aligned}M_{o}&=L+c\left ( \displaystyle \frac{d_{1}}{d_{1}+d_{2}} \right ) \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ L&=\textrm{tepi bawah kelas modus}\\ d_{1}&=\textrm{frekuensi kelas modus dengan kelas sebelumnya}\\ d_{2}&=\textrm{frekuensi kelas modus dengan kelas setelahnya}\\ c&=\textrm{panjang kelas} \end{aligned}\\\hline \end{array}$

E. Ukuran Letak Data

$\begin{array}{|c|l|}\hline 1.& \textrm{Kuartil}\quad \left ( Q_{i} \right )\\\hline &\begin{aligned}Q_{i}&=L_{i}+c\left ( \displaystyle \frac{\displaystyle \frac{i}{4}n-F_{i}}{f_{i}} \right ) \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ L_{i}&=\textrm{tepi bawah kelas kuartil ke}-i\\ n&=\textrm{ukuran data=total datum=total frekuensi}\\ f_{i}&=\textrm{frekuensi pada kelas kuartil ke}-i\\ F_{i}&=\textrm{frekuensi kumulatif sebelum kelas kuartil ke}-i\\ c&=\textrm{panjang kelas} \end{aligned}\\\hline \end{array}$.

$\begin{array}{|c|l|}\hline 2.& \textrm{Desil}\quad \left ( D_{i} \right )\\\hline &\begin{aligned}D_{i}&=L_{i}+c\left ( \displaystyle \frac{\displaystyle \frac{i}{10}n-F_{i}}{f_{i}} \right ) \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ L_{i}&=\textrm{tepi bawah kelas desil ke}-i\\ n&=\textrm{ukuran data=total datum=total frekuensi}\\ f_{i}&=\textrm{frekuensi pada kelas desil ke}-i\\ F_{i}&=\textrm{frekuensi kumulatif sebelum kelas desil ke}-i\\ c&=\textrm{panjang kelas} \end{aligned}\\\hline \end{array}$.

$\begin{array}{|c|l|}\hline 3.& \textrm{Persentil}\quad \left ( P_{i} \right )\\\hline &\begin{aligned}P_{i}&=L_{i}+c\left ( \displaystyle \frac{\displaystyle \frac{i}{100}n-F_{i}}{f_{i}} \right ) \end{aligned}\\\hline &\begin{aligned}\textrm{Keter}&\textrm{angan}:\\ L_{i}&=\textrm{tepi bawah kelas persentil ke}-i\\ n&=\textrm{ukuran data=total datum=total frekuensi}\\ f_{i}&=\textrm{frekuensi pada kelas persentil ke}-i\\ F_{i}&=\textrm{frekuensi kumulatif sebelum kelas persentil ke}-i\\ c&=\textrm{panjang kelas} \end{aligned}\\\hline \end{array}$.

F. Ukuran Penyebaran Data

$\begin{array}{|c|l|c|}\hline \textrm{No}&\: \: \: \: \textrm{Data Dispersi}&\textrm{Simbol}\\\hline 1.&\textrm{Jangkauan}&R\: \: \textrm{atau}\: \: J\\\hline 2.&\textrm{Jangkauan}&H\\ &\textrm{antarkuartil}&\\\hline 3.&\textrm{Simpangan}&Q_{d}\\ &\textrm{kuartil}&\\\hline 4.&\textrm{Langkah}&L\\\hline 5.&\textrm{Pagar dalam}&Q_{1}-L\\\hline 6.&\textrm{Pagar luar}&Q_{3}-L\\\hline 7.&\textrm{Simpangan}&SR\\ &\textrm{rata-rata}&\\\hline 8.&\textrm{Ragam/variansi}&S^{2}\\\hline 9&\textrm{Simpangan baku}&S\\\hline 10.&\textrm{Koefisien variansi}&V\\\hline \end{array}$.

G. Histogram

Diagram batang
Diagram garis
Line plot
Histogram dan poligon

H. Frekuensi Relatif

Daftar Pustaka

Johanes, Kastolan, & Sulasim. 2005. Kompetensi Matematika Program Basaha SMA Kelas XI. JAkarta: YUDHISTIRA.
Muklis. Ngapiningsih, & Astuti, A.Y. 2022. Buku Interaktif Matematika untuk SMA/MA/SMK/MAK Kelas X. Yogyakarta:PENERBIT INTAN PARIWARA.
Noormandiri. 2022. Matematika untuk SMA/MA Kelas X Kurikulum Merdeka. Jakarta: ERLANGGA.
Tim Penyusun. ....... Belajar Praktis Matematika Mata Pelajaran Wajib untuk SMA/MA Kelas XII. Klaten. VIVA PAKARINDO

Contoh Soal 8 Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 36.&\textrm{Persamaan lingkaran yang menyinggung}\\ &\textrm{sumbu X serta melalui titik potong}\\ &\textrm{lingkaran}\: \: (x+1)^{2}+(y+2)^{2}=1\: \: \textrm{dan}\\ &x^{2}+y^{2}+3x+3y+4=0\: \: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-4x+2y+4=0\\ &\textrm{b}.\quad x^{2}+y^{2}-4x+2y-4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-4x-2y-4=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}+4x+2y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}+4x+2y-4=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=(x+1)^{2}+(y+2)^{2}=1\\ &\qquad \Leftrightarrow x^{2}+y^{2}+2x+4y+4=0\\ &\bullet \: L_{2}=x^{2}+y^{2}+3x+3y+4=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-x+y=0\Leftrightarrow y=x\\ &\color{blue}\textrm{Dengan cara coba-coba, maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}+2x+4y+4+p(-x+y)=0\\ &\color{blue}\textrm{Untuk}\: \: p=1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4+(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+x+5y+4=0\\ &\color{blue}\textrm{Untuk}\: \: p=-1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+3x+3y+4=0\\ &\color{blue}\textrm{Dan untuk}\: \: p=-2\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-2(-x+y)=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}+4x+2y+4=0 \end{aligned} \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya} \end{array}$

DAFTAR PUSTAKA

Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Contoh Soal 7 Materi Hubungan Dua Lingkaran

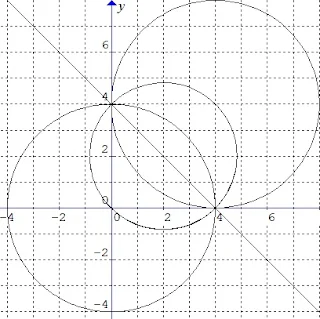
$\begin{array}{ll}\\ 31.&\textrm{Persamaan lingkaran yang melalui titik}\\ &(0,0)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x-8y-11=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-6y-22=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-12x+10y=0\\ &\textrm{b}.\quad x^{2}+y^{2}+8x-10y=0\\ &\textrm{c}.\quad x^{2}+y^{2}-8x+12y=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-8x-10y=0\\ &\textrm{e}.\quad x^{2}+y^{2}+12x-8y=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x-8y-11=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-6y-22=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-2x-2y+11=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (0,0), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x-8y-11 +p(-2x-2y+11)=0\\ &\Leftrightarrow 0^{2}+0^{2}-0-0-11+p(0+11)=0\\ &\Leftrightarrow p=\color{blue}1 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x-8y-11+(-2x-2y+11)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-10y=0 \end{aligned} \end{array}$.

Berikut ilustrasi gambarnya

$\begin{array}{ll}\\ 32.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (8,4)\: \: \textrm{dan titik potong lingkaran}\: x^{2}+y^{2}=16\\ &\textrm{dan}\: \: x^{2}+y^{2}-4x-4y=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-8x-8y-16=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x+8y+16=0\\ &\textrm{c}.\quad \color{red}x^{2}+y^{2}-8x-8y+16=0\\ &\textrm{d}.\quad x^{2}+y^{2}+8x+8y-16=0\\ &\textrm{e}.\quad x^{2}+y^{2}+8x+8y+16=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-16=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-4y=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=4x+4y-16=0\\ &\Leftrightarrow x+y=4\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (8,4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-16+p(x+y-4)=0\\ &\Leftrightarrow 8^{2}+4^{2}-16+p(8+4-4)=0\\ &\Leftrightarrow -8p=\color{blue}64\color{black}\Leftrightarrow p=\color{blue}-8 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-16-8(x+y-4)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-8y+16=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya} \end{array}$.

$\begin{array}{ll}\\ 33.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (7,-4)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x+8y-27=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-26x+4y+121=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-36x-2y+121=0\\ &\textrm{b}.\quad x^{2}+y^{2}+24x-4y-222=0\\ &\textrm{c}.\quad 3x^{2}+3y^{2}-18x+2y-121=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-36x+2y+195=0\\ &\textrm{e}.\quad x^{2}+y^{2}+24x+2y+195=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x+8y-27=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-26x+4y+121=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=20x+4y-148=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (7,-4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x+8y-27\\ &\qquad+p(20x+4y-148)=0\\ &\Leftrightarrow 7^{2}+(-4)^{2}-42-32-27\\ &\qquad+p(140-16-148)=0\\ &\Leftrightarrow -24p=\color{blue}36\color{black}\Leftrightarrow p=\color{blue}-\displaystyle \frac{3}{2} \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x+8y-27\\ &\qquad-\displaystyle \frac{3}{2}(20x+4y-148)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-36x+2y+195=0 \end{aligned} \end{array}$.

Berikut ilustrasi gambarnya

Jika dimensi gambar diperkecil menjadi

$\begin{array}{ll}\\ 34.&\textrm{Persamaan lingkaran yang melalui perpotongan}\\&\textrm{lingkaran}\: \: x^{2}+y^{2}-12x+6y+20=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-16x-14y+64=0\: \: \textrm{serta pusatnya}\\ &\textrm{terletak pada garis}\: \: 8x-3y-19=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-20x-34y+108=0\\ &\textrm{b}.\quad x^{2}+y^{2}-16x+12y+96=0\\ &\textrm{c}.\quad x^{2}+y^{2}-12x+20y+88=0\\ &\textrm{d}.\quad x^{2}+y^{2}+16x-24y+108=0\\ &\textrm{e}.\quad x^{2}+y^{2}+22x-34y+96=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa persamaan lingkaran}:\\ &\bullet \: L_{1}=x^{2}+y^{2}-12x+6y+20=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-16x-14y+64=0\\ &\textrm{Persamaan tali busurnya (garis kuasa)}\\ &\textrm{adalah}:\\ &L_{1}(x,y)-L_{2}(x,y)\\ &=4x+20y-44=0\Leftrightarrow \color{blue}x=11-5y\\ &\textrm{Selanjutnya dengan substitusi }\\ &\begin{aligned}&x^{2}+y^{2}-12x+6y+20=0\\ &\Leftrightarrow (x-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (\color{blue}11-5y\color{black}-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (y-5y)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow 26y^2-44y+9=0 \end{aligned}\\ &\textrm{Sehingga dengan}\: \: \color{red}\textrm{memodifikasi}\\ &\begin{aligned}&26y^2-44y+9=0\\ &\Leftrightarrow 25y^2-44y+y^2+9=0\\ &\quad\textrm{arahkan ke bentuk kuadrat sempurna}\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+8=0\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+17^{2}-17^{2}+8=0\\ &\Leftrightarrow (5y-1)^{2}+(y-17)^{2}-281=0\\ &\quad \textrm{ingat bahwa ada tali busur}\: \: \color{blue}5y=11-x\\ &\Leftrightarrow (\color{blue}11-x\color{black}-1)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow (10-x)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow x^{2}-20x+100+y^{2}-34y+289-281=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-20x-34y+108=0 \end{aligned} \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$

$\begin{array}{ll}\\ 35.&\textrm{Persamaan lingkaran dengan titik pusat}\\ &\textrm{pada garis}\: \: x+2y-3=0\: \: \textrm{dan melalui}\\ &\textrm{titik potong dua lingkaran}\\ &x^{2}+y^{2}-2x-4y+1=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-2y+4=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-6x+7=0\\ &\textrm{b}.\quad x^{2}+y^{2}-3y+4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-2y+1=0\\ &\textrm{d}.\quad x^{2}+y^{2}-2x-4y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}-3x-2y+7=0\\\\ &\textbf{Jawab}:\\ &\color{blue}\textbf{Alternatif 1}\\ &\textrm{Gunakan cara pembahasan sebagaimana pada}\\ &\textrm{nomor-nomor sebelumnya}\\ &\color{blue}\textbf{Alternatif 2}\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}-2x-4y+1=0,\: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+y^{2}-4x-2y+4=0\\ &\textrm{Persamaan}\: \: \color{red}\textrm{tali busur}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}-2x-4y+1\\ &-(x^{2}+y^{2}-4x-2y+4)=0\\ &\Leftrightarrow 2x-2y-3=0\\ &\textrm{Selanjutnya perlu ditentukan juga}\\&\textrm{Persamaan}\: \: \color{red}\textrm{berkas lingkaran}\: \color{black}\textrm{melalui}\\ &\textrm{titik-titik potong kedua lingkaran}\\ &\textrm{di atas adalah}:\\ &L_{1}+\lambda L_{2}=0\\ &x^{2}+y^{2}-2x-4y+1\\ &\qquad+\lambda \left ( x^{2}+y^{2}-4x-2y+4 \right )=0\\ &\Leftrightarrow (1+\lambda )x^{2}+(1+\lambda )y^{2}-(2+4\lambda )x\\ &\qquad -(4+2\lambda )y+1+4\lambda =0\\ &\textrm{Saat}\: \: \lambda =-1,\: \textrm{maka persamaan berkas}\\ &\textrm{lingkarannya adalah}:\: 2x-2y-3=0\\ &\textrm{Hal ini hasilnya sama persis saat kita}\\ &\textrm{menentukan persamaan}\: \color{red}\textrm{tali busur}\: \color{black}\textrm{di atas}\\ &\textrm{Selanjutnya kita ambil}\\ &L_{2}-(L_{1}+\lambda L_{2})=0\\ &\Leftrightarrow x^{2}+y^{2}-4x-2y+4-(2x-2y-3)=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-6x+7=0 \end{aligned} \end{array}$.

Gambar mula-mula

Lingkaran baru yang berpusat di (3,0)

Contoh Soal 6 Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 26.&\textrm{Diketahui lingkaran-lingkaran}\\ & x^{2}+y^{2}-2x+3y+k=0\: \: \textrm{dan}\: \\ &x^{2}+y^{2}+8x-6y-7=0\: \: \textrm{saling}\\ &\textrm{berpotongan ortogonal saat}\: \: k=\: ....\\ &\textrm{a}.\quad \color{red}-10\\ &\textrm{b}.\quad -3\\ &\textrm{c}.\quad 1\\ &\textrm{d}.\quad 5\\ &\textrm{e}.\quad 8\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan tabel berikut}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}-2x+3y+k=0&\begin{cases} P_{1} &=\left ( 1,-\displaystyle \frac{3}{2} \right ) \\ r_{1} & = \sqrt{\displaystyle \frac{13-4k}{4}} \end{cases}\\\hline \begin{aligned}L_{2}&\equiv x^{2}+y^{2}+8x-6y-7=0 \end{aligned}&\begin{cases} P_{2} &=\left ( -4,3 \right ) \\ r_{2} & = \sqrt{32} \end{cases}\\\hline \end{array} \\ &\textrm{Syarat dua lingkaran berpotongan ortogonal}\\ &\begin{aligned}&\left (P_{1}P_{2} \right )^{2}=r_{1}^{2}+r_{2}^{2}\\ &\Leftrightarrow \left ( 1+4 \right )^{2}+\left ( -\displaystyle \frac{3}{2}-3 \right )^{2}=\left ( \sqrt{\displaystyle \frac{13-4k}{4}} \right )^{2}+\sqrt{32}^{2}\\ &\Leftrightarrow \: 25+\displaystyle \frac{81}{4}=\displaystyle \frac{13-4k}{4}+32\\ &\Leftrightarrow \: 100+81=13-4k+128\\ &\Leftrightarrow \: k=-10 \end{aligned} \\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

$\begin{array}{ll}\\ 27.&\textrm{Persamaan lingkaran yang berpotongan}\\ &\textrm{lingkaran lain}\: \: x^{2}+y^{2}+2x+y-11=0\\ &\textrm{secara tegak lurus dan melalui}\: \: (4,3)\: \: \textrm{serta}\\ &\textrm{pusatnya pada}\: \: 9x+4y=37\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-10x+4y+3=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x+10y+6=0\\ &\textrm{c}.\quad x^{2}+y^{2}+4x-8y+7=0\\ &\textrm{d}.\quad x^{2}+y^{2}+6x+y+5=0\\ &\textrm{e}.\quad x^{2}+y^{2}+12x+6y+5=0\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan tabel berikut}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x+y-11=0&\begin{cases} P_{1} &=\left ( -1,-\displaystyle \frac{1}{2} \right ) \\ r_{1} & = \sqrt{\displaystyle \frac{49}{4}}=\displaystyle \frac{7}{2} \end{cases}\\\hline \begin{aligned}L_{2}&\equiv (x-a)^{2}+(y-b)^{2}=r^{2} \end{aligned}&\begin{cases} P_{2} &=\left ( a,b \right ) \\ r_{2} & = r \end{cases}\\\hline \end{array}\\ &\textrm{Karena berpotongan tegak lurus, maka}\\ &\begin{aligned}&\left (P_{1}P_{2} \right )^{2}=r_{1}^{2}+r_{2}^{2}\\ &\Leftrightarrow \left ( -1-a \right )^{2}+\left ( -\displaystyle \frac{1}{2}-b \right )^{2}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow a^{2}+2a+1+b^{2}+b+\displaystyle \frac{1}{4}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow \color{blue}a^{2}+b^{2}+2a+b+\displaystyle \frac{5}{4}=\displaystyle \frac{49}{4}+r^{2}\\ &\Leftrightarrow a^{2}+b^{2}+2a+b-11=r^{2}\: .......(1)\\ \end{aligned} \\ &\textrm{Selanjutnya}\\ &\begin{aligned}&\textrm{Lingkaran}\: \: L_{2}\: \: \textrm{melalui titik}\: \: (4,3), \textrm{artinya}\\ &\textrm{bahwa}\: :\: (4-a)^{2}+(3-b)^{2}=r^{2}\\ &\Leftrightarrow a^{2}-8a+16+b^{2}-6b+9=r^{2}\\ &\Leftrightarrow a^{2}+b^{2}-8a-6b+25=r^{2}\: .......(2)\\ &\textrm{Pusat lingkaran}\: \: L_{2}\: \: \textrm{melalui garis}\: \: 9x+4y=37\\ &\textrm{artinya}:\: 9a+4b=37\: ...............(3)\\ \end{aligned}\\ &\begin{aligned}&\textrm{Dengan eliminasi}\: 1\: \&\: 2\: \: \textrm{dapat diperoleh}:\\ &\begin{array}{rll} a^{2}+b^{2}-8a-6b+25&=r^{2}&\\ a^{2}+b^{2}+2a+b-11&=r^{2}&-\\\hline -10a-7b+36&=0&\textrm{atau}\\ 10a+7b&=36&......(4) \end{array}\\ &\textrm{Dari persamaan}\: 3\: \&\: 4\: \: \textrm{dapat diperoleh}:\\ & \end{aligned}\\ &\begin{array}{rll} 10a+7b&=36&(\times 4)\\ 9a+4b&=37&(\times 7)\\\hline 40a+28b&=144&\\ 63a+28b&=259&\\\hline -23a\: \quad\quad&=-115&\\ a&=\displaystyle \frac{-115}{-23}&=5\\ 10(5)+7b&=36&\\ 7b&=-14\\ b&=-2 \end{array}\\ &\textrm{Adapun langkah berikutnya}\\ &\begin{aligned}&L_{2}\equiv (4-a)^{2}+(3-b)^{2}=r^{2}\\ &L_{2}\equiv (4-5)^{2}+(3+2)^{2}=r^{2}\\ &L_{2}\equiv r^{2}=25+1=26\\ &\textrm{Sehingga},\: L_{2}\equiv (x-5)^{2}+(y+2)^{2}=26\\ &\Leftrightarrow x^{2}+y^{2}-10x+4y+25+4-26=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-10x+4y+3=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$.

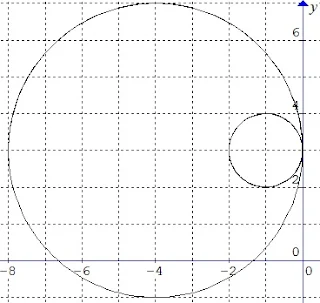
Jika diperjelas dengan tambahan garis 9x+4y=37

$\begin{array}{ll}\\ 28.&\textrm{Diketahui lingkaran pertama berpusat di}\: \: (1,2)\\ &\textrm{dan menyinggung garis}\: \: 3x-4y+10=0.\\ &\textrm{Jika ada lingkaran kedua dengan pusat}\: \: (4,6)\\ &\textrm{dan menyinggung lingkaran yang pertama},\\ &\textrm{maka persamaan lingkaran yang kedua}\\ &\textrm{tersebut adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-8x-12y+48=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x-12y+43=0\\ &\textrm{c}.\quad \color{red}x^{2}+y^{2}-8x-12y+36=0\\ &\textrm{d}.\quad x^{2}+y^{2}-8x-12y+27=0\\ &\textrm{e}.\quad x^{2}+y^{2}-8x-12y+16=0\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui bahwa kedua lingkaran saling}\\ &\color{blue}\textrm{bersinggungan di luar},\: \color{black}\textrm{maka}\\ &\begin{aligned}r_{1}+r_{2}&=P_{1}P_{2}\\ &=\sqrt{(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}\\ &=\sqrt{(1-4)^{2}+(2-6)^{2}}\\ &=\sqrt{3^{2}+4^{2}}=\sqrt{5^{2}}=5 \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned}r_{\textrm{pertama}}&=\left |\displaystyle \frac{3(1)-4(2)+10}{\sqrt{3^{2}+4^{2}}} \right |\\ &=\left | \displaystyle \frac{3-8+10}{\sqrt{5^{2}}} \right |=\left | \displaystyle \frac{5}{5} \right |=\left | 1 \right |=1\\ \textrm{sehingga} &\\ r_{\textrm{kedua}}&=5-r_{\textrm{pertama}}=5-1=4 \end{aligned}\\ &\textrm{maka persamaan lingkaran keduanya adalah}:\\ &\begin{aligned}&(x-4)^{2}+(y-6)^{2}=4^{2}\\ &\Leftrightarrow x^{2}-8x+16+y^{2}-12y+36=16\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-8x-12y+36=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$.

$\begin{array}{ll}\\ 29.&\textrm{Garis kuasa (tali busur sekutu)}\\ &\textrm{dari lingkaran}\\ &L_{1}\equiv x^{2}+y^{2}+6x-4y-12=0\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-12y=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 3x+4y+9=0\\ &\textrm{b}.\quad 3x-4y-8=0\\ &\textrm{c}.\quad 3x-4y+7=0\\ &\textrm{d}.\quad 3x+4y-7=0\\ &\textrm{e}.\quad \color{red}3x+4y-6=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}+6x-4y-12=0,\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-12y=0\\ &\textrm{Persamaan}\: \: \color{red}\textrm{garis kuasa}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}+6x-4y-12\\ &-(x^{2}+y^{2}-12y)=0\\ &\Leftrightarrow 6x+8y-12=0\\ &\Leftrightarrow \color{red}3x+4y-6=0 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 30.&\textrm{Jika dua lingkaran}\\ & x^{2}+y^{2}=9\: \: \textrm{dan}\\ &x^{2}+y^{2}-4y+2y+3=0\: \: \textrm{yang}\\ &\textrm{berpotongan di}\: \: (x_{1},y_{1})\: \: \textrm{dan}\: \: (x_{2},y_{2}),\\ &\textrm{maka nilai}\: \: 5(x_{1}+x_{2})\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}24\\ &\textrm{b}.\quad 26\\ &\textrm{c}.\quad 28\\ &\textrm{d}.\quad 30\\ &\textrm{e}.\quad 32\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}-9=0\: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+y^{2}-4x+2y+3\\ &\textrm{Persamaan}\: \: \color{red}\textrm{garis kuasa}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}-9\\ &-(x^{2}+y^{2}-4y+2y+3)=0\\ &\Leftrightarrow 4x-2y-12=0\\ &\Leftrightarrow 2x-y-6=0\\ &\Leftrightarrow y=6-2x \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned}&x^{2}+y^{2}-9=0\\ &\Leftrightarrow x^{2}+(6-2x)^{2}-9=0\\ &\Leftrightarrow x^{2}+36-24x+4x^{2}-9=0\\ &\Leftrightarrow 5x^{2}-24x+27=0\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{576-540}}{10}\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{36}}{10}=\frac{24\pm 6}{10}\\ &\Leftrightarrow x_{1,2}=\displaystyle \frac{24\pm \sqrt{36}}{10}=\frac{24\pm 6}{10}\\ &\Leftrightarrow \quad x_{1}=3\: \: \textrm{atau}\: \: x_{2}=1,8\\ &\textrm{maka}\: \: 5(x_{1}+x_{2})=5\left ( 3+1,8 \right )=\color{red}24 \end{aligned} \end{array}$.

Contoh Soal 5 Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 21.&\textrm{Titik Kuasa dari lingkaran-lingkaran}\\ &\textrm{berikut}\\ &L_{1}\equiv x^{2}+y^{2}+x+y-14=0\\ &L_{2}\equiv x^{2}+y^{2}=13\\ &L_{3}\equiv x^{2}+y^{2}+3x-2y-26=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}(3,-2)\\ &\textrm{b}.\quad (2,-3)\\ &\textrm{c}.\quad (-3,2)\\ &\textrm{d}.\quad (-2,3)\\ &\textrm{e}.\quad (3,2)\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{aligned}&\begin{array}{lrlll} (L_{1})&x^{2}+y^{2}+x+y&=&14\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &x+y&=&1&....(1) \end{array}\\ &\textrm{dan}\\ &\begin{array}{lrlll} (L_{3})&x^{2}+y^{2}+3x-2y&=&26\\ (L_{2})&x^{2}+y^{2}&=&13&-\\\hline &3x-2y&=&13&....(2) \end{array}\\ &\textrm{Selanjutnya kita eliminasi}\: (1)\& (2)\\ &\textrm{dan hasilnya adalah}:\\ &\begin{array}{rrlrl} \color{blue}(2)&3x-2y&=&13\\ \color{blue}(1)&3x+3y&=&3&-\qquad (\times 3)\\\hline &-5y&=&10&\\ &y&=&\color{red}-2&\Rightarrow x=\color{red}3 \end{array}\\ &\textrm{Jadi, titik kuasa ketiganya}: (3,-2) \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$

$\begin{array}{ll}\\ 22.&\textrm{Titik-titik potong dari persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-2)^{2}+y^{2}=10\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-2)^{2}=10\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad (3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{b}.\quad \color{red}(3,3)\: \: \textrm{dan}\: \: (-1,-1)\\ &\textrm{c}.\quad (3,-3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{d}.\quad (-3,3)\: \: \textrm{dan}\: \: (1,1)\\ &\textrm{e}.\quad (-3,-3)\: \: \textrm{dan}\: \: (-1,-1)\\\\ &\textbf{Jawab}:\\ &\color{blue}\textrm{Alternatif 1}\\ &\textrm{Dengan substitusi opsi pilihan jawaban}\\ &\textrm{maka akan ketemu jawabannya langsung}\\ &\color{blue}\textrm{Alternatif 2}\\ &\textrm{Dengan eliminasi dan ilustrasi gambar}\\ &\begin{array}{lrlll} (L_{1})&(x-2)^{2}+y^{2}&=&10\\ (L_{2})&x^{2}+(y-2)^{2}&=&10&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-4x&=&6\\ (L_{2})&x^2+y^2-4y&=&6&-\\\hline &-4x+4y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array} \\ &\textrm{Jelas opsi jawaban c, d salah}\\ &\textrm{karena}\: \: y=x,\\ &\textbf{Dengan bantuan ilustrasi, pilihan jawaban}\\ &\textbf{akan tampak dengan jelas} \end{array}$.

$\begin{array}{ll}\\ 23.&\textrm{Persamaan tali busur persekutuan dua}\\ &\textrm{lingkaran}\: \: L_{1}\equiv (x-3)^{2}+y^{2}=16\: \: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+(y-3)^{2}=16\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad y=-2x\\ &\textrm{b}.\quad y=-x\\ &\textrm{c}.\quad \color{red}y=x\\ &\textrm{d}.\quad y=2x\\ &\textrm{e}.\quad y=\displaystyle \frac{1}{2}x\\\\ &\textbf{Jawab}:\\ &\textrm{Dengan eliminasi, kita mendapatkan}\\ &\begin{array}{lrlll} (L_{1})&(x-3)^{2}+y^{2}&=&16\\ (L_{2})&x^{2}+(y-3)^{2}&=&16&\\&\color{blue}\textrm{menjadi}\\ (L_{1})&x^2+y^2-6x&=&9\\ (L_{2})&x^2+y^2-6y&=&9&-\\\hline &-6x+6y&=&0&\\ &\color{blue}\textrm{maka hasilnya}\\ &y&=&x \end{array}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

$\begin{array}{ll}\\ 24.&\textrm{Banyaknya garis singgung persekutuan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+2x-6y+9=0\\ &\textrm{dan}\: \: x^{2}+y^{2}+8x-6y+9=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 0\\ &\textrm{b}.\quad \color{red}1\\ &\textrm{c}.\quad 2\\ &\textrm{d}.\quad 3\\ &\textrm{e}.\quad 4\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x-6y+9=0&\begin{cases} P_{1} &=(-1,3) \\ r_{1} & = 1 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+8x-6y+9=0&\begin{cases} P_{2} &=(-4,3) \\ r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{Perhatikan pula bahwa}\: \: r_{2}-r_{1}=4-1=3\\ &\begin{aligned}&\textrm{Karena}\: \: P_{1}P_{2}=r_{2}-r_{1},\: \textrm{hal ini berarti lingkaran}\\ &L_{1}\: \: \textrm{bersinggungan di dalam dengan lingkaran}\: L_{2}\\ &\textrm{Sehingga kedua lingkaran ini hanya akan }\\ &\textrm{memiliki}\: \: \color{red}\textrm{satu}\: \: \color{black}\textrm{garis singgung persekutuan} \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

$\begin{array}{ll}\\ 25.&\textrm{Persamaan lingkaran dengan jari-jari}\: \: 5\\ &\textrm{dan menyinggung lingkaran lain}\\ & x^{2}+y^{2}-2x-4y-20=0\: \: \: \textrm{di titik}\\ &(5,5)\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{b}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-2x-4y-120=0\\ &\textrm{e}.\quad x^{2}+y^{2}-2x-4y-120=0\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahi bahwa}\\ &\begin{aligned}&\begin{array}{rrlll} (L_{1})&(x-a)^2+(y-b)^{2}&=&5^{2}\\ (L_{2})&x^{2}+y^{2}-2x-4y&=&20& \end{array} \\ &\textrm{Titik singgung dua lingkaran}\\ &\textrm{di titik}\: \: (5,5),\: \textrm{artinya}\\ &\begin{pmatrix} 5\\ 5 \end{pmatrix}=\displaystyle \frac{\begin{pmatrix} a\\ b \end{pmatrix}+\begin{pmatrix} 1\\ 2 \end{pmatrix}}{2}\\ &\Leftrightarrow \begin{pmatrix} 10\\ 10 \end{pmatrix}=\begin{pmatrix} a\\ b \end{pmatrix}+\begin{pmatrix} 1\\ 2 \end{pmatrix}\\ &\Leftrightarrow \begin{pmatrix} a\\ b \end{pmatrix}=\begin{pmatrix} 10-1\\ 10-2 \end{pmatrix}=\begin{pmatrix} 9\\ 8 \end{pmatrix} \end{aligned}\\ &\begin{aligned}&\textrm{maka persamaan lingkarannya adalah}:\\ &\Leftrightarrow (x-9)^{2}+(y-8)^{2}=5^{2}\\ &\Leftrightarrow x^{2}+y^{2}-18x-16y+120=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$.

Contoh Soal 4 Materi Lingkaran dan Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 16.&\textrm{Salah satu garis singgung yang bersudut}\: \: 120^{\circ}\\ &\textrm{terhadap sumbu x positif terhadap lingkaran}\\ &\textrm{dengan ujung diameter titik}\: \: (7,6)\: \textrm{dan}\: \: (1,-2)\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}y=-x\sqrt{3}+4\sqrt{3}+12\\ &\textrm{b}.\quad y=-x\sqrt{3}-4\sqrt{3}+8\\ &\textrm{c}.\quad y=-x\sqrt{3}+4\sqrt{3}-4\\ &\textrm{d}.\quad y=-x\sqrt{3}-4\sqrt{3}-8\\ &\textrm{e}.\quad y=-x\sqrt{3}+4\sqrt{3}+22\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline \textrm{Pusat Lingkaran}&\textrm{Gradien Garis Singgung}\\\hline \begin{aligned}&(a,b)\\ &=\left ( \displaystyle \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )\\ &=\left ( \displaystyle \frac{7+1}{2},\frac{6+(-2)}{2} \right )\\ &=(4,2) \end{aligned}&\begin{aligned}m&=\tan 120^{\circ}\\ &=-\tan \left ( 180^{\circ}-60^{\circ} \right )\\ &=-\tan 60^{\circ}\\ &=-\sqrt{3}\\ &\\ \end{aligned} \\\hline \textrm{Jari-jari}&\textrm{Garis Singgung}\\\hline \begin{aligned}r&=\textrm{jarak titik}\\ &\: \: \: \: \: \, \textrm{singgung ke pusat}\\ &=\sqrt{(7-4)^{2}+(6-2)^{2}}\\ &=\sqrt{3^{2}+4^{2}}\\ &=\sqrt{25}\\ &=5\\ &\\ &\\ & \end{aligned}&\begin{aligned} &(y-b)=m(x-a)\pm r\sqrt{1+m^{2}}\\ &\Leftrightarrow (y-2)=-\sqrt{3}(x-4)\pm 5\sqrt{1+(-\sqrt{3})^{2}}\\ &\Leftrightarrow y-2=-\sqrt{3}x+4\sqrt{3}\pm 5\sqrt{1+4}\\ &\Leftrightarrow y=-\sqrt{3}x+4\sqrt{3}+2\pm 10\\ &\Leftrightarrow y=\begin{cases} -\sqrt{3}x+4\sqrt{3}+2+ 10 \\ -\sqrt{3}x+4\sqrt{3}+2- 10 \end{cases}\\ &\Leftrightarrow y=\begin{cases} \color{red}-\sqrt{3}x+4\sqrt{3}+12 & \\ -\sqrt{3}x+4\sqrt{3}-8 & \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Berikut ilustrasi gambarnya} \end{array}$.

Dengan ilustrasi tambahan

$\begin{array}{ll}\\ 17.&\textrm{Salah satu garis singgung lingkaran}\\\ & x^{2}+y^{2}=10\: \: \textrm{yang ditarik dari}\\ &\textrm{titik}\: \: (4,2)\: \: \textrm{adalah}....\\ &\textrm{a}.\quad \color{red}x+3y=10\\ &\textrm{b}.\quad x-3y=10\\ &\textrm{c}.\quad -x-3y=10\\ &\textrm{d}.\quad 2x+y=10\\ &\textrm{e}.\quad x+2y=10\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline \begin{aligned}&\textrm{Garis Singgung}\\ &\quad\quad \textrm{di titik}\\ &(x_{1},y_{1})=(4,2) \end{aligned}&\begin{aligned}&\textrm{Tahapan menentukan}\\ &\quad\qquad \textrm{harga}\: \: m\\ & \end{aligned}\\\hline \begin{aligned}&y-y_{1}=m(x-x_{1})\\ &y-2=m(x-4)\\ &y=mx-4m+2\\ &\\ &\\ &\\ & \end{aligned}&\begin{aligned}&x^{2}+y^{2}=10\\ &x^{2}+\left ( mx-4m+2 \right )^{2}=10\\ &x^{2}+m^{2}x^{2}+16m^{2}+4-8m^{2}x+4mx-16m=10\\ &x^{2}+m^{2}x^{2}+16m^{2}-8m^{2}x+4mx-16m-6=0\\ &(1+m^{2})x^{2}+(4m-8m^{2})x+16m^{2}-16m-6=0\\ &\begin{cases} a & =1+m^{2} \\ b & =4m-8m^{2} \\ c & =16m^{2}-16m-6 \end{cases} \end{aligned}\\\hline \end{array}\\ &\begin{aligned}&\textrm{Syarat menyinggung}\: \: D=0\\ &b^{2}-4ac=0\\ &\left ( 4m-8m^{2} \right )^{2}-4\left ( 1+m^{2} \right )\left ( 16m^{2}-16m-6 \right )=0\\ &16m^{2}-64m^{3}+64m^{4}-64m^{2}+64m+24-64m^{4}+64m^{3}+24m^{2}=0\\ &-24m^{2}+64m+24=0\\ &-3m^{2}+8m+3=0\\ &(m-3)(3m+1)=0\\ &m=3\: \: \textrm{atau}\: \: m=-\displaystyle \frac{1}{3}\\ &m=\begin{cases} 3 & \Rightarrow y=3x-10\\ &\Rightarrow 3x-y=10\\ -\displaystyle \frac{1}{3} & \Rightarrow y=-\displaystyle \frac{1}{3}x+\frac{4}{3}+2\\ &\Rightarrow \color{red}x+3y=10 \end{cases} \end{aligned} \end{array}$.

$.\qquad\begin{aligned}&\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned}$

$\begin{array}{ll}\\ 18.&\textrm{Diketahui persamaan lingkaran}\: \: x^{2}+y^{2}=r^{2}\\ &\textrm{dan sebuah titik di luar lingkaran}\: \: M(a,b)\\ &\textrm{Posisi garis}\: \: ax+by=r^{2}\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{menyinggung lingkaran}\\ &\textrm{b}.\quad \color{red}\textrm{memotong lingkaran di dua titik}\\ &\textrm{c}.\quad \textrm{melalui titik pusat lingkaran}\\ &\textrm{d}.\quad \textrm{tidak memotong lingkaran}\\ &\textrm{e}.\quad \textrm{tidak ada yang benar}\\\\ &\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\\ &\bullet \quad L\equiv x^{2}+y^{2}=r^{2}\\ &\bullet \quad M(a,b)\: \: \textrm{di luar lingkaran}\: \: L\\ &\color{purple}\textrm{Selanjutnya perhatikan penjelasan berikut}\\ &\begin{aligned}&\textrm{Karena}\: M(a,b)\: \textrm{di luar lingkaran}\: L,\: \textrm{maka}\\ &\textrm{maka salah satu dari}\: \: a\: \: \textrm{atau}\: \: b\: \: \textrm{atau keduanya}\\ &\textrm{akan lebih besar nilanya dari pada}\: \: r.\\ &\textrm{Misalkan kita pilih}\: \: a>r\\ &\color{blue}\textrm{Ambil posisi saat memotong sumbu}-X,\: \color{black}y=0\\ &\begin{aligned}&\textrm{Untuk lingkaran}\: \: x^{2}+y^{2}=r^{2}\\ &\bullet \quad y=0\Rightarrow x^{2}+0^{2}=r^{2}\Rightarrow x=\left | r \right |\\ &\textrm{Untuk garis}\: \: ax+by=r^{2}\\ &\bullet \quad y=0\Rightarrow ax=r^{2}\Rightarrow x=\displaystyle \frac{r^{2}}{a}\\ &\textrm{Dari sini tampak posisi}\: \: x=\color{red}\left | r \right |> \displaystyle \frac{r^{2}}{a}\geq 0 \end{aligned}\\ &\textrm{Sehingga kesimpulannya adalah}:\\ &\color{red}\textrm{garis tersebut akan selalu memotong lingkaran} \end{aligned}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

$\begin{array}{ll}\\ 19.&\textrm{Dua lingkaran dengan persamaan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+6x-8y+21=0\\ &\textrm{dan}\: \: x^{2}+y^{2}+10x-8y+25=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{berpotongan di luar titik}\\ &\textrm{b}.\quad \textrm{tidak berpotongan atau bersinggungan}\\ &\textrm{c}.\quad \textrm{bersinggungan luar}\\ &\textrm{d}.\quad \color{red}\textrm{bersinggungan dalam}\\ &\textrm{e}.\quad \textrm{sepusat}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+6x-8y+21=0&\begin{cases} P_{1} &=(-3,4) \\ r_{1} & = 2 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+10x-8y+25=0&\begin{cases} P_{2} &=(-5,4) \\ r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{dan}\\ &\begin{array}{|c|c|}\hline \textrm{Jarak kedua pusat}&\textrm{Jumlah/selisih jari-jari}\\\hline \begin{aligned}&\left (P_{1}P_{2} \right )\\ &=\sqrt{(-3+5)^{2}+(4-4)^{2}}\\ &=\sqrt{2^{2}+0^{2}}=\sqrt{4}=2 \end{aligned}&\begin{aligned}\begin{cases} r_{1}+r_{2} & =2+4=6 \\ \left |r_{1}-r_{2} \right | & =\left | 2-4 \right |=2 \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Karena nilai}\: \: \color{red}P_{1}P_{2}\color{black}=\color{red}\left |r_{1}-r_{2} \right |\color{black}=\color{red}2\\ &\textrm{hal ini menunjukkan keduanya bersinggungan}\\ &\color{blue}\textrm{di dalam}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$ .

$\begin{array}{ll}\\ 20.&\textrm{Dua lingkaran dengan persamaan}\\ &\textrm{lingkaran-lingkaran}\: x^{2}+y^{2}+2x-6y+9=0\\ &\textrm{dan}\: \: x^{2}+y^{2}+8x-6y+9=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \textrm{berpotongan}\\ &\textrm{b}.\quad \color{red}\textrm{bersinggungan di dalam}\\ &\textrm{c}.\quad \textrm{bersinggungan luar}\\ &\textrm{d}.\quad \textrm{tidak berpotongan}\\ &\textrm{e}.\quad \textrm{sepusat}\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan bahwa}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}+2x-6y+9=0&\begin{cases} P_{1} &=(-1,3) \\ r_{1} & = 1 \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}+8x-6y+9=0&\begin{cases} P_{2} &=(-4,3) \\ r_{2} & = 4 \end{cases}\\\hline \end{array} \\ &\textrm{dan}\\ &\begin{array}{|c|c|}\hline \textrm{Jarak kedua pusat}&\textrm{Jumlah/selisih jari-jari}\\\hline \begin{aligned}&\left (P_{1}P_{2} \right )\\ &=\sqrt{(-1+4)^{2}+(3-3)^{2}}\\ &=\sqrt{3^{2}+0^{2}}=\sqrt{9}=3 \end{aligned}&\begin{aligned}\begin{cases} r_{1}+r_{2} & =1+4=5 \\ \left |r_{1}-r_{2} \right | & =\left | 1-4 \right |=3 \end{cases} \end{aligned}\\\hline \end{array}\\ &\textrm{Karena nilai}\: \: \color{red}P_{1}P_{2}\color{black}=\color{red}\left |r_{1}-r_{2} \right |\color{black}=\color{red}3\\ &\textrm{hal ini menunjukkan keduanya bersinggungan}\\ &\color{blue}\textrm{di dalam}\\ &\textbf{Sebagai ilustrasi perhatikan gambar berikut} \end{array}$.

DAFTAR PUSTAKA

Budi, W. S. 2010. Bahan Ajar Persiapan Menuju Olimpiade Sain Nasional/Internasional Matematika 3. Jakarta: ZAMRUD KEMALA.
Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Contoh Soal 3 Materi Lingkaran

$\begin{array}{ll}\\ 11.&\textrm{Lingkaran}\: \: x^{2}+y^{2}+2ax+2by+c=0\\ &\textrm{menyinggung sumbu Y jika}\: \: c\: =....\\ &\textrm{A}.\quad ab\\ &\textrm{B}.\quad ab^{2}\\ &\textrm{C}.\quad a^{2}b\\ &\textrm{D}.\quad a^{2}\\ &\textrm{E}.\quad \color{red}b^{2}\\\\ &\textbf{Jawab}:\\ &\color{blue}\textbf{Alternatif 1}\\ &\begin{aligned}&x^{2}+y^{2}+2ax+2by+c=0\\ &x=0\Rightarrow 0^{2}+y^{2}+2a.0+2by+c=0\\ &y^{2}+2by+c=0\begin{cases} a & =1 \\ b & =2b \\ c & =c \end{cases}\\ &\textrm{Syarat menyinggung}\: \textrm{adalah}:\\ &D=b^{2}-4ac=0\\ &\Leftrightarrow (2b)^{2}-4.1.c=0\\ &\Leftrightarrow 4c=4b^{2}\\ &\Leftrightarrow c=\color{red}b^{2} \end{aligned} \\\\ &\color{blue}\textbf{Alternatif 2}\\ &\begin{aligned}&x^{2}+y^{2}+2ax+2by+c=0\\ &\Leftrightarrow x^{2}+2ax+a^{2}+y^{2}+2by+b^{2}+c-a^{2}-b^{2}=0\\ &\Leftrightarrow (x+a)^{2}+(y+b)^{2}=a^{2}+b^{2}-c\\ &\textrm{Karena menyinggung sumbu-Y, maka}\: \: R=a \\ &\textrm{Sehingga}\: \: R^{2}=a^{2}+b^{2}-c=a^{2}\\ &\Leftrightarrow b^{2}-c=0\\ &\Leftrightarrow b^{2}=c\\ &\Leftrightarrow c=\color{red}b^{2} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Diketahui pusat lingkaran L terletak dikuadran}\\ &\textrm{I dan berada di sepanjang garis}\: \: y=2x.\: \: \textrm{Jika}\\ &\textrm{lingkaran L menyinggung sumbu Y di titik}\\ &(0,6),\: \textrm{maka persamaan lingkaran L adalah}\: ....\\ &\textrm{A}.\quad x^{2}+y^{2}-3x-6y=0\\ &\textrm{B}.\quad x^{2}+y^{2}+6x+12y-108=0\\ &\textrm{C}.\quad x^{2}+y^{2}+12x+6y-72=0\\ &\textrm{D}.\quad x^{2}+y^{2}-12x-6y=0\\ &\textrm{E}.\quad \color{red}x^{2}+y^{2}-6x-12y+36=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&(x-a)^{2}+(y-b)^{2}=r^{2},\\ &\textrm{menyinggung titik}\: \: (0,6)\\ &\textrm{berarti pusat lingkaran L juga terletak}\\ &\textrm{pada garis}\: \: y=6.\: \: \textrm{Hal ini menunjukkan bahwa }\\ &\textrm{pusat lingkaran}\: \: \, \: \textrm{L berpusat di}\: \: (x,2x)=(\frac{y}{2},y),\\ &\textrm{dengan}\: \: y=6.\, \: \textrm{Dari informasi di atas, }\\ &\textrm{didapatlah pusat lingkaran berada di titik}\: \: (3,6).\\ &\textrm{Sehingga persamaan lingkarannya adalah}:\\ &(x-3)^{2}+(y-6)^{2}=3^{2}\: \: \textrm{ingat}\: \: r=\textrm{absis}\: \: x=3\\ &\Leftrightarrow (x-3)^{2}+(y-6)^{2}=x^{2}-6x+9+y^{2}+12x+36=9\\ &\Leftrightarrow \, \color{red}x^{2}+y^{2}-6x+12y+36=0\\ &\color{purle}\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Persamaan garis singgung lingkaran}\\ &x^{2}+y^{2}+8x-3y-24=0,\: \: \textrm{di titik}\\ & (2,4)\: \: \textrm{adalah}\: ....\\ &\textrm{A}.\quad 12x-5y-44=0\\ &\textrm{B}.\quad \color{red}12x+5y-44=0\\ &\textrm{C}.\quad 12x-y-50=0\\ &\textrm{D}.\quad 12x+y-50=0\\ &\textrm{E}.\quad 12x+y+50=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&x^{2}+y^{2}+8x-3y-24\\ &\Leftrightarrow x^{2}+8x+16+y^{2}-3y+\displaystyle \frac{9}{4}-24=16+\frac{9}{4}\\ &\Leftrightarrow \: (x+4)^{2}+(y-\frac{3}{2})^{2}=16+\frac{9}{4}+24=42\frac{1}{4}\\ &\textrm{Persamaan garis singgung lingkar}\textrm{an lingkaran }\\ &\textrm{di titik}\: \: (x_{1},y_{1})\: \: \textrm{adalah}:\\ &(x_{1}+4)(x+4)+(y_{1}-\frac{3}{2})(y-\frac{3}{2})=42\frac{1}{4},\\ &\textrm{untuk}\: \: (x_{1},y_{1})=(2,4),\: \textrm{maka}\\ &(2+4)(x+4)+(4-\frac{3}{2})(y-\frac{3}{2})=\frac{169}{4}\\ &\Leftrightarrow 6(x+4)+\frac{5}{2}(y-\frac{3}{2})=\frac{169}{4}\\ &\Leftrightarrow 24(x+4)+5(2y-3)=169\\ &\Leftrightarrow 24x+96+10y-15=169\\ &\Leftrightarrow 24x+10y=169-96+15=88\\ &\Leftrightarrow \color{red}12x+5y-44=0\\ &\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Sebuah garis singgung}\: \: g\: \: \textrm{menyinggung }\\ &\textrm{lingkaran yang berpusat di}\: \: (-2,5)\: \: \textrm{dan}\\ &\textrm{berjari-jari}\: \: 2\sqrt{10}\: \: \textrm{di titk}\: \: (4,3),\: \textrm{maka }\\ &\textrm{persamaan garis singgung}\: \: g\: \: \textrm{adalah}\: .... \\ &\textrm{A}.\quad y=3x+9\\ &\textrm{B}.\quad \color{red}y=3x-9\\ &\textrm{C}.\quad y=-3x+9\\ &\textrm{D}.\quad y=-3x-9\\ &\textrm{E}.\quad y=3x+21\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&(x-a)^{2}+(y-b)^{2}=r^{2}\\ &\begin{cases} \textrm{Pusat} & =(-2,5) \\ \textrm{r} & =2\sqrt{10} \end{cases} \\ &\textrm{maka persamaan lingkarannya}:\\ &(x+2)^{2}+(y-5)^{2}=(2\sqrt{10})^{2}\\ &\Leftrightarrow (x_{1}+2)(x+2)+(y_{1}-5)(y-5)=40,\\ &\textrm{menyingung garis}\: \: g\: \: \textrm{di}\: (4,3)\\ &(4+2)(x+2)+(3-5)(y-5)=40\\ &\Leftrightarrow 6x+12-2y+10=40\\ &\Leftrightarrow 6x-2y=40-12-10\\ &\Leftrightarrow 3x-y=9\\ &\Leftrightarrow -y=-3x+9\\ &\Leftrightarrow \color{red}y=3x-9\\ &\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 15.&\textrm{Suatu lingkaran dengan titik pusatnya terletak }\\ &\textrm{pada kurva}\: \: y=\sqrt{x}\: \: \textrm{dan melalui titik asal}\: \: O(0,0).\\ & \textrm{Jika diketahui absis titik pusat lingkaran tersebut }\\ &\textrm{adalah}\: \: a,\: \: \textrm{maka persamaan garis singgung }\\ &\textrm{lingkaran yang melalui titik}\: \: O\: \: \textrm{tersebut adalah}\: ....\\ &\textrm{A}.\quad y=-x\\ &\textrm{B}.\quad \color{red}y=-x\sqrt{a}\\ &\textrm{C}.\quad y=-ax\\ &\textrm{D}.\quad y=-2x\sqrt{2}\\ &\textrm{E}.\quad y=-2ax\\\\ &\textbf{Jawab}:\\ &\begin{array}{|l|c|l|}\hline \begin{aligned}&\textrm{Pusat}\\ &\textrm{lingkaran}\\ &\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Gradien garis singgung}\\ &\textrm{yang tegak lurus dengan }\\ &\textrm{garis yang melalui titik}\\ &\textrm{pusat lingkaran yang }\\ &\textrm{bergradien}\: \: m_{L} \end{aligned}&\begin{aligned}&\textrm{Persamaan garis }\\ &\textrm{singgung yang }\\ &\textrm{melalui titik asal}\\ &O(0,0)\\ & \end{aligned}\\\hline \begin{aligned}&(a,b)\\ &=\left ( a,\sqrt{a} \right )\\ &\\ &\\ & \end{aligned}&\color{blue}\begin{aligned}&m.m_{1}=-1\\ &m.\frac{y}{x}=-1\\ &m=-\frac{x}{y}=-\displaystyle \frac{a}{\sqrt{a}}\\ &\: \: \: \, =-\sqrt{a} \end{aligned}&\begin{aligned}y&=mx,\\ & \textrm{karena melalui}\\ &\textrm{titik asal}\\ y&=-\sqrt{a}x,\\ y&=\color{red}-x\sqrt{a} \end{aligned}\\\hline \end{array} \end{array}$.

Contoh Soal 2 Materi Lingkaran

$\begin{array}{ll}\\ 6.&\textrm{Diketahui lingkaran}\: \: x^{2}+y^{2}+4x+ky-12=0\\ &\textrm{melalui titik}\: \: (-2,8)\: \: \textrm{maka jari-jari lingkaran}\\ &\textrm{tersebut adalah}....\\ &\textrm{A}.\quad 1\\ &\textrm{B}.\quad \color{red}5\\ &\textrm{C}.\quad 6\\ &\textrm{D}.\quad 12\\ &\textrm{E}.\quad 25\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui ingkaran berpusat di}\: \left ( -2,-\displaystyle \frac{1}{2}k \right ),\\ &\textrm{yaitu}:\\ &x^{2}+y^{2}+4x+ky-12=0\\ & \textrm{melalui}\: \: (-2,8)\: \: \textrm{berarti }\\ &(-2)^{2}+8^{2}+4(-2)+k.8-12=0\\ &4+64-8-12+8k=0\\ &48+8k=0\\ &k=\color{blue}-6\\ &\textrm{Sehingga}\: \: r=\sqrt{\displaystyle \frac{4^{2}}{4}+\frac{(-6)^{2}}{4}-(-12)}\\ &\qquad\qquad \: \: \: =\sqrt{\displaystyle 4+9+12}=\sqrt{25}=\color{red}5\\ \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 7.&\textrm{Persmaan lingkaran}\: \: x^{2}+y^{2}+px+8y+9=0\\ &\textrm{menyinggung sumbu X. Pusat lingkaran tersebut }\\ &\textrm{adalah}\: ....\\ &\textrm{A}.\quad (6,-4)\\ &\textrm{B}.\quad (6,6)\\ &\textrm{C}.\quad \color{red}(3,-4)\\ &\textrm{D}.\quad (-6,-4)\\ &\textrm{E}.\quad (3,4)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textbf{Lingkaran}\: \: x^{2}+y^{2}+px+8y+9=0\\ &\textrm{maka,}\\ &x^{2}+px+y^{2}+8y+9=0\\ &\left ( x+\displaystyle \frac{1}{2}p \right )^{2}-\displaystyle \frac{1}{4}p^{2}+(y+4)^{2}-16+9=0\\ &\Leftrightarrow \left ( x+\displaystyle \frac{1}{2}p \right )^{2}+(y+4)^{2}=7+\displaystyle \frac{1}{4}p^{2}\\ &\textrm{karena menyinggung sumbu-X,}\: \: \: \: R=b=4,\\ & \textrm{sehingga}\\ &7+\displaystyle \frac{1}{4}p^{2}=4^{2}\\ &\Leftrightarrow \displaystyle \frac{1}{4}p^{2}=16-7=9\Leftrightarrow p^{2}=36\Leftrightarrow p=\color{blue}\pm 6\\ &p=-6\: \Rightarrow \: x^{2}+y^{2}-6x+8y+9=0\\ &\quad\Rightarrow \textrm{pusatnya adalah}\: \: \left ( -\displaystyle \frac{A}{2},-\frac{B}{2} \right )=\color{red}(3,-4)\\ &p=6\: \: \: \, \: \Rightarrow \: x^{2}+y^{2}+6x+8y+9=0\\ &\quad\Rightarrow \textrm{pusatnya adalah}\: \: \left ( -\displaystyle \frac{A}{2},-\frac{B}{2} \right )=\color{red}(-3,-4)\\ &\color{purple}\textrm{dan berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 8.&\textrm{Titik-titik berikut yang posisinya berada di luar }\\ &\textrm{lingkaran}\: \: x^{2}+y^{2}-2x+8y-32=0\: \: \textrm{adalah}.... \\ &\textrm{A}.\quad (0,0)\\ &\textrm{B}.\quad (-6,-4)\\ &\textrm{C}.\quad \color{red}(-3,2)\\ &\textrm{D}.\quad (3,1)\\ &\textrm{E}.\quad (4,1)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\begin{array}{|c|c|l|c|}\hline \color{blue}\textrm{Opsi}&\color{blue}\textrm{Titik}&\qquad\qquad\quad\color{blue}\textrm{Lingkaran}&\color{blue}\textrm{Keterangan}\\\hline \textrm{A}&(0,0)&0^{2}+0^{2}-2.0+8.0-32=-32&\textrm{dalam}\\\hline \textrm{B}&(-6,-4)&(-6)^{2}+(-4)^{2}-2(-6)+8(-4)-32=0&\textrm{pada}\\\hline \color{red}\textrm{C}&(-3,2)&(-3)^{2}+(2)^{2}-2(-3)+8(2)-32=3&\textbf{di luar}\\\hline \textrm{D}&(3,1)&3^{2}+1^{2}-2.3+8.1-32=-20&\textrm{dalam}\\\hline \textrm{E}&(4,1)&4^{2}+1^{2}-2.4+8.1-32=-15&\textrm{dalam}\\\hline \end{array} \\ &\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 9.&\textrm{Diketahui garis}\: \: x-2y=5\: \: \textrm{memotong lingkaran}\\ &x^{2}+y^{2}-4y+8y+10=0\: \: \textrm{di titik A dan B}.\\ &\textrm{Panjang ruas garis AB adalah}....\\ &\textrm{A}.\quad 4\sqrt{2}\\ &\textrm{B}.\quad \color{red}2\sqrt{5}\\&\textrm{C}.\quad \sqrt{10}\\ &\textrm{D}.\quad 5\\ &\textrm{E}.\quad 4\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\begin{aligned}&\textrm{Perhatikanlah bahwa garis}\: \: \color{blue}x-2y=5\\&\textrm{memotong lingkaran}\\ &x^{2}+y^{2}-4x+8y+10=0,\\ &\textrm{maka garis}\: \: \color{blue}x=2y+5\: \: \color{black}\textrm{disubstitusikan ke}\\ &\textrm{lingkaran tersebut, yaitu}:\\ &(\color{blue}2y+5\color{black})^{2}+y^{2}-4(\color{blue}2y+5\color{black})+8y+10=0\\ &4y^{2}+20y+25+y^{2}-8y-20+8y+10=0\\ &5y^{2}+20y+15=0\\ &y^{2}+4y+3=0\\ &(y+1)(y+3)=0\\ &y=-1\: \: \vee \: \: y=-3\\ &\textrm{untuk nilai}\\ & y=-3\Rightarrow x=2(-3)+5=-1,\quad A(-1,-3)\\ &y=-1\Rightarrow x=2(-1)+5=3,\qquad B(3,-1)\\ &\textrm{maka},\qquad \textrm{AB}=\sqrt{(3-(-1))^{2}+(-1-(-3))^{2}}\\ &=\sqrt{4^{2}+2^{2}}\\ &=\sqrt{16+4}\\ &=\sqrt{20}\\ &=\color{red}2\sqrt{5} \end{aligned}\\ &\color{purple}\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$ .

$\begin{array}{ll}\\ 10.&\textrm{Kekhususan persamaan lingkaran}\\ &x^{2}+y^{2}-6x-6y+6=0\: \: \textrm{adalah}....\\ &\textrm{A}.\quad \textrm{menyinggung sumbu X}\\ &\textrm{B}.\quad \textrm{menyinggung sumbu Y}\\ &\textrm{C}.\quad \textrm{berpusat di}\: \: O(0,0)\\ &\textrm{D}.\quad \color{red}\textrm{titik pusatnya terletak pada}\: \: x-y=0\\ &\textrm{E}.\quad \textrm{berjari-jari 3}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui persamaan lingkaran}\\ &x^{2}+y^{2}-6x-6y+6=0\\ &x^{2}-6x+9+y^{2}-6y+9+6=9+9\\ &(x-3)^{2}+(y-3)^{2}=18-6\\ &(x-3)^{2}+(y-3)^{2}=12\\ &(x-3)^{2}+(y-3)^{2}=\left ( 2\sqrt{3} \right )^{2}\\ &\textrm{lingkaran ini}\begin{cases} \textrm{Pusat} &=\color{blue}(3,3) \\ \textrm{Jari-jari} &=\color{blue}2\sqrt{3} \end{cases}\\ &\begin{array}{|c|l|c|}\hline \textrm{Opsi}&\qquad\qquad\qquad\textrm{Pernyataan}&\textrm{Keterangan}\\\hline \textrm{A}&\textrm{menyinggung sumbu X}&\textrm{tidak tepat}\\\hline \textrm{B}&\textrm{menyinggung sumbu Y}&\textrm{tidak tepat}\\\hline \textrm{C}&\textrm{berpusat di}\: \: O(0,0)&\textrm{tidak tepat}\\\hline \color{red}\textrm{D}&\color{red}\textrm{titik pusatnya terletak pada garis}\: \: x-y=0&\textbf{tepat}\\\hline \textrm{E}&\textrm{berjari-jari 3}&\textrm{tidak tepat}\\\hline \end{array} \\ &\textrm{Berikut ilustrasi gambarnya} \end{aligned} \end{array}$.

Contoh Soal 1 Materi Lingkaran

$\begin{array}{ll}\\ 1.&\textrm{Jari-jari lingkaran dengan persamaan}\: \: x^{2}+y^{2}=48\\ &\textrm{adalah}....\\ &\textrm{A}.\quad \displaystyle 3\sqrt{5}\\ &\textrm{B}.\quad \color{red}4\sqrt{3}\\ &\textrm{C}.\quad 5\sqrt{2}\\ &\textrm{D}.\quad \displaystyle 6\sqrt{3}\\ &\textrm{E}.\quad 7\\\\ &\textbf{Jawab}:\qquad \\ &\begin{aligned}r^{2}&=48\\ r&=\sqrt{48}\\ &=\sqrt{16.3}\\ &=4\sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Titik pusat lingkaran}\: \: (x-7)^{2}+(y+9)^{2}=48\\ &\textrm{adalah}....\\ &\textrm{A}.\quad \displaystyle (-7,-9)\\ &\textrm{B}.\quad (-7,9)\\ &\textrm{C}.\quad \color{red}(7,-9)\\ &\textrm{D}.\quad \displaystyle (7,6)\\ &\textrm{E}.\quad (15,48)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Jelas bahwa}\: \: \: (a,b)&=(-6,9) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Persamaan lingkaran yang berpusat di}\: \: P(-2,5)\\ &\textrm{dan melalui titik}\: \: T(3,4)\: \: \textrm{adalah}....\\ &\textrm{A}.\quad \color{red}(x+2)^{2}+(y-5)^{2}=26\\ &\textrm{B}.\quad (x-3)^{2}+(y+5)^{2}=36\\ &\textrm{C}.\quad (x+2)^{2}+(y-5)^{2}=82\\ &\textrm{D}.\quad (x-3)^{2}+(y+5)^{2}=82\\ &\textrm{E}.\quad (x+2)^{2}+(y+5)^{2}=82\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Persamaan Lingkaran Berpusat di}\: \: (a,b)\\ & \textrm{adalah}:\: (x-a)^{2}+(y-b)^{2}=r^{2}\\ &\begin{array}{|l|l|l|}\hline \textrm{Pusat di}\: \: P(-2,5)&\textrm{Melalui Titik}\: \: T(3,4)\\\hline \begin{aligned}(x-a)^{2}+(y-b)^{2}&=r^{2}\\ (x+2)^{2}+(y-5)^{2}&=r^{2}\\ &\\ & \end{aligned}&\begin{aligned}(x-a)^{2}+(y-b)^{2}&=r^{2}\\ (3+2)^{2}+(4-5)^{2}&=r^{2}\\ 5^{2}+(-1)^{2}&=r^{2}\\ 26&=r^{2} \end{aligned}\\\hline \begin{aligned}&\textrm{Sehinga persamaan}\\ &\textrm{lingkarannya} \end{aligned}&\begin{aligned}&\textrm{adalah}:\\ &(x+2)^{2}+(y-5)^{2}=r^{2}=26\\ &(x+2)^{2}+(y-5)^{2}=26\\ & \end{aligned}\\\hline \end{array} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Koordinat titik pusat dan jari-jari lingkaran}\: \: x^{2}+y^{2}-4x+6y+4=0\: \: \textrm{adalah}....\\ &\textrm{A}.\quad (-3,2)\: \: \textrm{dan}\: \: 3\\ &\textrm{B}.\quad (3,-2)\: \: \textrm{dan}\: \: 3\\ &\textrm{C}.\quad (-2,-3)\: \:\textrm{ dan}\: \: 3\\ &\textrm{D}.\quad \color{red}(2,-3)\: \: \textrm{dan}\: \: 3\\ &\textrm{E}.\quad (2,3)\: \: \textrm{dan}\: \: 3\\\\ &\textbf{Jawab}: \\ &\textbf{Alterntif 1}\\ &\begin{array}{|l|l|}\hline &{\textrm{Persamaan Lingkaran Berpusat di}\: \: (a,b)\: \: \textrm{dan berjari-jari}\: \: r\: \: \textrm{adalah}}\\ &{\begin{aligned}(x-a)^{2}+(y-b)^{2}&=r^{2}\\ x^{2}+y^{2}-4x+6y+4&=0\\ x^{2}-4x+y^{2}+6y+4&=0\\ x^{2}-4x+4-4+y^{2}+6y+9-9+4&=0\\ (x-2)^{2}-4+(y+3)^{2}-9+4&=0\\ (x-2)^{2}+(y+3)^{2}&=4+9-4\\ (x-2)^{2}+(y+3)^{2}&=9\\ (x-2)^{2}+(y-(-3))^{2}&=3^{2}\begin{cases} \textrm{Pusat} & =(2,-3) \\ \textrm{dan}\\ \: r & = 3 \end{cases} \end{aligned}}\\\hline \end{array}\\ &\textbf{Alterntif 2}\\ &\begin{aligned}\textrm{Diketahui}&\: \textrm{persamaan lingkaran}:\: \: x^{2}+y^{2}-4x+6y+4=0\begin{cases} A & =-4 \\ B & =6 \\ C & =4 \end{cases}\\ &x^{2}+y^{2}+Ax+By+C=0\\ &\begin{cases} \textrm{Pusat} & =\left ( -\displaystyle \frac{1}{2}A,\: -\frac{1}{2}B \right )=\left ( -\frac{1}{2}\cdots ,\: -\frac{1}{2}\cdots \right )=(\cdots ,\cdots ) \\ \textrm{Jari-jari} & =\sqrt{\displaystyle \frac{1}{4}A^{2}+\frac{1}{4}B^{2}-C}=\sqrt{\displaystyle \frac{1}{4}\cdots ^{2}+\frac{1}{4}\cdots ^{2}-\cdots }=\sqrt{\cdots } \end{cases} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 5.&\textrm{Suatu lingkaran}\: \: x^{2}+y^{2}-4x+2y+p=0\\ &\textrm{berjari-jari 3, maka nilai}\: \: p\: \: \textrm{adalah}....\\ &\textrm{A}.\quad -1\\ &\textrm{B}.\quad -2\\ &\textrm{C}.\quad -3\\ &\textrm{D}.\quad \color{red}-4\\ &\textrm{E}.\quad -5\\\\ &\textbf{Jawab}:\\ &\begin{aligned}r=\sqrt{\displaystyle \frac{A^{2}}{4}+\frac{B^{2}}{4}-C}&=3\\ \displaystyle \sqrt{\frac{(-4)^{2}}{4}+\frac{2^{2}}{4}-p}&=3\\ \displaystyle \frac{16}{4}+\frac{4}{4}-p&=9\\ 4+1-p&=9\\ -p&=9-5\\ p&=-4 \end{aligned} \end{array}$.

Hubungan Dua Lingkaran (Lanjutan)

Hubungan Dua Buah Lingkaran

Coba perhatikan ilustrasi beberapa lingkaran berikut

Sebagai penjelasan dari kondisi di atas adalah:

$\begin{array}{|c|c|l|}\hline \textbf{Kedudukan}&\textbf{Ilustrasi}&\qquad\qquad\: \textbf{Keterangan}\\\hline \left | L_{1}L_{2} \right |>r_{1}+r_{2}&\textbf{Gambar 1}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{dan tidak pula bersinggungan}\\ &\textrm{dan saling lepas} \end{aligned}\\\hline \left | L_{1}L_{2} \right |=0&\textbf{Gambar 5}&\textrm{Dikarenakan sepusat}\\\hline \left | L_{1}L_{2} \right |\leq r_{1}+r_{2}&\textbf{Gambar 6}&\textrm{Terletak di dalam lingkaran}\: \: L_{1} \\\hline \left | L_{1}L_{2} \right |=r_{1}+r_{2}&\textbf{Gambar 2}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{tetapi bersinggungan di luar} \end{aligned}\\\hline \left | L_{1}L_{2} \right |=r_{1}-r_{2}&\textbf{Gambar 3}&\begin{aligned}&\textrm{kedua lingkaran tidak berpotongan}\\ &\textrm{tetapi bersinggungan di dalam} \end{aligned}\\\hline \begin{cases} \left | L_{1}L_{2} \right | > r_{1}-r_{2} \\ \left | L_{1}L_{2} \right | < r_{1}+r_{2} \end{cases}&\textbf{Gambar 4}&\begin{aligned}&\textrm{kedua lingkaran berpotongan} \end{aligned}\\\hline \end{array}$.

$\begin{aligned}&\textbf{Kuasa}\\ &\begin{array}{|l|l|}\hline \textrm{Lingkaran}&\textrm{Posisi sebuah titik terhadap lingkaran}\\\hline \begin{aligned}&\textrm{Titik dua}\\ & \textrm{lingkaran} \end{aligned}&\begin{aligned}&\textrm{Tempat kedudukan titik-titik yang memiliki}\\ &\textrm{kuasa yang sama terhadap dua lingkaran} \end{aligned}\\\hline \begin{aligned}&\textrm{Garis tiga}\\ & \textrm{lingkaran} \end{aligned}&\begin{aligned}&\textrm{Tempat kedudukan titik yang memiliki}\\ &\textrm{kuasa yang sama terhadap tiga buah lingkaran} \end{aligned}\\\hline \end{array} \end{aligned}$.

$\begin{aligned}&\textbf{Berkas Lingkaran}\\ &\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\textrm{Posisi}&\qquad\qquad\textrm{Keterangan}\\\hline \begin{aligned}&\textrm{Berkas}\\ &\textrm{Lingkaran} \end{aligned}&\begin{aligned}&\textrm{Pada garis}\\ &\textrm{busur} \end{aligned}&\begin{aligned}&\textrm{Sejumlah lingkaran yang dapat }\\ &\textrm{dibuat melalui titik-titik potong }\\ &\textrm{kedua lingakaran itu}\end{aligned} \\\hline \end{array} \end{aligned}$.

$\begin{aligned}&\textbf{Tali Busur Sekutu}\\ &\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\textrm{Posisi}&\qquad\qquad\textrm{Keterangan}\\\hline \begin{aligned}&\textrm{Tali Busur}\\ &\textrm{Sekutu}\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Kedua}\\ &\textrm{lingkaran}\\ &\textrm{yang}\\ & \textrm{berpotongan} \end{aligned}&\begin{aligned}&\textrm{Ruas garis yang menghubungkan }\\ &\textrm{titik-titik potong irisan irisan }\\ &\textrm{kedua lingkaran tersebut}\\ & \end{aligned} \\\hline \end{array}\\ &\bullet \: \: \textrm{Persamaan Tali Busur Sekutunya adalah}:\: \color{blue}L_{1}-L_{2}=0\\ &\bullet \: \: \textrm{Persamaan yang melalui titik potong dan lingkaran (berkas)}\\ &\: \: \quad \textrm{itu adalah}:\: L_{3}=L_{1}+\color{red}p\color{black}(L_{1}-L_{2}),\: \: \textrm{atau}\: \: L_{3}=L_{1}+\color{red}p\color{black}L_{2}\\ &\: \: \quad \textrm{dengan}\: \: \color{red}p\: \: \color{black}\textrm{adalah suatu parameter (suatu patokan nilai)}\\ &\bullet \: \: \textrm{Luas daerah irisan}:\: (\theta _{1}r_{1}^{2}+\theta _{2}r_{2}^{2})-\displaystyle \frac{1}{2}(r_{1}^{2}\sin \theta _{1}+r_{2}^{2}\sin \theta _{2}) \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah kedudukan untuk dua buah lingkaran}\\ & L_{1}\equiv x^{2}+y^{2}-2x-4y+1=0\\ &\textrm{dan}\: \: L_{2}\equiv x^{2}+y^{2}-4x-2y-1=0.\\ & \textrm{Jika kedua lingkaran tersebut bersinggungan}\\ &\textrm{atau berpotongan, tentukanlah titik singgung atau potongnya} \\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|c|}\hline L_{1}&L_{2}\\\hline x^{2}+y^{2}-2x-4y+1=0&x^{2}+y^{2}-4x-2y-1=0\\\hline \begin{cases} P_{1} & :\left ( - \displaystyle \frac{1}{2}(-2),-\frac{1}{2}(-4) \right )=(1,2) \\ r &=\sqrt{\displaystyle \frac{1}{4}\left ( (-2)^{2}+(-4^{2}) \right )-1}\\ &=2 \end{cases}&\begin{cases} P_{2} & :\left ( - \displaystyle \frac{1}{2}(-4),-\frac{1}{2}(-2) \right )=(2,1) \\ r &= \sqrt{\displaystyle \frac{1}{4}\left ( (-4)^{2}+(-2^{2}) \right )-(-1)}\\ &=\sqrt{6} \end{cases}\\\hline \end{array}\\ &\begin{aligned}\textrm{Jarak ke}&\textrm{dua pusat lingkarannya adalah}\: \: P_{1}P_{2}\: \: \textrm{yaitu}:\\ P_{1}P_{2}&=\sqrt{(2-1)^{2}+(1-2)^{2}}\\ &=\sqrt{2}\\ \textrm{Karena n}&\textrm{ilai}\: \: P_{1}P_{2}=\sqrt{2}\: \: \textrm{dan nilai}\: \: P_{1}+P_{2}=2+\sqrt{6},\\ \textrm{sehingga}\: &P_{1}P_{2}<P_{1}+P_{2}\: \: \textrm{maka kedua lingkaran }\\ \textrm{itu berpo}&\textrm{tongan} \end{aligned} \end{array}$.

$.\qquad \begin{aligned}x^{2}+y^{2}-2x-4y+1&=0\: ..................(1)\\ x^{2}+y^{2}-4x-2y-1&=0\: ..................(2)\\ ----------&---\: ^{-}\\ 2x-2y+2&=0\\ y&=x+1\: ........................(3)\\ \textrm{persamaan}\: \: (3)\rightarrow (1)&\\ x^{2}+(x+1)^{2}-2x-&4(x+1)+1=0\\ x^{2}+x^{2}+2x+1-2x&-4x-4+1=0\\ 2x^{2}-4x-2&=0\Leftrightarrow x^{2}-2x-1=0\\ x_{1,2}&=\displaystyle \frac{-(-2)\pm \sqrt{(-2)^{2}-4.1(-1)}}{2}\\ &=\displaystyle \frac{2\pm \sqrt{8}}{2}=\displaystyle \frac{2\pm 2\sqrt{2}}{2}\begin{cases} x_{1} & =1+\sqrt{2}\: .........(4)\: \: \textbf{atau} \\ x_{2} & =1-\sqrt{2}\: .........(5) \end{cases}\\ \textrm{persamaan}\: \: (4)\rightarrow (3)&,\: y_{1}=1+\sqrt{2}+1=2+\sqrt{2}\\ \textrm{persamaan}\: \: (5)\rightarrow (3)&,\: y_{1}=1-\sqrt{2}+1=2-\sqrt{2}\\ \textrm{Sehingga titik poton}&\textrm{gnya ada 2 yaitu}:\\ &\color{red}\begin{cases} \left ( 1+\sqrt{2},2+\sqrt{2} \right )\: \: \textrm{dan} \\ \left ( 1-\sqrt{2},2-\sqrt{2} \right ) \end{cases}& \\\textrm{Berikut ilustrasinya} \end{aligned}$.

$\begin{array}{ll}\\ 2&\textrm{Dari contoh soal no.1, tentukanlah persamaan lingkaran }\\ &\textrm{yang melalui titik potong kedua lingkaran itu serta }\\ &\textrm{melalui titik pusat koordinat}\: \: O(0,0)\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Pada jawaban soal no.1 didapatkan persamaan }\\ &\textbf{tali busur}:L_{1}-L_{2}\equiv x-y+1=0\\ &\textrm{Sehingga persamaan }\\ &\textbf{berkas lingkaran}\textrm{nya adalah}:L_{3}=L_{1}+p\left (L_{1}-L_{2} \right )=0\\ &\, \, \: \qquad \Leftrightarrow L_{3}= \left (x^{2}+y^{2}-2x-4y+1 \right )+p(x-y+1)=0\\ &\textrm{Karena melalui titik asal}\: \: O(0,0),\: \textrm{maka}\\ &\, \, \: \qquad \Leftrightarrow (0+0-0-0+1)+p(0-0+1)=0\Leftrightarrow p=-1\\ &\textrm{Selanjutnya persamaan berkas lingkarannya akan menjadi}\\ &\, \, \: \qquad L_{3}\equiv x^{2}+y^{2}-2x-4y+1 -(x-y+1)=0\\ &\textrm{Jadi},\: L_{3}\equiv x^{2}+y^{2}-3x-3y=0 \\\\ &\textrm{Dan gambar berikut sebagai ilustrasinya} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3&\textrm{Diketahuin dua buah lingkaran}\\ & L_{1}\equiv x^{2}+y^{2}-15y+32=0\quad \: \textrm{dan}\\ & L_{2}\equiv x^{2}+y^{2}-18x+2y+32=0\\ &\textrm{Tunjukkan bahwa kedua lingkaran}\\ &\textrm{bersinggungan di luar dan tentukan}\\ &\textrm{titik singgungnya}\\\\ &\textbf{Jawab}:\\ &\color{blue}\textrm{Akan ditunjukkan kedua lingkaran saling}\\ &\textrm{bersinggungan di luar, yaitu:}\\ &\begin{array}{|l|l|l|}\hline \qquad\qquad\textrm{Lingakaran}&\qquad\textrm{Pusat/r}\\\hline L_{1}\equiv x^{2}+y^{2}-15y+32=0&\begin{cases} P_{1} &=(0,8) \\ r_{1} & = 4\sqrt{2} \end{cases}\\\hline L_{2}\equiv x^{2}+y^{2}-18x+2y+32=0&\begin{cases} P_{2} &=(9,-1) \\ r_{2} & = 5\sqrt{2} \end{cases}\\\hline \end{array}\\ &\textrm{Selanjutnya}\\ &\begin{array}{|l|l|}\hline \textrm{Hitungan jarak kedua pusat}&\textrm{Sebagai bandingan}\\\hline \begin{aligned}&\textrm{Pusat 1 lingkaran}\: P_{1}=(0,8)\\ &\textrm{Pusat 2 lingkaran}\: P_{2}=(9,-1)\\ &\textrm{maka jarak}\: \: \: P_{1}P_{2}\: \: \textrm{adalah}\\ &=\sqrt{(9-0)^{2}+(-1-8)^{2}}\\ &=\sqrt{9^{2}+9^{2}}=\sqrt{2\times 9^{2}}=\color{red}9\sqrt{2} \end{aligned}&\begin{aligned}P_{1}P_{2}&=r_{1}+r_{2}\\&=4\sqrt{2}+5\sqrt{2}\\&=\color{red}9\sqrt{2}\\ &\\ & \end{aligned}\\\hline \end{array}\\ &\color{blue}\textrm{Adapun koordinat titik singgungnya}:\\ &\begin{aligned}\begin{pmatrix} x\\ y \end{pmatrix}&=\displaystyle \frac{5\begin{pmatrix} 0\\ 8 \end{pmatrix}+4\begin{pmatrix} 9\\ -1 \end{pmatrix}}{5+4}=\displaystyle \frac{\begin{pmatrix} 5\times 0+4\times 9\\ 5\times 8+4\times (-1) \end{pmatrix}}{9}\\ &=\displaystyle \frac{\begin{pmatrix} 36\\ 36 \end{pmatrix}}{9}=\begin{pmatrix} 4\\ 4 \end{pmatrix} \end{aligned}\\ &\textrm{Sehingga koordinat titik potongnya adalah}:\: (4,4)\\ &\textbf{Sebagai gambaran perhatikan ilustrasi berikut} \end{array}$.

DAFTAR PUSTAKA

Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.