Latihan Soal 1 Persiapan PAS Gasal Matematika Wajib Kelas XII

 

Sebagai tambahan penjelasan berikut diilustrasikan panjang beberapa unsur dalam kubus

dan

Jika diberikan pernyataan-pernyataan sebagai berikut

(1) titik A terletak pada garis AB

(2) titik A terletak di luar garis BC

(3) titik A pada bidang ABFE

(4) titik A di luar bidang ABCD

Pernyataan yang benar dan sesuai dengan 

kondisi gambar di atas adalah ....

Jawab: e

Cukup jelas baik poin (1), (2), maupun (3)

Jika diberikan pernyataan-pernyataan sebagai berikut

(1) titik M terletak pada garis LM

(2) titik N terletak di luar garis KL

(3) titik R pada bidang KLMN

(4) titik K dilalui garis SN

Pernyataan yang benar dan sesuai dengan 

kondisi gambar di atas adalah ....

Jawab : a

Jawaban cukup jelas

Jika diberikan pernyataan-pernyataan sebagai berikut

(1) titik A pada bidang  

(2) titik B pada bidang  

(3) titik C di luar garis AB

(4) titik C tidak pada bidang  

Pernyataan yang benar dan sesuai dengan 

kondisi gambar di atas adalah ....

Jawab : d

Jawaban juga cukup jelas

Pernyataan berikut yang benar adalah ....

Jawab : c

Jawaban sudah cukup jelas

apabila masih ada kendala bisa disampaikan dikolom komentar

agar bisa diperjelas

Pernyataan berikut yang benar adalah ....

Jawab : b

Jawaban sudah cukup jelas

apabila masih ada kendala bisa disampaikan dikolom komentar

agar bisa diperjelas pemabahasannya

 

Latihan Soal 12 Persiapan PAS Gasal Matematika Wajib Kelas X

$\begin{array}{ll}\\ 106.&\textrm{Diberikan gambar daerah yang diarsir }\\ &\textrm{berikut ini}\: ....\\ \end{array}\\$.

$.\qquad \begin{array}{l}\\ \textrm{Daerah yang diarsir merupakan daerah }\\ \textrm{penyelesaian dari}\\ \textrm{a}.\quad y<-x^{2}-5x-14\\ \textrm{b}.\quad y>x^{2}-5x-14\\ \textrm{c}.\quad \color{red}y\leq x^{2}-5x-14\\ \textrm{d}.\quad y\geq x^{2}+5x-14\\ \textrm{e}.\quad y\leq x^{2}+5x+14\\\\ \textbf{Jawab}:\quad \textbf{c}\\ \begin{aligned}&\color{blue}\textbf{Alternatif  1}\\ &\textrm{Ambil titik uji saja}\: \: (0,0)\: \: \textrm{untuk menguji}\\ &\textrm{wilayah fungsi}\: \: y...x^{2}-5x-14\\ &\color{blue}\textbf{Alternatif  2}\\ &\textrm{Fungsi di atas adalah fungsi}:\\ &y=f(x)=ax^{2}+bx+c\\ &\textrm{Karena kurva menghadap ke atas, maka}\\ &\textrm{maka nilai}\: \: \textbf{a}\: \: \textrm{positif}\\ &\textrm{Jelas pilihan}\: \: \textbf{a}\: \: \textrm{salah}\\ &\textrm{karena}\: :\: a<0\\ &\textrm{Karena kurva puncaknya di kuadran IV}\\ &\textrm{maka nilai}\: \: \textbf{b}<0\: \: \\ &\textrm{Jelas pilihan}\: \: \textbf{d,e}\: \: \textrm{salah}\\ &\textrm{Karena kurva memotong sumbu-Y}\\ &\textrm{di bawah sumbu-X. maka nilai}\: c<0\\ &\textrm{Dan karena kurva berupa kurva}\: \textbf{mulus}\\ &\textrm{maka jawaban}\: \: \textbf{b}\: \: \textrm{juga salah}\\ &\textrm{karena jika digambar akan berupa}\\ &\textrm{kurva yang putus-putus}.\\ &\textrm{Jadi, jawaban yang mungkin adalah}\: :\: \textbf{c} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 107.&\textrm{Diberikan gambar daerah yang diarsir }\\ &\textrm{berikut ini}\: ....\\ \end{array}\\$.

$.\qquad \begin{array}{l}\\ \textrm{Daerah yang diarsir merupakan daerah }\\ \textrm{penyelesaian dari}\\ \textrm{a}.\quad x^{2}+y^{2}\leq 4\: ;\: x+2y\leq 4\\ \textrm{b}.\quad x^{2}+y^{2}\leq 4\: ;\: x+2y\geq 4\\ \textrm{c}.\quad x^{2}+y^{2}\leq 16\: ;\: y\geq x+1\\ \textrm{d}.\quad \color{red}x^{2}+y^{2}\leq 16\: ;\: y\leq x+1\\ \textrm{e}.\quad x^{2}+y^{2}\leq 16\: ;\: x-y\leq 1\\\\ \textbf{Jawab}:\quad \textbf{d}\\ \begin{aligned}&\textrm{Diketahui bahwa ada sebuah lingkaran}\\ &\textrm{dengan persamaan}:\: x^{2}+y^{2}=16\: \textrm{dan}\\ &\textrm{sebuah garis}\: \: y=x+1.\\ &\textrm{Ambil titik uji saja}\: \: (0,0)\: \: \textrm{untuk menguji}\\ &\textrm{wailayah lingkaran dan sekitar garis}\\ &\textrm{yaitu}:\\ &\bullet \quad (0,0)\Rightarrow 0^{2}+0^{2}...16\: \: \textrm{dan}\\ &\bullet \quad (0,0)\Rightarrow 0...0+1\\ &\textrm{Tentunya tanda yang tepat adalah}:\: \: \leq .\\ &\textrm{Sehingga wilayah yang terarsir di atas}\\ &\begin{cases} & x^{2}+y^{2}\leq 16 \\ & y\leq x+1 \end{cases} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 108.&\textrm{Diberikan gambar daerah yang diarsir }\\ &\textrm{berikut ini}\: ....\\ \end{array}\\$.

$.\qquad \begin{array}{l}\\ \textrm{Daerah yang diarsir merupakan daerah }\\ \textrm{penyelesaian dari}\\ \textrm{a}.\quad y\leq x^{2}+5x\: ;\: y\geq x-2\\ \textrm{b}.\quad y\leq x^{2}+5x\: ;\: y\geq x+2\\ \textrm{c}.\quad \color{red}y\leq x^{2}+5x\: ;\: y\leq x+2\\ \textrm{d}.\quad y\leq x^{2}-5x\: ;\: y\geq x+2\\ \textrm{e}.\quad y\leq x^{2}-5x\: ;\: y\leq x+2\\\\ \textbf{Jawab}:\quad \textbf{c}\\ \begin{aligned}&\textrm{Diketahui bahwa dua buah kurva, yaitu}\\ &\textrm{linear dan kuadrat}:\\ &\begin{cases} y... & ax^{2}+bx+c \\ y... & px+q \end{cases}\\ &\color{blue}\textbf{Alternatif 1}\\ &\textrm{Ambil titik uji saja}\: \: (0,0)\: \: \textrm{untuk menguji}\\ &\textrm{wilayah kedua kurva tersebut}\\ &\color{blue}\textbf{Alternatif 2}\\ &\textrm{Lihat titik ekstrim fungsi kuadratnya}\\ &\textrm{Karena berada di kuadran III, maka}\\ &\textrm{nilai}\: \: \textbf{b}>0,\: \: \textrm{akibatnya opsi jawaban}\\ &\textbf{d}\: \: \textrm{dan}\: \: \textbf{e}\: \: \textrm{salah}.\\ &\textrm{Dan karena garis linearnya (garis lurus)}\\ &\textrm{sumbu-Y di atas sumbu-X, maka jawaban}\\ & \textbf{a}\: \: \textrm{salah}\\ &\textrm{Tinggal opsi jawaban}\: \: \textbf{b}\: \: \textrm{dan}\: \: \textbf{c}\\ &\textrm{dengan titik uji}\: \: (0,0),\: \textrm{maka opsi}\: \: \textbf{c}\\ &\textrm{yang paling tepat} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 109.&\textrm{Diberikan gambar daerah yang diarsir }\\ &\textrm{berikut ini}\: ....\\ \end{array}\\$.

$.\qquad \begin{array}{l}\\ \textrm{Daerah yang merupakan daerah }\\ \textrm{penyelesaian dari}\\ \begin{cases} y &\geq x^{2}-1 \\ y & \leq 4-x^{2} \end{cases}\\ \textrm{Ditunjukkan oleh daerah}\\ \textrm{a}.\quad \color{red}\textbf{I}\\ \textrm{b}.\quad \textbf{II}\\ \textrm{c}.\quad \textbf{III}\\ \textrm{d}.\quad \textbf{IV}\\ \textrm{e}.\quad \textbf{V}\\\\ \textbf{Jawab}:\quad \textbf{a}\\ \begin{aligned}&\textrm{Dengan titik uji}\: \: (0,0)\: \: \textrm{didapatkan}\\ &\bullet \quad y \leq x^{2}-1\Rightarrow 0\geq 0-1\: \: \textbf{benar}\\ &\qquad\textrm{lihat ilustrasi gambar 109.a di bawah}\\ &\bullet \quad y \leq 4-x^{2} \Rightarrow 0\leq 4-0\: \: \textbf{benar}\\ &\qquad\textrm{lihat ilustrasi gambar 109.b di bawah}\\ &\textrm{Jika kedua gambar dikolaborasi menjadi}\\ &\textrm{gambar 109.c}\\ \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 110.&\textrm{Diberikan gambar daerah yang diarsir }\\ &\textrm{berikut ini}\: ....\\ \end{array}\\$.

$.\qquad \begin{array}{l}\\ \textrm{Daerah yang diarsir merupakan daerah }\\ \textrm{penyelesaian dari}\\ \begin{cases} 2y &\leq 3x^{2}-27 \\ y & \leq -2x-x^{2} \\ y & \leq -x^{2}-5 \end{cases}\\ \textrm{Ditunjukkan oleh daerah}\\ \textrm{a}.\quad \textbf{I}\\ \textrm{b}.\quad \textbf{II}\\ \textrm{c}.\quad \textbf{III}\\ \textrm{d}.\quad \textbf{IV}\\ \textrm{e}.\quad \color{red}\textbf{V}\\\\ \textbf{Jawab}:\quad \textbf{e}\\ \begin{aligned}&\textrm{Dengan titik uji}\: \: (0,0)\: \: \textrm{didapatkan}\\ &\bullet \quad 2y \leq 3x^{2}-27\Rightarrow 0\leq 0-27\: \: \textbf{salah}\\ &\bullet \quad y \leq -2x-x^{2} \Rightarrow 0\leq 0\: \: \textbf{bisa benar}\\ &\qquad \textrm{tetapi saat titiknya diganti}\\ &\qquad (1,0)\: \: \textrm{jelas tampak salahnya}\\ &\bullet \quad 2y \leq -x^{2}-5\Rightarrow 0\leq 0-5\: \: \textbf{salah}\\ &\textrm{Dari semua fakta di atas}\\ &\textrm{opsi e yang paling mungkin benar}\\ \end{aligned} \end{array}$

Lanjutan Materi 2 Sistem Pertidaksamaan Dua Variabel

 3. Sistem Pertidaksamaan Dua Variabel Kuadrat dan Kuadrat (SPDVKK)

Bentuk Persamaan (SPDVKK)

$\begin{aligned}&\textrm{Bentuk Umum}:\\ &\quad\begin{cases} ax^{2}+by^{2}+cxy+dx+ey+f=0 \\ px^{2}+qy^{2}+rxy+sx+ty+u=0 \end{cases} \end{aligned}$.

Perhatikan tabel berikut

$\begin{array}{|c|l|}\hline 1.&\textrm{Penyelesaian}\\ &y=y\\\hline 2.&\textrm{Proses}:\\ &\begin{aligned}&ax^{2}+bx+c=px^{2}+qx+r\\ &\textrm{dengan}\: \textrm{syarat}\\ &a-p\neq 0\\ &\textrm{diubah kebentuk umum}\\ &Ax^{2}+Bx+C=0\\ &\textrm{dengan}\\ &D=B^{2}-4AC \end{aligned}\\\hline 3.&\textrm{Sebagai Penjelasan}\\ &\begin{aligned} D&> 0\\ &\textrm{SPDVKK mempunyai }\\ &\textrm{2 penyelesaian berbeda}\\ D&=0\\ &\textrm{SPDVKK mempunyai }\\ &\textrm{1 penyelesaian saja}\\ D&< 0\\ &\textrm{SPDVKK tidak }\\ &\textrm{mempunyai penyelesaian} \end{aligned}\\\hline \end{array}$.

Bentuk Pertidaksamaan (SPtDVKK)

$\begin{aligned}&\textrm{Bentuk Umum}:\\ &y\geq ax^{2}+bx+c\\ &y\leq px^{2}+qx+r\\\\ &\underline{\textrm{Catatan}}:\\ &\textrm{Tanda Ketaksamaan bisa diganti}\\ &\textrm{dengan tanda ketaksamaan yang}\\ &\textrm{lainnya} \end{aligned}$

Bentuk Pertidaksamaan dari SPtDVKK adalah wilayah atau daerah dengan menentukan penyelesaian seperti persamaan langkah awalnya kemudian dibuatkan wilayah yang menunjukkan pertidaksamaannya. Wilayah SPtDVKK ini adalah irisan antara wilayah penyelesaian dari pertidaksamaan kuadrat yang pertama dengan wilayah penyelesaian pertidaksamaan kuadrat yang kedua.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Carilah ada/tidaknya penyelesaian }\\ &\textrm{dari SPDVKK berikut ini}.\\\\ &\begin{cases} y=-x^{2} \\ y=x^{2}+2x+1 \end{cases}\\\\ &\textrm{dan sketsalah tafsiran geometrinya}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &\begin{cases} y=-x^{2}\\ y=x^{2}+2x+1 \end{cases}\\ &\textrm{substitusikan}\: \: \: y=-x^{2}\quad \textrm{ke}\quad y=x^{2}+2x+1\\ &\textrm{sehingga diperoleh}\\ &-x^{2}=x^{2}+2x+1\\ &2x^{2}+2x+1=0\\ &\begin{cases} a=2 \\ b=-2 \\ c=1 \end{cases}\\ &\textrm{Karena, nilai}\: \: D=b^{2}-4ac\\ &=(-2)^{2}-4(2)(1)=4-8=-4< 0\\ &\textrm{maka diperoleh keterangan }\\ &\textrm{bahwa kedua parabola tersebut}\\ &\textbf{tidak berpotongan dan tidak bersinggungan} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan himpunan penyelesaian }\\ &\textrm{dari SPtDVLK berikut ini}\\ &\begin{cases} y\leq 4-x^{2} \\ y\leq x^{2}-2x-3 \end{cases}\\\\ &\textrm{Jika ada, sketsalah tafsiran geometrinya}\\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ \textbf{a}.&\textrm{Pembuat nol fungsi}\: ,\: \begin{cases} y & =4-x^{2} \\ y & =x^{2}-2x-3 \end{cases},\\ &\textrm{yaitu}:\\ &\textbf{Untuk}:\: \: y=f(x)=4-x^{2}\\ &4-x^{2}=0 \Rightarrow x^{2}=4\Rightarrow x=\pm 2\\ &\textrm{Jadi titik potongnya}:(-2,0)\: \: \textrm{dan}\: \: (2,0)\\ &\textrm{Titik puncak grafik fungsinya}\: \left ( x_{ss},y \right ),\\ &\textrm{yaitu}:\\ &x_{ss}=-\displaystyle \frac{b}{a}\: \: \textrm{atau}\: \: x_{ss}=\displaystyle \frac{x_{1}+x_{2}}{2}\\ &\Rightarrow x_{ss}=\displaystyle \frac{2+(-2)}{2}=\frac{0}{2}=\color{red}0\color{black},\: \: \textrm{maka}\\ &y=f(\color{red}0\color{black})=4-0^{2}=4\\ &\textrm{Jadi, titik puncaknya}:\: (0,4)\\ &\textbf{Dan untuk}:\: \: y=f(x)=x^{2}-2x-3\\ &x^{2}-2x-3=0\Rightarrow (x+1)(x-3)=0\\ &x=-1\: \: \textrm{atau}\: \: x=3\\ &\textrm{Jadi titik potongnya}:(-1,0)\: \: \textrm{dan}\: \: (3,0)\\ &\textrm{Titik puncak grafik fungsinya}\: \left ( x_{ss},y \right ),\\ &\textrm{yaitu}:\\ &x_{ss}=-\displaystyle \frac{b}{a}\: \: \textrm{atau}\: \: x_{ss}=\displaystyle \frac{x_{1}+x_{2}}{2}\\ &\Rightarrow x_{ss}=\displaystyle \frac{(-1)+3}{2}=\frac{2}{2}=\color{red}1\color{black},\: \: \textrm{maka}\\ &y=f(\color{red}1\color{black})=1^{2}-2(1)-3=-4\\ &\textrm{Jadi, titik puncaknya}:\: (0,-4)\\ \textbf{b}.&\textrm{Melakukan uji titik untuk menentukan}\\ &\textrm{wilayah pertidaksamaan, yaitu}:\\ &\textrm{Ambil titik bebas saja, misal kita pilih lagi}\\ &\textrm{titik}\: \: (0,0),\: \textrm{maka}\\ &\begin{aligned}(0,0)&\Rightarrow y\leq 4-x^{2}\\ &0\leq 4-0^{2}\Rightarrow 0\leq 4\: \: \textbf{benar}\\ (0,0)&\Rightarrow y\leq x^{2}-2x-3\: \\ &0\leq 0^{2}-2(0)-3\Rightarrow 0\leq -3\: \: \textbf{salah} \end{aligned}\\ &\textrm{ini berarti wilayah yang di dalamnya}\\ &\textrm{terdapat titik uji}\: \: (0,0)\: \: \textrm{bukan}\\ &\textrm{wilayah penyelesaian kedua pertidaksamaan}\\ &\textrm{tersebut}\\ \textbf{c}.&\textrm{Menggambar wilayah pertidaksamaan}\\ &\textrm{berikut ilustrasi gambarnya}\end{array} \end{array}$.

atau

DAFTAR PUSTAKA

1. Kanginan, M., Akhmad, G., Nurdiansyah, H. 2014. Matematika untuk SMA/MA Kelas X Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
2. Yuana, R.A., Indriyastuti. 2017. Matematika untuk Kelas X SMA dan MA Kelompok Mata Pelajaran Wajib. Solo: TIGA SERANGKAI PUSTAKA MANDIRI.

Lanjutan Materi 1 Sistem Pertidaksamaan Dua Variabel

 2. Sistem Pertidaksamaan Dua Variabel Linear Kuadrat (SPtDVLK)

Bentuk Persamaan (SPDVLK)

$\begin{aligned}&\textrm{Bentuk Umum}:\\ &\qquad\begin{cases} ax+by+c=0 \\ px^{2}+qy^{2}+rxy+sx+ty+u=0 \end{cases} \end{aligned}$.

Perhatikanlah tabel berikut

$\begin{array}{|c|l|}\hline 1.&\textrm{Penyelesaian}\\ &y=y\\\hline 2.&\textrm{Proses}:\\ &\begin{aligned}&ax+b=px^{2}+qx+r\\ &\textrm{diubah ke bentuk umum}\\ &Ax^{2}+Bx+C=0\\ &\textrm{dengan}\\ &D=B^{2}-4AC \end{aligned}\\\hline 3.&\textrm{Sebagai Penjelasan}\\ &\begin{aligned} D&> 0\\ &\textrm{SPDVLK mempunyai }\\ &\textrm{2 penyelesaian berbeda}\\ D&=0\\ &\textrm{SPDVLK mempunyai }\\ &\textrm{1 penyelesaian saja}\\ D&< 0\\ &\textrm{SPDVLK tidak }\\ &\textrm{mempunyai penyelesaian} \end{aligned}\\\hline \end{array}$.

Bentuk Pertidaksamaan (SPtDVLK)

$\begin{aligned}&\textrm{Bentuk Umum}:\\ &y\geq ax^{2}+bx+c\\ &y\leq px+q\\\\ &\underline{\textrm{Catatan}}:\\ &\textrm{Tanda Ketaksamaan bisa diganti}\\ &\textrm{dengan tanda ketaksamaan yang}\\ &\textrm{lainnya} \end{aligned}$

Bentuk Pertidaksamaan dari SPtDVLK adalah wilayah atau daerah dengan menentukan penyelesaian seperti persamaan langkah awalnya kemudian dibuatkan wilayah yang menunjukkan pertidaksamaannya. Wilayah SPtDVLK ini adalah irisan antara wilayah penyelesaian dari pertidaksamaan linear dan wilayah penyelesaian pertidaksamaan kuadrat.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Carilah ada/tidaknya penyelesaian }\\ &\textrm{dari SPDVLK berikut ini}\\ &\begin{cases} y=-x+2 \\ y=x^{2}-3x+2 \end{cases}\\\\ &\textrm{Jika ada, sketsalah tafsiran geometrinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &\begin{cases} y=-x+2 \\ y= x^{2}-3x+2 \end{cases}\\ &\textrm{maka}\\ &y=y\\ &x^{2}-3x+2=-x+2\\ &x^{2}-2x=0\\ &x(x-2)=0\\ &x=0\quad \textrm{atau}\quad x=2\\ &\textrm{selanjutnya}\: \textbf{hasil ini dapat kita}\\ &\textrm{substitusikan ke}\: \: y=-x+2\\ &\textrm{untuk mendapatkan nilai}\: \: \: \: y\: \: \: \: \textrm{yaitu}:\\ &\begin{cases} x=0 & \Rightarrow y=-0+2=2 ,\quad \textrm{diperoleh titik}\quad (0,2)\\ x=2 & \Rightarrow y=-2+2=0 ,\quad \textrm{diperoleh juga titik}\quad (2,0) \end{cases}\\ &\\ &\textrm{sehingga HP-nya}=\left \{ (0,2),(2,0) \right \}\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan himpunan penyelesaian }\\ &\textrm{dari SPtDVLK berikut ini}\\ &\begin{cases} x+y<4 \\ y\geq x^{2}-9 \end{cases}\\\\ &\textrm{Jika ada, sketsalah tafsiran geometrinya}\\\\ &\textbf{Jawab}:\\ &\begin{array}{ll}\\ \textbf{a}.&\textrm{Pembuat nol fungsi}\: ,\: y=f(x)=x^{2}-9,\\ & \textrm{yaitu}:\\ &x^{2}-9=0\Rightarrow x^{2}=9\Rightarrow x=\pm 3\\ &\textrm{Jadi titik potongnya}:(-3,0)\: \: \textrm{dan}\: \: (3,0)\\ &\textrm{Titik puncak grafik fungsinya}\: \left ( x_{ss},y \right ),\\ &\textrm{yaitu}:\\ &x_{ss}=-\displaystyle \frac{b}{a}\: \: \textrm{atau}\: \: x_{ss}=\displaystyle \frac{x_{1}+x_{2}}{2}\\ &\Rightarrow x_{ss}=\displaystyle \frac{3+(-3)}{2}=\frac{0}{2}=\color{red}0\color{black},\: \: \textrm{maka}\\ &y=f(\color{red}0\color{black})=0^{2}-9=-9\\ &\textrm{Jadi, titik puncaknya}:\: (0,-9)\\ \textbf{b}.&\textrm{Melakukan uji titik untuk menentukan}\\ &\textrm{wilayah pertidaksamaan, yaitu}:\\ &\textrm{Ambil titik bebas saja, misal kita pilih}\\ &\textrm{titik}\: \: (0,0),\: \textrm{maka}\\ &\begin{aligned}(0,0)&\Rightarrow y\geq x^{2}-9\\ &0\geq 0^{2}-9\Rightarrow 0\geq -9\: \: \textbf{benar}\\ (0,0)&\Rightarrow x+y<4\: \: \textrm{juga}\: \textbf{benar}\\ &0+0<4\Rightarrow 0<4 \end{aligned}\\ &\textrm{ini berarti wilayah yang di dalamnya}\\ &\textrm{terdapat titik uji}\: \: (0,0)\: \: \textrm{merupakan}\\ &\textrm{wilayah penyelesaian kedua pertidaksamaan}\\ &\textrm{tersebut}\\ \textbf{c}.&\textrm{Menggambar wilayah pertidaksamaan}\\ &\textrm{berikut ilustrasi gambarnya} \end{array} \end{array}$.

atau

$\begin{array}{ll}\\ 3.&\textrm{Tentukan himpunan penyelesaian }\\ &\textrm{dari SPtDVLK berikut ini}\\ &\begin{cases} y\leq -x+2 \\ y\geq x^{2}-3x+2 \end{cases}\\\\ &\textrm{Jika ada, sketsalah tafsiran geometrinya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Dengan cara sama seperti no. 2}:\\ &\textrm{ditambah dengan}\\ &\begin{cases} y=-x+2 \\ y= x^{2}-3x+2 \end{cases}\\ &\textrm{maka}\\ &y=y\\ &x^{2}-3x+2=-x+2\\ &x^{2}-2x=0\\ &x(x-2)=0\\ &x=0\quad \textrm{atau}\quad x=2\\ &\textrm{selanjutnya}\: \textbf{hasil ini dapat kita}\\ &\textrm{substitusikan ke}\: \: y=-x+2\\ &\textrm{untuk mendapatkan nilai}\: \: \: \: y\: \: \: \: \textrm{yaitu}:\\ &\begin{cases} x=0 & \Rightarrow y=-0+2=2 ,\quad \textrm{diperoleh titik}\quad (0,2)\\ x=2 & \Rightarrow y=-2+2=0 ,\quad \textrm{diperoleh juga titik}\quad (2,0) \end{cases}\\ &\\ &\textrm{sehingga titik potongnya}=\left \{ (0,2),(2,0) \right \}\\ &\textrm{Dan wilayah solusinya adalah irisan}\\ &\textrm{dari kedua pertidaksamaan tersebut}\\ &\textrm{Berikut Gambar wilayahnya} \end{aligned} \end{array}$.

atau

Sistem Pertidaksamaan Dua Variabel

Sebelumnya telah diketahui sistem persamaan linear dua variabel, silahkan lihat di sini.

1. Sistem Persamaan Dua Variabel Linear dan Kuadrat

Sebelumnya akan kita singgung dulu fungsi linear dan kuadrat sebagai mana tabel berikut:

Fungsi Linear

$\begin{aligned}&\\ \textrm{Fungsi}&\: \textrm{Linear adalah}:\\ &\textrm{fungsi di aman fungsi yang }\\ &\textrm{hanya memiliki satu variabel}\\ &\textrm{atau peubah dan berpangkat satu}.\\\\ \textrm{Misal},&\: \: \color{red}f:x \mapsto ax+b\\ & \end{aligned}$.

Dalam menentukan persamaan linear/garis lurus adalah:

$\begin{array}{|c|c|}\hline \textrm{Melalui titik}\: \: \left ( x_{1},y_{1} \right )&\textrm{Melalui titik}\: \: \left ( x_{1},y_{1} \right )\\ \textrm{dan bergradien}\: \: m&\textrm{dan}\: \: \left ( x_{2},y_{2} \right )\\\hline y=m\left ( x-x_{1} \right )+y_{1}&\displaystyle \frac{y-y_{1}}{y_{2}-y_{1}}=\displaystyle \frac{x-x_{1}}{x_{2}-x_{1}}\\ &\begin{aligned}\textrm{dengan}:&\\ m&=\displaystyle \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \end{aligned}\\\hline \textrm{Sejajar dengan} &\textrm{Tegak lurus dengan}\\ \textrm{garis bergradien}\: \: m_{1}&\textrm{garis bergradien}\: \: m_{1}\\\hline \textrm{Syarat dua garis}&\textrm{Syarat dua garis}\\\hline \textrm{Sejajar}\: \: m_{1}=m_{2}&\textrm{Tegak lurus}\: \: m_{1}\times m_{2}=-1\\\hline y=m_{2}\left ( x-x_{1} \right )+y_{1}&y=-\displaystyle \frac{1}{m_{2}}\left ( x-x_{1} \right )+y_{1}\\\hline \end{array}$

Fungsi Kuadrat

$\begin{array}{|l|l|}\hline \textrm{Pengertian}&\begin{aligned}&\textrm{Suatu fungsi yang berbentuk}\\ &f(x)=ax^{2}+bx+c\\ & a,\: b,\: c,\: \in \mathbb{R},\: a\neq 0 \end{aligned}\\\hline \textrm{Grafik Fungsi}&\textrm{Keterangan}\\\hline \textrm{Titik potong sumbu x}&\textrm{Jika ada}\\\hline &\begin{aligned}&\textrm{untuk titik potong}\\ &\textrm{terhadap sumbu x }\\ &\textrm{Jika y = 0 maka }\\ &ax^{2}+bx+c=0\\ &\textrm{Selanjutnya tinggal}\\ &\textrm{menentukan nilai D}\\ &D=b^{2}-4ac\: \: \textrm{adalah}\\ &\: \: \: \: \: \: \: \: \: \textrm{nilai diskriminan}.\\ &\textrm{Jika} \: D>0\\ &\textrm{maka grafik}\\ &\textrm{memotong sumbu x}\\ &\textrm{di dua tempat berbeda}\\ &\textrm{yaitu di} \: (x_{1},0)\: \textrm{dan}\: (x_{2},0).\\ &\textrm{dan jika D = 0}\\ &\textrm{maka grafik}\\ &\textrm{ hanya menyinggung}\\ &\textrm{sumbu x di satu titik}\\ &\textrm{yaitu di }\: (x_{1},0)\\ &\textrm{dan jika}\: D<0 \\ &\textrm{maka grafik}\\ &\textrm{tidak memotong}\\ &\textrm{atau menyinggung sumbu x} \end{aligned}\\\hline \textrm{Titik potong sumbu y}&\begin{aligned}&\textrm{titik potong terhadap}\\ &\textrm{sumbu y, jika x = 0}\\ &y=f(x)=ax^{2}+bx+c\\ &y=f(0)=a(0)^{2}+b(0)+c\\ &y=c \end{aligned}\\\hline \textrm{Sumbu Simetri (SS)}&x=\displaystyle \frac{-b}{2a}\\\hline \textrm{Titik Puncak}&\left ( \displaystyle \frac{-b}{2a},\displaystyle \frac{D}{-4a} \right )\\\hline \textrm{Posisi grafik}&\textrm{Jika}\: a>0\: \textrm{maka}\\ &\textrm{grafik terbuka ke atas}\\ &\textrm{Dan jika nilai}\: a<0\: \textrm{maka}\\ &\textrm{grafik terbuka ke bawah}\\\hline \end{array}$.

Selanjutnya cara membuat grafik fungsi kudratnya adalah sebagai berikut:

$\begin{array}{|c|c|}\hline \textrm{Jika memotong sumbu}-\textrm{X}&\textrm{Jika menyinggung sumbu}-\textrm{X}\\ \textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan}\: \left ( x_{2},0 \right )&\textrm{di titik}\: \left ( x_{1},0 \right )\: \textrm{dan melalui}\\ \textrm{dan melalui sebuah titik lain}&\textrm{sebuah titik lain} \\\hline &\\ y=f(x)=a\left ( x-x_{1} \right )\left ( x-x_{2} \right )&y=f(x)=a\left ( x-x_{1} \right )^{2}\\ &\\\hline \textrm{Jika grafik fungsi itu melalui}&\textrm{Jika grafik fungsi itu melalui}\\\hline \textrm{Titik puncak}\: \: P\left ( x_{p},y_{p} \right )\: \textrm{dan}&\textrm{tiga buah titik yaitu}\: \left ( x_{1},y_{1} \right )\\ \textrm{sebuah titik lain}&\left ( x_{2},y_{2} \right )\: \: \textrm{dan}\: \: \left ( x_{3},y_{3} \right )\\\hline &\\ y=f(x)=a\left ( x-x_{p} \right )^{2}+y_{p}&y=f(x)=ax^{2}+bx+c\\ &\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: f\: \: \textrm{adalah fungsi linear dengan}\\ & f(2)-f(-2)=8,\\ & \textrm{maka nilai dari}\: \: f(4)-f(-2)\: \: \textrm{adalah}\: ....\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\\ &f(x)=ax+b\\ &f(2)-f(-2)\\ &=\left (a(2)+b \right )-\left ( a(-2)+b \right )=8\\ &8=2a+2a\\ &8=4a\\ &2=a\\ &f(x)=2x+b,\quad \textrm{dengan}\: \: b\: \: \textrm{konstan}\\ &\textrm{Sehingga nilai}\quad\\ &f(4)-f(-2)=\left (2(4)+b \right )-\left (2(-2)+b \right )\\ &=8+b+4-b\\ &=\color{red}12 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Ubahlah}\: \: 8-6x-x^{2}\: \: \textrm{ke dalam bentuk}\\ & a-(x+b)^{2},\: \textrm{selanjutnya tentukan}\\ & \textrm{daerah hasil dari}\: \: f(x)=8-6x-x^{2}\\ & \textrm{untuk}\: \: x\: \: \textrm{bilangan real}\\ &\qquad(\textit{NTU Entrance Examination AO-level})\\\\ &\textbf{Jawab}:\\ &\begin{array}{|c|l|}\hline 1.&\color{blue}\textrm{Diketahui}\\\hline &\begin{aligned}\textrm{Misal}\quad\qquad&\\ 8-6x-x^{2}&=f(x)\\ f(x)&=-x^{2}-6x+8\\ &=-\left ( x^{2}+6x-8 \right )\\ &=-\left ( x^{2}+6x+9-17 \right )\\ &=-\left ( (x+3)^{2}-17 \right )\\ &=-(x+3)^{2}+17\\ & \end{aligned}\\\hline 2.&\color{blue}\textrm{Mencari koordinat}\: \: \left ( x_{SS},y_{SS} \right )\\\hline &\begin{aligned}f(x)&=-x^{2}-6x+8\left\{\begin{matrix} a=-1\\ b=-6\\ c=\: \: 8\: \: \end{matrix}\right.\\ \textrm{Maka}&\\ x_{SS}&=\frac{-b}{2a}=\displaystyle \frac{-(-6)}{2(-1)}\\ &=-3\\ y_{SS}&=f(-3)=-\left ( -3+3 \right )^{2}+17=17\\ \therefore &\left ( x_{SS},y_{SS} \right )=(-3,17) \end{aligned}\\\hline 3.&\color{blue}\textrm{Nilai fungsi}\\\hline &\begin{aligned}\textrm{Karena}&\: \: a=-1<0\\ \textrm{maka f}&\textrm{ungsi menghadap}\\ \textbf{ke ba}&\textbf{wah},\: \: \textrm{sehingga}\\ \textrm{daerah}&\: \: \textrm{hasilnya}\: \: \left (R_{f} \right )\\ \textrm{adalah}&:\\ &\left \{ -\infty <y\leq 17 \right \}\\ &\\ &\textrm{Berikut ilustrasinya} \end{aligned}\\\hline \end{array} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Jika}\: \: \alpha \: \: \textrm{dan}\: \: \beta \: \: \textrm{adalah akar-akar dari }\\ &\textrm{persamaan kuadrat}\: \: x^{2}+mx+m=0,\\ &\textrm{maka nilai}\: \: m\: \: \textrm{yang menyebabkan }\\ &\textrm{jumlah kuadrat akar-akar mencapai}\\ &\textrm{minimum adalah}\: ....\\ &\qquad \: \textbf{(UM UNDIP 2014 Mat Das)}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\: \: x^{2}+mx+m=0\\ & \textbf{persamaan kuadrat}\: \textrm{dalam}\: \: x,\\ & \textrm{maka}\\ &x^{2}+mx+m=x^{2}-(\alpha +\beta )x+(\alpha \beta )=0\\ &\begin{cases} \alpha +\beta &=-m \\ & \\ \alpha \beta &=m \end{cases}\\ &\textrm{Selanjutnya}\\ &\alpha ^{2}+\beta ^{2}=\left ( \alpha +\beta \right )^{2}-2\alpha \beta\\ &=(-m)^{2}-2m\: \: \textrm{dan dapat kita tuliskan sebagai}\\ &f(m)=m^{2}-2m\begin{cases} a &=1 \\ b &=-2 \\ c &=0 \end{cases} \\ &\textrm{fungsi kuadrat dalam}\: \: m,\\ &\textrm{sehingga kita perlu mencari titik}\: \: \left ( m_{SS},f\left ( m_{SS} \right ) \right ),\\ & \textrm{tetapi yang kita perlukan}\\ &\textrm{cuma}\: \: m-\textrm{nya saja, yaitu}:\: \: m=m_{SS},\\ &\textrm{dengan}\quad m_{SS}=\displaystyle \frac{-b}{2a}=\frac{-(-2)}{2.1}=1 \end{aligned} \end{array}$.

Latihan Soal 10 Persiapan PAS Gasal Matematika Wajib Kelas XI

 $\begin{array}{ll}\\ 91.&\textrm{Titik A(4,-4) dicerminkan terhadap}\\ &\textrm{garis}\: \: y=x\tan 15^{\circ}\: \: \textrm{menghasilkan}\\ &\textrm{bayangan}\: \: A'(a,b)\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad \sqrt{3}&&\textrm{d}.\quad \color{red}4\sqrt{3}\\ \textrm{b}.\quad 2\sqrt{3}&\textrm{c}.\quad 3\sqrt{3}&\textrm{e}.\quad 6\sqrt{3} \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ &\begin{aligned}\begin{pmatrix} a\\ b \end{pmatrix}&=\begin{pmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} \cos 2.15^{\circ}& \sin 2.15^{\circ}\\ \sin 2.15^{\circ} & -\cos 2.15^{\circ} \end{pmatrix}\begin{pmatrix} 4\\ -4 \end{pmatrix}\\ &=\begin{pmatrix} \cos 30^{\circ}&\sin 30^{\circ}\\ \sin 30^{\circ}&-\cos 30^{\circ} \end{pmatrix}\begin{pmatrix} 4\\ -4 \end{pmatrix}\\ &=\begin{pmatrix} \displaystyle \frac{1}{2}\sqrt{3} & \displaystyle \frac{1}{2}\\ \displaystyle \frac{1}{2} & -\displaystyle \frac{1}{2}\sqrt{3} \end{pmatrix}\begin{pmatrix} 4\\ -4 \end{pmatrix}\\ &=\begin{pmatrix} 2\sqrt{3}-2\\ 2+2\sqrt{3} \end{pmatrix}\\ &\begin{cases} a &=2\sqrt{3}-2 \\ b &=2+2\sqrt{3} \end{cases}\\ \textrm{mak}&\textrm{a nilai dari}\\ a+b&=\left ( 2\sqrt{3}-2+2+2\sqrt{3} \right )\\ &=4\sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 92.&\textrm{Lingkaran}\: \: x^{2}+y^{2}-5x+8y+7=0\\ & \textrm{ditranslasikan oleh}\: \: T=\begin{pmatrix} m\\ n \end{pmatrix}\: \: \textrm{menghasilkan}\\ &\textrm{bayangan}\: \: x^{2}+y^{2}-9x+2y+6=0.\\ & \textrm{Nilai}\: \: m+n=\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad 2&&\textrm{d}.\quad \color{red}5\\ \textrm{b}.\quad 3&\qquad\textrm{c}.\quad 4\qquad&\textrm{e}.\quad 6 \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{d}\\ &\begin{aligned}\textrm{Dik}&\textrm{etahui sebuah lingkaran dengan persamaan}:\\ & \color{blue}x^{2}+y^{2}-5x+8y+7=0\\ \textrm{kar}&\textrm{ena akibat translasi, maka}\\ &\begin{cases} x & =x'-m \\ y & =y'-n \end{cases}\\ &x^{2}+y^{2}-5x+8y+7=0\\ \textrm{seh}&\textrm{ingga}\\ &\Leftrightarrow \color{purple}(x'-m)^{2}+(y'-n)^{2}-5(x'-m)+8(y'-n)+7=0\\ &\Leftrightarrow \color{purple}x'^{2}+y'^{2}-2mx'-2ny'+m^{2}+n^{2}-5x'+5m+8y'-8n+7=0\\ &\Leftrightarrow \color{purple}x'^{2}+y'^{2}-(2m+5)x'+(8-2n)y'+m^{2}+n^{2}+5m-8n+7=0\\ &\qquad \equiv \: \color{purple}x'^{2}+y'^{2}-9x'+2y'+6=0\qquad (\color{black}\textbf{akhir bayangan})\\ &\begin{cases} 9 &=2m+5 \Rightarrow m=2\\ 2 & =8-2n \: \Rightarrow \, \: n=3 \end{cases}\\ \textrm{Jad}&\textrm{i , nilai}\: \: m+n=2+3=5\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 93.&\textrm{Jika titik A(-2,1) dicerminkan terhadap garis}\\ & y=-\displaystyle \frac{1}{3}x\sqrt{3}\: ,\: \textrm{maka bayangan dari}\\ &\textrm{titik \textit{A} tersebut adalah}\, ....\\ &\begin{array}{lll}\\ \textrm{a}.\quad A'\left ( 1-\displaystyle \frac{1}{2}\sqrt{3},-\displaystyle \frac{1}{2}+\sqrt{3} \right )&&\\ \textrm{b}.\quad \color{red}A'\left ( -1-\displaystyle \frac{1}{2}\sqrt{3},-\displaystyle \frac{1}{2}+\sqrt{3} \right )&\\ \textrm{c}.\quad A'\left (-1-\displaystyle \frac{1}{2}\sqrt{3},\displaystyle \frac{1}{2}-\sqrt{3} \right )&\\ \textrm{d}.\quad A'\left ( 1-\displaystyle \frac{1}{2}\sqrt{3},\displaystyle \frac{1}{2}-\sqrt{3} \right )\\ \textrm{e}.\quad A'\left ( -1+\displaystyle \frac{1}{2}\sqrt{3},-\displaystyle \frac{1}{2}+\sqrt{3} \right ) \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\begin{aligned}\textrm{Diketahui}&\: \textrm{bahwa}:\\ y&=-\displaystyle \frac{1}{3}x\sqrt{3}=\left ( -\displaystyle \frac{1}{3}\sqrt{3} \right )x\\ &=\left (-\tan 30^{\circ} \right )x=\tan \left ( 180^{\circ}-30^{\circ} \right )x\\ &=\tan 150^{\circ}.x\\ \textrm{maka}\: \: \theta &=150^{\circ}\quad \Rightarrow \quad 2\theta =300^{\circ}\\ \begin{pmatrix} x'\\ y' \end{pmatrix}&=\color{purple}\begin{pmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\color{purple}\begin{pmatrix} \cos 300^{\circ} & \sin 300^{\circ} \\ \sin 300^{\circ} & -\cos 300^{\circ} \end{pmatrix}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=\color{purple}\begin{pmatrix} \displaystyle \frac{1}{2} & -\displaystyle \frac{1}{2}\sqrt{3}\\ -\displaystyle \frac{1}{2}\sqrt{3} & -\displaystyle \frac{1}{2} \end{pmatrix}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=\begin{pmatrix} -1-\displaystyle \frac{1}{2}\sqrt{3}\\ \sqrt{3}-\displaystyle \frac{1}{2} \end{pmatrix} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 94.&\textrm{Bayangan titik A(2,4) dicerminkan }\\ &\textrm{terhadap garis}\: \: y-x=0\: \: \textrm{dilanjutkan}\\ &\textrm{ke garis}\: \: x\sqrt{3}-3y=0\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}A'\left ( 2+\sqrt{3},-1+2\sqrt{3} \right )&&\\ \textrm{b}.\quad A'\left ( 2+\sqrt{3},1-2\sqrt{3} \right )&\\ \textrm{c}.\quad A'\left ( 1-\sqrt{3},-2+\sqrt{3} \right )&\\ \textrm{d}.\quad A'\left ( -2+\sqrt{3},1+2\sqrt{3} \right )\\ \textrm{e}.\quad A'\left ( 2-\sqrt{3},1-2\sqrt{3} \right ) \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{a}\\ &\begin{aligned}\textrm{Dike}&\textrm{tahui bahwa}:\\ &\begin{cases} x\sqrt{3}-3y=0 & \Leftrightarrow y=\displaystyle \frac{1}{3}\sqrt{3}x\\ &\Leftrightarrow y=\tan 30^{\circ}.x\\\\ x-y=0 & \Leftrightarrow y=x \end{cases}\\\\ \begin{pmatrix} x'\\ y' \end{pmatrix}&=\begin{pmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{pmatrix}\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} \cos 2.30^{\circ} & \sin 2.30^{\circ} \\ \sin 2.30^{\circ} & -\cos 2.30^{\circ} \end{pmatrix}\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} \displaystyle \frac{1}{2} & \displaystyle \frac{1}{2}\sqrt{3}\\ \displaystyle \frac{1}{2}\sqrt{3} & -\displaystyle \frac{1}{2} \end{pmatrix}\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\begin{pmatrix} 2\\ 4 \end{pmatrix}\\ &=\begin{pmatrix} \sqrt{3}+2\\ -1+2\sqrt{3} \end{pmatrix} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 95.&\textrm{Jika}\: \: T_{1}=\begin{pmatrix} 1 & 2\\ 1 & 1 \end{pmatrix}\: \: \textrm{dan}\: \: T_{2}=\begin{pmatrix} -2 & 5\\ -1 & 3 \end{pmatrix}\\ &\textrm{maka bayangan garis}\: \: x+y+1=0\\ &\textrm{oleh}\: \: T_{2}\circ T_{1}\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}x-2y-1=0&&\\ \textrm{b}.\quad x+2y-1=0&\\ \textrm{c}.\quad x+2y+1=0&\\ \textrm{d}.\quad x-2y+1=0\\ \textrm{e}.\quad x+y-1=0 \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{a}\\ &\begin{aligned}\textrm{Dike}&\textrm{tahui bahwa}:\\ \begin{pmatrix} x'\\ y' \end{pmatrix}&=T_{2}\circ T_{1}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} -2 & 5\\ -1 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2\\ 1 & 1 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} -2+5 & -4+5\\ -1+3 & -2+3 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} 3 & 1\\ 2 & 1 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} 3x+y\\ 2x+y \end{pmatrix}\\ \textrm{Dipe}&\textrm{roleh}\\ &\begin{array}{lllllllll}\\ \quad x'&=3x+y\\ \quad y'&=2x+y\qquad\quad-\\\hline x'-y'&=x\\ \Leftrightarrow \quad x&=\color{red}x'-y'\qquad\color{black}....(1)\\ \color{blue}\textrm{maka}\\ \qquad y&=x'-3x\\ &=x'-3(x'-y')\\ &=\color{red}3y'-2x'\quad \color{black}....(2) \end{array}\\ \textrm{Sehin}&\textrm{gga}\\ x+y&+1=0\\ x'-&y'+3y'-2x'+1=0\\ -x'+&2y'+1=0\\ x'-&2y'-1=0\\ \textrm{maka}&\: \textrm{bayangan garisnya}\\ x-2&y-1=0 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 96.&\textrm{Garis}\: \: 2x+y+4=0\: \: \textrm{ditranslasikan}\\ &\textrm{oleh}\: \: \begin{pmatrix} -2\\ 5 \end{pmatrix}\: \: \textrm{dilanjutkan transformasi} \\ &\textrm{oleh}\: \: \begin{pmatrix} 1 & 2\\ 0 & 1 \end{pmatrix}\: \: \textrm{persamaan bayangannya}\\ &\textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad 2x+y+3=0&&\\ \textrm{b}.\quad \color{red}2x-3y+3=0&\\ \textrm{c}.\quad 2x+3y+3=0&\\ \textrm{d}.\quad 3x+2y+3=0\\ \textrm{e}.\quad 3x-2y+3=0 \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\begin{aligned}\textrm{Diket}&\textrm{ahui bahwa}:\\ \begin{pmatrix} x'\\ y' \end{pmatrix}\: &=\begin{pmatrix} x\\ y \end{pmatrix}+\begin{pmatrix} -2\\ 5 \end{pmatrix}=\begin{pmatrix} x-2\\ y+5 \end{pmatrix}\\ \begin{pmatrix} x''\\ y'' \end{pmatrix}&=\begin{pmatrix} 1 & 2\\ 0 & 1 \end{pmatrix}\begin{pmatrix} x'\\ y' \end{pmatrix}\\ &=\begin{pmatrix} 1 & 2\\ 0 & 1 \end{pmatrix}\begin{pmatrix} x-2\\ y+5 \end{pmatrix}\\ &=\begin{pmatrix} x-2+2y+10\\ y+5 \end{pmatrix}\\ &=\begin{pmatrix} x+2y+8\\ y+5 \end{pmatrix}\\ \textrm{Diper}&\textrm{oleh}\\ &\begin{array}{lllllllll}\\ \quad x''&=x+2y+8\\ \: \: \: 2y''&=2y+10\qquad\quad-\\\hline x''-2y''&=x-2\\ \Leftrightarrow \quad x&=\color{red}x''-2y''+2\: \color{black}....(1)\\ \color{blue}\textrm{maka}\\ \qquad y&=\color{red}y''-5\quad \color{black}\qquad....(2) \end{array}\\ \textrm{sehin}&\textrm{gga}\\ 2x+&y+4=0\\ 2(x''&-2y''+2)+(y''-5)+4=0\\ 2x''-&3y''+3=0\\ \textrm{maka}&\: \textrm{bayangan garisnya}\\ 2x-&3y+3=0 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 97.&\textrm{Diketahui}\: \: M\: \: \textrm{adalah pencerminan terhadap}\\ &\textrm{garis}\: \: y=-x\: \: \textrm{dan}\: \: T\: \: \textrm{adalah transformasi} \\ &\textrm{yang dinyatakan oleh matriks}\: \: \begin{pmatrix} 2 & 3\\ 0 & -1 \end{pmatrix}\\ &\textrm{Koordinat bayangan titik}\: \: A(2,-8)\: \: \textrm{oleh}\\ &\textrm{transformasi}\: \: M\: \: \textrm{dilanjutkan oleh}\: \: T\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad (-10,2)&&\\ \textrm{b}.\quad (-2,-10)&\\ \textrm{c}.\quad \color{red}(10,2)&\\ \textrm{d}.\quad (-10,-2)\\ \textrm{e}.\quad (2,10) \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{c}\\ &\begin{aligned}\textrm{Dike}&\textrm{tahui bahwa}:\\ \begin{pmatrix} x'\\ y' \end{pmatrix} &=\color{purple}T\circ M\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} 2 & 3\\ 0 & -1 \end{pmatrix}\begin{pmatrix} 0 & -1\\ -1 & 0 \end{pmatrix}\begin{pmatrix} 2\\ -8 \end{pmatrix}\\ &=\begin{pmatrix} 0-3 & -2+0\\ 0+1 & 0+0 \end{pmatrix}\begin{pmatrix} 2\\ -8 \end{pmatrix}\\ &=\begin{pmatrix} -3 & -2\\ 1 & 0 \end{pmatrix}\begin{pmatrix} 2\\ -8 \end{pmatrix}\\ &=\begin{pmatrix} -6+16\\ 2+0 \end{pmatrix}\\ &=\color{red}\begin{pmatrix} 10\\ 2 \end{pmatrix} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 98.&\textrm{Jika}\: \: W\: \: \textrm{adalah transformasi oleh}\\ &\textrm{matriks}\: \: \begin{pmatrix} 1 & 0\\ 3 & 1 \end{pmatrix},\: \: \textrm{maka titik mula}\\ &\textrm{dari}\: \: W'(-2,5)\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad (-11,-2)&&\\ \textrm{b}.\quad (11,-2)&\\ \textrm{c}.\quad \color{red}(-2,11)&\\ \textrm{d}.\quad (2,11)\\ \textrm{e}.\quad (12,11) \end{array}\\\\ &\textbf{Jawab}:\quad \textbf{c}\\ &\begin{aligned}\textrm{Dimi}&\textrm{salkan}:\\ A&=\begin{pmatrix} -2\\ 5 \end{pmatrix},\: \: \textrm{dan}\\ W&=\begin{pmatrix} 1 & 0\\ 3 & 1 \end{pmatrix},\: \: \textrm{serta}\: \: X=\begin{pmatrix} x\\ y \end{pmatrix}\\ \textrm{mak}&\textrm{a}\\ &\begin{array}{|c|}\hline \color{red}\begin{aligned}A&=BX\\ B^{-1}A&=B^{-1}BX\\ B^{-1}A&=I.X\\ B^{-1}A&=X\\ X&=B^{-1}A \end{aligned}\\\hline \end{array}\\ \begin{pmatrix} x\\ y \end{pmatrix}&=\displaystyle \frac{1}{\begin{vmatrix} 1 &0 \\ 3 & 1 \end{vmatrix}}\begin{pmatrix} 1 & 0\\ -3 & 1 \end{pmatrix}\begin{pmatrix} -2\\ 5 \end{pmatrix}\\ &=1.\begin{pmatrix} -2+0\\ 6+5 \end{pmatrix}\\ &=\color{red}\begin{pmatrix} -2\\ 11 \end{pmatrix} \end{aligned} \end{array}$.

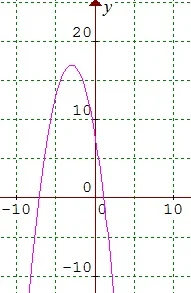
$\begin{array}{ll}\\ 99.&\textrm{Jika setiap titik pada grafik dengan}\\ &\textrm{dengan persamaan}\: \: y=\sqrt{x}\: \: \textrm{dicerminkan} \\ &\textrm{terhadap garis}\: \: y=x\: ,\: \textrm{maka persamaan}\\ &\textrm{grafik yang dihasilkan adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}y=x^{2}\: ,\: x\geq 0&&\\ \textrm{b}.\quad y=-\sqrt{x}\: ,\: x\geq 0&\\ \textrm{c}.\quad y=-x^{2}\: ,\: x\leq 0&\\ \textrm{d}.\quad y=\sqrt{-x}\: ,\: x\leq 0\\ \textrm{e}.\quad y=-\sqrt{-x}\: ,\: x\leq 0 \end{array}\\\\ &\quad\quad\qquad \textbf{UMB Tahun 2011 Kode 152}\\\\\\ &\textbf{Jawab}:\quad \textbf{a}\\ &\begin{aligned}\textrm{Dike}&\textrm{tahui bahwa}:\\ y&=\sqrt{x},\: \: \textrm{atau}\: \: y^{2}=x\\ \textbf{Alt}&\textbf{ernatif 1}\\ \textrm{mak}&\textrm{a}\: \: \textrm{saat dicerminkan terhadap}\\ \textrm{gari}&\textrm{s}\: \: y=x,\: \textrm{adalah}\: \: \color{red}x^{2}=y\\ \textrm{atau}&\: \: \color{red}y=x^{2}.\\ \textbf{Alt}&\textbf{ernatif 2}\\ \textrm{Jika}\: &\textrm{ingin dikerjakan dengan rumus}\\ \begin{pmatrix} x'\\ y' \end{pmatrix}&=M_{x=y}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\\ &=\begin{pmatrix} y\\ x \end{pmatrix}\\ \textrm{Sela}&\textrm{njutnya hasilnya disubstitusikan}\\ \textrm{ke p}&\textrm{ersamaan}\: \: y=\sqrt{x}\Rightarrow \color{red}x'=\sqrt{y'}\\ \sqrt{y'} &=x'\: \: \: \textrm{maka}\\ y'&=\left ( x' \right )^{2}\: \: \: \textrm{selanjutnya}\\ y&=x^{2} \end{aligned} \end{array}$.

Sebelum dicerminkan terhadap garis y=x

Gambar kurva/grafik setelah cerminkan terhadap garis y=x

$\begin{array}{ll}\\ 100.&\textrm{Transformasi}\: \: T\: \: \textrm{adalah pencerminan}\\ &\textrm{terhadap garis}\: \: y=\displaystyle \frac{x}{3}\: \: \textrm{dilanjutkan oleh} \\ &\textrm{pencerminan terhadap garis}\: \: y=-3x.\\ &\textrm{Matriks yang bersesuian dengan}\\ &\textrm{transformasi}\: \: T\: \: \textrm{adalah}\, ...\\ &\begin{array}{lll}\\ \textrm{a}.\quad \begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix}&&\\ \textrm{b}.\quad \color{red}\begin{pmatrix} -1 & 0\\ 0 & -1 \end{pmatrix}&\\ \textrm{c}.\quad \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}&\\ \textrm{d}.\quad \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}\\ \textrm{e}.\quad \begin{pmatrix} 0 & -1\\ -1 & 0 \end{pmatrix} \end{array}\\\\ &\quad\quad \textbf{SBMPTN Tahun 2013 Kode 433}\\\\\\ &\textbf{Jawab}:\quad \textbf{b}\\ &\begin{aligned}\textrm{Dike}&\textrm{tahui bahwa}:\\ \textrm{sebu}&\textrm{ah persamaan garis lurus}\\ \textrm{dapa}&\textrm{t dituliskan dengan}:\: y=\color{red}m\color{black}x\\ \textrm{Dike}&\textrm{tahui pula bahwa ada 2 garis}:\\ y_{1}&=\displaystyle \frac{1}{3}x\quad \textrm{dan}\: \: \: y_{2}=-3x\\ \textrm{seba}&\textrm{gai representasi transformasi}\: \: T.\\ \textrm{Kare}&\textrm{na}\: \: m_{1}\times m_{2}=\left ( \displaystyle \frac{1}{3} \right )(-3)=-1\\ \textrm{bera}&\textrm{rti 2 garis di atas saling tegak}\\ \textrm{luru}&\textrm{s dan hal ini seperti rotasi 2}\\ \textrm{kali}\: \: &90^{\circ}\: \: \textrm{atau}\: \: 180^{\circ}\\ \textrm{Jadi},&\: T=\color{purple}\begin{pmatrix} \cos 180^{\circ} & -\sin 180^{\circ}\\ \sin 180^{\circ} & \cos 180^{\circ} \end{pmatrix}\\ \Leftrightarrow &\: T=\color{red}\begin{pmatrix} -1 & 0\\ 0 & -1 \end{pmatrix} \end{aligned} \end{array}$.

DAFTAR PUSTAKA

1. Johanes, Kastolan, Sulasim, 2006. Kompetensi Matematika 3A SMA Kelas XII Program IPA Semester Pertama. Jakarta: YUDHISTIRA.
2. Nugroho, P. A. Gunarto, D. 2013. Big Bank Soal-Bahas MAtematika SMA/MA. Jakarta: WAHYUMEDIA.
3. Sharma,S.N., dkk. 2017. Jelajah Matematika SMA Kelas XI Program Wajib. Jakarta: YUDHISTIRA.