Sebelumnya telah dituliskan bahwa
$\begin{array}{ll}\\ \bullet &\sin \alpha =2\sin \displaystyle \frac{1}{2}\alpha \cos \frac{1}{2}\alpha \\ \bullet &\cos \alpha =\cos ^{2}\displaystyle \frac{1}{2}\alpha -\sin ^{2}\displaystyle \frac{1}{2}\alpha \\ \bullet &\tan \alpha =\displaystyle \frac{2\tan \displaystyle \frac{1}{2}\alpha }{1-\tan ^{2}\displaystyle \frac{1}{2}\alpha } \end{array}$.
B. 2. 1 Rumus Sudut Paruh untuk Sinus
Perhatikanlah Identitas trigonometri berikut
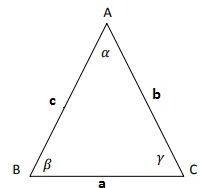
Perhatikanlah ilsutrasi segitiga ABC berikut
- $\sin ^{2}\alpha +\cos ^{2}\alpha =1$
- $\tan ^{2}\alpha -\sec ^{2}\alpha =-1$
- $\cot ^{2}\alpha -\csc ^{2}\alpha =-1$
- $\sin 2\alpha =2\sin \alpha \cos \alpha$
- $\cos 2\alpha =\cos ^{2}\alpha -\sin ^{2} \alpha$, dan
- $\cos 2\alpha =2\cos ^{2}\alpha -1$, serta
- $\cos 2\alpha =1 -2\sin ^{2} \alpha$
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Tunjukkan bahwa nilai}\: \: \tan \displaystyle \frac{1}{2}\alpha =\color{red}\displaystyle \frac{1-\cos \alpha }{\sin \alpha }\\\\ &\color{blue}\textbf{Bukti}:\\ &\textrm{Sebelumnya diketahui bahwa}:\\ &\begin{aligned}\tan \displaystyle \frac{1}{2}\alpha &=\pm \sqrt{\color{red}\displaystyle \frac{1-\cos \alpha }{1+\cos \alpha }},\: \textrm{maka}\\ &=\pm \sqrt{\displaystyle \frac{1-\cos \alpha }{1+\cos \alpha }\times \displaystyle \frac{1-\cos \alpha }{1-\cos \alpha }}\\ &=\pm \sqrt{\displaystyle \frac{\left ( 1-\cos \alpha \right )^{2}}{1-\cos ^{2}\alpha }}\\ &=\pm \sqrt{\displaystyle \frac{\left ( 1-\cos \alpha \right )^{2}}{\sin ^{2}\alpha }}\\ &=\displaystyle \color{red}\displaystyle \frac{1-\cos \alpha }{\sin \alpha }\qquad \color{black}\blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 2.&\textrm{Tunjukkan bahwa nilai}\: \: \tan \displaystyle \frac{1}{2}\alpha =\color{red}\displaystyle \frac{\sin \alpha }{1+\cos \alpha }\\\\ &\color{blue}\textbf{Bukti}:\\ &\textrm{Sebelumnya diketahui bahwa}:\\ &\begin{aligned}\tan \displaystyle \frac{1}{2}\alpha &=\displaystyle \color{red}\displaystyle \frac{1-\cos \alpha }{\sin \alpha },\: \color{black}\textrm{maka}\\ &=\displaystyle \frac{1-\cos \alpha }{\sin \alpha }\times \frac{1+\cos \alpha }{1+\cos \alpha }\\ &=\displaystyle \frac{1-\cos ^{2}\alpha }{\sin \alpha \left ( 1+\cos \alpha \right )}\\ &=\displaystyle \frac{\sin ^{2}\alpha }{\sin \alpha \left ( 1+\cos \alpha \right )}\\ &=\displaystyle \color{red}\displaystyle \frac{\sin \alpha }{1+\cos \alpha }\qquad \color{black}\blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 3.&\textrm{Tunjukkan bahwa nilai}\: \: \cos^{2} \displaystyle \frac{1}{2}\alpha =\color{red}\displaystyle \frac{1+\sec \alpha }{2\sec \alpha }\\\\ &\color{blue}\textbf{Bukti}:\\ &\textrm{Sebelumnya diketahui bahwa}:\\ &\begin{aligned}\cos^{2} \displaystyle \frac{1}{2}\alpha &=\displaystyle \color{red}\displaystyle \frac{1+\cos \alpha }{2 },\: \color{black}\textrm{maka}\\ &=\displaystyle \displaystyle \frac{1+\cos \alpha }{2}\times \displaystyle \frac{\displaystyle \frac{1}{\cos \alpha }}{\displaystyle \frac{1}{\cos \alpha }}\\ &=\displaystyle \frac{\displaystyle \frac{1}{\cos \alpha }+\displaystyle \frac{\cos \alpha }{\cos \alpha }}{\displaystyle \frac{2}{\cos \alpha }}\\ &=\displaystyle \frac{\sec \alpha +1}{2\sec \alpha }\\ &=\displaystyle \color{red}\displaystyle \frac{1+\sec \alpha }{2\sec \alpha }\qquad \color{black}\blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 4.&\textrm{Tunjukkan bahwa nilai}\: \: \sin \displaystyle \frac{1}{2}\alpha =\color{red}\displaystyle \frac{\sqrt{1+\sin \alpha }-\sqrt{1-\sin \alpha }}{2 }\\\\ &\color{blue}\textbf{Bukti}:\\ &\textrm{Sebelumnya diketahui bahwa}:\\ &\begin{aligned}\sin^{2} \displaystyle \frac{1}{2}\alpha &=\displaystyle \color{red}\displaystyle \frac{1-\cos \alpha }{2 },\: \color{black}\textrm{maka}\\ &=\displaystyle \frac{1-\sqrt{\cos ^{2}\alpha }}{2}\\ &=\displaystyle \frac{1-\sqrt{1-\sin ^{2}\alpha }}{2}\\ &=\displaystyle \frac{1-\sqrt{\left (1+\sin \alpha \right ).\left (1-\sin \alpha \right )}}{2}\\ &=\displaystyle \frac{1-\sqrt{\left (1+\sin \alpha \right ).\left (1-\sin \alpha \right )}}{2}\\ &=\displaystyle \frac{2+\sin \alpha -\sin \alpha -2\sqrt{\left (1+\sin \alpha \right ).\left (1-\sin \alpha \right )}}{4}\\ &=\displaystyle \frac{1+\sin \alpha +1-\sin \alpha -2\sqrt{\left (1+\sin \alpha \right ).\left (1-\sin \alpha \right )}}{4}\\ &=\displaystyle \frac{\left ( \sqrt{1+\sin \alpha }-\sqrt{1-\sin \alpha }\right )^{2}}{4}\\ &=\left (\displaystyle \frac{\left ( \sqrt{1+\sin \alpha }-\sqrt{1-\sin \alpha }\right )}{2} \right )^{2}\\ \sin \displaystyle \frac{1}{2}\alpha &=\displaystyle \color{red}\displaystyle \frac{\sqrt{1+\sin \alpha }-\sqrt{1-\sin \alpha }}{2 }\qquad \color{black}\blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 5.&\textrm{Dengan menggunakan rumus sudut}\\ &\textrm{paruh, tentukanlah nilai dari}\\ &\textrm{a}.\quad \cos \displaystyle \frac{\pi }{8},\qquad \textrm{b}.\quad \sin 15^{\circ}\qquad \textrm{c}.\quad \tan 15^{\circ}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Ingat baik sudut}\: \: \displaystyle \frac{\pi }{8}\: \: \textrm{atau}\: \: \displaystyle \frac{\pi }{4}\: \: \textrm{di kuadran I}\\ &\textrm{maka}\: \: \cos \displaystyle \frac{\pi }{8}\: \: \textrm{bertanda positif, sehingga}\\ &\begin{aligned}\textrm{a}.\quad \cos \displaystyle \frac{\pi }{8}&=\sqrt{\displaystyle \frac{1+\cos \displaystyle \frac{\pi }{4}}{2}}=\sqrt{\displaystyle \frac{1+\displaystyle \frac{1}{2}\sqrt{2}}{2}}\\ &=\sqrt{\displaystyle \frac{2+\sqrt{2}}{4}}=\color{red}\displaystyle \frac{1}{2}\sqrt{2+\sqrt{2}} \end{aligned}\\ &\textrm{Adapun untuk sudut}\: \: 15^{\circ}\: \: \textrm{ataupun}\: \: 30^{\circ}\\ &\textrm{akan berada di kuadran I akibatnya }\\ &\textrm{tandanya positif, sehingga}\\ &\begin{aligned}\textrm{b}.\quad \sin 15^{\circ}&=\sqrt{\displaystyle \frac{1-\cos 30^{\circ}}{2}}\\ &=\sqrt{\displaystyle \frac{1-\displaystyle \frac{1}{2}\sqrt{3}}{2}}=\sqrt{\displaystyle \frac{2-\sqrt{3}}{4}}\\ &=\color{red}\displaystyle \frac{1}{2}\sqrt{2-\sqrt{3}} \end{aligned}\\ &\textrm{Dan untuk sudut}\: \: \tan \displaystyle \frac{1}{2}\alpha =\displaystyle \frac{1-\cos \alpha }{\sin \alpha }\\ &\begin{aligned}\textrm{c}.\quad \tan 15^{\circ}&=\displaystyle \frac{1-\cos 30^{\circ} }{\sin 30^{\circ} }\\ &=\displaystyle \frac{1-\displaystyle \frac{1}{2}\sqrt{3}}{\displaystyle \frac{1}{2}}\\ &=\displaystyle \frac{\displaystyle \frac{\left ( 2-\sqrt{3} \right )}{2}}{\displaystyle \frac{1}{2}}\\ &=\color{red}2-\sqrt{3} \end{aligned} \end{array}$.
DAFTAR PUSTAKA
- Sukino. 2017. Matematika untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.