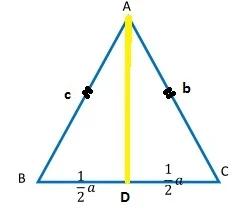
1. Identitas Trigonometri dalam Segitiga
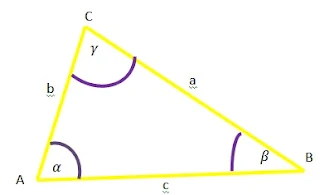
Perhatikan segitiga sembarang berikut

$\begin{aligned}&\textrm{Dalam Sebuah segitiga akan berlaku}\\ &\textrm{identitas berikut}\\ &1.\quad \sin \alpha +\sin \beta +\sin \gamma =4\cos \displaystyle \displaystyle \frac{\alpha }{2}\cos \displaystyle \frac{\beta }{2}\cos \displaystyle \frac{\gamma }{2}\\ &2.\quad \cos \alpha +\cos \beta +\cos \gamma =4\sin \displaystyle \displaystyle \frac{\alpha }{2}\sin \displaystyle \frac{\beta }{2}\sin \displaystyle \frac{\gamma }{2}+1\\ &3.\quad \tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma \\ &4.\quad \sin^{2} \alpha +\sin^{2} \beta +\sin^{2} \gamma =2\cos \alpha \cos \beta \cos \gamma +2\\ &5.\quad \sin 2\alpha +\sin 2\beta +\sin 2\gamma =4\sin \alpha \sin \beta \sin \gamma \\ &6.\quad \cot \displaystyle \frac{\alpha }{2}+\cot \frac{\beta}{2}+\cot \displaystyle \frac{\gamma }{2}=\cot \displaystyle \frac{\alpha }{2}+\cot \frac{\beta}{2}+\cot \displaystyle \frac{\gamma }{2}\\ &7.\quad \cot \alpha \cot \beta +\cot \alpha \cot \gamma + \cot \beta \cot \gamma =1 \end{aligned}$.
2. Segitiga dan Pertidaksamaan Segitiga
Pada sebuah segitiga pengklasifikasiannya dapat berdasarkan berdasarkan panjang sisinya ataupun jenis sudut-sudutnya. Berikut untuk klasifikasi berdasarkan panjang sisinya
$\begin{aligned} &\textrm{a}.\quad \textrm{sembarang}\\ &\textrm{b}.\quad \textrm{samakaki}\\ &\textrm{c}.\quad \textrm{samasisi}\\ \end{aligned}$.
Dan berdasarkan jenis sudutnya sebuah segitiga dapat dikategorikan dengan
$\begin{aligned} &\textrm{a}.\quad \textrm{lancip}\\ &\textrm{b}.\quad \textrm{siku-siku}\\ &\textrm{c}.\quad \textrm{tumpul}\\ \end{aligned}$.
Adapun berkaitan dengan segmen garis yang akan menjadi penyusun sebuah segitiga, maka sebuah segitiga hanya bisa dibuat dari ketiga segmen garis yang mana segemen garis yang terpanjang akan selalu lebih pendek dari pada jumlah panjang kedua segmen garis yang lainnya atau segmen garis yang terpendek akan selalu lebih panjang dari pada selisih panjang dari kedua segemn garis yang lainnya. Sifat tersebut lazim dinamkan dengan ketidaksamaan dalam segitiga.
$\begin{aligned} &\textbf{Pertidaksamaan dalam Segitiga}\\ &\begin{cases} a+b &>c \\ a+c &>b \\ b+c &>a \end{cases}\\ &\textbf{atau}\\ &\begin{cases} \left | a-b \right | &<c \\ \left | a-c \right | &<b \\ \left | b-c \right | &<a \end{cases} \end{aligned}$.
3. Ketaksamaan (Inequality)
Di sini yang akan dibahas adalah beberapa ketaksamaan secara umum yang tentunya sebagian berlaku pada segitiga untuk membantu para siswa dijenjang SMP atau SMA atau sederajat juga menjadi pengingat buat penulis sendiri, karena materi ini hampir menuntut daya nalar yang lebih dengan prasyarat telah terbiasa dengan soal-soal semisal aljabar dan trigonometri.
3. 1 Ketaksamaan QM-AM-GM-HM
Dalam setiap soal yang melibatkan ketaksamaan biasanya muncul dalam soal berkategori KSN (Kompetisi Sains Nasional) baik tingkat kabupaten, provinsi bahkan nasional maupun juga KSM (Kompetisi Sains Madrasah) dengan jenjang yang sama serta soal-soal dengan kategori kompetisi yang semisal. Model penyelesaian yang digunakan hampir sering akan melibatkan penggunaan ketaksamaan metode ini, yaitu QM-AM-GM-HM. Pada beberapa contoh soal di bawah dapat Anda cermati tentang penggunaan penyelesaian cara ini demikian pula pada halaman-halaman berikutnya pada blog ini akan dibahas beberapa soal dan diselesaikan dengan cara ini.
$\begin{aligned}&\textbf{Pada segitiga akan berlaku}\\ &\bullet \: \textrm{Quadratic Mean}=QM=\sqrt{\displaystyle \frac{a^{2}+b^{2}+c^{2}}{3}}\\ &\bullet \: \textrm{Arithmetic Mean}=AM= \frac{a+b+c}{3}\\ &\bullet \: \textrm{Geometric Mean}=GM=\sqrt[3]{abc}\\ &\bullet \: \textrm{Harmonic Mean}=HM=\displaystyle \frac{3}{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\\ \end{aligned}$.
Dengan kata lain QM adalah rataan kuadratik, AM adalah rataan aritmetik, dan GM adalah rataan geometri, serta HM rataan harmoni dan besarnya $QM\geq AM\geq GM\geq HM$.
$\begin{aligned}&\textrm{Misalkan diberikan}\: \: x_{1},x_{2},x_{3},\cdots ,x_{n}\\ & \textrm{bilangan real positif, maka hubungan }\\ &\textrm{ketaksamaan}\: \: \color{red}\textrm{QM-AM-GM-HM}\\ & \color{black}\textrm{dapat dituliskan}\\ &\sqrt{\displaystyle \frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+\cdots +x_{n}^{2}}{n}}\qquad\qquad \color{red}(\textrm{QM})\\ &\geq \displaystyle \frac{x_{1}+x_{2}+x_{3}+\cdots +x_{n}}{n}\: \: \: \quad\quad\quad \color{red}(\textrm{AM})\\ &\geq \sqrt[n]{x_{1}.x_{2}.x_{3}\cdots x_{n}}\: \: \: \: \qquad\qquad\qquad \color{red}(\textrm{GM})\\ &\geq \displaystyle \frac{n}{\displaystyle \frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}+\cdots +\frac{1}{x_{n}}}\quad\quad \color{red}(\textrm{HM}) \end{aligned}$.
Anda juga bisa klik di sini untuk QM, AM, GM, dan HM.
$\begin{aligned}&\textrm{Misalkan untuk}\: \: \color{blue}n=2\\ &\textrm{maka hubungan ketaksamaannya adalah}\\ &\sqrt{\displaystyle \frac{x_{1}^{2}+x_{2}^{2}}{2}}\geq \displaystyle \frac{x_{1}+x_{2}}{2}\geq \sqrt{x_{1}x_{2}}\geq \displaystyle \frac{2}{\displaystyle \frac{1}{x_{1}}+\frac{1}{x_{2}}} \end{aligned}$.
$\begin{aligned}&\textrm{Dan misalkan untuk}\: \: \color{blue}n=3\\ &\textrm{maka hubungan ketaksamaannya adalah}\\ &\sqrt{\displaystyle \frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}{3}}\geq \displaystyle \frac{x_{1}+x_{2}+x_{3}}{3}\geq \sqrt[3]{x_{1}x_{2}x_{3}}\geq \displaystyle \frac{3}{\displaystyle \frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}} \end{aligned}$.
Demikian seterusnya.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: \alpha ,\: \beta ,\: \: \textrm{dan}\: \: \gamma \: \: \textrm{adalah sudut}\\ & \textrm{pada segitiga ABC, buktikan bahwa}\\ &\sin 2\alpha +\sin 2\beta +\sin 2\gamma =4\sin \alpha \sin \beta \sin \gamma \\\\ &\textbf{Bukti}\\ &\begin{aligned}&\textrm{Dikatahui bahwa}\\ &\alpha +\beta =180^{\circ}-\gamma \\ &\textrm{Maka}\\ &\color{red}\sin 2\alpha +\sin 2\beta +\sin 2\gamma \\ &=2\sin \left ( \displaystyle \frac{2\alpha +2\beta }{2} \right )\cos \left ( \displaystyle \frac{2\alpha -2\beta }{2} \right )+2\sin \gamma \cos \gamma \\ &=2\sin (\alpha +\beta )\cos (\alpha -\beta )+2\sin \gamma \cos \gamma \\ &=2\sin \gamma \cos (\alpha -\beta )+2\sin \gamma \cos \gamma \\ &=2\sin \gamma \left (\cos (\alpha -\beta )+ \cos \gamma \right ) \\ &=2\sin \gamma \left ( \cos (\alpha -\beta )-\cos (\alpha +\beta ) \right )\\ &=2\sin \gamma \left ( -2\sin \alpha \sin (-\beta ) \right )\\ &=4\sin \gamma \sin \alpha \sin \beta \\ &=4 \sin \alpha \sin \beta \sin \gamma \qquad \blacksquare \\ \end{aligned} \end{array}$.
Catatan:
Kotak persegi kecil hitam diletakkan diakhir pembuktian menunjukkan pembuktian telah dianggap cukup dan memenuhi
$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: a\: \: \textrm{dan}\: \: b\: \: \textrm{adalah bilangan real}\\ &\textrm{positif, tunjukkan bahwa}\: \: \displaystyle \frac{a}{b}+\frac{b}{a}\geq 2\\\\ &\textbf{Bukti}:\\ &\color{red}\textrm{Alternatif 1}\\ &\begin{aligned}&\textrm{Dengan AM-GM}\\ &\displaystyle \frac{\displaystyle \frac{a}{b}+\frac{b}{a}}{2}\geq \sqrt{\displaystyle \frac{a}{b}.\frac{b}{a}}\\ &\Leftrightarrow \: \displaystyle \frac{\displaystyle \frac{a}{b}+\frac{b}{a}}{2}\geq 1\\ &\Leftrightarrow \: \displaystyle \frac{a}{b}+\frac{b}{a}\geq 2\qquad \blacksquare \end{aligned}\\ &\color{red}\textrm{Alternatif 2}\\ &\begin{aligned}&\left ( \sqrt{\displaystyle \frac{a}{b}}-\sqrt{\displaystyle \frac{b}{a}}\right )^{2}\geq 0\\ &\Leftrightarrow \: \displaystyle \frac{a}{b}-2+\displaystyle \frac{b}{a}\geq 0\\ &\Leftrightarrow \: \displaystyle \frac{a}{b}+\frac{b}{a}\geq 2\qquad \blacksquare \end{aligned}\\ \end{array}$.
$\begin{array}{ll}\\ 3.&\textrm{Untuk sembarang}\: \: x>0\\ &\textrm{Tunjukkan bahwa}\: \: \displaystyle \frac{x^{2}}{1+x^{4}}\leq \displaystyle \frac{1}{2}\\\\ &\textbf{Bukti}:\\ &\color{red}\textrm{Alternatif 1}\\ &\begin{aligned}&\textrm{Perhatikan bahwa}\: \: \left (x^{2}-1 \right )^{2}\geq 0\\ &\textrm{maka}\\ &\left (x^{2}-1 \right )^{2}=x^{4}-2x^{2}+1\geq 0\\ &\Leftrightarrow \: x^{4}+1\geq 2x^{2}\\ &\Leftrightarrow \: 1\geq \displaystyle \frac{2x^{2}}{x^{4}+1}\\ &\Leftrightarrow \: \displaystyle \frac{1}{2}\geq \displaystyle \frac{x^{2}}{x^{2}+1}\: \: \textrm{atau}\\ &\Leftrightarrow \: \displaystyle \frac{x^{2}}{x^{4}+1}\leq \displaystyle \frac{1}{2}\qquad \blacksquare \end{aligned} \\ &\color{red}\textrm{Alternatif 2}\\ &\begin{aligned} &\textrm{Dengan AM-GM}\\ &\displaystyle \frac{1+x^{4}}{2}\geq \sqrt{1\times x^{4}}\\ &\Leftrightarrow \: \displaystyle \frac{1+x^{4}}{2}\geq x^{2}\\ &\Leftrightarrow \: \displaystyle \frac{1+x^{4}}{x^{2}}\geq 2\\ &\Leftrightarrow \: \displaystyle \frac{x^{2}}{1+x^{4}}\leq \displaystyle \frac{1}{2} \qquad \blacksquare \\ \end{aligned} \\ &\color{red}\textrm{Alternatif 3}\\ &\begin{aligned} &\displaystyle \frac{x^{2}}{1+x^{4}}=\displaystyle \frac{1}{\displaystyle \frac{1}{x^{2}}+x^{2}}\\ &\textrm{Dengan AM-GM}\\ &\displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}\geq \sqrt{\displaystyle \frac{1}{x^{2}}\times x^{2}}\\ &\Leftrightarrow \: \displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}\geq 1\\ &\Leftrightarrow \: \displaystyle \frac{1}{\displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}}\leq 1\\ &\Leftrightarrow \: \displaystyle \frac{2}{\displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}}\leq 1\\ &\Leftrightarrow \: \displaystyle \frac{1}{\displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}}\leq \displaystyle \frac{1}{2}\\ &\Leftrightarrow \: \displaystyle \frac{1}{\displaystyle \frac{\displaystyle \frac{1}{x^{2}}+x^{2}}{2}}=\displaystyle \frac{x^{2}}{1+x^{4}}\leq \displaystyle \frac{1}{2}\qquad \blacksquare \\ \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 4.&\textrm{Jika}\: \: a,b,c\: \: \textrm{adalah sisi segitiga yang}\\ &\textrm{memenuhi}\: \: a+b+c=1,\: \textrm{tunjukkan}\\ &\textrm{bahwa}\: \: ab+ac+bc\leq \displaystyle \frac{1}{2}\\\\ &\textbf{Bukti}:\\ &\begin{aligned}&(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc\\ &\Leftrightarrow \: 1=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc\\ &\Leftrightarrow \: 2ab+2ac+2bc=1-\left (a^{2}+b^{2}+c^{2} \right )\\ &\Leftrightarrow \: ab+bac+bc=\displaystyle \frac{1}{2}-\displaystyle \frac{1}{2}\left ( a^{2}+b^{2}+c^{2} \right )\\ &\Leftrightarrow \: ab+bac+bc\leq \displaystyle \frac{1}{2}\qquad \blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 5.&\textrm{Jika}\: \: a,b,c\: \: \textrm{adalah bilangan real positif}\\ &\textrm{dengan}\: \: a+b+c=1,\: \textrm{tunjukkan}\\ &\textrm{bahwa}\: \: \left ( \displaystyle \frac{1}{a}-1 \right )\left ( \displaystyle \frac{1}{b}-1 \right )\left ( \displaystyle \frac{1}{c}-1 \right )\geq 8\\\\ &\textbf{Bukti}:\\ &\begin{aligned}&\textrm{Telah diketahui bahwa}:\: a+b+c=1 \\ &\textrm{Dengan ketaksamaan AM-GM kita}\\ &\textrm{bisa mendapatkan}\\ &\bullet \: \: \displaystyle \frac{a+b}{2}\geq \sqrt{ab}\Leftrightarrow a+b\geq 2\sqrt{ab}\\ &\bullet \: \: \displaystyle \frac{b+c}{2}\geq \sqrt{bc}\Leftrightarrow b+c\geq 2\sqrt{bc}\\ &\bullet \: \: \displaystyle \frac{c+a}{2}\geq \sqrt{ca}\Leftrightarrow c+a\geq 2\sqrt{ca}\\ &\textrm{Selanjutnya kembali kepersoalan, yaitu}:\\ &\begin{aligned} \left ( \displaystyle \frac{1}{a}-1 \right )&\left ( \displaystyle \frac{1}{b}-1 \right )\left ( \displaystyle \frac{1}{c}-1 \right )\\ &= \left ( \displaystyle \frac{1-a}{a} \right )\left ( \displaystyle \frac{1-b}{b} \right )\left ( \displaystyle \frac{1-c}{c} \right )\\ &= \left ( \displaystyle \frac{b+c}{a} \right )\left ( \displaystyle \frac{a+c}{b} \right )\left ( \displaystyle \frac{a+b}{c} \right )\\ &\geq \left (\displaystyle \frac{2\sqrt{bc}}{a} \right )\left ( \displaystyle \frac{2\sqrt{ac}}{b} \right )\left ( \displaystyle \frac{2\sqrt{ab}}{c} \right )\\ &\geq \left (\displaystyle \frac{8\sqrt{(abc)^{2}}}{abc} \right )\\ &\geq \displaystyle \frac{8abc}{abc}\\ &\geq 8\qquad \blacksquare \end{aligned} \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 6.&\textrm{Jika}\: \: a,b,c\: \: \textrm{adalah bilangan real positif}\\ &\textrm{dengan}\: \: a+b+c=1,\: \textrm{tunjukkan}\\ &\textrm{bahwa}\: \: \left ( \displaystyle \frac{1}{a}+1 \right )\left ( \displaystyle \frac{1}{b}+1 \right )\left ( \displaystyle \frac{1}{c}+1 \right )\geq 64\\\\ &\textbf{Bukti}:\\ &\begin{aligned} &\left ( \displaystyle \frac{1}{a}+1 \right )\left ( \displaystyle \frac{1}{b}+1 \right )\left ( \displaystyle \frac{1}{c}+1 \right )\\ &=\displaystyle \frac{1}{abc}+\left (\displaystyle \frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca} \right )+\left (\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )+1\\ &\textrm{Dengan AM-GM kita mendapatkan}\\ &\bullet \: \: \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq 3\sqrt[3]{\displaystyle \frac{1}{abc}}\\ &\bullet \: \: \displaystyle \frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\geq 3\sqrt[3]{\displaystyle \frac{1}{(abc)^{2}}}\\ &\textrm{Kita tulis sintak prosesnya di atas}\\ &=1+\left (\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )+\left (\displaystyle \frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca} \right )+\displaystyle \frac{1}{abc}\\ &\geq 1+3\sqrt[3]{\displaystyle \frac{1}{abc}}+3\sqrt[3]{\displaystyle \frac{1}{(abc)^{2}}}+\sqrt[3]{\displaystyle \frac{1}{(abc)^{3}}}\\ &\geq 1+3\sqrt[3]{\displaystyle \frac{1}{abc}}+3\sqrt[3]{\displaystyle \frac{1}{(abc)^{2}}}+\sqrt[3]{\displaystyle \frac{1}{(abc)^{3}}}\\ &=\left ( 1+\displaystyle \frac{1}{\sqrt[3]{abc}} \right )^{3}\\ &\textrm{Karena}\: \: \sqrt[3]{abc}\leq \displaystyle \frac{a+b+c}{3}=\displaystyle \frac{1}{3},\: \textrm{maka}\\ &\left ( \displaystyle \frac{1}{a}+1 \right )\left ( \displaystyle \frac{1}{b}+1 \right )\left ( \displaystyle \frac{1}{c}+1 \right )\geq \left ( 1+\displaystyle \frac{1}{\sqrt[3]{abc}} \right )^{3}\\ &\: \qquad\qquad\qquad\qquad\qquad\quad\quad \geq \left ( 1+\displaystyle \frac{1}{\left (\frac{1}{3} \right )} \right )^{3}\\ &\: \qquad\qquad\qquad\qquad\qquad\quad\quad \geq \left ( 1+3 \right )^{4}\\ &\: \qquad\qquad\qquad\qquad\qquad\quad\quad \geq 4^{4}\\ &\: \qquad\qquad\qquad\qquad\qquad\quad\quad \geq 64\qquad \blacksquare \end{aligned} \end{array}$.
DAFTAR PUSTAKA
- Bintari, N., Gunarto, D. 2007. Panduan Menguasai Soal-Soal Olimpiade Matematika Nasional dan Internasional. Yogyakarta: INDONESIA CERDAS.
- Budhi, W.S. 2014. Matematika 4: Bahan Ajar Persiapan Menuju Olimpiade Matematika Sain Nasional/Internasional SMA. Jakarta: TRISULA ADISAKTI.
- Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.