PAS MATEMATIKA BLOG

Contoh Soal Vektor di Dimensi Dua (Kelas X Matematika Peminatan) Bagian 2

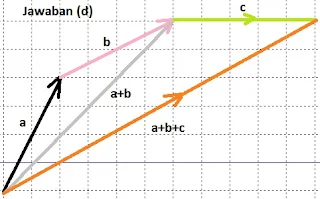
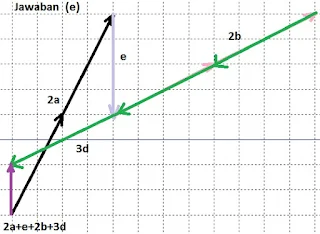
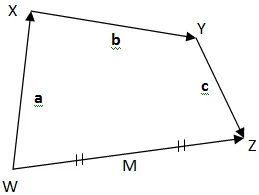
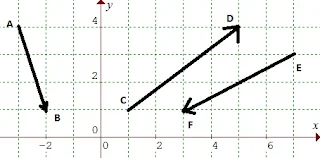
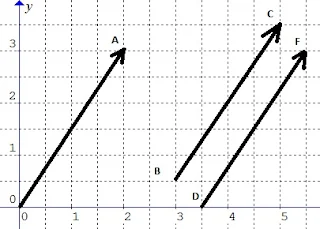
$\begin{array}{ll}\\ 4.&\color{blue}\textrm{Perhatikanlah ilustrasi gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Nyatakanlah vektor-vektor di atas dalam}\\ &\textrm{a}.\quad \textrm{vektor kolom}\\ &\textrm{b}.\quad \textrm{vektor baris}\\ &\textrm{c}.\quad \textrm{vektor basis}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Vektor di atas saat dinyatakan dengan}\\ &\begin{array}{|c|l|l|l|}\hline \textrm{No}&\quad\textrm{Kolom}&\qquad\textrm{Baris}&\qquad\textrm{Basis}\\\hline 1&\bar{a}=\begin{pmatrix} 2\\ 4 \end{pmatrix}&\bar{a}=\begin{pmatrix} 2, & 4 \end{pmatrix}&\bar{a}=2\bar{i}+4\bar{j}\\\hline 2&\bar{b}=\begin{pmatrix} 4\\ 2 \end{pmatrix}&\bar{b}=\begin{pmatrix} 4, & 2 \end{pmatrix}&\bar{b}=4\bar{i}+2\bar{j}\\\hline 3&\bar{c}=\begin{pmatrix} 5\\ 0 \end{pmatrix}&\bar{c}=\begin{pmatrix} 5, & 0 \end{pmatrix}&\bar{c}=5\bar{i}\\\hline 4&\bar{d}=\begin{pmatrix} -2\\ -4 \end{pmatrix}&\bar{d}=\begin{pmatrix} -2, & -4 \end{pmatrix}&\bar{d}=-2\bar{i}-4\bar{j}\\\hline 5&\bar{e}=\begin{pmatrix} 0\\ -4 \end{pmatrix}&\bar{e}=\begin{pmatrix} 0, & -4 \end{pmatrix}&\bar{e}=-4\bar{j}\\\hline 6&\bar{f}=\begin{pmatrix} 3\\ -3 \end{pmatrix}&\bar{f}=\begin{pmatrix} 3, & -3 \end{pmatrix}&\bar{f}=3\bar{i}-3\bar{j}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 5&\textrm{Tentukanlah panjang atau besar dari}\\ &\textrm{vektor-vektor berikut}\\ &\textrm{a}.\quad \bar{a}=\begin{pmatrix} -4\\ 3 \end{pmatrix}\quad\quad\quad \textrm{d}.\quad \bar{d}=\begin{pmatrix} 6, &-8 \end{pmatrix}\\ &\textrm{b}.\quad \bar{b}=\begin{pmatrix} 5\\ 0 \end{pmatrix}\qquad\quad\quad \textrm{e}.\quad \bar{e}=2\bar{i}+4\bar{j}\\ &\textrm{c}.\quad \bar{c}=\begin{pmatrix} 4, & -6 \end{pmatrix}\: \qquad \textrm{f}.\quad \bar{f}=-5\bar{i}+12\bar{j}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Lambang panjang suatu vektor adalah}:\\ &\color{red}\left | \begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}},\: \: \color{black}\textrm{maka}\\ &\bullet \: \left | \bar{a} \right |=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5\\ &\bullet \: \left | \bar{b} \right |=\sqrt{5^{2}+0^{2}}=\sqrt{25}=5\\ &\bullet \: \left | \bar{c} \right |=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\\ &\bullet \: \left | \bar{d} \right |=\sqrt{6^{2}+(-8)^{2}}=\sqrt{36+64}=\sqrt{100}=10\\ &\bullet \: \left | \bar{e} \right |=\sqrt{2^{2}+4^{2}}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\\ &\bullet \: \left | \bar{f} \right |=\sqrt{(-5)^{2}+12^{2}}=\sqrt{25+144}=\sqrt{169}=13 \end{array}$

$\begin{array}{ll}\\ 6&\textrm{Pada soal no.4 di atas dengan menggunakan}\\ &\textrm{aturan segitiga dan jajar genjang, gambarlah}\\ &\textrm{vektor-vektor berikut pada kertas berpertak}\\ &\textrm{a}.\quad \bar{a}+\bar{b}\qquad\qquad\qquad \textrm{d}.\quad \left ( \bar{a}+\bar{b} \right )+\bar{c}\\ &\textrm{b}.\quad \bar{b}+\bar{c}\, \qquad\qquad\qquad \textrm{e}.\quad 2\bar{a}+\bar{e}+2\bar{b}+3\bar{d}\\ &\textrm{c}.\quad \bar{a}+\left (\bar{b}+\bar{c} \right )\: \: \quad \qquad \textrm{f}.\quad 2\left ( \bar{a}+\bar{b}+\bar{c}+\bar{d}+\bar{e} \right )\\\\ &\textrm{Jawab}:\\ \end{array}$

Contoh Soal Vektor di Dimensi Dua (Kelas X Matematika Peminatan) Bagian 1

Perhatikanlah gambar berikut untuk menjawab soal no.1

$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: \overline{XW}=\textbf{a}\: ,\: \overline{XY}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{YZ}=\textbf{c}\\ &\textrm{Nyatakan dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{WY}\qquad\qquad\qquad \textrm{d}.\quad\overline{WZ}\\ &\textrm{b}. \quad\overline{XZ}\qquad\qquad\qquad \: \textrm{e}.\quad\overline{WM}\\ &\textrm{c}.\quad\overline{ZX}\qquad\qquad\qquad \: \: \textrm{f}.\quad\overline{MY}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{WY}&=\overline{WX}+\overline{XY}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{XZ}&=\overline{XY}+\overline{YZ}=\textbf{b}+\textbf{c}\\ \textrm{c}.\quad\overline{ZX}&=\overline{ZY}+\overline{YX}=-\textbf{c}+(-\textbf{b})=-\textbf{b}-\textbf{c}\\ &=-(\textbf{b}+\textbf{c})\\ &\textrm{atau}\\ \overline{ZX}&=-\overline{XZ}=-(\textbf{b}+\textbf{c})\\ \textrm{d}.\quad \overline{WZ}&=\overline{WX}+\overline{XY}+\overline{YZ}\\ &=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{e}.\quad \overline{WM}&=\displaystyle \frac{1}{2}\overline{WZ}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{MY}&=\overline{MZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\overline{WZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )+(-\textbf{c})\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )-\textbf{c}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}-\textbf{c} \right )\end{aligned} \end{array}$

Perhatikanlah gambar berikut untuk menjawab soal no.2

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: \overline{PQ}=\textbf{a}\: ,\: \overline{QR}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{RS}=\textbf{c}\\ &\textrm{dan titik}\: \: \textbf{E}\: \: \textrm{dan}\: \: \textbf{F}\: \: \textrm{adalah titik tegah}\\ &\overline{RS}\: \: \textrm{dan}\: \: \overline{QS},\\ &\textrm{nyatakanlah dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{PR}\qquad\qquad\qquad \textrm{e}.\quad\overline{PF}\\ &\textrm{b}. \quad\overline{RP}\qquad\qquad\qquad \textrm{f}.\quad\overline{SF}\\ &\textrm{c}.\quad\overline{PS}\qquad\qquad\qquad \: \textrm{g}.\quad\overline{FR}\\ &\textrm{d}.\quad\overline{QE}\qquad\qquad\qquad \textrm{h}.\quad\overline{EF}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{PR}&=\overline{PQ}+\overline{QR}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{RP}&=\overline{RQ}+\overline{QP}=-\textbf{b}-\textbf{a}=-\left ( \textbf{a}+\textbf{b} \right )\\ \textrm{c}.\quad\overline{PS}&=\overline{PQ}+\overline{QR}+\overline{RS}=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{d}.\quad \overline{QE}&=\overline{QR}+\overline{RE}=\overline{QR}+\displaystyle \frac{1}{2}\overline{RS}\\ &=\textbf{b}+\displaystyle \frac{1}{2}\textbf{c}\\ \textrm{e}.\quad \overline{PF}&=\overline{PQ}+\overline{QF}=\overline{PQ}+\displaystyle \frac{1}{2}\overline{QS}\\ &=\overline{PQ}+\displaystyle \frac{1}{2}\left ( \overline{QR}+\overline{RS} \right )\\ &=\displaystyle \frac{1}{2}\left ( 2\textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{SF}&=\displaystyle \frac{1}{2}\overline{SQ}=\displaystyle \frac{1}{2}\left (\overline{SR}+\overline{RQ} \right )=\displaystyle \frac{1}{2}\left ( -\textbf{c}+(-\textbf{b}) \right )\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )\\ \textrm{g}.\quad \overline{FR}&=\overline{FQ}+\overline{QR}=\displaystyle \frac{1}{2}\overline{SQ}+\overline{QR}\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )+\textbf{b}=\displaystyle \frac{1}{2}\left ( \textbf{b}-\textbf{c} \right )\\ \textrm{h}.\quad \overline{EF}&=\overline{ES}+\overline{SF}=\displaystyle \frac{1}{2}\overline{RS}+\displaystyle \frac{1}{2}\overline{SQ}\\ &=\displaystyle \frac{1}{2}\textbf{c}+\left ( -\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right ) \right )=-\displaystyle \frac{1}{2}\textbf{b} \end{aligned} \end{array}$

$\color{red}\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Jika pada titik P bekerja 3 buah gaya}\\ &\textrm{seperti pada gambar di bawah, lukislah}\\ &\textrm{vektor}\\ &\qquad\qquad \textbf{r}=\textbf{a}+\textbf{b}+\textbf{c}\\\\ &\textrm{Jawab}:\\ &\textrm{Dengan aturan poligon kita akan}\\ &\textrm{mendapatkan gambar berikut} \end{array}$

Materi Vektor Lanjutan 2 (Kelas X Matematika Peminatan)

$\color{blue}\textrm{K. Operasi Vektor}$

$\color{blue}\textrm{1. Penjumlahan}$

$\color{blue}\textrm{1. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut

Penjumlahan di atas adalah penjumlahan menurut aturan segitiga,

perhatikan pula pemisalan berikut

$\begin{aligned}&\textrm{Menurut aturan segitiga}\\ &\overline{AB}+\overline{BC}=\bar{a}+\bar{b}=\overline{AC},\quad \color{red}\textrm{Selanjutnya}\\ &\overline{AC}+\overline{CD}=\bar{a}+\bar{b}+\bar{c}=\overline{AD},\quad \color{red}\textrm{maka}\\ &\overline{AD}+\overline{DE}=\bar{a}+\bar{b}+\bar{c}+\bar{d}=\overline{AE} \end{aligned}$

Pada penjumlahan dengan vektor adalah tetap (tidak berubah)

$\begin{aligned} &\overline{a}+\overline{0}=\overline{0}+\overline{a}=\overline{a}\\ &\textrm{Sehingga vektor nol disebut sebagai}\\ &\color{red}\textbf{elemen identitas} \end{aligned}$

$\color{blue}\textrm{1. 2 Secara Aljabar}$

Misal

$\begin{aligned} &\overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}\: \: \textrm{dan}\: \: \overline{b}=\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}\\ &\textrm{maka secara aljabar}\\ &\color{red}\overline{a}+\overline{b}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}+\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}=\begin{pmatrix} x_{1}+x_{2}\\ y_{1}+y_{2} \end{pmatrix} \end{aligned}$

Perhatikan kembali gambar berikut (lihat pada pembahasan sebelumnya)

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Titik A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}+\overline{CD}=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}=\begin{pmatrix} 1+4\\ (-3)+3 \end{pmatrix}=\color{blue}\begin{pmatrix} 5\\ 0 \end{pmatrix} \end{aligned}$

Dan untuk contoh yang lain adalah:

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: ,\: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{EF}=\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}+\overline{CD}+\overline{EF}\\ &=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}+\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &=\begin{pmatrix} 1+4+(-4)\\ (-3)+3+(-2) \end{pmatrix}=\color{blue}\begin{pmatrix} 1\\ -2 \end{pmatrix} \end{aligned}$

$\color{blue}\textrm{2. Pengurangan}$

$\color{blue}\textrm{2. 1 Secara Geometri}$

Pada pengurangan vektor $\overline{a}\: \: \: \color{red}\textrm{oleh}\: \: \: \color{black}\overline{b}$ dapat didefinisikan sebagai:

$\overline{a}-\overline{b}=\overline{a}+\left ( -\overline{b} \right )$. Perhatikanlah ilustrasi secara geometri berikut:

$\color{blue}\textrm{2. 2 Secara Aljabar}$

$\begin{aligned}&\textrm{Misalkan}\: \: \: \overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}\: \: \textrm{dan}\: \: \overline{b}=\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}\\ &\textrm{maka}\: \: -\overline{b}=\begin{pmatrix} -x_{2}\\ -y_{2} \end{pmatrix}\\ &\color{red}\textrm{Selanjutnya}\\ &\overline{a}-\overline{b}=\overline{a}+\left ( -\overline{b} \right )=\color{red}\begin{pmatrix} x_{1}-x_{2}\\ y_{1}-y_{2} \end{pmatrix} \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Pada contoh soal bahasan penjumlahan di atas, perhatikan lagi bahwa

Titik A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}-\overline{CD}=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} -4\\ -3 \end{pmatrix}=\begin{pmatrix} 1-4\\ (-3)-3 \end{pmatrix}=\color{blue}\begin{pmatrix} -3\\ -6 \end{pmatrix} \end{aligned}$

$\color{blue}\textrm{3. Perkalian dengan Skalar}$

$\color{blue}\textrm{3. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut!

$\color{blue}\textrm{3. 2 Secara Aljabar}$

Perkalian suatu skalar dengan suatu vektor tergantung pada skalarnya. Jika suatu skalar k dengan $\color{red}k>0$, maka perkalian ini akan menghasilkan vektor baru yang besarnya sekian k kali dari vektor semula atau $\color{red}k\left | \overline{a} \right |$ dan arahnya searah dengan vektor yang dikalikan. Demikian sebaliknya, jika nilai $\color{red}k<0$, maka besar vektor hasil perkaliannya adalah $\color{red}k\left | \overline{a} \right |$ dengan arah yang berlawanan dari vektor semula.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Misalkan diketahui vektor-vektor sebagai berikut:

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: ,\: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{EF}=\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\textrm{dengan muculnya skalar adalah}:\\ &\color{red}3\overline{AB}+4\overline{CD}-5\overline{EF}\\ &=3\begin{pmatrix} 1\\ -3 \end{pmatrix}+4\begin{pmatrix} 4\\ 3 \end{pmatrix}-5\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &=\begin{pmatrix} 3.1+4.4+(-5).(-4)\\ 3.(-3)+4.3+(-5).(-2) \end{pmatrix}=\color{blue}\begin{pmatrix} 39\\ 13 \end{pmatrix} \end{aligned}$

DAFTAR PUSTAKA

Kuntarti, Sulistiyono, & Kurnianingsih, S. 2005. Matematika untuk SMA dan MA Kelas XII Program Ilmu Alam. Jakarta: PT. Gelora Aksara Pratama

Materi Vektor Lanjutan (Kelas X Matematika Peminatan)

$\color{blue}\textrm{D. Modulus Vektor}$

Modulus suatu vektor adalah ukuran (panjang) suatu vektor. Dalam hal ini modulus suatu vektor adalah besar/panjang suatu vektor.

Lihat pada pembahasan sebelumnya tentang panjang vektor di $\color{red}\textrm{R}^{2}$ di sini.

Dalam menuliskan modulus/panjang vektor ini digunakan notasi $\left | \overline{a} \right |$ jika vektornya $\overline{a}$.

Bila $\color{red}\overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix},\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\sqrt{x_{1}^{2}+y_{1}^{2}}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

Perhatikanlah ilustrasi gambar berikut

Tentukanlah modulus/panjang vektor $\overline{u}$ ?

Jawab:

$\begin{aligned}&\textrm{Diketahui bahwa vektor}\: \: \color{red}\overline{u}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\\ &\textrm{maka modulus vektor}\: \: \overline{u}\\ &=\left | \overline{u} \right |\\ &=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}\\ &=\color{red}2\sqrt{13} \end{aligned}$

$\color{blue}\textrm{E. Vektor Posisi dan Vektor Bebas}$

Perhatikanlah ilustrasi berikut

Vektor yang titik pangkalnya berada di titik O(0,0), maka vektor tersebut dinamakan vektor posisi. Pada gambar di atas titik A rekatif terhadapa O(0,0), maka $\color{red}\overline{OA}$ disebut vektor posisi A terhadap titik O(0,0) dan vektor yang lainnya dinamakan vektor bebas. Pada gambar di atas $\color{red}\overline{BC}\: \&\: \overline{DF}$ adalah contoh vektor bebasnya.

$\color{blue}\textrm{F. Kesamaan Dua Vektor}$

Perhatikanlah dua vektor bebas pada gambar di atas, cukup jelas secara geometri tampak panjang vektor $\color{red}\overline{BC}\: \&\: \overline{DF}$ sama. Dan secara aljabar dapat ditunjukkan juga bahwa:

$\color{red}\overline{BC}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \&\: \color{red}\overline{DF}=\begin{pmatrix} 4\\ 6 \end{pmatrix}$.

$\begin{aligned}&\textbf{Secara aljabar}\: \textrm{pula dua vektor}\\ &\textrm{dikatakan sama, jika komponen}\\ &\textrm{komponen yang bersesuaian sama}\\ &\begin{pmatrix} a_{1}\\ a_{2} \end{pmatrix}=\begin{pmatrix} b_{1}\\ b_{2} \end{pmatrix}\Rightarrow \begin{cases} a_{1} & =b_{1} \\ a_{2} & =b_{2} \end{cases} \end{aligned}$.

Secara definisi

$\overline{a}=\overline{b}\: \: \begin{cases} \bullet & \left | \overline{a} \right |=\left | \overline{b} \right | \\\\ \bullet & \textrm{arah}\: \: \overline{a}=\textrm{arah}\: \: \overline{b} \end{cases}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{aligned}1.\quad&\textrm{Tentukan nilai}\: x\: \textrm{dan}\: y\: \textrm{jika}\: \begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} 2\\ 5 \end{pmatrix}\\ &\textbf{Jawab}:\\ &\textrm{Jelas bahwa jawabannya adalah}\\ &x=2,\: \textrm{dan}\: y=5 \end{aligned}$.

$\begin{aligned}2.\quad&\textrm{Tentukan nilai}\: x\: \textrm{dan}\: y\: \textrm{jika}\: \begin{pmatrix} x+y\\ x-y \end{pmatrix}=\begin{pmatrix} 9\\ 1 \end{pmatrix}\\ &\textbf{Jawab}:\\ &\textrm{Jelas bahwa jawabannya adalah}\\ &x+y=9\\ &x-y=1\\ &------\quad \: +\\ &2x\quad =10\\ &\qquad x=\displaystyle \frac{10}{2}=5\\ &\textrm{dan}\: \: x+y=9\Leftrightarrow 5+y=9\Leftrightarrow v=9-5=4\\ &\textrm{Jadi},\: \: x=5,\: \: \textrm{dan}\: \: y=4 \end{aligned}$.

$\color{blue}\textrm{G. Vektor Negatif}$

Perhatikanlah ilustrasi berikut

$\color{red}\overline{a}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \color{black}\&\: \: \color{red}\overline{b}=\color{black}\begin{pmatrix} -4\\ -6 \end{pmatrix}=-\color{red}\begin{pmatrix} 4\\ 6 \end{pmatrix}$

Vektor $\color{red}-\: \overline{a}=\overline{b}$ memiliki ukuran yang sama dengan $\overline{a}$.

Selanjutnya vektor $\color{red}\overline{a}=-\: \overline{b}\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\left | \overline{b} \right |$

$\color{blue}\textrm{H. Vektor Satuan}$

Perhatikanlah ilustrasi berikut

Jika diketahui $\color{red}\overline{a}\: \color{black}\&\: \: \color{red}\overline{b}$ seperti gambar di atas, maka

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{a} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{b} \end{cases}$

Dan panjang dari vektor satuan ini adalah selalu satu satuan.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Tentukanlah vektor satuan dari dua vektor pada gambar di atas?

Jawab:

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} -2\\ 5 \end{pmatrix}}{\sqrt{(-2)^{2}+5^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{29}}\begin{pmatrix} -2\\ 5 \end{pmatrix}=\displaystyle \frac{1}{29}\sqrt{29}\begin{pmatrix} -2\\ 5 \end{pmatrix} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} 6\\ 4 \end{pmatrix}}{\sqrt{6^{2}+4^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{52}}\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{1}{26}\sqrt{52}\begin{pmatrix} 6\\ 4 \end{pmatrix} \end{cases}$

$\color{blue}\textrm{I. Vektor Basis}$

Vektor satuan yang saling tegak lurus. Didalam ruang dimensi dua terdapat dua vektir basis., yaitu:

$\bar{i}=\color{red}\begin{pmatrix} 1\\ 0 \end{pmatrix}\: \: \color{black}\textrm{dan}\: \: \bar{j}=\color{blue}\begin{pmatrix} 0\\ 1 \end{pmatrix}$

$\begin{aligned}&\textrm{Misalkan vektor}\: \: \bar{u}=\color{red}\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}\\ &\textrm{dapat dinyatakan dalam kombinasi linear}\\ &\textrm{vektor basis}\: \: \bar{i}\: \: \textrm{dan}\: \: \bar{j}\: \: \textrm{di atas, yaitu}\\ &\bar{u}=\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}=u_{1}\begin{pmatrix} 1\\ 0 \end{pmatrix}+u_{2}\begin{pmatrix} 0\\ 1 \end{pmatrix}\\ &\textrm{maka akan menjadi}\\ &\bar{u}=u_{1}\bar{i}+u_{2}\bar{j}\\ &\textrm{SEBAGAI CONTOH}\\ &\overline{AB}=\begin{pmatrix} 5\\ 8 \end{pmatrix}\: \: \color{blue}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=5\bar{i}+8\bar{j}\\ &\textrm{Demikian juga jika}\\ &\overline{CD}=\begin{pmatrix} -3\\ -8 \end{pmatrix}\: \: \color{red}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=-3\bar{i}-8\bar{j}\\ \end{aligned}$

$\color{blue}\textrm{J. Vektor Nol}$

Jika vektor $\overline{a}=\overline{b}$ , maka $\overline{a}-\overline{b}=0$.

$\textbf{0}$ disebut sebagai vektor ol.

Sebagai tabahan penjelasan vektor $\textbf{0}$ tidak mempunyai besar dan arahnya tak tentu.

Vektor (Kelas X Matematika Peminatan)

$\color{blue}\textrm{A. Pendahuluan}$

Vektor adalah besaran yang memiliki panjang/besar sekaligus memiliki arah. Secara geometri, vektor digambarkan dengan anak panah (ruas garis berarah) yang mana memiliki titik pangkal dan titik ujung.

Perhatikanlah ilustrasi berikut

Perhatikanlah vektor b pada gambar di atas. Vektor tersebut dilambangkan dengan sebuah huruf b kecil tebal yang memiliki titik pangkal pada koordinat kartesius di titik $\left ( \displaystyle -\frac{5}{2},-\frac{3}{2} \right )$ dan berujung di titik $\left ( \displaystyle -1,2 \right )$ . Selain vektor b dituliskan dengan sebuah huruf kecil tercetak tebal dapat juga dituliskan dengan sebuah huruf kecil tanpa tercetak tebal tapi diberi anak panah kecil atau ruas garis di atasnya, yaitu : $\vec{a},\: \bar{a}$.

$\color{red}\textrm{Berikut cara penulisan notasi vektor}$

Menggunakan dua huruf kapital yang di atasnya ada anak panah, misalnya $\overline{PQ},\: \overline{RS},\: \: \textrm{dan}\: \: \overline{AZ}$
Menggunakan dua huruf kapital yang di atasnya diberikan anak panah, seperti $\overrightarrow{PQ},\: \overrightarrow{RS},\: \: \textrm{dan}\: \: \overrightarrow{AZ}$
Menggunakan sebauah huruf kecil tercetak tebal seperti pembahasan sebelumnya di atas, yaitu : $\textbf{a},\: \textbf{b},\: \textbf{c},\: \textbf{d},\: \: \textrm{dan}\: \: \textbf{e}$
Menggunakan sebuah huruf kecil yang di atsnya diberikan anak panah, misalnya: $\vec{a},\: \vec{b},\: \vec{c},\: \vec{d},\: \: \textrm{dan}\: \: \vec{e}$
Menggunakan sebuah huruf kecil yang bawahnya diberi garis
Menggunakan sebuah huruf kecil yang di atasnya diberi ruas garis, seperti $\bar{a},\: \bar{b},\: \bar{c},\: \bar{d},\: \: \textrm{dan}\: \: \bar{e}$

$\color{blue}\textrm{B. Vektor pada}\: \: \textrm{R}^{2}$

Vektor di $\color{blue}\textrm{R}^{2}$ adalah sebuah vektor yang diwakili oleh sebuah garis berarah dalam sebuah bidang datar atau Cartesius.

Perhatikanlah ilustrasi berikut

Misalkan pada salah satu vektor pada gambar di atas, ambil contoh $\overline{AB}$ . Vektor tersebut dilambangkan secara geometri dengan $\overline{AB}$ dan dibaca "vektor AB" yang berarti "vektor dari titik A ke titik B", dengan titik A sebagai titik pangkal dan B sebagai titik ujung. Sedangkan penulisan vektor secara aljabar dapat dinyatakan dalam matriks kolom atau matrik baris.

Pada $\color{blue}\textrm{R}^{2}$ (penulisan vektor pada ruang dimensi dua) penulisan vektor ini dituliskan dengan $\overline{AB}$, dengan

$\overline{AB}=\begin{pmatrix} \textrm{komponen horisontal}\\ \textrm{komponen vertikal} \end{pmatrix}$

Sehingga pada ilustrasi gambar di atas vektor-vektorya dapat dituliskan sebagai:

$\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix},\: \: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix},\: \: \&\: \: \overline{EF}=\begin{pmatrix} -4\\ -2 \end{pmatrix}$

atau

$\overline{AB}=\begin{bmatrix} 1, & -3 \end{bmatrix},\: \: \overline{CD}=\begin{bmatrix} 4, & 3 \end{bmatrix},\: \: \&\: \: \overline{EF}=\begin{bmatrix} -4, & -2 \end{bmatrix}$

$\color{blue}\textrm{C. Panjang Vektor}$

Panjang suatu vektor dilambangkan dengan tanda harga mutlak. Misal pada gambar di atas pada bahasan vekor di $\color{blue}\textrm{R}^{2}$, yaitu:

$\left | \overline{AB} \right |,\: \left | \overline{CD} \right |,\: \: \&\: \: \left | \overline{EF} \right |$.

Misalkan suatu vektor $\bar{u}$ dengan $\bar{u}=\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}$, maka panjang dari vektor $\bar{u}$ ini dapat ditentukan dengan

= $\left | \bar{u} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}}$.

Sehingga pada gambar di atas, panjang/besar vektornya dapat kita tentukan, yaitu:

$\begin{aligned}\bullet \: \left | \overline{AB} \right |&=\color{red}\sqrt{1^{2}+(-3)^{2}}=\sqrt{1+9}\\ &=\sqrt{10}\\ \bullet \: \left | \overline{CD} \right |&=\color{red}\sqrt{4^{2}+3^{2}}=\sqrt{16+9}\\ &=\sqrt{25}=5\\ \bullet \: \left | \overline{EF} \right |&=\color{red}\sqrt{(-4)^{2}+(-2)^{2}}=\sqrt{16+4}\\ &=\sqrt{20}=2\sqrt{5} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

1. Perhatikanlah gambar berikut

$\begin{array}{ll}\\ . &\textrm{Nyatakan vektor pada gambar di atas}\\ &\textrm{secara aljabar dan tentukan panjangnya}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{array}{ll}\\ \bullet &\textrm{Secara aljabar dinyatakan}\\ &\overrightarrow{a}=\begin{pmatrix} 6\\ -1 \end{pmatrix}=(6,-1)\\ &\overrightarrow{b}=\begin{pmatrix} 10\\ 5 \end{pmatrix}=(10,5)\\ &\overrightarrow{c}=\begin{pmatrix} -3\\ -6 \end{pmatrix}=(-3,-6)\\ \bullet &\textrm{Besar/panjang vektornya adalah}\\ &\left | \overrightarrow{a} \right |=\sqrt{6^{2}+(-1)^{2}}=\sqrt{36+1}=\sqrt{37}\\ &\left | \overrightarrow{b} \right |=\sqrt{10^{2}+5^{2}}=\sqrt{100+25}=\sqrt{125}\\ &\left | \overrightarrow{c} \right |=\sqrt{(-3)^{2}+(-6)^{2}}=\sqrt{9+36}\\ &\quad =\sqrt{45}=3\sqrt{5} \end{array} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan panjang vektor berikut}\\ &\textrm{a}.\quad \begin{pmatrix} 3\\ 4 \end{pmatrix},\qquad\qquad\qquad \textrm{b}.\quad\begin{pmatrix} 6\\ 9 \end{pmatrix}\\\\ &\color{blue}\textbf{Jawab}:\\ &\left | \begin{pmatrix} 3\\ 4 \end{pmatrix} \right |=\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}=5\\\\ &\left | \begin{pmatrix} 6\\ 9 \end{pmatrix} \right |=\sqrt{6^{2}+9^{2}}=\sqrt{36+81}=\sqrt{117} \end{array}$

Kedudukan Titik terhadap Lingkaran (Kelas XI)

$\color{blue}\textrm{D. Kedudukan Titik Terhadap Lingkaran }$.

Kedudukan sebuah titik terhadap sebuah lingkaran yang berpusat di O(0,0) memiliki 3 kemungkinan, yaitu:

jika titik A(x,y) di dalam lingkaran, maka berlaku $x^{2}+y^{2}<r^{2}$.
jika titik A(x,y) pada lingkaran, maka berlaku $x^{2}+y^{2}=r^{2}$, dan
jika titik A(x,y) di luar lingkaran, maka berlaku $x^{2}+y^{2}>r^{2}$.

Demikian juga kedudukan sebuah titik terhadap sebuah lingkaran yang berpusat di $(a,b)$ memiliki 3 kemungkinan, yaitu:

jika titik A(x,y) di dalam lingkaran, maka berlaku $(x-a)^{2}+(y-b)^{2}<r^{2}$ atau $x^{2}+y^{2}+Ax+By+C<0$.
jika titik A(x,y) pada lingkaran, maka berlaku $(x-a)^{2}+(y-b)^{2}=r^{2}$ atau $x^{2}+y^{2}+Ax+By+C=0$.
jika titik A(x,y) di luar lingkaran, maka berlaku $(x-a)^{2}+(y-b)^{2}>r^{2}$ atau $x^{2}+y^{2}+Ax+By+C>0$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Sebuah lingkaran yang berpusat pada }\\ &\textrm{pangkal koordinat}\\ &\textrm{a}.\quad \textrm{Tentukanlah persamaan lingkaran }\\ &\qquad\textrm{yang berjari-jari 5}\\ &\textrm{b}.\quad \textrm{Gambarlah lingkaran (pada soal a.) }\\ &\qquad\textrm{pada kertas grafiks}\\ &\textrm{c}.\quad \textrm{Lukislah titik-titik dari},\\ &\qquad A(2,3),\: B(4,3),\: \: \textrm{dan}\: \: C(3,6).\\ &\textrm{d}.\quad \textrm{Nyatakan kedudukan titik-titik}\\ &\qquad A,\: B,\: \textrm{dan}\: C\: \textrm{terhadap lingkaran. }\\ &\qquad\textrm{Di dalam, pada, atau}\\ &\qquad\textrm{beradakah di luar lingkaran}\\ &\textbf{Jawab}:\\ &\textrm{Perhatikanlah ilustrasi berikut} \end{array}$.

$\begin{aligned}\textrm{a}.\quad&\textrm{Diketahui}\: \: r=5\\ &\begin{aligned}&x^{2}+y^{2}=5^{2}\\ &\qquad\qquad \updownarrow\\ &x^{2}+y^{2}=25\\ &\textrm{atau}\\ &L\equiv \left \{ (x,y)|x^{2}+y^{2}=25 \right \} \end{aligned}\\ \textrm{b}.\quad&\textrm{Lihat gambar di atas}\\ \textrm{c}.\quad&\textrm{Lihat juga gambar di atas}\\ \textrm{d}.\quad&\textrm{Dari gambar jelas bahwa}:\\ &\begin{matrix} \bullet \quad \textrm{Titik}\: \: A(2,3)\: \textrm{berada di dalam lingkaran}\\ \textrm{atau}:(2)^{2}+(3)^{2}=4+9=13<\color{red}25\\ \bullet \quad \textrm{Titik}\: \: A(4,3)\: \textrm{berada pada lingkaran}\: \: \: \: \: \: \: \\ \textrm{atau}:(4)^{2}+(3)^{2}=16+9=25=\color{red}25\\ \bullet \quad \textrm{Titik}\: \: A(3,6)\: \textrm{berada di luar lingkaran}\: \: \: \,\\ \textrm{atau}:(3)^{2}+(6)^{2}=9+36=45>\color{red}25\\ \end{matrix} \end{aligned}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah persamaan lingkaran}\\ &\textrm{yang berpusat di pangkal koordinat}\\ &\textrm{dan melalui titik}\: \: P(5,-3)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Diketahui}&\: \textrm{pusat lingkaran di pangkal }\\ \textrm{koordinat}&\: \: O(0,0)\: \: \textrm{serta lingkaran}\\ \textrm{yang mela}&\textrm{lui titik}\: \: P(5,-3),\: \textrm{maka}\\ r&=\sqrt{(x_{p}-0)^{2}+(y_{p}-0)^{2}}\\ &=\sqrt{5^{2}+(-3)^{2}}\\ &=\sqrt{25+9}\\ &=\sqrt{34}\\ \textrm{Sehingga }&,\: \textrm{persamaan lingkarannya adalah}\\ L&\equiv x^{2}+y^{2}=r^{2}\Leftrightarrow x^{2}+y^{2}=\color{red}34 \end{aligned}\end{array}$.

DAFTAR PUSTAKA

Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Sobirin. 2006. Kompas Matematika Strategi Praktis Menguasai Tes Matematika SMA Kelas 2. Jakarta: KAWAN PUSTAKA.
Wirodikromo, S. 2007. Matematika Jilid 2 IPA untuk Kelas XI. Jakarta: ERLANGGA.

Lingkaran (Matematika Peminatan Kelas XI)

$\color{blue}\textrm{A. Definisi Lingkaran}$.

Secara definisi lingkaran adalah tempat kedudukam titik-titik yang berjarak sama terhadap satu titik tertentu. Selanjutnya titik tertentu disebut sebagai pusat lingkaran sedangkan jarak yang salalu sama terhadapa titik tertentu tersebut disebut sebagai jari-jari atau radius (r).

Sebagai ilustrasi berikut diberikan gambar berkaitan kedudukan titik-titik tersebut

$\color{blue}\textrm{B. Persamaan Lingkaran Berpusat di O(0,0) }$.

Persamaan sebuah lingkaran dengan dengan jari-jari $r$ dan berpusat di titik pusat koordinat dapat dilustrasikan sebagai berikut

Misalkan sebuah titik $\textrm{P}(x,y)$ terletak pada sebuah lingkaran yang berpusat di O(0,0). Dan titik $\textrm{P}'(x,0)$ adalah proyeksi titik P pada sumbu-X sehingga $\bigtriangleup \textrm{OP}'\textrm{P}$ berupa sebuah segitiga siku-siku di $\textrm{P}'$. Dengan rumus Pythagoras kita mendapatkan

$\begin{aligned}&OP^{2}=(OP')^{2}+(PP')^{2}\\ &\Leftrightarrow \: r^{2}=x^{2}+y^{2}\\ &\Leftrightarrow r=\sqrt{x^{2}+y^{2}} \end{aligned}$

Untuk lebih memudahkan pemahaman Anda, perhatikanlah ilustrasi berikut

Sehingga dapat disimpulkan persamaan lingkaran yang berpusat di O(0,0) adalah:

$\begin{array}{|ccc|}\hline &&\\ &\color{red}x^{2}+y^{2}=r^{2}&\\ &&\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukan persamaan lingkaran yang }\\ & \textrm{berpusat di O dan berjari-jari}\: \: \displaystyle \frac{1}{2}\sqrt{10}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui pusat lingkaran di O}\\ &\textrm{dengan jarijari}\: \: r=\displaystyle \frac{1}{2}\sqrt{10}\\ &\textrm{Persamaan lingkarannya adalah}:\\ &\color{red}x^{2}+y^{2}=r^{2}\\ &\Leftrightarrow \: x^{2}+y^{2}=\left ( \displaystyle \frac{1}{2}\sqrt{10} \right )^{2}\\ &\Leftrightarrow \: x^{2}+y^{2}=\displaystyle \frac{10}{4},\quad \textrm{atau}\\ &\Leftrightarrow \: x^{2}+y^{2}=\displaystyle \frac{5}{2}\\ &\textrm{Jadi, persamaan lingkarannya}\\ &\textrm{adalah}\: \: \: x^{2}+y^{2}=\displaystyle \frac{5}{2} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukan pusat dan jari-jari lingkaran}\\ & \textrm{yang memenuhi persamaan}\: \: \\ &x^{2}+y^{2}=6\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui persamaan lingkaran}\\ &\: \: x^{2}+y^{2}=6\\ &\textrm{maka }\\ &\bullet \: \: \textrm{pusat lingkaran adalah O}\\ &\qquad\color{red}x^{2}+y^{2}=r^{2}\\ &\bullet \: \: \textrm{dengan jari-jarinya adalah}\\ &\qquad r^{2}=6\Rightarrow \color{red}r=\sqrt{6}\\ &\textrm{Jadi, pusat lingkaran di O dengan}\\ &\textrm{jari-jari sebesar}\: \: r=\sqrt{6} \end{aligned} \end{array}$.

$\color{blue}\textrm{C. Persamaan Lingkaran Berpusat di (a,b)}$.

Perhatikanlah ilustrasi berikut

Pada ilustrasi gambar di atas ditunjukkan sebuah lingkaran berpusat di $N(a,b)$ dengan jari-jari $r$, misalkan kita ambil sebuah titik $P(x,y)$ pada keliling lingkaran, maka $NP=r$.

$\begin{aligned}&\sqrt{(x-a)^{2}+(y-b)^{2}}=r^{2}\\ &\color{red}(x-a)^{2}+(y-b)^{2}=r^{2}\\ &\textrm{persamaan di atas adalah}\: \: \textbf{Bentuk Umum}\\ &\textrm{dari}\: \: \textbf{Persamaan Lingkaran}\: \: \textrm{yang}\\ &\textrm{berpusat di}\: \: (a,b) \end{aligned}$

Selanjutnya perhatikanlah rangkuman berikut

$\begin{array}{|l|c|c|}\hline \textrm{Lingkaran} &x^{2}+y^{2}=r^{2}&(x-p)^{2}+(y-q)^{2}=r^{2}\\\hline \textrm{Pusat}&(0,0)&(p,q)\\\hline \textrm{Jari-jari}&r&r\\\hline \begin{aligned}&\textrm{Pesamaan garis}\\ &\textrm{singgung melalui}\\ &\textrm{titik}\: \: (x_{1},y_{1})\\ &\textrm{pada lingkaran} \end{aligned}&x_{1}x+y_{1}y=r^{2}&\begin{aligned}&(x_{1}-p)(x-p)\\ &\: +(y_{1}-q)(y-q)=r^{2} \end{aligned}\\\hline \begin{aligned}&\textrm{Persamaan garis}\\ &\textrm{singgung dengan}\\ &\textrm{gradien}\: \: m \end{aligned}&\begin{aligned}&y=mx\\ &\: \pm r\sqrt{m^{2}+1} \end{aligned}&\begin{aligned}&(y-q)=m(x-a)\\ &\: \pm r\sqrt{m^{2}+1} \end{aligned}\\\hline \end{array}$.

Kusus untuk yang pusat $(a,b)$ adalah:

$\begin{array}{|l|c|}\hline \textrm{Lingkaran} &x^{2}+y^{2}+Ax+By+C=0\\\hline \textrm{Pusat}&\left ( -\frac{1}{2}A,-\frac{1}{2}B \right )\\\hline \textrm{Jari-jari}&r=\sqrt{\displaystyle \frac{1}{4}\left ( A^{2}+B^{2} \right )-C}\\\hline \begin{aligned}&\textrm{Pesamaan garis}\\ &\textrm{singgung melalui}\\ &\textrm{titik}\: \: (x_{1},y_{1})\\ &\textrm{pada lingkaran} \end{aligned}&\begin{aligned}&x_{1}x+y_{1}y\\ &\: +\displaystyle \frac{A}{2}(x_{1}+x)\\ &\: +\displaystyle \frac{B}{2}(y_{1}+y)+C=0 \end{aligned}\\\hline \begin{aligned}&\textrm{Persamaan garis}\\ &\textrm{singgung dengan}\\ &\textrm{gradien}\: \: m \end{aligned}&\begin{aligned}&y+\frac{1}{2}B=m(x+\frac{1}{2}A)\\ &\: \pm \sqrt{\displaystyle \frac{1}{4}\left ( A^{2}+B^{2} \right )-C}.\sqrt{m^{2}+1} \end{aligned}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Tentukan persamaan lingkaran yang }\\ & \textrm{berpusat di (0,-2) dan berjari-jari}\: \: 5\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui pusat lingkaran berpusat}\\ &\textrm{di}\: \: (0,-2)\: \: \textrm{dan berjari-jari}\: r=5\\ &\textrm{Persamaan lingkarannya adalah}:\\ &\color{red}(x-a)^{2}+(y-b)^{2}=r^{2}\\ &\Leftrightarrow \: (x-0)^{2}+(y-(-2))^{2}=\left ( 5 \right )^{2}\\ &\Leftrightarrow \: x^{2}+(y+2)^{2}=25,\quad \textrm{atau}\\ &\Leftrightarrow \: x^{2}+y^{2}+4y+4=25\\ &\textrm{Jadi, persamaan lingkarannya}\\ &\textrm{adalah}\: \: \: x^{2}+y^{2}+4y-21=0 \end{aligned} \end{array}$,

$\begin{array}{ll}\\ 2.&\textrm{Tentukan persamaan lingkaran}\\ & \textrm{yang berpusat di titik}\: \: M(1,3)\\ &\textrm{dan melalui titik}\: \: N(-2,5)\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui jari-jari lingkaran}\\ &r=MN=\sqrt{(x_{M}-x_{N})^{2}+()^{2}}\\ &\Leftrightarrow \: \: =\sqrt{(-2-1)^{2}+(5-3)^{2}}\\ &\Leftrightarrow \: \: =\sqrt{(-3)^{2}+2^{2}}\\ &\Leftrightarrow \: \: =\sqrt{9+4}=\sqrt{13}\\ &\textrm{maka}\\ &\textrm{persamaan lingkarannya adalah}\\ &(x-1)^{2}+(y-3)^{2}=r^{2}\\ &\Leftrightarrow \: (x-1)^{2}+(y-3)^{2}=\left ( \sqrt{13} \right )^{2}\\ &\Leftrightarrow \: (x-1)^{2}+(y-3)^{2}=13\\ &\textrm{Jadi, jari-jari lingkarannya}\\ &\textrm{adalah}\: \: \sqrt{13}\: .\: \textrm{Dan persamaan}\\ &\textrm{lingkarannya adalah}:\: (x-1)^{2}+(y-3)^{2}=13 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah pusat dan jari-jari lingkaran berikut?}\\ &\textrm{a}.\quad L\equiv (x+1)^{2}+(y+2)^{2}=9\\ &\textrm{b}.\quad L\equiv (x+1)^{2}+(y-2)^{2}=9\\ &\textrm{c}.\quad L\equiv (x-1)^{2}+(y+2)^{2}=9\\ &\textrm{d}.\quad L\equiv (x-1)^{2}+(y-2)^{2}=9\\ &\textrm{e}.\quad L\equiv (x+3)^{2}+(y-3)^{2}=9\\ &\textrm{f}.\quad L\equiv (x-1)^{2}+(y-2)^{2}=25\\ &\textrm{g}.\quad L\equiv (x-1)^{2}+y^{2}=27\\ &\textrm{h}.\quad L\equiv x^{2}+(y-1)^{2}=27\\\\ &\textrm{Jawab}:\\ &L\equiv (x+1)^{2}+(y+2)^{2}=9,\: \: \textrm{pusat di}\: \: (-1,-2)\\ &\textrm{dan jari-jarinya adalah}\: \: \sqrt{9}=3\\ &\textrm{Soal yang belum dibahas silahkan }\\ &\textrm{diselesaikan sendiri sebagai latihan} \end{array}$.

$\begin{array}{ll}\\ 4.&\textrm{Tentukanlah pusat dan jari-jari dari }\\ &\textrm{persamaan lingkaran}\\\ & L\equiv 2x^{2}+2y^{2}-2x+6y-3=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Persamaan lingkaran}\\\ & L\equiv 2x^{2}+2y^{2}-2x+6y-3=0\\ &\Leftrightarrow \color{blue}x^{2}+y^{2}-x+3y-\displaystyle \frac{3}{2}=0\color{red}\begin{cases} A & =-1 \\ B & =3 \\ C & =-\displaystyle \frac{3}{2} \end{cases}\\ &\textrm{maka}\: \: \begin{cases} \textrm{Pusat} & =\left ( -\displaystyle \frac{-1}{2},- \frac{3}{2}\right )=\left ( \displaystyle \frac{1}{2},-\frac{3}{2} \right ) \\ \textrm{Jari-jari} & =r=\sqrt{\displaystyle \frac{(-1)^{2}}{4}+\frac{3^{2}}{4}-\left ( -\frac{3}{2} \right )}\\ &=\sqrt{\displaystyle \frac{1}{4}+\frac{9}{4}+\frac{6}{4}}=\sqrt{4}=2 \end{cases}\\ &\textrm{Jadi, lingkaran}\: \: 2x^{2}+2y^{2}-2x+6y-3=0\\\ & \textrm{berpusat di} \: \: \left ( \displaystyle \frac{1}{2},-\frac{3}{2} \right )\: \: \textrm{dan berjari-jari}\: \: 2\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 5.&\textrm{Diketahui persamaan lingkaran}\\\ &L\equiv 2x^{2}+2y^{2}-4x+3py-30=0\\ & \textrm{dan melalui titik}\: \: (-2,1).\: \textrm{Tentukanlah }\\ &\textrm{persamaan lingkaran baru yang} \\ &\textrm{kosentris(sepusat) dan panjang jari-jarinya}\\ &\textrm{dua kali panjang jari-jari lingkaran semula?}\\\\ &\textbf{Jawab}\\ &\begin{aligned}&\textrm{Diketahui persamaan lingkaran}\\ &2x^{2}+2y^{2}-4x+3py-30=0,\: \: \textrm{melalui}\\ &(-2,1), \: \: \textrm{maka}\\ &\begin{aligned}&\textrm{kita tentukan harga}\: \: p\: \: \textrm{dulu, yaitu}:\\ &2(-2)^{2}+2(1)^{2}-4(-2)+3p(1)-30=0\\ &\Leftrightarrow \: \: 8+2+8+3p-30=0\\ &\Leftrightarrow \: \: 3p=12\\ &\Leftrightarrow \: \: \color{red}p=4 \end{aligned}\\ &\textrm{Akibatnya persamaan lingkaran menjadi}\\ &\begin{aligned}&2x^{2}+2y^{2}-4x+12y-30=0\\ &\Leftrightarrow \: \: x^{2}+y^{2}-2x+6y-15=0 \end{aligned}\\ &\begin{aligned}&\begin{cases} \color{blue}\textrm{Pusat}: \\ \left ( -\displaystyle \frac{1}{2}A,-\frac{1}{2}B \right )\\ =\left ( -\displaystyle \frac{1}{2}.(-2),-\frac{1}{2},6 \right )\\ =(1,-3) \\\\ \color{blue}\textrm{Jari-jari }:\\ \begin{aligned}r&=\sqrt{\left ( -\frac{1}{2}A \right )^{2}+\left ( -\frac{1}{2}B \right )-C}\\ &=\sqrt{1^{2}+(-3)^{2}-(-15)}\\ &=\sqrt{1+9+15}=5 \end{aligned} \end{cases} \\ & \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned}&\textrm{Persamaan}\: \textrm{lingkaran baru }\\ &\textrm{dengan pusat}\: \: (1,-3)\: \: \textrm{dan jari-jari}\\ & r_{\textrm{baru}}=2r=2.5=10\\ &(x-1)^{2}+(y+3)^{2}=(10)^{2}\\ &\Leftrightarrow \: \: x^{2}-2x+1+y^{2}+6x+9=100\\ &\Leftrightarrow \: \: \color{red}x^{2}+y^{2}-2x+6y-90=0\end{aligned} \end{aligned} \end{array}$

Berikut ilustrasi gambarnya

Contoh Soal 14 (Segitiga dan Ketaksamaan)

$\begin{array}{ll}\\ 66.&\textrm{Diberikan}\: \: a,b,c>0,\: \: \textrm{tunjukkan bahwa}\\ &\displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\geq 6\\\\ &\textbf{Bukti}:\\ &\color{red}\textrm{Alternatif 1}\\ &\textrm{Dengan mengaplikasikan AM-GM-HM}\\ &\textrm{pada}\: \: \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\: \: \textrm{kita dapat menemukan}\\ &\color{blue}\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\color{black}\geq \displaystyle \frac{3}{(abc)^{.^{\frac{1}{3}}}}\geq \color{blue}\displaystyle \frac{9}{a+b+c}\\ &\textrm{Jika kedua ruas dikalikan dengan}\: \: \color{red}a+b+c\color{black},\\ &\textrm{maka}\\ &\color{blue}3+\displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\color{black}\geq \color{blue}\displaystyle \frac{9(a+b+c)}{a+b+c}\\ &\Leftrightarrow \displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\geq 6\qquad \blacksquare \\ &\begin{aligned}&\color{red}\textrm{Alternatif 2}\\ &\textrm{Asumsikan}\: \: a\leq b\leq c,\: \textrm{maka}\: \: a+b\leq a+c\leq b+c\\ &\textrm{dan}\: \: \displaystyle \frac{1}{c}\leq \frac{1}{b}\leq \frac{1}{a}.\\ &\textrm{Perhatikan bahwa}\\ & (a+b\leq a+c\leq b+c)\: \: \textrm{dan}\: \: \displaystyle \frac{1}{c}\leq \frac{1}{b}\leq \frac{1}{a}\\ &\textrm{memiliki kemonotonan yang sama}\\ &\textrm{maka dengan}\: \: \textbf{ketaksamaan Renata}\\ &\textrm{dapat diperoleh bentuk}\\ &(b+c).\displaystyle \frac{1}{a}+(c+a).\displaystyle \frac{1}{b}+(a+b).\displaystyle \frac{1}{c}\geq (b+c).\displaystyle \frac{1}{b}+(c+a).\displaystyle \frac{1}{c}+(a+b).\displaystyle \frac{1}{a}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \doteq 1+\displaystyle \frac{c}{b}+1+\frac{a}{c}+1+\frac{b}{a}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \doteq 3+\frac{c}{b}+\frac{a}{c}+\frac{b}{a}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \doteq 3+3\left ( \displaystyle \frac{abc}{abc} \right )^{.^{\frac{1}{3}}}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \doteq 3+3\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \doteq 6\qquad \blacksquare \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 67.&\textrm{Diberikan}\: \: a,b,c>0,\: \: \textrm{tunjukkan kebenaran}\\ &\textbf{ketaksamaan Nesbitt}\: \textrm{berikut}\\ &\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \frac{3}{2}\\\\ &\textbf{Bukti}:\\ &\color{blue}\textrm{Alternatif 1}\\ &\begin{aligned}&\textrm{Asumsikan},\\ &\color{red}\begin{cases} & a\geq b\geq c \\ & \displaystyle \frac{1}{b+c}\geq \frac{1}{a+c}\geq \frac{1}{a+b} \end{cases} \\ &\textrm{Dengan}\: \: \textbf{Ketaksamaan Chebyshev}\\ &\displaystyle \frac{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}{3}\geq \displaystyle \frac{(a+b+c)}{3}\left ( \displaystyle \frac{\left (\displaystyle \frac{1}{b+c}+ \frac{1}{a+c}+ \frac{1}{a+b} \right )}{3} \right )\\ &\textrm{Dengan AM-HM dan}\: K=\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\\ &\Leftrightarrow \displaystyle \frac{K}{3}\geq \displaystyle \frac{(a+b+c)}{3}\left ( \displaystyle \frac{3}{(b+c)+(a+c)+(a+b)} \right )\\ &\Leftrightarrow K\geq \displaystyle \frac{3(a+b+c)}{2(a+b+c)}\\ &\Leftrightarrow K\geq \displaystyle \frac{3}{2}\\ &\Leftrightarrow \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \displaystyle \frac{3}{2}\qquad \blacksquare \end{aligned}\\ &\color{blue}\textrm{Alternatif 2}\\ &\begin{aligned}&\color{magenta}\textbf{Pertama},\: \color{black}\textrm{asumsikan}\\ &\color{red}\begin{cases} & a\geq b\geq c \\ & \displaystyle \frac{1}{b+c}\geq \frac{1}{a+c}\geq \frac{1}{a+b} \end{cases} \\ &\textrm{Dengan}\: \: \textbf{Ketaksamaan Chebyshev}\\ &3\left (\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq (a+b+c)\left (\displaystyle \frac{1}{b+c}+ \frac{1}{a+c}+ \frac{1}{a+b} \right )\\ &\color{magenta}\textbf{Kedua},\: \color{black}\textrm{asumsikan}\\ &\color{red}\begin{cases} & a+b\geq a+c\geq b+c \\ & \displaystyle \frac{1}{a+b}\leq \frac{1}{a+c}\leq \frac{1}{b+c} \end{cases} \\ &\textrm{Dengan}\: \: \textbf{Ketaksamaan Chebyshev}\\ &3\left (\displaystyle \frac{a+b}{a+b}+\frac{a+c}{a+c}+\frac{b+c}{b+c} \right )\leq (a+b+a+c+b+c)\left (\displaystyle \frac{1}{a+b}+ \frac{1}{a+c}+ \frac{1}{b+c} \right )\\ &\Leftrightarrow 3(1+1+1)\leq 2(a+b+c)\left (\displaystyle \frac{1}{a+b}+ \frac{1}{a+c}+ \frac{1}{b+c} \right )\\ &\Leftrightarrow \displaystyle \frac{9}{2}\leq (a+b+c)\left (\displaystyle \frac{1}{a+b}+ \frac{1}{a+c}+ \frac{1}{b+c} \right )\\ &\textrm{Dari dua ketaksamaan di atas didapatkan}\\ &3\left (\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq \displaystyle \frac{9}{2}\\ &\Leftrightarrow \left (\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq \displaystyle \frac{3}{2}\qquad \blacksquare \end{aligned} \end{array}$

$\begin{array}{ll}\\ 68.&\textrm{Jika}\: \: a,b,c>0\: ,\: \textrm{dengan}\: \: a\neq b\neq c\\ &\textrm{tunjukkan bahwa}\\ &\left ( a^{3}+b^{3}+c^{3} \right )> \displaystyle \frac{(a+b+c)^{3}}{9}> 3abc\\\\ &\textbf{Bukti}:\\ &\textrm{Dengan}\: \textbf{ketaksamaan Chebyshev}\\ &\textrm{untuk}\: \: a\geq b\geq c,\: \textrm{dapat diperoleh bentuk}\\ &\displaystyle \frac{\left ( a^{3}+b^{3}+c^{3} \right )}{3}> \left ( \displaystyle \frac{a+b+c}{3} \right )\left ( \displaystyle \frac{a+b+c}{3} \right )\left ( \displaystyle \frac{a+b+c}{3} \right )\\ &\Leftrightarrow \displaystyle \frac{\left ( a^{3}+b^{3}+c^{3} \right )}{3}> \left ( \displaystyle \frac{a+b+c}{3} \right )^{3}> \left ( \displaystyle \frac{3\sqrt[3]{abc}}{3} \right )^{3}\\ &\Leftrightarrow \displaystyle \frac{\left ( a^{3}+b^{3}+c^{3} \right )}{3}> \displaystyle \frac{(a+b+c)^{3}}{27}> abc\\ &\Leftrightarrow \left ( a^{3}+b^{3}+c^{3} \right )> \displaystyle \frac{(a+b+c)^{3}}{9}> 3abc\quad \blacksquare \end{array}$.

$\begin{array}{ll}\\ 69.&\textrm{tunjukkan bahwa untuk}\: \: n\: \: \textrm{bilangan asli}\\&\textrm{berlaku}\\ &\displaystyle \frac{1}{\sqrt{n}}\left (1+\sqrt{\displaystyle \frac{1}{2}}+\sqrt{\displaystyle \frac{1}{3}}+\cdots +\sqrt{\displaystyle \frac{1}{n}} \right )\leq (2n-1)^{.^{\frac{1}{4}}}\\\\ &\textbf{Bukti}:\\ &\textrm{Dengan}\: \textbf{ketaksamaan Chebyshev}\\&\textrm{untuk}:\: \left ( 1\geq \displaystyle \frac{1}{2}\geq \frac{1}{3}\geq \cdots \geq \frac{1}{n} \right )\\ &\textrm{dapat diperoleh bentuk berikut}\\ &\left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )^{2}\leq n\left ( 1+\displaystyle \frac{1}{2.2}+\frac{1}{3.3}+\cdots +\frac{1}{n.n} \right )\\ &\Leftrightarrow \left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )^{2}\leq n\left ( 1+\displaystyle \frac{1}{1.2}+\frac{1}{2.3}+\cdots +\frac{1}{(n-1).n} \right )\\ &\Leftrightarrow \left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )^{2}\leq n\left ( 1+\left (1-\displaystyle \frac{1}{2} \right )+\left (\displaystyle \frac{1}{2}-\frac{1}{3} \right )+\cdots +\left (\displaystyle \frac{1}{(n-1)}-\frac{1}{n} \right ) \right )\\ &\Leftrightarrow \left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )^{2}\leq n\left ( 1+1-\displaystyle \frac{1}{n} \right )=n\left ( 2-\displaystyle \frac{1}{n} \right )\\&\Leftrightarrow \left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )\leq \sqrt{2n-1}\quad \color{red}..........(1)\\ &\textrm{Gunakan lagi}\: \textbf{ketaksamaan Chebyshev}\\ &\left (1+\sqrt{\displaystyle \frac{1}{2}}+\sqrt{\displaystyle \frac{1}{3}}+\cdots +\sqrt{\displaystyle \frac{1}{n}} \right )^{2}\leq n\left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )\\ &\Leftrightarrow \displaystyle \frac{1}{n}\left (1+\sqrt{\displaystyle \frac{1}{2}}+\sqrt{\displaystyle \frac{1}{3}}+\cdots +\sqrt{\displaystyle \frac{1}{n}} \right )^{2}\leq \left (1+ \displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \right )\: \: \color{red}...(2)\\&\textrm{Dari ketaksamaan (1) dan (2), dapat diperoleh}\\ & \displaystyle \frac{1}{n}\left (1+\sqrt{\displaystyle \frac{1}{2}}+\sqrt{\displaystyle \frac{1}{3}}+\cdots +\sqrt{\displaystyle \frac{1}{n}} \right )^{2}\leq \sqrt{2n-1}=(2n-1)^{.^{\frac{1}{2}}}\\ &\Leftrightarrow \displaystyle \frac{1}{\sqrt{n}}\left (1+\sqrt{\displaystyle \frac{1}{2}}+\sqrt{\displaystyle \frac{1}{3}}+\cdots +\sqrt{\displaystyle \frac{1}{n}} \right )\leq (2n-1)^{.^{\frac{1}{4}}}\qquad \blacksquare \end{array}$.

$\begin{array}{ll}\\ 70.&(\textbf{OSN 2011})\\ &\textrm{Jika}\: \: a,b,c>0\: ,\: \textrm{dengan}\: \: abc=1\\ &\textrm{Jika diketahui}\\ &a^{2011}+b^{2011}+c^{2011}< \displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\\ &\textrm{tunjukkan bahwa}\\ &(a+b+c)> \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\\\\ &\textbf{Bukti}:\\ &\textrm{Asumsikan}\\&\color{red}\begin{cases} &a\geq b\geq c \\ &\displaystyle \frac{1}{c}\geq \frac{1}{b}\geq \frac{1}{a} \end{cases}\\ &\textrm{Dengan}\: \textbf{ketaksamaan Chebyshev}\\ &\textrm{Perhatikan}\\ &\begin{aligned}&\displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\geq \displaystyle \frac{1}{3}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\left ( \displaystyle \frac{1}{a^{2010}}+\frac{1}{b^{2010}}+\frac{1}{c^{2010}} \right )\\ &\Leftrightarrow \displaystyle \frac{1}{a^{2010}}+\frac{1}{b^{2010}}+\frac{1}{c^{2010}}\geq \displaystyle \frac{1}{3}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\left ( \displaystyle \frac{1}{a^{2009}}+\frac{1}{b^{2009}}+\frac{1}{c^{2009}} \right )\\ &\Leftrightarrow \displaystyle \frac{1}{a^{2009}}+\frac{1}{b^{2009}}+\frac{1}{c^{2009}}\geq \displaystyle \frac{1}{3}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\left ( \displaystyle \frac{1}{a^{2008}}+\frac{1}{b^{2008}}+\frac{1}{c^{2008}} \right )\\ &\qquad\qquad \vdots \\ &\Leftrightarrow \displaystyle \frac{1}{a^{3}}+\frac{1}{b^{3}}+\frac{1}{c^{3}}\geq \displaystyle \frac{1}{3}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\left ( \displaystyle \frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}} \right )\\ &\Leftrightarrow \displaystyle \frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}\geq \displaystyle \frac{1}{3}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )\\ &\textrm{Sehingga}\\ &\displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\geq \displaystyle \frac{1}{3^{2010}}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )^{2011}\: \: \color{red}.....(1) \end{aligned} \\&\color{red}\textrm{dan}\\ &\begin{aligned}&a^{2011}+b^{2011}+c^{2011}\geq \displaystyle \frac{1}{3}(a+b+c)(a^{2010}+b^{2010}+c^{2010})\\ &\Leftrightarrow a^{2010}+b^{2010}+c^{2010}\geq \displaystyle \frac{1}{3}(a+b+c)(a^{2009}+b^{2009}+c^{2009})\\ &\Leftrightarrow a^{2009}+b^{2009}+c^{2009}\geq \displaystyle \frac{1}{3}(a+b+c)(a^{2008}+b^{2008}+c^{2008})\\&\qquad\qquad \vdots \\&\Leftrightarrow a^{3}+b^{3}+c^{3}\geq \displaystyle \frac{1}{3}(a+b+c)(a^{2}+b^{2}+c^{2})\\&\Leftrightarrow a^{2}+b^{2}+c^{2}\geq \displaystyle \frac{1}{3}(a+b+c)(a+b+c)\\ &\textrm{Sehingga}\\ &\Leftrightarrow a^{2011}+b^{2011}+c^{2011}\geq \displaystyle \frac{1}{3^{2010}}(a+b+c)^{2011}\: \: \color{red}........(2) \end{aligned}\\ &\begin{aligned}&\color{purple}\textrm{Dari ketaksamaan (1) dan (2) didapatkan}\\ &\frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\geq \displaystyle \frac{1}{3^{2010}}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )^{2011}\\ &>a^{2011}+b^{2011}+c^{2011}\geq \displaystyle \frac{1}{3^{2010}}(a+b+c)^{2011}\\ &\color{blue}\textrm{atau}\\ &\displaystyle \sum_{\textrm{siklik}}^{.}\displaystyle \frac{1}{a^{2011}}\geq \displaystyle \frac{1}{3^{2010}}\left ( \displaystyle \sum_{\textrm{siklik}}^{.}\displaystyle \frac{1}{a}\right )^{2011}> \displaystyle \sum_{\textrm{siklik}}^{.}a^{2011}\geq \displaystyle \frac{1}{3^{2010}}\left ( \displaystyle \sum_{\textrm{siklik}}^{.} \right )^{2011}\\ &\Leftrightarrow \displaystyle \frac{1}{3^{2010}}\left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )^{2011}>\displaystyle \frac{1}{3^{2010}}(a+b+c)^{2011}\\ &\Leftrightarrow \left ( \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )> (a+b+c)\\&\Leftrightarrow \: a+b+c< \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\qquad \blacksquare \end{aligned} \end{array}$.

DAFTAR PUSTAKA

Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.

Contoh Soal 13 (Segitiga dan Ketaksamaan)

$.\quad\qquad\begin{aligned}&\color{red}\textrm{Mengenal penulisan pola}\: \textbf{Siklik dan Simetri}\\ &\textrm{Misal untuk}\: \: n=3,\: \: \textrm{pada penulisan unsur}\\ &x,y,\: \: \textrm{dan}\: \: z,\: \textrm{maka}\\ &\begin{array}{|l|l|}\hline \textbf{Pola Siklik}&\textbf{Pola Simetri}\\\hline\begin{aligned}\displaystyle \sum_{\textrm{siklik}}^{.}x^{2}=x^{2}+y^{2}+z^{2}\\ &\\ &\\ &\\ &\\ & \end{aligned} &\begin{aligned}\displaystyle\sum_{\textrm{sym}}^{.}x^{2}&=x^{2}+x^{2}\\ &+y^{2}+y^{2}\\ \\ &+z^{2}+z^{2}\\ \\ &=2\left (x^{2}+y^{2}+z^{2} \right ) \end{aligned}\\ \begin{aligned}\displaystyle \sum_{\textrm{siklik}}^{.}x^{3}=x^{3}+y^{3}+z^{3}\end{aligned}&\begin{aligned}\displaystyle \sum_{\textrm{sym}}^{.}x^{3}=2\left (x^{3}+y^{3}+z^{3} \right ) \end{aligned}\\ \begin{aligned}\displaystyle \sum_{\textrm{siklik}}^{.}x^{2}y=x^{2}y+y^{2}z+z^{2}x\\ &\\ &\\ & \end{aligned}&\begin{aligned}\displaystyle \sum_{\textrm{sym}}^{.}x^{2}y&=x^{2}y+x^{2}z\\ &+y^{2}x+y^{2}z\\\\ &+z^{2}x+z^{2}y \end{aligned}\\ \begin{aligned}\displaystyle \sum_{\textrm{siklik}}^{.}xyz&=xyz+yzx+zxy\\ &=3xyz \end{aligned}&\begin{aligned}\displaystyle \sum_{\textrm{sym}}^{.}xyz&=xyz+xzy+\cdots \\ &=6xyz \end{aligned} \\\hline \end{array} \end{aligned}$.

$\begin{array}{ll}\\ 61.&(\textbf{IMO 1995})\\ &\textrm{Jika}\: \: a,b,c\: \: \textrm{bilangan-bilangan real positif}\\ &\textrm{dengan}\: \: abc=1,\: \: \textrm{maka tunjukkan bahwa}\\ &\displaystyle \frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(c+a)}+\frac{1}{c^{3}(a+b)}\geq \displaystyle \frac{3}{2}\\\\ &\textbf{Bukti}\\ &\begin{aligned}&\textrm{Misalkan}\: \: x=\displaystyle \frac{1}{a},\: y=\displaystyle \frac{1}{b},\: \: \textrm{dan}\: \: z=\displaystyle \frac{1}{c},\\ & \textrm{maka}\\ &\displaystyle \frac{1}{a^{3}(b+c)}+\frac{1}{b^{3}(c+a)}+\frac{1}{c^{3}(a+b)}\\ &=\displaystyle \frac{x^{3}yz}{y+z}+ \frac{y^{3}xz}{x+z}+ \frac{z^{3}xy}{x+y},\: \: \textrm{karena}\: xyz=1\\ &=\displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y}\\ &\textrm{Dengan ketaksamaan}\: \textbf{Cauchy-Schwarz}\\ &\left ( 2\displaystyle \sum_{\textrm{siklik}}^{.}y+z \right )\left ( \displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y} \right )\geq (x+y+z)^{2}\\ &\Leftrightarrow \left ( \displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y} \right )\geq \displaystyle \frac{(x+y+z)^{2}}{2(x+y+z)}\\ &\Leftrightarrow \left ( \displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y} \right )\geq \displaystyle \frac{(a+b+c)}{2}\\ &\Leftrightarrow \left ( \displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y} \right )\geq \displaystyle \frac{3\sqrt[3]{xyz}}{2}\\ &\Leftrightarrow \left ( \displaystyle \frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y} \right )\geq \displaystyle \frac{3}{2}\qquad \blacksquare \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 62.&\textrm{Diketahui} \: \: a,b\: \: \textrm{bilangan real positif}\\&\textrm{Tunjukkan bahwa}\: \: \displaystyle \frac{a^{2}}{b}+\frac{b^{2}}{a}\geq a+b\\\\ &\textbf{Bukti}\\ &\textrm{Asumsikan bahwa}\: \: a\geq b,\: \textrm{maka}\: \: a^{2}\geq b^{2}\\&\textrm{dan}\: \: \displaystyle \frac{1}{b}\geq \frac{1}{a}.\\ &\textrm{Perhatikan bahwa baik}\: \left ( a^{2},b^{2} \right )\: \textrm{dan}\: \left ( \displaystyle \frac{1}{b}, \frac{1}{a} \right)\\ &\textrm{adalah kumpulan dua barisan yang monoton}\\ &\textrm{sama yaitu sama-sama naik. Sehingga}\\ &\textrm{dengan}\: \: \textbf{ketaksamaan Renata}\: \textrm{diperoleh}\\ &a^{2}.\displaystyle \frac{1}{b}+b^{2}.\displaystyle \frac{1}{a}\geq a^{2}.\displaystyle \frac{1}{a}+b^{2}.\displaystyle \frac{1}{b}\\ &\Leftrightarrow \displaystyle \frac{a^{2}}{b}+\frac{b^{2}}{a}\geq a+b\qquad \blacksquare \end{array}$.

$\begin{array}{ll}\\ 63.&\textrm{Diberikan}\: \: a,b,c>0,\: \: \textrm{tunjukkan bahwa}\\ &\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\geq a+b+c\\\\ &\textbf{Bukti}:\\ &\color{red}\textrm{Alternatif 1}\\ &\textrm{Dengan AM-GM diperoleh}\\ &\bullet \: \: \displaystyle \frac{a}{c}+\frac{c}{a}\geq 2\Leftrightarrow \displaystyle \frac{c}{a}\geq 2-\displaystyle \frac{a}{c}\\ &\bullet \: \: \displaystyle \frac{b}{c}+\frac{c}{b}\geq 2\Leftrightarrow \displaystyle \frac{b}{c}\geq 2-\displaystyle \frac{c}{b}\\ &\bullet \: \: \displaystyle \frac{a}{b}+\frac{b}{a}\geq 2\Leftrightarrow \displaystyle \frac{a}{b}\geq 2-\displaystyle \frac{b}{a}\\ &\textrm{Sehingga}\\ &\begin{aligned}\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}&\geq a\left ( 2-\displaystyle \frac{c}{b} \right )+b\left ( 2-\displaystyle \frac{a}{c} \right )+c\left ( 2-\displaystyle \frac{b}{a} \right )\\ &=2a-\displaystyle \frac{ac}{b}+2b-\displaystyle \frac{ab}{c}+2c-\displaystyle \frac{bc}{a}\\ \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}&\geq 2(a+b+c)-\left ( \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b} \right )\\ 2&\left ( \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b} \right )\geq 2(a+b+c)\\ \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}&\geq a+b+c\qquad \blacksquare \end{aligned}\\ &\color{red}\textrm{Alternatif 2}\\ &\textrm{Dengan ketaksamaan Renata}\\ &\begin{aligned}&\textrm{Asumsikan}\: \: a\geq b\geq c,\: \textrm{maka}\: \: ab\geq ca\geq bc\\ &\textrm{dan}\: \: \displaystyle \frac{1}{c}\geq \frac{1}{b}\geq \frac{1}{a}.\\ &\textrm{Perhatikan bahwa}\\ & (ab\geq ca\geq bc)\: \: \textrm{dan}\: \: \left ( \displaystyle \frac{1}{c}\geq \frac{1}{b}\geq \frac{1}{a} \right )\\ &\textrm{memiliki kemonotonan yang sama}\\ &\textrm{maka dengan}\: \: \textbf{ketaksamaan Renata}\\ &\textrm{dapat diperoleh bentuk}\\ &ab.\displaystyle \frac{1}{c}+ac.\displaystyle \frac{1}{b}+bc.\displaystyle \frac{1}{a}\geq ab.\displaystyle \frac{1}{b}+ac.\displaystyle \frac{1}{a}+bc.\displaystyle \frac{1}{c}\\ &\Leftrightarrow \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\geq a+c+b\\ &\Leftrightarrow \displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\geq a+b+c\qquad \blacksquare \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 64.&\textrm{Diberikan}\: \: a,b,c>0,\: \: \textrm{tunjukkan kebenaran}\\ &\textbf{ketaksamaan Nesbitt}\: \textrm{berikut}\\ &\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geq \frac{3}{2}\\\\ &\textbf{Bukti}:\\ &\color{red}\textrm{Alternatif 1}\\ &\textrm{Dengan AM-GM diperoleh}\\ &\displaystyle \frac{(a+b)+(b+c)+(c+a)}{3}\geq \displaystyle \frac{3}{\displaystyle \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}}\\ &\Leftrightarrow ((a+b)+(b+c)+(c+a))\left ( \displaystyle \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a} \right )\geq 9\\ &\Leftrightarrow 2\left ( \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )+6\geq 9\\ &\Leftrightarrow 2\left ( \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq 3\\ &\Leftrightarrow \left ( \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq \displaystyle \frac{3}{2}\qquad \blacksquare \\ &\color{red}\textrm{Alternatif 2}\\ &\textrm{Dengan ketaksamaan Renata}\\ &\begin{aligned}&\textrm{Asumsikan}\: \: a\leq b\leq c,\: \textrm{maka}\: \: a+b\leq a+c\leq b+c\\ &\textrm{dan}\: \: \displaystyle \frac{1}{b+c}\leq \frac{1}{a+c}\leq \frac{1}{a+b}.\\ &\textrm{Perhatikan bahwa}\\ & (a\leq b\leq c)\: \: \textrm{dan}\: \: \displaystyle \frac{1}{b+c}\leq \frac{1}{a+c}\leq \frac{1}{a+b}\\ &\textrm{memiliki kemonotonan yang sama}\\ &\textrm{maka dengan}\: \: \textbf{ketaksamaan Renata}\\ &\textrm{dapat diperoleh bentuk}\\ &a.\displaystyle \frac{1}{b+c}+b.\displaystyle \frac{1}{a+c}+c.\displaystyle \frac{1}{a+b}\geq b.\displaystyle \frac{1}{b+c}+c.\displaystyle \frac{1}{a+c}+a.\displaystyle \frac{1}{a+b}\\ &\textrm{dan}\\ &a.\displaystyle \frac{1}{b+c}+b.\displaystyle \frac{1}{a+c}+c.\displaystyle \frac{1}{a+b}\geq c.\displaystyle \frac{1}{b+c}+a.\displaystyle \frac{1}{a+c}+b.\displaystyle \frac{1}{a+b}\\ &\textrm{Jika dijumlahkan keduanya, maka}\\ &2\left ( \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq 3\\ &\Leftrightarrow \left ( \displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \right )\geq \displaystyle \frac{3}{2}\qquad \blacksquare \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 65.&(\textbf{OSN 2015})\\ &\textrm{Diberikan}\: \: a,b,c>0,\: \: \textrm{Buktikan bahwa}\\ &\sqrt{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}}+\sqrt{\displaystyle \frac{b}{c+a}+\frac{c}{a+b}}+\sqrt{\displaystyle\frac{c}{a+b}+ \frac{a}{b+c}}\geq 3\\\\ &\textbf{Bukti}:\\ &\textrm{Perhatikan bukti soal no. 4 di atas}\\ &\textrm{Dengan}\: \: \textbf{keksamaan Renata}\: \: \textrm{dapat diperoleh}\\ &\displaystyle \frac{a}{b+c}+\frac{b}{a+c}\geq \frac{b}{b+c}+\frac{a}{a+c}\\ &\textrm{Misalkan}\\ &x=b+c,\: y=c+a,\: y=a+b,\: \textrm{maka}\\ &\displaystyle \frac{a}{b+c}+\frac{b}{a+c}\geq \frac{b}{b+c}+\frac{a}{a+c}\\ &\Leftrightarrow \displaystyle \frac{a}{b+c}+\frac{b}{a+c}\geq \frac{y+z-x}{2x}+\frac{x+z-y}{2y}\\ &\begin{aligned} &\Leftrightarrow \sqrt{ \displaystyle \frac{a}{b+c}+\frac{b}{a+c}}\geq \sqrt{\frac{y+z-x}{2x}+\frac{x+z-y}{2y}}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: = \sqrt{\displaystyle \frac{1}{2}}\sqrt{\displaystyle \frac{y}{x}+\frac{z}{x}-1+\frac{x}{y}+\frac{z}{y}-1}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: \: \textrm{dengan AM-GM}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: \geq \displaystyle \frac{1}{\sqrt{2}}\sqrt{\displaystyle \frac{z}{x}+\frac{z}{y}+2\sqrt{\frac{y}{x}.\frac{x}{y}}-2}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: = \displaystyle \frac{1}{\sqrt{2}}\sqrt{\displaystyle \frac{z}{x}+\frac{z}{y}+2-2}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: \geq \displaystyle \frac{1}{\sqrt{2}}\sqrt{\displaystyle \frac{z}{x}+\frac{z}{y}}\\ &\Leftrightarrow \quad\quad\quad\quad \quad\quad\quad\: \: \geq \displaystyle \frac{\sqrt{2}}{\sqrt{2}}\sqrt{\displaystyle \frac{z^{2}}{xy}}=\displaystyle \sqrt{\displaystyle \frac{z^{2}}{xy}}\\ \end{aligned}\\ &\begin{aligned} &\bullet \: \sqrt{ \displaystyle \frac{a}{b+c}+\frac{b}{a+c}} \geq \displaystyle \sqrt{\displaystyle \frac{z^{2}}{xy}}\\ &\bullet \: \sqrt{ \displaystyle \frac{b}{c+a}+\frac{c}{a+b}}\geq \sqrt{\displaystyle \frac{x^{2}}{yz}}\\ &\bullet \: \sqrt{ \displaystyle \frac{c}{a+b}+\frac{a}{b+c}}\geq \sqrt{\displaystyle \frac{y^{2}}{xz}} \end{aligned}\\ &\begin{aligned} &\textrm{Selanjutnya}\\ &\sqrt{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}}+\sqrt{\displaystyle \frac{b}{c+a}+\frac{c}{a+b}}+\sqrt{\displaystyle\frac{c}{a+b}+ \frac{a}{b+c}}\\ &\geq \displaystyle \sqrt{\displaystyle \frac{z^{2}}{xy}}+\sqrt{\displaystyle \frac{x^{2}}{yz}}+\sqrt{\displaystyle \frac{y^{2}}{xz}}\\ &\textrm{Dengan AM-GM lagi}\\ &\geq 3\sqrt[3]{\sqrt{\displaystyle \frac{z^{2}}{xy}}\times \sqrt{\displaystyle \frac{x^{2}}{yz}}\times \sqrt{\displaystyle \frac{y^{2}}{xz}}}\\ &\geq 3\sqrt[3]{\sqrt{\displaystyle \frac{(xyz)^{2}}{(xyz)^{2}}}}\\ &\geq 3\qquad \blacksquare \end{aligned} \end{array}$

DAFTAR PUSTAKA

Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.

WEBSITE

https://holdenlee.github.io/high_school/omc/23-rearrange.pdf diakses 18 Januari 2022.
https://www.gotohaggstrom.com/Advanced%20inequality%20manipulations.pdf diakses 20 Januari 2022

Contoh Soal 12 (Segitiga dan Ketaksamaan)

$\begin{array}{ll}\\ 56.&(\textbf{OSK 2018})\\ &\textrm{Diketahui bilangan real}\: \: x\: \: \textrm{dan}\: \: y\\ &\textrm{yang memenuhi}\: \: \displaystyle \frac{1}{2}< \frac{x}{y}< 2\\ &\textrm{Nilai minimum}\: \: \displaystyle \frac{x}{2y-x}+\frac{2y}{2x-y}\: \: \textrm{adalah}\: ....\\\\ &\textbf{Jawab}\\ &\begin{aligned}&\color{red}\textrm{Alternatif 1}\\ &\textrm{Misal}\: \: t=\displaystyle \frac{x}{y}\\ &\textrm{Misalkan juga}\: \: f(t)=\displaystyle \frac{x}{2y-x}+\displaystyle \frac{2y}{2x-y}\\ &\textrm{maka}\: \: f(t)=\displaystyle \frac{2t^{2}-3t+4}{-2t^{2}+5t-2}\\ &\bullet \:\textrm{Agar minimum, maka}\: \: f'(t)=0\\ &\: \: \: \: \: \textrm{Sehingga}\\ &\: \: \: \: \: f'(t)=4t^{2}+8t-14=0\\ &\: \: \: \: \Leftrightarrow t_{1,2}=-1\pm \displaystyle \frac{3}{2}\sqrt{2}\\ &\: \: \: \: \textrm{Pilih yang positif, yaitu}\: \: t=-1+ \displaystyle \frac{3}{2}\sqrt{2}\\ &\bullet \: \textrm{Dengan proses substistusi harga}\: \: t\\ &\: \: \: \: \textrm{di atas, maka akan didapatkan }\\ &\: \: \: \: \textrm{nilai}\: \: f(t)=1+\displaystyle \frac{4}{3}\sqrt{2} \end{aligned} \\ &\begin{aligned}&\color{red}\textrm{Alternatif 2}\\ &\textrm{Menurut bentuk}\: \: \displaystyle \frac{1}{2}< \frac{x}{y}< 2\\ &\textrm{jelas bahwa baik}\: \: 2y-x\: \: \textrm{dan}\: \: 2x-y \\ &\textrm{keduanya}\: \textbf{positif}\\ &\color{purple}\textrm{Lihat tabel berikut}\\ &\begin{array}{|c|c|c|}\hline \textrm{Bentuk}&\textrm{Pengecekan 1}&\textrm{Pengecekan 2}\\\hline \begin{aligned}&\displaystyle \frac{1}{2}< \frac{x}{y}< 2\\ &\textrm{Jelas bahwa}\\ &x,y\neq 0\\ &\\ &\\ &\\ &\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Saat}\: \: (\times y)\\ &\textrm{Yaitu}:\\ &\displaystyle \frac{1}{2}(y)< \frac{x}{y}(y)< 2(y)\\ &\Leftrightarrow \displaystyle \frac{1}{2}y< x< 2y\\ &\textrm{Jelas bahwa}\\ &2y-x>0\\ &\\ &\\ & \end{aligned}&\begin{aligned}&\textrm{Saat dibali posisinya}\\ &\displaystyle \frac{1}{2}< \frac{y}{x}< 2\\ &\textrm{Saat}\: \: (\times x)\\ &\textrm{Yaitu}:\\ &\displaystyle \frac{1}{2}(x)< \frac{y}{x}(x)< 2(x)\\ &\Leftrightarrow \displaystyle \frac{1}{2}x< y< 2x\\ &\textrm{Jelas bahwa}\\ &2x-y>0 \end{aligned}\\\hline \end{array}\\ &\textrm{Saat masing-masing}\\ &\bullet \: \displaystyle \frac{x}{2y-x}=\displaystyle \frac{1}{3}+\frac{2}{3}\left ( \displaystyle \frac{2x-y}{2y-x} \right )\: \: \: \textrm{dan}\\ &\bullet \: \displaystyle \frac{2y}{2x-y}=\displaystyle \frac{2}{3}+\frac{4}{3}\left ( \displaystyle \frac{2y-x}{2x-y} \right )\\ &\color{blue}\textrm{Dengan ketaksamaan AM-GM diperoleh}\\ &\begin{aligned} \displaystyle \frac{x}{2y-x}+\displaystyle \frac{2y}{2x-y}&=1+\frac{2}{3}\left ( \displaystyle \frac{2x-y}{2y-x} \right )+\frac{4}{3}\left ( \displaystyle \frac{2y-x}{2x-y} \right )\\ &\geq 1+2\sqrt{\frac{2}{3}\left ( \displaystyle \frac{2x-y}{2y-x} \right )\frac{4}{3}\left ( \displaystyle \frac{2y-x}{2x-y} \right )}\\ &= 1+2\sqrt{\displaystyle \frac{8}{9}}\\ &=1+2\left ( \displaystyle \frac{2}{3} \right )\sqrt{2}\\ &=1+\displaystyle \frac{4}{3}\sqrt{2} \end{aligned} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 57.&\textrm{Diketahui}\: \: a,b\: \: \textrm{bilangan real positif}\\ &\textrm{dan}\: \: a+b=1.\: \textrm{Tunjukkan bahwa}\\ &\qquad \left ( a+\displaystyle \frac{1}{a} \right )^{2}+\left ( b+\displaystyle \frac{1}{b} \right )^{2}\geq \displaystyle \frac{25}{2}\\\\ &\textbf{Bukti}\\ \end{array}$.

$\: \: \: \quad\begin{aligned}&\color{purple}\textrm{Dengan AM-GM kita akan mendapatkan}\\ &1=a+b\geq 2\sqrt{ab}\Leftrightarrow \displaystyle \frac{1}{2}\geq \sqrt{ab}\Leftrightarrow 2\leq \displaystyle \frac{1}{\sqrt{ab}}\\ &\Leftrightarrow \displaystyle \frac{1}{\sqrt{ab}}\geq 2\Leftrightarrow \displaystyle \frac{1}{ab}\geq 4\\ &\color{red}\textrm{Perhatikan soal, dengan CS-Engel}\: \color{black}\textrm{akan}\\ &\textrm{didapatkan}\\ &\begin{aligned} &(1+1)\left (\displaystyle \frac{\left ( a+\frac{1}{a} \right )^{2}}{1} +\displaystyle \frac{\left ( b+\frac{1}{b} \right )^{2}}{1} \right )\geq \left (a+\frac{1}{a}+b+\frac{1}{b} \right )^{2}\\ &\Leftrightarrow 2\left (\left (\displaystyle a+\frac{1}{a} \right)^{2} +\left (b+\frac{1}{b} \right )^{2} \right )\geq \left (a+b+\frac{1}{a}+\frac{1}{b} \right )^{2}\\ &\Leftrightarrow \left (\displaystyle a+\frac{1}{a} \right )^{2} +\left (b+\frac{1}{b} \right )^{2}\geq \displaystyle \frac{1}{2}\left ( 1+\displaystyle \frac{a+b}{ab} \right )^{2}\\ &\Leftrightarrow \left (\displaystyle a+\frac{1}{a} \right )^{2} +\left (b+\frac{1}{b} \right )^{2}\geq\displaystyle \frac{1}{2}\left ( 1+\displaystyle \frac{1}{ab} \right )^{2}\\ &\Leftrightarrow \left (\displaystyle a+\frac{1}{a} \right )^{2} +\left (b+\frac{1}{b} \right )^{2}\geq\displaystyle \frac{1}{2}(1+4)^{2}\\ &\Leftrightarrow \left (\displaystyle a+\frac{1}{a} \right )^{2} +\left (b+\frac{1}{b} \right )^{2}\geq \displaystyle \frac{1}{2}\times 25\\ &\Leftrightarrow \left (\displaystyle a+\frac{1}{a} \right )^{2} +\left (b+\frac{1}{b} \right )^{2}\geq \displaystyle \frac{25}{2}\qquad \blacksquare \end{aligned} \end{aligned}$.

$\begin{array}{ll}\\ 58.&\textrm{Jika}\: \: a,b\: \: \textrm{bilangan positif, buktikan}\\ &\textrm{a}.\quad 2(a^{2}+b^{2})\geq (a+b)^{2}\\ &\textrm{b}.\quad 4(a^{3}+b^{3})\geq (a+b)^{3}\\ &\textrm{c}.\quad 8(a^{4}+b^{4})\geq (a+b)^{4}\\ &\textrm{d}.\quad 16(a^{5}+b^{5})\geq (a+b)^{5}\\ &\textrm{e}.\quad 32(a^{6}+b^{6})\geq (a+b)^{6}\\ &\textrm{f}.\quad 64(a^{7}+b^{7})\geq (a+b)^{7}\\ &\textrm{g}.\quad 128(a^{8}+b^{8})\geq (a+b)^{8}\\\\ &\textbf{Bukti}:\\ &\textrm{Akan ditunjukkan bukti poin 6.c saja}\\ &\textrm{untuk poin yang lain, silahkan pembaca}\\ &\textrm{sekalian untuk dibuktikan sendiri sebagai}\\ &\textrm{bahan latihan mandiri}.\\ &\textrm{Adapun bukti poin 6.c adalah sebagaimana}\\ &\textrm{berikut ini}\\ &\begin{aligned} &\color{red}\textrm{Dengan ketaksamaan CS-Engel}\: \color{black}\textrm{akan}\\ &\textrm{didapatkan}\\ &\bullet \: \: (1+1)(a^{4}+b^{4})\geq (a^{2}+b^{2})^{2}\\ &\: \quad\Leftrightarrow 2\left (a^{4}+b^{4} \right )\geq (a^{2}+b^{2})^{2}\: \color{red}..........(1)\\ &\bullet \: \: (1+1)(a^{2}+b^{2})\geq (a+b)^{2}\\ &\: \quad\Leftrightarrow 2\left (a^{2}+b^{2} \right )\geq \displaystyle (a+b)^{2},\quad (\textrm{kuadratkan})\\ &\: \quad \Leftrightarrow 4\displaystyle \left (a^{2}+b^{2} \right )^{2}\geq (a+b)^{4}\\ &\: \quad \Leftrightarrow \left (a^{2}+b^{2} \right )^{2}\geq \displaystyle \frac{(a+b)^{4}}{4}\: \color{red}...........(2)\\ &\textrm{Dari (1) dan (2) didapatkan hubungan}\\ &2\left (a^{4}+b^{4} \right )\geq \left (a^{2}+b^{2} \right )^{2}\geq \displaystyle \frac{(a+b)^{4}}{4}\\ &\Leftrightarrow 8\left ( a^{4}+b^{4} \right )\geq 4\left ( a^{2}+b^{2} \right )^{2}\geq (a+b)^{4}\\ &\Leftrightarrow 8\left ( a^{4}+b^{4} \right )\geq (a+b)^{4}\qquad \blacksquare \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 59.&\textrm{Jika}\: \: x,y,z\: \: \textrm{adalah bilangan real positif}\\ &\textrm{dengan}\: \: x^{2}+y^{2}+z^{2}=27.\: \textrm{Tunjukkan}\\ & \textrm{bahwa}\: \: x^{3}+y^{3}+z^{3}\geq 81\\\\ &\textbf{Bukti}\\ &\color{red}\textrm{Pada contoh soal no.2 terdapat}\\ &(ax+by+cz)^{2}\leq (a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})\\ &\textrm{ganti mengganti}\: \: a=b=c=1,\: \textrm{maka menjadi}\\ &(x+y+z)^{2}\leq (1^{2}+1^{2}+1^{2})(x^{2}+y^{2}+z^{2})\\ &\Leftrightarrow (x+y+z)^{2}\leq (3)(x^{2}+y^{2}+z^{2})\: \color{red}........(1)\\ &\textrm{Selanjutnya dengan mengganti dengan}\\ &x^{.^{\frac{3}{2}}},y^{.^{\frac{3}{2}}},z^{.^{\frac{3}{2}}}\: \: \textrm{dan}\: \: x^{.^{\frac{1}{2}}},y^{.^{\frac{1}{2}}},z^{.^{\frac{1}{2}}},\: \textrm{pada}\\ &(ax+by+cz)^{2}\leq (a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})\\ &\textrm{Kita akan dapatkan}\\ &(x^{2}+y^{2}+z^{2})\leq (x^{3}+y^{3}+z^{3})(x+y+z)\: \color{red}........(2)\\ &\textrm{Jika masing-masing ruas dikuadratkan, maka}\\ &(x^{2}+y^{2}+z^{2})^{4}\leq (x^{3}+y^{3}+z^{3})^{2}(x+y+z)^{2}\\ &\Leftrightarrow (x^{2}+y^{2}+z^{2})^{4} \leq 3(x^{3}+y^{3}+z^{3})^{2}\left ( x^{2}+y^{2}+z^{2} \right )\\ &\Leftrightarrow (x^{2}+y^{2}+z^{2})^{3} \leq 3(x^{3}+y^{3}+z^{3})^{2}\\ &\Leftrightarrow (27)^{3}\leq 3(x^{3}+y^{3}+z^{3})^{2}\\ &\Leftrightarrow 3^{9}\leq 3(x^{3}+y^{3}+z^{3})^{2}\\ &\Leftrightarrow 3^{8}\leq (x^{3}+y^{3}+z^{3})^{2}\\ &\Leftrightarrow (x^{3}+y^{3}+z^{3})^{2}\geq 3^{8}\\ &\Leftrightarrow (x^{3}+y^{3}+z^{3})\geq 3^{.^{\frac{8}{2}}}\\ &\Leftrightarrow (x^{3}+y^{3}+z^{3})\geq 3^{4}=81\qquad \blacksquare \end{array}$.

$\begin{array}{ll}\\ 60.&\textrm{Untuk}\: \: a,b,c,d\: \: \textrm{adalah bilangan real }\\ &\textrm{positif, tunjukkan bahwa}\\ &\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{4}{c}+\frac{16}{d}\geq \displaystyle \frac{64}{a+b+c+d}\\\\ &\textbf{Bukti}\\ &\begin{aligned}&\color{red}\textrm{Dengan ketaksamaan CS-Engel}\\ &(a+b+c+d)\left (\displaystyle \frac{1^{2}}{a}+\displaystyle \frac{1^{2}}{b}+\displaystyle \frac{2^{2}}{c}+\displaystyle \frac{4^{2}}{d} \right )\geq (1+1+2+4)^{2}\\ &\Leftrightarrow \displaystyle \frac{1^{2}}{a}+\displaystyle \frac{1^{2}}{b}+\displaystyle \frac{2^{2}}{c}+\displaystyle \frac{4^{2}}{d}\geq \displaystyle \frac{(1+1+2+4)^{2}}{a+b+c+d}\\ &\Leftrightarrow \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{4}{c}+\frac{16}{d}\geq \displaystyle \frac{64}{a+b+c+d}\quad \blacksquare \end{aligned} \end{array}$.

DAFTAR PUSTAKA

Muslim, M.S. 2020. Kumpulan Soal dan Pembahasan Olimpiade Matematika SMA Tahun 2007-2019 Tingkat Kota/Kabupaten. Bandung: YRAMA WIDYA.
Widodo, T. 2018. Booklet OSN SMA 2018: Soal dan Solusi OSK, OSP, OSN SMA Bidang Matematika.
Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.