Materi Vektor Lanjutan 2 (Kelas X Matematika Peminatan)

 $\color{blue}\textrm{K. Operasi Vektor}$

$\color{blue}\textrm{1. Penjumlahan}$

$\color{blue}\textrm{1. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut

Penjumlahan di atas adalah penjumlahan menurut aturan segitiga, 

perhatikan pula pemisalan berikut

$\begin{aligned}&\textrm{Menurut aturan segitiga}\\ &\overline{AB}+\overline{BC}=\bar{a}+\bar{b}=\overline{AC},\quad \color{red}\textrm{Selanjutnya}\\ &\overline{AC}+\overline{CD}=\bar{a}+\bar{b}+\bar{c}=\overline{AD},\quad \color{red}\textrm{maka}\\ &\overline{AD}+\overline{DE}=\bar{a}+\bar{b}+\bar{c}+\bar{d}=\overline{AE} \end{aligned}$

Pada penjumlahan dengan vektor adalah tetap (tidak berubah)

$\begin{aligned} &\overline{a}+\overline{0}=\overline{0}+\overline{a}=\overline{a}\\ &\textrm{Sehingga vektor nol disebut sebagai}\\ &\color{red}\textbf{elemen identitas} \end{aligned}$

$\color{blue}\textrm{1. 2 Secara Aljabar}$

Misal  

$\begin{aligned} &\overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}\: \: \textrm{dan}\: \: \overline{b}=\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}\\ &\textrm{maka secara aljabar}\\ &\color{red}\overline{a}+\overline{b}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}+\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}=\begin{pmatrix} x_{1}+x_{2}\\ y_{1}+y_{2} \end{pmatrix} \end{aligned}$

Perhatikan kembali gambar berikut (lihat pada pembahasan sebelumnya) 

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

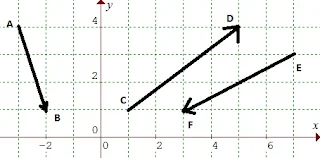
Titik  A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}+\overline{CD}=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}=\begin{pmatrix} 1+4\\ (-3)+3 \end{pmatrix}=\color{blue}\begin{pmatrix} 5\\ 0 \end{pmatrix} \end{aligned}$

Dan untuk contoh yang lain adalah:

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: ,\: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{EF}=\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}+\overline{CD}+\overline{EF}\\ &=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}+\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &=\begin{pmatrix} 1+4+(-4)\\ (-3)+3+(-2) \end{pmatrix}=\color{blue}\begin{pmatrix} 1\\ -2 \end{pmatrix} \end{aligned}$

$\color{blue}\textrm{2. Pengurangan}$

$\color{blue}\textrm{2. 1 Secara Geometri}$

Pada pengurangan vektor $\overline{a}\: \: \: \color{red}\textrm{oleh}\: \: \: \color{black}\overline{b}$  dapat didefinisikan sebagai:

$\overline{a}-\overline{b}=\overline{a}+\left ( -\overline{b} \right )$. Perhatikanlah ilustrasi secara geometri berikut:

$\color{blue}\textrm{2. 2 Secara Aljabar}$

$\begin{aligned}&\textrm{Misalkan}\: \: \: \overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix}\: \: \textrm{dan}\: \: \overline{b}=\begin{pmatrix} x_{2}\\ y_{2} \end{pmatrix}\\ &\textrm{maka}\: \: -\overline{b}=\begin{pmatrix} -x_{2}\\ -y_{2} \end{pmatrix}\\ &\color{red}\textrm{Selanjutnya}\\ &\overline{a}-\overline{b}=\overline{a}+\left ( -\overline{b} \right )=\color{red}\begin{pmatrix} x_{1}-x_{2}\\ y_{1}-y_{2} \end{pmatrix} \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Pada contoh soal bahasan penjumlahan di atas, perhatikan lagi bahwa

Titik  A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\color{red}\overline{AB}-\overline{CD}=\begin{pmatrix} 1\\ -3 \end{pmatrix}+\begin{pmatrix} -4\\ -3 \end{pmatrix}=\begin{pmatrix} 1-4\\ (-3)-3 \end{pmatrix}=\color{blue}\begin{pmatrix} -3\\ -6 \end{pmatrix} \end{aligned}$

$\color{blue}\textrm{3. Perkalian dengan Skalar}$

$\color{blue}\textrm{3. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut!

$\color{blue}\textrm{3. 2 Secara Aljabar}$

Perkalian suatu skalar dengan suatu vektor tergantung pada skalarnya. Jika suatu skalar  k  dengan  $\color{red}k>0$,  maka perkalian ini akan menghasilkan vektor baru yang besarnya sekian  k  kali dari vektor semula  atau  $\color{red}k\left | \overline{a} \right |$   dan arahnya searah dengan vektor yang dikalikan. Demikian sebaliknya, jika nilai  $\color{red}k<0$, maka besar vektor hasil perkaliannya adalah  $\color{red}k\left | \overline{a} \right |$  dengan arah yang berlawanan dari vektor semula.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

Misalkan diketahui vektor-vektor sebagai berikut:

$\begin{aligned} &\overline{AB}=\begin{pmatrix} 1\\ -3 \end{pmatrix}\: ,\: \overline{CD}=\begin{pmatrix} 4\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overline{EF}=\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &\textrm{maka penjumlahan secara Aljabar}\\ &\textrm{dengan muculnya skalar adalah}:\\ &\color{red}3\overline{AB}+4\overline{CD}-5\overline{EF}\\ &=3\begin{pmatrix} 1\\ -3 \end{pmatrix}+4\begin{pmatrix} 4\\ 3 \end{pmatrix}-5\begin{pmatrix} -4\\ -2 \end{pmatrix}\\ &=\begin{pmatrix} 3.1+4.4+(-5).(-4)\\ 3.(-3)+4.3+(-5).(-2) \end{pmatrix}=\color{blue}\begin{pmatrix} 39\\ 13 \end{pmatrix} \end{aligned}$

DAFTAR PUSTAKA

1. Kuntarti, Sulistiyono, & Kurnianingsih, S. 2005. Matematika untuk SMA dan MA Kelas XII Program Ilmu Alam. Jakarta: PT. Gelora Aksara Pratama