Distribusi Peluang Diskrit

$\begin{array}{rl}\text{D. 1}.& \text{Distribusi Peluang Diskrit}\end{array}$

$\begin{array}{rl}& \text{Misalkan}X\text{adalah variabel acak diskrit}\\ & \text{dari nilai}:x_1,x_2,x_3,x_4,\cdots ,x_k,\text{dan}\\ & P\text{adalah seluruh nilai peluang untuk}:\\ & p_1,p_2,p_3,p_4,\cdots ,p_k,\text{maka nilai untuk}\\ & p_1+p_2+p_3+p_4+\cdots +p_k=1\\ & \mathbf{\text{dan}}\\ & \text{Fungsi}f(x)=P(X=x)\text{yang mempunyai}\\ & \text{nilai}{p}_1,p_2,p_3,p_4,\cdots ,p_k,\text{pada variabel}\\ & X=x_1,x_2,x_3,x_4,\cdots ,x_k,\text{disebut fungsi}\\ & \text{kepekatan peluang dari variabel acak}X.\\ & \text{Selanjutnya jika kita gambar grafik}f(x)\\ & \text{terhadap}x,\text{maka kita akan grafik yang}\\ & \text{dinamakan dengan}\mathbf{\text{grafik peluang}}\end{array}$

Suatu fungsi  $f(x)=P(X=x)$  disebut fungsi peluang (probabilitas) dari  $X$, jika memenuhi syarat-syarat:

$\begin{array}{c}(\text{i})f(x)\ge 0\text{untuk semua}x\\ \\ (\text{ii})\sum _{i=1}^{n}f\left(x_i\right)=f(x_1)+f(x_2)+f(x_3)+...+f(x_n)=1\end{array}$

$\text{CONTOH SOAL}$

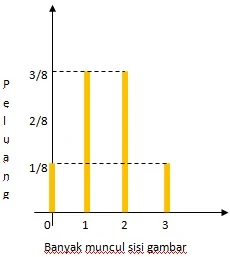
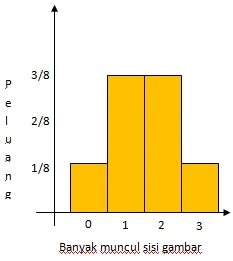
$\begin{array}{l}\\ 1.& \text{Pada percobaan melempar 3 koin identik}\\ & \text{sekaligus bersama-sama. Variabel acak}\\ & \text{dalam hal ini pada kejadian muncul sisi}\\ & \text{gambar, tentukan}\\ & \text{a}.\text{distribusi peluangnya}\\ & \text{b}.\text{tabel fungsi peluangnya}\\ & \text{c}.\text{grafik fungsi peluangnya}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Diketahui dari soal}\text{variabel acak}\\ & \text{pada kejadian di atas adalah munculnya}\\ & \text{sisi gambar pada pelemparan 3 koin}\\ & \text{maka}\end{array}\\ & \begin{array}{rl}\text{a}.& \text{Distribusi peluangnya}\\ & \begin{array}{|lcccccccc|}\hline \text{Sampel}& AAA& AAG& AGA& AGG& GAA& GAG& GGA& GGG\\ \text{Muncul}(G)& 0& 1& 1& 2& 1& 2& 2& 3\\ \hline\end{array}\\ \text{b}.& \text{Tabel fungsi peluangnya}\\ & x=\text{muncul kejadian sisi gambar}(G)\\ & \begin{array}{|cccccc|}\hline x& 0& 1& 2& 3& \text{Jumlah}\\ f(x)& {\displaystyle \frac{1}{8}}& {\displaystyle \frac{3}{8}}& {\displaystyle \frac{3}{8}}& {\displaystyle \frac{1}{8}}& 1\\ \hline\end{array}\\ \text{c}.& \text{Grafik fungsi peluangnya adalah}\\ & \end{array}\end{array}$

 

$\begin{array}{l}\\ 2.& \text{Pada sebuah kotak terdapat 2 kelereng}\\ & \text{biru dan 4 kelereng merah. Tiga kereng}\\ & \text{diambil secara acak. Tentukanlah distribusi}\\ & \text{peluang}x\text{jika}x\text{menyatakan banyaknya}\\ & \text{terambilnya bola biru}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{|lc|}\hline \text{Nama}& \text{Perhitungan}\\ \text{Banyak}& \\ \text{titik sampel}& \begin{array}{rl}{C}_3^6& ={\displaystyle \frac{6!}{3!(6-3)!}=20}\end{array}\\ \text{Banyak cara}& \\ \text{mendapatkan bola biru}& C_x^2\\ \text{Banyak cara}& \\ \text{mendapatkan bola merah}& C_{3-x}^4\\ \hline\end{array}\end{array}$

$.\begin{array}{|ll|}\hline \text{Distribusi peluang}& \text{Perhitungan}\\ P(X=x)=f(x)& f(x)={\displaystyle \frac{{\displaystyle C_x^2.C_{3-x}^4}}{{\displaystyle C_3^6}},}\\ \text{untuk}& \begin{array}{rl}x& =0,1,2\end{array}\\ x=0\Rightarrow P(x=0)& f(x)={\displaystyle \frac{{\displaystyle C_0^2.C_{3-0}^4}}{{\displaystyle C_3^6}}}\\ & .={\displaystyle \frac{{\displaystyle C_0^2.C_3^4}}{{\displaystyle C_3^6}}={\displaystyle \frac{{\displaystyle \frac{2!}{0!2!}\times \frac{4!}{3!1!}}}{{\displaystyle \frac{6!}{3!3!}}}}}\\ & .={\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2}\\ x=1\Rightarrow P(x=1)& f(x)={\displaystyle \frac{{\displaystyle C_1^2.C_{3-1}^4}}{{\displaystyle C_3^6}}}\\ & .={\displaystyle \frac{{\displaystyle C_1^2.C_2^4}}{{\displaystyle C_3^6}}={\displaystyle \frac{{\displaystyle \frac{2!}{1!1!}\times \frac{4!}{2!2!}}}{{\displaystyle \frac{6!}{3!3!}}}}}\\ & .={\displaystyle \frac{2!4!3!3!}{2!2!6!}=0,6}\\ x=2\Rightarrow P(x=2)& f(x)={\displaystyle \frac{{\displaystyle C_2^2.C_{3-2}^4}}{{\displaystyle C_3^6}}}\\ & .={\displaystyle \frac{{\displaystyle C_2^2.C_1^4}}{{\displaystyle C_3^6}}={\displaystyle \frac{{\displaystyle \frac{2!}{2!0!}\times \frac{4!}{1!3!}}}{{\displaystyle \frac{6!}{3!3!}}}}}\\ & .={\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2}\\ \hline\end{array}$

$\begin{array}{l}\\ 3.& \text{Tunjukkan bahwa fungsi}P(x)={\displaystyle \frac{x+2}{12}}\\ & \text{untuk}x=1,2,\text{dan}3\text{merupakan fungsi}\\ & \text{peluang}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}\text{Perhatik}& \text{an bahwa}\\ \bullet P(1)& ={\displaystyle \frac{1+2}{12}=\frac{3}{12}=\frac{1}{4}}\\ \bullet P(2)& ={\displaystyle \frac{2+2}{12}=\frac{4}{12}=\frac{1}{3}}\\ \bullet P(3)& ={\displaystyle \frac{5+2}{12}=\frac{5}{12}}\\ \text{Sehing}& \text{ga}{\displaystyle \sum _{i=1}^{3}P(i)={\displaystyle \frac{3}{12}+\frac{4}{12}+\frac{5}{12}=\frac{12}{12}=1}}\\ & \{\begin{array}{ll}(\text{i})& \text{Peluangnya berada}0\le P(i)\le 1\\ (\text{ii})& \text{dan nilai totolnya}={\displaystyle \sum _{i=1}^{3}P(i)=1}\end{array}\\ \text{Jadi},& \text{fungsi}P(x)={\displaystyle \frac{x+2}{12}\text{untuk}x=1,2,\text{dan}3}\\ & \mathbf{\text{merupakan fungsi peluang}}\end{array}\end{array}$

$\begin{array}{l}\\ 4.& \text{Diketahui fungsi peluang adalah}P(x)={\displaystyle \frac{m}{x+1}}\\ & \text{untuk}x=0,1,2,\text{dan}3.\text{Tentukanlah}\\ & \text{a}.\text{nilai}m\\ & \text{b}.\text{nilai}P(x\le 2)\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}\text{a}.& {\displaystyle \sum _{i=0}^{3}P(i)=1}\\ & \iff {\displaystyle \frac{m}{0+1}+\frac{m}{1+1}+\frac{m}{2+1}+\frac{m}{3+1}=1}\\ & \iff m+{\displaystyle \frac{m}{2}+\frac{m}{3}+\frac{m}{4}=1}\\ & \iff \left({\displaystyle \frac{12+6+4+3}{12}}\right)m=1\\ & \iff m={\displaystyle \frac{12}{25}}\\ \text{b}.& P(x\le 2)=P(x=0)+P(x=1)+P(x=2)\\ & \iff m+{\displaystyle \frac{m}{2}+\frac{m}{3}=1}\\ & \iff \left({\displaystyle \frac{6+3+2}{6}}\right)m={\displaystyle \frac{11}{6}m}\\ & \iff ={\displaystyle \frac{11}{6}\left({\displaystyle \frac{12}{25}}\right)=\frac{22}{25}}\end{array}\end{array}$

$\begin{array}{l}\\ 5.& \text{Diketahui fungsi}f(x)=\{\begin{array}{ll}{\displaystyle \frac{x}{6}}& \text{untuk}x=1,2,3\\ \\ 0& \text{untuk}x\text{yang lain}\end{array}\\ & \text{adalah suatu fungsi peluang/probabilitas}\\ & \text{dari pubah/variabel acak}X.\text{Tentukanlah}\\ & \text{a}.\text{distribusi peluangnya untuk}X\\ & \text{b}.P(X=2),P(X<3),\text{dan}P(X\ge 2)\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}\text{a}.& \text{Distribusi peluangnya adalah}:\\ & \begin{array}{|cccccccc|}\hline X=x& 1& 2& 3& 4& 5& \cdots & \text{Jumlah}\\ P(X=x)& {\displaystyle \frac{1}{6}}& {\displaystyle \frac{2}{6}}& {\displaystyle \frac{3}{6}}& 0& 0& 0& 1\\ \hline\end{array}\\ \text{b}.& \text{Karena}f(x)=\{\begin{array}{ll}{\displaystyle \frac{x}{6}}& \text{untuk}x=1,2,3\\ \\ 0& \text{untuk}x\text{yang lain}\end{array}\\ & \text{maka}\\ & \bullet P(X=2)={\displaystyle \frac{2}{6}}\\ & \bullet P(X<3)=P(X=1)+P(X=2)\\ & ={\displaystyle \frac{1}{6}+\frac{2}{6}}\\ & ={\displaystyle \frac{3}{6}=\frac{1}{2}}\\ & \bullet P(X\ge 2)=P(X=2)+P(X=3)\\ & ={\displaystyle \frac{2}{6}+\frac{3}{6}}\\ & ={\displaystyle \frac{5}{6}}\end{array}\end{array}$

$\begin{array}{l}\\ 6.& \text{Diketahui fungsi peluang variabel}X\\ & f(x)=\{\begin{array}{ll}{\displaystyle \frac{x+2}{14}}& \text{untuk}x=0,1,2,\text{dan}3\\ \\ 0& \text{untuk}x\text{yang lain}\end{array}\\ & \text{Tentukanlah}\\ & \text{a}.\text{bahwa}X\text{merupakan variabel acak diskrit}\\ & \text{b}.P(X=4),F(2),P(1<X\le 3),\\ & \text{dan}P(X\ge 1)\text{serta}P(|X-2|\le 1)\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}\text{a}.& \text{Distribusi peluangnya adalah}:\\ & \overline{)\begin{array}{cccccc}X=x& 0& 1& 2& 3& \text{Jumlah}\\ P(X=x)& {\displaystyle \frac{2}{14}}& {\displaystyle \frac{3}{14}}& {\displaystyle \frac{4}{14}}& {\displaystyle \frac{5}{14}}& 1\end{array}}\\ & \text{Karena}{\displaystyle \sum _{x=0}^{3}f(x)=1,\text{serta}}\\ & 0\le {\displaystyle \frac{2}{14},\frac{3}{14},\frac{4}{14},\frac{5}{14}<1.\text{Sehingga syarat}}\\ & 0\le f(x)<1\text{dan}\sum f(x)=1\mathbf{\text{terpenuhi}}\\ & \text{Jadi, terbukti}X\text{adalah variabel acak diskrit}\\ \text{b}.& \bullet P(X=4)=f(4)=0\\ & \bullet F(2)=P(X\le 2)\\ & =P(X=0)+P(X=1)+P(X=2)\\ & =f(0)+f(1)+f(2)\\ & ={\displaystyle \frac{2}{14}+\frac{3}{14}+\frac{4}{14}=\frac{9}{14}}\\ & \bullet P(1<X\le 3)=P(X=2)+P(X=3)\\ & =f(2)+f(3)={\displaystyle \frac{4}{14}+\frac{5}{14}={\displaystyle \frac{9}{14}}}\\ & \bullet P(X\ge 1)=f(1)+f(2)+f(3)\\ & ={\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}={\displaystyle \frac{12}{14}}}\\ & \bullet P(|X-2|\le 1)=P(-1\le X-2\le 1)\\ & =P(1\le X\le 3)\\ & =f(1)+f(2)+f(3)\\ & ={\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}={\displaystyle \frac{12}{14}}}\end{array}\end{array}$

$\begin{array}{l}\\ 7.& \text{Distribusipeluang acak X disajikan dalam tabel berikut}\\ & \begin{array}{|cccc|}\hline x& 2& 3& 4\\ f(x)& {\displaystyle \frac{1}{8}}& k+{\displaystyle \frac{1}{8}}& 2k\\ \hline\end{array}\\ & \text{Jika X merupakan variabel acak diskret, tentukanlah}\\ & \text{a}.\text{nilai textit{k}}\\ & \text{b}.\text{nilai}\text{P}(\text{X}\ge 3)-\text{F}(3)\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\text{a}.\sum f(x)& =f(2)+f(3)+f(4)=1\\ \iff & {\displaystyle \frac{1}{8}+k+\frac{1}{8}+2k=1}\\ \iff & 3k=1-{\displaystyle \frac{2}{8}=\frac{6}{8}}\\ \iff & k={\displaystyle \frac{2}{8}=\frac{1}{4}}\\ \text{b}.\text{P}(\text{X}\ge 3& )-\text{F}(3)=\text{P}(\text{X}\ge 3)-\text{P}(\text{X}\le 3)\\ & =f(3)+f(4)-(f(2)+f(3))\\ & =f(4)-f(2)\\ & =2\left({\displaystyle \frac{1}{4}}\right)-\frac{1}{8}\\ & ={\displaystyle \frac{4}{8}-\frac{1}{8}=\frac{3}{8}}\end{array}\end{array}$

DAFTAR PUSTAKA

1. Noormandiri. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
2. Kurnia, N., dkk. 2018. Jelajah Matematika SMA Kelas XII Peminatan MIPA. Bogor: YUDHISTIRA.