Contoh Soal Numerasi Lanjutan Persiapan Asesmen Nasional (AN)

$\text{CONTOH SOAL 6}$.

Perhatikan ilustrasi gambar berikut

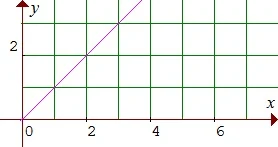
Sebuah titik (x,y) diambil secara acak dari dalam persegi panjang yang terbentuk dari titik (0,0), (4,0), (4,1) dan (1,0). Probabilitas x<y adalah ... .

$\begin{array}{l}\\ \text{A}.& {\displaystyle \frac{1}{8}}& & & \text{D}.& {\displaystyle \frac{1}{2}}\\ \\ \text{B}.& {\displaystyle \frac{1}{4}}& \text{C}.& {\displaystyle \frac{3}{8}}& \text{E}.& {\displaystyle \frac{3}{4}}\end{array}$.

$\text{SOLUSI SOAL 6}$.

Jika gambar diperjelas dengan kertas berpetak akan tampak dengan jelas luasnya, yaitu

Tampak Jelas bahwa luas daerah yang dibatasi oleh  $f(x)=y=x$ dengan $x<y$ adalah ${\displaystyle \frac{1}{2}}$.

Perhatikan ilustrasi berikut

Dan jelas juga bahwa total luas persegi pajang di atas adalah 4 satuan luas serta luas daerah. Sehingga probabilitas bahwa titik (x,y) yang dipilih secara acak pada persegi panjang di atas dengan x<y adalah:

$\begin{array}{rl}\text{Probabilitas}& ={\displaystyle \frac{\left({\displaystyle \frac{1}{2}}\right)}{4}}\\ & ={\displaystyle \frac{1}{8}}\end{array}$.

Jadi, opsi jawaban di atas adalah A.

$\text{CONTOH SOAL 7}$.

Perhatikan ilustrasi gambar berikut

Sebuah titik P akan dipilih secara acak dari bagian dalam sebuah segilima dengan koordinat titik sudut  $A(0,2)$, $B(4,0)$, $C(2\pi +1,1)$, $C(2\pi +1,4)$, dan  $E(0,4)$. Probabilitas bahwa  $\mathrm{\angle }APB$  sebuah sudut tumpul adalah ... .

$\begin{array}{l}\\ \text{A}.& {\displaystyle \frac{1}{5}}& & & \text{D}.& {\displaystyle \frac{3}{8}}\\ \\ \text{B}.& {\displaystyle \frac{1}{4}}& \text{C}.& {\displaystyle \frac{5}{16}}& \text{E}.& {\displaystyle \frac{1}{2}}\end{array}$.

$\text{SOLUSI SOAL 7}$.

Sebelumnya perlu dingat bahwa sudut tumpul adalah sudut yang lebih besar dari  ${90}^{\circ }$. Selanjutnya perhatikan gambar berikut

Gambar di atas menunjukkan sebuah titik P dengan  $\mathrm{\angle }APB={90}^{\circ }$. Dalam hal ini titik P terletak pada keliling dari setengah lingkaran dengan pusat lingkaran (2,1) terletak pada ruas garis AB dengan jari-jari

$\begin{array}{rl}r& =\sqrt{2^2+1^2}=\sqrt{5}\end{array}$. Dantitik yang berada di luar setengah lingkaran tetapi masih dalam segilima ABCDE tersebut akan memiliki  $\mathrm{\angle }APB<{90}^{\circ }$ dan titik-tik yang berada di dalam setengah lingkrang ini akan memiliki sudut  $\mathrm{\angle }APB>{90}^{\circ }$. Sehingga untuk menentukan probabilitas $\mathrm{\angle }APB$ tumpul adalah sama saja kita menentukan probabilitas untuk $\mathrm{\angle }APB>{90}^{\circ }$, yaitu:

$\begin{array}{rl}\text{Probabilitasnya}& ={\displaystyle \frac{\mathbf{\text{Luas setengah lingkaran}}}{\mathbf{\text{Luas segilima}}ABCDE}}\\ & ={\displaystyle \frac{{\displaystyle \frac{1}{2}\pi \times {\left(\sqrt{5}\right)}^2}}{(2\pi +1)\times 4-\left({\displaystyle \frac{1}{2}\times 2\times 4}\right)}}\\ & ={\displaystyle \frac{{\displaystyle \frac{1}{2}\left(5\pi \right)}}{8\pi }}\\ & ={\displaystyle \frac{5}{16}}\end{array}$.

$\text{CONTOH SOAL 8}$.

Gambar 0, 1, 2, dan 3 berturut-turut terdiri atas 1, 5, 13, dan 25 persegi satuan sebagaimana ilustrasi gambar berikut

Jika pola di atas berlanjut, maka persegi satuan pada gambar ke-100 adalah ... .

$\begin{array}{l}\\ \text{A}.& 10.401& & & \text{D}.& 39.801\\ \\ \text{B}.& 19.801& \text{C}.& 20.201& \text{E}.& 40.801\end{array}$.

$\text{SOLUSI SOAL 8}$.

Untuk memudahkan penghitungan persegi kecil, ada baiknya kita susun menjadi susunan persegi agak besar dengan melengkapkan persegi-persegi kecil dikeempat pojoknya sebagaimana ilustrasi berikut

Setelah ditambah kotak warna pink, maka perhitungan jumlah kotak warna hijau pada gambar ke-n akan semakin mudah, yaitu:

mulai dari gambar pertama atau suku ke-0, maka 

$\begin{array}{rl}{U}_n& =(2n+1{)}^2-4.{\displaystyle \frac{n(n+1)}{2}}\\ & =4n^2+4n+1-2n^2-2n\\ & =2n^2+2n+1\\ \text{ma}& \text{ka suku ke-100 (gambar ke-100)}\\ U_{100}& ={2.100}^2+2.100+1\\ & =20.201\end{array}$.

$\text{CONTOH SOAL 9}$.

Pada persegi panjang ABCD diketahui AD = 1, Titik P berada di ruas garis AB. Ruas garis DB dan DP membagi tiga sudut $\mathrm{\angle }ADC$, maka keliling $△BDP$ adalah ... .

$\begin{array}{l}\\ \text{A}.& 3+{\displaystyle \frac{\sqrt{3}}{3}}& & & \text{D}.& {\displaystyle \frac{3+3\sqrt{5}}{2}}\\ \\ \text{B}.& 2+{\displaystyle \frac{4\sqrt{3}}{3}}& \text{C}.& 2+2\sqrt{2}& \text{E}.& 2+{\displaystyle \frac{5\sqrt{3}}{3}}\end{array}$.

$\text{SOLUSI SOAL 9}$.

Karena $\overline{DB}\text{dan}\overline{DP}$ membagi sudut ADC menjadi tiga bagian yang sama besar, maka 

$\mathrm{\angle }CBD=\mathrm{\angle }BDP=\mathrm{\angle }PDA={30}^{\circ }$,

maka

$\begin{array}{rl}AP& =AD\tan \mathrm{\angle }PAD=1.\tan {30}^{\circ }={\displaystyle \frac{1}{3}\sqrt{3}}\\ DP& ={\displaystyle \frac{AD}{\cos {30}^{\circ }}={\displaystyle \frac{1}{{\displaystyle \frac{1}{2}\sqrt{3}}}={\displaystyle \frac{2}{\sqrt{3}}=\frac{2}{3}\sqrt{3}}}}\\ AB& =AD\mathrm{\angle }BDA=1.\tan {60}^{\circ }=1.\sqrt{3}=\sqrt{3}\\ DB& =\sqrt{D{A}^2+A{B}^2}=\sqrt{1+{\left(\sqrt{3}\right)}^2}\\ & =\sqrt{1+3}=\sqrt{4}=2\end{array}$.

Sehingga keliling  

$\begin{array}{rl}△BDP& =BD+DP+PB\\ & =2+{\displaystyle \frac{2}{3}\sqrt{3}+(\sqrt{3}-{\displaystyle \frac{1}{3}\sqrt{3}})}\\ & =2+{\displaystyle \frac{4}{3}\sqrt{3}}\end{array}$.

Jadi, jawaban yang tepat adalah opsi B.

$\text{CONTOH SOAL 10}$.

Manakah di antara kerucut berikut ini yang terbentuk dari sektor lingkaran bersudut ${252}^{\circ }$ dan jari-jari 10 dengan cara menyambungkan kedua sisinya yang lurus?

A.  

B. 

. 

C. 

 

D. 

E. 

$\text{SOLUSI SOAL 10}$.

Keliling lingkaran yang bagiannya terpotong adalah  $2\pi \times 10=20\pi$ dan bagian dari luas lingkaran yang akan menjadi selimut kerucut adalah:

${\displaystyle \frac{{252}^{\circ }}{{360}^{\circ }}\times 20\pi =14\pi }$. Perhatikan gambar berikut

Sehingga keliling lingkaran sebagai alas kerucut adalah $14\pi$. 

Dari fakta ini, maka lingkaran sebagai alas kerucut akan memiliki jari-jari:

$\begin{array}{rl}{L}_{⨀\text{alas}}& =2\pi r\\ r& ={\displaystyle \frac{L_{⨀\text{alas}}}{2\pi }}\\ & ={\displaystyle \frac{14\pi }{2\pi }}\\ & =7\end{array}$

Jadi, pilihan jawaban yang tepat adalah gambar opsi C.

DAFTAR PUSTAKA

1. Faires, J. Douglas. 2006. Langkah Pertama Menuju Olimpiade Matematika Menggunakan Kompetisi Matematika Amerika, ed. ke-3. Terjemahan: Tim Penerjemah. Pakar Raya, Bandung. 307 hal.