PAS MATEMATIKA BLOG: binomial distribution

Tampilkan postingan dengan label binomial distribution. Tampilkan semua postingan

Distribusi Binomial

Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 3)

$\begin{array}{ll}\\ 11.&\textrm{Suatu tes dengan pilihan jawaban }\\ &\textrm{benar-salah berjumlah 8 soal}\\ &\textrm{Supaya lulus tes, peserta diharuskan }\\ &\textrm{menjawab benar minimal 50}\%\\ &\textrm{Peluang seseorang dianggap lulus tes }\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad \displaystyle 0,2188\qquad\qquad\quad\qquad \quad\textrm{d}.\quad 0,6367\\ &\textrm{b}.\quad \displaystyle \color{red}0,2734\quad \: \color{black}\textrm{c}.\quad 0,3633\quad\quad \textrm{e}.\quad 0,7266\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang benar}=\displaystyle \frac{1}{2},\qquad \textrm{dan}\: \: \\ &q=\textbf{Peluang Salah}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P(X=x)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &P\left ( X=50\%(8)=4 \right )=\begin{pmatrix} 8\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{4}\times \left ( \frac{1}{2} \right )^{8-4}\\ &\qquad =\displaystyle \frac{8!}{4!\times 4!}\left ( \displaystyle \frac{1}{2} \right )^{4+4}\\ &\qquad =70\times \displaystyle \frac{1}{256}\\ &\qquad =\color{red}0,2734 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Sebuah kotak berisi 20 bola dengan }\\ &\textrm{rincian 12 boal berwarna kuning dan }\\ &\textrm{sisanya berwarna hijau. Dari kotak} \\ &\textrm{diambil 6 bola secara acak. Peluang}\\ &\textrm{terambil 4 bola hijau adalah}....\\ &\textrm{a}.\quad \displaystyle 0,1238\quad\quad\qquad\qquad \qquad\textrm{d}.\quad 0,8132\\ &\textrm{b}.\quad \color{red}\displaystyle 0,1382\: \quad \color{black}\textrm{c}.\quad 0,3110\quad\quad \textrm{e}.\quad 0,9590\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang bola kuning}\\ &\: \: =\displaystyle \frac{C_{1}^{12}}{C_{1}^{20}}=\displaystyle \frac{12}{20}=\frac{3}{5},\\ &q=\textbf{Peluang bola hijau}=1-\displaystyle \frac{3}{5}=\frac{2}{5}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &f(4)=\begin{pmatrix} 6\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{2}{5} \right )^{4}\times \left ( \frac{3}{5} \right )^{6-4}\\ &\qquad =\displaystyle \frac{6!}{2!\times 4!}\left ( \displaystyle \frac{16}{625} \right )\times \left ( \displaystyle \frac{9}{25} \right )\\ &\qquad =15\times \displaystyle \frac{144}{15625}=\frac{2160}{15625}\\ &\qquad =\color{red}0,1382 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 13.&\textrm{Dua dadu dilambungkan 5 kali}\\ &\textrm{Peluang muncul pasangan mata dadu}\\ &\textrm{berjumlah 4 sampai dengan 7 }\\ &\textrm{sebanyak 4 kali adalah}\: ....\\ &\textrm{a}.\quad \displaystyle 0,1503\: \: \: \: \qquad\qquad\quad\quad \quad\textrm{d}.\quad 0,1583\\ &\textrm{b}.\quad \displaystyle 0,1553\quad \textrm{c}.\quad \color{red}0,1563\quad\quad \color{black}\textrm{e}.\quad 0,1593\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang mata dadu berjumlah 4 sampai 7}\\ &\: \: =\displaystyle \frac{18}{36}=\frac{1}{2},\qquad \textrm{dan}\: \: \\ &q=\textbf{Peluang bola hijau}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &f(4)=P\left ( X=4 \right )=\begin{pmatrix} 5\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{4}\times \left ( \frac{1}{2} \right )^{5-4}\\ &\qquad =\displaystyle \frac{5!}{1!\times 4!}\left ( \displaystyle \frac{1}{16} \right )\times \left (\frac{1}{2} \right )\\ &\qquad =5\times \displaystyle \frac{1}{32}=\frac{5}{32}\\ &\qquad =\color{red}0,1563 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 14.&\textrm{Peluang seseorang sembih dari }\\ &\textrm{penyakit jantung adalah 0,6}\\ &\textrm{Jika 7 orang penderita ini menjalani }\\ &\textrm{operasi, maka peluang 3 sampai}\\ &\textrm{6 orang sembuh adalah}... .\\ &\textrm{a}.\quad \displaystyle 0,0629\qquad\qquad\quad\qquad \quad\textrm{d}.\quad \color{red}0,6822\\ &\textrm{b}.\quad \displaystyle 0,2613\quad \textrm{c}.\quad 0,2898\quad\quad \: \textrm{e}.\quad 0,9720\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang sembuh}=0,6,\qquad \textrm{maka}\: \: \\ &q=\textbf{Peluang tidak sembuh}=1-0,6=0,4\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &P\left ( 3\leq X\leq 6 \right )=P\left ( X\leq 6 \right )-P\left ( X\leq 3 \right )\\ &=C_{4}^{7}(0,6)^{4}(0,4)^{3}+C_{5}^{7}(0,6)^{5}(0,4)^{2}+C_{6}^{7}(0,6)^{6}(0,4)^{1}\\ &=35\times 0,0082944+21\times 0,0124416+7\times 0,0186624\\ &=0,290304+0,2612736+0,1306368\\ &=\color{red}0,6822144 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 15.&\textrm{Peluang seseorang mendapatkan reaksi }\\ &\textrm{buruk setelah disuntik adalah 0,0005}\\ &\textrm{Dari 4000 orang yang disuntik, maka }\\ &\textrm{peluang seseorang mendapatkan reaksi}\\ & \textrm{ada 2 orang adalah}.....\\ &\textrm{a}.\quad \displaystyle \frac{1}{2}e^{-2}\\ &\textrm{b}.\quad e^{-2}\\ &\textrm{c}.\quad \color{red}2e^{-2}\\ &\textrm{d}.\quad \displaystyle \frac{1}{2}e^{2}\\ &\textrm{e}.\quad 2e^{2}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Di atas adalah contoh kasus }\\ &\textrm{permasalahan}\: \: \textbf{Distribusi Poisson}\\ &P\left ( X=x \right )=f(x)=\left\{\begin{matrix} \displaystyle \frac{e^{-\lambda }.\lambda ^{x}}{x!}\: \: ,\: \: x=0,1,2,3,\cdots \\\ 0,\quad \textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{matrix}\right.\\ &P\left ( X=2 \right )=\displaystyle \frac{e^{-np}.(np)^{2}}{2!}\\ &\qquad =\displaystyle \frac{e^{-(4000.0,0005)}.(4000.0,0005)^{2}}{2!}\\ &\qquad =\displaystyle \frac{e^{-2}.2^{2}}{2}\\ &\qquad =\color{red}2e^{-2} \end{aligned} \end{array}$

Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 2)

$\begin{array}{ll}\\ 6.&\textrm{Pengundian terhadap mata uang }\\ &\textrm{yang homogen sebanyak 10 kali}\\ &\textrm{Peluang untuk mendapatkan 6 }\\ &\textrm{muka angka adalah}\: ....\\ &\textrm{a}.\quad 0,1172\\ &\textrm{b}.\quad \color{red}0,2051\\ &\textrm{c}.\quad 0,2461\\ &\textrm{d}.\quad 0,2651\\ &\textrm{e}.\quad 0,2852\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang Angka}=\displaystyle \frac{1}{2},\quad \textrm{dan}\: \: \\ &q=\textbf{Bukan Angka}\\ &\: \: =\textbf{Peluang Gambar}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P(x;n;p)=P(X=x)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &\textrm{maka}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &f(6)=P\left ( X=6 \right )=\begin{pmatrix} 10\\ 6 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{6}\times \left ( \frac{1}{2} \right )^{10-6}\\ &\qquad =\displaystyle \frac{10!}{6!\times 4!}\left ( \displaystyle \frac{1}{2} \right )^{6+4}\\ &\qquad =210\times \displaystyle \frac{1}{1024}\\ &\qquad =\color{red}0,2051 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Pada pengundian terhadap mata uang identik},\\ &\textrm{sebanyak 10 kali, peluang distribusi binomial} \\ &\textrm{untuk mendapatkan 7 muka gambar adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.\quad \displaystyle 0,2653&&\textrm{d}.\quad \displaystyle 0,7522\\ \textrm{b}.\quad \displaystyle \color{red}0,1172&\textrm{c}.\quad \displaystyle 0,2653&\textrm{e}.\quad 0,2422 \end{array}\\\\ &\textrm{Jawab}:\\ &\textrm{Uraian berikut sekaligus tambahan}\\ &\textrm{penjelasan pada uraian jawaban}\\ &\color{blue}\textrm{soal no. 6 di atas}\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &\textrm{Ingat sebuah koin ada 2 muka}\\ &\textrm{yaitu muka gambar (G) dan angka (A)}\\ &\color{red}\textrm{misalkan}\\ &A=\textrm{kejadian muncul muka gambar}\\ &\textrm{maka peluangnya adalah}\: \: \displaystyle \frac{1}{2}\\ &\textrm{Selanjutnya di sini disimbolkan dengan}\: \: \: \color{blue}p=\displaystyle \frac{1}{2}\\ &\color{red}\textrm{Demikian juga misalkan}\\ &B=\textrm{kejadian muncul muka angka}\\ &\textrm{maka peluang juga}\: \displaystyle \frac{1}{2}\\ &\textrm{Di sini dituliskan dengan}\: \: \: \color{blue}q=\displaystyle \frac{1}{2}\\ f(7)&=\begin{pmatrix} 10\\ 7 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{7}\left ( \displaystyle \frac{1}{2} \right )^{10-7}\\ &=\begin{pmatrix} 10\\ 7 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{7}\left ( \displaystyle \frac{1}{2} \right )^{3}\\ &=\displaystyle \frac{10!}{7!\times (10-7)!}\left ( \displaystyle \frac{1}{2} \right )^{7+3}\\ &=\displaystyle \frac{10.9.8.\not{7!}}{\not{7!}.3.2.1}\left ( \displaystyle \frac{1}{1024} \right ) \\ &=\color{red}0,1172 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Sebuah uang logam dilempar sebanyak 8}\\ &\textrm{kali. Peluang muncul gambar sebanyak}\\ &\textrm{5 kali adalah}\: ....\\ &\begin{array}{llllllll}\\ \textrm{a}.&\displaystyle \frac{3}{32}&&&\textrm{d}.&\displaystyle \color{red}\frac{7}{32}\\\\ \textrm{b}.&\displaystyle \frac{4}{32}&\textrm{c}.&\displaystyle \frac{5}{32}&\textrm{e}.&\displaystyle \frac{9}{32} \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(5)&=\begin{pmatrix} 8\\ 5 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{5}\left ( \displaystyle \frac{1}{2} \right )^{8-5}\\ &=\begin{pmatrix} 8\\ 5 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{5}\left ( \displaystyle \frac{1}{2} \right )^{3}\\ &=\displaystyle \frac{8!}{5!\times (8-5)!}\left ( \displaystyle \frac{1}{2} \right )^{5+3}\\ &=\displaystyle \frac{8.7.6.5!}{5!.3.2.1}\left ( \displaystyle \frac{1}{256} \right ) \\ &=\displaystyle \frac{8.7}{256}\\ &=\color{red}\displaystyle \frac{7}{32} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 9.&\textrm{Pada pelemparan sebuah koin sebanyak 4 kali}\\ &\textrm{Peluang didapatkannya dua angka pada} \\ &\textrm{pelemparan tersebut adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.\quad \displaystyle 0,123&&\textrm{d}.\quad \displaystyle 0,232\\ \textrm{b}.\quad \displaystyle 0,135&\textrm{c}.\quad \displaystyle 0,154&\textrm{e}.\quad \color{red}0,375 \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(2)&=\begin{pmatrix} 4\\ 2 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{2}\left ( \displaystyle \frac{1}{2} \right )^{4-2}\\ &=\begin{pmatrix} 4\\ 2 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{2}\left ( \displaystyle \frac{1}{2} \right )^{2}\\ &=\displaystyle \frac{4!}{2!\times (4-2)!}\left ( \displaystyle \frac{1}{2} \right )^{2+2}\\ &=\displaystyle \frac{4.3.2!}{2!.2.1}\left ( \displaystyle \frac{1}{16} \right ) \\ &=\color{red}0,375 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 10.&\textrm{Dari data survei didapatkan bahwa}\\ &\textrm{satu dari lima orang telah berkunjung}\\ &\textrm{ke dokter dalam sembarang bulan yang}\\ &\textrm{ditanyakan. Jika 10 orang dipilih secara}\\ &\textrm{acak, peluang 3 orang telah berkunjung}\\ &\textrm{ke dokter bulan lalu adalah}\: ....\\ &\begin{array}{llllllll}\\ \textrm{a}.&\displaystyle 0,125&&&\textrm{d}.&\displaystyle \color{red}0,201\\\\ \textrm{b}.&\displaystyle 0,174&\textrm{c}.&\displaystyle 0,182&\textrm{e}.&\displaystyle 0,423 \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(3)&=\begin{pmatrix} 10\\ 3 \end{pmatrix}\left ( \displaystyle \frac{1}{5} \right )^{3}\left ( \displaystyle \frac{4}{5} \right )^{10-3}\\ &=\begin{pmatrix} 10\\ 3 \end{pmatrix}\left ( \displaystyle \frac{1}{5} \right )^{3}\left ( \displaystyle \frac{4}{5} \right )^{7}\\ &=\displaystyle \frac{10!}{3!\times 7!}\left ( \displaystyle \frac{1}{125} \right )\left ( \displaystyle \frac{4^{7}}{5^{7}} \right )\\ &=\cdots \\ &=\color{red}\displaystyle 0,201 \end{aligned} \end{array}$

Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 1)

$\begin{array}{ll}\\ 1.&\textrm{Manakah yang merupakan data diskrit dari pernyataan berikut}\\ &\textrm{a}.\quad \textrm{Suhu Badan Anton ketika sakit mencapai}\: \: 40^{\circ}C\\ &\textrm{b}.\quad \textrm{Kecepatan mobil yang sedang melaju adalah}\: \: 100\: \: km/jam\\ &\textrm{c}.\quad \textrm{Tinggi tiang bendaera di madrasah Budi adalah 4 m}\\ &\textrm{d}.\quad \color{red}\textrm{Jumlah guru yang mengajar di MA Futuhiyah }\\ &\qquad \color{red}\textrm{sebanyak 30 orang}\\ &\textrm{e}.\quad \textrm{Berat bayi yang baru lahir adalah 3.500 gram}\\\\ &\textrm{Jawab}:\\ &\textrm{Alasannya dikarena hasil mencacah} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Jika Anda mengumpulkan nilai raport}\\ &\textrm{teman-teman sekelas Anda untuk pelajaran}\\ &\textrm{ matematika, maka data yang Anda peroleh }\\ &\textrm{adalah}....\\ &\textrm{a}.\quad \color{red}\textrm{data diskrit}\\ &\textrm{b}.\quad \textrm{data kontinu}\\ &\textrm{c}.\quad \textrm{data kualitatif}\\ &\textrm{d}.\quad \textrm{Populasi}\\ &\textrm{e}.\quad \textrm{Sampel}\\\\ &\textrm{Jawab}:\\ &\textrm{Dengan catatan nilainya cacah} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Ukuran yang dihitung dari seluruh data }\\ &\textrm{dalam populasi adalah}\: ....\\ &\textrm{a}.\quad \textrm{data kuantitatif}\\ &\textrm{b}.\quad \textrm{data kualitatif}\\ &\textrm{c}.\quad \textrm{Statistik}\\ &\textrm{d}.\quad \textrm{Statistika}\\ &\textrm{e}.\quad \color{red}\textrm{Parameter}\\\\ &\textrm{Jawab}:\\ &\textrm{Parameter adalah ukuran dari }\\ &\textrm{seluruh data atau populasi} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui distribusi peluang suatu }\\ &\textrm{variabel acak diskrit sebagai berikut}\\ &\begin{array}{|c|c|c|c|c|}\hline x&0&1&2&3\\\hline f(x)&m&0,26&3m&0,42\\\hline \end{array}\\ &\textrm{Peluang nilai X minimal berharga 2 adalah}\\ &\textrm{a}.\quad 0,24\\ &\textrm{b}.\quad 0,34\\ &\textrm{c}.\quad 0,42\\ &\textrm{d}.\quad 0,58\\ &\textrm{e}.\quad \color{red}0,66\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}\: \: X\: \: \textrm{adalah variabel }\\ &\textrm{acak diskrit, maka}\: \: \sum f(x)=1\\ &F(c)=P(X\leq c)=\displaystyle \sum_{x=0}^{x=c}f(x)\\ &=f(0)+f(1)+f(2)+f(3)+\cdots +f(c)=1\\ &\textrm{dalam hal soal}\: \textrm{di atas, maka kita tentukan}\\ &\textrm{nilai}\: \: \color{blue}m\: \: \color{black}\textrm{dulu}\\ &F(3)=P(X\leq 3)=\displaystyle \sum_{x=0}^{x=3}f(x)\\ &=f(0)+f(1)+f(2)+f(3)=1\\ &1=m+0,26+3m+0,42=4m+0,68\\ &4m=1-0.68=0,32\\ &m=0.08, \qquad \textrm{sehingga}\\ &P(2\leq X\leq 3)=f(2)+f(3)=3m+0,42\\ &=3(0,08)+0,42=0,24+0,42=\color{red}0,66 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Diketahui fungsi peluang suatu }\\ &\textrm{variabel acak kontinu adalah}\\ &f(y)=\left\{\begin{matrix} 0,\quad \textrm{untuk \textit{y} yang lain}\\\\ \displaystyle \frac{2y+k}{50},\: \: \textrm{untuk}\: \: 0\leq y\leq 5 \end{matrix}\right.\\ &\textrm{Nilai}\: \: P\left ( \left | Y-1 \right |\leq 2 \right )\: \: \textrm{adalah}....\\ &\textrm{a}.\quad \displaystyle \frac{7}{25}\qquad\qquad\qquad\qquad \textrm{d}.\quad \frac{14}{25}\\\\ &\textrm{b}.\quad \displaystyle \frac{9}{25}\qquad \textrm{c}.\quad \color{red}\frac{12}{25}\qquad\quad \color{black}\textrm{e}.\quad \frac{18}{25}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\int_{0}^{5}\displaystyle \frac{2y+k}{50}\: dy=1\\ &1=\int_{0}^{5}\displaystyle \frac{2y+k}{50}\: dy\\ &50=\int_{0}^{5}(2y+k)dy\\ &50=y^{2}+ky|_{0}^{5}=5^{2}+5k=25+5k\\ &k=5\\ &\color{blue}P(\left | Y-1 \right |\leq 2)=P\left ( -2\leq Y-1\leq 2 \right )\\ &=P\left ( -1\leq Y\leq 3 \right )\\ &=f(-1)+f(0)+f(1)+f(2)+f(3)\\ &=\int_{0}^{3}\left ( \displaystyle \frac{2y+5}{50} \right )dy\\ &=\displaystyle \frac{1}{50}\left ( y^{2}+5y \right )|_{0}^{3}\\ &=\displaystyle \frac{1}{50}\left ( 9+15 \right )=\displaystyle \frac{24}{50}=\color{red}\frac{12}{25} \end{aligned} \end{array}$

Distribusi Binomial

$\color{blue}\begin{aligned}\textrm{E}.\quad&\textrm{Binomial Newton} \end{aligned}$

$\color{blue}\begin{aligned}\textrm{E. 1}.\quad&\textrm{Binomial Newton} \end{aligned}$

$\begin{aligned}&\textrm{Perhatikanlah susunan bilangan berikut}\\\\ &\begin{array}{|c|l|}\hline &\\ 1=C_{0}^{\color{red}1}\quad 1=C_{1}^{\color{red}1}&(a+b)^{\color{red}1}\\ &\\ 1=C_{0}^{\color{red}2}\quad 2=C_{1}^{\color{red}2}\quad 1=C_{2}^{\color{red}2}&(a+b)^{\color{red}2}\\ &\\ 1=C_{0}^{\color{red}3}\quad 3=C_{1}^{\color{red}3}\quad 3=C_{2}^{\color{red}3}\quad 1=C_{3}^{\color{red}3}&(a+b)^{\color{red}3}\\ &\\ 1=C_{0}^{\color{red}4}\quad 4=C_{1}^{\color{red}4}\quad 6=C_{2}^{\color{red}4}\quad 4=C_{3}^{\color{red}4}\quad 1=C_{4}^{\color{red}4}&(a+b)^{\color{red}4}\\ \vdots &\: \: \quad\vdots \\ dst&(a+b)^{\color{red}\cdots }\\ &\\ \vdots&\: \: \quad\vdots \\ &(a+b)^{\color{red}n}\\\hline \end{array}\\\\ &\textrm{Susunan bilangan-bilangan di atas selanjutnya}\\ &\textrm{dinamakan}\: \: \: \textbf{Segitiga Pascal}\\ & \end{aligned}$

$\begin{aligned}&\textrm{Bilangan}\: \: C_{r}^{n}=\begin{pmatrix} n\\ r \end{pmatrix}\: \: \textrm{merupakan koefisien}\\ &\textrm{dari binomial}\: \: (a+b)^{n}\\ &\textrm{Selanjutnya perhatikanlah bahwa untuk}\\ &n=1,2,3,4,\cdots \: \: \: \textrm{berlaku}\\ &\color{red}\begin{aligned}(a+b)^{n}\color{black}=\, &\color{red}C_{0}^{n}a^{n}b^{0}+C_{1}^{n}a^{n-1}b^{1}+C_{2}^{n}a^{n-2}b^{2}\\ &+C_{3}^{n}a^{n-3}b^{3}+\cdots +C_{n-3}^{n}a^{3}b^{n-3}\\ &+C_{n-2}^{n}a^{2}b^{n-2}+C_{n-1}^{n}a^{1}b^{n-1}+C_{n}^{n}a^{0}b^{n}\\ &\color{black}=\displaystyle \sum_{r=0}^{n}C_{r}^{\color{red}n}a^{\color{red}n\color{black}-r}b^{r} \end{aligned}\\ & \end{aligned}$

$\color{blue}\textrm{E. 2 Perluasan Binomial Newton}$

$\begin{aligned}&\textrm{Untuk bilangan real}\: \: n\: \: \textrm{dan bilangan}\\ &\textrm{non negatif}\: \: r,\: \: \textrm{serta}\: \: \left | A \right |<1,\: \textrm{berlaku}:\\ &(1+A)^{n}=\displaystyle \sum_{r=0}^{n}C_{r}^{n}A^{r} \end{aligned}$

$\color{blue}\textrm{E. 3 Teorema Multinomial}$

Pada bentuk multinomial dengan ekspresi $(x_{1}+x_{2}+x_{3}+\cdots +x_{r})^{n}$ dengan n dan r bilangan bulat positif, maka koefisien dari $\color{red}x_{1}^{n_{1}}x_{2}^{n_{2}}x_{3}^{n_{3}}\cdots x_{r}^{n_{r}}$ adalah $\displaystyle \frac{n!}{n_{1}!n_{2}!n_{3}!\cdots n_{r}!}$ dinotasikan dengan $\begin{pmatrix} n\\\\ n_{1},n_{2},n_{3},\cdots ,n_{r} \end{pmatrix}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Misalkan untuk}\: \: n\: \: \textrm{bilangan bulat}\\ &\textrm{Positif. Tunjukklan bahwa}\\ &\textrm{a}.\quad (1+x)^{n}=\displaystyle \sum_{r=0}^{n}C_{r}^{n}x^{r}=\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}x^{r}\\ &\textrm{b}.\quad \begin{pmatrix} n\\ 0 \end{pmatrix}+\begin{pmatrix} n\\ 1 \end{pmatrix}+\begin{pmatrix} n\\ 2 \end{pmatrix}+\cdots +\begin{pmatrix} n\\ n \end{pmatrix}=2^{n}\\\\ &\textbf{Bukti}\\ &\color{red}\begin{aligned}\color{black}\textrm{a}.\quad(1+x)&^{n}\\ \color{black}=\, &\color{red}C_{0}^{n}1^{n}x^{0}+C_{1}^{n}1^{n-1}x^{1}+C_{2}^{n}1^{n-2}x^{2}\\ &+C_{3}^{n}1^{n-3}x^{3}+\cdots +C_{n-3}^{n}1^{3}x^{n-3}\\ &+C_{n-2}^{n}1^{2}x^{n-2}+C_{n-1}^{n}1^{1}x^{n-1}+C_{n}^{n}1^{0}x^{n}\\ =\, &\color{red}C_{0}^{n}+C_{1}^{n}x+C_{2}^{n}x^{2} +C_{3}^{n}x^{3}+\cdots \\ &+C_{n-3}^{n}x^{n-3} +C_{n-2}^{n}x^{n-2}+C_{n-1}^{n}x^{n-1}\\ &+C_{n}^{n}x^{n}\\ \color{black}\textrm{atau}&\: \color{black}\textrm{dengan bentuk lain}\\ =\, &\begin{pmatrix} n\\ 0 \end{pmatrix}+\begin{pmatrix} n\\ 1 \end{pmatrix}x+\begin{pmatrix} n\\ 2 \end{pmatrix}x^{2}+\begin{pmatrix} n\\ 3 \end{pmatrix}x^{3}\\ &+\cdots +\begin{pmatrix} n\\ n-3 \end{pmatrix}x^{n-3}+\begin{pmatrix} n\\ n-2 \end{pmatrix}x^{n-2}\\ &+\begin{pmatrix} n\\ n-1 \end{pmatrix}x^{n-1}+\begin{pmatrix} n\\ n \end{pmatrix}x^{n}\\ \color{black}=&\color{black}\displaystyle \sum_{r=0}^{n}\begin{pmatrix} \color{red}n\\ r \end{pmatrix}x^{r} \end{aligned}\\ &\color{red}\begin{aligned}\color{black}\textrm{b}.\quad(1+x)&^{n}\: \: \color{black}\textrm{lihat jawaban poin}\: \: a,\: \: \textrm{saat}\: \: \color{blue}x=1\\ \color{black}(1+1)&^{n}\color{red} \color{black}=\color{red}\begin{pmatrix} n\\ 0 \end{pmatrix}+\begin{pmatrix} n\\ 1 \end{pmatrix}1+\begin{pmatrix} n\\ 2 \end{pmatrix}1^{2}+\begin{pmatrix} n\\ 3 \end{pmatrix}1^{3}\\ &+\cdots +\begin{pmatrix} n\\ n-3 \end{pmatrix}1^{n-3}+\begin{pmatrix} n\\ n-2 \end{pmatrix}1^{n-2}\\ &+\begin{pmatrix} n\\ n-1 \end{pmatrix}1^{n-1}+\begin{pmatrix} n\\ n \end{pmatrix}1^{n}\\ \color{black}(2)&^{n}\color{red} \color{black}=\color{red}\begin{pmatrix} n\\ 0 \end{pmatrix}+\begin{pmatrix} n\\ 1 \end{pmatrix}+\begin{pmatrix} n\\ 2 \end{pmatrix}+\begin{pmatrix} n\\ 3 \end{pmatrix}\\ &+\cdots +\begin{pmatrix} n\\ n-1 \end{pmatrix}+\begin{pmatrix} n\\ n \end{pmatrix}\\ \color{black}=&\color{black}\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}\\ \color{black}\textrm{Sehing}&\color{black}\textrm{ga}\\ 2^{n}&=\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Misalkan untuk}\: \: n\: \: \textrm{bilangan bulat}\\ &\textrm{Positif. Tunjukklan bahwa}\\ & \begin{pmatrix} n\\ 0 \end{pmatrix}-\begin{pmatrix} n\\ 1 \end{pmatrix}+\begin{pmatrix} n\\ 2 \end{pmatrix}-\cdots +(-1)^{n}\begin{pmatrix} n\\ n \end{pmatrix}=0\\\\ &\textbf{Bukti}\\ &\textrm{Sebelumnya diketahui bahwa}\\ &\begin{aligned}&(a+b)^{n}=\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}a^{n-r}b^{r}\\ &\qquad\qquad\qquad \color{blue}\textrm{atau}\\ &\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}a^{n-r}b^{r}=(a+b)^{n}\\ &\blacklozenge \quad \textrm{saat}\: \: \color{blue}a=b=1,\: \: \color{black}\textrm{maka}\\ &\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}1^{n-r}1^{r}=(1+1)^{n}\\ &\Leftrightarrow \displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}=2^{n}\: ...\: (\color{red}\textrm{bukti no. 1.b})\\ &\blacklozenge \quad \textrm{saat}\: \: \color{blue}a=1\: \&\: b=-1\: \: \color{black}\textrm{maka}\\ &\displaystyle \sum_{r=0}^{n}\begin{pmatrix} n\\ r \end{pmatrix}1^{n-r}(-1)^{r}=(1-1)^{n}=0\\ &\textrm{Sehingga}\\ &\begin{pmatrix} n\\ 0 \end{pmatrix}-\begin{pmatrix} n\\ 1 \end{pmatrix}+\begin{pmatrix} n\\ 2 \end{pmatrix}-\cdots +(-1)^{n}\begin{pmatrix} n\\ n \end{pmatrix}=0\quad \blacksquare \end{aligned} \end{array}$

$\color{blue}\begin{aligned}\textrm{E}.\quad&\textrm{Distribusi Binomial} \end{aligned}$

Perhatikan materi Binomial Newton di atas berkaitan dengan distribusi binomial. Misalkan suatu kejadian yang hanya memberikan dua hasil saja $\color{red}a$ dan $\color{red}b$ saja seperti melambungkan sebuah uang koin yang akan menghasilkan 2 hasil saja yang mungkin, yaitu antara sisi gambar $\color{red}G$ atau muncul sisi angka $\color{red}A$ atau pada contoh lainnya adalah ketika seseorang yang menunggu hasil hasil ujian yang jelas hasilnya kemungkinannya cuma dua, yaitu lulus atau tidak lulus.

Percobaan acak yang hanya memberikan 2 hasil saja disebut percobaan $\color{red}Bernoulli$. Selanjujtnya percobaan Bernoulli yang dilakukan sebanyak $\color{blue}n$ kali dinamakan dengan $\color{red}\textrm{percobaan}\: \textrm{Binomial}$.

Variabel acak $\color{red}X$ yanmg mana nilai-nilainya ditentukan oleh hasil dari percobaan binomial disebut sebagai Variabel Acak Binomial.

Berikut ciri-ciri percobaan binomial

Percobaan dilakukan secara berulang sebanyak $\color{red}n$ kali, dengan $\color{red}n$ bilangan bulat positif
Setiap percobaan memiliki dua macam hasil saja dan saling berkomplemen, yaitu kejadian yang diharapkan (disebut sukses) dan kejadian yang tidak diharapkan (disebut tidak sukses)
Peluang setiap kejadian bersifat tetap untuk setiap percobaan dan jumlah peluangnya baik sukses maupun yang tidak sukses sama dengan 1. Misalkan peluang suksesny adalah $\color{red}p$, maka peluang gagalnya adalah $\color{red}q=1-p$
Setiap percobaan bebas $\color{red}(independent)$ satu sama lainnya, artinya hasil percobaan yang satu tidak mempengaruhi percobaan yang lain.

Secara umum rumus fungsi $\color{red}\textrm{distribusi binomial}$ adalah:

$\begin{aligned}&f(x)=P(x;n;p)=\color{red}C(n,x)p^{x}q^{n-x}\color{black}=\color{red}\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &\textbf{Keterangan}:\\ &\bullet \: C(n,x)=\begin{pmatrix} n\\ x \end{pmatrix}=\color{blue}\textrm{koefisien bibonial}\\ &\bullet \: x=\textrm{banyak kejadian yang diharapkan},\\ &\quad\qquad \textrm{dengan nilai}\: \: x=0,1,2,3,\cdots ,n\\ &\bullet \: p=\textrm{peluang kejadian yang diharapkan}\\ &\bullet \: q=\textrm{peluang kejadian yang tidak diharapkan} \end{aligned}$

Jika rumus dari fungsi peluang di atas dijabarkan akan menjadi berupa bentuk penjumlahan, maka

$\begin{aligned}F(t)&=P(X\leq t)\\ &=\displaystyle \sum_{x=0}^{x=t}\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &=\begin{pmatrix} n\\ 0 \end{pmatrix}p^{0}q^{n-0}+\begin{pmatrix} n\\ 1 \end{pmatrix}+p^{1}q^{n-1}+\begin{pmatrix} n\\ 2 \end{pmatrix}p^{2}q^{n-2}+\cdots +\begin{pmatrix} n\\ t \end{pmatrix}p^{t}q^{n-t} \end{aligned}$

Dan rumus di atas karena tidak sepenuhnya sampai $\color{red}n$ , maka akan diperoleh fungsi binomial. kumulatif.

Hasil perhitungan $\color{red}f(x)=P(x;n;p)$ juga dapat dilihat dalam tabel distribusi binomial. Sebagai contohnya adalah $\color{red}P(2;4;0,05)$ yang berarti $\color{red}x=2$, $\color{red}n=4$, dan $\color{red}p=0,05$ berikut tabelnya:

(Sumber: Buku Siswa Matematika Kelas XII, penulis Tasari, dkk, 2016; hal :126, PT.INTAN PARIWARA)

Sedangkan untuk mencari nilai fungsi peluang distribusi binomial kumulatif, misalkan diberikan $F(2)=P(X\leq 2)$ dari $\color{red}P(2;4;0,05)$ perhatikanlah tabel distribusi untuk distribusi peluang kumulatif dari sumber buku yang sama tetapi terdapat pada halaman berikutnya dengan melihat kolom $\color{red}p=0,05$ , lalu perhatikan baris $\color{red}x=2$ untuk $\color{red}n=2$. Berikut tabelnya

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Dari sebuah survei didapatkan bahwa}\\ &\textrm{1 dari 5 orang berkata bah dia telah}\\ &\textrm{mengunjungi dokter dalam sembarang}\\ &\textrm{bulan. Jika 10 orang dipilih secara acak}\\ &\textrm{maka peluang 3 orang telah berkunjung}\\ &\textrm{ke dokter pada bulan kemaren adalah}\: ....\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&n=10, \: x=3,\: p=\displaystyle \frac{1}{5},\: q=\frac{4}{5}\\ &\textrm{maka}\\ &P(3;10;\displaystyle \frac{1}{5})=\begin{pmatrix} 10\\ 3 \end{pmatrix}\left ( \displaystyle \frac{1}{5} \right )^{3}\left ( \displaystyle \frac{4}{5} \right )^{7} \end{aligned}\\ &\quad\qquad\qquad=\color{red}0,201 \end{array}$

$\LARGE\colorbox{yellow}{TAMBAHAN}$

$\color{blue}\begin{aligned}\textrm{F}.\quad&\textrm{Dsitribusi Poisson} \end{aligned}$

Perhatikanlah rumus ditribusi binomial berikut

$\begin{aligned}&f(x)=P(x;n;p)\\ &=\color{red}C(n,x)p^{x}q^{n-x}\color{black}=\color{red}\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ \end{aligned}$

Saat harga $\color{blue}p$ sebagai lmabang sukses tersebut sangat kecil atau kecil sekali dapat juga dikatakan $\color{blue}p\rightarrow 0$, dan percobaan dilakukan banyak sekali atau $\color{blue}n\rightarrow \infty$ , maka penggunaan formula binomial akan terasa sulit. Dan untuk tetap mendapatkan nilai seperti hasil pada perhitungan dengan rumus binomial tersebut, maka digunakan pendekatan nilai dengan menggunkan rumus Distribusi Poisson berikut:

$f(x)=P(X=x)=\color{red}P(x;\lambda )=\displaystyle \frac{\lambda ^{x}}{x!}.e^{-\lambda }$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 2.&\textrm{Pada tiap 100 lembarkertas produksi}\\ &\textrm{suatu pabrikdiperkirakan terdapat 1}\\ &\textrm{lembar yang rusak. Tentukanlah}\\ &\textrm{kemungkinan mendapat selembar kertas}\\ &\textrm{dari 20 lembar yang diambil secara acak}\\ &\textrm{dari hasil produksi tersebut}!\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad &n=10, \: x=1,\: p=\displaystyle \frac{1}{100},\: q=\frac{99}{100}\\ &\textrm{maka penghitungan dengan}\\ &\textrm{rumus}\: \textbf{Distribusi Binomial}\\ &P(1;20;\displaystyle \frac{1}{100})=\begin{pmatrix} 20\\ 1 \end{pmatrix}\left ( \displaystyle \frac{1}{100} \right )^{1}\left ( \displaystyle \frac{99}{100} \right )^{19}\\ &=\cdots \\ \textrm{b}.\quad&\textrm{Dengan rumus}\: \textbf{Distribusi poisson}\\ &\bullet \quad n=20\rightarrow \textrm{terlalu besar, dan}\\ &\bullet \quad p=\displaystyle \frac{1}{100}\rightarrow \textrm{terlalu kecil, maka}\\ &\textrm{dengan}\: \: \lambda =np=20\times \displaystyle \frac{1}{100}=\color{blue}0,2\\ &\textrm{dan}\: \: \: e=2,7183\: \: (\textrm{bilangan Euler})\\ &f(x)=P(X=x)=\displaystyle \frac{\lambda ^{x}}{x!}.e^{-\lambda }\\ &f(1)=\displaystyle \frac{(0,2)^{1}.e^{-0,2}}{1!}\\ &\qquad =0,2\times 0,409\\ &\qquad =\color{red}0,0818 \end{aligned} \end{array}$

DAFTAR PUSTAKA

Bintari, N. 2009. Master Juara Olimpiade Matematika SMA Nasional dan Internasional. Yogyakarta: PUSTAKA WIDYATAMA.
Kanginan, M., Terzalgi, Y. 2014. Matematika untuk SMA-MA/SMK Kelas XI. Bandung: SEWU.
Rasiman, Rahmawati, N., D. 2012. Matematika Diskrit. Semarang: IKIP PGRI Semarang Press.
Sharma, dkk. 2017. Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta: YUDHISTIRA.
Tasari, Sksin, N., Miyanto, & Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: PT. INTAN PARIWARA.
Yuliatun. 2019. Matematika IPA Kelas XII SMA/MA Semester Genap. Solo: INDONESIA JAYA

Distribusi Peluang Kontinue

$\color{blue}\begin{aligned}\textrm{D. 2}.\quad&\textrm{Distribusi Peluang Kontinue} \end{aligned}$

Jika pada distribusi peluang diskrit nilai x diperjelas lagi menjadi nilai eksak atau kontinue, maka distribusi peluangnya akan berubah menjadi distribusi peluang kontinu.

Luas seluruh daerah di dalam kurva memiliki luas 1. Luas daerah pada wilayah yang diarsi (warna kuning) yang terletak antara X=a dan X=b dapat dinyatakan dengan : $P(a\leq X\leq b)=\displaystyle \int_{a}^{b}f(x)\: \: dx$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Fungsi peluang lama bicara seorang}\\ &\textrm{operator sebagai berikut}\\ &f(x)=\begin{cases} kx &\textrm{untuk}\: \: 0\leq k\leq 5 \\ k(10-x)&\textrm{untuk}\: \: 5\leq k\leq 10\\ \qquad 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{Nilai}\: \: k\\ &\textrm{b}.\quad \textrm{Peluang operator telpon berbicara}\\ &\qquad \textrm{lebih dari 8 menit}\\ &\qquad \textrm{Peluang operator telpon berbicara}\\ &\qquad \textrm{2 sampai 4 menit}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Karena}\: \: f(x)\: \: \textrm{adalah fungsi peluang, maka}\\ &\displaystyle \int_{0}^{5}kx\: dx+\int_{5}^{10}k(10-x)\: dx=1\\ &\Leftrightarrow \left [ \displaystyle \frac{1}{2}kx^{2} \right ]_{0}^{5}+\left [ 10kx-\displaystyle \frac{1}{2}kx^{2} \right ]_{5}^{10}=1\\ &\Leftrightarrow \displaystyle \frac{1}{2}k(5^{2}-0^{2})+\left ( 10k(10-5)-\displaystyle \frac{1}{2}k(10^{2}-5^{2}) \right )=1\\ &\Leftrightarrow \displaystyle \frac{1}{2}k(25)+10k(5)-\displaystyle \frac{1}{2}k(100-25)=1\\ &\Leftrightarrow \displaystyle \frac{25}{2}k+50k-\displaystyle \frac{75}{2}k=1\\ &\Leftrightarrow 50k-25k=1\\ &\Leftrightarrow 25k=1\\ &\Leftrightarrow k=\color{red}\displaystyle \frac{1}{25}\\ \textrm{b}.\quad&\textrm{Misalkan saja}\\ &X=\textrm{lama operator telpon bicara}\\ &\textrm{Peluang operator berbicara lebih}\\ &\textrm{dari 8 menit}=P(X>8),\\ &P(X>8)=P(8<X\leq 10)\\ &\quad\qquad =\displaystyle \int_{8}^{10}k(10-x)\: dx\\ &\quad\qquad =\displaystyle \int_{8}^{10}\frac{1}{25}(10-x)\: dx\\ &\quad\qquad =\displaystyle \frac{1}{25}\left [ 10x-\displaystyle \frac{1}{2}x^{2} \right ]_{8}^{10}\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 10(10-8)-\displaystyle \frac{1}{2}(10^{2}-8^{2}) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 10.(2)-\displaystyle \frac{1}{2}(100-64) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}\left ( 20-\displaystyle \frac{1}{2}(36) \right )\\ &\quad\qquad =\displaystyle \frac{1}{25}(20-18)\\ &\quad\qquad =\displaystyle \frac{1}{25}(2)=\color{red}\frac{2}{25}=0,08\\ \textrm{c}.\quad&\textrm{Peluang operator telpon berbicara}\\ &P(2\leq X\leq 4)\\ &=\displaystyle \int_{2}^{4}kx\: dx\\ &=\displaystyle \int_{2}^{4}\displaystyle \frac{1}{25}x\: dx\\ &=\displaystyle \frac{1}{25}\left [ \displaystyle \frac{1}{2}x^{2} \right ]_{2}^{4}\\ &=\displaystyle \frac{1}{25}\times \frac{1}{2}(4^{2}-2^{2})\\ &=\displaystyle \frac{1}{50}(16-4)\\ &=\color{red}\displaystyle \frac{12}{50}=0,24 \end{aligned} \end{array}$

DAFTAR PUSTAKA

Kurnia, N., dkk. 2018. Jelajah Matematika SMA Kelas XII Peminatan MIPA. Bogor: YUDHISTIRA.
Tasari. Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.

Distribusi Peluang Diskrit

$\color{blue}\begin{aligned}\textrm{D. 1}.\quad&\textrm{Distribusi Peluang Diskrit} \end{aligned}$

$\begin{aligned} &\textrm{Misalkan}\: \: X\: \: \textrm{adalah variabel acak diskrit}\\ &\textrm{dari nilai}\: :\: \: x_{1},\: x_{2},\: x_{3},\: x_{4},\: \cdots \: ,\: x_{k},\: \textrm{dan}\\ &P\: \textrm{adalah seluruh nilai peluang untuk}\: :\\ &p_{1},\: p_{2},\: p_{3},\: p_{4},\: \cdots \: ,p_{k}, \textrm{maka nilai untuk}\\ &\color{blue}p_{1}+ p_{2}+ p_{3}+ p_{4}+ \cdots +p_{k}=1\\ &\textbf{dan}\\ &\textrm{Fungsi}\: \: f(x) =P(X=x)\: \: \textrm{yang mempunyai}\\ &\textrm{nilai}\: \: p_{1},\: p_{2},\: p_{3},\: p_{4},\: \cdots \: ,p_{k},\: \textrm{pada variabel}\\ &X=x_{1},\: x_{2},\: x_{3},\: x_{4},\: \cdots \: ,\: x_{k},\: \textrm{disebut fungsi}\\ &\textrm{kepekatan peluang dari variabel acak}\: \: X.\\ &\textrm{Selanjutnya jika kita gambar grafik}\: \: f(x)\\ &\textrm{terhadap}\: \: x,\: \textrm{maka kita akan grafik yang}\\ &\textrm{dinamakan dengan}\: \: \color{red}\textbf{grafik peluang} \end{aligned}$

Suatu fungsi $f(x)=P(X=x)$ disebut fungsi peluang (probabilitas) dari $X$, jika memenuhi syarat-syarat:

$\color{blue}\begin{matrix} (\textrm{i})\quad f(x)\geq 0\: \: \: \textrm{untuk semua}\: \: x\qquad\qquad\qquad\qquad\qquad\qquad\: \: \\\\ (\textrm{ii})\quad \sum_{i=1}^{n}f\left ( x_{i} \right )=\color{red}f(x_{1})+f(x_{2})+f(x_{3})+...+f(x_{n})=\color{black}1 \end{matrix}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

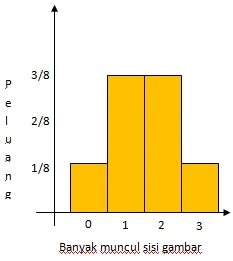
$\begin{array}{ll}\\ 1.&\textrm{Pada percobaan melempar 3 koin identik}\\ &\textrm{sekaligus bersama-sama. Variabel acak}\\ &\textrm{dalam hal ini pada kejadian muncul sisi}\\ &\textrm{gambar, tentukan}\\ &\textrm{a}.\: \: \textrm{distribusi peluangnya}\\ &\textrm{b}.\: \: \textrm{tabel fungsi peluangnya}\\ &\textrm{c}.\: \: \textrm{grafik fungsi peluangnya}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui dari soal}\: \: \color{red}\textrm{variabel acak}\\ &\textrm{pada kejadian di atas adalah munculnya}\\ &\textrm{sisi gambar pada pelemparan 3 koin}\\ &\textrm{maka} \end{aligned}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya}\\ &\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline \textrm{Sampel}&AAA&AA\color{red}G&A\color{red}G\color{black}A&A\color{red}GG&\color{red}G\color{black}AA&\color{red}G\color{black}A\color{red}G&\color{red}GG\color{black}A&\color{red}GGG\\\hline \textrm{Muncul}\: \color{red}(G)&0&1&1&2&1&2&2&3\\\hline \end{array}\\ \textrm{b}.\quad&\textrm{Tabel fungsi peluangnya}\\ &x=\textrm{muncul kejadian sisi gambar}\: \: \color{red}(G)\\ &\begin{array}{|c|c|c|c|c|c|}\hline x&0&1&2&3&\color{red}\textrm{Jumlah}\\\hline f(x)&\displaystyle \frac{1}{8}&\displaystyle \frac{3}{8}&\displaystyle \frac{3}{8}&\displaystyle \frac{1}{8}&\color{red}1\\\hline \end{array}\\ \textrm{c}.\quad&\textrm{Grafik fungsi peluangnya adalah}\\ & \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Pada sebuah kotak terdapat 2 kelereng}\\ &\textrm{biru dan 4 kelereng merah. Tiga kereng}\\ &\textrm{diambil secara acak. Tentukanlah distribusi}\\ &\textrm{peluang}\: \: \color{red}x\: \: \color{black}\textrm{jika}\: \: \color{red}x\: \: \color{black}\textrm{menyatakan banyaknya}\\ &\textrm{terambilnya bola biru}\\\\ &\textbf{Jawab}:\\ &\begin{array}{|l|c|}\hline \qquad\qquad\textrm{Nama}&\textrm{Perhitungan}\\\hline \textrm{Banyak}&\\ \textrm{titik sampel}&\begin{aligned}C_{3}^{6}&=\displaystyle \frac{6!}{3!(6-3)!}=20 \end{aligned}\\\hline \textrm{Banyak cara}&\\ \textrm{mendapatkan bola biru}&C_{x}^{2}\\\hline \textrm{Banyak cara}&\\ \textrm{mendapatkan bola merah}&C_{3-x}^{4}\\\hline \end{array} \end{array}$

$.\quad \: \begin{array}{|l|l|}\hline \color{red}\textrm{Distribusi peluang}&\qquad\quad\color{red}\textrm{Perhitungan}\\\hline P(X=x)=f(x)&f(x)=\displaystyle \frac{\displaystyle C_{x}^{2}.C_{3-x}^{4}}{\displaystyle C_{3}^{6}},\\ \textrm{untuk}&\begin{aligned}x&=0,1,2 \end{aligned}\\\hline x=0\Rightarrow P(x=0)&f(x)=\displaystyle \frac{\displaystyle C_{0}^{2}.C_{3-0}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{0}^{2}.C_{3}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{0!2!}\times \frac{4!}{3!1!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2\\\hline x=1\Rightarrow P(x=1)&f(x)=\displaystyle \frac{\displaystyle C_{1}^{2}.C_{3-1}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{1}^{2}.C_{2}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{1!1!}\times \frac{4!}{2!2!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!2!6!}=0,6\\\hline x=2\Rightarrow P(x=2)&f(x)=\displaystyle \frac{\displaystyle C_{2}^{2}.C_{3-2}^{4}}{\displaystyle C_{3}^{6}}\\ &.\: \: \, \quad=\displaystyle \frac{\displaystyle C_{2}^{2}.C_{1}^{4}}{\displaystyle C_{3}^{6}}=\displaystyle \frac{\displaystyle \frac{2!}{2!0!}\times \frac{4!}{1!3!}}{\displaystyle \frac{6!}{3!3!}}\\ &.\: \: \, \quad=\displaystyle \frac{2!4!3!3!}{2!3!6!}=0,2\\\hline \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tunjukkan bahwa fungsi}\: \: P(x)=\displaystyle \frac{x+2}{12}\\ &\textrm{untuk}\: \: x=1,2,\: \textrm{dan}\: \: 3\: \: \textrm{merupakan fungsi}\\ &\textrm{peluang}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Perhatik}&\textrm{an bahwa}\\ \bullet \quad P(1)&=\displaystyle \frac{1+2}{12}=\frac{3}{12}=\frac{1}{4}\\ \bullet \quad P(2)&=\displaystyle \frac{2+2}{12}=\frac{4}{12}=\frac{1}{3} \\ \bullet \quad P(3)&=\displaystyle \frac{5+2}{12}=\frac{5}{12} \\ \textrm{Sehing}&\textrm{ga}\: \: \displaystyle \sum_{i=1}^{3}P(i)=\displaystyle \frac{3}{12}+\frac{4}{12}+\frac{5}{12}=\color{red}\frac{12}{12}=1\\ &\begin{cases} (\textrm{i}) & \textrm{Peluangnya berada}\: \: \color{red}0\leq P(i)\leq 1 \\ (\textrm{ii}) & \textrm{dan nilai totolnya}=\displaystyle \color{red}\sum_{i=1}^{3}P(i)=1 \end{cases}\\ \textrm{Jadi},\: &\textrm{fungsi}\: \: P(x)=\displaystyle \frac{x+2}{12}\: \: \textrm{untuk}\: \: x=1,2,\: \textrm{dan}\: \: 3\\ &\textbf{merupakan fungsi peluang} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui fungsi peluang adalah}\: \: P(x)=\displaystyle \frac{\color{red}m}{x+1}\\ &\textrm{untuk}\: \: x=0,1,2,\: \textrm{dan}\: \: 3\: .\: \textrm{Tentukanlah}\\ &\textrm{a}.\: \: \textrm{nilai}\: \: \color{red}m\\ &\textrm{b}.\: \: \textrm{nilai}\: \: \color{red}P(x\leq 2)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\displaystyle \sum_{i=0}^{3}P(i)=\color{blue}1\\ &\Leftrightarrow \displaystyle \frac{\color{red}m}{0+1}+\frac{\color{red}m}{1+1}+\frac{\color{red}m}{2+1}+\frac{\color{red}m}{3+1}=1\\ &\Leftrightarrow \color{red}m\color{black}+\displaystyle \frac{\color{red}m}{2}+\frac{\color{red}m}{3}+\frac{\color{red}m}{4}=1\\ &\Leftrightarrow \left (\displaystyle \frac{12+6+4+3}{12} \right )\color{red}m\color{black}=1\\ &\Leftrightarrow \color{red}m\color{black}=\displaystyle \frac{12}{25}\\ \textrm{b}.\quad&P(x\leq 2)=P(x=0)+P(x=1)+P(x=2)\\ &\Leftrightarrow \color{red}m\color{black}+\displaystyle \frac{\color{red}m}{2}+\frac{\color{red}m}{3}=1\\ &\Leftrightarrow \left ( \displaystyle \frac{6+3+2}{6} \right )\color{red}m\color{black}=\displaystyle \frac{11}{6}\color{red}m\\ &\Leftrightarrow \quad =\displaystyle \frac{11}{6}\left ( \displaystyle \frac{12}{25} \right )=\frac{22}{25} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Diketahui fungsi}\: \: f(x)=\begin{cases} \displaystyle \frac{x}{6} &\textrm{untuk}\: \: x=1,2,3 \\\\ 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{adalah suatu fungsi peluang/probabilitas}\\ &\textrm{dari pubah/variabel acak}\: \: X.\: \: \textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{distribusi peluangnya untuk}\: \: X\\ &\textrm{b}.\quad P(X=2),\: P(X< 3),\: \textrm{dan}\: P(X\geq 2)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya adalah}:\\ &\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline X=x&1&2&3&4&5&\cdots &\textrm{Jumlah}\\\hline P(X=x)&\displaystyle \frac{1}{6}&\displaystyle \frac{2}{6}&\displaystyle \frac{3}{6}&\color{red}0&\color{red}0&\color{red}0&\color{blue}1\\\hline \end{array}\\ \textrm{b}.\quad &\textrm{Karena}\: \: f(x)=\begin{cases} \color{red}\displaystyle \frac{x}{6} &\textrm{untuk}\: \: x=1,2,3 \\\\ 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{maka}\\ &\bullet P(X=2)=\color{red}\displaystyle \frac{2}{6}\\ &\bullet P(X<3)=P(X=1)+P(X=2)\\ &\: \quad\qquad \qquad =\displaystyle \frac{1}{6}+\frac{2}{6}\\ &\: \quad\qquad \qquad =\displaystyle \frac{3}{6}=\color{red}\frac{1}{2}\\ &\bullet P(X\geq 2)=P(X=2)+P(X=3)\\ &\: \quad\qquad \qquad =\displaystyle \frac{2}{6}+\frac{3}{6}\\ &\: \quad\qquad \qquad =\color{red}\displaystyle \frac{5}{6} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 6.&\textrm{Diketahui fungsi peluang variabel}\: \: X\\ &f(x)=\begin{cases} \displaystyle \frac{x+2}{14} &\textrm{untuk}\: \: x=0,1,2,\: \: \textrm{dan}\: \: 3 \\\\ \quad 0 &\textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{bahwa}\: \: X\: \: \textrm{merupakan variabel acak diskrit}\\ &\textrm{b}.\quad P(X=4),\: F(2),\: P(1<X\leq 3),\\ &\qquad \textrm{dan}\: P(X\geq 1)\: \: \textrm{serta}\: \: P(\left |X-2 \right |\leq 1)\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Distribusi peluangnya adalah}:\\ &\begin{array}{|c|c|c|c|c|c|c}\hline X=x&0&1&2&3&\textrm{Jumlah}\\\hline P(X=x)&\displaystyle \frac{2}{14}&\displaystyle \frac{3}{14}&\displaystyle \frac{4}{14}&\displaystyle \frac{5}{14}&1\\\hline \end{array} \\ &\textrm{Karena}\: \: \displaystyle \sum_{x=0}^{3}f(x)=1,\: \textrm{serta}\\ &0\leq \displaystyle \frac{2}{14},\: \frac{3}{14},\: \frac{4}{14},\: \frac{5}{14}<1.\: \textrm{Sehingga syarat}\\ &0\leq f(x)<1\: \: \textrm{dan}\: \: \sum f(x)=1\: \: \: \color{red}\textbf{terpenuhi}\\ &\textrm{Jadi, terbukti}\: \: X\: \: \textrm{adalah variabel acak diskrit}\\ \textrm{b}.\quad&\bullet P(X=4)=f(4)=\color{red}0\\ &\bullet F(2)=P(X\leq 2)\\ &\quad\qquad=P(X=0)+P(X=1)+P(X=2)\\ &\quad\qquad=f(0)+f(1)+f(2)\\ &\quad\qquad=\displaystyle \frac{2}{14}+\frac{3}{14}+\frac{4}{14}=\color{red}\frac{9}{14}\\ &\bullet P(1<X\leq 3)=P(X=2)+P(X=3)\\ &\quad\qquad =f(2)+f(3)=\displaystyle \frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{9}{14}\\ &\bullet P(X\geq 1)=f(1)+f(2)+f(3)\\ &\quad\qquad =\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{12}{14}\\ &\bullet P(\left | X-2 \right |\leq 1)=P(-1\leq X-2\leq 1)\\ &\quad\qquad =P(1\leq X\leq 3)\\ &\quad\qquad =f(1)+f(2)+f(3)\\ &\quad\qquad =\displaystyle \frac{3}{14}+\frac{4}{14}+\frac{5}{14}=\color{red}\displaystyle \frac{12}{14} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Distribusipeluang acak X disajikan dalam tabel berikut}\\ &\begin{array}{|c|c|c|c|}\hline x&2&3&4\\\hline f(x)&\displaystyle \frac{1}{8}&k+\displaystyle \frac{1}{8}&2k\\\hline \end{array}\\ &\textrm{Jika X merupakan variabel acak diskret, tentukanlah}\\ &\textrm{a}.\quad \textrm{nilai \textit{k}}\\ &\textrm{b}.\quad \textrm{nilai}\: \: \textrm{P}(\textrm{X}\geq 3)-\textrm{F}(3)\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad \sum f(x)&=f(2)+f(3)+f(4)=1\\ \Leftrightarrow \quad &\displaystyle \frac{1}{8}+k+\frac{1}{8}+2k=1\\ \Leftrightarrow \quad &3k=1-\displaystyle \frac{2}{8}=\frac{6}{8}\\ \Leftrightarrow \quad &k=\displaystyle \frac{2}{8}=\color{red}\frac{1}{4}\\ \textrm{b}.\quad \textrm{P}(\textrm{X}\, \geq 3&)-\textrm{F}(3)=\textrm{P}(\textrm{X}\geq 3)-\textrm{P}(\textrm{X}\leq 3)\\ &=f(3)+f(4)-\left ( f(2)+f(3) \right )\\ &=f(4)-f(2)\\ &=2\left ( \displaystyle \frac{1}{4} \right )-\frac{1}{8}\\ &=\displaystyle \frac{4}{8}-\frac{1}{8}=\color{red}\frac{3}{8} \end{aligned} \end{array}$

DAFTAR PUSTAKA

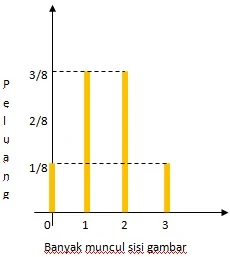
Noormandiri. 2017. Matematika Jilid 3 untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Kurnia, N., dkk. 2018. Jelajah Matematika SMA Kelas XII Peminatan MIPA. Bogor: YUDHISTIRA.

Fungsi Distribusi

Variabel Acak (Lanjutan Materi Distribusi Binomial)

$\color{blue}\textrm{C. Variabel Acak}$

Suatu besaran yang nilainya hanya tunggal dalam konsep matematis disebut sebagai konstanta, sedangkan besaran yang memungkinkan nilainya berbeda-beda disebut sebagai variabel/peubah.

Berkaitan dengan konsep variabel acak, pada contoh berikut akan diberikan contoh kejadian pelemparan sebuah uang koin sebanyak tiga kali dan didapatkan gambarannya sebagai berikut:

$\begin{aligned} \color{blue}\textrm{Mula}\: \, &(1)\quad (2)\quad (3)\quad \color{blue}\textbf{Ruang sampel}\\ \color{red}\textbf{Mulai}&\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (A,A,A)\\ G\rightarrow (A,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (A,G,A)\\ G\rightarrow (A,G,G) \end{matrix}\right. \end{matrix}\right.\\ G\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (G,A,A)\\ G\rightarrow (G,A,G) \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (G,G,A)\\ G\rightarrow (G,G,G) \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. \end{aligned}$.

Ruang sampel yang kita dapatkan dari ilustrasi pelemparan sebuah koin sebanyak tiga kali di atas adalah: S={(A,A,A),(A,A,G),(A,G,A),(A,G,G),(G,A,A),(G,A,G),(G,G,A),(G,G,G)}, sehingga $n(S)=8$.

Selanjutnya dalam fungsi atau pemetaan $S\rightarrow R$ yang memetakan setiap anggota S (ruang sampel) ke X (range=daerah hasil), jika X adalah kejadian munculnya nilai sisi A dari cara acak pelemparan uang koin di atas, maka kita akan memiliki data sebagaimana di bawah.

$\begin{aligned}&\textrm{Perhatikanlah ilustrasi berikut}\\ &\begin{aligned} \color{blue}\textrm{Mula}\: \, &(1)\quad (2)\quad (3)\quad \color{blue}\textbf{Ruang sampel}\quad \textbf{Nilai}\\ \textbf{Mulai}&\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow \color{magenta}(A,A,A)\rightarrow \rightarrow \rightarrow X=3\\ G\rightarrow (A,A,G)\rightarrow \rightarrow \rightarrow X=2 \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (A,G,A)\rightarrow \rightarrow \rightarrow X=2\\ G\rightarrow (A,G,G)\rightarrow \rightarrow \rightarrow X=1 \end{matrix}\right. \end{matrix}\right.\\ G\left\{\begin{matrix} A\left\{\begin{matrix} A\rightarrow (G,A,A)\rightarrow \rightarrow \rightarrow X=2\\ G\rightarrow (G,A,G)\rightarrow \rightarrow \rightarrow X=1 \end{matrix}\right.\\ G\left\{\begin{matrix} A\rightarrow (G,G,A)\rightarrow \rightarrow \rightarrow X=1\\ G\rightarrow \color{red}(G,G,G)\rightarrow \rightarrow \rightarrow X=0 \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. \end{aligned}\\ &\textrm{Jadi, nilai}\: \: X\: \: \textrm{yang mungkin}=\color{red}0,1,2,\: \color{black}\textrm{atau}\: \color{red}3 \end{aligned}$

Perhatikanlah contoh ilustrasi di atas, nilai X ternyata tidak memiliki nilai tunggal. Karena X tidak memiliki nilai tunggal, maka X selanjutnya disebut dengan variabel. Dan variabel seperti ini yang nilainya ditentukan oleh percobaan sehingga akan mendapatkan beberapa kemungkinan selanjutnya disebut dengan variabel acak. Sehingga X pada contoh di atas adalah salah satu contoh untuk variabel acak.

Sebagai tambahan penjelasan perhatikan pula tabel berikut

$\begin{array}{|l|l|l|}\hline \textrm{No}&\textrm{Istilah}&\qquad\qquad\qquad\textrm{Penjelasan}\\\hline 8&\textrm{Cara}&\color{blue}\textrm{atau radom}.\: \textrm{yaitu setiap elemen populasi}\\ &\textrm{Acak}&\textrm{memiliki kesempatan yang yang sama}\\ &&\textrm{sehingga bersifat objektif}\\\hline 9&\textrm{Ruang}&\textrm{Himpunan dari semua hasil yang mungkin}\\ &\textrm{Sampel}&\textrm{dari sebuah percobaan}\\\hline 10&\textrm{Variabel}&\textrm{Suatu fungsi (aturan) yang memetakan }\\ &\textrm{Acak}&\textrm{setiap anggota ruang sampel dengan}\\ &(\textrm{VA})&\textrm{sebuah bilangan riil. Biasanya dinotasikan}\\ &&\textrm{dengan huruf besar, sedangkan nilai}\\ &&\textrm{variabel acaknya dinotasikan dengan}\\ &&\textrm{huruf kecil}\\\hline 11&(\textrm{VA})&\textrm{Jika VA tersebut memiliki sejumlah nilai}\\ &\textrm{Diskrit}&\textrm{yang dapat dihitung(berupa bilangan}\\ &&\textrm{bulat positif)}\\\hline 12&\textrm{VA}&\textrm{Sebaliknya yaitu berupa bilangan yang}\\ &\textrm{Kontinu}&\textrm{tidak bulat}\\\hline \end{array}$.

Tabel di atas adalah tabel lanjutan dari tabel pada halaman ini.

Perlu untuk dimengerti pada kasus pemisalan di atas untuk kejadian $(X=0)$ adalah ekivalen dengan kejadian $\left \{ (G,G,G) \right \}$ dengan nilai $n\left \{ (X=0) \right \}=1$, sehingga peluang untuk kejadian ini adalah:

$P\left \{ (X=0) \right \}=\displaystyle \frac{n\left \{ (X=0) \right \}}{n(S)}=\displaystyle \frac{1}{8}$.

Selanjutnya untuk penulisan singkat dari perhitungan di atas adalah:

$P(X=0) =\displaystyle \frac{n\left \{ (X=0) \right \}}{n(S)}=\displaystyle \frac{1}{8}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Sebuah koin dilempar sebanyak tiga kali}\\ &\textrm{tentukan peluang mendapatkan tepat}\\ &\textrm{dua angka (contoh kasus variabel acak diskrit)}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Misalkan},\: X=\textrm{banyak kejadian muncul sisi angka} \end{aligned}\\ &\begin{aligned}&\textrm{Perhatikan uraian sampel pada materi di atas}\\ &\textrm{ada 2 sisi angka : AAG,AGA,GAA}\\ &\textrm{sehingga peluangnya}=P(X=2),\: \: \textrm{dan nilainya}\\ &P(X=2)=\displaystyle \frac{n(X=2)}{n(S)}=\color{red}\frac{3}{8} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tunjukkan bahwa total semua kejadian}\\ &\textrm{pada soal No.1 di atas, adalah 1}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Perhatikan lagi ilustrasi nilai}\: \: X\: \: \textrm{yang}\\ &\textrm{mungkin, yaitu}:\: 0,1,2,\: \: \textrm{dan}\: \: 3\\ &\textrm{Karena semua kejadian saling lepas},\\ &\textrm{maka}\\ &P(X=0\cup X=1\cup X=2\cup X=3)\\ &=P(0\leq X\leq 3)\\ &=P(X=0)+P(X=1)+P(X=2)+P(X=3)\\ &=\displaystyle \frac{1}{8}+\frac{3}{8}+\frac{3}{8}+\frac{1}{8}\\ &=\displaystyle \frac{8}{8}=\color{red}1\qquad \color{black}\textbf{(terbukti)} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Pada gambar berikut diberikan ilustrasi}\\ &\textrm{papan putar} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Jika}\: \: X_{1}\: \: \textrm{menyatakan perolehan angka pada}\\&\textrm{papan catur A. dan}\: \: X_{2}\: \: \textrm{menyatakan perolehan}\\ &\textrm{angka pada catur B. Tunjukkan bahwa}\\ &Y=X_{1}+X_{2}\: \: \textrm{adalah}\: \textbf{variabel acak diskrit}\\\\ &\textbf{Jawab}:\\ &\textrm{Pada papan putar A, peluang munculnya}\\ &\textrm{angka 2 dan 3 adalah sama, yaitu}:\\ &P(A2)=P(A3)=\displaystyle \frac{1}{4}\\ &catatan: \: \textrm{luas A1 = luas A2+A3}\\ &\textrm{Sedangkan pada papan putar B peluangnya}\\ &\textrm{sama yaitu}:P(B1)+P(B2)+P(B3)=\displaystyle \frac{1}{3} \end{aligned}$.

$.\qquad\begin{array}{|l|l|l|}\hline Y=X_{1}+X_{2}&\textrm{Hasil}&\textrm{Peluang}\: P(Y)\\\hline 2=1+1&(A1,B1)&\displaystyle \frac{2}{4}\times \frac{1}{3}=\frac{2}{12}\\\hline \begin{aligned}3&=1+2\\ &=2+1 \end{aligned}&\begin{aligned}&(A1,B2)\\ &(A2,B1) \end{aligned}&\begin{aligned}&\displaystyle \frac{2}{4}\times \frac{1}{3}\\ &+\displaystyle \frac{1}{4}\times \frac{1}{3}=\frac{3}{12} \end{aligned}\\\hline \begin{aligned}4&=1+3\\ &=2+2\\ &=3+1 \end{aligned}&\begin{aligned}&(A1.B3)\\ &(A2,B2)\\ &(A3,B1)\end{aligned}&\begin{aligned}&\displaystyle \frac{2}{4}\times \frac{1}{3}+\frac{1}{4}\times \frac{1}{3}\\ &+\frac{1}{4}\times \frac{1}{3}=\frac{4}{12} \end{aligned}\\\hline \begin{aligned}5&=2+3\\ &=3+2 \end{aligned}&\begin{aligned}&(A2,B3)\\ &(A3,B2) \end{aligned}&\begin{aligned}&\displaystyle \frac{1}{4}\times \frac{1}{3}\\ &+\displaystyle \frac{1}{4}\times \frac{1}{3}=\frac{2}{12} \end{aligned}\\\hline 6=3+3&(A3,B3)&\displaystyle \frac{1}{4}\times \frac{1}{3}=\frac{1}{12}\\\hline \end{array}$.

$.\qquad\begin{aligned}&\textrm{Dari tabel di atas diperoleh bahwa}\\ &P(Y=2\cup Y=3\cup Y=4\cup Y=5\cup Y=6)\\ &=P(2\leq Y\leq 6)\\ &=P(Y=2)+P(Y=3)+\cdots +P(Y=6)\\ &=\displaystyle \frac{2}{12}+\frac{3}{12}+\frac{4}{12}+\frac{2}{12}+\frac{1}{12}=\frac{12}{12}=1\\ &\textrm{Dari hasil di atas, maka dapat disimpulkan}\\ &Y=X_{1}+X_{2}\: \: \textrm{dengan nilai numeriknya}\\ &\textrm{adalah}\: y=2,3,4,5,6\: \: \textrm{adalah bilangan}\\ &\textrm{bulat, maka}\: \: Y\: \: \textrm{adalah}\: \: \textbf{variabel acak}\\ &\textbf{diskrit} \end{aligned}$.

DAFTAR PUSTAKA

Kanginan, M., Nurdiansyah, H, Akhmad, G. 2016. Matematika untuk SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.

Lanjutan 2 Contoh Soal Kombinasi (Dsitribusi Binomial)

$\begin{array}{ll}\\ 11.&\textrm{Berapa banyak cara dapat memilih untuk}\\ &\textrm{3 perwakilan dari 10 anggota suatu}\\ &\textrm{kelompok, jika}\\ &\textrm{a. tanpa perlakuan khusus}\\ &\textrm{b. salah seorang harus terpilih}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Dengan tanpa perlakuan}\\ &\textrm{memilih 3 orang dari 10 orang adalah}:\\ &C(10,3)=\displaystyle \frac{10!}{3!(10-3)!}=\frac{10!}{3!\times 7!}=\color{blue}120\\ \textrm{b}.\quad&\textrm{Dengan perlakuan 1 orang terpilih}\\ &\color{red}(\textrm{1 orang ini artinya tidak perlu diperhitungkan})\\ &\textrm{memilih 2 orang dari 9 orang adalah}:\\ &C(9,2)=\displaystyle \frac{9!}{2!(9-2)!}=\frac{9!}{2!\times 8!}=\color{blue}36 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Berapa banyak cara dapat memilih 2 buku}\\ &\textrm{matematika dan 3 buku fisika serta 4 buku}\\ &\textrm{ekonomi pada suatu lemari buku yang}\\ &\textrm{di dalamnya terdapat 10 buku matematika,}\\ &\textrm{11 buku fisika dan 12 buku ekonomi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Banyak}\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,2)\times C(11,3)\times C(12,4)\\ &=\displaystyle \frac{10!}{2!\times 8!}\times \frac{11!}{3!\times 8!}\times \frac{12!}{4!\times 8!}\\ &=\displaystyle \frac{10\times 9}{1\times 2}\times \frac{11\times 10\times 9}{1\times 2\times 3}\times \frac{12\times 11\times 10\times 9}{1\times 2\times 3\times 4}\\ &=\color{red}3675375 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Berapa banyak cara dapat memilih 3 tas}\\ &\textrm{dan 4 dompet serta 5 kunci kotak motor}\\ &\textrm{di atas meja yang di atasnya telah tersedia}\\ &\textrm{10 tas, 11 dompet serta 12 kunci kontak}\\ &\textrm{motor}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Banyak}\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,3)\times C(11,4)\times C(12,5)\\ &=\displaystyle \frac{10!}{3!\times 7!}\times \frac{11!}{4!\times 7!}\times \frac{12!}{5!\times 7!}\\ &=\displaystyle \frac{10\times 9\times 8}{1\times 2\times 3}\times \frac{11\times 10\times 9\times 8}{1\times 2\times 3\times 4}\times \frac{12\times 11\times 10\times 9\times 8}{1\times 2\times 3\times 4\times 5}\\ &=120\times 330\times 792\\ &=\color{red}31363200 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Suatu kelompok yang terdiri dari 20 remaja}\\ &\textrm{a}.\quad \textrm{Jika mereka saling berjabat tangan}\\ &\qquad \textrm{seseorang dengan lainnya hanya satu kali}\\ &\qquad \textrm{maka banyak jabat tangan yang terjadi}?\\ &\textrm{b}.\quad \textrm{Jika mereka membentuk regu voly, maka}\\ &\qquad \textrm{berapa banyak regu voly yang terbentuk}?\\ &\textrm{c}.\quad \textrm{Jika mereka membentuk regu sepak bola},\\ &\qquad \textrm{maka banyak regu sepak bola yang terbentuk}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\: \: n=20\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Karena jabat tangan dilakukan hanya hanya}\\ &\textrm{pada dua remaja yang berbeda dan urutan}\\ &\textrm{tidak diperlukan, maka hal ini persoalan}\\ &\textrm{kombinasi. Sehingga banyaknya jabat tangan}\\ &\begin{pmatrix} n\\ r \end{pmatrix}=\displaystyle \frac{n!}{r!(n-r)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20!}{2!(20-2)!}=\frac{20!}{2!\times 18!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20.19.\not{18!}}{2.\not{18!}}=\color{red}190\\ \textrm{b}.\quad&\textrm{Karena satu regu voli ada 6 orang, maka}\\ &\begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!(20-6)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!\times 14!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\color{red}\displaystyle \frac{20.19.18.17.16.15.\not{14!}}{720\times \not{14!}}\\ \textrm{c}.\quad&\textrm{Karena satu regu terdiri dari 11 orang},\\ &\textrm{maka}\\ &\begin{pmatrix} 20\\ 11 \end{pmatrix}=\displaystyle \frac{20!}{11!(20-11)!}=\color{red}\frac{20!}{11!\times 9!} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 15.&\textrm{Jajargenjang yang dapat dibuat oleh}\\ &\textrm{himpunan empat garis sejajar yang}\\ &\textrm{berpotongan dengan garis yang terhimpun}\\ &\textrm{dalam 7 garis sejajar adalah}\: ....\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa kombinasi dari dua himpunan}\\ &\textrm{garis sejajar yang masing-masing berjumlah}\\ &\textrm{4 dan 7 garis, maka}\: \color{red}\textrm{banyak jajar genjang}\\ &\begin{aligned}&=\begin{pmatrix} 4\\ 2 \end{pmatrix}\times \begin{pmatrix} 7\\ 2 \end{pmatrix}\\ &=\displaystyle \frac{4!}{2!(4-2)!}\times \frac{7!}{2!\times (7-2)!}\\ &=\displaystyle \frac{4\times 3\times \not{2!}}{2\times \not{2!}}\times \frac{7\times 6\times \not{5!}}{2\times \not{5!}}\\ &=6\times 21\\ &=\color{red}126\: \: \color{black}\textrm{jajar genjang} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 16.&\textrm{Diketahui segi enam beraturan. Tentukanlah}\\ &\textrm{a}.\quad \textrm{Banyak diagonal dapat dibentuk}?\\ &\textrm{b}.\quad \textrm{Banyak segi tiga di dalamnya}?\\ &\textrm{c}.\quad \textrm{Banyak perpotongan diagonal-diagonal}\\ &\qquad \textrm{jika tidak ada titik-titik perpotongan}\\ &\qquad \textrm{yang sama}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui segi}-n\: \: \textrm{dengan}\: \: n=6\\ &\textrm{Dan perlu diingat bahwa di sini tidak diperlukan}\\ &\textrm{urutan mana yang perlu didahulukan, maka}\\ &\textrm{rumus kombinasi yang perlu digunakan, yaitu}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Banyak diagonalnya adalah}:\\ &\begin{pmatrix} n\\ 2\end{pmatrix}-n=\displaystyle \frac{n(n-3)}{2}\\ &\Leftrightarrow \qquad\quad=\displaystyle \frac{6.(6-3)}{2}=\frac{6.3}{2}=\color{red}9\\ \textrm{b}.\quad&\textrm{Banyaknya segi tiga, berarti melibatkan}\\ &\textrm{tiga garis, maka}\\ &\begin{pmatrix} 6\\ 3 \end{pmatrix}=\displaystyle \frac{6!}{3!\times (6-3)!}=\frac{6\times 5\times 4\times \not{3!}}{6\times \not{3!}}=\color{red}20\\ \textrm{c}.\quad&\textrm{Satu buah titik potong dapat dibentuk}\\ &\textrm{dengan dua garis ekuivalen dengan empat}\\ &\textrm{buah titik sudut, maka banyaknya titik}\\ &\textrm{potong adalah}:\\ &\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{6!}{4!\times (6-4)!}=\frac{6!}{4!\times 2!}=\color{red}15 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 17.&\textrm{Perhatikalah dua ilustrasi gambar berikut} \end{array}$

Gambar (1)

Gambar (2)

$\begin{array}{ll}\\ .\quad\: \, &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{jalur terpendek dari titik A ke B}\\ &\qquad \textrm{pada gambar (1)}\\ &\textrm{b}.\quad \textrm{jalur terpendek dari titik P ke Q}\\ &\qquad \textrm{pada gambar (2)}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Perhatikanlah bahwa langkah dari titik A}\\ &\textrm{ke titik B harus terdiri dari 8 langkah, yaitu}\\ &\textrm{3 langkah ke kanan dan 5 langkah ke atas}\\ &\textrm{Karena yang diinginkan lintasan terpendek}\\ &\textrm{dan tidak ada kekhususn harus dimulai dari}\\ &\textrm{mana, maka banyaknya langkah berbdeda}\\ &\textrm{dan terpendek adalah}:\\ &\begin{pmatrix} 8\\ 3 \end{pmatrix}\: \: \color{red}\textrm{atau}\: \: \color{black}\begin{pmatrix} 8\\ 5 \end{pmatrix}.\: \textrm{Misal kita hitung salah}\\ &\textrm{satunya saja}:\\ &\begin{pmatrix} 8\\ 3 \end{pmatrix}=\displaystyle \frac{8!}{3!(8-5)!}=\frac{8!}{3!\times 5!}=\frac{8.7.6.\not{5!}}{6.\not{5!}}=\color{red}56 \end{aligned} \end{array}$

$.\qquad\: \, \begin{aligned}\textrm{b}.\quad&\textrm{Untuk poin b, perhatikanlah ilustrasi}\\ &\textrm{gambar berikut(untuk memudahkan}\\ &\textrm{perhitungan). Tempatkan titik-titik}\\ &\textrm{bantu A, B, C, D, E, dan F seperti}\\ &\textrm{pada gambar berikut} \end{aligned}$

$.\qquad\: \, \begin{aligned}.\quad&\textrm{Perhatikanlah untuk setiap lintasan}\\ &\textrm{terpendek dari titik P ke titik Q}\\ &\textrm{dapat dipastikan akan melewati}\\ &\textrm{titik A, B, C, dan D. Sehingga dari}\\ &\textrm{keempat titik itulah akan diperoleh}\\ &\textrm{rute PAQ, PBQ, PCQ, dan PDQ}.\\ &\textrm{Sehingga banyak rute terpendek dari}\\ &\textrm{titik P ke Q yang selanjutnya kita}\\ &\textrm{simbolkan dengan}\: \: \color{red}\#PQ\: \: \color{black}\textrm{adalah}:\\ &\begin{aligned}\color{red}\#PQ&=\#PAQ+\#PBQ+\#PCQ+\#PDQ\\ &=\begin{pmatrix} 4\\ 0 \end{pmatrix}\begin{pmatrix} 5\\ 0 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}\begin{pmatrix} 5\\ 1 \end{pmatrix}+\color{magenta}\#PECQ+\#PFCQ+\#PFDQ\\ &=1.1+4.5+\color{magenta}\begin{pmatrix} 3\\ 2 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\begin{pmatrix} 3\\ 2 \end{pmatrix}\color{black}+\color{magenta}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 2 \end{pmatrix}\color{black}+\color{magenta}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\\ &=1+20+\color{magenta}3.1.3\color{black}+\color{magenta}3.3.3\color{black}+\color{magenta}3.1.1\\ &=1+20+9+27+3\\ &=\color{red}60 \end{aligned} \end{aligned}$.

$\begin{array}{ll}\\ 18.&\textrm{Berapa banyak cara memilih 3 dari}\\ &\textrm{7 hari yang disediakan}\\ &\textrm{(penglangan diperbolehkan)}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\begin{cases} n & =7\: \: \textrm{(hari)} \\ r & =3\: \:(\textrm{hari} ) \\ \bullet & \textrm{Pengulangan dibolehkan} \end{cases}\\ &=\begin{pmatrix} n+r-1\\ r \end{pmatrix}\\ &=\begin{pmatrix} 7+3-1\\ 3 \end{pmatrix}\\ &=\begin{pmatrix} 9\\ 3 \end{pmatrix}=\displaystyle \frac{9!}{3!(9-3)!}=\displaystyle \frac{9!}{3!\times 6!}=\displaystyle \frac{9\times 8\times 7}{1\times 2\times 3}\\ &=\color{red}84 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 19.&\textrm{Sebuah toko roti menjual 8 jenis roti}\\ &\textrm{Jika seseorang membeli 12 buah roti}\\ &\textrm{dengan setiap jenis minimal 1 buah}\\ &\textrm{berapa banyak kemungkinannya}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui}\begin{cases} n & =12\: \: \textrm{(buah)} \\ r & =8\: \:(\textrm{jenis roti} ) \\ \bullet & \textrm{Pengulangan dibolehkan} \\ \bullet & \textrm{minimal 1 jenis roti} \end{cases}\\ &=\begin{pmatrix} n-r+(r-1)\\ (r-1) \end{pmatrix}=\begin{pmatrix} n-1\\ r-1 \end{pmatrix}\\ &=\begin{pmatrix} 12-1\\ 8-1 \end{pmatrix}\\ &=\begin{pmatrix} 11\\ 7 \end{pmatrix}=\displaystyle \frac{11!}{7!(11-7)!}=\displaystyle \frac{11!}{7!\times 4!}\\&=\displaystyle \frac{11\times 10\times 9\times 8}{1\times 2\times 3\times 4}\\ &=\color{red}330 \end{aligned} \end{array}$.

DAFTAR PUSTAKA

Bintari, N. 2009. Master Juara Olimpiade Matematika SMA Nasional dan Internasional. Yogyakarta: PUSTAKA WIDYATAMA.
Ibrahim, Mussafi, N, S, M. 2013. Pengantar Kombinatorika dan Teori Graf. Yogyakarta: GRAHA ILMU.
Johnaes, Kastolan, & Sulasim. 2004. Kompetensi Matematika SMA Kelas 2 Semester 1 Program Ilmu Sosial KBK 2004. Jakarta: YUDHISTIRA.
Kanginan, M., Terzalgi, Y. 2014. Matematika untuk SMA-MA/SMK Kelas XI (Wajib). Bandung: SRIKANDI EMPAT WIDYA UTAMA.
Kartini, Suprapto, Subandi, & Setiyadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Sobirin. 2006. Kompas Matematika: Strategi Praktis Menguasai Tes Matematika (SMA Kelas XI IPA). Jakarta: KAWAN PUSTAKA.
Sukino. 2011. Maestro Olimpiade Matematika SMP Seri B. Jakarta: ERLANGGA.
Susyanto, N, 2012. Tutor Senior Olimpiade Matematika Lima Benua Tingkat SMP. Yogyakarta: KENDI MAS MEDIA.
Tampomas, H. 1999. SeribuPena Matematika SMU Jilid 2 Kelas 2 Berdasarkan Kurikulum 1994 Suplemen CBPP 1999. Jakarta: ERLANGGA.

Lanjutan 1 Contoh Soal Kombinasi (Distribusi Binomial)

$\begin{array}{ll}\\ 4.&\textrm{Bentuk sederhana dari}\\ &\textrm{a}.\quad \displaystyle 5!+6!+7!\\ &\textrm{b}.\quad \displaystyle \frac{(n+1)!}{(n-1)!}\\ &\textrm{c}.\quad \displaystyle \frac{(n+2)!}{n!}\\ &\textrm{d}.\quad \displaystyle \frac{(n-2)!}{(n+1)!}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&5!+6!+7!=5!+6.5!+7.6.5!\\ &\quad\quad\quad\quad \: \: \: \: =(1+6+42).5!\\ &\quad\quad\quad\quad \: \: \: \: =49.5!=49.120=5880\\ \textrm{b}.\quad&\displaystyle \frac{(n+1)!}{(n-1)!}=\frac{(n+1)n(n-1)!}{(n-1)!}\\ &\quad\quad\quad\: \: \: =(n+1)n=n^{2}+n\\ \textrm{c}.\quad&\displaystyle \frac{(n+2)!}{n!}=\frac{(n+1)(n+1)n!}{n!}\\ &\quad\quad\quad\: \: \: =(n+2)(n+1)\\ &\quad\quad\quad\: \: \: =n^{2}+3n+2\\ \textrm{d}.\quad&\displaystyle \frac{(n-2)!}{(n+1)!}=\frac{(n-2)!}{(n+1)n(n-1)(n-2)!}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{(n+1)n(n-1)}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{n^{3}-n} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad \displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\textrm{b}.\quad \displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\textrm{c}.\quad \displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\Leftrightarrow \displaystyle \frac{n(n-1)(n-2) \not{(n-3)!}.\not{3!}}{6.5.\not{4}.\not{3!}\not{(n-3)}!}=\frac{33}{\not{4}}\\ &\Leftrightarrow n(n-1)(n-2)=33.6.5=11.10.9\\ &\Leftrightarrow n(n-1)(n-2)=11.(11-1).(11-2)\\ &\Leftrightarrow \qquad\qquad\qquad \: n=11\\ \textrm{b}.\quad&\displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \displaystyle \frac{3-2.8+56}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \frac{43}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow 43=5n+3\Leftrightarrow 5n=40\Leftrightarrow n=8\\ \textrm{c}.\quad &\displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\ &\Leftrightarrow 4n=\displaystyle \frac{5!2!10!}{7!5!5!}\\ &\Leftrightarrow 4n=\displaystyle \frac{\not{5!}2!10.9.8.\not{7!}}{\not{7!}5!\not{5!}}\\&\Leftrightarrow \: \: n=3 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 6.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad P(n,2)=42\\ &\textrm{b}.\quad 7.P(n,3)=6.P(n+1,3)\\ &\textrm{c}.\quad 3.P(n,4)=P(n-1,5)\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&P(n,2)=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=\displaystyle \frac{n\times (n-1)\times (n-2)!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle n\times (n-1)=7.6=7.(7-1)\\ &\Leftrightarrow n=7\\ \textrm{b}.\quad&7.P(n,3)=6.P(n+1,3)\\ &\displaystyle \frac{7.n!}{(n-3)!}=\frac{6(n+1)!}{(n+1-3)!}\\ &\displaystyle \frac{7\not{n!}}{(n-3)!}=\frac{6.(n+1).\not{n!}}{(n-2)!}\\ &\Leftrightarrow \frac{7}{\not{(n-3)!}}=\frac{6n+6}{(n-1)\not{(n-3)!}}\\ &\Leftrightarrow 7(n-2)=6n+6\\ &\Leftrightarrow 7n-6n=6+14\Leftrightarrow n=20\\ \textrm{c}.\quad&3.P(n,4)=P(n-1,5)\\ &\Leftrightarrow \displaystyle \frac{3.n!}{(n-4)!}=\frac{(n-1)!}{(n-1-5)!}\\ &\Leftrightarrow \frac{3.n.\not{(n-1)!}}{(n-4)!}=\frac{\not{(n-1)!}}{(n-6)!}\\ &\Leftrightarrow \frac{3n}{(n-4)(n-5).\not{(n-6)!}}=\frac{1}{\not{(n-6)!}}\\ &\Leftrightarrow 3n=(n-4)(n-5)\\ &\Leftrightarrow 3n=n^{2}-9n+20\\ &\Leftrightarrow n^{2}-12n+20=0\\ &\Leftrightarrow (n-2)(n-10)=0\\ &\Leftrightarrow n=2\: \: \color{red}\textrm{tidak memenuhi}\: \: \color{black}\textrm{atau}\: \: n=10\\ &\textrm{jadi},\: \: n=10 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Jika 10 siswa akan dipilih 4 orang untuk}\\ &\textrm{menjadi ketua kelas, wakil, sekretaris dan}\\ &\textrm{seorang bendahara, maka banyak susunan}\\ &\textrm{terjadi adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Penyusunan memerlukan urutan}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\Leftrightarrow P(10,4)=\displaystyle \frac{10!}{(10-4)!}=\frac{10!}{6!}\\ &\Leftrightarrow \qquad\qquad =\displaystyle \frac{10\times 9\times 8\times 7\times \not{6!}}{\not{6!}}\\ &\Leftrightarrow \qquad\qquad =5040 \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Jika dari kota A ke kota B terdapat 3 jalur.}\\ &\textrm{Dan dari kota B ke kota C terdapat 4 jalur,}\\ &\textrm{serta dari kota C sampai ke kota D ada 5 jalur}\\ &\textrm{Banyak jalan dari kota A ke kota D adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Jalur yang ada semuanya berbeda}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\begin{aligned}\textrm{a}&\textrm{dari A ke B ada 3 jalur cukup pilih satu, maka}\\ &\bullet \quad P(3,1)=\displaystyle \frac{3!}{(3-1)!}=\frac{3!}{2!}=3\\ \textrm{b}&\textrm{dari B ke C ada 4 jalur cukup pilih satu, maka}\\ &\bullet \quad P(4,1)=\displaystyle \frac{4!}{(4-1)!}=\frac{4!}{3!}=4\\ \textrm{c}&\textrm{dari C ke D ada 5 jalur cukup pilih satu, maka}\\ &\bullet \quad P(5,1)=\displaystyle \frac{5!}{(5-1)!}=\frac{5!}{4!}=5 \end{aligned}\\ &\textrm{Jadi, total jalur yang dapat di lalui dari A sampai D adalah}:\\ &\qquad P(3,1)\times P(4,1)\times P(5,1)=3\times 4\times 5=\color{red}60 \end{array}$

$\begin{array}{ll}\\ 9.&\textrm{Jika di suatu kelas terdapat 4 orang akan dipilih 3 orang }\\ &\textrm{untuk menjadi ketua, sekretaris, dan bendahara}.\\ &\textrm{Tentukanlah banyak cara memilih 3 orang tersebut?}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Karena ada 4 orang, misal A, B, C, dan D yang}\\ &\textrm{akan dipilih 3 orang untuk menduduki posisi} \\ &\textrm{ketua, sekretaris, dan bendahara, maka kita tinggal}\\ &\textrm{buat permutasinya, yaitu posisi ketua dapat dipilih }\\ &\textrm{dengan 4 cara, sekretaris dapat dipilih dengan 3 cara}, \\ &\textrm{dan bendahara dapat dipilih dengan 2 cara. atau} \\ &\color{blue} P(4,3)=\displaystyle \frac{4!}{(4-3)!}=\frac{4!}{1!}=\frac{4\times 3\times 2\times 1}{1}=24\: \: \textrm{cara}\\ &\textrm{Berikut ilustrasinya dengan diagram pohon} \end{aligned} \end{array}$

$\color{red}\begin{cases} A&\begin{cases} B & \begin{cases} C &\rightarrow ABC\\ D & \rightarrow ABD \end{cases} \\ C & \begin{cases} B &\rightarrow ACB\\ D & \rightarrow ACD \end{cases} \\ D & \begin{cases} B &\rightarrow ADB \\ C &\rightarrow ADC \end{cases} \end{cases} \\ \\ B&\begin{cases} A & \begin{cases} C &\rightarrow BAC\\ D & \rightarrow BAD \end{cases} \\ C & \begin{cases} A &\rightarrow BCA\\ D & \rightarrow BCD \end{cases} \\ D & \begin{cases} A &\rightarrow BDA \\ C &\rightarrow BDC \end{cases} \end{cases} \\ \\ C&\begin{cases} A & \begin{cases} B &\rightarrow CAB\\ D & \rightarrow CAD \end{cases} \\ B & \begin{cases} A &\rightarrow CBA\\ D & \rightarrow CBD \end{cases} \\ D & \begin{cases} A &\rightarrow CDA \\ B &\rightarrow CDB \end{cases} \end{cases} \\ \\ D&\begin{cases} A & \begin{cases} B &\rightarrow DAB\\ C & \rightarrow DAC \end{cases} \\ B & \begin{cases} A &\rightarrow DBA\\ C & \rightarrow DBC \end{cases} \\ C & \begin{cases} A &\rightarrow DCA \\ B &\rightarrow DCB \end{cases} \end{cases} \end{cases}$

$\begin{array}{ll}\\ 10.&\textrm{Seorang anak akan mengambil 4 buah bola dari}\\ &\textrm{10 warna yang berbeda. Berapakah banyak}\\ &\textrm{kombinasi warna yang berbeda yang diambil}\\ &\textrm{oleh Andi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}n=10&\: \: \textrm{dan}\: \: r=4\\ C(n,r)&=\displaystyle \frac{n!}{r!(n-r)!}\\ C(10,4)&=\displaystyle \frac{10!}{4!(10-4)!}\\ &=\displaystyle \frac{10!}{4!\times 6!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6!}{(4\times 3\times 2\times 1)\times 6!}\\ &=420\: \: \textrm{kombinasi warna bola berbeda} \end{aligned} \end{array}$

DAFTAR PUSTAKA

Johnaes, Kastolan, & Sulasim. 2004. Kompetensi Matematika SMA Kelas 2 Semester 1 Program Ilmu Sosial KBK 2004. Jakarta: YUDHISTIRA.
Kartini, Suprapto, Subandi, & Setiyadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Sobirin. 2006. Kompas Matematika Strategi Praktis Menguasai Tes Matematika. Jakarta: KAWAN PUSTAKA.

Distribusi Binomial (Matematika Peminatan kelas XII SMA/MA)

$\color{blue}\textrm{A. Pendahuluan Distribusi Binomial}$

$\begin{aligned}&\left\{\begin{matrix} (1)\: \textrm{Review}\begin{cases} \textrm{Peluang} \begin{cases} \textrm{Populasi} \\ \textrm{Sampel}\begin{cases} \textrm{Acak} \\ \textrm{Bukan Acak}.\quad \end{cases} \end{cases} \\ \textrm{Kombiasi} & \end{cases}\\ (2)\: \textrm{Variabel Acak}\begin{cases} \textrm{Diskrit} & .\qquad\qquad\qquad\qquad \\ \textrm{Kontinue} & \end{cases}\\ (3)\: \textrm{Distribusi}\begin{cases} \textrm{Distribusi Peluang Variabel Acak} & \\ \textrm{Fungsi Distribusi Kumulatif} & \\ \textrm{Variabel Acak Binomial}&\\ \textrm{Distribusi Binomial} \end{cases}\\ \end{matrix}\right. \end{aligned}$

$\color{blue}\textrm{Penjelasan}$

$\begin{array}{|c|l|l|}\hline \textrm{No}&\quad\textrm{Istilah}&\qquad\qquad\qquad\textrm{Penjelasan}\\\hline 1&\textrm{Statistika}&\textrm{Ilmu tentang pengumpulan, pengolahan},\\ &&\textrm{penganalisaan serta penarikan kesimpulan}\\ &&\textrm{data. Selanjutnya akan dibagi dua yaitu}\\ &&\color{blue}\textrm{deskriptif dan inferensia}\\\hline 2&\textrm{Statistik}&\color{red}\textrm{Kumpulan data/ukuran sampel}\\\hline 3&\textrm{Parameter}&\textrm{Ukuran populasi}\\\hline 4&\textrm{Populasi}&\color{blue}\textrm{Keseluruhan/semua anggota objek/data}\\\hline 5&\textrm{Sampel}&\color{blue}\textrm{Subjek/Objek yang mewakili populasi}\\\hline 6&\textrm{Sesus}&\textrm{Penelitian seluruh data (populasi)}\\\hline 7&\textrm{Tekik}&\textrm{Cara pengambilan data terbatas pada}\\ &\textrm{Sampling}&\textrm{sebagian saja dari populasi yang diteliti}\\\hline \end{array}$.

$\color{blue}\textrm{B. Kombinasi, Peluang, dan Variabel Acak}$.

Untuk memulai bahasan ini kita sertakan pengertian yang berkaitan dengan kombinasi yaitu adalah permutasi. Perhatikanlah tabel berikut

$\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\qquad\qquad\qquad\textrm{Permutasi}&\qquad\qquad\qquad\textrm{Kombinasi}\\\hline \textrm{Definisi}&\begin{aligned}&\textrm{Permutasi r unsur dari n unsur}\\ &\textrm{adalah banyaknya kemungkinan}\\ &\textrm{urutan r unsur yang dipilih}\\ &\textrm{dari n unsur yang tersedia}.\\ & \textrm{Tiap unsur berbeda dan}\: r\leq n\\ &\end{aligned}&\begin{aligned}&\textrm{Kombinasi r unsur dan n unsur}\\ &\textrm{adalah banyaknya kemungkinan}\\ &\textrm{tidak terurut dalam pemilihan}\\ &\textrm{r unsur yang diambil dari n}\\ & \textrm{unsur yang tersedia. Tiap unsur}\\ &\textrm{berbeda dan}\: \: r\leq n \end{aligned}\\\hline \textrm{Tipe}&\begin{aligned}&\textrm{Bentuk khusus kaidah}\\ &\textrm{perkalian} \end{aligned}&\begin{aligned}&\textrm{Bentuk khusus dari bentuk}\\ &\textrm{permutasi} \end{aligned}\\\hline \textrm{Notasi}&_{n}P_{r},\: P_{n}^{r},\: \textrm{atau}\: \: P(n,k)&_{n}C_{r},\: C_{r}^{n},\: \binom{n}{r},\: \textrm{atau}\: \: C(n,r)\\\hline \textrm{Rumus}&P(n,r)=\displaystyle \frac{n!}{(n-r)!}&\binom{n}{r}=C(n,r)=\displaystyle \frac{n!}{r!(n-r)!}\\\hline \end{array}$.

$\begin{aligned}&\color{red}\textrm{Sebagai catatan bahwa}\\&n!=1\times 2\times 3\times \cdots \times (n-1)\times n \end{aligned}$

Selanjutnya yang akan kita bahas berkaitan bab ini adalah kombinasi beserta contohnya. Perhatikan pula tabel berikut

$\begin{array}{|c|c|}\hline \color{red}\textrm{Kombinasi}&\textrm{Kombinasi dalam}\\ \textrm{dengan pengulangan}&\color{red}\textrm{Binom Newton}\\\hline \begin{aligned}&C(n+r-1,r)\\ &=C(n+r-1,n-1)\\ &\binom{n+r-1}{r}\\ &=\binom{n+r-1}{n-1} \end{aligned}&\begin{aligned}&(x+y)^{n}\\ &=\sum_{k=o}^{n}\binom{n}{r}x^{n-k}y^{k}\\\\ &\textrm{Koefisien untuk}\\ &x^{n-k}y^{k},\: \textrm{yaitu}\\ &\textrm{suku ke}-(k+1)\\ &\textrm{adalah}\: \binom{n}{r} \end{aligned}\\\hline \end{array}$.

serta

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah nilai}\\ &\begin{array}{lll}\\ \textrm{a}.\quad 3!&\textrm{e}.\quad \displaystyle \frac{6!}{4!}&\textrm{i}.\quad \displaystyle \frac{2!}{0!}+\frac{3!}{1!}+\frac{4!}{2!}\\ \textrm{b}.\quad 5!&\textrm{f}.\quad \displaystyle \frac{10!}{6!}&\textrm{j}.\quad \displaystyle \frac{2!}{0!}\times \frac{3!}{1!}+\frac{4!}{2!}\\ \textrm{c}.\quad 0!+1!+2!+3!&\textrm{g}.\quad \displaystyle \frac{7!}{3!\times 4!}&\textrm{k}.\quad \displaystyle \frac{3\times 4!}{3!(5!-5!)}\\ \textrm{d}.\quad (2!)!+(3!)!&\textrm{h}.\quad \displaystyle \frac{13!}{12!+12!}&\textrm{l}.\quad \displaystyle \frac{3!+5!+7!}{4!+6!}\end{array}\\\\ &\textrm{Jawab}:\\\\ &\begin{array}{l}\\ \textrm{a}.\quad 3!=3.2.1=6\\ \textrm{b}.\quad 5!=5.4.3.2.1=120\\ \begin{aligned}\textrm{c}.\quad 0!+1!+2!+3!&=1+1+2+6\\ &=10 \end{aligned}\\ \begin{aligned}\textrm{d}.\quad (2!)!+(3!)!&=2!+6!\\ &=2+720\\ &=722 \end{aligned}\\ \textrm{e}.\quad \displaystyle \frac{6!}{4!}=\frac{720}{24}=30\quad \textrm{atau}\quad \displaystyle \frac{6!}{4!}=\displaystyle \frac{6.5.\not{4}.\not{3}.\not{2}.\not{1}}{\not{4}.\not{3}.\not{2}.\not{1}}=6.5=30\\ \textrm{f}.\quad \displaystyle \frac{10!}{6!}=\frac{10.9.8.7.6.5.4.3.2.1}{6.5.4.3.2.1}=.... (\textrm{silahkan diselesaikan sendiri})\\ \textrm{g}.\quad \displaystyle \frac{7!}{3!\times 4!}=\frac{7.6.5.4.3.2.1}{(3.2.1)\times (4.3.2.1)}=.... (\textrm{silahkan juga diselesaikan sendiri})\\ \vdots \\ (\textrm{silahkan selanjutnya diselesaikan sendiri}) \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Sederhanakanlah}\\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle \frac{n!}{(n-1)!}&\textrm{e}.\quad \displaystyle \frac{1}{n!}+\frac{n}{(n+1)!}-\frac{1}{(n-1)!}\\ \textrm{b}.\quad \displaystyle \frac{(n+2)!}{(n+1)!}&\textrm{f}.\quad \displaystyle \frac{(4n)!}{(4n+1)!}+\frac{(4n)!}{(4n-1)!}\\ \textrm{c}.\quad \displaystyle \frac{(2n)!}{(2n+1)!}&\textrm{g}.\quad \displaystyle \frac{1}{n}-\frac{n!}{(n-1).(n-2)!}\\ \textrm{d}.\quad \displaystyle \frac{(n+2)!}{(n^{2}+3n+2)}&\textrm{h}.\quad 1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\end{array}\\\\ &\textrm{Jawab}:\\\\ &\begin{array}{l}\\ \textrm{a}.\quad \displaystyle \frac{n!}{(n-1)!}=\frac{n.(n-1)!}{(n-1)!}=n\\ \textrm{b}.\quad \displaystyle \frac{(n+2)!}{(n+1)!}=\frac{(n+2).(n+1)!}{(n+1)!}=n+2\\ \textrm{c}.\quad \displaystyle \frac{(2n)!}{(2n+1)!}=\frac{(2n)!}{(2n+1).(2n)!}=\frac{1}{2n+1}\\ \textrm{d}.\quad \displaystyle \frac{(n+2)!}{n^{2}+3n+2}=\frac{(n+2)!}{(n+2).(n+1)}=\frac{(n+2).(n+1).n!}{(n+2).(n+1)}=n!\\ \vdots \\ (\textrm{silahkan selanjutnya diselesaikan sendiri sebagai latihan})\\ \vdots \\ \begin{aligned}\textrm{h}.\quad &1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\\ & =(2-1).1!+(3-1).2!+(4-1).3!+(5-1).4!+...+(n+1-1).n!\\ &=2.1!+3.2!+4.3!+5.4!+...+(n+1).n!-1!-2!-3!-4!-...-n!\\ &=2!+3!+4!+5!+...+(n+1)!-\left ( 1!+2!+3!+4!+...+n! \right )\\ &=(n+1)!-1 \end{aligned} \end{array} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Sederhanakanlah bentuk penjumlahan berikut}\\ &\displaystyle \frac{3}{1!+2!+3!}+\frac{4}{2!+3!+4!}+\frac{5}{3!+4!+5!}+\cdots +\displaystyle \frac{100}{98!+99!+100!}\\\\ &\textrm{Jawab}:\\\\ &\begin{aligned}&\textrm{Perhatikan}\, \: \textrm{bahwa}\\ &\displaystyle \frac{3}{1!+2!+3!}=\frac{3}{1+2+6}=\frac{3}{9}=\frac{1}{3}\times \frac{2}{2}=\frac{2}{1\times 2\times 3}=\frac{2}{3!}=\frac{3-1}{3!}=\frac{3}{3!}-\frac{1}{3!}=\frac{3}{2!\times 3}-\frac{1}{3!}=\frac{1}{2!}-\frac{1}{3!}\\ &\textrm{sehingga}\\ &\frac{3}{1!+2!+3!}=\frac{1}{2!}-\frac{1}{3!}\\ &\displaystyle \frac{4}{2!+3!+4!}=\cdots =\frac{1}{3!}-\frac{1}{4!}\\ &\displaystyle \frac{5}{3!+4!+5!}=\cdots =\frac{1}{4!}-\frac{1}{5!}\\ &\vdots \\ &\displaystyle \frac{100}{98!+99!+100!}=\cdots =\frac{1}{99!}-\frac{1}{100!}\\ &---------------------------\\ &\qquad\qquad\qquad\qquad\quad\quad =\frac{1}{2!}-\frac{1}{100!} \end{aligned} \end{array}$.