Contoh 3 Soal dan Pembahasan Materi Permutasi dan Kombinasi

$\begin{array}{ll}\\ 11.&\textrm{Dalam suatu rapat mengelilingi meja bundar}\\ &\textrm{yang dihadiri sebanyak 7 orang}\\ &\textrm{a}.\quad \textrm{ada berapa susunan yang terjadi}?\\ &\textrm{b}.\quad \textrm{Jika A dan B bagian dari 7 orang ini}\\ &\qquad \textrm{duduknya selalu berdampingan, maka}\\ &\qquad \textrm{posisi duduk yang terbentuk sejumlah}?\\ &\textrm{c}.\quad \textrm{Jika seperti poin b, tetapi yang}\\ &\qquad \textrm{duduk berdampingan atau saling berdekatan}\\ &\qquad \textrm{adalah A, B, dan C}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\: \: n=7\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Posisi duduk melingkarnya}\\ &=(7-1)!=6!=\color{red}720\\ &\textbf{atau}\\ &n=r=7\: \: \textrm{orang, maka}\\ &=\displaystyle \frac{P(7,7)}{7}=6!=\color{red}720\\ \textrm{b}.\quad&\textrm{Ada syarat A dan B berdampingan, maka}\\ &\textrm{A dan B dihitung 1 objek dulu, sehingga total}\\ &\textrm{objek ada 1 objek ditambah sisanya = 6 objek}.\\ &\textrm{Dari 6 objek ini yang dianggap duduk melingkar}\\ &\textrm{dengan 2 orang (A dan B) bisa gantian posisi}.\\ &\textrm{sehingga}\\ &(6-1)!\times 2!=5!\times 2!=\color{red}240\\ &\textbf{atau}\\ &=\displaystyle \frac{P(6,6)}{6}\times P(2,2)\\ &=5!\times 2!=120\times 2=\color{red}240\\ \textrm{b}.\quad&\textrm{3 orang (A, B, dan C) dianggap 1 objek}\\ &\textrm{dulu sehigga yang duduk posisi melingkar}\\ &\textrm{dianggap 5 orang, sehingga perhitungannya}\\ &=\displaystyle \frac{P(5,5)}{5}\times P(3,3)\\ &=24\times 6=\color{red}144 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Suatu kelompok yang terdiri dari 20 remaja}\\ &\textrm{a}.\quad \textrm{Jika mereka saling berjabat tangan}\\ &\qquad \textrm{seseorang dengan lainnya hanya satu kali}\\ &\qquad \textrm{maka banyak jabat tangan yang terjadi}?\\ &\textrm{b}.\quad \textrm{Jika mereka membentuk regu voly, maka}\\ &\qquad \textrm{berapa banyak regu voly yang terbentuk}?\\ &\textrm{c}.\quad \textrm{Jika mereka membentuk regu sepak bola},\\ &\qquad \textrm{maka banyak regu sepak bola yang terbentuk}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\: \: n=20\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Karena jabat tangan dilakukan hanya hanya}\\ &\textrm{pada dua remaja yang berbeda dan urutan}\\ &\textrm{tidak diperlukan, maka hal ini persoalan}\\ &\textrm{kombinasi. Sehingga banyaknya jabat tangan}\\ &\begin{pmatrix} n\\ r \end{pmatrix}=\displaystyle \frac{n!}{r!(n-r)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20!}{2!(20-2)!}=\frac{20!}{2!\times 18!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20.19.\not{18!}}{2.\not{18!}}=\color{red}190\\ \textrm{b}.\quad&\textrm{Karena satu regu voli ada 6 orang, maka}\\ &\begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!(20-6)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!\times 14!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\color{red}\displaystyle \frac{20.19.18.17.16.15.\not{14!}}{720\times \not{14!}}\\ \textrm{c}.\quad&\textrm{Karena satu regu terdiri dari 11 orang},\\ &\textrm{maka}\\ &\begin{pmatrix} 20\\ 11 \end{pmatrix}=\displaystyle \frac{20!}{11!(20-11)!}=\color{red}\frac{20!}{11!\times 9!} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 13.&\textrm{Jajargenjang yang dapat dibuat oleh}\\ &\textrm{himpunan empat garis sejajar yang}\\ &\textrm{berpotongan dengan garis yang terhimpun}\\ &\textrm{dalam 7 garis sejajar adalah}\: ....\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa kombinasi dari dua himpunan}\\ &\textrm{garis sejajar yang masing-masing berjumlah}\\ &\textrm{4 dan 7 garis, maka}\: \color{red}\textrm{banyak jajar genjang}\\ &\begin{aligned}&=\begin{pmatrix} 4\\ 2 \end{pmatrix}\times \begin{pmatrix} 7\\ 2 \end{pmatrix}\\ &=\displaystyle \frac{4!}{2!(4-2)!}\times \frac{7!}{2!\times (7-2)!}\\ &=\displaystyle \frac{4\times 3\times \not{2!}}{2\times \not{2!}}\times \frac{7\times 6\times \not{5!}}{2\times \not{5!}}\\ &=6\times 21\\ &=\color{red}126\: \: \color{black}\textrm{jajar genjang} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 14.&\textrm{Diketahui segi enam beraturan. Tentukanlah}\\ &\textrm{a}.\quad \textrm{Banyak diagonal dapat dibentuk}?\\ &\textrm{b}.\quad \textrm{Banyak segi tiga di dalamnya}?\\ &\textrm{c}.\quad \textrm{Banyak perpotongan diagonal-diagonal}\\ &\qquad \textrm{jika tidak ada titik-titik perpotongan}\\ &\qquad \textrm{yang sama}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui segi}-n\: \: \textrm{dengan}\: \: n=6\\ &\textrm{Dan perlu diingat bahwa di sini tidak diperlukan}\\ &\textrm{urutan mana yang perlu didahulukan, maka}\\ &\textrm{rumus kombinasi yang perlu digunakan, yaitu}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Banyak diagonalnya adalah}:\\ &\begin{pmatrix} n\\ 2\end{pmatrix}-n=\displaystyle \frac{n(n-3)}{2}\\ &\Leftrightarrow \qquad\quad=\displaystyle \frac{6.(6-3)}{2}=\frac{6.3}{2}=\color{red}9\\ \textrm{b}.\quad&\textrm{Banyaknya segi tiga, berarti melibatkan}\\ &\textrm{tiga garis, maka}\\ &\begin{pmatrix} 6\\ 3 \end{pmatrix}=\displaystyle \frac{6!}{3!\times (6-3)!}=\frac{6\times 5\times 4\times \not{3!}}{6\times \not{3!}}=\color{red}20\\ \textrm{c}.\quad&\textrm{Satu buah titik potong dapat dibentuk}\\ &\textrm{dengan dua garis ekuivalen dengan empat}\\ &\textrm{buah titik sudut, maka banyaknya titik}\\ &\textrm{potong adalah}:\\ &\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{6!}{4!\times (6-4)!}=\frac{6!}{4!\times 2!}=\color{red}15 \end{aligned} \end{array}$

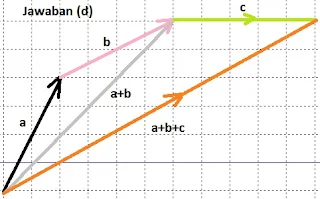
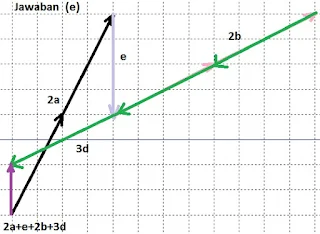
$\begin{array}{ll}\\ 15.&\textrm{Perhatikalah dua ilustrasi gambar berikut} \end{array}$

Gambar (1)

Gambar (2)

$\begin{array}{ll}\\ .\quad\: \, &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{jalur terpendek dari titik A ke B}\\ &\qquad \textrm{pada gambar (1)}\\ &\textrm{b}.\quad \textrm{jalur terpendek dari titik P ke Q}\\ &\qquad \textrm{pada gambar (2)}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Perhatikanlah bahwa langkah dari titik A}\\ &\textrm{ke titik B harus terdiri dari 8 langkah, yaitu}\\ &\textrm{3 langkah ke kanan dan 5 langkah ke atas}\\ &\textrm{Karena yang diinginkan lintasan terpendek}\\ &\textrm{dan tidak ada kekhususn harus dimulai dari}\\ &\textrm{mana, maka banyaknya langkah berbdeda}\\ &\textrm{dan terpendek adalah}:\\ &\begin{pmatrix} 8\\ 3 \end{pmatrix}\: \: \color{red}\textrm{atau}\: \: \color{black}\begin{pmatrix} 8\\ 5 \end{pmatrix}.\: \textrm{Misal kita hitung salah}\\ &\textrm{satunya saja}:\\ &\begin{pmatrix} 8\\ 3 \end{pmatrix}=\displaystyle \frac{8!}{3!(8-5)!}=\frac{8!}{3!\times 5!}=\frac{8.7.6.\not{5!}}{6.\not{5!}}=\color{red}56 \end{aligned} \end{array}$

$.\qquad\: \, \begin{aligned}\textrm{b}.\quad&\textrm{Untuk poin b, perhatikanlah ilustrasi}\\ &\textrm{gambar berikut(untuk memudahkan}\\ &\textrm{perhitungan). Tempatkan titik-titik}\\ &\textrm{bantu A, B, C, D, E, dan F seperti}\\ &\textrm{pada gambar berikut} \end{aligned}$

$.\qquad\: \, \begin{aligned}.\quad&\textrm{Perhatikanlah untuk setiap lintasan}\\ &\textrm{terpendek dari titik P ke titik Q}\\ &\textrm{dapat dipastikan akan melewati}\\ &\textrm{titik A, B, C, dan D. Sehingga dari}\\ &\textrm{keempat titik itulah akan diperoleh}\\ &\textrm{rute PAQ, PBQ, PCQ, dan PDQ}.\\ &\textrm{Sehingga banyak rute terpendek dari}\\ &\textrm{titik P ke Q yang selanjutnya kita}\\ &\textrm{simbolkan dengan}\: \: \color{red}\#PQ\: \: \color{black}\textrm{adalah}:\\ &\begin{aligned}\color{red}\#PQ&=\#PAQ+\#PBQ+\#PCQ+\#PDQ\\ &=\begin{pmatrix} 4\\ 0 \end{pmatrix}\begin{pmatrix} 5\\ 0 \end{pmatrix}+\begin{pmatrix} 4\\ 3 \end{pmatrix}\begin{pmatrix} 5\\ 1 \end{pmatrix}+\color{magenta}\#PECQ+\#PFCQ+\#PFDQ\\ &=1.1+4.5+\color{magenta}\begin{pmatrix} 3\\ 2 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\begin{pmatrix} 3\\ 2 \end{pmatrix}\color{black}+\color{magenta}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 2 \end{pmatrix}\color{black}+\color{magenta}\begin{pmatrix} 3\\ 1 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\begin{pmatrix} 3\\ 0 \end{pmatrix}\\ &=1+20+\color{magenta}3.1.3\color{black}+\color{magenta}3.3.3\color{black}+\color{magenta}3.1.1\\ &=1+20+9+27+3\\ &=\color{red}60 \end{aligned} \end{aligned}$

DAFTAR PUSTAKA

1. Bintari, N. 2009. Master Juara Olimpiade Matematika SMA Nasional dan Internasional. Yogyakarta: PUSTAKA WIDYATAMA.
2. Ibrahim, Mussafi, N, S, M. 2013. Pengantar Kombinatorika dan Teori Graf. Yogyakarta: GRAHA ILMU.
3. Kanginan, M., Terzalgi, Y. 2014. Matematika untuk SMA-MA/SMK Kelas XI (Wajib). Bandung: SRIKANDI EMPAT WIDYA UTAMA.
4. Sobirin. 2006. Kompas Matematika: Strategi Praktis Menguasai Tes Matematika (SMA Kelas XI IPA). Jakarta: KAWAN PUSTAKA.
5. Sukino. 2011. Maestro Olimpiade Matematika SMP Seri B. Jakarta: ERLANGGA.
6. Susyanto, N, 2012. Tutor Senior Olimpiade Matematika Lima Benua Tingkat SMP. Yogyakarta: KENDI MAS MEDIA.
7. Tampomas, H. 1999. SeribuPena Matematika SMU Jilid 2 Kelas 2 Berdasarkan Kurikulum 1994 Suplemen CBPP 1999. Jakarta: ERLANGGA.

Contoh 2 Soal dan Pembahasan Materi Permutasi dan Kombinasi

$\begin{array}{ll}\\ 6.&\textrm{Dari angka-angka 2,3,5,6,7, dan 9 dibuat}\\ &\textrm{susunan bilangan}\\ &\textrm{a. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka berlainan}\\ &\textrm{b. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka boleh berulang}\\ &\textrm{c. berapa banyak bilangan ganjil yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan}\\ &\textrm{d. berapa banyak bilangan genap yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan}\\ &\textrm{e. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka berlainan yang lebih dari 2021}\\ &\textrm{f. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka boleh berulang yang lebih dari 2021}\\ &\textrm{g. berapa banyak bilangan genap yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan yang lebih dari 2021}\\ &\textrm{h. berapa banyak bilangan ganjil yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan yang lebih dari 2021}\\\\ &\color{blue}\textbf{Jawab}:\\  \end{array}$

$.\quad\: \, \begin{aligned}\textrm{a}.\quad&P(6,4)=\displaystyle \frac{6!}{(6-2)!}=\frac{6!}{2!}=6.5.4.3=\color{red}360\\ \textrm{b}.\quad&P(6,1)^{4}=6^{4}=\color{red}1296\\ \textrm{c}.\quad&\textrm{Untuk digit satuan ditentukan dulu, yaitu}\\ &\textrm{karena digit ganjil ada 4, maka ada 4 pilihan}\\ &\textrm{sisanya disebar ke slot ribuan sampai puluhan}\\ &\textrm{maka}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{red}\textrm{ratusan}&\textrm{puluhan}&\color{red}\textrm{satuan}\\\hline P(5,1)&P(4,1)&P(3,1)&P(4,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}\\ &\textrm{Sehingga banyak bilangan yg terjadi}\\ &P(5,1).P(4,1).P(3,1).P(4,1)=5.4.3.4=\color{red}240\\ \textrm{d}.\quad&\textbf{Cara pertama}\\ &\textrm{Semisal dengan jawaban poin c, Karena}\\ &\textrm{digit genap ada 2, maka digit satuan ada}\\ &\textrm{2 pilihan, sisanya disebar, yaitu}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{red}\textrm{ratusan}&\textrm{puluhan}&\color{red}\textrm{satuan}\\\hline P(5,1)&P(4,1)&P(3,1)&P(2,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}\\ &\textrm{Sehingga banyak bilangan yg terjadi}\\ &P(5,1).P(4,1).P(3,1).P(2,1)=5.4.3.2=\color{red}120\\ &\textbf{Cara kedua}\\ &\textrm{Jawaban poin a dikurangi poin c, yaitu}\\ &360-240=\color{red}120 \end{aligned}$

$.\quad\: \, \begin{aligned}\textrm{e}.\quad&\textbf{Cara Pertama}\\ &\textrm{Karena digit pilihannya, 2,3,5,6,7, dan 9}\\ &\textrm{disusun bagaimanapun bilangan 4 digit}\\ &\textrm{yang diambilkan dari bilangan di atas}\\ &\textrm{pasti semunya akan lebih besar dari 2021}\\ &\textrm{maka banyaknya bilangan yang terjadi}\\ &\textrm{adalah}:\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{magenta}\textrm{ratusan}&\textrm{puluhan}&\color{magenta}\textrm{satuan}\\\hline P(6,1)&P(5,1)&P(4,1)&P(3,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}>2021\\ &\textrm{Sehingga totalnya banyaknya}\\ &P(6,1)\times P(5,1)\times P(4,1)\times P(3,1)\\ &=6.5.4.3=\color{red}360\\ &\textbf{Cara Kedua}\\ &\textrm{Sama seperti jawaban pada poin a}\\ \textrm{f}.\quad&\textrm{Sama persis jawaban poin b, yaitu}\\ &P(6,1)^{4}=6^{4}=\color{red}1296\\ &\textrm{Jika diuraikan adalah sebagai berikut}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{magenta}\textrm{ratusan}&\textrm{puluhan}&\color{magenta}\textrm{satuan}\\\hline P(6,1)&P(6,1)&P(6,1)&P(6,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}>2021 \end{aligned}$

$\begin{array}{ll}\\ 7.&\textrm{Andi akan mengambil 4 buah bola dari}\\ &\textrm{10 warna yang berbeda. Berapakah banyak}\\ &\textrm{kombinasi warna yang berbeda yang diambil}\\ &\textrm{oleh Andi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}n=10&\: \: \textrm{dan}\: \: r=4\\ C(n,r)&=\displaystyle \frac{n!}{r!(n-r)!}\\ C(10,4)&=\displaystyle \frac{10!}{4!(10-4)!}\\ &=\displaystyle \frac{10!}{4!\times 6!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6!}{(4\times 3\times 2\times 1)\times 6!}\\ &=420\: \: \textrm{kombinasi warna bola berbeda} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Berapa banyak cara dapat memilih untuk}\\ &\textrm{3 perwakilan dari 10 anggota suatu}\\ &\textrm{kelompok, jika}\\ &\textrm{a. tanpa perlakuan khusus}\\ &\textrm{b. salah seorang harus terpilih}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Dengan tanpa perlakuan}\\ &\textrm{memilih 3 orang dari 10 orang adalah}:\\ &C(10,3)=\displaystyle \frac{10!}{3!(10-3)!}=\frac{10!}{3!\times 7!}=\color{blue}120\\ \textrm{b}.\quad&\textrm{Dengan perlakuan 1 orang terpilih}\\ &\color{red}(\textrm{1 orang ini artinya tidak perlu diperhitungkan})\\ &\textrm{memilih 2 orang dari 9 orang adalah}:\\ &C(9,2)=\displaystyle \frac{9!}{2!(9-2)!}=\frac{9!}{2!\times 8!}=\color{blue}36 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 9.&\textrm{Berapa banyak cara dapat memilih 2 buku}\\ &\textrm{matematika dan 3 buku fisika serta 4 buku}\\ &\textrm{ekonomi pada suatu lemari buku yang}\\ &\textrm{di dalamnya terdapat 10 buku matematika,}\\ &\textrm{11 buku fisika dan 12 buku ekonomi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Banyak}&\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,2)\times C(11,3)\times C(12,4)\\ &=\displaystyle \frac{10!}{2!\times 8!}\times \frac{11!}{3!\times 8!}\times \frac{12!}{4!\times 8!}\\ &=\displaystyle \frac{10\times 9}{1\times 2}\times \frac{11\times 10\times 9}{1\times 2\times 3}\times \frac{12\times 11\times 10\times 9}{1\times 2\times 3\times 4}\\ &=\color{red}3675375 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 10.&\textrm{Banyak susunan huruf yang berbeda}\\ &\textrm{pada satu baris yang dapat dibentuk}\\ &\textrm{dari huruf-huruf pada kata "MATEMATIKA"}\\ &\textrm{adalah}\: ....\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{cases} \textrm{Jumlah huruf} & n=\color{red}10 \\ \textrm{Penyusunnya}\, , & \text{ yaitu }: \begin{cases} M & \text{ jumlah } =2 \\ A & \text{ jumlah } =3 \\ T & \text{ jumlah } =2 \\ E & \text{ banyak } =1 \\ I & \text{ banyak } =1 \\ K & \text{ banyak } =1 \end{cases} \end{cases}\\ &\textrm{Sehingga}\\ &\begin{aligned}P(10;2,3,2,1,1,1)&=\displaystyle \frac{\color{red}10\color{black}!}{2!.3!.2!.1!.1!.1!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6\times 5\times 4}{4}\\ &=10\times 9\times 8\times 7\times 6\times 5\\ &=\color{red}151200 \end{aligned} \end{array}$

Contoh 1 Soal dan Pembahasan Materi Permutasi dan Kombinasi

$\begin{array}{ll}\\ 1.&\textrm{Bentuk sederhana dari}\\ &\textrm{a}.\quad \displaystyle 5!+6!+7!\\ &\textrm{b}.\quad \displaystyle \frac{(n+1)!}{(n-1)!}\\ &\textrm{c}.\quad \displaystyle \frac{(n+2)!}{n!}\\ &\textrm{d}.\quad \displaystyle \frac{(n-2)!}{(n+1)!}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&5!+6!+7!=5!+6.5!+7.6.5!\\ &\quad\quad\quad\quad \: \: \: \: =(1+6+42).5!\\ &\quad\quad\quad\quad \: \: \: \: =49.5!=49.120=5880\\ \textrm{b}.\quad&\displaystyle \frac{(n+1)!}{(n-1)!}=\frac{(n+1)n(n-1)!}{(n-1)!}\\ &\quad\quad\quad\: \: \: =(n+1)n=n^{2}+n\\ \textrm{c}.\quad&\displaystyle \frac{(n+2)!}{n!}=\frac{(n+1)(n+1)n!}{n!}\\ &\quad\quad\quad\: \: \: =(n+2)(n+1)\\ &\quad\quad\quad\: \: \: =n^{2}+3n+2\\ \textrm{d}.\quad&\displaystyle \frac{(n-2)!}{(n+1)!}=\frac{(n-2)!}{(n+1)n(n-1)(n-2)!}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{(n+1)n(n-1)}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{n^{3}-n} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad \displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\textrm{b}.\quad \displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\textrm{c}.\quad \displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\Leftrightarrow \displaystyle \frac{n(n-1)(n-2) \not{(n-3)!}.\not{3!}}{6.5.\not{4}.\not{3!}\not{(n-3)}!}=\frac{33}{\not{4}}\\ &\Leftrightarrow n(n-1)(n-2)=33.6.5=11.10.9\\ &\Leftrightarrow n(n-1)(n-2)=11.(11-1).(11-2)\\ &\Leftrightarrow \qquad\qquad\qquad \: n=11\\ \textrm{b}.\quad&\displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \displaystyle \frac{3-2.8+56}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \frac{43}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow 43=5n+3\Leftrightarrow 5n=40\Leftrightarrow n=8\\ \textrm{c}.\quad &\displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\ &\Leftrightarrow 4n=\displaystyle \frac{5!2!10!}{7!5!5!}\\ &\Leftrightarrow 4n=\displaystyle \frac{\not{5!}2!10.9.8.\not{7!}}{\not{7!}5!\not{5!}}\\&\Leftrightarrow \: \: n=3 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad P(n,2)=42\\ &\textrm{b}.\quad 7.P(n,3)=6.P(n+1,3)\\ &\textrm{c}.\quad 3.P(n,4)=P(n-1,5)\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&P(n,2)=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=\displaystyle \frac{n\times (n-1)\times (n-2)!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle n\times (n-1)=7.6=7.(7-1)\\ &\Leftrightarrow n=7\\ \textrm{b}.\quad&7.P(n,3)=6.P(n+1,3)\\ &\displaystyle \frac{7.n!}{(n-3)!}=\frac{6(n+1)!}{(n+1-3)!}\\ &\displaystyle \frac{7\not{n!}}{(n-3)!}=\frac{6.(n+1).\not{n!}}{(n-2)!}\\ &\Leftrightarrow \frac{7}{\not{(n-3)!}}=\frac{6n+6}{(n-1)\not{(n-3)!}}\\ &\Leftrightarrow 7(n-2)=6n+6\\ &\Leftrightarrow 7n-6n=6+14\Leftrightarrow n=20\\ \textrm{c}.\quad&3.P(n,4)=P(n-1,5)\\ &\Leftrightarrow \displaystyle \frac{3.n!}{(n-4)!}=\frac{(n-1)!}{(n-1-5)!}\\ &\Leftrightarrow \frac{3.n.\not{(n-1)!}}{(n-4)!}=\frac{\not{(n-1)!}}{(n-6)!}\\ &\Leftrightarrow \frac{3n}{(n-4)(n-5).\not{(n-6)!}}=\frac{1}{\not{(n-6)!}}\\ &\Leftrightarrow 3n=(n-4)(n-5)\\ &\Leftrightarrow 3n=n^{2}-9n+20\\ &\Leftrightarrow n^{2}-12n+20=0\\ &\Leftrightarrow (n-2)(n-10)=0\\ &\Leftrightarrow n=2\: \: \color{red}\textrm{tidak memenuhi}\: \: \color{black}\textrm{atau}\: \: n=10\\ &\textrm{jadi},\: \: n=10 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Jika 10 siswa akan dipilih 4 orang untuk}\\ &\textrm{menjadi ketua kelas, wakil, sekretaris dan}\\ &\textrm{seorang bendahara, maka banyak susunan}\\ &\textrm{terjadi adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Penyusunan memerlukan urutan}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\Leftrightarrow P(10,4)=\displaystyle \frac{10!}{(10-4)!}=\frac{10!}{6!}\\ &\Leftrightarrow \qquad\qquad =\displaystyle \frac{10\times 9\times 8\times 7\times \not{6!}}{\not{6!}}\\ &\Leftrightarrow \qquad\qquad =5040 \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Jika dari kota A ke kota B terdapat 3 jalur.}\\ &\textrm{Dan dari kota B ke kota C terdapat 4 jalur,}\\ &\textrm{serta dari kota C sampai ke kota D ada 5 jalur}\\ &\textrm{Banyak jalan dari kota A ke kota D adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Jalur yang ada semuanya berbeda}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\begin{aligned}\textrm{a}&\textrm{dari A ke B ada 3 jalur cukup pilih satu, maka}\\ &\bullet \quad P(3,1)=\displaystyle \frac{3!}{(3-1)!}=\frac{3!}{2!}=3\\ \textrm{b}&\textrm{dari B ke C ada 4 jalur cukup pilih satu, maka}\\ &\bullet \quad P(4,1)=\displaystyle \frac{4!}{(4-1)!}=\frac{4!}{3!}=4\\ \textrm{c}&\textrm{dari C ke D ada 5 jalur cukup pilih satu, maka}\\ &\bullet \quad P(5,1)=\displaystyle \frac{5!}{(5-1)!}=\frac{5!}{4!}=5 \end{aligned}\\ &\textrm{Jadi, total jalur yang dapat di lalui dari A sampai D adalah}:\\ &\qquad P(3,1)\times P(4,1)\times P(5,1)=3\times 4\times 5=\color{red}60 \end{array}$

Notasi Faktorial, Permutasi dan Kombinasi

 $\color{blue}\textrm{C. Faktorial}$

Perhatikanlah tabel berikut yang berisi perkalian bilangan terurut pada bilangan asli

$\begin{array}{|c|}\hline n!=1\times 2\times 3\times 4\times \cdots \times (n-2)\times (n-1)\times n\\ \textbf{atau}\\ n!=n\times (n-1)\times (n-2)\times \cdots \times 4\times 3\times 2\times 1\\ \color{red}\textrm{dengan}\\ (n+1)!=(n+1)\times n!\: \: \textrm{untuk}\: \: n\geq 1,\: n\in \mathbb{N}\\ \color{blue}\textrm{serta didefinisikan bahwa}\\ 0!= 1!=1\\ \colorbox{yellow}{CONTOH}\\ 0!=1\\ 1!=1\\ 2!=2\times 1=2\\ 3!=3\times 2\times 1=6\\ 4!=4\times 3\times 2\times 1=24\\ 5!=5\times 4\times 3\times 2\times 1=120\\ 6!=6\times 5\times 4\times 3\times 2\times 1=720\\ \\ \vdots \\ \\ \color{black}n!=n\times (n-1)\times (n-2)\times \cdots \times 4\times 3\times 2\times 1\\\hline \end{array}$

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah nilai}\\ &\begin{array}{lll}\\ \textrm{a}.\quad 3!&\textrm{e}.\quad \displaystyle \frac{6!}{4!}&\textrm{i}.\quad \displaystyle \frac{2!}{0!}+\frac{3!}{1!}+\frac{4!}{2!}\\ \textrm{b}.\quad 5!&\textrm{f}.\quad \displaystyle \frac{10!}{6!}&\textrm{j}.\quad \displaystyle \frac{2!}{0!}\times \frac{3!}{1!}+\frac{4!}{2!}\\ \textrm{c}.\quad 0!+1!+2!+3!&\textrm{g}.\quad \displaystyle \frac{7!}{3!\times 4!}&\textrm{k}.\quad \displaystyle \frac{3\times 4!}{3!(5!-5!)}\\ \textrm{d}.\quad (2!)!+(3!)!&\textrm{h}.\quad \displaystyle \frac{13!}{12!+12!}&\textrm{l}.\quad \displaystyle \frac{3!+5!+7!}{4!+6!}\end{array}\\\\ &\textrm{Jawab}:\\\\ &\begin{array}{l}\\ \textrm{a}.\quad 3!=3.2.1=6\\ \textrm{b}.\quad 5!=5.4.3.2.1=120\\ \begin{aligned}\textrm{c}.\quad 0!+1!+2!+3!&=1+1+2+6\\ &=10 \end{aligned}\\ \begin{aligned}\textrm{d}.\quad (2!)!+(3!)!&=2!+6!\\ &=2+720\\ &=722 \end{aligned}\\ \textrm{e}.\quad \displaystyle \frac{6!}{4!}=\frac{720}{24}=30\quad \textrm{atau}\quad \displaystyle \frac{6!}{4!}=\displaystyle \frac{6.5.\not{4}.\not{3}.\not{2}.\not{1}}{\not{4}.\not{3}.\not{2}.\not{1}}=6.5=30\\ \textrm{f}.\quad \displaystyle \frac{10!}{6!}=\frac{10.9.8.7.6.5.4.3.2.1}{6.5.4.3.2.1}=.... (\textrm{silahkan diselesaikan sendiri})\\ \textrm{g}.\quad \displaystyle \frac{7!}{3!\times 4!}=\frac{7.6.5.4.3.2.1}{(3.2.1)\times (4.3.2.1)}=.... (\textrm{silahkan juga diselesaikan sendiri})\\ \vdots \\ (\textrm{silahkan selanjutnya diselesaikan sendiri}) \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Sederhanakanlah}\\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle \frac{n!}{(n-1)!}&\textrm{e}.\quad \displaystyle \frac{1}{n!}+\frac{n}{(n+1)!}-\frac{1}{(n-1)!}\\ \textrm{b}.\quad \displaystyle \frac{(n+2)!}{(n+1)!}&\textrm{f}.\quad \displaystyle \frac{(4n)!}{(4n+1)!}+\frac{(4n)!}{(4n-1)!}\\ \textrm{c}.\quad \displaystyle \frac{(2n)!}{(2n+1)!}&\textrm{g}.\quad \displaystyle \frac{1}{n}-\frac{n!}{(n-1).(n-2)!}\\ \textrm{d}.\quad \displaystyle \frac{(n+2)!}{(n^{2}+3n+2)}&\textrm{h}.\quad 1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\end{array}\\\\ &\textrm{Jawab}:\\\\ &\begin{array}{l}\\ \textrm{a}.\quad \displaystyle \frac{n!}{(n-1)!}=\frac{n.(n-1)!}{(n-1)!}=n\\ \textrm{b}.\quad \displaystyle \frac{(n+2)!}{(n+1)!}=\frac{(n+2).(n+1)!}{(n+1)!}=n+2\\ \textrm{c}.\quad \displaystyle \frac{(2n)!}{(2n+1)!}=\frac{(2n)!}{(2n+1).(2n)!}=\frac{1}{2n+1}\\ \textrm{d}.\quad \displaystyle \frac{(n+2)!}{n^{2}+3n+2}=\frac{(n+2)!}{(n+2).(n+1)}=\frac{(n+2).(n+1).n!}{(n+2).(n+1)}=n!\\ \vdots \\ (\textrm{silahkan selanjutnya diselesaikan sendiri sebagai latihan})\\ \vdots \\ \begin{aligned}\textrm{h}.\quad &1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\\ & =(2-1).1!+(3-1).2!+(4-1).3!+(5-1).4!+...+(n+1-1).n!\\ &=2.1!+3.2!+4.3!+5.4!+...+(n+1).n!-1!-2!-3!-4!-...-n!\\ &=2!+3!+4!+5!+...+(n+1)!-\left ( 1!+2!+3!+4!+...+n! \right )\\ &=(n+1)!-1 \end{aligned} \end{array} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Sederhanakanlah bentuk penjumlahan berikut}\\ &\displaystyle \frac{3}{1!+2!+3!}+\frac{4}{2!+3!+4!}+\frac{5}{3!+4!+5!}+\cdots +\displaystyle \frac{100}{98!+99!+100!}\\\\ &\textrm{Jawab}:\\\\ &\begin{aligned}\textrm{Perhatikan}&\, \: \textrm{bahwa}\\ &\displaystyle \frac{3}{1!+2!+3!}=\frac{3}{1+2+6}=\frac{3}{9}=\frac{1}{3}\times \frac{2}{2}=\frac{2}{1\times 2\times 3}=\frac{2}{3!}=\frac{3-1}{3!}=\frac{3}{3!}-\frac{1}{3!}=\frac{3}{2!\times 3}-\frac{1}{3!}=\frac{1}{2!}-\frac{1}{3!}\\ &\textrm{sehingga}\\ &\frac{3}{1!+2!+3!}=\frac{1}{2!}-\frac{1}{3!}\\ &\displaystyle \frac{4}{2!+3!+4!}=\cdots =\frac{1}{3!}-\frac{1}{4!}\\ &\displaystyle \frac{5}{3!+4!+5!}=\cdots =\frac{1}{4!}-\frac{1}{5!}\\ &\vdots \\ &\displaystyle \frac{100}{98!+99!+100!}=\cdots =\frac{1}{99!}-\frac{1}{100!}\\ &---------------------------\\ &\qquad\qquad\qquad\qquad\quad\quad =\frac{1}{2!}-\frac{1}{100!} \end{aligned} \end{array}$

$\color{blue}\textrm{D. Permutasi dan Kombinasi}$

$\begin{array}{|l|l|l|}\hline \textrm{Istilah}&\qquad\qquad\qquad\textrm{Permutasi}&\qquad\qquad\qquad\textrm{Kombinasi}\\\hline \textrm{Definisi}&\begin{aligned}&\textrm{Permutasi r unsur dari n unsur adalah}\\ &\textrm{banyaknya kemungkinan urutan r buah}\\ &\textrm{unsur yang dipilih dari n unsur}\\ &\textrm{yang tersedia}.\: \textrm{Tiap unsur berbeda dan}\\ & r\leq n \end{aligned}&\begin{aligned}&\textrm{Kombinasi r unsur dan n unsur adalah}\\ &\textrm{banyaknya kemungkinan tidak terurut}\\ &\textrm{dalam pemilihan r unsur yang diambil}\\ &\textrm{dari n unsur yang tersedia}.\: \textrm{Tiap unsur}\\ &\textrm{berbeda dan}\: \: r\leq n \end{aligned}\\\hline \textrm{Tipe}&\textrm{Bentuk khusus kaidah perkalian}&\textrm{Bentuk khusus permutasi}\\\hline \textrm{Notasi}&_{n}P_{r},\: P_{n}^{r},\: \textrm{atau}\: \: P(n,k)&_{n}C_{r},\: C_{r}^{n},\: \binom{n}{r},\: \textrm{atau}\: \: C(n,r)\\\hline \textrm{Rumus}&P(n,r)=\displaystyle \frac{n!}{(n-r)!}&\binom{n}{r}=C(n,r)=\displaystyle \frac{n!}{r!(n-r)!}\\\hline \end{array}$

Selanjutnya perhatikanlah tabel berikut

$\begin{array}{|c|c|c|}\hline \textrm{Permutasi}&\textrm{Permutasi}\\ \textrm{dengan unsur yang sama}&\textrm{Siklis}\\\hline \begin{aligned}&P(n;n_{1},n_{2},n_{3},...,n_{k})\\ &=\displaystyle \frac{P(n,n)}{n_{1}!n_{2}!n_{3}!...n_{k}!}\\ &=\displaystyle \frac{n!}{n_{1}!n_{2}!n_{3}!...n_{k}!} \end{aligned}&\begin{aligned}&\begin{cases} \textrm{Siklis} & =(n-1)! \\\\ \textrm{Kalung} & =\displaystyle \frac{(n-1)!}{2} \end{cases} \end{aligned}\\\hline \end{array}$

dan

$\begin{array}{|c|c|}\hline \textrm{Kombinasi}&\textrm{Kombinasi dalam}\\ \textrm{dengan pengulangan}&\textrm{Binom Newton}\\\hline \begin{aligned}&C(n+r-1,r)\\ &=C(n+r-1,n-1)\\ &\binom{n+r-1}{r}\\ &=\binom{n+r-1}{n-1} \end{aligned}&\begin{aligned}&(x+y)^{n}\\ &=\sum_{k=o}^{n}\binom{n}{r}x^{n-k}y^{k}\\\\ &\textrm{Koefisien untuk}\\ &x^{n-k}y^{k},\: \textrm{yaitu}\\ &\textrm{suku ke}-(k+1)\\ &\textrm{adalah}\: \binom{n}{r} \end{aligned}\\\hline \end{array}$

serta

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Jika di suatu kelas terdapat 4 orang akan dipilih 3 orang }\\ &\textrm{untuk menjadi ketua, sekretaris, dan bendahara}.\\ &\textrm{Tentukanlah banyak cara memilih 3 orang tersebut?}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Karena ada 4 orang, misal A, B, C, dan D yang}\\ &\textrm{akan dipilih 3 orang untuk menduduki posisi} \\ &\textrm{ketua, sekretaris, dan bendahara, maka kita tinggal}\\ &\textrm{buat permutasinya, yaitu posisi ketua dapat dipilih }\\ &\textrm{dengan 4 cara, sekretaris dapat dipilih dengan 3 cara}, \\ &\textrm{dan bendahara dapat dipilih dengan 2 cara. atau} \\ &\color{blue} P(4,3)=\displaystyle \frac{4!}{(4-3)!}=\frac{4!}{1!}=\frac{4\times 3\times 2\times 1}{1}=24\: \: \textrm{cara}\\ &\textrm{Berikut ilustrasinya dengan diagram pohon} \end{aligned} \end{array}$

$\color{red}\begin{cases} A&\begin{cases} B & \begin{cases} C &\rightarrow ABC\\ D & \rightarrow ABD \end{cases} \\ C & \begin{cases} B &\rightarrow ACB\\ D & \rightarrow ACD \end{cases} \\ D & \begin{cases} B &\rightarrow ADB \\ C &\rightarrow ADC \end{cases} \end{cases} \\ \\ B&\begin{cases} A & \begin{cases} C &\rightarrow BAC\\ D & \rightarrow BAD \end{cases} \\ C & \begin{cases} A &\rightarrow BCA\\ D & \rightarrow BCD \end{cases} \\ D & \begin{cases} A &\rightarrow BDA \\ C &\rightarrow BDC \end{cases} \end{cases} \\ \\ C&\begin{cases} A & \begin{cases} B &\rightarrow CAB\\ D & \rightarrow CAD \end{cases} \\ B & \begin{cases} A &\rightarrow CBA\\ D & \rightarrow CBD \end{cases} \\ D & \begin{cases} A &\rightarrow CDA \\ B &\rightarrow CDB \end{cases} \end{cases} \\ \\ D&\begin{cases} A & \begin{cases} B &\rightarrow DAB\\ C & \rightarrow DAC \end{cases} \\ B & \begin{cases} A &\rightarrow DBA\\ C & \rightarrow DBC \end{cases} \\ C & \begin{cases} A &\rightarrow DCA \\ B &\rightarrow DCB \end{cases} \end{cases} \end{cases}$

$\begin{array}{ll}\\ 2.&\textrm{Seorang anak akan mengambil 4 buah bola dari}\\ &\textrm{10 warna yang berbeda. Berapakah banyak}\\ &\textrm{kombinasi warna yang berbeda yang diambil}\\ &\textrm{oleh Andi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}n=10&\: \: \textrm{dan}\: \: r=4\\ C(n,r)&=\displaystyle \frac{n!}{r!(n-r)!}\\ C(10,4)&=\displaystyle \frac{10!}{4!(10-4)!}\\ &=\displaystyle \frac{10!}{4!\times 6!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6!}{(4\times 3\times 2\times 1)\times 6!}\\ &=420\: \: \textrm{kombinasi warna bola berbeda} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Berapa banyak cara dapat memilih untuk}\\ &\textrm{3 perwakilan dari 10 anggota suatu}\\ &\textrm{kelompok, jika}\\ &\textrm{a. tanpa perlakuan khusus}\\ &\textrm{b. salah seorang harus terpilih}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Dengan tanpa perlakuan}\\ &\textrm{memilih 3 orang dari 10 orang adalah}:\\ &C(10,3)=\displaystyle \frac{10!}{3!(10-3)!}=\frac{10!}{3!\times 7!}=\color{blue}120\\ \textrm{b}.\quad&\textrm{Dengan perlakuan 1 orang terpilih}\\ &\color{red}(\textrm{1 orang ini artinya tidak perlu diperhitungkan})\\ &\textrm{memilih 2 orang dari 9 orang adalah}:\\ &C(9,2)=\displaystyle \frac{9!}{2!(9-2)!}=\frac{9!}{2!\times 8!}=\color{blue}36 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Berapa banyak cara dapat memilih 2 buku}\\ &\textrm{matematika dan 3 buku fisika serta 4 buku}\\ &\textrm{ekonomi pada suatu lemari buku yang}\\ &\textrm{di dalamnya terdapat 10 buku matematika,}\\ &\textrm{11 buku fisika dan 12 buku ekonomi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Banyak}&\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,2)\times C(11,3)\times C(12,4)\\ &=\displaystyle \frac{10!}{2!\times 8!}\times \frac{11!}{3!\times 8!}\times \frac{12!}{4!\times 8!}\\ &=\displaystyle \frac{10\times 9}{1\times 2}\times \frac{11\times 10\times 9}{1\times 2\times 3}\times \frac{12\times 11\times 10\times 9}{1\times 2\times 3\times 4}\\ &=\color{red}3675375 \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Johnaes, Kastolan, & Sulasim. 2004. Kompetensi Matematika SMA Kelas 2 Semester 1 Program Ilmu Sosial KBK 2004. Jakarta: YUDHISTIRA.
2. Kartini, Suprapto, Subandi, & Setiyadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
3. Sobirin. 2006. Kompas Matematika Strategi Praktis Menguasai Tes Matematika. Jakarta: KAWAN PUSTAKA.

Vektor di Dimensi Tiga

$\color{blue}\textrm{A. Vektor Di Ruang}$

Perhatikanlah ilustrasi gambar berikut

$\begin{array}{|c|c|}\hline \textrm{Nama}&\textbf{R}^{3}\\\hline \textrm{Vektor Satuan}&\textrm{Ruang (Bidang XYZ)}\\\hline \hat{e}_{\bar{a}}=\displaystyle \frac{\bar{a}}{\left | \bar{a} \right |}&\begin{cases} i= &\textrm{vektor satuan} \\ &\textrm{yang searah sumbu X}\\ j= &\textrm{Vektor satuan}\\ &\textrm{yang searah sumbu Y}\\ k=&\textrm{Vektor satuan}\\ &\textrm{searah sumbu Z} \end{cases} \\\hline \textrm{Vektor nol}&\overrightarrow{O}=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}\\\hline \textrm{Vektor posisi}&\overrightarrow{OP}=\vec{p}=\begin{pmatrix} p_{1}\\ p_{2}\\ p_{3} \end{pmatrix}=p_{1}\bar{i}+p_{2}\bar{j}+p_{3}\bar{j}\\\hline \textrm{Besar Vektor}&\overrightarrow{OP}=\sqrt{p_{1}^{2}+p_{2}^{2}+p_{3}^{2}}\\\hline \end{array}$

$\color{blue}\textrm{B. Operasi Vektor}$

$\color{blue}\textrm{1. Sifat-Sifat Aljabar Vektor}$

$\begin{array}{|l|l|l|}\hline 1.&\textrm{Komutatif penjumlahan}&\vec{a}+\vec{b}=\vec{b}+\vec{a}\\\hline 2.&\textrm{Asosiatif penjumlahan}&\left ( \vec{a}+\vec{b} \right )+\vec{c}=\vec{a}+\left ( \vec{b}+\vec{c} \right )\\\hline 3.&\textrm{Elemen Identitas}&\vec{a}+\vec{0}=\vec{0}+\vec{a}=\vec{a}\\\hline 4.&\textrm{Invers Penjumlahan}&\vec{a}+\left ( -\vec{a} \right )=\left ( -\vec{a} \right )+\vec{a}=\vec{0}\\\hline 5.&\textrm{Perkalian dengan skalar}&k\left ( l\vec{a} \right )=\left ( kl \right )\vec{a}\\ &&k\left ( \vec{a}+ \vec{b} \right )=k\vec{a}+k\vec{b}\\ &&k\left ( \vec{a}- \vec{b} \right )=k\vec{a}-k\vec{b}\\\hline 6.&\begin{aligned}&\textrm{Jika A, B, dan C segaris }\\ &\color{blue}\textrm{(Kolinear)} \end{aligned}&\begin{cases} \overrightarrow{AB}=k\overrightarrow{BC} \\ \overrightarrow{AC}=k\overrightarrow{AB} \\ dll \end{cases}\\\hline \end{array}$.

$\begin{array}{|c|c|}\hline \color{blue}\textrm{Vektor}&\color{blue}\textrm{Contoh}\\\hline \vec{z}=a\vec{i}+b\vec{j}+c\vec{k}&\begin{aligned}&\textrm{diketahui}\: \: \vec{p}=\vec{i}-2\vec{j}+2\vec{k}\\ &\textrm{maka pangjang vektor}\: \: \vec{p}\: \: \textrm{adalah}\\ &\left | \vec{p} \right |=\sqrt{1^{2}+(-2)^{2}+2^{2}}\\ &\quad\: \: =\sqrt{1+4+4}=\sqrt{9}=3 \end{aligned}\\\hline &\begin{aligned}&\textrm{Vektor satuan dari}\: \: \vec{p}\: \: \textrm{adalah}\\ &\vec{e}_{\vec{p}}=\frac{\vec{p}}{\left | \vec{p} \right |}=\displaystyle \frac{\begin{pmatrix} 1\\ -2\\ 2 \end{pmatrix}}{3}\\ &=\displaystyle \frac{1}{3}\begin{pmatrix} 1\\ -2\\ 2 \end{pmatrix}=\displaystyle \begin{pmatrix} \frac{1}{3}\\ -\frac{2}{3}\\ \frac{2}{3} \end{pmatrix} \end{aligned}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui vektor-vektor}\: \overrightarrow{a}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}\\ &\overrightarrow{b}=\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix},\: \: \textrm{dan}\: \: \overrightarrow{c}=\begin{pmatrix} 7\\ 0\\ 4 \end{pmatrix},\\ & \textrm{tentukanlah hasil dari}\\ &\textrm{a}.\quad \overrightarrow{a}+\overrightarrow{b}\\ &\textrm{b}.\quad 6\overrightarrow{a}+2\overrightarrow{b}\\ &\textrm{c}.\quad 2\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\\ &\textrm{d}.\quad \displaystyle \frac{1}{2}\overrightarrow{c}-\overrightarrow{a}+\displaystyle \frac{3}{4}\overrightarrow{b}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}\quad&\overrightarrow{a}+\overrightarrow{b}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}+\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix}\\ &=\begin{pmatrix} 2+(-3)\\ 1+(-5)\\ (-4)+2 \end{pmatrix}\\ &=\begin{pmatrix} 2-3\\ 1-5\\ -4+2 \end{pmatrix}=\color{red}\begin{pmatrix} -1\\ -4\\ -2 \end{pmatrix}\\ \textrm{b}.\quad&6\overrightarrow{a}+2\overrightarrow{b}=6\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}+2\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix}\\ &=\begin{pmatrix} 18-6\\ 6-10\\ -24+4 \end{pmatrix}=\color{red}\begin{pmatrix} 12\\ -4\\ -20 \end{pmatrix}\\ \textrm{c}.\quad&2\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\\ &2\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}-\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix}+\begin{pmatrix} 7\\ 0\\ 4 \end{pmatrix}\\ &=\begin{pmatrix} 4+3+7\\ 2+5+0\\ -8-2+4 \end{pmatrix}=\color{red}\begin{pmatrix} 17\\ 7\\ -6 \end{pmatrix}\\ \textrm{d}.\quad&\displaystyle \frac{1}{2}\overrightarrow{c}-\overrightarrow{a}+\displaystyle \frac{3}{4}\overrightarrow{b}=\cdots \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui vektor-vektor}\: \overrightarrow{a}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}\\ &\textrm{tentukanlah}\: \: \left | \overrightarrow{a} \right |\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\left | \overrightarrow{a} \right |&=\sqrt{2^{2}+1^{2}+(-4)^{2}}\\ &=\sqrt{4+1+16}\\ &=\color{red}\sqrt{21} \end{aligned} \end{array}$

$\color{blue}\textrm{2. Perkalian Skalar Dua Vektor}$

Konsep perkalian skalar dua buah vektor di ruang sama persis dengan konsep di bidang, yaitu:

$\color{red}\overrightarrow{a}\cdot \overrightarrow{b}=\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |\cos \theta$.

Misalkan diketahui

$\color{red}\begin{aligned}&\overrightarrow{a}=\begin{pmatrix} a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}, \overrightarrow{b}=\begin{pmatrix} b_{1}\\ b_{2}\\ b_{3} \end{pmatrix},\: \: \color{black}\textrm{maka}\\ & \overrightarrow{a} \cdot \overrightarrow{b} =\color{black}\begin{pmatrix} a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}\cdot \begin{pmatrix} b_{1}\\ b_{2}\\ b_{3} \end{pmatrix}\\ &\qquad\quad =\color{black}a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Diketahui vektor-vektor}\: \overrightarrow{a}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}\\ &\overrightarrow{b}=\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix},\: \: \textrm{dan}\: \: \overrightarrow{c}=\begin{pmatrix} 7\\ 0\\ 4 \end{pmatrix},\\ & \textrm{tentukanlah hasil dari}\\ &\textrm{a}.\quad \overrightarrow{a}\cdot \overrightarrow{b}\\ &\textrm{b}.\quad \overrightarrow{a}\cdot \overrightarrow{c}\\ &\textrm{c}.\quad \overrightarrow{b}\cdot \overrightarrow{c}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}\quad&\overrightarrow{a}\cdot \overrightarrow{b}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}\cdot \begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix}\\ &=(2)(-3)+(1)(-5)+(-4)(2)\\ &=-6-5-8=\color{red}-19\\ \textrm{b}\quad&\overrightarrow{a}\cdot \overrightarrow{c}=\begin{pmatrix} 2\\ 1\\ -4 \end{pmatrix}\cdot \begin{pmatrix} 7\\ 0\\ 4 \end{pmatrix}\\ &=(2)(7)+(1)(0)+(-4)(4)\\ &=14+0-16=\color{red}-2\\ \textrm{c}\quad&\overrightarrow{b}\cdot \overrightarrow{c}=\begin{pmatrix} -3\\ -5\\ 2 \end{pmatrix}\cdot \begin{pmatrix} 7\\ 0\\ 4 \end{pmatrix}\\ &=(-3)(7)+(-5)(0)+(2)(4)\\ &=-21+0+8=\color{red}-13 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah nilai}\: \: t\: \: \textrm{jika}\\ & \overrightarrow{p}=3\bar{i}+t\bar{j}+\bar{k}\: \: \textrm{dan}\: \: \overrightarrow{p}\cdot \overrightarrow{p}=13\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}&\overrightarrow{p}\cdot \overrightarrow{p}=13\\ &\overrightarrow{p}\cdot \overrightarrow{p}=\left | \overrightarrow{p} \right |\left | \overrightarrow{p} \right |\cos 0^{\circ}=13,\\ &\qquad\qquad \color{blue}\textrm{ingat bahwa}\: \: \angle \left ( \overrightarrow{p},\overrightarrow{p} \right )=0^{\circ}\\ &\qquad\qquad \color{blue}\textrm{dan nilai}\: \: \cos 0^{\circ}=1,\\ & \color{black}\textrm{maka}\\ &\overrightarrow{p}\cdot \overrightarrow{p}=\left | \overrightarrow{p} \right |^{2}.1=13\Leftrightarrow \left | \overrightarrow{p} \right |^{2}=13\\ &\Leftrightarrow \left (\sqrt{3^{2}+t^{2}+1^{2}} \right )^{2}=13\\ &\Leftrightarrow 3^{2}+t^{2}+1^{2}=13\\ &\Leftrightarrow 9+t^{2}+1=13\\ &\Leftrightarrow t^{2}=13-9-1=10\\ &\Leftrightarrow t^{2}=3\\ &\Leftrightarrow t=\color{red}\pm \sqrt{3} \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Diketahui}\: \: \overrightarrow{p}=\begin{pmatrix} -2\\ 1\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{q}=\begin{pmatrix} 4\\ -1\\ t \end{pmatrix}\\ &\textrm{Jika}\: \: \overrightarrow{p}\: \: \textrm{tegak lurus}\: \: \overrightarrow{q}\: \: \textrm{maka}\\ &\textrm{tentukanlah nilai}\: \: t\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}\\ &\overrightarrow{p}=\begin{pmatrix} -2\\ 1\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{q}=\begin{pmatrix} 4\\ -1\\ t \end{pmatrix}\\ &\textrm{dengan}\: \: \overrightarrow{p}\: \: \textrm{dan}\: \: \overrightarrow{q}\: \: \textrm{tegak lurus}\\ &\textrm{artinya}\: \: \color{blue}\angle \left ( \overrightarrow{p},\overrightarrow{q} \right )=90^{\circ}.\: \color{black}\textrm{Sehingga}\\ &\textrm{nilai}\: \: \color{blue}\cos 90^{\circ}=0\\ &\textrm{maka}\\ &\overrightarrow{p}\cdot \overrightarrow{q}=\left | \overrightarrow{p} \right |\left | \overrightarrow{q} \right |\cos \theta \\ &\overrightarrow{p}\cdot \overrightarrow{q}=\left | \overrightarrow{p} \right |\left | \overrightarrow{q} \right |\cdot 0=0\\ &\Leftrightarrow \: \begin{pmatrix} -2\\ 1\\ 3 \end{pmatrix}\cdot \begin{pmatrix} 4\\ -1\\ t \end{pmatrix}=0\\ &\Leftrightarrow \: (-2)(4)+(1)(-1)+(3)(t)=0\\ &\Leftrightarrow \: -8-1+3t=0\\ &\Leftrightarrow \: 3t=9\\ &\Leftrightarrow \: t=\color{red}3 \end{aligned} \end{array}$.

DAFTAR PUSTAKA

1. Yuana, R.A., Indriyastuti. 2017. Persektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan Matematika dan Ilmu Alam. Solo: PT TIGA SERANGKAI MANDIRI.

Lanjutan Contoh Soal Vektor Dimensi Dua (Bagian 3)

$\begin{array}{ll}\\ 7&\textrm{Jika}\: \: \bar{a}=\begin{pmatrix} 4\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \bar{b}=\begin{pmatrix} 1\\ 2 \end{pmatrix}\\ &\textrm{tentukanlah}\\ &\textrm{a}.\quad \bar{a}+\bar{b}\qquad\qquad\qquad \textrm{d}.\quad \left ( 3\bar{a}+3\bar{b} \right )\\ &\textrm{b}.\quad \bar{b}+\bar{a}\, \qquad\qquad\qquad \textrm{e}.\quad 2(\bar{a}-\bar{b})\\ &\textrm{c}.\quad 3(\bar{a}+ \bar{b})\: \: \, \, \: \qquad \qquad \textrm{f}.\quad 2 \bar{a}-2\bar{b}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}\quad &\bar{a}+\bar{b}=\begin{pmatrix} 4\\ -3 \end{pmatrix}+\begin{pmatrix} 1\\ 2 \end{pmatrix}=\begin{pmatrix} 4+1\\ -3+2 \end{pmatrix}=\begin{pmatrix} 5\\ -1 \end{pmatrix}\\ \textrm{b}\quad &\bar{b}+\bar{a}=\begin{pmatrix} 1\\ 2 \end{pmatrix}+\begin{pmatrix} 4\\ -3 \end{pmatrix}=\begin{pmatrix} 1+4\\ 2+(-3) \end{pmatrix}=\begin{pmatrix} 5\\ -1 \end{pmatrix}\\ \textrm{c}\quad &\cdots \\ \textrm{d}\quad &3\bar{a}+3\bar{b}=3\begin{pmatrix} 4\\ -3 \end{pmatrix}+3\begin{pmatrix} 1\\ 2 \end{pmatrix}\\ &=\begin{pmatrix} 12\\ -9 \end{pmatrix}+\begin{pmatrix} 3\\ 6 \end{pmatrix}=\begin{pmatrix} 12+3\\ -9+6 \end{pmatrix}=\begin{pmatrix} 15\\ -3 \end{pmatrix}\\ \textrm{e}\quad &\cdots \\ \textrm{f}\quad &\cdots \end{aligned} \end{array}$

$\begin{array}{ll}\\ 8.&\textrm{Perhatikanlah gambar berikut} \end{array}$.

$.\qquad\begin{array}{ll}\\ &\textrm{Pada Balok ABCD.EFGH diatas diketahui }\\ &\textrm{DA = 4 cm, DC = 5 cm, dan DH 3 cm}.\\ &\textrm{Misalkan}\: \: \vec{i}\: \: \textrm{adalah vektor satuan dengan arah }\\ &\textrm{sama dengan}\: \: \overrightarrow{DA},\: \vec{j}\: \: \textrm{adalah vektor satuan }\\ &\textrm{dengan arah sama}\: \: \overrightarrow{DC}\: ,\: \textrm{dan}\: \: \vec{k}\\ &\textrm{adalah vektor satuan dengan arah sama dengan}\: \: \overrightarrow{DH}.\: \\ &\textrm{Nyatakanlah vektor-vektor berikut dalam vektor}\: \: \vec{i},\: \vec{j}\: \textrm{dan}\: \: \vec{k}.\\ &\begin{array}{ll}\\ \textrm{a}.&\overrightarrow{DA},\: \: \overrightarrow{DC}\: \: \textrm{dan} \: \: \overrightarrow{DH}\\ \textrm{b}.&\overrightarrow{DB}\: \: \: \: \textrm{dan}\: \: \overrightarrow{DF}\\ \textrm{c}.&\overrightarrow{DP}\: \: \textrm{jika}\: \: P\: \: \textrm{titik tengan}\: \: EF\\ \textrm{d}.&\overrightarrow{DQ}\: \: \textrm{jika}\: \: Q\: \: \textrm{titik pada perpanjangan}\\ & FG\: \: \textrm{dengan}\: \: FG=GQ\end{array} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Jawab}:\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{a}.&\begin{cases} \overrightarrow{DA}=4\vec{i}\\ \overrightarrow{DC}=5\vec{j} \\ \overrightarrow{DH}=3\vec{k} \end{cases}\\ &\\ &\\ \end{aligned}&\begin{aligned}\textrm{b}.\: \overrightarrow{DB}&=\overrightarrow{DC}+\overrightarrow{CB}\\ &=\overrightarrow{DC}+\overrightarrow{DA}\\ &=5\vec{j}+4\vec{i}\\ \overrightarrow{DF}&=\overrightarrow{DB}+\overrightarrow{BF}\\ &=4\vec{i}+5\vec{j}+3\vec{k} \end{aligned}\\\hline \end{array}\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{c}.\: \overrightarrow{DP}&=\overrightarrow{DE}+\overrightarrow{EP}\\ &=\overrightarrow{DA}+\overrightarrow{AE}+\overrightarrow{EP}\\ &=4\vec{i}+3\vec{k}+\frac{1}{2}\overrightarrow{EF}\\ &=4\vec{i}+3\vec{k}+\frac{1}{2}\overrightarrow{DC}\\ &= 4\vec{i}+3\vec{k}+\frac{1}{2}\left ( 5\vec{j} \right )\\ &=4\vec{i}+\frac{5}{2}\vec{j}+3\vec{k}\end{aligned}&\begin{aligned}\textrm{d}.\: \overrightarrow{DQ}&=\overrightarrow{DG}+\overrightarrow{GQ}\\ &=\overrightarrow{DC}+\overrightarrow{CG}+\overrightarrow{GQ}\\ &=\overrightarrow{DC}+\overrightarrow{DH}+\overrightarrow{AD}\\ &=\overrightarrow{DC}+\overrightarrow{DH}-\overrightarrow{DA}\\ &=5\vec{j}+3\vec{k}-4\vec{i}\\ &\\ &\\ & \end{aligned}\\\hline \end{array} \end{aligned}$

$\begin{array}{ll}\\ 9.&\textrm{Diketahui}\: \: \vec{a}=\begin{pmatrix} -5\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \vec{b}=\begin{pmatrix} 6\\ -2 \end{pmatrix}.\\ & \textrm{Tentukanlah}\\ &\textrm{a}.\quad \vec{a}-\vec{b}\qquad\qquad \textrm{b}.\quad \vec{b}-\vec{a}\\ &\textrm{c}.\quad 4\left ( \vec{a}-\vec{b} \right )\qquad\qquad \textrm{d}.\quad 4\vec{a}-4\vec{b}\\\\ &\textrm{Jawab}:\\ &\begin{array}{llll}\\ \begin{aligned}a.\quad \vec{a}-\vec{b}&=\vec{a}+\left ( -\vec{b} \right )\\ &=\begin{pmatrix} -5\\ 3 \end{pmatrix}+\begin{pmatrix} -6\\ 2 \end{pmatrix}\\ &=\begin{pmatrix} -11\\ 5 \end{pmatrix} \end{aligned}&\\ \begin{aligned}b.\quad \vec{b}-\vec{a}&=\vec{b}+\left ( -\vec{a} \right )\\ &=\begin{pmatrix} 6\\ -2 \end{pmatrix}+\begin{pmatrix} 5\\ -3 \end{pmatrix}\\ &=\begin{pmatrix} 11\\ -5 \end{pmatrix} \end{aligned}\\ \begin{aligned}c.\quad 4\left ( \vec{a}-\vec{b} \right )&=4\begin{pmatrix} -11\\ 5 \end{pmatrix}\\ &=\begin{pmatrix} -44\\ 20 \end{pmatrix}\\ & \end{aligned}&\\ \end{array} \end{array}$

$\begin{array}{ll}\\ 10.&\textrm{Diketahui}\: \: \vec{p}=\begin{pmatrix} 4\\ -3 \end{pmatrix}\: \: \textrm{dan}\: \: \vec{q}=\begin{pmatrix} 1\\ 2 \end{pmatrix}.\\ & \textrm{Tentukanlah}\\ &\textrm{a}.\quad \vec{p}+\vec{q}\qquad\qquad \textrm{b}.\quad \vec{q}+\vec{p}\\ &\textrm{c}.\quad 4\left ( \vec{p}+\vec{q} \right )\qquad\qquad \textrm{d}.\quad 4\vec{p}+4\vec{q}\\ &\textrm{e}.\quad 4\left ( \vec{p}-\vec{q} \right )\: \: \quad\quad \textrm{f}.\quad 4\vec{p}-4\vec{q}\\\\ &\textrm{Jawab}:\\ &\begin{array}{llll}\\ \begin{aligned}a.\quad \vec{p}+\vec{q}&=\begin{pmatrix} 4\\ -3 \end{pmatrix}+\begin{pmatrix} 1\\ 2 \end{pmatrix}\\ &=\begin{pmatrix} 5\\ -1 \end{pmatrix} \end{aligned}&\begin{aligned}b.\quad \vec{q}+\vec{p}&=\begin{pmatrix} 1\\ 2 \end{pmatrix}+\begin{pmatrix} 4\\ -3 \end{pmatrix}\\ &=\begin{pmatrix} 5\\ -1 \end{pmatrix} \end{aligned}&&\\ \end{array} \end{array}$

$\begin{array}{ll}\\ 11.&\textrm{Pada contoh soal No. 8 tentukanlah }\\ &\textrm{panjang vektor}\: \: \overrightarrow{DA},\: \overrightarrow{DP}\: \textrm{dan}\: \: \overrightarrow{DQ}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\left |\overrightarrow{DA} \right |=4\: cm,\\ &\left |\overrightarrow{DP} \right |^{2}=\left | \overrightarrow{DE} \right |^{2}+\left | \overrightarrow{EP} \right |^{2}\\ &=\left | \overrightarrow{DA} \right |^{2}+\left | \overrightarrow{AE} \right |^{2}+\left | \overrightarrow{EP} \right |^{2}\\ &=4^{2}+3^{2}+\left ( \frac{5}{2} \right )^{2}\\ &=16+9+\frac{25}{4}\\ &\left | \overrightarrow{DP} \right |=\sqrt{\frac{125}{4}}\\ &=\displaystyle \frac{5}{2}\sqrt{5}\: cm,\: \: \textrm{dan}\\ &\left | \overrightarrow{DQ} \right |^{2}=\left | \overrightarrow{DG} \right |^{2}+\left | \overrightarrow{GQ} \right |^{2}\\ &=\left | \overrightarrow{DC} \right |^{2}+\left | \overrightarrow{CG} \right |^{2}+\left | \overrightarrow{GQ} \right |^{2}\\ &=5^{2}+3^{2}+4^{2}\\ &=25+9+16\\ &=50\\ &\left | \overrightarrow{DQ} \right |&=\sqrt{50}\\ &=5\sqrt{2}\: cm \end{aligned} \end{array}$

$\begin{array}{ll}\\ 12.&\textrm{Perhatikanlah gambar di bawah ini}\\ &\textrm{dan nyatakan titik-titik pada gambar }\\ &\textrm{tersebut dalam vektor posisi}\\ \end{array}$

$.\qquad\begin{aligned}&\textrm{Jawab}:\\ &\textrm{Perhatikanlah gambar berikut} \end{aligned}$

$.\qquad\begin{array}{|l|l|}\hline \textrm{Titik}&\textrm{Vektor Posisi}\\\hline P(5,3)&\vec{p}=\begin{pmatrix} 5\\ 3 \end{pmatrix}\\\hline Q(2,-3)&\vec{q}=\begin{pmatrix} 2\\ -3 \end{pmatrix}\\\hline R(-5,-1)&\vec{r}=\begin{pmatrix} -5\\ -1 \end{pmatrix}\\\hline S(-3,7)&\vec{s}=\begin{pmatrix} -3\\ 7 \end{pmatrix}\\\hline \end{array}$

$\begin{array}{ll}\\ 13.&\textrm{Perhatikanlah gambar pada soal No. 12 di atas. }\\ &\textrm{Tentukanlah vektor-vektor berikut}\\ &\textrm{a}.\quad \overrightarrow{PQ}\\ &\textrm{b}.\quad \overrightarrow{PS}\\ &\textrm{c}.\quad \overrightarrow{QS}\\ &\textrm{d}.\quad \overrightarrow{QP}+\overrightarrow{PS}\\\\ &\textrm{Jawab}:\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{a}.\quad \overrightarrow{PQ}&=\overrightarrow{PO}+\overrightarrow{OQ}\\ &=-\overrightarrow{OP}+\overrightarrow{OQ}\\ &=\overrightarrow{OQ}-\overrightarrow{OP}\\ &=\vec{q}-\vec{p}\\ &=\begin{pmatrix} 2\\ -3 \end{pmatrix}-\begin{pmatrix} 5\\ 3 \end{pmatrix}\\ &=\begin{pmatrix} -3\\ -6 \end{pmatrix} \end{aligned}&\begin{aligned}\textrm{b}.\quad \overrightarrow{PS}&=\vec{s}-\vec{p}\\ \textrm{dengan }&\textrm{cara semisal poin a}\\ \overrightarrow{PS}&=\begin{pmatrix} -3\\ 7 \end{pmatrix}-\begin{pmatrix} 5\\ 3 \end{pmatrix}\\ &=\begin{pmatrix} -8\\ 4 \end{pmatrix}\\ &\\ & \end{aligned} \\\hline \end{array}\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{c}.\quad \overrightarrow{QS}&=\vec{s}-\vec{q}\\ &=\begin{pmatrix} -3\\ 7 \end{pmatrix}-\begin{pmatrix} 2\\ -3 \end{pmatrix}\\ &=\begin{pmatrix} -5\\ 10 \end{pmatrix} \end{aligned}&\begin{aligned}\textrm{d}.\quad \overrightarrow{QP}+\overrightarrow{PS}&=\overrightarrow{QS}\\ &=\begin{pmatrix} -5\\ 10 \end{pmatrix}\\ \textrm{lihat jawaban}&\textrm{ poin c} \end{aligned}\\\hline \end{array} \end{array}$

Contoh Soal Vektor di Dimensi Dua (Matematika Peminatan Kelas X) Bagian 2

$\begin{array}{ll}\\ 4.&\color{blue}\textrm{Perhatikanlah ilustrasi gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Nyatakanlah vektor-vektor di atas dalam}\\ &\textrm{a}.\quad \textrm{vektor kolom}\\ &\textrm{b}.\quad \textrm{vektor baris}\\ &\textrm{c}.\quad \textrm{vektor basis}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Vektor di atas saat dinyatakan dengan}\\ &\begin{array}{|c|l|l|l|}\hline \textrm{No}&\quad\textrm{Kolom}&\qquad\textrm{Baris}&\qquad\textrm{Basis}\\\hline 1&\bar{a}=\begin{pmatrix} 2\\ 4 \end{pmatrix}&\bar{a}=\begin{pmatrix} 2, & 4 \end{pmatrix}&\bar{a}=2\bar{i}+4\bar{j}\\\hline 2&\bar{b}=\begin{pmatrix} 4\\ 2 \end{pmatrix}&\bar{b}=\begin{pmatrix} 4, & 2 \end{pmatrix}&\bar{b}=4\bar{i}+2\bar{j}\\\hline 3&\bar{c}=\begin{pmatrix} 5\\ 0 \end{pmatrix}&\bar{c}=\begin{pmatrix} 5, & 0 \end{pmatrix}&\bar{c}=5\bar{i}\\\hline 4&\bar{d}=\begin{pmatrix} -2\\ -4 \end{pmatrix}&\bar{d}=\begin{pmatrix} -2, & -4 \end{pmatrix}&\bar{d}=-2\bar{i}-4\bar{j}\\\hline 5&\bar{e}=\begin{pmatrix} 0\\ -4 \end{pmatrix}&\bar{e}=\begin{pmatrix} 0, & -4 \end{pmatrix}&\bar{e}=-4\bar{j}\\\hline 6&\bar{f}=\begin{pmatrix} 3\\ -3 \end{pmatrix}&\bar{f}=\begin{pmatrix} 3, & -3 \end{pmatrix}&\bar{f}=3\bar{i}-3\bar{j}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 5&\textrm{Tentukanlah panjang atau besar dari}\\ &\textrm{vektor-vektor berikut}\\ &\textrm{a}.\quad \bar{a}=\begin{pmatrix} -4\\ 3 \end{pmatrix}\quad\quad\quad \textrm{d}.\quad \bar{d}=\begin{pmatrix} 6, &-8 \end{pmatrix}\\ &\textrm{b}.\quad \bar{b}=\begin{pmatrix} 5\\ 0 \end{pmatrix}\qquad\quad\quad \textrm{e}.\quad \bar{e}=2\bar{i}+4\bar{j}\\ &\textrm{c}.\quad \bar{c}=\begin{pmatrix} 4, & -6 \end{pmatrix}\: \qquad \textrm{f}.\quad \bar{f}=-5\bar{i}+12\bar{j}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Lambang panjang suatu vektor adalah}:\\ &\color{red}\left | \begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}},\: \: \color{black}\textrm{maka}\\ &\bullet \: \left | \bar{a} \right |=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5\\ &\bullet \: \left | \bar{b} \right |=\sqrt{5^{2}+0^{2}}=\sqrt{25}=5\\ &\bullet \: \left | \bar{c} \right |=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\\ &\bullet \: \left | \bar{d} \right |=\sqrt{6^{2}+(-8)^{2}}=\sqrt{36+64}=\sqrt{100}=10\\ &\bullet \: \left | \bar{e} \right |=\sqrt{2^{2}+4^{2}}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\\ &\bullet \: \left | \bar{f} \right |=\sqrt{(-5)^{2}+12^{2}}=\sqrt{25+144}=\sqrt{169}=13 \end{array}$

$\begin{array}{ll}\\ 6&\textrm{Pada soal no.4 di atas dengan menggunakan}\\ &\textrm{aturan segitiga dan jajar genjang, gambarlah}\\ &\textrm{vektor-vektor berikut pada kertas berpertak}\\ &\textrm{a}.\quad \bar{a}+\bar{b}\qquad\qquad\qquad \textrm{d}.\quad \left ( \bar{a}+\bar{b} \right )+\bar{c}\\ &\textrm{b}.\quad \bar{b}+\bar{c}\, \qquad\qquad\qquad \textrm{e}.\quad 2\bar{a}+\bar{e}+2\bar{b}+3\bar{d}\\ &\textrm{c}.\quad \bar{a}+\left (\bar{b}+\bar{c} \right )\: \: \quad \qquad \textrm{f}.\quad 2\left ( \bar{a}+\bar{b}+\bar{c}+\bar{d}+\bar{e} \right )\\\\ &\textrm{Jawab}:\\ \end{array}$

Lanjutan Materi Vektor : Proyeksi Ortogonal Suatu Vektor

$\color{blue}\begin{aligned}\textrm{A}.\quad&\textrm{Panjang Proyeksi Ortogonal Suatu}\\ &\textrm{Vektor pada vektor lain} \end{aligned}$.

Perhatikanlah ilstrasi gambar yang dibentuk dari dua vektor berikut

Pada gambar di atas 

$\begin{array}{|c|c|}\hline \triangle \textrm{OAC}&\angle \left ( \overrightarrow{a},\overrightarrow{b} \right )\\\hline \begin{aligned}\cos \theta &=\displaystyle \frac{\left | \overrightarrow{c} \right |}{\left | \overrightarrow{a} \right |}\\ \Leftrightarrow \left | \overrightarrow{c} \right |&=\left | \overrightarrow{a} \right |\cos \theta \: \: ........(1) \end{aligned}&\begin{aligned}\cos \theta &=\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |}\: \: ........(2) \end{aligned}\\\hline \end{array}$.

$\begin{aligned}\textrm{Dari}\: \: (1)\: \: &\textrm{dan} \: \: (2)\: \: \textrm{diperoleh}\\ \left | \overrightarrow{c} \right |&=\left | \overrightarrow{a} \right |\cos \theta \\ &=\left | \overrightarrow{a} \right |\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |} \right )\\ &=\color{red}\left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right | \end{aligned}$

$\color{blue}\begin{aligned}\textrm{B}.\quad&\textrm{Proyeksi Ortogonal Suatu Vektor}\\ &\textrm{pada vektor lain} \end{aligned}$.

$\begin{array}{|c|}\hline {\textrm{Perhatikan pula misal}\: \: \hat{c}\: \: \textrm{adalah vektor satuan dari}\: \: \overrightarrow{c}\: \: \textrm{dan}\: \: \overrightarrow{b},}\\\hline \begin{aligned}\textrm{maka}\: \: \: \overrightarrow{c}&=\left | \overrightarrow{c} \right |\hat{c} \end{aligned}\qquad\qquad \textrm{dan}\qquad\qquad \begin{aligned}\overrightarrow{b}&=\left | \overrightarrow{b} \right |\hat{b}=\left | \overrightarrow{b} \right |\hat{c} \end{aligned}\\\hline {\begin{aligned}\textrm{Sehingga}&\: \: \textbf{proyeksi ortogonal vektor}\: \: \overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\: \: \textrm{adalah}:\\ \overrightarrow{c}&=\left | \overrightarrow{c} \right |\hat{b}\\ &=\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right )\left ( \displaystyle \frac{\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right )\\ &=\left (\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |^{2}} \right )\overrightarrow{b} \end{aligned}}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui vektor}\: \: \overrightarrow{a}=\begin{pmatrix} 3\\ 2 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{b}=\begin{pmatrix} -2\\ 1 \end{pmatrix}.\\ & \textrm{Tentukanlah proyeksi ortogonal vektor}\\ &\overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\: \: \textrm{dan tentukanlah panjangnya} \\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{Misalkan}&\: \: \overrightarrow{c}\: \: \textrm{adalah vektor proyeksi yang dimaksud, }\\ &\textrm{maka}\\ \overrightarrow{c}&=\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |^{2}} \right )\overrightarrow{b}\\ &=\displaystyle \frac{\begin{pmatrix} 3\\ 2 \end{pmatrix}.\begin{pmatrix} -2\\ 1 \end{pmatrix}}{(-2)^{2}+1^{2}}.\overrightarrow{b}=\frac{3.(-2)+2.1}{4+1}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=-\frac{4}{5}\begin{pmatrix} -2\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{8}{5}\\ -\frac{4}{5} \end{pmatrix}\quad \textbf{atau}\\ &=\color{red}\frac{8}{5}\bar{i}-\frac{4}{5}\bar{j} \end{aligned}\\ &\begin{aligned}\textrm{Dan panjang}\: \: &\textrm{vektor proyeksi yang dimaksud adalah}:\\ \left |\overrightarrow{c} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right |\\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ 2 \end{pmatrix}.\begin{pmatrix} -2\\ 1 \end{pmatrix}}{\sqrt{(-2)^{2}+1^{2}}} \right |=\left |\frac{3.(-2)+2.1}{\sqrt{4+1}} \right |\\ &=\left |-\frac{4}{\sqrt{5}} \right |\\ &=\displaystyle \frac{4}{\sqrt{5}}=\color{red}\frac{4}{5}\sqrt{5} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui vektor}\: \: \overrightarrow{a}=3\bar{i}-2\bar{j}+2\bar{k}\: \: \textrm{dan}\: \: \overrightarrow{b}=2\bar{i}-2\bar{j}+\bar{k}\\ &\textrm{Tentukanlah panjang vektor proyeksi ortogonal}\\ &\textrm{a}.\quad \overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\qquad\qquad\qquad \textrm{b}.\quad \overrightarrow{a}\: \: \textrm{pada}\: \: \left ( \overrightarrow{a}+\overrightarrow{b} \right ) \\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad\textrm{Misal}&\textrm{kan}\: \: \overrightarrow{c}\: \: \textrm{adalah vektor proyeksi yang dimaksud,}\\ & \textrm{maka panjanynya}\\ \left |\overrightarrow{c} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right | \\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ -2\\ 2 \end{pmatrix}.\begin{pmatrix} 2\\ -2\\ 1 \end{pmatrix}}{\sqrt{2^{2}+(-2)^{2}+1^{2}}} \right |=\left |\frac{3.2+(-2).(-2)+2.1}{\sqrt{4+4+1}} \right |\\ &=\left | \displaystyle \frac{12}{3} \right |=\color{red}4 \end{aligned}\\ &\begin{aligned}\textrm{b}.\quad\textrm{Misal}&\textrm{kan}\: \: \overrightarrow{f}\: \: \textrm{adalah vektor proyeksi yang dimaksud,}\\ & \textrm{maka panjanynya}\\ \left |\overrightarrow{f} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\left (\overrightarrow{a}+\overrightarrow{b} \right )}{\left |\overrightarrow{a}+ \overrightarrow{b} \right |} \right |\\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ -2\\ 2 \end{pmatrix}.\begin{pmatrix} 3+2\\ -2+(-2)\\ 2+1 \end{pmatrix}}{\sqrt{(3+2)^{2}+(-2+(-2))^{2}+(2+1)^{2}}} \right |\\ &=\left |\frac{3.5+(-2).(-4)+2.3}{\sqrt{25+16+9}} \right |\\ &=\left |\frac{29}{\sqrt{50}} \right |\\ &=\displaystyle \frac{29}{5\sqrt{2}}=\color{red}\frac{29}{10}\sqrt{5} \end{aligned} \end{array}$

Lanjutan Materi Perkalian Skalar Dua Vektor Di Ruang Dimensi Dua (Matematika Peminatan Kelas X)

$\color{blue}\textrm{L. Operasi Perkalian Dua Buah Vektor}$

Perhatikanlah ilustrasi berikut

Bentuk perkalian dari ilustrasi dua vektor di atas dinotasikan dengan  $\color{black}\bar{a}\bullet \bar{b}$. Dimisalkan sebuah vektor  $\color{black}\bar{a}$  dan  vektor  $\color{black}\bar{b}$  membentuk sudut  $\theta$ , maka perkalian skalar dua vektor didefinisikan dengan

$\color{black}\bar{a}\bullet \bar{b}=\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta ,\: \: \color{blue}\textrm{dengan}\: \: \color{black}0^{\circ}\leq \theta \leq 180^{\circ}$

Misalkan diberikan dua vektor   

$\begin{aligned}&\bar{a}=\color{red}\begin{pmatrix} a_{1}\\ a_{2} \end{pmatrix}\: \: \color{black}\textrm{dan}\: \: \bar{b}=\color{blue}\begin{pmatrix} b_{1}\\ b_{2} \end{pmatrix}\\ &\textrm{Sesuai definisi, maka}\\ &\bar{a}\bullet \bar{b}=\color{red}\bar{a_{1}}\color{blue}\bar{b_{1}}\color{black}+\color{red}\bar{a_{2}}\color{blue}\bar{b_{2}} \end{aligned}$

Sebagai bukti diberikan uraian berikut

Perhatikanlah   $\triangle \textbf{AOB}$   di atas, saat kita menentukan ruas garis  AB  yang terbentuk dari vektor posisi  $\color{black}\bar{a}$  dan  $\color{black}\bar{b}$ dengan sudut pengapitnya adalah  $\theta$, maka kita dapat menggunakan aturan COSINUS, yaitu:

$\color{purple}\begin{aligned}\left | \overline{AB} \right |^{2}&=\left | \overline{OA} \right |^{2}+\left | \overline{OB} \right |^{2}-2\left | \overline{OA} \right |\left | \overline{OB} \right |\cos \theta \\ (b_{1}-a_{1})^{2}&+(b_{2}-a_{2})^{2}=a_{1}^{2}+a_{2}^{2}+b_{1}^{2}+b_{2}^{2}-2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta \\ -2a_{1}b_{1}-&2a_{2}b_{2}=-2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta \\ \displaystyle 2a_{1}b_{1}+&2a_{2}b_{2}=\displaystyle 2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta\\ &\textbf{Karena}\\ &\color{blue}\bar{a}\bullet \bar{b}=\displaystyle 2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta\\ \displaystyle 2a_{1}b_{1}+&2a_{2}b_{2}=\bar{a}\bullet \bar{b}\: \: \: \color{black}\blacksquare \end{aligned}$

Dan dari bentuk di atas kita juga akan mendapatkan bentuk:

$\cos \theta =\displaystyle \frac{\bar{a}\bullet \bar{b}}{\left | \bar{a} \right |\left | \bar{b} \right |}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Jika diketahui}\: \: \left | \bar{a} \right |=5,\: \: \textrm{dan}\: \: \left | \bar{b} \right |=8\\ &\textrm{dan kedua vektor itu membentuk sudut}\: \: 60^{\circ}\\ &\textrm{maka nilai}\: \: \bar{a}\bullet \bar{b}=....\\\\ &\textrm{Jawab}\\ &\begin{aligned}\bar{a}\bullet \bar{b}&=\left | \bar{a} \right |\left | \bar{b} \right |\cos \angle \left ( \bar{a},\bar{b} \right )\\ &=5.8.\cos 60^{\circ}\\ &=40\times \displaystyle \frac{1}{2}\\ &=20 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Jika diketahui vektor}\: \: \bar{a} =\begin{pmatrix} 15\\ -11 \end{pmatrix},\: \: \textrm{dan}\: \: \bar{b}=\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &\textrm{Tentukanlah nilai}\: \: \bar{a}\bullet \bar{b}\\\\ &\textrm{Jawab}\\ &\color{blue}\begin{aligned}\bar{a}\bullet \bar{b}&=\begin{pmatrix} 15\\ -11 \end{pmatrix}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=(15)(-2)+(-11)(1)\\ &=-30+(-11)\\ &=-30-11\\ &=-41 \end{aligned} \end{array}$

$\color{blue}\textrm{M. Perbandingan Vektor}$

Perhatikanlah ilustrasi gambar berikut!

Dari gambar tersebut di atas diketahui bahwa titik P dan Q dengan koordinat masing-masing adalah  $(x_{1},y_{1})$  dan  $(x_{1},y_{1})$, dan  $\overrightarrow{PT}:\overrightarrow{TQ}=m:n$ , mak vektor posisi titik T adalah $\vec{t}=\displaystyle \frac{n\vec{p}+m\vec{q}}{m+n}$.

Berikut paparan buktinya

$\begin{aligned}\overrightarrow{PT}:\overrightarrow{TQ}&=m:n\\ \displaystyle \frac{\overrightarrow{PT}}{\overrightarrow{TQ}}&=\frac{m}{n}\\ \displaystyle \frac{\vec{t}-\vec{p}}{\vec{q}-\vec{t}}&=\frac{m}{n}\\ n\left ( \vec{t}-\vec{p} \right )&=m\left ( \vec{q}-\vec{t} \right )\\ n\vec{t}-n\vec{p}&=m\vec{q}-m\vec{t}\\ m\vec{t}+n\vec{t}&=m\vec{q}+n\vec{p}\\ \vec{t}\left ( m+n \right )&=n\vec{p}+m\vec{q}\\ \vec{t}&=\color{red}\displaystyle \frac{n\vec{p}+m\vec{q}}{m+n}\qquad\quad \color{black}\blacksquare \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Perhatikanlah gambar pada soal No. 6 di atas. }\\ &\textrm{Jika titik T terletak pada}\: \overrightarrow{SP},\: \textrm{sehingga}\\&\: \: \overrightarrow{ST}:\overrightarrow{TP}=1:3,\: \textrm{maka}\\ &\textrm{a}.\quad \textrm{Tentukanlah koordinat titik T}\:\\ &\textrm{b}.\quad \textrm{Jika titik M terletak di tengah-tengah}\: \: \overrightarrow{SP},\\ &\qquad \textrm{tentukanlah koordinat titik M}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{a}.\quad \vec{t}&=\displaystyle \frac{3\vec{s}+\vec{p}}{3+1}\\ &=\displaystyle \frac{3\begin{pmatrix} -3\\ 7 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix}}{3+1}\\ &=\displaystyle \frac{1}{4}\left ( \begin{pmatrix} -9\\ 21 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix} \right )\\ &=\displaystyle \frac{1}{4}\begin{pmatrix} -4\\ 24 \end{pmatrix}\\ &=\begin{pmatrix} -1\\ 6 \end{pmatrix}\\ \textrm{jadi}&\: \textrm{koordinat titik}\: \color{red}T(-1,6) \end{aligned}&\begin{aligned}\textrm{b}.\quad \vec{m}&=\displaystyle \frac{1}{2}\left ( \vec{s}+\vec{p} \right )\\ &=\displaystyle \frac{1}{2}\left ( \begin{pmatrix} -3\\ 7 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix} \right )\\ &=\displaystyle \frac{1}{2}\begin{pmatrix} 2\\ 10 \end{pmatrix}\\ &=\begin{pmatrix} 1\\ 5 \end{pmatrix}\\ \textrm{Jadi}&\: \textrm{koordinat titik}\: \color{red}M(1,5)\\ &\\ &\\ & \end{aligned}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui}\: \: \vec{u}=\begin{pmatrix} -8\\ 2 \end{pmatrix}\: \textrm{dan}\: \: \vec{v}=\begin{pmatrix} -4\\ m \end{pmatrix}.\\ &\textrm{Tentukan}\: \: m\: \: \textrm{jika}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\overrightarrow{u}&=k\vec{v}\\ &\quad (\textrm{vektor}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah})\\ \begin{pmatrix} -8\\ 2 \end{pmatrix}&=k\begin{pmatrix} -4\\ m \end{pmatrix}=\begin{pmatrix} -4k\\ mk \end{pmatrix}\\ -8&=-4m\: \: \Rightarrow \: \: m=\displaystyle \frac{-8}{-4}=2\\ \textrm{Jadi}\: &\: \color{red}m=2\\ \end{aligned} \end{array}$

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Perhatikanlah gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad &\textrm{Nyatakan vektor-vektor pada gambar }\\ &\textrm{di atas ke dalam bentuk}\\ &\textrm{a}.\quad \textrm{Vektor kolom}\\ &\textrm{b}.\quad \textrm{Vektor baris}\\ &\textrm{c}.\quad \textrm{Vektor basis} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Pada soal No. 1 di atas, gambarkanlah }\\ &\textrm{vektor-vektor berikut pada kertas berpetak}\\ &\textrm{a}.\quad \vec{a}+\vec{b}\\ &\textrm{b}.\quad \vec{b}+\vec{c}\\ &\textrm{c}.\quad \vec{c}+\vec{d}\\ &\textrm{d}.\quad (\vec{a}+\vec{b})+\vec{c}\\ &\textrm{e}.\quad \vec{b}+(\vec{c}+\vec{d})\\ &\textrm{f}.\quad (\vec{a}+\vec{b})+(\vec{c}+\vec{d})\\ &\textrm{g}.\quad (\vec{a}+\vec{b})-(\vec{c}+\vec{d})\\ &\textrm{h}.\quad \vec{a}+\vec{b}+\vec{c}+\vec{d}+\vec{e}+\vec{f}\\ &\textrm{i}.\quad \vec{a}-\vec{b}+\vec{c}-\vec{d}+\vec{e}-\vec{f}\end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar pada soal No. 6 di atas.}\\ &\textrm{Jika titik T terletak pada}\: \: \overrightarrow{SP},\: \textrm{sehingga}\\ &\overrightarrow{ST}:\overrightarrow{TP}=2:3,\: \textrm{maka}\\ &\textrm{a}.\quad \textrm{Tentukanlah koordinat titik T}\:\\ &\textrm{b}.\quad \textrm{Jika titik M terletak di tengah-tengah}\: \: \overrightarrow{SP},\\ &\qquad \textrm{tentukanlah koordinat titik M}\\ \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui}\: \: \vec{u}=\begin{pmatrix} 16\\ -2 \end{pmatrix}\: \textrm{dan}\: \: \vec{v}=\begin{pmatrix} -4\\ m \end{pmatrix}.\\ &\textrm{Tentukan}\: \: m\: \: \textrm{jika}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah}\end{array}$

DAFTAR PUSTAKA

1. Kuntarti, Sulistiyono, & Kurnianingsih, S. 2005. Matematika untuk SMA dan MA Kelas XII Program Ilmu Alam. Jakarta: PT. Gelora Aksara Pratama.
2. Yuana, R. A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan dan Ilmu Alam. Solo: PT TIGA SERANGKAI PUSTAKA MANDIRI.

Lanjutan Materi Polinom : Akar-Akar Persamaan Polinom

$\color{blue}\textbf{1. Pencarian akar-akar persamaan polinom}$

Persamaan suku banyak/polinom  $a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0$  dengan  $n>1\: \: \textrm{dan}\: \: a_{n}\neq 0$  paling sedikit memiliki sebuah akar riil atau imajiner. Pada bahasan ini untuk mendapatkan akar-akar rasional perlu dilakukan cara coba-coba. Misalkan  $x=h$  kita pilih, selanjutnya tinggal kita buktikan bahwa apakah  $x=h$ apakah akar polinom tersebut atau tidak, jika $f(h)=0$, maka $x=h$ adalah termasuk akar dari polinom tersebut, tetapi jika tidak  atau  $f(h) \neq 0$, maka $x=h$ bukan akar yang diinginkan.

Beberapa petunjuk agar  $x=h$  terarah sebagai akar polinom

• Misalkan  $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}$  dengan  $r$  adalah faktor dari  $a_{0}$, dan  $s$  adalah faktor dari  $a_{n}$, maka akar-akar rasional jika ada adalah  $x=h=\color{red}\displaystyle \frac{r}{s}$.
• Jika pada langkah pertama di atas ditemukan sebuah akar rasional katakanlah  $x=h_{1}$, maka tentukan hasil bagi  $f(x)$  dengan  $x=h_{1}$  ini. Misalkan hasil baginya adalah  $h_{1}(x)$  atau  $\color{blue}f(x)=(x-h_{1})h_{1}(x)$, maka langkah berikutnya carilah akar dari  $h_{1}(x)$ ini. Dan jika didapatkan akar dari  $h_{1}(x)$  adalah  $x=h_{2}$, maka tentukanlah hasil bagi  dari  $h_{1}(x)$  oleh  $x=h_{2}$, katakanlah hasilnya  $h_{2}(x)$, maka  $\color{blue}f(x)=(x-h_{1})(x-h_{2})h_{2}(x)$ demikian seterusnya.

$\color{blue}\textbf{2. Jumlah dan hasil kali akar-akar polinom}$

Untuk fungsi  derajat 2 maka berlaku seperti menentukan rumus jumlah dan selisih pada persamaan kuadrat. Tetapi untuk polinom berderajat tiga  $f(x)=ax^{3}+bx^{2}+cx+d$  saat  $f(x)=0$, maka berlaku

$\begin{aligned}f(x)&=\color{red}ax^{3}+bx^{2}+cx+d\: \: \color{black}\textrm{dengan}\\ &x_{1},\: x_{2},\: x_{3}\: \: \textrm{adalah akar-akarnya, maka}\\ \bullet \: \: &x_{1}+x_{2}+x_{3}=-\displaystyle \frac{b}{a}\\ \bullet \: \: &x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3}=\displaystyle \frac{c}{a}\\ \bullet \: \: &x_{1}\times x_{2}\times x_{3}=-\displaystyle \frac{d}{a}\\ \end{aligned}$

$\begin{aligned}\textrm{Unt}&\textrm{uk yang berderajat empat}\\ f(x)&=\color{red}ax^{4}+bx^{3}+cx^{2}+dx+e\: \: \color{black}\textrm{saat}\: \: f(x)=0\\ &\textrm{dengan}\: \: \: x_{1},\: x_{2},\: x_{3},\: x_{4}\: \textrm{adalah akar-akarnya},\\ &\textrm{maka}\\ \bullet \: \: &x_{1}+x_{2}+x_{3}+x_{4}=-\displaystyle \frac{b}{a}\\ \bullet \: \: &x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{3}+...+x_{3}x_{4}=\displaystyle \frac{c}{a}\\ \bullet \: \: &x_{1} x_{2} x_{3}+x_{1} x_{2} x_{4}+x_{1}x_{3}x_{4}+x_{2} x_{3} x_{4}=-\displaystyle \frac{d}{a}\\ \bullet \: \: &x_{1} x_{2} x_{3}x_{4}=\displaystyle \frac{e}{a} \end{aligned}$

$\begin{aligned}&\color{blue}\textbf{Rumus Tambahan}\\ &\bullet \: \: \: x_{1}^{2}+x_{2}^{2}=\left ( x_{1}+x_{2} \right )^{2}-2x_{1}x_{2}\\ &\bullet \: \: \: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\\ &\qquad =\left ( x_{1}+x_{2}+x_{3} \right )^{2}-2\left ( x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3} \right )\\ &\bullet \: \: \: x_{1}^{3}+x_{2}^{3}+x_{3}^{3}\\ &\qquad =\left ( x_{1}+x_{2}+x_{3} \right )^{3}-3x_{1}x_{2}x_{3}\left ( x_{1}+x_{2}+x_{3} \right ) \end{aligned}$

$\begin{aligned}&\color{blue}\textbf{Teorema Vieta berkaitan polinom}\\ &\textrm{Persamaan polinom berderajat}\: \: n\\ &\color{red}a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0\\ &\textrm{dengan akar-akar}:\: \: \color{purple}x_{1},\: x_{2},\: x_{3},\: \cdots \: ,x_{n},\\ &\textrm{maka}:\\ &\bullet \quad x_{1}+x_{2}+x_{3}+\cdots +x_{n}=\color{blue}-\displaystyle \frac{a_{n-1}}{a_{n}}\\ &\bullet \quad x_{1}x_{2}+x_{1}x_{3}+\cdots +x_{2}x_{3}+\cdots +x_{n-1}x_{n}=\color{magenta}\displaystyle \frac{a_{n-2}}{a_{n}}\\ &\bullet \quad x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+\cdots +x_{n-2}x_{n-1}x_{n}=\color{blue}-\displaystyle \frac{a_{n-3}}{a_{n}}\\ &\qquad\qquad\qquad \vdots \\ &\bullet \quad x_{1}x_{2}x_{3}\cdots x_{n}=\color{magenta}(-1)^{n}.\displaystyle \frac{a_{0}}{a_{n}} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Jika akar-akar dari polinom}\\ &x^{3}+2x^{2}-5x-6=0\: \: \textrm{adalah}\\ &x_{1},\: x_{2},\: \: \textrm{dan}\: \: x_{3},\: \textrm{tentukanlah nilai}\\ &\textrm{a}.\quad x_{1}+ x_{2}+ x_{3}\\ &\textrm{b}.\quad x_{1}x_{2}+ x_{1}x_{3}+ x_{2}x_{3}\\ &\textrm{c}.\quad x_{1}\times x_{2}\times x_{3}\\ &\textrm{d}.\quad x_{1}^{2}+ x_{2}^{2}+ x_{3}^{2}\\\\ &\textrm{Jawab}:\\ &\textrm{Diketahui bahwa}:\: \: \color{red}x^{3}+2x^{2}-5x-6=0\\ &\textrm{dengan koefisien-koefisien variabelnya}\\ & a_{3}=1,\: a_{2}=2,\: a_{1}=-5,\: \: \textrm{dan}\: \: a_{0}=-6\\ &\textrm{Menurut}\: \: \textbf{Teorema Vieta},\: \textrm{maka}\\ &\textrm{a}.\quad x_{1}+ x_{2}+ x_{3}=-\displaystyle \frac{a_{2}}{a_{3}}=-\frac{2}{1}=\color{red}-2\\ &\textrm{b}.\quad x_{1}x_{2}+ x_{1}x_{3}+ x_{2}x_{3}=\displaystyle \frac{a_{1}}{a_{3}}=\displaystyle \frac{-5}{1}=\color{red}-5\\ &\textrm{c}.\quad x_{1}\times x_{2}\times x_{3}=-\displaystyle \frac{a_{0}}{a_{3}}=-\displaystyle \frac{-6}{1}=\color{red}6\\ &\textrm{d}.\quad x_{1}^{2}+ x_{2}^{2}+ x_{3}^{2}\\ &\quad\quad =\left ( x_{1}+x_{2}+x_{3} \right )^{2}-2\left ( x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3} \right )\\ &\quad\quad =(-2)^{2}-2(-5)=4+10=\color{red}14 \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui polinom}\: \: x^{3}+3x-1=0\\ &\textrm{dengan akar-akar}\: \: \alpha ,\: \beta ,\: \textrm{dan}\: \: \gamma \\ &\textrm{tentukanlah nilai}\: \: \alpha^{3} +\beta^{3} + \gamma^{3} \\\\ &\textrm{Jawab}:\\ &\textrm{Pandang polinom}\: \: \color{red}x^{3}+3x-1=0\\ &\textrm{dengan}:\: a_{3}=1,\: a_{2}=0,\: a_{1}=3,\: a_{0}=-1\\ &\textrm{maka bentuk nilai dari akar-akarnya}\\ &\textrm{yaitu}:\\ &\bullet \quad \alpha ^{3}+3\alpha -1=0\: \: .......(1)\\ &\bullet \quad \beta ^{3}+3\beta -1=0\: \: .......(2)\\ &\bullet \quad \gamma ^{3}+3\gamma -1=0\: \: .......(3)\\ &\textrm{Ketika persamaan}\: \: (1)+(2)+(3)\: \: \textrm{maka}\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left (\alpha +\beta +\gamma \right ) -3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left ( \displaystyle \frac{a_{2}}{a_{3}} \right )-3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left ( 0 \right )-3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}=\color{red}3 \end{array}$

Daftar Pustaka

1. Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Kelas XI untuk SMA dan MA Program Studi Ilmu Alam. Klaten: INTAN PARIWARA.
2. Nugroho, P. A., Gunarto, D. 2013. Big Bank Soal+Bahas Matematika SMA/MA Kelas 1, 2, 3. Jakarta: WAHYUMEDIA.
3. Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT.
4. Sunardi, Waluyo, S., Sutrisno, Subagya. 2005. Matematika 2 untuk SMA Kelas XI IPA. Jakarta: BUMI AKSARA.
5. Sukino, S., Intan, T. S., Santiago, Y. E. 2015. Pena Emas Olimpiade Sains Nasional Matematika untuk SMP Seri Kinomatika 1: Seleksi Tingkat Sekolah dan Seleksi Tingkat Kabupaten\Kota. Bandung: YRAMA WIDYA.
6. Sukino. 2016. Matematika untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Lanjutan Materi Polinom : Teorema Sisa dan Teorema Faktor

 $\textbf{1. Teorema Sisa}$

Sebelumnya telah diketahui bahwa jika suatu polinom  $\textbf{f(x)}$ dibagi oleh  $\textbf{g(x)}$ dengan hasil bagi  $\textbf{h(x)}$  dan sisa pembagian berupa  $\textbf{s(x)}$, maka kondisi tersebut dapat dituliskan dengan

$f(x)=g(x)\times h(x)+s(x)$

Selanjutnya apabila  $\textbf{f(x)}$  berderajat  $\color{blue}n$  dibagi oleh  $\textbf{g(x)}$ berderajat  $\color{blue}m$, maka hasil bagi  $\textbf{h(x)}$  akan berderajat  $\color{blue}n-m$  dan sisa pembagian maksimum berderajat $\color{blue}m-1$.

Perhatikan kembali contoh soal sebelumnya yaitu:

Dari paparan di atas apabila disederhanakan, maka:

$\begin{aligned}\textrm{Jika}\: &\textrm{polinomial}\: \: f(x)\: \: \textrm{dibagi oleh}\\ \textrm{a}.\quad&g(x)=(x-a),\: \: s(x)=\color{red}f(a)\\ \textrm{b}.\quad&g(x)=(x+a),\: \: s(x)=\color{red}f(-a)\\ \textrm{c}.\quad&g(x)=(ax-b),\: \: s(x)=\color{red}f\left ( \displaystyle \frac{b}{a} \right )\\ \textrm{d}.\quad&g(x)=(ax+b),\: \: s(x)=\color{red}f\left (- \displaystyle \frac{b}{a} \right )\\ \textrm{e}.\quad&g(x)=(x-a)(x-b)\\ &\quad s(x)=\displaystyle \frac{x-a}{b-a}\color{red}f(b)\color{black}+\frac{x-b}{a-b}\color{red}f(a)\\ \textrm{f}.\quad&g(x)=(x-a)(x-b)(x-c)\\ &\quad s(x)=\displaystyle \frac{(x-a)(x-b)}{(c-a)(c-b)}\color{red}f(c)\\ &\: \qquad +\displaystyle \frac{(x-a)(x-c)}{(b-a)(b-c)}\color{red}f(b)\\ &\: \qquad +\displaystyle \frac{(x-b)(x-c)}{(a-b)(a-c)}\color{red}f(a) \end{aligned}$

$\textbf{2. Teorema Faktor}$

Pada pembagian sebuah bilangan bahwa suatu bilangan dikatakan habis terbagi jika pembaginya adalah faktor dari bilangan tersebut. Sebagai misal 15 faktornya adalah: 1,3,5, dan 15. Dan pada bahasan materi tentang pemfaktoran pada persamaan kuadrat saat Anda duduk di kelas X sebagai misal  $x^{2}+x-6$ akan habis terbagi oleh  $x+3$  dan  $x-2$. Demikian juga  ketika  $x^{2}+2x-8$  akan habis terbagi oleh  $x+4$  dan  $x-2$. Selanjutnya pembagi-pembagi tersebut kita namakan sebagai faktor dari yang dibagi tersebut.

Untuk selanjutnya toerema faktor dinyatakan:

• Jika  $(x-h)$ adalah faktor dari  $f(x)$  jika dan hanya jika  $f(h)=0$
• Jika  $(ax+h)$  merupakan faktor dari  $f(x)$  jika dan hanya jika  $f\left ( \displaystyle \frac{-h}{a} \right )=0$