Contoh Soal Vektor di Dimensi Dua (Matematika Peminatan Kelas X) Bagian 2

$\begin{array}{ll}\\ 4.&\color{blue}\textrm{Perhatikanlah ilustrasi gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Nyatakanlah vektor-vektor di atas dalam}\\ &\textrm{a}.\quad \textrm{vektor kolom}\\ &\textrm{b}.\quad \textrm{vektor baris}\\ &\textrm{c}.\quad \textrm{vektor basis}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Vektor di atas saat dinyatakan dengan}\\ &\begin{array}{|c|l|l|l|}\hline \textrm{No}&\quad\textrm{Kolom}&\qquad\textrm{Baris}&\qquad\textrm{Basis}\\\hline 1&\bar{a}=\begin{pmatrix} 2\\ 4 \end{pmatrix}&\bar{a}=\begin{pmatrix} 2, & 4 \end{pmatrix}&\bar{a}=2\bar{i}+4\bar{j}\\\hline 2&\bar{b}=\begin{pmatrix} 4\\ 2 \end{pmatrix}&\bar{b}=\begin{pmatrix} 4, & 2 \end{pmatrix}&\bar{b}=4\bar{i}+2\bar{j}\\\hline 3&\bar{c}=\begin{pmatrix} 5\\ 0 \end{pmatrix}&\bar{c}=\begin{pmatrix} 5, & 0 \end{pmatrix}&\bar{c}=5\bar{i}\\\hline 4&\bar{d}=\begin{pmatrix} -2\\ -4 \end{pmatrix}&\bar{d}=\begin{pmatrix} -2, & -4 \end{pmatrix}&\bar{d}=-2\bar{i}-4\bar{j}\\\hline 5&\bar{e}=\begin{pmatrix} 0\\ -4 \end{pmatrix}&\bar{e}=\begin{pmatrix} 0, & -4 \end{pmatrix}&\bar{e}=-4\bar{j}\\\hline 6&\bar{f}=\begin{pmatrix} 3\\ -3 \end{pmatrix}&\bar{f}=\begin{pmatrix} 3, & -3 \end{pmatrix}&\bar{f}=3\bar{i}-3\bar{j}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 5&\textrm{Tentukanlah panjang atau besar dari}\\ &\textrm{vektor-vektor berikut}\\ &\textrm{a}.\quad \bar{a}=\begin{pmatrix} -4\\ 3 \end{pmatrix}\quad\quad\quad \textrm{d}.\quad \bar{d}=\begin{pmatrix} 6, &-8 \end{pmatrix}\\ &\textrm{b}.\quad \bar{b}=\begin{pmatrix} 5\\ 0 \end{pmatrix}\qquad\quad\quad \textrm{e}.\quad \bar{e}=2\bar{i}+4\bar{j}\\ &\textrm{c}.\quad \bar{c}=\begin{pmatrix} 4, & -6 \end{pmatrix}\: \qquad \textrm{f}.\quad \bar{f}=-5\bar{i}+12\bar{j}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Lambang panjang suatu vektor adalah}:\\ &\color{red}\left | \begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}},\: \: \color{black}\textrm{maka}\\ &\bullet \: \left | \bar{a} \right |=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5\\ &\bullet \: \left | \bar{b} \right |=\sqrt{5^{2}+0^{2}}=\sqrt{25}=5\\ &\bullet \: \left | \bar{c} \right |=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\\ &\bullet \: \left | \bar{d} \right |=\sqrt{6^{2}+(-8)^{2}}=\sqrt{36+64}=\sqrt{100}=10\\ &\bullet \: \left | \bar{e} \right |=\sqrt{2^{2}+4^{2}}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\\ &\bullet \: \left | \bar{f} \right |=\sqrt{(-5)^{2}+12^{2}}=\sqrt{25+144}=\sqrt{169}=13 \end{array}$

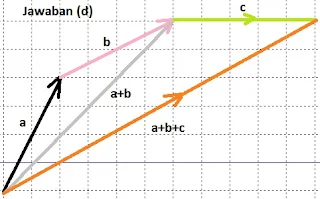
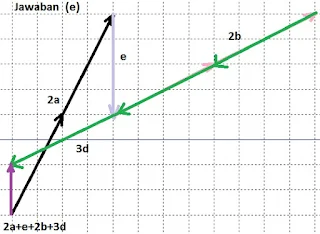
$\begin{array}{ll}\\ 6&\textrm{Pada soal no.4 di atas dengan menggunakan}\\ &\textrm{aturan segitiga dan jajar genjang, gambarlah}\\ &\textrm{vektor-vektor berikut pada kertas berpertak}\\ &\textrm{a}.\quad \bar{a}+\bar{b}\qquad\qquad\qquad \textrm{d}.\quad \left ( \bar{a}+\bar{b} \right )+\bar{c}\\ &\textrm{b}.\quad \bar{b}+\bar{c}\, \qquad\qquad\qquad \textrm{e}.\quad 2\bar{a}+\bar{e}+2\bar{b}+3\bar{d}\\ &\textrm{c}.\quad \bar{a}+\left (\bar{b}+\bar{c} \right )\: \: \quad \qquad \textrm{f}.\quad 2\left ( \bar{a}+\bar{b}+\bar{c}+\bar{d}+\bar{e} \right )\\\\ &\textrm{Jawab}:\\ \end{array}$