Contoh Soal Vektor di Dimensi Dua (Matematika Peminatan Kelas X) Bagian 1

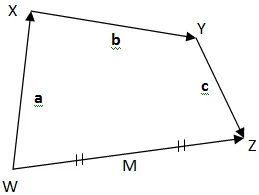
 Perhatikanlah gambar berikut untuk menjawab soal no.1

$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: \overline{XW}=\textbf{a}\: ,\: \overline{XY}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{YZ}=\textbf{c}\\ &\textrm{Nyatakan dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{WY}\qquad\qquad\qquad \textrm{d}.\quad\overline{WZ}\\ &\textrm{b}. \quad\overline{XZ}\qquad\qquad\qquad \: \textrm{e}.\quad\overline{WM}\\ &\textrm{c}.\quad\overline{ZX}\qquad\qquad\qquad \: \: \textrm{f}.\quad\overline{MY}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{WY}&=\overline{WX}+\overline{XY}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{XZ}&=\overline{XY}+\overline{YZ}=\textbf{b}+\textbf{c}\\ \textrm{c}.\quad\overline{ZX}&=\overline{ZY}+\overline{YX}=-\textbf{c}+(-\textbf{b})=-\textbf{b}-\textbf{c}\\ &=-(\textbf{b}+\textbf{c})\\ &\textrm{atau}\\ \overline{ZX}&=-\overline{XZ}=-(\textbf{b}+\textbf{c})\\ \textrm{d}.\quad \overline{WZ}&=\overline{WX}+\overline{XY}+\overline{YZ}\\ &=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{e}.\quad \overline{WM}&=\displaystyle \frac{1}{2}\overline{WZ}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{MY}&=\overline{MZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\overline{WZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )+(-\textbf{c})\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )-\textbf{c}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}-\textbf{c} \right )\end{aligned} \end{array}$

Perhatikanlah gambar berikut untuk menjawab soal no.2

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: \overline{PQ}=\textbf{a}\: ,\: \overline{QR}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{RS}=\textbf{c}\\ &\textrm{dan titik}\: \: \textbf{E}\: \: \textrm{dan}\: \: \textbf{F}\: \: \textrm{adalah titik tegah}\\ &\overline{RS}\: \: \textrm{dan}\: \: \overline{QS},\\ &\textrm{nyatakanlah dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{PR}\qquad\qquad\qquad \textrm{e}.\quad\overline{PF}\\ &\textrm{b}. \quad\overline{RP}\qquad\qquad\qquad \textrm{f}.\quad\overline{SF}\\ &\textrm{c}.\quad\overline{PS}\qquad\qquad\qquad \: \textrm{g}.\quad\overline{FR}\\ &\textrm{d}.\quad\overline{QE}\qquad\qquad\qquad \textrm{h}.\quad\overline{EF}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{PR}&=\overline{PQ}+\overline{QR}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{RP}&=\overline{RQ}+\overline{QP}=-\textbf{b}-\textbf{a}=-\left ( \textbf{a}+\textbf{b} \right )\\ \textrm{c}.\quad\overline{PS}&=\overline{PQ}+\overline{QR}+\overline{RS}=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{d}.\quad \overline{QE}&=\overline{QR}+\overline{RE}=\overline{QR}+\displaystyle \frac{1}{2}\overline{RS}\\ &=\textbf{b}+\displaystyle \frac{1}{2}\textbf{c}\\ \textrm{e}.\quad \overline{PF}&=\overline{PQ}+\overline{QF}=\overline{PQ}+\displaystyle \frac{1}{2}\overline{QS}\\ &=\overline{PQ}+\displaystyle \frac{1}{2}\left ( \overline{QR}+\overline{RS} \right )\\ &=\displaystyle \frac{1}{2}\left ( 2\textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{SF}&=\displaystyle \frac{1}{2}\overline{SQ}=\displaystyle \frac{1}{2}\left (\overline{SR}+\overline{RQ} \right )=\displaystyle \frac{1}{2}\left ( -\textbf{c}+(-\textbf{b}) \right )\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )\\ \textrm{g}.\quad \overline{FR}&=\overline{FQ}+\overline{QR}=\displaystyle \frac{1}{2}\overline{SQ}+\overline{QR}\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )+\textbf{b}=\displaystyle \frac{1}{2}\left ( \textbf{b}-\textbf{c} \right )\\ \textrm{h}.\quad \overline{EF}&=\overline{ES}+\overline{SF}=\displaystyle \frac{1}{2}\overline{RS}+\displaystyle \frac{1}{2}\overline{SQ}\\ &=\displaystyle \frac{1}{2}\textbf{c}+\left ( -\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right ) \right )=-\displaystyle \frac{1}{2}\textbf{b} \end{aligned} \end{array}$

$\color{red}\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Jika pada titik P bekerja 3 buah gaya}\\ &\textrm{seperti pada gambar di bawah, lukislah}\\ &\textrm{vektor}\\ &\qquad\qquad \textbf{r}=\textbf{a}+\textbf{b}+\textbf{c}\\\\ &\textrm{Jawab}:\\ &\textrm{Dengan aturan poligon kita akan}\\ &\textrm{mendapatkan gambar berikut} \end{array}$