Lanjutan Materi Vektor Di Ruang Dimensi Dua (Matematika Peminatan Kelas X)

$\color{blue}\textrm{E. Modulus Vektor}$

Modulus suatu vektor adalah ukuran (panjang) suatu vektor. Dalam hal ini modulus suatu vektor adalah besar/panjang suatu vektor.

Lihat pada pembahasan sebelumnya tentang panjang vektor di  $\color{red}\textrm{R}^{2}$  di sini.

Dalam menuliskan modulus/panjang vektor ini digunakan notasi  $\left | \overline{a} \right |$  jika vektornya $\overline{a}$. 

Bila  $\color{red}\overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix},\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\sqrt{x_{1}^{2}+y_{1}^{2}}$

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

Perhatikanlah ilustrasi gambar berikut

Tentukanlah modulus/panjang vektor  $\overline{u}$ ?

Jawab:

$\begin{aligned}&\textrm{Diketahui bahwa vektor}\: \: \color{red}\overline{u}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\\ &\textrm{maka modulus vektor}\: \: \overline{u}\\ &=\left | \overline{u} \right |\\ &=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}\\ &=\color{red}2\sqrt{13} \end{aligned}$

$\color{blue}\textrm{F. Vektor Posisi dan Vektor Bebas}$

Perhatikanlah ilustrasi berikut

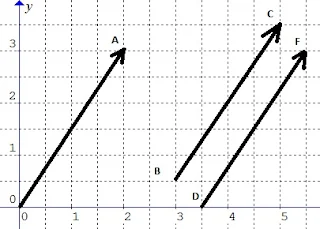
Vektor yang titik pangkalnya berada di titik O(0,0), maka vektor tersebut dinamakan vektor posisi. Pada gambar di atas titik A rekatif terhadapa O(0,0), maka  $\color{red}\overline{OA}$ disebut vektor posisi A terhadap titik O(0,0) dan vektor yang lainnya dinamakan vektor bebas. Pada gambar di atas  $\color{red}\overline{BC}\: \&\: \overline{DF}$  adalah contoh vektor bebasnya.

$\color{blue}\textrm{G. Kesamaan Dua Vektor}$

Perhatikanlah dua vektor bebas pada gambar di atas, cukup jelas secara geometri tampak panjang vektor $\color{red}\overline{BC}\: \&\: \overline{DF}$  sama. Dan secara aljabar dapat ditunjukkan juga bahwa:

$\color{red}\overline{BC}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \&\: \color{red}\overline{DF}=\begin{pmatrix} 4\\ 6 \end{pmatrix}$

Secara definisi

$\overline{a}=\overline{b}\: \: \begin{cases} \bullet & \left | \overline{a} \right |=\left | \overline{b} \right | \\\\ \bullet & \textrm{arah}\: \: \overline{a}=\textrm{arah}\: \: \overline{b} \end{cases}$

$\color{blue}\textrm{H. Vektor Negatif}$

Perhatikanlah ilustrasi berikut

$\color{red}\overline{a}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \color{black}\&\: \: \color{red}\overline{b}=\color{black}\begin{pmatrix} -4\\ -6 \end{pmatrix}=-\color{red}\begin{pmatrix} 4\\ 6 \end{pmatrix}$

Vektor  $\color{red}-\: \overline{a}=\overline{b}$ memiliki ukuran yang sama dengan   $\overline{a}$.

Selanjutnya vektor  $\color{red}\overline{a}=-\: \overline{b}\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\left | \overline{b} \right |$

$\color{blue}\textrm{I. Vektor Satuan}$

Perhatikanlah ilustrasi berikut

Jika diketahui  $\color{red}\overline{a}\: \color{black}\&\: \: \color{red}\overline{b}$ seperti gambar di atas, maka

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{a} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{b} \end{cases}$ 

Dan panjang dari vektor satuan ini adalah selalu satu satuan.

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

Tentukanlah vektor satuan dari dua vektor pada gambar di atas?

Jawab:

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} -2\\ 5 \end{pmatrix}}{\sqrt{(-2)^{2}+5^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{29}}\begin{pmatrix} -2\\ 5 \end{pmatrix}=\displaystyle \frac{1}{29}\sqrt{29}\begin{pmatrix} -2\\ 5 \end{pmatrix} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} 6\\ 4 \end{pmatrix}}{\sqrt{6^{2}+4^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{52}}\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{1}{26}\sqrt{52}\begin{pmatrix} 6\\ 4 \end{pmatrix} \end{cases}$

$\color{blue}\textrm{J. Vektor Basis}$

Vektor satuan yang saling tegak lurus. Didalam ruang dimensi dua terdapat dua vektir basis., yaitu:

$\bar{i}=\color{red}\begin{pmatrix} 1\\ 0 \end{pmatrix}\: \: \color{black}\textrm{dan}\: \: \bar{j}=\color{blue}\begin{pmatrix} 0\\ 1 \end{pmatrix}$

$\begin{aligned}&\textrm{Misalkan vektor}\: \: \bar{u}=\color{red}\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}\\ &\textrm{dapat dinyatakan dalam kombinasi linear}\\ &\textrm{vektor basis}\: \: \bar{i}\: \: \textrm{dan}\: \: \bar{j}\: \: \textrm{di atas, yaitu}\\ &\bar{u}=\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}=u_{1}\begin{pmatrix} 1\\ 0 \end{pmatrix}+u_{2}\begin{pmatrix} 0\\ 1 \end{pmatrix}\\ &\textrm{maka akan menjadi}\\ &\bar{u}=u_{1}\bar{i}+u_{2}\bar{j}\\ &\textrm{SEBAGAI CONTOH}\\ &\overline{AB}=\begin{pmatrix} 5\\ 8 \end{pmatrix}\: \: \color{blue}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=5\bar{i}+8\bar{j}\\ &\textrm{Demikian juga jika}\\ &\overline{CD}=\begin{pmatrix} -3\\ -8 \end{pmatrix}\: \: \color{red}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=-3\bar{i}-8\bar{j}\\ \end{aligned}$

$\color{blue}\textrm{K. Vektor Nol}$

Jika vektor  $\overline{a}=\overline{b}$ , maka $\overline{a}-\overline{b}=0$.

$\textbf{0}$  disebut sebagai vektor ol.

Sebagai tabahan penjelasan vektor  $\textbf{0}$  tidak mempunyai besar dan arahnya tak tentu.