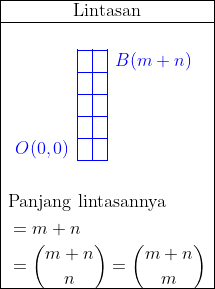Distribusi Binomial (Matematika Peminatan kelas XII SMA/MA)

 $\text{A. Pendahuluan Distribusi Binomial}$

$\begin{array}{rl}& \{\begin{array}{c}(1)\text{Review}\{\begin{array}{l}\text{Peluang}\{\begin{array}{l}\text{Populasi}\\ \text{Sampel}\{\begin{array}{l}\text{Acak}\\ \text{Bukan Acak}.\end{array}\end{array}\\ \text{Kombiasi}& \end{array}\\ (2)\text{Variabel Acak}\{\begin{array}{ll}\text{Diskrit}& .\\ \text{Kontinue}& \end{array}\\ (3)\text{Distribusi}\{\begin{array}{ll}\text{Distribusi Peluang Variabel Acak}& \\ \text{Fungsi Distribusi Kumulatif}& \\ \text{Variabel Acak Binomial}& \\ \text{Distribusi Binomial}\end{array}\end{array}\end{array}$

$\text{Penjelasan}$

$\begin{array}{|cll|}\hline \text{No}& \text{Istilah}& \text{Penjelasan}\\ 1& \text{Statistika}& \text{Ilmu tentang pengumpulan, pengolahan},\\ & & \text{penganalisaan serta penarikan kesimpulan}\\ & & \text{data. Selanjutnya akan dibagi dua yaitu}\\ & & \text{deskriptif dan inferensia}\\ 2& \text{Statistik}& \text{Kumpulan data/ukuran sampel}\\ 3& \text{Parameter}& \text{Ukuran populasi}\\ 4& \text{Populasi}& \text{Keseluruhan/semua anggota objek/data}\\ 5& \text{Sampel}& \text{Subjek/Objek yang mewakili populasi}\\ 6& \text{Sesus}& \text{Penelitian seluruh data (populasi)}\\ 7& \text{Tekik}& \text{Cara pengambilan data terbatas pada}\\ & \text{Sampling}& \text{sebagian saja dari populasi yang diteliti}\\ \hline\end{array}$.

$\text{B. Kombinasi, Peluang, dan Variabel Acak}$.

Untuk memulai bahasan ini kita sertakan pengertian yang berkaitan dengan kombinasi yaitu adalah permutasi. Perhatikanlah tabel berikut

$\begin{array}{|lll|}\hline \text{Istilah}& \text{Permutasi}& \text{Kombinasi}\\ \text{Definisi}& \begin{array}{rl}& \text{Permutasi r unsur dari n unsur}\\ & \text{adalah banyaknya kemungkinan}\\ & \text{urutan r unsur yang dipilih}\\ & \text{dari n unsur yang tersedia}.\\ & \text{Tiap unsur berbeda dan}r\le n\\ & \end{array}& \begin{array}{rl}& \text{Kombinasi r unsur dan n unsur}\\ & \text{adalah banyaknya kemungkinan}\\ & \text{tidak terurut dalam pemilihan}\\ & \text{r unsur yang diambil dari n}\\ & \text{unsur yang tersedia. Tiap unsur}\\ & \text{berbeda dan}r\le n\end{array}\\ \text{Tipe}& \begin{array}{rl}& \text{Bentuk khusus kaidah}\\ & \text{perkalian}\end{array}& \begin{array}{rl}& \text{Bentuk khusus dari bentuk}\\ & \text{permutasi}\end{array}\\ \text{Notasi}& {}_n{P}_r,P_n^r,\text{atau}P(n,k)& {}_n{C}_r,C_r^n,(\genfrac{}{}{0ex}{}{n}{r}),\text{atau}C(n,r)\\ \text{Rumus}& P(n,r)={\displaystyle \frac{n!}{(n-r)!}}& (\genfrac{}{}{0ex}{}{n}{r})=C(n,r)={\displaystyle \frac{n!}{r!(n-r)!}}\\ \hline\end{array}$.

$\begin{array}{rl}& \text{Sebagai catatan bahwa}\\ & n!=1\times 2\times 3\times \cdots \times (n-1)\times n\end{array}$

Selanjutnya yang akan kita bahas berkaitan bab ini adalah kombinasi beserta contohnya. Perhatikan pula tabel berikut

$\begin{array}{|cc|}\hline \text{Kombinasi}& \text{Kombinasi dalam}\\ \text{dengan pengulangan}& \text{Binom Newton}\\ \begin{array}{rl}& C(n+r-1,r)\\ & =C(n+r-1,n-1)\\ & (\genfrac{}{}{0ex}{}{n+r-1}{r})\\ & =(\genfrac{}{}{0ex}{}{n+r-1}{n-1})\end{array}& \begin{array}{rl}& (x+y{)}^n\\ & =\sum _{k=o}^n(\genfrac{}{}{0ex}{}{n}{r})x^{n-k}{y}^k\\ \\ & \text{Koefisien untuk}\\ & x^{n-k}{y}^k,\text{yaitu}\\ & \text{suku ke}-(k+1)\\ & \text{adalah}(\genfrac{}{}{0ex}{}{n}{r})\end{array}\\ \hline\end{array}$.

serta

$\text{CONTOH SOAL}$

$\begin{array}{l}\\ 1.& \text{Tentukanlah nilai}\\ & \begin{array}{l}\\ \text{a}.3!& \text{e}.{\displaystyle \frac{6!}{4!}}& \text{i}.{\displaystyle \frac{2!}{0!}+\frac{3!}{1!}+\frac{4!}{2!}}\\ \text{b}.5!& \text{f}.{\displaystyle \frac{10!}{6!}}& \text{j}.{\displaystyle \frac{2!}{0!}\times \frac{3!}{1!}+\frac{4!}{2!}}\\ \text{c}.0!+1!+2!+3!& \text{g}.{\displaystyle \frac{7!}{3!\times 4!}}& \text{k}.{\displaystyle \frac{3\times 4!}{3!(5!-5!)}}\\ \text{d}.(2!)!+(3!)!& \text{h}.{\displaystyle \frac{13!}{12!+12!}}& \text{l}.{\displaystyle \frac{3!+5!+7!}{4!+6!}}\end{array}\\ \\ & \text{Jawab}:\\ \\ & \begin{array}{c}\\ \text{a}.3!=3.2.1=6\\ \text{b}.5!=5.4.3.2.1=120\\ \begin{array}{rl}\text{c}.0!+1!+2!+3!& =1+1+2+6\\ & =10\end{array}\\ \begin{array}{rl}\text{d}.(2!)!+(3!)!& =2!+6!\\ & =2+720\\ & =722\end{array}\\ \text{e}.{\displaystyle \frac{6!}{4!}=\frac{720}{24}=30\text{atau}{\displaystyle \frac{6!}{4!}={\displaystyle \frac{6.5.\text{⧸}4.\text{⧸}3.\text{⧸}2.\text{⧸}1}{\text{⧸}4.\text{⧸}3.\text{⧸}2.\text{⧸}1}=6.5=30}}}\\ \text{f}.{\displaystyle \frac{10!}{6!}=\frac{10.9.8.7.6.5.4.3.2.1}{6.5.4.3.2.1}=....(\text{silahkan diselesaikan sendiri})}\\ \text{g}.{\displaystyle \frac{7!}{3!\times 4!}=\frac{7.6.5.4.3.2.1}{(3.2.1)\times (4.3.2.1)}=....(\text{silahkan juga diselesaikan sendiri})}\\ ⋮\\ (\text{silahkan selanjutnya diselesaikan sendiri})\end{array}\end{array}$

$\begin{array}{l}\\ 2.& \text{Sederhanakanlah}\\ & \begin{array}{l}\\ \text{a}.{\displaystyle \frac{n!}{(n-1)!}}& \text{e}.{\displaystyle \frac{1}{n!}+\frac{n}{(n+1)!}-\frac{1}{(n-1)!}}\\ \text{b}.{\displaystyle \frac{(n+2)!}{(n+1)!}}& \text{f}.{\displaystyle \frac{(4n)!}{(4n+1)!}+\frac{(4n)!}{(4n-1)!}}\\ \text{c}.{\displaystyle \frac{(2n)!}{(2n+1)!}}& \text{g}.{\displaystyle \frac{1}{n}-\frac{n!}{(n-1).(n-2)!}}\\ \text{d}.{\displaystyle \frac{(n+2)!}{(n^2+3n+2)}}& \text{h}.1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\end{array}\\ \\ & \text{Jawab}:\\ \\ & \begin{array}{c}\\ \text{a}.{\displaystyle \frac{n!}{(n-1)!}=\frac{n.(n-1)!}{(n-1)!}=n}\\ \text{b}.{\displaystyle \frac{(n+2)!}{(n+1)!}=\frac{(n+2).(n+1)!}{(n+1)!}=n+2}\\ \text{c}.{\displaystyle \frac{(2n)!}{(2n+1)!}=\frac{(2n)!}{(2n+1).(2n)!}=\frac{1}{2n+1}}\\ \text{d}.{\displaystyle \frac{(n+2)!}{n^2+3n+2}=\frac{(n+2)!}{(n+2).(n+1)}=\frac{(n+2).(n+1).n!}{(n+2).(n+1)}=n!}\\ ⋮\\ (\text{silahkan selanjutnya diselesaikan sendiri sebagai latihan})\\ ⋮\\ \begin{array}{rl}\text{h}.& 1.1!+2.2!+3.3!+4.4!+5.5!+...+n.n!\\ & =(2-1).1!+(3-1).2!+(4-1).3!+(5-1).4!+...+(n+1-1).n!\\ & =2.1!+3.2!+4.3!+5.4!+...+(n+1).n!-1!-2!-3!-4!-...-n!\\ & =2!+3!+4!+5!+...+(n+1)!-(1!+2!+3!+4!+...+n!)\\ & =(n+1)!-1\end{array}\end{array}\end{array}$

$\begin{array}{l}\\ 3.& \text{Sederhanakanlah bentuk penjumlahan berikut}\\ & {\displaystyle \frac{3}{1!+2!+3!}+\frac{4}{2!+3!+4!}+\frac{5}{3!+4!+5!}+\cdots +{\displaystyle \frac{100}{98!+99!+100!}}}\\ \\ & \text{Jawab}:\\ \\ & \begin{array}{rl}& \text{Perhatikan}\text{bahwa}\\ & {\displaystyle \frac{3}{1!+2!+3!}=\frac{3}{1+2+6}=\frac{3}{9}=\frac{1}{3}\times \frac{2}{2}=\frac{2}{1\times 2\times 3}=\frac{2}{3!}=\frac{3-1}{3!}=\frac{3}{3!}-\frac{1}{3!}=\frac{3}{2!\times 3}-\frac{1}{3!}=\frac{1}{2!}-\frac{1}{3!}}\\ & \text{sehingga}\\ & \frac{3}{1!+2!+3!}=\frac{1}{2!}-\frac{1}{3!}\\ & {\displaystyle \frac{4}{2!+3!+4!}=\cdots =\frac{1}{3!}-\frac{1}{4!}}\\ & {\displaystyle \frac{5}{3!+4!+5!}=\cdots =\frac{1}{4!}-\frac{1}{5!}}\\ & ⋮\\ & {\displaystyle \frac{100}{98!+99!+100!}=\cdots =\frac{1}{99!}-\frac{1}{100!}}\\ & ---------------------------\\ & =\frac{1}{2!}-\frac{1}{100!}\end{array}\end{array}$.

Contoh Soal Vektor di Dimensi Dua (Kelas X Matematika Peminatan) Bagian 2

 $\begin{array}{l}\\ 4.& \text{Perhatikanlah ilustrasi gambar berikut}\end{array}$

$\begin{array}{l}\\ .& \text{Nyatakanlah vektor-vektor di atas dalam}\\ & \text{a}.\text{vektor kolom}\\ & \text{b}.\text{vektor baris}\\ & \text{c}.\text{vektor basis}\\ \\ & \text{Jawab}:\\ & \text{Vektor di atas saat dinyatakan dengan}\\ & \begin{array}{|clll|}\hline \text{No}& \text{Kolom}& \text{Baris}& \text{Basis}\\ 1& \overline{a}=\left(\begin{array}{c}2\\ 4\end{array}\right)& \overline{a}=\left(\begin{array}{cc}2,& 4\end{array}\right)& \overline{a}=2\overline{i}+4\overline{j}\\ 2& \overline{b}=\left(\begin{array}{c}4\\ 2\end{array}\right)& \overline{b}=\left(\begin{array}{cc}4,& 2\end{array}\right)& \overline{b}=4\overline{i}+2\overline{j}\\ 3& \overline{c}=\left(\begin{array}{c}5\\ 0\end{array}\right)& \overline{c}=\left(\begin{array}{cc}5,& 0\end{array}\right)& \overline{c}=5\overline{i}\\ 4& \overline{d}=\left(\begin{array}{c}-2\\ -4\end{array}\right)& \overline{d}=\left(\begin{array}{cc}-2,& -4\end{array}\right)& \overline{d}=-2\overline{i}-4\overline{j}\\ 5& \overline{e}=\left(\begin{array}{c}0\\ -4\end{array}\right)& \overline{e}=\left(\begin{array}{cc}0,& -4\end{array}\right)& \overline{e}=-4\overline{j}\\ 6& \overline{f}=\left(\begin{array}{c}3\\ -3\end{array}\right)& \overline{f}=\left(\begin{array}{cc}3,& -3\end{array}\right)& \overline{f}=3\overline{i}-3\overline{j}\\ \hline\end{array}\end{array}$

$\begin{array}{l}\\ 5& \text{Tentukanlah panjang atau besar dari}\\ & \text{vektor-vektor berikut}\\ & \text{a}.\overline{a}=\left(\begin{array}{c}-4\\ 3\end{array}\right)\text{d}.\overline{d}=\left(\begin{array}{cc}6,& -8\end{array}\right)\\ & \text{b}.\overline{b}=\left(\begin{array}{c}5\\ 0\end{array}\right)\text{e}.\overline{e}=2\overline{i}+4\overline{j}\\ & \text{c}.\overline{c}=\left(\begin{array}{cc}4,& -6\end{array}\right)\text{f}.\overline{f}=-5\overline{i}+12\overline{j}\\ \\ & \text{Jawab}:\\ & \text{Lambang panjang suatu vektor adalah}:\\ & \left|\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)\right|=\sqrt{u_1^2+u_2^2},\text{maka}\\ & \bullet \left|\overline{a}\right|=\sqrt{(-4{)}^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\\ & \bullet \left|\overline{b}\right|=\sqrt{5^2+0^2}=\sqrt{25}=5\\ & \bullet \left|\overline{c}\right|=\sqrt{4^2+6^2}=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\\ & \bullet \left|\overline{d}\right|=\sqrt{6^2+(-8{)}^2}=\sqrt{36+64}=\sqrt{100}=10\\ & \bullet \left|\overline{e}\right|=\sqrt{2^2+4^2}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\\ & \bullet \left|\overline{f}\right|=\sqrt{(-5{)}^2+{12}^2}=\sqrt{25+144}=\sqrt{169}=13\end{array}$

$\begin{array}{l}\\ 6& \text{Pada soal no.4 di atas dengan menggunakan}\\ & \text{aturan segitiga dan jajar genjang, gambarlah}\\ & \text{vektor-vektor berikut pada kertas berpertak}\\ & \text{a}.\overline{a}+\overline{b}\text{d}.(\overline{a}+\overline{b})+\overline{c}\\ & \text{b}.\overline{b}+\overline{c}\text{e}.2\overline{a}+\overline{e}+2\overline{b}+3\overline{d}\\ & \text{c}.\overline{a}+(\overline{b}+\overline{c})\text{f}.2(\overline{a}+\overline{b}+\overline{c}+\overline{d}+\overline{e})\\ \\ & \text{Jawab}:\end{array}$

Contoh Soal Vektor di Dimensi Dua (Kelas X Matematika Peminatan) Bagian 1

 Perhatikanlah gambar berikut untuk menjawab soal no.1

$\begin{array}{l}\\ 1.& \text{Jika}\overline{XW}=\mathbf{\text{a}},\overline{XY}=\mathbf{\text{b}},\text{dan}\overline{YZ}=\mathbf{\text{c}}\\ & \text{Nyatakan dalam vektor},\mathbf{\text{a}},\mathbf{\text{b}},\mathrm{\&}\mathbf{\text{c}}\\ & \text{untuk vektor-vektor berikut}\\ & \text{a}.\overline{WY}\text{d}.\overline{WZ}\\ & \text{b}.\overline{XZ}\text{e}.\overline{WM}\\ & \text{c}.\overline{ZX}\text{f}.\overline{MY}\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\text{a}.\overline{WY}& =\overline{WX}+\overline{XY}=\mathbf{\text{a}}+\mathbf{\text{b}}\\ \text{b}.\overline{XZ}& =\overline{XY}+\overline{YZ}=\mathbf{\text{b}}+\mathbf{\text{c}}\\ \text{c}.\overline{ZX}& =\overline{ZY}+\overline{YX}=-\mathbf{\text{c}}+(-\mathbf{\text{b}})=-\mathbf{\text{b}}-\mathbf{\text{c}}\\ & =-(\mathbf{\text{b}}+\mathbf{\text{c}})\\ & \text{atau}\\ \overline{ZX}& =-\overline{XZ}=-(\mathbf{\text{b}}+\mathbf{\text{c}})\\ \text{d}.\overline{WZ}& =\overline{WX}+\overline{XY}+\overline{YZ}\\ & =\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}}\\ \text{e}.\overline{WM}& ={\displaystyle \frac{1}{2}\overline{WZ}}\\ & ={\displaystyle \frac{1}{2}(\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}})}\\ \text{f}.\overline{MY}& =\overline{MZ}+\overline{ZY}\\ & ={\displaystyle \frac{1}{2}\overline{WZ}+\overline{ZY}}\\ & ={\displaystyle \frac{1}{2}(\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}})+(-\mathbf{\text{c}})}\\ & ={\displaystyle \frac{1}{2}(\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}})-\mathbf{\text{c}}}\\ & ={\displaystyle \frac{1}{2}(\mathbf{\text{a}}+\mathbf{\text{b}}-\mathbf{\text{c}})}\end{array}\end{array}$

Perhatikanlah gambar berikut untuk menjawab soal no.2

$\begin{array}{l}\\ 2.& \text{Jika}\overline{PQ}=\mathbf{\text{a}},\overline{QR}=\mathbf{\text{b}},\text{dan}\overline{RS}=\mathbf{\text{c}}\\ & \text{dan titik}\mathbf{\text{E}}\text{dan}\mathbf{\text{F}}\text{adalah titik tegah}\\ & \overline{RS}\text{dan}\overline{QS},\\ & \text{nyatakanlah dalam vektor},\mathbf{\text{a}},\mathbf{\text{b}},\mathrm{\&}\mathbf{\text{c}}\\ & \text{untuk vektor-vektor berikut}\\ & \text{a}.\overline{PR}\text{e}.\overline{PF}\\ & \text{b}.\overline{RP}\text{f}.\overline{SF}\\ & \text{c}.\overline{PS}\text{g}.\overline{FR}\\ & \text{d}.\overline{QE}\text{h}.\overline{EF}\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\text{a}.\overline{PR}& =\overline{PQ}+\overline{QR}=\mathbf{\text{a}}+\mathbf{\text{b}}\\ \text{b}.\overline{RP}& =\overline{RQ}+\overline{QP}=-\mathbf{\text{b}}-\mathbf{\text{a}}=-(\mathbf{\text{a}}+\mathbf{\text{b}})\\ \text{c}.\overline{PS}& =\overline{PQ}+\overline{QR}+\overline{RS}=\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}}\\ \text{d}.\overline{QE}& =\overline{QR}+\overline{RE}=\overline{QR}+{\displaystyle \frac{1}{2}\overline{RS}}\\ & =\mathbf{\text{b}}+{\displaystyle \frac{1}{2}\mathbf{\text{c}}}\\ \text{e}.\overline{PF}& =\overline{PQ}+\overline{QF}=\overline{PQ}+{\displaystyle \frac{1}{2}\overline{QS}}\\ & =\overline{PQ}+{\displaystyle \frac{1}{2}(\overline{QR}+\overline{RS})}\\ & ={\displaystyle \frac{1}{2}(2\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}})}\\ \text{f}.\overline{SF}& ={\displaystyle \frac{1}{2}\overline{SQ}={\displaystyle \frac{1}{2}(\overline{SR}+\overline{RQ})={\displaystyle \frac{1}{2}(-\mathbf{\text{c}}+(-\mathbf{\text{b}}))}}}\\ & =-{\displaystyle \frac{1}{2}(\mathbf{\text{b}}+\mathbf{\text{c}})}\\ \text{g}.\overline{FR}& =\overline{FQ}+\overline{QR}={\displaystyle \frac{1}{2}\overline{SQ}+\overline{QR}}\\ & =-{\displaystyle \frac{1}{2}(\mathbf{\text{b}}+\mathbf{\text{c}})+\mathbf{\text{b}}={\displaystyle \frac{1}{2}(\mathbf{\text{b}}-\mathbf{\text{c}})}}\\ \text{h}.\overline{EF}& =\overline{ES}+\overline{SF}={\displaystyle \frac{1}{2}\overline{RS}+{\displaystyle \frac{1}{2}\overline{SQ}}}\\ & ={\displaystyle \frac{1}{2}\mathbf{\text{c}}+(-{\displaystyle \frac{1}{2}(\mathbf{\text{b}}+\mathbf{\text{c}})})=-{\displaystyle \frac{1}{2}\mathbf{\text{b}}}}\end{array}\end{array}$

$\begin{array}{l}\\ 3.& \text{Perhatikanlah gambar berikut}\end{array}$

$\begin{array}{l}\\ .& \text{Jika pada titik P bekerja 3 buah gaya}\\ & \text{seperti pada gambar di bawah, lukislah}\\ & \text{vektor}\\ & \mathbf{\text{r}}=\mathbf{\text{a}}+\mathbf{\text{b}}+\mathbf{\text{c}}\\ \\ & \text{Jawab}:\\ & \text{Dengan aturan poligon kita akan}\\ & \text{mendapatkan gambar berikut}\end{array}$

Materi Vektor Lanjutan 2 (Kelas X Matematika Peminatan)

 $\text{K. Operasi Vektor}$

$\text{1. Penjumlahan}$

$\text{1. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut

Penjumlahan di atas adalah penjumlahan menurut aturan segitiga, 

perhatikan pula pemisalan berikut

$\begin{array}{rl}& \text{Menurut aturan segitiga}\\ & \overline{AB}+\overline{BC}=\overline{a}+\overline{b}=\overline{AC},\text{Selanjutnya}\\ & \overline{AC}+\overline{CD}=\overline{a}+\overline{b}+\overline{c}=\overline{AD},\text{maka}\\ & \overline{AD}+\overline{DE}=\overline{a}+\overline{b}+\overline{c}+\overline{d}=\overline{AE}\end{array}$

Pada penjumlahan dengan vektor adalah tetap (tidak berubah)

$\begin{array}{rl}& \bar{a}+\bar{0}=\bar{0}+\bar{a}=\bar{a}\\ & \text{Sehingga vektor nol disebut sebagai}\\ & \mathbf{\text{elemen identitas}}\end{array}$

$\text{1. 2 Secara Aljabar}$

Misal  

$\begin{array}{rl}& \bar{a}=\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)\text{dan}\bar{b}=\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)\\ & \text{maka secara aljabar}\\ & \bar{a}+\bar{b}=\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)+\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=\left(\begin{array}{c}{x}_1+x_2\\ y_1+y_2\end{array}\right)\end{array}$

Perhatikan kembali gambar berikut (lihat pada pembahasan sebelumnya) 

$\text{CONTOH SOAL}$.

Titik  A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{array}{rl}& \overline{AB}=\left(\begin{array}{c}1\\ -3\end{array}\right)\text{dan}\overline{CD}=\left(\begin{array}{c}4\\ 3\end{array}\right)\\ & \text{maka penjumlahan secara Aljabar}\\ & \overline{AB}+\overline{CD}=\left(\begin{array}{c}1\\ -3\end{array}\right)+\left(\begin{array}{c}4\\ 3\end{array}\right)=\left(\begin{array}{c}1+4\\ (-3)+3\end{array}\right)=\left(\begin{array}{c}5\\ 0\end{array}\right)\end{array}$

Dan untuk contoh yang lain adalah:

$\begin{array}{rl}& \overline{AB}=\left(\begin{array}{c}1\\ -3\end{array}\right),\overline{CD}=\left(\begin{array}{c}4\\ 3\end{array}\right)\text{dan}\overline{EF}=\left(\begin{array}{c}-4\\ -2\end{array}\right)\\ & \text{maka penjumlahan secara Aljabar}\\ & \overline{AB}+\overline{CD}+\overline{EF}\\ & =\left(\begin{array}{c}1\\ -3\end{array}\right)+\left(\begin{array}{c}4\\ 3\end{array}\right)+\left(\begin{array}{c}-4\\ -2\end{array}\right)\\ & =\left(\begin{array}{c}1+4+(-4)\\ (-3)+3+(-2)\end{array}\right)=\left(\begin{array}{c}1\\ -2\end{array}\right)\end{array}$

$\text{2. Pengurangan}$

$\text{2. 1 Secara Geometri}$

Pada pengurangan vektor $\bar{a}\text{oleh}\bar{b}$  dapat didefinisikan sebagai:

$\bar{a}-\bar{b}=\bar{a}+(-\bar{b})$. Perhatikanlah ilustrasi secara geometri berikut:

$\text{2. 2 Secara Aljabar}$

$\begin{array}{rl}& \text{Misalkan}\bar{a}=\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)\text{dan}\bar{b}=\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)\\ & \text{maka}-\bar{b}=\left(\begin{array}{c}-x_2\\ -y_2\end{array}\right)\\ & \text{Selanjutnya}\\ & \bar{a}-\bar{b}=\bar{a}+(-\bar{b})=\left(\begin{array}{c}{x}_1-x_2\\ y_1-y_2\end{array}\right)\end{array}$.

$\text{CONTOH SOAL}$.

Pada contoh soal bahasan penjumlahan di atas, perhatikan lagi bahwa

Titik  A(-3,4) , B(-2,1) , C(1,1) , D(5,4) , E(7,3) & F(3,1)

$\begin{array}{rl}& \overline{AB}=\left(\begin{array}{c}1\\ -3\end{array}\right)\text{dan}\overline{CD}=\left(\begin{array}{c}4\\ 3\end{array}\right)\\ & \text{maka penjumlahan secara Aljabar}\\ & \overline{AB}-\overline{CD}=\left(\begin{array}{c}1\\ -3\end{array}\right)+\left(\begin{array}{c}-4\\ -3\end{array}\right)=\left(\begin{array}{c}1-4\\ (-3)-3\end{array}\right)=\left(\begin{array}{c}-3\\ -6\end{array}\right)\end{array}$

$\text{3. Perkalian dengan Skalar}$

$\text{3. 1 Secara Geometri}$

Perhatikanlah ilustrasi berikut!

$\text{3. 2 Secara Aljabar}$

Perkalian suatu skalar dengan suatu vektor tergantung pada skalarnya. Jika suatu skalar  k  dengan  $k>0$,  maka perkalian ini akan menghasilkan vektor baru yang besarnya sekian  k  kali dari vektor semula  atau  $k\left|\bar{a}\right|$   dan arahnya searah dengan vektor yang dikalikan. Demikian sebaliknya, jika nilai  $k<0$, maka besar vektor hasil perkaliannya adalah  $k\left|\bar{a}\right|$  dengan arah yang berlawanan dari vektor semula.

$\text{CONTOH SOAL}$.

Misalkan diketahui vektor-vektor sebagai berikut:

$\begin{array}{rl}& \overline{AB}=\left(\begin{array}{c}1\\ -3\end{array}\right),\overline{CD}=\left(\begin{array}{c}4\\ 3\end{array}\right)\text{dan}\overline{EF}=\left(\begin{array}{c}-4\\ -2\end{array}\right)\\ & \text{maka penjumlahan secara Aljabar}\\ & \text{dengan muculnya skalar adalah}:\\ & 3\overline{AB}+4\overline{CD}-5\overline{EF}\\ & =3\left(\begin{array}{c}1\\ -3\end{array}\right)+4\left(\begin{array}{c}4\\ 3\end{array}\right)-5\left(\begin{array}{c}-4\\ -2\end{array}\right)\\ & =\left(\begin{array}{c}3.1+4.4+(-5).(-4)\\ 3.(-3)+4.3+(-5).(-2)\end{array}\right)=\left(\begin{array}{c}39\\ 13\end{array}\right)\end{array}$

DAFTAR PUSTAKA

1. Kuntarti, Sulistiyono, & Kurnianingsih, S. 2005. Matematika untuk SMA dan MA Kelas XII Program Ilmu Alam. Jakarta: PT. Gelora Aksara Pratama

Materi Vektor Lanjutan (Kelas X Matematika Peminatan)

 

$\text{D. Modulus Vektor}$

Modulus suatu vektor adalah ukuran (panjang) suatu vektor. Dalam hal ini modulus suatu vektor adalah besar/panjang suatu vektor.

Lihat pada pembahasan sebelumnya tentang panjang vektor di  ${\text{R}}^2$  di sini.

Dalam menuliskan modulus/panjang vektor ini digunakan notasi  $\left|\bar{a}\right|$  jika vektornya $\bar{a}$. 

Bila  $\bar{a}=\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right),\text{maka}\left|\bar{a}\right|=\sqrt{x_1^2+y_1^2}$

$\text{CONTOH SOAL}$

Perhatikanlah ilustrasi gambar berikut

Tentukanlah modulus/panjang vektor  $\bar{u}$ ?

Jawab:

$\begin{array}{rl}& \text{Diketahui bahwa vektor}\bar{u}=\left(\begin{array}{c}4\\ 6\end{array}\right)\\ & \text{maka modulus vektor}\bar{u}\\ & =\left|\bar{u}\right|\\ & =\sqrt{4^2+6^2}=\sqrt{16+36}=\sqrt{52}\\ & =2\sqrt{13}\end{array}$

$\text{E. Vektor Posisi dan Vektor Bebas}$

Perhatikanlah ilustrasi berikut

Vektor yang titik pangkalnya berada di titik O(0,0), maka vektor tersebut dinamakan vektor posisi. Pada gambar di atas titik A rekatif terhadapa O(0,0), maka  $\overline{OA}$ disebut vektor posisi A terhadap titik O(0,0) dan vektor yang lainnya dinamakan vektor bebas. Pada gambar di atas  $\overline{BC}\mathrm{\&}\overline{DF}$  adalah contoh vektor bebasnya.

$\text{F. Kesamaan Dua Vektor}$

Perhatikanlah dua vektor bebas pada gambar di atas, cukup jelas secara geometri tampak panjang vektor $\overline{BC}\mathrm{\&}\overline{DF}$  sama. Dan secara aljabar dapat ditunjukkan juga bahwa:

$\overline{BC}=\left(\begin{array}{c}4\\ 6\end{array}\right)\mathrm{\&}\overline{DF}=\left(\begin{array}{c}4\\ 6\end{array}\right)$.

$\begin{array}{rl}& \mathbf{\text{Secara aljabar}}\text{pula dua vektor}\\ & \text{dikatakan sama, jika komponen}\\ & \text{komponen yang bersesuaian sama}\\ & \left(\begin{array}{c}{a}_1\\ a_2\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)\Rightarrow \{\begin{array}{ll}{a}_1& =b_1\\ a_2& =b_2\end{array}\end{array}$.

Secara definisi

$\bar{a}=\bar{b}\{\begin{array}{ll}\bullet & \left|\bar{a}\right|=\left|\bar{b}\right|\\ \\ \bullet & \text{arah}\bar{a}=\text{arah}\bar{b}\end{array}$

$\text{CONTOH SOAL}$.

$\begin{array}{rl}1.& \text{Tentukan nilai}x\text{dan}y\text{jika}\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}2\\ 5\end{array}\right)\\ & \mathbf{\text{Jawab}}:\\ & \text{Jelas bahwa jawabannya adalah}\\ & x=2,\text{dan}y=5\end{array}$.

$\begin{array}{rl}2.& \text{Tentukan nilai}x\text{dan}y\text{jika}\left(\begin{array}{c}x+y\\ x-y\end{array}\right)=\left(\begin{array}{c}9\\ 1\end{array}\right)\\ & \mathbf{\text{Jawab}}:\\ & \text{Jelas bahwa jawabannya adalah}\\ & x+y=9\\ & x-y=1\\ & ------+\\ & 2x=10\\ & x={\displaystyle \frac{10}{2}=5}\\ & \text{dan}x+y=9\iff 5+y=9\iff v=9-5=4\\ & \text{Jadi},x=5,\text{dan}y=4\end{array}$.

$\text{G. Vektor Negatif}$

Perhatikanlah ilustrasi berikut

$\bar{a}=\left(\begin{array}{c}4\\ 6\end{array}\right)\mathrm{\&}\bar{b}=\left(\begin{array}{c}-4\\ -6\end{array}\right)=-\left(\begin{array}{c}4\\ 6\end{array}\right)$

Vektor  $-\bar{a}=\bar{b}$ memiliki ukuran yang sama dengan   $\bar{a}$.

Selanjutnya vektor  $\bar{a}=-\bar{b}\text{maka}\left|\bar{a}\right|=\left|\bar{b}\right|$

$\text{H. Vektor Satuan}$

Perhatikanlah ilustrasi berikut

Jika diketahui  $\bar{a}\mathrm{\&}\bar{b}$ seperti gambar di atas, maka

$\{\begin{array}{ll}{\displaystyle \frac{\bar{a}}{\left|\bar{a}\right|}}& \text{adalah vektor satuan dari vektor}\bar{a}\\ \\ {\displaystyle \frac{\bar{b}}{\left|\bar{b}\right|}}& \text{adalah vektor satuan dari vektor}\bar{b}\end{array}$ 

Dan panjang dari vektor satuan ini adalah selalu satu satuan.

$\text{CONTOH SOAL}$.

Tentukanlah vektor satuan dari dua vektor pada gambar di atas?

Jawab:

$\{\begin{array}{ll}{\displaystyle \frac{\bar{a}}{\left|\bar{a}\right|}}& ={\displaystyle \frac{\left(\begin{array}{c}-2\\ 5\end{array}\right)}{\sqrt{(-2{)}^2+5^2}}}\\ & ={\displaystyle \frac{1}{\sqrt{29}}\left(\begin{array}{c}-2\\ 5\end{array}\right)={\displaystyle \frac{1}{29}\sqrt{29}\left(\begin{array}{c}-2\\ 5\end{array}\right)}}\\ \\ {\displaystyle \frac{\bar{b}}{\left|\bar{b}\right|}}& ={\displaystyle \frac{\left(\begin{array}{c}6\\ 4\end{array}\right)}{\sqrt{6^2+4^2}}}\\ & ={\displaystyle \frac{1}{\sqrt{52}}\left(\begin{array}{c}6\\ 4\end{array}\right)={\displaystyle \frac{1}{26}\sqrt{52}\left(\begin{array}{c}6\\ 4\end{array}\right)}}\end{array}$

$\text{I. Vektor Basis}$

Vektor satuan yang saling tegak lurus. Didalam ruang dimensi dua terdapat dua vektir basis., yaitu:

$\overline{i}=\left(\begin{array}{c}1\\ 0\end{array}\right)\text{dan}\overline{j}=\left(\begin{array}{c}0\\ 1\end{array}\right)$

$\begin{array}{rl}& \text{Misalkan vektor}\overline{u}=\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)\\ & \text{dapat dinyatakan dalam kombinasi linear}\\ & \text{vektor basis}\overline{i}\text{dan}\overline{j}\text{di atas, yaitu}\\ & \overline{u}=\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)=u_1\left(\begin{array}{c}1\\ 0\end{array}\right)+u_2\left(\begin{array}{c}0\\ 1\end{array}\right)\\ & \text{maka akan menjadi}\\ & \overline{u}=u_1\overline{i}+u_2\overline{j}\\ & \text{SEBAGAI CONTOH}\\ & \overline{AB}=\left(\begin{array}{c}5\\ 8\end{array}\right)\text{dalam vektor basis menjadi}\\ & \overline{AB}=5\overline{i}+8\overline{j}\\ & \text{Demikian juga jika}\\ & \overline{CD}=\left(\begin{array}{c}-3\\ -8\end{array}\right)\text{dalam vektor basis menjadi}\\ & \overline{AB}=-3\overline{i}-8\overline{j}\end{array}$

$\text{J. Vektor Nol}$

Jika vektor  $\bar{a}=\bar{b}$ , maka $\bar{a}-\bar{b}=0$.

$\mathbf{\text{0}}$  disebut sebagai vektor ol.

Sebagai tabahan penjelasan vektor  $\mathbf{\text{0}}$  tidak mempunyai besar dan arahnya tak tentu. 

Vektor (Kelas X Matematika Peminatan)

 $\text{A. Pendahuluan}$

Vektor adalah besaran yang memiliki panjang/besar sekaligus memiliki arah. Secara geometri, vektor digambarkan dengan anak panah (ruas garis berarah) yang mana memiliki titik pangkal dan titik ujung.

Perhatikanlah ilustrasi berikut

Perhatikanlah vektor  b  pada gambar di atas. Vektor tersebut dilambangkan dengan sebuah huruf  b  kecil tebal yang memiliki titik pangkal pada koordinat kartesius di titik  $\left({\displaystyle -\frac{5}{2},-\frac{3}{2}}\right)$  dan berujung di titik $\left({\displaystyle -1,2}\right)$ . Selain vektor b dituliskan dengan sebuah huruf kecil tercetak tebal dapat juga dituliskan dengan sebuah huruf kecil tanpa tercetak tebal tapi diberi anak panah kecil  atau ruas garis di atasnya, yaitu :  $\overrightarrow{a},\overline{a}$.

$\text{Berikut cara penulisan notasi vektor}$

1. Menggunakan dua huruf kapital yang di atasnya ada anak panah, misalnya  $\overline{PQ},\overline{RS},\text{dan}\overline{AZ}$
2. Menggunakan dua huruf kapital yang di atasnya diberikan anak panah, seperti  $\overrightarrow{PQ},\overrightarrow{RS},\text{dan}\overrightarrow{AZ}$
3. Menggunakan sebauah huruf kecil tercetak tebal seperti pembahasan sebelumnya di atas, yaitu :  $\mathbf{\text{a}},\mathbf{\text{b}},\mathbf{\text{c}},\mathbf{\text{d}},\text{dan}\mathbf{\text{e}}$
4. Menggunakan sebuah huruf kecil yang di atsnya diberikan anak panah, misalnya:  $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{d},\text{dan}\overrightarrow{e}$
5. Menggunakan sebuah huruf kecil yang bawahnya diberi garis
6. Menggunakan sebuah huruf kecil yang di atasnya diberi ruas garis, seperti  $\overline{a},\overline{b},\overline{c},\overline{d},\text{dan}\overline{e}$

$\text{B. Vektor pada}{\text{R}}^2$

Vektor di  ${\text{R}}^2$ adalah sebuah vektor yang diwakili oleh sebuah garis berarah dalam sebuah bidang datar atau Cartesius.

Perhatikanlah ilustrasi berikut

Misalkan pada salah satu vektor pada gambar di atas, ambil contoh $\overline{AB}$ . Vektor tersebut dilambangkan secara geometri dengan $\overline{AB}$  dan dibaca "vektor AB" yang berarti "vektor dari titik A ke titik B", dengan titik A sebagai titik pangkal dan B sebagai titik ujung. Sedangkan penulisan vektor secara aljabar dapat dinyatakan dalam matriks kolom atau matrik baris.

Pada   ${\text{R}}^2$  (penulisan vektor pada ruang dimensi dua) penulisan vektor ini dituliskan dengan  $\overline{AB}$, dengan 

$\overline{AB}=\left(\begin{array}{c}\text{komponen horisontal}\\ \text{komponen vertikal}\end{array}\right)$

Sehingga pada ilustrasi gambar di atas vektor-vektorya dapat dituliskan sebagai:

$\overline{AB}=\left(\begin{array}{c}1\\ -3\end{array}\right),\overline{CD}=\left(\begin{array}{c}4\\ 3\end{array}\right),\mathrm{\&}\overline{EF}=\left(\begin{array}{c}-4\\ -2\end{array}\right)$

atau

$\overline{AB}=\left[\begin{array}{cc}1,& -3\end{array}\right],\overline{CD}=\left[\begin{array}{cc}4,& 3\end{array}\right],\mathrm{\&}\overline{EF}=\left[\begin{array}{cc}-4,& -2\end{array}\right]$

$\text{C. Panjang Vektor}$

Panjang suatu vektor dilambangkan dengan tanda harga mutlak. Misal pada gambar di atas pada bahasan vekor di  ${\text{R}}^2$, yaitu:

$\left|\overline{AB}\right|,\left|\overline{CD}\right|,\mathrm{\&}\left|\overline{EF}\right|$.

Misalkan suatu vektor  $\overline{u}$ dengan  $\overline{u}=\left(\begin{array}{c}{u}_1\\ u_2\end{array}\right)$, maka panjang dari vektor  $\overline{u}$  ini dapat ditentukan dengan 

= $\left|\overline{u}\right|=\sqrt{u_1^2+u_2^2}$.

Sehingga pada gambar di atas, panjang/besar vektornya dapat kita tentukan, yaitu:

$\begin{array}{rl}\bullet \left|\overline{AB}\right|& =\sqrt{1^2+(-3{)}^2}=\sqrt{1+9}\\ & =\sqrt{10}\\ \bullet \left|\overline{CD}\right|& =\sqrt{4^2+3^2}=\sqrt{16+9}\\ & =\sqrt{25}=5\\ \bullet \left|\overline{EF}\right|& =\sqrt{(-4{)}^2+(-2{)}^2}=\sqrt{16+4}\\ & =\sqrt{20}=2\sqrt{5}\end{array}$

$\text{CONTOH SOAL}$.

1. Perhatikanlah gambar berikut

$\begin{array}{l}\\ .& \text{Nyatakan vektor pada gambar di atas}\\ & \text{secara aljabar dan tentukan panjangnya}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{l}\\ \bullet & \text{Secara aljabar dinyatakan}\\ & \overrightarrow{a}=\left(\begin{array}{c}6\\ -1\end{array}\right)=(6,-1)\\ & \overrightarrow{b}=\left(\begin{array}{c}10\\ 5\end{array}\right)=(10,5)\\ & \overrightarrow{c}=\left(\begin{array}{c}-3\\ -6\end{array}\right)=(-3,-6)\\ \bullet & \text{Besar/panjang vektornya adalah}\\ & \left|\overrightarrow{a}\right|=\sqrt{6^2+(-1{)}^2}=\sqrt{36+1}=\sqrt{37}\\ & \left|\overrightarrow{b}\right|=\sqrt{{10}^2+5^2}=\sqrt{100+25}=\sqrt{125}\\ & \left|\overrightarrow{c}\right|=\sqrt{(-3{)}^2+(-6{)}^2}=\sqrt{9+36}\\ & =\sqrt{45}=3\sqrt{5}\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Tentukan panjang vektor berikut}\\ & \text{a}.\left(\begin{array}{c}3\\ 4\end{array}\right),\text{b}.\left(\begin{array}{c}6\\ 9\end{array}\right)\\ \\ & \mathbf{\text{Jawab}}:\\ & \left|\left(\begin{array}{c}3\\ 4\end{array}\right)\right|=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5\\ \\ & \left|\left(\begin{array}{c}6\\ 9\end{array}\right)\right|=\sqrt{6^2+9^2}=\sqrt{36+81}=\sqrt{117}\end{array}$

Kedudukan Titik terhadap Lingkaran (Kelas XI)

$\text{D. Kedudukan Titik Terhadap Lingkaran }$.

Kedudukan sebuah titik terhadap sebuah lingkaran yang berpusat di O(0,0) memiliki 3 kemungkinan, yaitu:

• jika titik A(x,y) di dalam lingkaran, maka berlaku  $x^2+y^2<r^2$.
• jika titik A(x,y) pada lingkaran, maka berlaku  $x^2+y^2=r^2$, dan
• jika titik A(x,y) di luar lingkaran, maka berlaku  $x^2+y^2>r^2$.

Demikian juga kedudukan sebuah titik terhadap sebuah lingkaran yang berpusat di $(a,b)$ memiliki 3 kemungkinan, yaitu:

• jika titik A(x,y) di dalam lingkaran, maka berlaku $(x-a{)}^2+(y-b{)}^2<r^2$  atau  $x^2+y^2+Ax+By+C<0$.
• jika titik A(x,y) pada lingkaran, maka berlaku $(x-a{)}^2+(y-b{)}^2=r^2$  atau  $x^2+y^2+Ax+By+C=0$.
• jika titik A(x,y) di luar lingkaran, maka berlaku $(x-a{)}^2+(y-b{)}^2>r^2$  atau  $x^2+y^2+Ax+By+C>0$.

$\text{CONTOH SOAL}$.

$\begin{array}{l}\\ 1.& \text{Sebuah lingkaran yang berpusat pada }\\ & \text{pangkal koordinat}\\ & \text{a}.\text{Tentukanlah persamaan lingkaran }\\ & \text{yang berjari-jari 5}\\ & \text{b}.\text{Gambarlah lingkaran (pada soal a.) }\\ & \text{pada kertas grafiks}\\ & \text{c}.\text{Lukislah titik-titik dari},\\ & A(2,3),B(4,3),\text{dan}C(3,6).\\ & \text{d}.\text{Nyatakan kedudukan titik-titik}\\ & A,B,\text{dan}C\text{terhadap lingkaran. }\\ & \text{Di dalam, pada, atau}\\ & \text{beradakah di luar lingkaran}\\ & \mathbf{\text{Jawab}}:\\ & \text{Perhatikanlah ilustrasi berikut}\end{array}$.

$\begin{array}{rl}\text{a}.& \text{Diketahui}r=5\\ & \begin{array}{rl}& x^2+y^2=5^2\\ & \updownarrow \\ & x^2+y^2=25\\ & \text{atau}\\ & L\equiv \{(x,y)|x^2+y^2=25\}\end{array}\\ \text{b}.& \text{Lihat gambar di atas}\\ \text{c}.& \text{Lihat juga gambar di atas}\\ \text{d}.& \text{Dari gambar jelas bahwa}:\\ & \begin{array}{c}\bullet \text{Titik}A(2,3)\text{berada di dalam lingkaran}\\ \text{atau}:(2{)}^2+(3{)}^2=4+9=13<25\\ \bullet \text{Titik}A(4,3)\text{berada pada lingkaran}\\ \text{atau}:(4{)}^2+(3{)}^2=16+9=25=25\\ \bullet \text{Titik}A(3,6)\text{berada di luar lingkaran}\\ \text{atau}:(3{)}^2+(6{)}^2=9+36=45>25\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Tentukanlah persamaan lingkaran}\\ & \text{yang berpusat di pangkal koordinat}\\ & \text{dan melalui titik}P(5,-3)\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}\text{Diketahui}& \text{pusat lingkaran di pangkal }\\ \text{koordinat}& O(0,0)\text{serta lingkaran}\\ \text{yang mela}& \text{lui titik}P(5,-3),\text{maka}\\ r& =\sqrt{(x_p-0{)}^2+(y_p-0{)}^2}\\ & =\sqrt{5^2+(-3{)}^2}\\ & =\sqrt{25+9}\\ & =\sqrt{34}\\ \text{Sehingga }& ,\text{persamaan lingkarannya adalah}\\ L& \equiv x^2+y^2=r^2\iff x^2+y^2=34\end{array}\end{array}$.

DAFTAR PUSTAKA

1. Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
2. Sobirin. 2006. Kompas Matematika Strategi Praktis Menguasai Tes Matematika SMA Kelas 2. Jakarta: KAWAN PUSTAKA.
3. Wirodikromo, S. 2007. Matematika Jilid 2 IPA untuk Kelas XI. Jakarta: ERLANGGA.

Lingkaran (Matematika Peminatan Kelas XI)

 $\text{A. Definisi Lingkaran}$.

Secara definisi lingkaran adalah tempat kedudukam titik-titik yang berjarak sama terhadap satu titik tertentu. Selanjutnya titik tertentu disebut sebagai pusat lingkaran sedangkan jarak yang salalu sama terhadapa titik tertentu tersebut disebut sebagai jari-jari atau radius (r).

Sebagai ilustrasi berikut diberikan gambar berkaitan kedudukan titik-titik tersebut

$\text{B. Persamaan Lingkaran Berpusat di O(0,0) }$.

Persamaan sebuah lingkaran dengan dengan jari-jari  $r$  dan berpusat di titik pusat koordinat dapat dilustrasikan sebagai berikut

Misalkan sebuah titik  $\text{P}(x,y)$  terletak pada sebuah lingkaran yang berpusat di O(0,0). Dan titik ${\text{P}}^{\prime }(x,0)$ adalah proyeksi titik  P  pada sumbu-X sehingga  $△{\text{OP}}^{\prime }\text{P}$   berupa sebuah segitiga siku-siku di ${\text{P}}^{\prime }$. Dengan rumus Pythagoras kita mendapatkan

$\begin{array}{rl}& O{P}^2=(O{P}^{\prime }{)}^2+(P{P}^{\prime }{)}^2\\ & \iff r^2=x^2+y^2\\ & \iff r=\sqrt{x^2+y^2}\end{array}$

Untuk lebih memudahkan pemahaman Anda, perhatikanlah ilustrasi berikut

Sehingga dapat disimpulkan persamaan lingkaran yang berpusat di O(0,0) adalah:

$\begin{array}{|ccc|}\hline & & \\ & x^2+y^2=r^2& \\ & & \\ \hline\end{array}$.

$\text{CONTOH SOAL}$.

$\begin{array}{l}\\ 1.& \text{Tentukan persamaan lingkaran yang }\\ & \text{berpusat di O dan berjari-jari}{\displaystyle \frac{1}{2}\sqrt{10}}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Diketahui pusat lingkaran di O}\\ & \text{dengan jarijari}r={\displaystyle \frac{1}{2}\sqrt{10}}\\ & \text{Persamaan lingkarannya adalah}:\\ & x^2+y^2=r^2\\ & \iff x^2+y^2={\left({\displaystyle \frac{1}{2}\sqrt{10}}\right)}^2\\ & \iff x^2+y^2={\displaystyle \frac{10}{4},\text{atau}}\\ & \iff x^2+y^2={\displaystyle \frac{5}{2}}\\ & \text{Jadi, persamaan lingkarannya}\\ & \text{adalah}{x}^2+y^2={\displaystyle \frac{5}{2}}\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Tentukan pusat dan jari-jari lingkaran}\\ & \text{yang memenuhi persamaan}\\ & x^2+y^2=6\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Diketahui persamaan lingkaran}\\ & x^2+y^2=6\\ & \text{maka }\\ & \bullet \text{pusat lingkaran adalah O}\\ & x^2+y^2=r^2\\ & \bullet \text{dengan jari-jarinya adalah}\\ & r^2=6\Rightarrow r=\sqrt{6}\\ & \text{Jadi, pusat lingkaran di O dengan}\\ & \text{jari-jari sebesar}r=\sqrt{6}\end{array}\end{array}$.

$\text{C. Persamaan Lingkaran Berpusat di (a,b)}$.

Perhatikanlah ilustrasi berikut

Pada ilustrasi gambar di atas ditunjukkan sebuah lingkaran berpusat di $N(a,b)$ dengan jari-jari  $r$, misalkan kita ambil sebuah titik $P(x,y)$ pada keliling lingkaran, maka $NP=r$.

$\begin{array}{rl}& \sqrt{(x-a{)}^2+(y-b{)}^2}=r^2\\ & (x-a{)}^2+(y-b{)}^2=r^2\\ & \text{persamaan di atas adalah}\mathbf{\text{Bentuk Umum}}\\ & \text{dari}\mathbf{\text{Persamaan Lingkaran}}\text{yang}\\ & \text{berpusat di}(a,b)\end{array}$

Selanjutnya perhatikanlah rangkuman berikut

$\begin{array}{|lcc|}\hline \text{Lingkaran}& x^2+y^2=r^2& (x-p{)}^2+(y-q{)}^2=r^2\\ \text{Pusat}& (0,0)& (p,q)\\ \text{Jari-jari}& r& r\\ \begin{array}{rl}& \text{Pesamaan garis}\\ & \text{singgung melalui}\\ & \text{titik}(x_1,y_1)\\ & \text{pada lingkaran}\end{array}& x_{1}x+y_{1}y=r^2& \begin{array}{rl}& (x_1-p)(x-p)\\ & +(y_1-q)(y-q)=r^2\end{array}\\ \begin{array}{rl}& \text{Persamaan garis}\\ & \text{singgung dengan}\\ & \text{gradien}m\end{array}& \begin{array}{rl}& y=mx\\ & \pm r\sqrt{m^2+1}\end{array}& \begin{array}{rl}& (y-q)=m(x-a)\\ & \pm r\sqrt{m^2+1}\end{array}\\ \hline\end{array}$.

Kusus untuk yang pusat  $(a,b)$ adalah:

$\begin{array}{|lc|}\hline \text{Lingkaran}& x^2+y^2+Ax+By+C=0\\ \text{Pusat}& (-\frac{1}{2}A,-\frac{1}{2}B)\\ \text{Jari-jari}& r=\sqrt{{\displaystyle \frac{1}{4}(A^2+B^2)-C}}\\ \begin{array}{rl}& \text{Pesamaan garis}\\ & \text{singgung melalui}\\ & \text{titik}(x_1,y_1)\\ & \text{pada lingkaran}\end{array}& \begin{array}{rl}& x_{1}x+y_{1}y\\ & +{\displaystyle \frac{A}{2}(x_1+x)}\\ & +{\displaystyle \frac{B}{2}(y_1+y)+C=0}\end{array}\\ \begin{array}{rl}& \text{Persamaan garis}\\ & \text{singgung dengan}\\ & \text{gradien}m\end{array}& \begin{array}{rl}& y+\frac{1}{2}B=m(x+\frac{1}{2}A)\\ & \pm \sqrt{{\displaystyle \frac{1}{4}(A^2+B^2)-C}}.\sqrt{m^2+1}\end{array}\\ \hline\end{array}$.

$\text{CONTOH SOAL}$.

$\begin{array}{l}\\ 1.& \text{Tentukan persamaan lingkaran yang }\\ & \text{berpusat di (0,-2) dan berjari-jari}5\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Diketahui pusat lingkaran berpusat}\\ & \text{di}(0,-2)\text{dan berjari-jari}r=5\\ & \text{Persamaan lingkarannya adalah}:\\ & (x-a{)}^2+(y-b{)}^2=r^2\\ & \iff (x-0{)}^2+(y-(-2){)}^2={\left(5\right)}^2\\ & \iff x^2+(y+2{)}^2=25,\text{atau}\\ & \iff x^2+y^2+4y+4=25\\ & \text{Jadi, persamaan lingkarannya}\\ & \text{adalah}{x}^2+y^2+4y-21=0\end{array}\end{array}$,

$\begin{array}{l}\\ 2.& \text{Tentukan persamaan lingkaran}\\ & \text{yang berpusat di titik}M(1,3)\\ & \text{dan melalui titik}N(-2,5)\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Diketahui jari-jari lingkaran}\\ & r=MN=\sqrt{(x_M-x_N{)}^2+({)}^2}\\ & \iff =\sqrt{(-2-1{)}^2+(5-3{)}^2}\\ & \iff =\sqrt{(-3{)}^2+2^2}\\ & \iff =\sqrt{9+4}=\sqrt{13}\\ & \text{maka}\\ & \text{persamaan lingkarannya adalah}\\ & (x-1{)}^2+(y-3{)}^2=r^2\\ & \iff (x-1{)}^2+(y-3{)}^2={\left(\sqrt{13}\right)}^2\\ & \iff (x-1{)}^2+(y-3{)}^2=13\\ & \text{Jadi, jari-jari lingkarannya}\\ & \text{adalah}\sqrt{13}.\text{Dan persamaan}\\ & \text{lingkarannya adalah}:(x-1{)}^2+(y-3{)}^2=13\end{array}\end{array}$.

$\begin{array}{l}\\ 3.& \text{Tentukanlah pusat dan jari-jari lingkaran berikut?}\\ & \text{a}.L\equiv (x+1{)}^2+(y+2{)}^2=9\\ & \text{b}.L\equiv (x+1{)}^2+(y-2{)}^2=9\\ & \text{c}.L\equiv (x-1{)}^2+(y+2{)}^2=9\\ & \text{d}.L\equiv (x-1{)}^2+(y-2{)}^2=9\\ & \text{e}.L\equiv (x+3{)}^2+(y-3{)}^2=9\\ & \text{f}.L\equiv (x-1{)}^2+(y-2{)}^2=25\\ & \text{g}.L\equiv (x-1{)}^2+y^2=27\\ & \text{h}.L\equiv x^2+(y-1{)}^2=27\\ \\ & \text{Jawab}:\\ & L\equiv (x+1{)}^2+(y+2{)}^2=9,\text{pusat di}(-1,-2)\\ & \text{dan jari-jarinya adalah}\sqrt{9}=3\\ & \text{Soal yang belum dibahas silahkan }\\ & \text{diselesaikan sendiri sebagai latihan}\end{array}$.

$\begin{array}{l}\\ 4.& \text{Tentukanlah pusat dan jari-jari dari }\\ & \text{persamaan lingkaran}\\ & L\equiv 2x^2+2y^2-2x+6y-3=0\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Persamaan lingkaran}\\ & L\equiv 2x^2+2y^2-2x+6y-3=0\\ & \iff x^2+y^2-x+3y-{\displaystyle \frac{3}{2}=0\{\begin{array}{ll}A& =-1\\ B& =3\\ C& =-{\displaystyle \frac{3}{2}}\end{array}}\\ & \text{maka}\{\begin{array}{ll}\text{Pusat}& =(-{\displaystyle \frac{-1}{2},-\frac{3}{2}})=\left({\displaystyle \frac{1}{2},-\frac{3}{2}}\right)\\ \text{Jari-jari}& =r=\sqrt{{\displaystyle \frac{(-1{)}^2}{4}+\frac{3^2}{4}-(-\frac{3}{2})}}\\ & =\sqrt{{\displaystyle \frac{1}{4}+\frac{9}{4}+\frac{6}{4}}}=\sqrt{4}=2\end{array}\\ & \text{Jadi, lingkaran}2x^2+2y^2-2x+6y-3=0\\ & \text{berpusat di}\left({\displaystyle \frac{1}{2},-\frac{3}{2}}\right)\text{dan berjari-jari}2\end{array}\end{array}$.

$\begin{array}{l}\\ 5.& \text{Diketahui persamaan lingkaran}\\ & L\equiv 2x^2+2y^2-4x+3py-30=0\\ & \text{dan melalui titik}(-2,1).\text{Tentukanlah }\\ & \text{persamaan lingkaran baru yang}\\ & \text{kosentris(sepusat) dan panjang jari-jarinya}\\ & \text{dua kali panjang jari-jari lingkaran semula?}\\ \\ & \mathbf{\text{Jawab}}\\ & \begin{array}{rl}& \text{Diketahui persamaan lingkaran}\\ & 2x^2+2y^2-4x+3py-30=0,\text{melalui}\\ & (-2,1),\text{maka}\\ & \begin{array}{rl}& \text{kita tentukan harga}p\text{dulu, yaitu}:\\ & 2(-2{)}^2+2(1{)}^2-4(-2)+3p(1)-30=0\\ & \iff 8+2+8+3p-30=0\\ & \iff 3p=12\\ & \iff p=4\end{array}\\ & \text{Akibatnya persamaan lingkaran menjadi}\\ & \begin{array}{rl}& 2x^2+2y^2-4x+12y-30=0\\ & \iff x^2+y^2-2x+6y-15=0\end{array}\\ & \begin{array}{rl}& \{\begin{array}{l}\text{Pusat}:\\ (-{\displaystyle \frac{1}{2}A,-\frac{1}{2}B})\\ =(-{\displaystyle \frac{1}{2}.(-2),-\frac{1}{2},6})\\ =(1,-3)\\ \\ \text{Jari-jari }:\\ \begin{array}{rl}r& =\sqrt{{(-\frac{1}{2}A)}^2+(-\frac{1}{2}B)-C}\\ & =\sqrt{1^2+(-3{)}^2-(-15)}\\ & =\sqrt{1+9+15}=5\end{array}\end{array}\\ & \end{array}\\ & \text{Selanjutnya}\\ & \begin{array}{rl}& \text{Persamaan}\text{lingkaran baru }\\ & \text{dengan pusat}(1,-3)\text{dan jari-jari}\\ & r_{\text{baru}}=2r=2.5=10\\ & (x-1{)}^2+(y+3{)}^2=(10{)}^2\\ & \iff x^2-2x+1+y^2+6x+9=100\\ & \iff x^2+y^2-2x+6y-90=0\end{array}\end{array}\end{array}$

Berikut ilustrasi gambarnya

Contoh Soal 14 (Segitiga dan Ketaksamaan)

 $\begin{array}{l}\\ 66.& \text{Diberikan}a,b,c>0,\text{tunjukkan bahwa}\\ & {\displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\ge 6}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Alternatif 1}\\ & \text{Dengan mengaplikasikan AM-GM-HM}\\ & \text{pada}{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\text{kita dapat menemukan}}\\ & {\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge {\displaystyle \frac{3}{(abc{)}^{{.}^{\frac{1}{3}}}}\ge {\displaystyle \frac{9}{a+b+c}}}}\\ & \text{Jika kedua ruas dikalikan dengan}a+b+c,\\ & \text{maka}\\ & 3+{\displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\ge {\displaystyle \frac{9(a+b+c)}{a+b+c}}}\\ & \iff {\displaystyle \frac{b+c}{a}+\frac{c+a}{b}+\frac{a+b}{c}\ge 6◼}\\ & \begin{array}{rl}& \text{Alternatif 2}\\ & \text{Asumsikan}a\le b\le c,\text{maka}a+b\le a+c\le b+c\\ & \text{dan}{\displaystyle \frac{1}{c}\le \frac{1}{b}\le \frac{1}{a}.}\\ & \text{Perhatikan bahwa}\\ & (a+b\le a+c\le b+c)\text{dan}{\displaystyle \frac{1}{c}\le \frac{1}{b}\le \frac{1}{a}}\\ & \text{memiliki kemonotonan yang sama}\\ & \text{maka dengan}\mathbf{\text{ketaksamaan Renata}}\\ & \text{dapat diperoleh bentuk}\\ & (b+c).{\displaystyle \frac{1}{a}+(c+a).{\displaystyle \frac{1}{b}+(a+b).{\displaystyle \frac{1}{c}\ge (b+c).{\displaystyle \frac{1}{b}+(c+a).{\displaystyle \frac{1}{c}+(a+b).{\displaystyle \frac{1}{a}}}}}}}\\ & \doteq 1+{\displaystyle \frac{c}{b}+1+\frac{a}{c}+1+\frac{b}{a}}\\ & \doteq 3+\frac{c}{b}+\frac{a}{c}+\frac{b}{a}\\ & \doteq 3+3{\left({\displaystyle \frac{abc}{abc}}\right)}^{{.}^{\frac{1}{3}}}\\ & \doteq 3+3\\ & \doteq 6◼\end{array}\end{array}$.

$\begin{array}{l}\\ 67.& \text{Diberikan}a,b,c>0,\text{tunjukkan kebenaran}\\ & \mathbf{\text{ketaksamaan Nesbitt}}\text{berikut}\\ & {\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge \frac{3}{2}}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Alternatif 1}\\ & \begin{array}{rl}& \text{Asumsikan},\\ & \{\begin{array}{ll}& a\ge b\ge c\\ & {\displaystyle \frac{1}{b+c}\ge \frac{1}{a+c}\ge \frac{1}{a+b}}\end{array}\\ & \text{Dengan}\mathbf{\text{Ketaksamaan Chebyshev}}\\ & {\displaystyle \frac{{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}}{3}\ge {\displaystyle \frac{(a+b+c)}{3}\left({\displaystyle \frac{\left({\displaystyle \frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}}\right)}{3}}\right)}}\\ & \text{Dengan AM-HM dan}K={\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\\ & \iff {\displaystyle \frac{K}{3}\ge {\displaystyle \frac{(a+b+c)}{3}\left({\displaystyle \frac{3}{(b+c)+(a+c)+(a+b)}}\right)}}\\ & \iff K\ge {\displaystyle \frac{3(a+b+c)}{2(a+b+c)}}\\ & \iff K\ge {\displaystyle \frac{3}{2}}\\ & \iff {\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge {\displaystyle \frac{3}{2}◼}}\end{array}\\ & \text{Alternatif 2}\\ & \begin{array}{rl}& \mathbf{\text{Pertama}},\text{asumsikan}\\ & \{\begin{array}{ll}& a\ge b\ge c\\ & {\displaystyle \frac{1}{b+c}\ge \frac{1}{a+c}\ge \frac{1}{a+b}}\end{array}\\ & \text{Dengan}\mathbf{\text{Ketaksamaan Chebyshev}}\\ & 3\left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge (a+b+c)\left({\displaystyle \frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}}\right)\\ & \mathbf{\text{Kedua}},\text{asumsikan}\\ & \{\begin{array}{ll}& a+b\ge a+c\ge b+c\\ & {\displaystyle \frac{1}{a+b}\le \frac{1}{a+c}\le \frac{1}{b+c}}\end{array}\\ & \text{Dengan}\mathbf{\text{Ketaksamaan Chebyshev}}\\ & 3\left({\displaystyle \frac{a+b}{a+b}+\frac{a+c}{a+c}+\frac{b+c}{b+c}}\right)\le (a+b+a+c+b+c)\left({\displaystyle \frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}}\right)\\ & \iff 3(1+1+1)\le 2(a+b+c)\left({\displaystyle \frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}}\right)\\ & \iff {\displaystyle \frac{9}{2}\le (a+b+c)\left({\displaystyle \frac{1}{a+b}+\frac{1}{a+c}+\frac{1}{b+c}}\right)}\\ & \text{Dari dua ketaksamaan di atas didapatkan}\\ & 3\left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge {\displaystyle \frac{9}{2}}\\ & \iff \left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge {\displaystyle \frac{3}{2}◼}\end{array}\end{array}$ 

$\begin{array}{l}\\ 68.& \text{Jika}a,b,c>0,\text{dengan}a\ne b\ne c\\ & \text{tunjukkan bahwa}\\ & (a^3+b^3+c^3)>{\displaystyle \frac{(a+b+c{)}^3}{9}>3abc}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Dengan}\mathbf{\text{ketaksamaan Chebyshev}}\\ & \text{untuk}a\ge b\ge c,\text{dapat diperoleh bentuk}\\ & {\displaystyle \frac{(a^3+b^3+c^3)}{3}>\left({\displaystyle \frac{a+b+c}{3}}\right)\left({\displaystyle \frac{a+b+c}{3}}\right)\left({\displaystyle \frac{a+b+c}{3}}\right)}\\ & \iff {\displaystyle \frac{(a^3+b^3+c^3)}{3}>{\left({\displaystyle \frac{a+b+c}{3}}\right)}^3>{\left({\displaystyle \frac{3\sqrt[3]{abc}}{3}}\right)}^3}\\ & \iff {\displaystyle \frac{(a^3+b^3+c^3)}{3}>{\displaystyle \frac{(a+b+c{)}^3}{27}>abc}}\\ & \iff (a^3+b^3+c^3)>{\displaystyle \frac{(a+b+c{)}^3}{9}>3abc◼}\end{array}$.

$\begin{array}{l}\\ 69.& \text{tunjukkan bahwa untuk}n\text{bilangan asli}\\ & \text{berlaku}\\ & {\displaystyle \frac{1}{\sqrt{n}}(1+\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{1}{3}}}+\cdots +\sqrt{{\displaystyle \frac{1}{n}}})\le (2n-1{)}^{{.}^{\frac{1}{4}}}}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Dengan}\mathbf{\text{ketaksamaan Chebyshev}}\\ & \text{untuk}:(1\ge {\displaystyle \frac{1}{2}\ge \frac{1}{3}\ge \cdots \ge \frac{1}{n}})\\ & \text{dapat diperoleh bentuk berikut}\\ & {(1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})}^2\le n(1+{\displaystyle \frac{1}{2.2}+\frac{1}{3.3}+\cdots +\frac{1}{n.n}})\\ & \iff {(1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})}^2\le n(1+{\displaystyle \frac{1}{1.2}+\frac{1}{2.3}+\cdots +\frac{1}{(n-1).n}})\\ & \iff {(1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})}^2\le n(1+(1-{\displaystyle \frac{1}{2}})+\left({\displaystyle \frac{1}{2}-\frac{1}{3}}\right)+\cdots +\left({\displaystyle \frac{1}{(n-1)}-\frac{1}{n}}\right))\\ & \iff {(1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})}^2\le n(1+1-{\displaystyle \frac{1}{n}})=n(2-{\displaystyle \frac{1}{n}})\\ & \iff (1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})\le \sqrt{2n-1}..........(1)\\ & \text{Gunakan lagi}\mathbf{\text{ketaksamaan Chebyshev}}\\ & {(1+\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{1}{3}}}+\cdots +\sqrt{{\displaystyle \frac{1}{n}}})}^2\le n(1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})\\ & \iff {\displaystyle \frac{1}{n}{(1+\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{1}{3}}}+\cdots +\sqrt{{\displaystyle \frac{1}{n}}})}^2\le (1+{\displaystyle \frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}})...(2)}\\ & \text{Dari ketaksamaan (1) dan (2), dapat diperoleh}\\ & {\displaystyle \frac{1}{n}{(1+\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{1}{3}}}+\cdots +\sqrt{{\displaystyle \frac{1}{n}}})}^2\le \sqrt{2n-1}=(2n-1{)}^{{.}^{\frac{1}{2}}}}\\ & \iff {\displaystyle \frac{1}{\sqrt{n}}(1+\sqrt{{\displaystyle \frac{1}{2}}}+\sqrt{{\displaystyle \frac{1}{3}}}+\cdots +\sqrt{{\displaystyle \frac{1}{n}}})\le (2n-1{)}^{{.}^{\frac{1}{4}}}◼}\end{array}$.

$\begin{array}{l}\\ 70.& (\mathbf{\text{OSN 2011}})\\ & \text{Jika}a,b,c>0,\text{dengan}abc=1\\ & \text{Jika diketahui}\\ & a^{2011}+b^{2011}+c^{2011}<{\displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}}\\ & \text{tunjukkan bahwa}\\ & (a+b+c)>{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Asumsikan}\\ & \{\begin{array}{ll}& a\ge b\ge c\\ & {\displaystyle \frac{1}{c}\ge \frac{1}{b}\ge \frac{1}{a}}\end{array}\\ & \text{Dengan}\mathbf{\text{ketaksamaan Chebyshev}}\\ & \text{Perhatikan}\\ & \begin{array}{rl}& {\displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\ge {\displaystyle \frac{1}{3}\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)\left({\displaystyle \frac{1}{a^{2010}}+\frac{1}{b^{2010}}+\frac{1}{c^{2010}}}\right)}}\\ & \iff {\displaystyle \frac{1}{a^{2010}}+\frac{1}{b^{2010}}+\frac{1}{c^{2010}}\ge {\displaystyle \frac{1}{3}\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)\left({\displaystyle \frac{1}{a^{2009}}+\frac{1}{b^{2009}}+\frac{1}{c^{2009}}}\right)}}\\ & \iff {\displaystyle \frac{1}{a^{2009}}+\frac{1}{b^{2009}}+\frac{1}{c^{2009}}\ge {\displaystyle \frac{1}{3}\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)\left({\displaystyle \frac{1}{a^{2008}}+\frac{1}{b^{2008}}+\frac{1}{c^{2008}}}\right)}}\\ & ⋮\\ & \iff {\displaystyle \frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\ge {\displaystyle \frac{1}{3}\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)\left({\displaystyle \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}\right)}}\\ & \iff {\displaystyle \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge {\displaystyle \frac{1}{3}\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)}}\\ & \text{Sehingga}\\ & {\displaystyle \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\ge {\displaystyle \frac{1}{3^{2010}}{\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)}^{2011}.....(1)}}\end{array}\\ & \text{dan}\\ & \begin{array}{rl}& a^{2011}+b^{2011}+c^{2011}\ge {\displaystyle \frac{1}{3}(a+b+c)(a^{2010}+b^{2010}+c^{2010})}\\ & \iff a^{2010}+b^{2010}+c^{2010}\ge {\displaystyle \frac{1}{3}(a+b+c)(a^{2009}+b^{2009}+c^{2009})}\\ & \iff a^{2009}+b^{2009}+c^{2009}\ge {\displaystyle \frac{1}{3}(a+b+c)(a^{2008}+b^{2008}+c^{2008})}\\ & ⋮\\ & \iff a^3+b^3+c^3\ge {\displaystyle \frac{1}{3}(a+b+c)(a^2+b^2+c^2)}\\ & \iff a^2+b^2+c^2\ge {\displaystyle \frac{1}{3}(a+b+c)(a+b+c)}\\ & \text{Sehingga}\\ & \iff a^{2011}+b^{2011}+c^{2011}\ge {\displaystyle \frac{1}{3^{2010}}(a+b+c{)}^{2011}........(2)}\end{array}\\ & \begin{array}{rl}& \text{Dari ketaksamaan (1) dan (2) didapatkan}\\ & \frac{1}{a^{2011}}+\frac{1}{b^{2011}}+\frac{1}{c^{2011}}\ge {\displaystyle \frac{1}{3^{2010}}{\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)}^{2011}}\\ & >a^{2011}+b^{2011}+c^{2011}\ge {\displaystyle \frac{1}{3^{2010}}(a+b+c{)}^{2011}}\\ & \text{atau}\\ & {\displaystyle \sum _{\text{siklik}}^{.}{\displaystyle \frac{1}{a^{2011}}\ge {\displaystyle \frac{1}{3^{2010}}{\left({\displaystyle \sum _{\text{siklik}}^{.}{\displaystyle \frac{1}{a}}}\right)}^{2011}>{\displaystyle \sum _{\text{siklik}}^{.}{a}^{2011}\ge {\displaystyle \frac{1}{3^{2010}}{\left({\displaystyle \sum _{\text{siklik}}^{.}}\right)}^{2011}}}}}}\\ & \iff {\displaystyle \frac{1}{3^{2010}}{\left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)}^{2011}>{\displaystyle \frac{1}{3^{2010}}(a+b+c{)}^{2011}}}\\ & \iff \left({\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\right)>(a+b+c)\\ & \iff a+b+c<{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}◼}\end{array}\end{array}$.

DAFTAR PUSTAKA

1. Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.

Contoh Soal 13 (Segitiga dan Ketaksamaan)

 $.\begin{array}{rl}& \text{Mengenal penulisan pola}\mathbf{\text{Siklik dan Simetri}}\\ & \text{Misal untuk}n=3,\text{pada penulisan unsur}\\ & x,y,\text{dan}z,\text{maka}\\ & \begin{array}{|ll|}\hline \mathbf{\text{Pola Siklik}}& \mathbf{\text{Pola Simetri}}\\ \begin{array}{r}{\displaystyle \sum _{\text{siklik}}^{.}{x}^2=x^2+y^2+z^2}\\ & \\ & \\ & \\ & \\ & \end{array}& \begin{array}{rl}{\displaystyle \sum _{\text{sym}}^{.}{x}^2}& =x^2+x^2\\ & +y^2+y^2\\ \\ & +z^2+z^2\\ \\ & =2(x^2+y^2+z^2)\end{array}\\ \begin{array}{r}{\displaystyle \sum _{\text{siklik}}^{.}{x}^3=x^3+y^3+z^3}\end{array}& \begin{array}{r}{\displaystyle \sum _{\text{sym}}^{.}{x}^3=2(x^3+y^3+z^3)}\end{array}\\ \begin{array}{r}{\displaystyle \sum _{\text{siklik}}^{.}{x}^{2}y=x^{2}y+y^{2}z+z^{2}x}\\ & \\ & \\ & \end{array}& \begin{array}{rl}{\displaystyle \sum _{\text{sym}}^{.}{x}^{2}y}& =x^{2}y+x^{2}z\\ & +y^{2}x+y^{2}z\\ \\ & +z^{2}x+z^{2}y\end{array}\\ \begin{array}{rl}{\displaystyle \sum _{\text{siklik}}^{.}xyz}& =xyz+yzx+zxy\\ & =3xyz\end{array}& \begin{array}{rl}{\displaystyle \sum _{\text{sym}}^{.}xyz}& =xyz+xzy+\cdots \\ & =6xyz\end{array}\\ \hline\end{array}\end{array}$.

$\begin{array}{l}\\ 61.& (\mathbf{\text{IMO 1995}})\\ & \text{Jika}a,b,c\text{bilangan-bilangan real positif}\\ & \text{dengan}abc=1,\text{maka tunjukkan bahwa}\\ & {\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}\ge {\displaystyle \frac{3}{2}}}\\ \\ & \mathbf{\text{Bukti}}\\ & \begin{array}{rl}& \text{Misalkan}x={\displaystyle \frac{1}{a},y={\displaystyle \frac{1}{b},\text{dan}z={\displaystyle \frac{1}{c},}}}\\ & \text{maka}\\ & {\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}}\\ & ={\displaystyle \frac{x^{3}yz}{y+z}+\frac{y^{3}xz}{x+z}+\frac{z^{3}xy}{x+y},\text{karena}xyz=1}\\ & ={\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\\ & \text{Dengan ketaksamaan}\mathbf{\text{Cauchy-Schwarz}}\\ & \left(2{\displaystyle \sum _{\text{siklik}}^{.}y+z}\right)\left({\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\right)\ge (x+y+z{)}^2\\ & \iff \left({\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\right)\ge {\displaystyle \frac{(x+y+z{)}^2}{2(x+y+z)}}\\ & \iff \left({\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\right)\ge {\displaystyle \frac{(a+b+c)}{2}}\\ & \iff \left({\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\right)\ge {\displaystyle \frac{3\sqrt[3]{xyz}}{2}}\\ & \iff \left({\displaystyle \frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}}\right)\ge {\displaystyle \frac{3}{2}◼}\end{array}\end{array}$.

$\begin{array}{l}\\ 62.& \text{Diketahui}a,b\text{bilangan real positif}\\ & \text{Tunjukkan bahwa}{\displaystyle \frac{a^2}{b}+\frac{b^2}{a}\ge a+b}\\ \\ & \mathbf{\text{Bukti}}\\ & \text{Asumsikan bahwa}a\ge b,\text{maka}{a}^2\ge b^2\\ & \text{dan}{\displaystyle \frac{1}{b}\ge \frac{1}{a}.}\\ & \text{Perhatikan bahwa baik}(a^2,b^2)\text{dan}\left({\displaystyle \frac{1}{b},\frac{1}{a}}\right)\\ & \text{adalah kumpulan dua barisan yang monoton}\\ & \text{sama yaitu sama-sama naik. Sehingga}\\ & \text{dengan}\mathbf{\text{ketaksamaan Renata}}\text{diperoleh}\\ & a^2.{\displaystyle \frac{1}{b}+b^2.{\displaystyle \frac{1}{a}\ge a^2.{\displaystyle \frac{1}{a}+b^2.{\displaystyle \frac{1}{b}}}}}\\ & \iff {\displaystyle \frac{a^2}{b}+\frac{b^2}{a}\ge a+b◼}\end{array}$.

$\begin{array}{l}\\ 63.& \text{Diberikan}a,b,c>0,\text{tunjukkan bahwa}\\ & {\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+b+c}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Alternatif 1}\\ & \text{Dengan AM-GM diperoleh}\\ & \bullet {\displaystyle \frac{a}{c}+\frac{c}{a}\ge 2\iff {\displaystyle \frac{c}{a}\ge 2-{\displaystyle \frac{a}{c}}}}\\ & \bullet {\displaystyle \frac{b}{c}+\frac{c}{b}\ge 2\iff {\displaystyle \frac{b}{c}\ge 2-{\displaystyle \frac{c}{b}}}}\\ & \bullet {\displaystyle \frac{a}{b}+\frac{b}{a}\ge 2\iff {\displaystyle \frac{a}{b}\ge 2-{\displaystyle \frac{b}{a}}}}\\ & \text{Sehingga}\\ & \begin{array}{rl}{\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}}& \ge a(2-{\displaystyle \frac{c}{b}})+b(2-{\displaystyle \frac{a}{c}})+c(2-{\displaystyle \frac{b}{a}})\\ & =2a-{\displaystyle \frac{ac}{b}+2b-{\displaystyle \frac{ab}{c}+2c-{\displaystyle \frac{bc}{a}}}}\\ {\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}}& \ge 2(a+b+c)-\left({\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}}\right)\\ 2& \left({\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}}\right)\ge 2(a+b+c)\\ {\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}}& \ge a+b+c◼\end{array}\\ & \text{Alternatif 2}\\ & \text{Dengan ketaksamaan Renata}\\ & \begin{array}{rl}& \text{Asumsikan}a\ge b\ge c,\text{maka}ab\ge ca\ge bc\\ & \text{dan}{\displaystyle \frac{1}{c}\ge \frac{1}{b}\ge \frac{1}{a}.}\\ & \text{Perhatikan bahwa}\\ & (ab\ge ca\ge bc)\text{dan}\left({\displaystyle \frac{1}{c}\ge \frac{1}{b}\ge \frac{1}{a}}\right)\\ & \text{memiliki kemonotonan yang sama}\\ & \text{maka dengan}\mathbf{\text{ketaksamaan Renata}}\\ & \text{dapat diperoleh bentuk}\\ & ab.{\displaystyle \frac{1}{c}+ac.{\displaystyle \frac{1}{b}+bc.{\displaystyle \frac{1}{a}\ge ab.{\displaystyle \frac{1}{b}+ac.{\displaystyle \frac{1}{a}+bc.{\displaystyle \frac{1}{c}}}}}}}\\ & \iff {\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+c+b}\\ & \iff {\displaystyle \frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}\ge a+b+c◼}\end{array}\end{array}$.

$\begin{array}{l}\\ 64.& \text{Diberikan}a,b,c>0,\text{tunjukkan kebenaran}\\ & \mathbf{\text{ketaksamaan Nesbitt}}\text{berikut}\\ & {\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\ge \frac{3}{2}}\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Alternatif 1}\\ & \text{Dengan AM-GM diperoleh}\\ & {\displaystyle \frac{(a+b)+(b+c)+(c+a)}{3}\ge {\displaystyle \frac{3}{{\displaystyle \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}}}}}\\ & \iff ((a+b)+(b+c)+(c+a))\left({\displaystyle \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}}\right)\ge 9\\ & \iff 2\left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)+6\ge 9\\ & \iff 2\left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge 3\\ & \iff \left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge {\displaystyle \frac{3}{2}◼}\\ & \text{Alternatif 2}\\ & \text{Dengan ketaksamaan Renata}\\ & \begin{array}{rl}& \text{Asumsikan}a\le b\le c,\text{maka}a+b\le a+c\le b+c\\ & \text{dan}{\displaystyle \frac{1}{b+c}\le \frac{1}{a+c}\le \frac{1}{a+b}.}\\ & \text{Perhatikan bahwa}\\ & (a\le b\le c)\text{dan}{\displaystyle \frac{1}{b+c}\le \frac{1}{a+c}\le \frac{1}{a+b}}\\ & \text{memiliki kemonotonan yang sama}\\ & \text{maka dengan}\mathbf{\text{ketaksamaan Renata}}\\ & \text{dapat diperoleh bentuk}\\ & a.{\displaystyle \frac{1}{b+c}+b.{\displaystyle \frac{1}{a+c}+c.{\displaystyle \frac{1}{a+b}\ge b.{\displaystyle \frac{1}{b+c}+c.{\displaystyle \frac{1}{a+c}+a.{\displaystyle \frac{1}{a+b}}}}}}}\\ & \text{dan}\\ & a.{\displaystyle \frac{1}{b+c}+b.{\displaystyle \frac{1}{a+c}+c.{\displaystyle \frac{1}{a+b}\ge c.{\displaystyle \frac{1}{b+c}+a.{\displaystyle \frac{1}{a+c}+b.{\displaystyle \frac{1}{a+b}}}}}}}\\ & \text{Jika dijumlahkan keduanya, maka}\\ & 2\left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge 3\\ & \iff \left({\displaystyle \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}}\right)\ge {\displaystyle \frac{3}{2}◼}\end{array}\end{array}$.

$\begin{array}{l}\\ 65.& (\mathbf{\text{OSN 2015}})\\ & \text{Diberikan}a,b,c>0,\text{Buktikan bahwa}\\ & \sqrt{{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}}}+\sqrt{{\displaystyle \frac{b}{c+a}+\frac{c}{a+b}}}+\sqrt{{\displaystyle \frac{c}{a+b}+\frac{a}{b+c}}}\ge 3\\ \\ & \mathbf{\text{Bukti}}:\\ & \text{Perhatikan bukti soal no. 4 di atas}\\ & \text{Dengan}\mathbf{\text{keksamaan Renata}}\text{dapat diperoleh}\\ & {\displaystyle \frac{a}{b+c}+\frac{b}{a+c}\ge \frac{b}{b+c}+\frac{a}{a+c}}\\ & \text{Misalkan}\\ & x=b+c,y=c+a,y=a+b,\text{maka}\\ & {\displaystyle \frac{a}{b+c}+\frac{b}{a+c}\ge \frac{b}{b+c}+\frac{a}{a+c}}\\ & \iff {\displaystyle \frac{a}{b+c}+\frac{b}{a+c}\ge \frac{y+z-x}{2x}+\frac{x+z-y}{2y}}\\ & \begin{array}{rl}& \iff \sqrt{{\displaystyle \frac{a}{b+c}+\frac{b}{a+c}}}\ge \sqrt{\frac{y+z-x}{2x}+\frac{x+z-y}{2y}}\\ & \iff =\sqrt{{\displaystyle \frac{1}{2}}}\sqrt{{\displaystyle \frac{y}{x}+\frac{z}{x}-1+\frac{x}{y}+\frac{z}{y}-1}}\\ & \iff \text{dengan AM-GM}\\ & \iff \ge {\displaystyle \frac{1}{\sqrt{2}}\sqrt{{\displaystyle \frac{z}{x}+\frac{z}{y}+2\sqrt{\frac{y}{x}.\frac{x}{y}}-2}}}\\ & \iff ={\displaystyle \frac{1}{\sqrt{2}}\sqrt{{\displaystyle \frac{z}{x}+\frac{z}{y}+2-2}}}\\ & \iff \ge {\displaystyle \frac{1}{\sqrt{2}}\sqrt{{\displaystyle \frac{z}{x}+\frac{z}{y}}}}\\ & \iff \ge {\displaystyle \frac{\sqrt{2}}{\sqrt{2}}\sqrt{{\displaystyle \frac{z^2}{xy}}}={\displaystyle \sqrt{{\displaystyle \frac{z^2}{xy}}}}}\end{array}\\ & \begin{array}{rl}& \bullet \sqrt{{\displaystyle \frac{a}{b+c}+\frac{b}{a+c}}}\ge {\displaystyle \sqrt{{\displaystyle \frac{z^2}{xy}}}}\\ & \bullet \sqrt{{\displaystyle \frac{b}{c+a}+\frac{c}{a+b}}}\ge \sqrt{{\displaystyle \frac{x^2}{yz}}}\\ & \bullet \sqrt{{\displaystyle \frac{c}{a+b}+\frac{a}{b+c}}}\ge \sqrt{{\displaystyle \frac{y^2}{xz}}}\end{array}\\ & \begin{array}{rl}& \text{Selanjutnya}\\ & \sqrt{{\displaystyle \frac{a}{b+c}+\frac{b}{c+a}}}+\sqrt{{\displaystyle \frac{b}{c+a}+\frac{c}{a+b}}}+\sqrt{{\displaystyle \frac{c}{a+b}+\frac{a}{b+c}}}\\ & \ge {\displaystyle \sqrt{{\displaystyle \frac{z^2}{xy}}}+\sqrt{{\displaystyle \frac{x^2}{yz}}}+\sqrt{{\displaystyle \frac{y^2}{xz}}}}\\ & \text{Dengan AM-GM lagi}\\ & \ge 3\sqrt[3]{\sqrt{{\displaystyle \frac{z^2}{xy}}}\times \sqrt{{\displaystyle \frac{x^2}{yz}}}\times \sqrt{{\displaystyle \frac{y^2}{xz}}}}\\ & \ge 3\sqrt[3]{\sqrt{{\displaystyle \frac{(xyz{)}^2}{(xyz{)}^2}}}}\\ & \ge 3◼\end{array}\end{array}$

DAFTAR PUSTAKA

1. Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.

WEBSITE

1. https://holdenlee.github.io/high_school/omc/23-rearrange.pdf diakses 18 Januari 2022.
2. https://www.gotohaggstrom.com/Advanced%20inequality%20manipulations.pdf  diakses 20 Januari 2022