Contoh Soal 14 (Segitiga dan Ketaksamaan)
Contoh 3 Soal Permutasi dan Kombinasi (Matematika Wajib Kelas XII)
$\begin{array}{ll}\\ 11.&\textrm{Dalam suatu rapat mengelilingi meja bundar}\\ &\textrm{yang dihadiri sebanyak 7 orang}\\ &\textrm{a}.\quad \textrm{ada berapa susunan yang terjadi}?\\ &\textrm{b}.\quad \textrm{Jika A dan B bagian dari 7 orang ini}\\ &\qquad \textrm{duduknya selalu berdampingan, maka}\\ &\qquad \textrm{posisi duduk yang terbentuk sejumlah}?\\ &\textrm{c}.\quad \textrm{Jika seperti poin b, tetapi yang}\\ &\qquad \textrm{duduk berdampingan atau saling berdekatan}\\ &\qquad \textrm{adalah A, B, dan C}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\: \: n=7\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Posisi duduk melingkarnya}\\ &=(7-1)!=6!=\color{red}720\\ &\textbf{atau}\\ &n=r=7\: \: \textrm{orang, maka}\\ &=\displaystyle \frac{P(7,7)}{7}=6!=\color{red}720\\ \textrm{b}.\quad&\textrm{Ada syarat A dan B berdampingan, maka}\\ &\textrm{A dan B dihitung 1 objek dulu, sehingga total}\\ &\textrm{objek ada 1 objek ditambah sisanya = 6 objek}.\\ &\textrm{Dari 6 objek ini yang dianggap duduk melingkar}\\ &\textrm{dengan 2 orang (A dan B) bisa gantian posisi}.\\ &\textrm{sehingga}\\ &(6-1)!\times 2!=5!\times 2!=\color{red}240\\ &\textbf{atau}\\ &=\displaystyle \frac{P(6,6)}{6}\times P(2,2)\\ &=5!\times 2!=120\times 2=\color{red}240\\ \textrm{b}.\quad&\textrm{3 orang (A, B, dan C) dianggap 1 objek}\\ &\textrm{dulu sehigga yang duduk posisi melingkar}\\ &\textrm{dianggap 5 orang, sehingga perhitungannya}\\ &=\displaystyle \frac{P(5,5)}{5}\times P(3,3)\\ &=24\times 6=\color{red}144 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 12.&\textrm{Suatu kelompok yang terdiri dari 20 remaja}\\ &\textrm{a}.\quad \textrm{Jika mereka saling berjabat tangan}\\ &\qquad \textrm{seseorang dengan lainnya hanya satu kali}\\ &\qquad \textrm{maka banyak jabat tangan yang terjadi}?\\ &\textrm{b}.\quad \textrm{Jika mereka membentuk regu voly, maka}\\ &\qquad \textrm{berapa banyak regu voly yang terbentuk}?\\ &\textrm{c}.\quad \textrm{Jika mereka membentuk regu sepak bola},\\ &\qquad \textrm{maka banyak regu sepak bola yang terbentuk}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa}\: \: n=20\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Karena jabat tangan dilakukan hanya hanya}\\ &\textrm{pada dua remaja yang berbeda dan urutan}\\ &\textrm{tidak diperlukan, maka hal ini persoalan}\\ &\textrm{kombinasi. Sehingga banyaknya jabat tangan}\\ &\begin{pmatrix} n\\ r \end{pmatrix}=\displaystyle \frac{n!}{r!(n-r)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20!}{2!(20-2)!}=\frac{20!}{2!\times 18!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 2 \end{pmatrix}=\displaystyle \frac{20.19.\not{18!}}{2.\not{18!}}=\color{red}190\\ \textrm{b}.\quad&\textrm{Karena satu regu voli ada 6 orang, maka}\\ &\begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!(20-6)!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\displaystyle \frac{20!}{6!\times 14!}\\ &\Leftrightarrow \begin{pmatrix} 20\\ 6 \end{pmatrix}=\color{red}\displaystyle \frac{20.19.18.17.16.15.\not{14!}}{720\times \not{14!}}\\ \textrm{c}.\quad&\textrm{Karena satu regu terdiri dari 11 orang},\\ &\textrm{maka}\\ &\begin{pmatrix} 20\\ 11 \end{pmatrix}=\displaystyle \frac{20!}{11!(20-11)!}=\color{red}\frac{20!}{11!\times 9!} \end{aligned} \end{array}$
$\begin{array}{ll}\\ 13.&\textrm{Jajargenjang yang dapat dibuat oleh}\\ &\textrm{himpunan empat garis sejajar yang}\\ &\textrm{berpotongan dengan garis yang terhimpun}\\ &\textrm{dalam 7 garis sejajar adalah}\: ....\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui bahwa kombinasi dari dua himpunan}\\ &\textrm{garis sejajar yang masing-masing berjumlah}\\ &\textrm{4 dan 7 garis, maka}\: \color{red}\textrm{banyak jajar genjang}\\ &\begin{aligned}&=\begin{pmatrix} 4\\ 2 \end{pmatrix}\times \begin{pmatrix} 7\\ 2 \end{pmatrix}\\ &=\displaystyle \frac{4!}{2!(4-2)!}\times \frac{7!}{2!\times (7-2)!}\\ &=\displaystyle \frac{4\times 3\times \not{2!}}{2\times \not{2!}}\times \frac{7\times 6\times \not{5!}}{2\times \not{5!}}\\ &=6\times 21\\ &=\color{red}126\: \: \color{black}\textrm{jajar genjang} \end{aligned} \end{array}$
$\begin{array}{ll}\\ 14.&\textrm{Diketahui segi enam beraturan. Tentukanlah}\\ &\textrm{a}.\quad \textrm{Banyak diagonal dapat dibentuk}?\\ &\textrm{b}.\quad \textrm{Banyak segi tiga di dalamnya}?\\ &\textrm{c}.\quad \textrm{Banyak perpotongan diagonal-diagonal}\\ &\qquad \textrm{jika tidak ada titik-titik perpotongan}\\ &\qquad \textrm{yang sama}?\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Diketahui segi}-n\: \: \textrm{dengan}\: \: n=6\\ &\textrm{Dan perlu diingat bahwa di sini tidak diperlukan}\\ &\textrm{urutan mana yang perlu didahulukan, maka}\\ &\textrm{rumus kombinasi yang perlu digunakan, yaitu}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Banyak diagonalnya adalah}:\\ &\begin{pmatrix} n\\ 2\end{pmatrix}-n=\displaystyle \frac{n(n-3)}{2}\\ &\Leftrightarrow \qquad\quad=\displaystyle \frac{6.(6-3)}{2}=\frac{6.3}{2}=\color{red}9\\ \textrm{b}.\quad&\textrm{Banyaknya segi tiga, berarti melibatkan}\\ &\textrm{tiga garis, maka}\\ &\begin{pmatrix} 6\\ 3 \end{pmatrix}=\displaystyle \frac{6!}{3!\times (6-3)!}=\frac{6\times 5\times 4\times \not{3!}}{6\times \not{3!}}=\color{red}20\\ \textrm{c}.\quad&\textrm{Satu buah titik potong dapat dibentuk}\\ &\textrm{dengan dua garis ekuivalen dengan empat}\\ &\textrm{buah titik sudut, maka banyaknya titik}\\ &\textrm{potong adalah}:\\ &\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{6!}{4!\times (6-4)!}=\frac{6!}{4!\times 2!}=\color{red}15 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 15.&\textrm{Perhatikalah dua ilustrasi gambar berikut} \end{array}$
DAFTAR PUSTAKA
- Bintari, N. 2009. Master Juara Olimpiade Matematika SMA Nasional dan Internasional. Yogyakarta: PUSTAKA WIDYATAMA.
- Ibrahim, Mussafi, N, S, M. 2013. Pengantar Kombinatorika dan Teori Graf. Yogyakarta: GRAHA ILMU.
- Kanginan, M., Terzalgi, Y. 2014. Matematika untuk SMA-MA/SMK Kelas XI (Wajib). Bandung: SRIKANDI EMPAT WIDYA UTAMA.
- Sobirin. 2006. Kompas Matematika: Strategi Praktis Menguasai Tes Matematika (SMA Kelas XI IPA). Jakarta: KAWAN PUSTAKA.
- Sukino. 2011. Maestro Olimpiade Matematika SMP Seri B. Jakarta: ERLANGGA.
- Susyanto, N, 2012. Tutor Senior Olimpiade Matematika Lima Benua Tingkat SMP. Yogyakarta: KENDI MAS MEDIA.
- Tampomas, H. 1999. SeribuPena Matematika SMU Jilid 2 Kelas 2 Berdasarkan Kurikulum 1994 Suplemen CBPP 1999. Jakarta: ERLANGGA.
Contoh 2 Soal Permutasi dan Kombinasi (Matematika Wajib Kelas XII)
$\begin{array}{ll}\\ 6.&\textrm{Dari angka-angka 2,3,5,6,7, dan 9 dibuat}\\ &\textrm{susunan bilangan}\\ &\textrm{a. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka berlainan}\\ &\textrm{b. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka boleh berulang}\\ &\textrm{c. berapa banyak bilangan ganjil yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan}\\ &\textrm{d. berapa banyak bilangan genap yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan}\\ &\textrm{e. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka berlainan yang lebih dari 2021}\\ &\textrm{f. berapa banyak bilangan yang terdiri dari 4}\\ &\: \quad \textrm{angka boleh berulang yang lebih dari 2021}\\ &\textrm{g. berapa banyak bilangan genap yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan yang lebih dari 2021}\\ &\textrm{h. berapa banyak bilangan ganjil yang terdiri}\\ &\: \quad \textrm{dari 4 angka berlainan yang lebih dari 2021}\\\\ &\color{blue}\textbf{Jawab}:\\ \end{array}$
$.\quad\: \, \begin{aligned}\textrm{a}.\quad&P(6,4)=\displaystyle \frac{6!}{(6-2)!}=\frac{6!}{2!}=6.5.4.3=\color{red}360\\ \textrm{b}.\quad&P(6,1)^{4}=6^{4}=\color{red}1296\\ \textrm{c}.\quad&\textrm{Untuk digit satuan ditentukan dulu, yaitu}\\ &\textrm{karena digit ganjil ada 4, maka ada 4 pilihan}\\ &\textrm{sisanya disebar ke slot ribuan sampai puluhan}\\ &\textrm{maka}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{red}\textrm{ratusan}&\textrm{puluhan}&\color{red}\textrm{satuan}\\\hline P(5,1)&P(4,1)&P(3,1)&P(4,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}\\ &\textrm{Sehingga banyak bilangan yg terjadi}\\ &P(5,1).P(4,1).P(3,1).P(4,1)=5.4.3.4=\color{red}240\\ \textrm{d}.\quad&\textbf{Cara pertama}\\ &\textrm{Semisal dengan jawaban poin c, Karena}\\ &\textrm{digit genap ada 2, maka digit satuan ada}\\ &\textrm{2 pilihan, sisanya disebar, yaitu}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{red}\textrm{ratusan}&\textrm{puluhan}&\color{red}\textrm{satuan}\\\hline P(5,1)&P(4,1)&P(3,1)&P(2,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}\\ &\textrm{Sehingga banyak bilangan yg terjadi}\\ &P(5,1).P(4,1).P(3,1).P(2,1)=5.4.3.2=\color{red}120\\ &\textbf{Cara kedua}\\ &\textrm{Jawaban poin a dikurangi poin c, yaitu}\\ &360-240=\color{red}120 \end{aligned}$
$.\quad\: \, \begin{aligned}\textrm{e}.\quad&\textbf{Cara Pertama}\\ &\textrm{Karena digit pilihannya, 2,3,5,6,7, dan 9}\\ &\textrm{disusun bagaimanapun bilangan 4 digit}\\ &\textrm{yang diambilkan dari bilangan di atas}\\ &\textrm{pasti semunya akan lebih besar dari 2021}\\ &\textrm{maka banyaknya bilangan yang terjadi}\\ &\textrm{adalah}:\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{magenta}\textrm{ratusan}&\textrm{puluhan}&\color{magenta}\textrm{satuan}\\\hline P(6,1)&P(5,1)&P(4,1)&P(3,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}>2021\\ &\textrm{Sehingga totalnya banyaknya}\\ &P(6,1)\times P(5,1)\times P(4,1)\times P(3,1)\\ &=6.5.4.3=\color{red}360\\ &\textbf{Cara Kedua}\\ &\textrm{Sama seperti jawaban pada poin a}\\ \textrm{f}.\quad&\textrm{Sama persis jawaban poin b, yaitu}\\ &P(6,1)^{4}=6^{4}=\color{red}1296\\ &\textrm{Jika diuraikan adalah sebagai berikut}\\ &\begin{array}{|c|c|c|c|}\hline \color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}&\color{blue}\textrm{kotak}\\ 1&2&3&4\\\hline \textrm{digit}&\textrm{digit}&\textrm{digit}&\textrm{digit}\\ \textrm{ribuan}&\color{magenta}\textrm{ratusan}&\textrm{puluhan}&\color{magenta}\textrm{satuan}\\\hline P(6,1)&P(6,1)&P(6,1)&P(6,1)\\ \textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}&\textrm{pilihan}\\\hline \end{array}>2021 \end{aligned}$
$\begin{array}{ll}\\ 7.&\textrm{Andi akan mengambil 4 buah bola dari}\\ &\textrm{10 warna yang berbeda. Berapakah banyak}\\ &\textrm{kombinasi warna yang berbeda yang diambil}\\ &\textrm{oleh Andi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}n=10&\: \: \textrm{dan}\: \: r=4\\ C(n,r)&=\displaystyle \frac{n!}{r!(n-r)!}\\ C(10,4)&=\displaystyle \frac{10!}{4!(10-4)!}\\ &=\displaystyle \frac{10!}{4!\times 6!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6!}{(4\times 3\times 2\times 1)\times 6!}\\ &=420\: \: \textrm{kombinasi warna bola berbeda} \end{aligned} \end{array}$
$\begin{array}{ll}\\ 8.&\textrm{Berapa banyak cara dapat memilih untuk}\\ &\textrm{3 perwakilan dari 10 anggota suatu}\\ &\textrm{kelompok, jika}\\ &\textrm{a. tanpa perlakuan khusus}\\ &\textrm{b. salah seorang harus terpilih}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Dengan tanpa perlakuan}\\ &\textrm{memilih 3 orang dari 10 orang adalah}:\\ &C(10,3)=\displaystyle \frac{10!}{3!(10-3)!}=\frac{10!}{3!\times 7!}=\color{blue}120\\ \textrm{b}.\quad&\textrm{Dengan perlakuan 1 orang terpilih}\\ &\color{red}(\textrm{1 orang ini artinya tidak perlu diperhitungkan})\\ &\textrm{memilih 2 orang dari 9 orang adalah}:\\ &C(9,2)=\displaystyle \frac{9!}{2!(9-2)!}=\frac{9!}{2!\times 8!}=\color{blue}36 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 9.&\textrm{Berapa banyak cara dapat memilih 2 buku}\\ &\textrm{matematika dan 3 buku fisika serta 4 buku}\\ &\textrm{ekonomi pada suatu lemari buku yang}\\ &\textrm{di dalamnya terdapat 10 buku matematika,}\\ &\textrm{11 buku fisika dan 12 buku ekonomi}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Banyak}&\: \textrm{cara pemilihan tersebut adalah}:\\ &=C(10,2)\times C(11,3)\times C(12,4)\\ &=\displaystyle \frac{10!}{2!\times 8!}\times \frac{11!}{3!\times 8!}\times \frac{12!}{4!\times 8!}\\ &=\displaystyle \frac{10\times 9}{1\times 2}\times \frac{11\times 10\times 9}{1\times 2\times 3}\times \frac{12\times 11\times 10\times 9}{1\times 2\times 3\times 4}\\ &=\color{red}3675375 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 10.&\textrm{Banyak susunan huruf yang berbeda}\\ &\textrm{pada satu baris yang dapat dibentuk}\\ &\textrm{dari huruf-huruf pada kata "MATEMATIKA"}\\ &\textrm{adalah}\: ....\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{cases} \textrm{Jumlah huruf} & n=\color{red}10 \\ \textrm{Penyusunnya}\, , & \text{ yaitu }: \begin{cases} M & \text{ jumlah } =2 \\ A & \text{ jumlah } =3 \\ T & \text{ jumlah } =2 \\ E & \text{ banyak } =1 \\ I & \text{ banyak } =1 \\ K & \text{ banyak } =1 \end{cases} \end{cases}\\ &\textrm{Sehingga}\\ &\begin{aligned}P(10;2,3,2,1,1,1)&=\displaystyle \frac{\color{red}10\color{black}!}{2!.3!.2!.1!.1!.1!}\\ &=\displaystyle \frac{10\times 9\times 8\times 7\times 6\times 5\times 4}{4}\\ &=10\times 9\times 8\times 7\times 6\times 5\\ &=\color{red}151200 \end{aligned} \end{array}$
Ketaksamaan Holder
3. Ketaksamaan Holder
DAFTAR PUSTAKA
- Chen, E. 2014. A Brief Introduction to Olympiad Inequalities.
- Riasat, S. 2008. Basics of Olympiad Inequalities.
- Todinov, M.T. 2020. Risk And Uncertaintly Reduction by Using Algebraic Inequalities. Boca Raton: CRC Press.
- Tung. K.Y. 2013. Ayo Raih Medali Emas Olimpiade Matematika SMA. Yogyakarta: ANDI.
- Young, B. 2009. Seri Buku Olimpiade Matematika Strategi Menyelesaikan Soal-Soal Olimpiade Matematika: Ketaksamaan (Inequality). Bandung: PAKAR RAYA.
Contoh 1 Soal Permutasi dan Kombinasi (Matematika Wajib Kelas XII)
$\begin{array}{ll}\\ 1.&\textrm{Bentuk sederhana dari}\\ &\textrm{a}.\quad \displaystyle 5!+6!+7!\\ &\textrm{b}.\quad \displaystyle \frac{(n+1)!}{(n-1)!}\\ &\textrm{c}.\quad \displaystyle \frac{(n+2)!}{n!}\\ &\textrm{d}.\quad \displaystyle \frac{(n-2)!}{(n+1)!}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&5!+6!+7!=5!+6.5!+7.6.5!\\ &\quad\quad\quad\quad \: \: \: \: =(1+6+42).5!\\ &\quad\quad\quad\quad \: \: \: \: =49.5!=49.120=5880\\ \textrm{b}.\quad&\displaystyle \frac{(n+1)!}{(n-1)!}=\frac{(n+1)n(n-1)!}{(n-1)!}\\ &\quad\quad\quad\: \: \: =(n+1)n=n^{2}+n\\ \textrm{c}.\quad&\displaystyle \frac{(n+2)!}{n!}=\frac{(n+1)(n+1)n!}{n!}\\ &\quad\quad\quad\: \: \: =(n+2)(n+1)\\ &\quad\quad\quad\: \: \: =n^{2}+3n+2\\ \textrm{d}.\quad&\displaystyle \frac{(n-2)!}{(n+1)!}=\frac{(n-2)!}{(n+1)n(n-1)(n-2)!}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{(n+1)n(n-1)}\\ &\quad\quad\quad\: \: \: =\displaystyle \frac{1}{n^{3}-n} \end{aligned} \end{array}$
$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad \displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\textrm{b}.\quad \displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\textrm{c}.\quad \displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\displaystyle \frac{n!3!}{6!(n-3)!}=\frac{33}{4}\\ &\Leftrightarrow \displaystyle \frac{n(n-1)(n-2) \not{(n-3)!}.\not{3!}}{6.5.\not{4}.\not{3!}\not{(n-3)}!}=\frac{33}{\not{4}}\\ &\Leftrightarrow n(n-1)(n-2)=33.6.5=11.10.9\\ &\Leftrightarrow n(n-1)(n-2)=11.(11-1).(11-2)\\ &\Leftrightarrow \qquad\qquad\qquad \: n=11\\ \textrm{b}.\quad&\displaystyle \frac{3}{8!}-\frac{2}{7!}+\frac{1}{6!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \displaystyle \frac{3-2.8+56}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow \frac{43}{8!}=\frac{5n+3}{8!}\\ &\Leftrightarrow 43=5n+3\Leftrightarrow 5n=40\Leftrightarrow n=8\\ \textrm{c}.\quad &\displaystyle \frac{7!}{5!2!}:\frac{10!}{5!5!}=1:4n\\ &\Leftrightarrow 4n=\displaystyle \frac{5!2!10!}{7!5!5!}\\ &\Leftrightarrow 4n=\displaystyle \frac{\not{5!}2!10.9.8.\not{7!}}{\not{7!}5!\not{5!}}\\&\Leftrightarrow \: \: n=3 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah nilai}\: \: n\: \: \textrm{yang memenuhi}\\ &\textrm{persamaan berikut}\\ &\textrm{a}.\quad P(n,2)=42\\ &\textrm{b}.\quad 7.P(n,3)=6.P(n+1,3)\\ &\textrm{c}.\quad 3.P(n,4)=P(n-1,5)\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&P(n,2)=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle \frac{n!}{(n-2)!}=\displaystyle \frac{n\times (n-1)\times (n-2)!}{(n-2)!}=42\\ &\Leftrightarrow \displaystyle n\times (n-1)=7.6=7.(7-1)\\ &\Leftrightarrow n=7\\ \textrm{b}.\quad&7.P(n,3)=6.P(n+1,3)\\ &\displaystyle \frac{7.n!}{(n-3)!}=\frac{6(n+1)!}{(n+1-3)!}\\ &\displaystyle \frac{7\not{n!}}{(n-3)!}=\frac{6.(n+1).\not{n!}}{(n-2)!}\\ &\Leftrightarrow \frac{7}{\not{(n-3)!}}=\frac{6n+6}{(n-1)\not{(n-3)!}}\\ &\Leftrightarrow 7(n-2)=6n+6\\ &\Leftrightarrow 7n-6n=6+14\Leftrightarrow n=20\\ \textrm{c}.\quad&3.P(n,4)=P(n-1,5)\\ &\Leftrightarrow \displaystyle \frac{3.n!}{(n-4)!}=\frac{(n-1)!}{(n-1-5)!}\\ &\Leftrightarrow \frac{3.n.\not{(n-1)!}}{(n-4)!}=\frac{\not{(n-1)!}}{(n-6)!}\\ &\Leftrightarrow \frac{3n}{(n-4)(n-5).\not{(n-6)!}}=\frac{1}{\not{(n-6)!}}\\ &\Leftrightarrow 3n=(n-4)(n-5)\\ &\Leftrightarrow 3n=n^{2}-9n+20\\ &\Leftrightarrow n^{2}-12n+20=0\\ &\Leftrightarrow (n-2)(n-10)=0\\ &\Leftrightarrow n=2\: \: \color{red}\textrm{tidak memenuhi}\: \: \color{black}\textrm{atau}\: \: n=10\\ &\textrm{jadi},\: \: n=10 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 4.&\textrm{Jika 10 siswa akan dipilih 4 orang untuk}\\ &\textrm{menjadi ketua kelas, wakil, sekretaris dan}\\ &\textrm{seorang bendahara, maka banyak susunan}\\ &\textrm{terjadi adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Penyusunan memerlukan urutan}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\Leftrightarrow P(10,4)=\displaystyle \frac{10!}{(10-4)!}=\frac{10!}{6!}\\ &\Leftrightarrow \qquad\qquad =\displaystyle \frac{10\times 9\times 8\times 7\times \not{6!}}{\not{6!}}\\ &\Leftrightarrow \qquad\qquad =5040 \end{array}$
$\begin{array}{ll}\\ 5.&\textrm{Jika dari kota A ke kota B terdapat 3 jalur.}\\ &\textrm{Dan dari kota B ke kota C terdapat 4 jalur,}\\ &\textrm{serta dari kota C sampai ke kota D ada 5 jalur}\\ &\textrm{Banyak jalan dari kota A ke kota D adalah}\: ....\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Jalur yang ada semuanya berbeda}\\ &\textrm{maka perlu digunakan permutasi, yaitu}:\\ &P(n,r)=\displaystyle \frac{n!}{(n-r)!}\\ &\begin{aligned}\textrm{a}&\textrm{dari A ke B ada 3 jalur cukup pilih satu, maka}\\ &\bullet \quad P(3,1)=\displaystyle \frac{3!}{(3-1)!}=\frac{3!}{2!}=3\\ \textrm{b}&\textrm{dari B ke C ada 4 jalur cukup pilih satu, maka}\\ &\bullet \quad P(4,1)=\displaystyle \frac{4!}{(4-1)!}=\frac{4!}{3!}=4\\ \textrm{c}&\textrm{dari C ke D ada 5 jalur cukup pilih satu, maka}\\ &\bullet \quad P(5,1)=\displaystyle \frac{5!}{(5-1)!}=\frac{5!}{4!}=5 \end{aligned}\\ &\textrm{Jadi, total jalur yang dapat di lalui dari A sampai D adalah}:\\ &\qquad P(3,1)\times P(4,1)\times P(5,1)=3\times 4\times 5=\color{red}60 \end{array}$
Lanjutan Materi 3 Persamaan Garis Singgung Lingkaran Melalui Titik di Luar Lingkaran
D. Persamaan Garis Singgung Lingkaran Melalui Titik di Luar Lingkaran
Coba perhatikan ilustrasi berikut
DAFTAR PUSTAKA
- Kanginan, M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Lanjutan Materi 2 Persamaan Garis Singgung Lingkaran (dengan Gradien m)
C. Garis Singgung dengan Gradien m
Perhatikan ilustrasi berikut
- Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
- Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.
Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 3)
$\begin{array}{ll}\\ 11.&\textrm{Suatu tes dengan pilihan jawaban }\\ &\textrm{benar-salah berjumlah 8 soal}\\ &\textrm{Supaya lulus tes, peserta diharuskan }\\ &\textrm{menjawab benar minimal 50}\%\\ &\textrm{Peluang seseorang dianggap lulus tes }\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad \displaystyle 0,2188\qquad\qquad\quad\qquad \quad\textrm{d}.\quad 0,6367\\ &\textrm{b}.\quad \displaystyle \color{red}0,2734\quad \: \color{black}\textrm{c}.\quad 0,3633\quad\quad \textrm{e}.\quad 0,7266\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang benar}=\displaystyle \frac{1}{2},\qquad \textrm{dan}\: \: \\ &q=\textbf{Peluang Salah}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P(X=x)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &P\left ( X=50\%(8)=4 \right )=\begin{pmatrix} 8\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{4}\times \left ( \frac{1}{2} \right )^{8-4}\\ &\qquad =\displaystyle \frac{8!}{4!\times 4!}\left ( \displaystyle \frac{1}{2} \right )^{4+4}\\ &\qquad =70\times \displaystyle \frac{1}{256}\\ &\qquad =\color{red}0,2734 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 12.&\textrm{Sebuah kotak berisi 20 bola dengan }\\ &\textrm{rincian 12 boal berwarna kuning dan }\\ &\textrm{sisanya berwarna hijau. Dari kotak} \\ &\textrm{diambil 6 bola secara acak. Peluang}\\ &\textrm{terambil 4 bola hijau adalah}....\\ &\textrm{a}.\quad \displaystyle 0,1238\quad\quad\qquad\qquad \qquad\textrm{d}.\quad 0,8132\\ &\textrm{b}.\quad \color{red}\displaystyle 0,1382\: \quad \color{black}\textrm{c}.\quad 0,3110\quad\quad \textrm{e}.\quad 0,9590\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang bola kuning}\\ &\: \: =\displaystyle \frac{C_{1}^{12}}{C_{1}^{20}}=\displaystyle \frac{12}{20}=\frac{3}{5},\\ &q=\textbf{Peluang bola hijau}=1-\displaystyle \frac{3}{5}=\frac{2}{5}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &f(4)=\begin{pmatrix} 6\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{2}{5} \right )^{4}\times \left ( \frac{3}{5} \right )^{6-4}\\ &\qquad =\displaystyle \frac{6!}{2!\times 4!}\left ( \displaystyle \frac{16}{625} \right )\times \left ( \displaystyle \frac{9}{25} \right )\\ &\qquad =15\times \displaystyle \frac{144}{15625}=\frac{2160}{15625}\\ &\qquad =\color{red}0,1382 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 13.&\textrm{Dua dadu dilambungkan 5 kali}\\ &\textrm{Peluang muncul pasangan mata dadu}\\ &\textrm{berjumlah 4 sampai dengan 7 }\\ &\textrm{sebanyak 4 kali adalah}\: ....\\ &\textrm{a}.\quad \displaystyle 0,1503\: \: \: \: \qquad\qquad\quad\quad \quad\textrm{d}.\quad 0,1583\\ &\textrm{b}.\quad \displaystyle 0,1553\quad \textrm{c}.\quad \color{red}0,1563\quad\quad \color{black}\textrm{e}.\quad 0,1593\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang mata dadu berjumlah 4 sampai 7}\\ &\: \: =\displaystyle \frac{18}{36}=\frac{1}{2},\qquad \textrm{dan}\: \: \\ &q=\textbf{Peluang bola hijau}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &f(4)=P\left ( X=4 \right )=\begin{pmatrix} 5\\ 4 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{4}\times \left ( \frac{1}{2} \right )^{5-4}\\ &\qquad =\displaystyle \frac{5!}{1!\times 4!}\left ( \displaystyle \frac{1}{16} \right )\times \left (\frac{1}{2} \right )\\ &\qquad =5\times \displaystyle \frac{1}{32}=\frac{5}{32}\\ &\qquad =\color{red}0,1563 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 14.&\textrm{Peluang seseorang sembih dari }\\ &\textrm{penyakit jantung adalah 0,6}\\ &\textrm{Jika 7 orang penderita ini menjalani }\\ &\textrm{operasi, maka peluang 3 sampai}\\ &\textrm{6 orang sembuh adalah}... .\\ &\textrm{a}.\quad \displaystyle 0,0629\qquad\qquad\quad\qquad \quad\textrm{d}.\quad \color{red}0,6822\\ &\textrm{b}.\quad \displaystyle 0,2613\quad \textrm{c}.\quad 0,2898\quad\quad \: \textrm{e}.\quad 0,9720\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang sembuh}=0,6,\qquad \textrm{maka}\: \: \\ &q=\textbf{Peluang tidak sembuh}=1-0,6=0,4\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &\textrm{maka}\\ &P\left ( 3\leq X\leq 6 \right )=P\left ( X\leq 6 \right )-P\left ( X\leq 3 \right )\\ &=C_{4}^{7}(0,6)^{4}(0,4)^{3}+C_{5}^{7}(0,6)^{5}(0,4)^{2}+C_{6}^{7}(0,6)^{6}(0,4)^{1}\\ &=35\times 0,0082944+21\times 0,0124416+7\times 0,0186624\\ &=0,290304+0,2612736+0,1306368\\ &=\color{red}0,6822144 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 15.&\textrm{Peluang seseorang mendapatkan reaksi }\\ &\textrm{buruk setelah disuntik adalah 0,0005}\\ &\textrm{Dari 4000 orang yang disuntik, maka }\\ &\textrm{peluang seseorang mendapatkan reaksi}\\ & \textrm{ada 2 orang adalah}.....\\ &\textrm{a}.\quad \displaystyle \frac{1}{2}e^{-2}\\ &\textrm{b}.\quad e^{-2}\\ &\textrm{c}.\quad \color{red}2e^{-2}\\ &\textrm{d}.\quad \displaystyle \frac{1}{2}e^{2}\\ &\textrm{e}.\quad 2e^{2}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Di atas adalah contoh kasus }\\ &\textrm{permasalahan}\: \: \textbf{Distribusi Poisson}\\ &P\left ( X=x \right )=f(x)=\left\{\begin{matrix} \displaystyle \frac{e^{-\lambda }.\lambda ^{x}}{x!}\: \: ,\: \: x=0,1,2,3,\cdots \\\ 0,\quad \textrm{untuk}\: \: x\: \: \textrm{yang lain} \end{matrix}\right.\\ &P\left ( X=2 \right )=\displaystyle \frac{e^{-np}.(np)^{2}}{2!}\\ &\qquad =\displaystyle \frac{e^{-(4000.0,0005)}.(4000.0,0005)^{2}}{2!}\\ &\qquad =\displaystyle \frac{e^{-2}.2^{2}}{2}\\ &\qquad =\color{red}2e^{-2} \end{aligned} \end{array}$
Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 2)
$\begin{array}{ll}\\ 6.&\textrm{Pengundian terhadap mata uang }\\ &\textrm{yang homogen sebanyak 10 kali}\\ &\textrm{Peluang untuk mendapatkan 6 }\\ &\textrm{muka angka adalah}\: ....\\ &\textrm{a}.\quad 0,1172\\ &\textrm{b}.\quad \color{red}0,2051\\ &\textrm{c}.\quad 0,2461\\ &\textrm{d}.\quad 0,2651\\ &\textrm{e}.\quad 0,2852\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&p=\textbf{Peluang Angka}=\displaystyle \frac{1}{2},\quad \textrm{dan}\: \: \\ &q=\textbf{Bukan Angka}\\ &\: \: =\textbf{Peluang Gambar}=1-\displaystyle \frac{1}{2}=\frac{1}{2}\\ &f(x)=P(x;n;p)=P(X=x)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &\textrm{maka}\\ &f(x)=P\left ( X=x \right )=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}.q^{n-x}\\ &f(6)=P\left ( X=6 \right )=\begin{pmatrix} 10\\ 6 \end{pmatrix}\times \left ( \displaystyle \frac{1}{2} \right )^{6}\times \left ( \frac{1}{2} \right )^{10-6}\\ &\qquad =\displaystyle \frac{10!}{6!\times 4!}\left ( \displaystyle \frac{1}{2} \right )^{6+4}\\ &\qquad =210\times \displaystyle \frac{1}{1024}\\ &\qquad =\color{red}0,2051 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 7.&\textrm{Pada pengundian terhadap mata uang identik},\\ &\textrm{sebanyak 10 kali, peluang distribusi binomial} \\ &\textrm{untuk mendapatkan 7 muka gambar adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.\quad \displaystyle 0,2653&&\textrm{d}.\quad \displaystyle 0,7522\\ \textrm{b}.\quad \displaystyle \color{red}0,1172&\textrm{c}.\quad \displaystyle 0,2653&\textrm{e}.\quad 0,2422 \end{array}\\\\ &\textrm{Jawab}:\\ &\textrm{Uraian berikut sekaligus tambahan}\\ &\textrm{penjelasan pada uraian jawaban}\\ &\color{blue}\textrm{soal no. 6 di atas}\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ &\textrm{Ingat sebuah koin ada 2 muka}\\ &\textrm{yaitu muka gambar (G) dan angka (A)}\\ &\color{red}\textrm{misalkan}\\ &A=\textrm{kejadian muncul muka gambar}\\ &\textrm{maka peluangnya adalah}\: \: \displaystyle \frac{1}{2}\\ &\textrm{Selanjutnya di sini disimbolkan dengan}\: \: \: \color{blue}p=\displaystyle \frac{1}{2}\\ &\color{red}\textrm{Demikian juga misalkan}\\ &B=\textrm{kejadian muncul muka angka}\\ &\textrm{maka peluang juga}\: \displaystyle \frac{1}{2}\\ &\textrm{Di sini dituliskan dengan}\: \: \: \color{blue}q=\displaystyle \frac{1}{2}\\ f(7)&=\begin{pmatrix} 10\\ 7 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{7}\left ( \displaystyle \frac{1}{2} \right )^{10-7}\\ &=\begin{pmatrix} 10\\ 7 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{7}\left ( \displaystyle \frac{1}{2} \right )^{3}\\ &=\displaystyle \frac{10!}{7!\times (10-7)!}\left ( \displaystyle \frac{1}{2} \right )^{7+3}\\ &=\displaystyle \frac{10.9.8.\not{7!}}{\not{7!}.3.2.1}\left ( \displaystyle \frac{1}{1024} \right ) \\ &=\color{red}0,1172 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 8.&\textrm{Sebuah uang logam dilempar sebanyak 8}\\ &\textrm{kali. Peluang muncul gambar sebanyak}\\ &\textrm{5 kali adalah}\: ....\\ &\begin{array}{llllllll}\\ \textrm{a}.&\displaystyle \frac{3}{32}&&&\textrm{d}.&\displaystyle \color{red}\frac{7}{32}\\\\ \textrm{b}.&\displaystyle \frac{4}{32}&\textrm{c}.&\displaystyle \frac{5}{32}&\textrm{e}.&\displaystyle \frac{9}{32} \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(5)&=\begin{pmatrix} 8\\ 5 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{5}\left ( \displaystyle \frac{1}{2} \right )^{8-5}\\ &=\begin{pmatrix} 8\\ 5 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{5}\left ( \displaystyle \frac{1}{2} \right )^{3}\\ &=\displaystyle \frac{8!}{5!\times (8-5)!}\left ( \displaystyle \frac{1}{2} \right )^{5+3}\\ &=\displaystyle \frac{8.7.6.5!}{5!.3.2.1}\left ( \displaystyle \frac{1}{256} \right ) \\ &=\displaystyle \frac{8.7}{256}\\ &=\color{red}\displaystyle \frac{7}{32} \end{aligned} \end{array}$
$\begin{array}{ll}\\ 9.&\textrm{Pada pelemparan sebuah koin sebanyak 4 kali}\\ &\textrm{Peluang didapatkannya dua angka pada} \\ &\textrm{pelemparan tersebut adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.\quad \displaystyle 0,123&&\textrm{d}.\quad \displaystyle 0,232\\ \textrm{b}.\quad \displaystyle 0,135&\textrm{c}.\quad \displaystyle 0,154&\textrm{e}.\quad \color{red}0,375 \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(2)&=\begin{pmatrix} 4\\ 2 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{2}\left ( \displaystyle \frac{1}{2} \right )^{4-2}\\ &=\begin{pmatrix} 4\\ 2 \end{pmatrix}\left ( \displaystyle \frac{1}{2} \right )^{2}\left ( \displaystyle \frac{1}{2} \right )^{2}\\ &=\displaystyle \frac{4!}{2!\times (4-2)!}\left ( \displaystyle \frac{1}{2} \right )^{2+2}\\ &=\displaystyle \frac{4.3.2!}{2!.2.1}\left ( \displaystyle \frac{1}{16} \right ) \\ &=\color{red}0,375 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 10.&\textrm{Dari data survei didapatkan bahwa}\\ &\textrm{satu dari lima orang telah berkunjung}\\ &\textrm{ke dokter dalam sembarang bulan yang}\\ &\textrm{ditanyakan. Jika 10 orang dipilih secara}\\ &\textrm{acak, peluang 3 orang telah berkunjung}\\ &\textrm{ke dokter bulan lalu adalah}\: ....\\ &\begin{array}{llllllll}\\ \textrm{a}.&\displaystyle 0,125&&&\textrm{d}.&\displaystyle \color{red}0,201\\\\ \textrm{b}.&\displaystyle 0,174&\textrm{c}.&\displaystyle 0,182&\textrm{e}.&\displaystyle 0,423 \end{array}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}f(x)&=P(x;n;p)=\begin{pmatrix} n\\ x \end{pmatrix}p^{x}q^{n-x}\\ f(3)&=\begin{pmatrix} 10\\ 3 \end{pmatrix}\left ( \displaystyle \frac{1}{5} \right )^{3}\left ( \displaystyle \frac{4}{5} \right )^{10-3}\\ &=\begin{pmatrix} 10\\ 3 \end{pmatrix}\left ( \displaystyle \frac{1}{5} \right )^{3}\left ( \displaystyle \frac{4}{5} \right )^{7}\\ &=\displaystyle \frac{10!}{3!\times 7!}\left ( \displaystyle \frac{1}{125} \right )\left ( \displaystyle \frac{4^{7}}{5^{7}} \right )\\ &=\cdots \\ &=\color{red}\displaystyle 0,201 \end{aligned} \end{array}$
Contoh Soal dan Pembahasan Distribusi Binomial (Bagian 1)
$\begin{array}{ll}\\ 1.&\textrm{Manakah yang merupakan data diskrit dari pernyataan berikut}\\ &\textrm{a}.\quad \textrm{Suhu Badan Anton ketika sakit mencapai}\: \: 40^{\circ}C\\ &\textrm{b}.\quad \textrm{Kecepatan mobil yang sedang melaju adalah}\: \: 100\: \: km/jam\\ &\textrm{c}.\quad \textrm{Tinggi tiang bendaera di madrasah Budi adalah 4 m}\\ &\textrm{d}.\quad \color{red}\textrm{Jumlah guru yang mengajar di MA Futuhiyah }\\ &\qquad \color{red}\textrm{sebanyak 30 orang}\\ &\textrm{e}.\quad \textrm{Berat bayi yang baru lahir adalah 3.500 gram}\\\\ &\textrm{Jawab}:\\ &\textrm{Alasannya dikarena hasil mencacah} \end{array}$
$\begin{array}{ll}\\ 2.&\textrm{Jika Anda mengumpulkan nilai raport}\\ &\textrm{teman-teman sekelas Anda untuk pelajaran}\\ &\textrm{ matematika, maka data yang Anda peroleh }\\ &\textrm{adalah}....\\ &\textrm{a}.\quad \color{red}\textrm{data diskrit}\\ &\textrm{b}.\quad \textrm{data kontinu}\\ &\textrm{c}.\quad \textrm{data kualitatif}\\ &\textrm{d}.\quad \textrm{Populasi}\\ &\textrm{e}.\quad \textrm{Sampel}\\\\ &\textrm{Jawab}:\\ &\textrm{Dengan catatan nilainya cacah} \end{array}$
$\begin{array}{ll}\\ 3.&\textrm{Ukuran yang dihitung dari seluruh data }\\ &\textrm{dalam populasi adalah}\: ....\\ &\textrm{a}.\quad \textrm{data kuantitatif}\\ &\textrm{b}.\quad \textrm{data kualitatif}\\ &\textrm{c}.\quad \textrm{Statistik}\\ &\textrm{d}.\quad \textrm{Statistika}\\ &\textrm{e}.\quad \color{red}\textrm{Parameter}\\\\ &\textrm{Jawab}:\\ &\textrm{Parameter adalah ukuran dari }\\ &\textrm{seluruh data atau populasi} \end{array}$
$\begin{array}{ll}\\ 4.&\textrm{Diketahui distribusi peluang suatu }\\ &\textrm{variabel acak diskrit sebagai berikut}\\ &\begin{array}{|c|c|c|c|c|}\hline x&0&1&2&3\\\hline f(x)&m&0,26&3m&0,42\\\hline \end{array}\\ &\textrm{Peluang nilai X minimal berharga 2 adalah}\\ &\textrm{a}.\quad 0,24\\ &\textrm{b}.\quad 0,34\\ &\textrm{c}.\quad 0,42\\ &\textrm{d}.\quad 0,58\\ &\textrm{e}.\quad \color{red}0,66\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}\: \: X\: \: \textrm{adalah variabel }\\ &\textrm{acak diskrit, maka}\: \: \sum f(x)=1\\ &F(c)=P(X\leq c)=\displaystyle \sum_{x=0}^{x=c}f(x)\\ &=f(0)+f(1)+f(2)+f(3)+\cdots +f(c)=1\\ &\textrm{dalam hal soal}\: \textrm{di atas, maka kita tentukan}\\ &\textrm{nilai}\: \: \color{blue}m\: \: \color{black}\textrm{dulu}\\ &F(3)=P(X\leq 3)=\displaystyle \sum_{x=0}^{x=3}f(x)\\ &=f(0)+f(1)+f(2)+f(3)=1\\ &1=m+0,26+3m+0,42=4m+0,68\\ &4m=1-0.68=0,32\\ &m=0.08, \qquad \textrm{sehingga}\\ &P(2\leq X\leq 3)=f(2)+f(3)=3m+0,42\\ &=3(0,08)+0,42=0,24+0,42=\color{red}0,66 \end{aligned} \end{array}$
$\begin{array}{ll}\\ 5.&\textrm{Diketahui fungsi peluang suatu }\\ &\textrm{variabel acak kontinu adalah}\\ &f(y)=\left\{\begin{matrix} 0,\quad \textrm{untuk \textit{y} yang lain}\\\\ \displaystyle \frac{2y+k}{50},\: \: \textrm{untuk}\: \: 0\leq y\leq 5 \end{matrix}\right.\\ &\textrm{Nilai}\: \: P\left ( \left | Y-1 \right |\leq 2 \right )\: \: \textrm{adalah}....\\ &\textrm{a}.\quad \displaystyle \frac{7}{25}\qquad\qquad\qquad\qquad \textrm{d}.\quad \frac{14}{25}\\\\ &\textrm{b}.\quad \displaystyle \frac{9}{25}\qquad \textrm{c}.\quad \color{red}\frac{12}{25}\qquad\quad \color{black}\textrm{e}.\quad \frac{18}{25}\\\\ &\textrm{Jawab}:\\ &\begin{aligned}&\int_{0}^{5}\displaystyle \frac{2y+k}{50}\: dy=1\\ &1=\int_{0}^{5}\displaystyle \frac{2y+k}{50}\: dy\\ &50=\int_{0}^{5}(2y+k)dy\\ &50=y^{2}+ky|_{0}^{5}=5^{2}+5k=25+5k\\ &k=5\\ &\color{blue}P(\left | Y-1 \right |\leq 2)=P\left ( -2\leq Y-1\leq 2 \right )\\ &=P\left ( -1\leq Y\leq 3 \right )\\ &=f(-1)+f(0)+f(1)+f(2)+f(3)\\ &=\int_{0}^{3}\left ( \displaystyle \frac{2y+5}{50} \right )dy\\ &=\displaystyle \frac{1}{50}\left ( y^{2}+5y \right )|_{0}^{3}\\ &=\displaystyle \frac{1}{50}\left ( 9+15 \right )=\displaystyle \frac{24}{50}=\color{red}\frac{12}{25} \end{aligned} \end{array}$
Persamaan Garis Singgung Lingkaran
A. Pendahuluan
Kita sebelumnya telah membahasas kedudukan suatu lingkaran terhadap suatu garis. Terkait dengan garis singgung lingkaran suatu lingkaran dapat memiliki sekian banyak garis singgung dan tentunya lebih dari satu garis singgung jika ingin dibuat. Garis singgung lingkaran adalah suatu garis yang memotong lingkaran tepat di satu titik. Masih ingat kembali kedudukan suatu garis terhadap lingkaran saat nilai $D=b^{2}-4ac=0$, dari sanalah akhir dari penyelesaian masalah yang terkait dengan ini.
B. Garis Singgung Melalui Sebuah Titik pada Lingkaran
Misalkan suatu titik $P(x_{1},y_{1})$ terdapat pada (keliling) lingkaran $x^{2}+y^{2}=r^{2}$, maka berakibat akan memiliki gradien dari garis OP berupa $m_{\textrm{P}}=\displaystyle \frac{y_{1}}{x_{1}}$.
Perhatikan dua ilustrasi berikut
Ilustrasi berikutnya menjadi seperti berikut
Perhatikan tiga ilustrasi di atas, jika titik P adalah titik sinngung lingkaran $x^{2}+y^{2}=r^{2}$, maka gradien garis singgung lingkarannya, misal kita namakan $m_{l}$ adalah $m_{l}=-\displaystyle \frac{x_{1}}{y_{1}}$, sehingga persamaan garis singgungnya yang melalui titik P tersebut dan bergradien $m_{l}=-\displaystyle \frac{x_{1}}{y_{1}}$ adalah:
$\begin{aligned}y-y_{1}&=-\displaystyle \frac{x_{1}}{y_{1}}\left ( x-x_{1} \right )\\ \Leftrightarrow y_{1}y-&y_{1}^{2}=-x_{1}x+x_{1}^{2}\\ \Leftrightarrow x_{1}x+&y_{1}y=x_{1}^{2}+y_{1}^{2}\\ \Leftrightarrow x_{1}x+&y_{1}y=r^{2}\\\\ \textrm{Jadi, per}&\textrm{samaan garis singgungnya adalah}:\\ &\quad \LARGE\boxed{x_{1}x+y_{1}y=r^{2}} \end{aligned}$.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
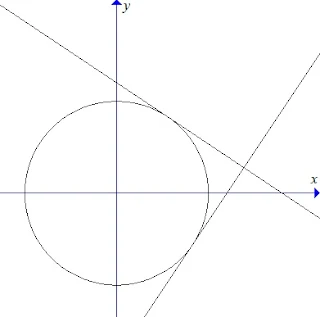
$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah persamaan lingkaran yang }\\ &\textrm{berpusat di pangkal koordinat dan}\\ &\textrm{menyinggung}\: \: k\equiv 2x+y-5=0\\\\ &\textbf{Jawab}:\\ &\textrm{Perhatikan ilustrasi berikut} \end{array}$.
- Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
- Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
- Sobirin. 2006. Kompas Matematika Strategi Praktis Menguasai Tes Matematika SMA Kelas 2. Jakarta: KAWAN PUSTAKA.
- Wirodikromo, S. 2007. Matematika Jilid 2 IPA untuk Kelas XI. Jakarta: ERLANGGA.