Latihan Soal 5 Persiapan PAS Gasal Matematika Wajib Kelas XI

 $\begin{array}{ll}\\ 41.&\textrm{Pada gambar berikut ini, pertidaksamaan}\\ &\textrm{yang memenuhi adalah}\\\\ \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&2x+y-4\leq 0,\: 2x+3y-6\geq 0,\: x\geq 0,\: y\geq 0\\ \textrm{b}.&2x+y-4\geq 0,\: 2x+3y-6\leq 0,\: x\geq 0,\: y\geq 0\\ \textrm{c}.&2x+y-4\leq 0,\: 2x+3y-6\leq 0,\: x\geq 0,\: y\geq 0\\ \color{red}\textrm{d}.&\left (2x+y-4 \right )\left (2x+3y-6 \right )\leq 0,\: x\geq 0,\: y\geq 0\\ \textrm{e}.&\left (2x+y-4 \right )\left (2x+3y-6 \right )\geq 0,\: x\geq 0,\: y\geq 0\\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\textrm{Misalkan titik potong kedua garis adalah M}\\ &\color{magenta}\textrm{Persamaan garisnya sebelah kiri M}:\\ &(1)\: 4x+2y-8=0\\ &\: \: \: \quad\textrm{kendala}:2x+y-4\leq 0\\ &(2)\: 2x+3y=6\\ &\: \: \: \quad \textrm{kendala}:2x+3y-6\geq 0\\ &(3)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(4)\: x=0,\: \: \textrm{kendala}:x\geq 0\\ &\color{blue}\textrm{Persamaan garisnya sebelah kanan M}:\\ &(5)\: 4x+2y-8=0\\ &\: \: \: \quad\textrm{kendala}:2x+y-4\geq 0\\ &(6)\: 2x+3y=6\\ &\: \: \: \quad \textrm{kendala}:2x+3y-6\leq 0\\ &(7)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(8)\: x=0,\: \: \textrm{kendala}:x\geq 0 \end{aligned}$

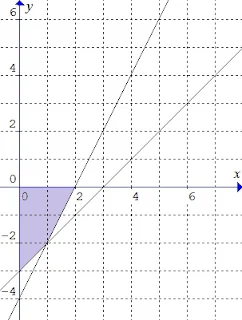
$\begin{array}{ll}\\ 42.&\textrm{Pada gambar berikut ini, pertidaksamaan}\\ &\textrm{yang memenuhi adalah}\\\\ \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \color{red}\textrm{a}.&2x-y-4\leq 0,\: x-y-3\leq 0,\: x\geq 0,\: y\geq 0\\ \textrm{b}.&2x-y-4\geq 0,\: x-y-3\geq 0,\: x\geq 0,\: y\leq 0\\ \textrm{c}.&2x-y-4\leq 0,\: x-y-3\geq 0,\: x\geq 0,\: y\leq 0\\ \textrm{d}.&\left (2x-y-4 \right )\left (x-y-3 \right )\geq 0,\: x\geq 0,\: y\leq 0\\ \textrm{e}.&\left (2x-y-4 \right )\left (x-y-3 \right )\leq 0,\: x\geq 0,\: y\leq 0\\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\color{blue}\textrm{Misalkan titik potong kedua garis adalah M}\\ &\color{magenta}\textrm{Persamaan garisnya di atas M dan model}\\ &\color{magenta}\textrm{matematikanya adalah sebagai berikut}:\\ &(1)\: -3x+3y=-9\\ &\: \: \: \quad\textrm{garisnya menjadi}:\: -3x+3y+9=0\\ &\: \: \: \quad\textrm{maka}:\: -x+y+3=0\\ &\: \: \: \quad\textrm{kendala}:-x+y+3\geq 0,\: \: \textrm{atau}\\ &\: \: \: \quad\color{blue}\textrm{kendala}:x-y-3\leq 0\\ &(2)\: -4x+2y=-8\\ &\: \: \: \quad\textrm{garisnya menjadi}:\: -4x+2y+8=0\\ &\: \: \: \quad\textrm{maka}:\: -2x+y+4=0\\ &\: \: \: \quad\textrm{kendala}:-2x+y+4\geq 0,\: \: \textrm{atau}\\ &\: \: \: \quad \quad\color{blue}\textrm{kendala}:2x-y-4\leq 0\\ &(3)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(4)\: x=0,\: \: \textrm{kendala}:x\geq 0\\ \end{aligned}$

$\begin{array}{ll}\\ 43.&\textrm{Seorang penjual hewan kurban memiliki}\\ &\textrm{15 kandang ternak untuk memelihara sapi}\\ &\textrm{dan kambing. Setiap kandang hanya berisi}\\ &\textrm{kambing saja atau sapi saja. Setiap kandang}\\ &\textrm{dapat menampung sapi sebanyak 20 ekor}\\ &\textrm{atau kambing sebanyak 38 ekor. Penjual}\\ &\textrm{hewan kurban tersebut menaksir biaya}\\ &\textrm{perawatan yang dikeluarkan untuk setiap}\\ &\textrm{kandang sapi setiap bulannya sebesar}\\ &Rp500.000,00\: \: \textrm{dan kambing}\: \: Rp300.000,00.\\ &\textrm{Sementara itu, jumlah hewan yang}\\ &\textrm{direncanakan tidak lebih dari 300 ekor}.\\ &\textrm{Jika banyak kandang yang berisi sapi}\\ &\textrm{disebut}\: \: x\: \: \textrm{dan banyak kandang yang berisi}\\ &\textrm{kambing disebut}\: \: y,\: \: \textrm{sistem pertidaksamaan}\\ &\textrm{yang harus dipenuhi oleh}\: \: x\: \: \textrm{dan}\: \: y\: \: \textrm{serta}\\ &\textrm{fungsi objektif untuk meminimumkan biaya}\\ &\textrm{perawatan hewan kurban adalah}.... \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&x\geq 0,\: y\geq 0,\: 20x+38y\leq 15,\: x+y\leq 300\\ &\textrm{minimum}\: \: f(x,y)=500.000x+300.000y\\ \textrm{b}.&x\geq 0,\: y\geq 0,\: 38x+20y\leq 15,\:x+y\leq 300 \\ &\textrm{minimum}\: \: f(x,y)=500.000x+300.000y\\ \textrm{c}.&x\geq 0,\: y\geq 0,\: 28x+30y\leq 300,\:x+y\leq 15 \\ &\textrm{minimum}\: \: f(x,y)=500.000x+300.000y\\ \textrm{d}.&x\geq 0,\: y\geq 0,\: 38x+20y\leq 300,\:x+y\leq 15 \\ &\textrm{minimum}\: \: f(x,y)=500.000x+300.000y\\ \color{red}\textrm{e}.&x\geq 0,\: y\geq 0,\: 20x+38y\leq 300,\:x+y\leq 15 \\ &\textrm{minimum}\: \: f(x,y)=500.000x+300.000y\\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\color{blue}\textrm{Misalkan titik potong kedua garis adalah M}\\ &\color{magenta}\textrm{Misalkan sapi}=x,\: \: \textrm{kambing}=y,\: \: \textrm{maka}\\ &(1)\: \textrm{Sapi}+\textrm{Kambing}= 15\: \: \textrm{ekor}\\ &\: \: \: \quad \textrm{persamaan garisnya}:\\ &\: \: \: \quad x+y= 15,\: \: \textrm{dan}\\ &\: \: \: \quad\textrm{kendalanya}:x+y\leq 15\\ &(2)\: \textrm{Daya tampung kandang}\\ &\: \: \: \quad \textrm{persamaan garisnya}:\\ &\: \: \: \quad20x+38y=300\\ &\: \: \: \quad \textrm{kendala}:20x+38y\leq 300\\ &(3)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(4)\: x=0,\: \: \textrm{kendala}:x\geq 0\\ &(5)\: \color{red}\textrm{Fungsi optimumnya adalah}:\\ &\: \: \: \color{blue}\quad f(x,y)=500.000x+300.000y \end{aligned}$

$\begin{array}{ll}\\ 44.&\textrm{Suatu perusahaan bangunan merencanakan}\\ &\textrm{pembangunan paling banyak 150 unit rumah}\\ &\textrm{untuk disewakan kepada 500 orang. Ada dua}\\ &\textrm{jenis rumah, yaitu rumah jenis A dengan}\\ &\textrm{kapasitas 4 orang yang akan disewakan dengan}\\ &\textrm{harga}\: \: Rp2.000.000,00\: \: \textrm{per tahun dan rumah}\\ &\textrm{jenis B dengan kapasitas 6 orang yang disewakan}\\ &Rp2.500.000,00\: \: \textrm{per tahun. Jika rumah jenis}\\ &\textrm{A dibuat sebanyak}\: \: x\: \: \textrm{unit dan jenis B sebanyak}\\ &y\: \: \textrm{unit},\: \color{blue}\textbf{model matematika}\: \color{black}\textrm{dari masalah tersebut}\\ &\textrm{adalah}\:.... \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&x\geq 0,\: y\geq 0,\: x+y\leq 100,\: 4x+6y\leq 500\\ \color{red}\textrm{b}.&x\geq 0,\: y\geq 0,\: x+y\leq 150,\:4x+6y\leq 500 \\ \textrm{c}.&x\geq 0,\: y\geq 0,\: x+y\leq 200,\:4x+6y\leq 250 \\ \textrm{d}.&x\geq 0,\: y\geq 0,\: x+y\leq 200,\:6x+4y\leq 250 \\ \textrm{e}.&x\geq 0,\: y\geq 0,\: x+y\leq 500,\:6x+4y\leq 250 \\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Model matematikanya adalah}:\\ &\color{magenta}\textrm{Misalkan rumah jenis A}=x,\: \: \textrm{jenis B}=y,\: \: \textrm{maka}\\ &(1)\: \textrm{Jenis A}+\textrm{Jenis B}= 150\: \: \textrm{unit}\\ &\: \: \: \quad \textrm{persamaan garisnya}:\\ &\: \: \: \quad x+y= 150,\: \: \textrm{dan}\\ &\: \: \: \quad\textrm{kendalanya}:x+y\leq 150\\ &(2)\: \textrm{Kapasitas atau daya tampung}\\ &\: \: \: \quad \textrm{Rumah jenis A muat 4 orang dan jenis B}\\ &\: \: \: \quad \textrm{6 orang sedangkan targetnya 500 orang, maka}\\ &\: \: \: \quad \textrm{persamaan garisnya}:\\ &\: \: \: \quad 4x+6y=500\\ &\: \: \: \quad \textrm{kendala}:4x+6y\leq 500\\ &(3)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(4)\: x=0,\: \: \textrm{kendala}:x\geq 0\\ &(5)\: \color{red}\textrm{Fungsi optimumnya adalah}:\\ &\: \: \: \color{blue}\quad f(x,y)=2.000.000x+2.500.000y \end{aligned}$

$\begin{array}{ll}\\ 45.&\textrm{Pedagang teh mempunyai lemari yang hanya}\\ &\textrm{cukup ditempati 40 boks teh. Teh A dibeli}\\ &\textrm{dengan harga}\: \: Rp6.000,00\: \: \textrm{setiap boks dan teh B}\\ &\textrm{dibeli dengan harga}\: \: Rp8.000,00\: \: \textrm{setiap boks}\\ &\textrm{Jika pedang tersebut mempunyai modal sebesar}\\ &Rp300.000,00\: \: \textrm{untuk membeli}\: \: x\: \: \textrm{boks teh A dan}\\ &y\: \: \textrm{boks teh B, maka sistem pertidaksamaan dari}\\ &\textrm{permasalahan tersebut adalah}\: .... \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&3x+4y\geq 150,\: x+y\geq 40,\: x\geq 0,\: y\geq 0\\ \color{red}\textrm{b}.&3x+4y\leq 150,\: x+y\leq 40,\:x\geq 0,y\geq 0 \\ \textrm{c}.&3x+4y\geq 150,\: x+y\leq 40,\:x\geq 0,\: y\geq 0 \\ \textrm{d}.&6x+8y\leq 300,\: x+y\geq 40,\:x\geq 0,\: y\geq 0 \\ \textrm{e}.&8x+4y\leq 300,\: x+y\leq 40,\:x\geq 0,\: y\geq 0 \\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{aligned}$.

$\begin{array}{ll}\\ 46.&\textrm{Pada pertidaksamaan}\\ & 2y\geq x\: ;\: y\leq 2x\: ;\: 2y+x\leq 20\: ;\: x+y\geq 9\\ &\textrm{Nilai maksimum untuk}\: \: \color{red}3y-x\: \: \color{black}\textrm{dicapai saat}\: ....\\\\ \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&\textrm{P}\\ \textrm{b}.&\textrm{Q}\\ \color{red}\textrm{c}.&\textrm{R}\\ \textrm{d}.&\textrm{S}\\ \textrm{e}.&\textrm{T}\\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\textrm{Dengan membuat garis(selidik)}:f(x,y)=3y-x\\ &\color{blue}\textrm{digeser dari bawah ke atas, maka akan didapatkan}\\ &\color{blue}\textrm{titik sudut(verteks) yang diinginkan}\\ & \end{aligned}$

$\begin{array}{ll}\\ 47.&\textrm{Nilai minimum dari}\: \: -2x+4y+6\\ &\textrm{untuk}\: \: x\: \: \textrm{dan}\: \: y\: \: \textrm{yang memenuhi}\\ &\begin{cases} 2x+y-20 &\leq 0 \\ 2x-y+10&\geq 0 \\ x+y-5 &\geq 0 \\ x-2y-5 &\leq 0 \\ x\geq 0 & \\ y\geq 0 & \end{cases}\\ &\textrm{adalah}\: ....\\ &\begin{array}{ll}\\ \textrm{a}.&-14\\ \textrm{b}.&-11\\ \textrm{c}.&-9\\ \textrm{d}.&-6\\ \color{red}\textrm{e}.&-4\\ \end{array}\\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\textrm{Diketahui fungsi objektif}:f(x,y)=-2x+4y+6\\ &\color{blue}\textrm{dan kendala-kendalanya}\\ &\begin{cases} 2x+y-20 &\leq 0 \\ 2x-y+10&\geq 0 \\ x+y-5 &\geq 0 \\ x-2y-5 &\leq 0 \\ x\geq 0 & \\ y\geq 0 & \end{cases}\\ &\color{blue}\textrm{maka daerah penyelesaiannya adalah}: \end{aligned}$

$.\: \: \: \quad\begin{aligned}&\textrm{Dan persamaan garisnya adalah}\\ &\begin{cases} \textrm{L}_{1}\equiv &2x+y=20 \\ \textrm{L}_{2}\equiv &2x-y=-10\\ \textrm{L}_{3}\equiv &x+y=5 \\\textrm{L}_{4} \equiv &x-2y=5 \end{cases}\\ &\color{blue}\textrm{Perpotongan untuk garis}\: \: \textrm{L}_{1}\&\textrm{L}_{2}\\ &\textrm{akan didapatkan titik C}\: \left ( \displaystyle \frac{5}{2},15 \right )\\ &\color{blue}\textrm{Perpotongan untuk garis}\: \: \textrm{L}_{1}\&\textrm{L}_{4}\\ &\textrm{akan didapatkan titik B}\: \left ( \displaystyle 9,2 \right )\\ \end{aligned}$

$.\: \: \: \quad\begin{array}{|l|}\hline \begin{aligned}\color{red}\textrm{untuk}\: &\color{red}\textrm{mendapatkan titik potong}\\ \textrm{garis}:\: &\textrm{L}_{1}\&\textrm{L}_{2}\: \: \color{black}\textrm{adalah sebagai berikut}:\\ &\begin{cases} 2x+y & =20 \\ 2x-y & =-10 \end{cases}\\ &-------\: \: .^{-}\\ &\: \: \: \quad\quad\quad2y=30\\ &\: \qquad\qquad y=15\Rightarrow x=\displaystyle \frac{5}{2}\\ \textrm{Sehing}&\textrm{ga didapatkan titik}\: \: \left ( \displaystyle \frac{5}{2},15 \right ) \end{aligned} \\\hline \begin{aligned}\color{magenta}\textrm{untuk}\: &\color{red}\textrm{mendapatkan titik potong}\\ \textrm{garis}:\: &\textrm{L}_{1}\&\textrm{L}_{4}\: \: \color{black}\textrm{adalah sebagai berikut}:\\ &\begin{cases} 2x+y & =20 \\ x-2y & =5 \end{cases}\\ &\begin{cases} 4x+2y & =40 \\ x-2y & =5 \end{cases}\\ &-------\: \: .^{+}\\ &\qquad\quad\quad5x=45\\ &\: \: \qquad\qquad x=9\Rightarrow y=2\\ \textrm{Sehing}&\textrm{ga didapatkan titik}\: \: \left ( 9,2 \right ) \end{aligned}\\\hline \end{array}$

$.\: \: \: \quad\textrm{Selanjutnya}$

$.\: \: \: \quad\begin{array}{|c|c|c|}\hline \textrm{Verteks}&\color{magenta}\textrm{Nilai}:& \textrm{Keterangan}\\ &-2x+4y+6&\\\hline \textrm{A}(5,0)&-2(5)+4.0+6=-4&\color{blue}\textrm{Minimum}\\\hline \textrm{B}(9,2)&-2(9)+4.2+6=-4&\color{blue}\textrm{Minimum}\\\hline \textrm{C}\left ( \displaystyle \frac{5}{2},15 \right )&-2\left ( \displaystyle \frac{5}{2} \right )+4.15+6=61&\color{red}\textrm{Maksimum}\\\hline \textrm{D}(0,10)&-2.0+4.10+6=46&\\\hline \textrm{E}(0,5)&-2.0+4.5+6=26&\\\hline \end{array}$

$\begin{array}{ll}\\ 48.&\textrm{Nilai minimum}\: \: f(x,y)=3+4x-5y\\ &\textrm{untuk}\: \: x\: \: \textrm{dan}\: \: y\: \: \textrm{yang memenuhi}\\ &\begin{cases} -x+y &\leq 1 \\ x+2y&\geq 5 \\ 2x+y &\leq 10 \\ \end{cases}\\ &\textrm{adalah}\: ....\\ &\begin{array}{ll}\\ \textrm{a}.&-19\\ \textrm{b}.&-6\\ \color{red}\textrm{c}.&-5\\ \textrm{d}.&-3\\ \textrm{e}.&23\\ \end{array} \\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\textrm{Diketahui fungsi objektif}:f(x,y)=3+4x-5y\\ &\color{blue}\textrm{dan kendala-kendalanya}\\ &\begin{cases} -x+y &\leq 1 \\ x+2y&\geq 5 \\ 2x+y &\leq 10 \\ \end{cases}\\ &\color{blue}\textrm{maka daerah penyelesaiannya adalah}: \end{aligned}$

$.\: \: \: \quad\begin{array}{|c|c|c|}\hline \textrm{Verteks}&\color{magenta}\textrm{Nilai}:& \textrm{Keterangan}\\ &3+4x-5y&\\\hline \textrm{A}(1,2)&3+4.1-5.2=-3&\\\hline \textrm{B}(3,4)&3+4.3-5.4=-5&\color{blue}\textrm{Minimum}\\\hline \textrm{C}(5,0)&3+4.5-5.0=23&\color{red}\textrm{Maksimum}\\\hline \end{array}$

$\begin{array}{ll}\\ 49.&\textrm{Fungsi}\: \: f(x,y)=10x+15y\\ &\textrm{untuk}\: \: x\: \: \textrm{dan}\: \: y\: \: \textrm{yang memenuhi}\\ &\begin{cases} x &\geq 0 \\ y&\geq 0 \\ x &\leq 800 \\ x&+\: \: y\: \: \leq 1000\\ \end{cases}\\ &\textrm{mempunyai nilai maksimum}\: ....\\ &\begin{array}{ll}\\ \textrm{a}.&9.000\\ \textrm{b}.&11.000\\ \color{red}\textrm{c}.&13.000\\ \textrm{d}.&15.000\\ \textrm{e}.&16.000\\ \end{array} \\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\textrm{Diketahui fungsi objektif}:f(x,y)=10x+15y\\ &\color{blue}\textrm{dan kendala-kendalanya}\\ &\begin{cases} x &\geq 0 \\ y&\geq 0 \\ x &\leq 800 \\ x&+\: \: y\: \: \leq 1000\\ \end{cases}\\ &\color{blue}\textrm{maka daerah penyelesaiannya adalah}: \end{aligned}$

$.\: \: \: \quad\begin{array}{|c|c|c|}\hline \textrm{Verteks}&\color{magenta}\textrm{Nilai}:& \textrm{Keterangan}\\ &f(x,y)=10x+15y&\\\hline \textrm{A}(800,0)&800.10+0=8000&\color{red}\textrm{Minimum}\\\hline \textrm{B}(800,200)&800.10+15.200=11.000&\\\hline \textrm{C}(400,600)&10.400+15.600=13.000&\color{blue}\textrm{Maksimum}\\\hline \textrm{D}(0,600)&3+0+15.600=9.000&\\\hline \end{array}$

$\begin{array}{ll}\\ 50.&\textrm{Nilai maksimum fungsi sasaran}\\ & f(x,y)=4x+5y\\ &\textrm{untuk}\: \: x\: \: \textrm{dan}\: \: y\: \: \textrm{yang memenuhi}\\ &\begin{cases} x&\geq 0 \\ y&\geq 0 \\ (&2x+y-4\: )(\: 2x+3y-6\: )\: \: \leq 0\\ \end{cases}\\ &\textrm{adalah}\: ....\\ &\begin{array}{ll}\\ \textrm{a}.&11\\ \textrm{b}.&12\\ \textrm{c}.&16\\ \color{red}\textrm{d}.&20\\ \textrm{e}.&24\\ \end{array} \\ \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\textrm{Diketahui fungsi objektif}:f(x,y)=4x+5y\\ &\color{blue}\textrm{dan kendala-kendalanya}\\ &\begin{cases} x&\geq 0 \\ y&\geq 0 \\ (&2x+y-4\: )(\: 2x+3y-6\: )\: \: \leq 0\\ \end{cases}\\ &\color{blue}\textrm{maka daerah penyelesaiannya adalah}: \end{aligned}$

$.\: \: \: \quad\begin{aligned}\textrm{untuk}\: &\textrm{mendapatkan titik potongnya}\\ &\begin{cases} 2x+y & =4 \\ 2x+3y & =6 \end{cases}\\ &-------\: \: .^{-}\\ &\: \, \qquad-2y=-2\\ &\qquad\qquad y=1\Rightarrow x=\displaystyle \frac{3}{2}\\ \textrm{sehing}&\textrm{ga akan didapatkan}\\ \color{blue}\textrm{titik p}&\color{blue}\textrm{otongnya adalah}:\: \: \left ( \displaystyle \frac{3}{2},1 \right )\\ \textrm{Selanj}&\textrm{utnya, kita dapat menentukan}\\ \textrm{nilai}\: \: \: \: &\textrm{maksimunya dengan bantuan tabel berikut} \end{aligned}$

$.\: \: \: \quad\begin{array}{|c|c|c|}\hline \textrm{Verteks}&\color{magenta}\textrm{Nilai}:& \textrm{Keterangan}\\ &f(x,y)=4x+5y&\\\hline (2,0)&4.2+0=8&\color{red}\textrm{Minimum}\\\hline (3,0)&4.3+0=12&\\\hline \left ( \displaystyle \frac{3}{2},1 \right )&4.\left ( \displaystyle \frac{3}{2} \right )+5.1=11&\\\hline (0,2)&0+52=10&\\\hline (0,4)&0+5.4=20&\color{blue}\textrm{Maksimum}\\\hline \end{array}$

Latihan Soal 4 Persiapan PAS Gasal Matematika Wajib Kelas XI

 $\begin{array}{ll}\\ 31.&\textrm{Daerah yang diarsir berikut adalah himpunan}\\ &\textrm{penyelesaian pertidaksamaan dari}....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&y\geq 0,\: x-2y\geq -2,\: 3x+4y\leq 12\\ \textrm{b}.&y\geq 0,\: x-2y\geq -2,\: 3x+4y\geq 12\\ \textrm{c}.&y\geq 0,\: -2x+y\geq -2,\: 4x+3y\leq 12\\ \textrm{d}.&x\geq 0,\: -2x+y\leq -2,\: 4x+3y\geq 12\\ \textrm{e}.&x\geq 0,\: x-2y\leq -2,\: 3x+4y\leq 12 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\textrm{Cukup jelas. Anda bisa mengecek dengan titik uji} \end{array}$

$\begin{array}{ll}\\ 32.&\textrm{Daerah yang diarsir berikut adalah himpunan}\\ &\textrm{penyelesaian pertidaksamaan dari}....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&x\geq 0,\: 4x+y\geq 4,\: x+y\leq 2\\ \color{red}\textrm{b}.&x\geq 0,\: 4x+y\leq 4,\: x+y\geq 2\\ \textrm{c}.&x\geq 0,\: 4x+y> 4,\: x+y< 2\\ \textrm{d}.&x\geq 0,\: x+4y> 4,\: x+y< 2\\ \textrm{e}.&x\geq 0,\: x+4y\leq 4,\: x+y\geq 2 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Cukup jelas} \end{array}$

$\begin{array}{ll}\\ 33.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} 2x+y & \leq 24 \\ x+2y &\geq 12 \\ x-y & \geq -2 \end{cases}\\\\ &\textrm{adalah}\: ....\\ & \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 34.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} x+2y & \geq 6 \\ 4x+5y &\leq 20 \\ 2x+y & \geq 6 \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \color{red}\textrm{b}.&\textrm{II}\\ \textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 35.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} 2x+y & \geq 4 \\ x+y &\geq 3 \\ x-4y & \geq 4 \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$.

$\begin{array}{ll}\\ 36.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} -x+2y & \leq 2 \\ 4x+3y &\leq 12 \\ x \geq 0&\\ y\geq 0& \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{I}\: \: \textrm{dan}\: \: \textrm{IV}\\ \textrm{e}.&\textrm{II}\: \: \textrm{dan}\: \: \textrm{II} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 37.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} 5x+y & \geq 10\\ 2x+y &\leq 8 \\ y\geq 2& \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 38.&\textrm{Pada gambar berikut ini, yang merupakan}\\ &\textrm{himpunan penyelesaian sistem pertidaksamaan}\\\\ &\color{magenta}\begin{cases} x+y & \geq 4\\ x+2y &\leq 6 \\ y\geq 1& \end{cases}\\\\ &\textrm{adalah}\: ....\\ \end{array}$

$.\: \: \: \begin{array}{ll}\\ &\begin{array}{llll}\\ \textrm{a}.&\textrm{I}\\ \textrm{b}.&\textrm{II}\\ \color{red}\textrm{c}.&\textrm{III}\\ \textrm{d}.&\textrm{IV}\\ \textrm{e}.&\textrm{V} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Pembahasan juga diserahkan kepada pembaca} \end{array}$

$\begin{array}{ll}\\ 39.&(\textrm{SPMB 2003})\\ &\textrm{Daerah yang diarsir pada ilustrasi gambar berikut}\\ &\textrm{adalah himpunan semua}\: \: (x,y)\: \: \textrm{yang memenuhi} \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \color{red}\textrm{a}.&2x+y\leq 30,\: 3x+4y\leq 60,\: x\geq 0,\: y\geq 0\\ \textrm{b}.&2x+y\geq 30,\: 3x+4y\geq 60,\: x\geq 0,\: y\geq 0\\ \textrm{c}.&x+2y\geq 30,\: 3x+4y\geq 60,\: x\geq 0,\: y\geq 0\\ \textrm{d}.&x+2y\leq 30,\: 4x+3y\leq 60,\: x\geq 0,\: y\geq 0\\ \textrm{e}.&2x+y\geq 30,\: 4x+3y\leq 60,\: x\geq 0,\: y\geq 0 \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\color{blue}\textrm{Persamaan garisnya adalah}:\\ &(1)\: 15x+20y=300\\ &\: \: \: \quad\textrm{kendala}:3x+4y\leq 60\\ &(2)\: 30x+15y=450\\ &\: \: \: \quad \textrm{kendala}:2x+y\leq 30\\ &(3)\: y=0,\: \: \textrm{kendala}:y\geq 0 \\ &(4)\: x=0,\: \: \textrm{kendala}:x\geq 0 \end{aligned}$

$\begin{array}{ll}\\ 40.&(\textrm{SPMB 2004})\\ &\textrm{Daerah yang diarsir pada ilustrasi gambar berikut}\\ &\textrm{adalah himpunan penyelesaian yang dipenuhi oleh} \end{array}$

$.\: \: \: \quad\begin{array}{ll}\\ \textrm{a}.&6x+5y-30\leq 0,\: x+6y-6\leq 0,\: x-y\leq 0\\ \textrm{b}.&6x+5y-30\geq 0,\: x+6y-6\leq 0,\: x-y\leq 0\\ \color{red}\textrm{c}.&6+5y-30\leq 0,\: x+6y-6\geq 0,\: x-y\geq 0\\ \textrm{d}.&6x+5y-30\leq 0,\: x+6y-6\geq 0,\: x-y\leq 0\\ \textrm{e}.&6x+5y-30\geq 0,\: x+6y-6\geq 0,x-y\geq 0 \end{array}$

$.\: \: \: \quad\begin{aligned}&\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\color{blue}\textrm{Perhatikan bahwa kendala-kendalanya}:\\ &\begin{array}{|c|c|c|}\hline \begin{aligned}6x+5y&=6\times 5\\ 6x+5y&=30 \end{aligned}&\begin{aligned}x+6y&=1\times 6\\ x+6y&=6 \end{aligned}&\begin{aligned}x&=y\\ \end{aligned}\\\hline \textbf{Sebelah kiri}&\textbf{Sebelah kanan}&\\\hline \begin{aligned}6x+5y&\leq 30\\ 6x+5y-30&\leq 0 \end{aligned}&\begin{aligned}x+6y&\geq 6\\ x+6y-6&\geq 0 \end{aligned}&\begin{aligned}x&\geq y\\ x-y&\geq 0 \end{aligned}\\\hline \end{array} \end{aligned}$

Latihan Soal 3 Persiapan PAS Gasal Matematika Wajib Kelas XI

$\begin{array}{ll}\\ 21.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &3+6+12+24+...+\left ( 3.2^{n-1} \right )=3.\left ( 2^{n}-1 \right )\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k+1,\: \: \textrm{maka}\\ &\textrm{ruas kiri persamaan tersebut dapat dituliskan}\\ &\textrm{dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&3+6+12+24+...+ 3.2^{k+1} \\ \textrm{b}.&3+6+12+24+...+ 3.2^{k-1} \\ \color{red}\textrm{c}.&3+6+12+24+...+ 3.2^{k-1}+3.2^{k} \\ \textrm{d}.&3+6+12+24+...+ 3.2^{k-1}+3.2^{k+1} \\ \textrm{e}.&3+6+12+24+...+ 3.2^{k}+3.2^{k+1} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}&3+6+12+24+...+ 3.2^{n-1} =3.\left ( 2^{n}-1 \right )\\ &\color{red}3+6+12+24+...+ 3.2^{k-1}+3.2^{k}\color{black}=\color{blue}3.\left ( 2^{k+1}-1 \right ) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 22.&\textbf{(EBTANAS 1999)}\\ &\textrm{Nilai dari}\: \: \displaystyle \sum_{k=1}^{100}5k-\sum_{k=1}^{100}(2k-1)\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad 30.900\\ &\textrm{b}.\quad 30.500\\ &\textrm{c}.\quad 16.250\\ &\textrm{d}.\quad 15.450\\ &\textrm{e}.\quad \color{red}15.250\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\textrm{Diketahi}\\ &\begin{aligned}\displaystyle \sum_{k=1}^{100}5k-\sum_{k=1}^{100}(2k-1)&=\sum_{k=1}^{100}(5k-2k+1)\\ &=\displaystyle \sum_{k=1}^{100}(3k+1)\\ &=3\displaystyle \sum_{k=1}^{100}k+1.100\\ &=3\left ( \displaystyle \frac{100}{2}(1+100) \right )+100\\ &=3.(5.050)+100\\ &=15.150+100\\ &=\color{red}15.250\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 23.&\textbf{(EBTANAS 2000)}\\ &\textrm{Diketahui}\: \: \displaystyle \sum_{k=5}^{25}(2-pk)=0, \textrm{maka nilai}\\ & \displaystyle \sum_{k=5}^{25}pk= ... .\\ &\textrm{a}.\quad 20\\ &\textrm{b}.\quad 28\\ & \textrm{c}.\quad 30\\ &\textrm{d}.\quad \color{red}42\\ & \textrm{e}.\quad 112\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}\displaystyle \sum_{k=5}^{25}(2-pk)=\displaystyle \sum_{k=5}^{25}2-\sum_{k=5}^{25}pk&=0\\ \displaystyle \sum_{k=5-4}^{25-4}2-\sum_{k=5}^{25}pk&=0\\ \displaystyle \sum_{k=5}^{25}pk&=\displaystyle \sum_{k=1}^{21}2\\ &=21.2\\ &=\color{red}42 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 24.&\textbf{(EBTANAS 2000)}\\ &\textrm{Nilai dari}\: \: \displaystyle \sum_{k=1}^{7}\left ( \displaystyle \frac{1}{2} \right )^{k+1}=... .\\ &\textrm{a}.\quad \displaystyle \frac{127}{1024}\\\\ &\textrm{b}.\quad \displaystyle \frac{127}{256}\\\\ & \textrm{c}.\quad \displaystyle \frac{255}{512}\\\\ &\textrm{d}.\quad \displaystyle \frac{127}{128}\\\\ & \textrm{e}.\quad \displaystyle \frac{255}{256}\\\\ &\textrm{Jawab}:\quad \color{red}\textrm{b}\\ &\begin{aligned}&\displaystyle \sum_{k=1}^{7}\left ( \displaystyle \frac{1}{2} \right )^{k+1}\\ &=\left ( \displaystyle \frac{1}{2} \right )^{2}+\left ( \frac{1}{2} \right )^{3}+\left ( \frac{1}{2} \right )^{4}+\left ( \frac{1}{2} \right )^{5}+\left ( \frac{1}{2} \right )^{6}+\left ( \frac{1}{2} \right )^{7} +\left ( \displaystyle \frac{1}{2} \right )^{8}\\ &=\displaystyle \frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}\\ &=\displaystyle \frac{64+32+16+8+4+2+1}{256}\\ &=\color{red}\displaystyle \frac{127}{256} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 25.&\textbf{EBTANAS 1999}\\ &\textrm{Diketahui jumlah n suku pertama }\\ &\textrm{deret aritmetika dinyatakan sebagai}\\ &S_{n}=n^{2}+2n.\: \textrm{Beda dari deret tersebut }\\ &\textrm{adalah}\: ....\\ &\textrm{a}.\quad 3 \\ &\textrm{b}.\quad \color{red}2\\ & \textrm{c}.\quad 1\\ &\textrm{d}.\quad -2\\ & \textrm{e}.\quad -3\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\textrm{Diketahui bahwa}\: \: S_{n}=n^{2}+2n,\\ &\textrm{dengan}\: \begin{cases} S_{1} & =U_{1}=a \\ S_{2} & =U_{1}+U_{2} \\ S_{3} & =U_{1}+U_{2}+U_{3} \\ &\vdots \\ S_{n} & =U_{1}+U_{2}+U_{3}+\cdots +U_{n} \end{cases}\\ &\begin{aligned}\textrm{Beda}=b&=U_{2}-U_{1}\\ &=(S_{2}-S_{1})-S_{1}\\ &=S_{2}-2S_{1}\\ &=\left ( 2^{2}+2.(2) \right )-2\left ( 1^{2}+2.(1) \right )\\ &=\left ( 4+4 \right )-2\left ( 1+2 \right )=8-6\\ &=\color{red}2\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 26.&\textbf{(UMPTN 1994)}\\ &\textrm{Diketahui jumlah n suku pertama suatu }\\ &\textrm{deret dinyatakan sebagai}\quad S_{n}=12n-n^{2}.\\ & \textrm{Suku kelima dari deret tersebut adalah}\: ....\\ &\textrm{a}.\quad -1 \\ &\textrm{b}.\quad 1\\ & \textrm{c}.\quad -3\\ &\textrm{d}.\quad \color{red}3\\ & \textrm{e}.\quad 0\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\textrm{Diketahui bahwa}\\ &S_{n}=12n-n^{2}\\ &\begin{aligned}U_{5}&=S_{5}-S_{4}\\ &=\left ( 12.(5)-(5)^{2} \right )-\left ( 12.(4)-(4)^{2} \right )\\ &=\left ( 60-25 \right )-\left ( 48-16 \right )\\ &=\color{red}3\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 27.&\textbf{(UMPTN 1997)}\\ &\textrm{Diketahui}\: \: U_{n}\: \: \textrm{adalah suku ke - n }\\ &\textrm{deret aritmetika dengan}\\ &U_{1}+U_{2}+U_{3}=-9\: \: \textrm{dan}\\ & \: U_{3}+U_{4}+U_{5}=15.\\ & \textrm{Maka jumlah lima suku pertama}\\ &\textrm{deret aritmetika tersebut adalah}\: ....\\ &\textrm{a}.\quad 4\\ &\textrm{b}.\quad \color{red}5\\ &\textrm{c}.\quad 6\\ &\textrm{d}.\quad 15\\ &\textrm{e}.\quad 24\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\textrm{Diketahui bahwa}\\ &\begin{aligned}&U_{1}+U_{2}+U_{3}=-9,\\ &\Leftrightarrow a+(a+b)+(a+2b)=-9\\ &\Leftrightarrow \color{blue}3a+3b=-9\\ &U_{3}+U_{4}+U_{5}=15,\\ &\Leftrightarrow (a+2b)+(a+3b)+(a+4b)=15\\ &\Leftrightarrow \color{blue}3a+9b=15\quad _{-}\\ & -----------------\\ &\, \qquad\qquad\qquad -6b=-24\Rightarrow b=\color{red}4\\ &\, \qquad \textrm{sehingga akan diperoleh}\: \: a=\color{red}-7\\ &\textrm{Selanjutnya}\\ &S_{5}=\displaystyle \frac{5}{2}\left ( U_{1}+U_{5} \right )\\ &=\displaystyle \frac{5}{2}\left ( a+a+(5-1)b \right )\\ &=\displaystyle \frac{5}{2}\left ( -7-7+4.4 \right )\\ &=\displaystyle \frac{5}{2}(2)\\ &=\color{red}5\end{aligned} \end{array}$.

$\begin{array}{ll}\\ 28.&\textbf{(UN 2013)}\\ &\textrm{Diketahui suatu barisan aritmetika dengan }\\ &\textrm{suku ketiga adalah 4 dan suku ketujuhnya }\\ &\textrm{adalah 16. Jumlah 10 suku pertama dari }\\ &\textrm{deret tersebut adalah}\: ...\: .\\ &\textrm{a}.\quad \color{red}115\\ &\textrm{b}.\quad 125\\ & \textrm{c}.\quad 130\\ &\textrm{d}.\quad 135\\ &\textrm{e}.\quad \displaystyle 140\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\begin{aligned}U_{3}=a+2b&=4\\ U_{7}=a+6b&=16\quad _{-}\\ ------&--\\ -4b&=-12\\ b&=3\\ \textrm{Sehingga}&\: \textrm{didapatkan}\\ \textrm{nilai}\: \: a=&4-2b\\ =&4-2.3\\ =&-2 \end{aligned}\\ &\begin{aligned}&\textrm{Maka}\: \textrm{jumlah 10 suku pertama }\\ &\textrm{deret tersebut adalah}\\ &S_{n}=\displaystyle \frac{n}{2}\left ( 2a+(n-1)b \right )\\ &S_{10}=\displaystyle \frac{10}{2}\left ( 2.(-2)+(10-1).3 \right )\\ &\: \: \quad=5\left ( -4+27 \right )\\ &\: \: \quad=5(23)\\ &\: \: \quad=\color{red}115 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 29.&\textbf{(UN 2014)}\\ &\textrm{Diketahui tempat duduk gedung pertunjukan }\\ &\textrm{film diatur mulai dari baris depan ke belakang }\\ &\textrm{dengan banyak banyak baris dibelakang lebih }\\ &\textrm{4 kursi dari baris di depannya.}\\ &\textrm{Jika dalam gedung pertunjukan terdapat 15}\\ &\textrm{baris kursi dan baris terdepan ada 20 kursi, }\\ &\textrm{maka kapasitas gedung pertunjukan tersebut }\\ &\textrm{adalah}\: ...\: .\: \textrm{kursi}\\ &\textrm{a}.\quad 1200\\ &\textrm{b}.\quad 800\\ & \textrm{c}.\quad \color{red}720\\ &\textrm{d}.\quad 600\\ &\textrm{e}.\quad 300\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}\textrm{Diketahui}&\:\begin{cases} a &=U_{1}=20 \\ b & =4 \\ n & =15 \\ S_{n} & =\displaystyle \frac{n}{2}\left ( 2a+(n-1)b \right ) \end{cases}\\ &\\ & \end{aligned}\\ &\begin{aligned}S_{n}&=\displaystyle \frac{n}{2}\left ( 2a+(n-1)b \right )\\ &=\displaystyle \frac{15}{2}\left ( 2(20)+(15-1).4 \right )\\ &=15(20+28)\\ &=15(48)\\ &=\color{red}750 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 30.&\textbf{(UN 2015)}\\ &\textrm{Diketahui suatu barisan aritmetika dengan }\\ &\textrm{suku ke-3 adalah 2 dan suku ke-8 adalah -13}.\\ &\textrm{Jumlah 20 suku pertama dari deret tersebut }\\ &\textrm{adalah}\: ...\: .\\ &\textrm{a}.\quad -580\\ &\textrm{b}.\quad -490\\ &\textrm{c}.\quad -440\\ &\textrm{d}.\quad \color{red}-410\\ &\textrm{e}.\quad -380\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}U_{3}=a+2b&=2\\ U_{8}=a+7b&=-13\quad _{-}\\ ------&---\\ -5b&=15\\ b&=-3\\ \textrm{Sehingga}&\: \textrm{didapatkan}\\ \textrm{nilai}\: \: a=&2-2b\\ =&2-2.(-3)\\ =&8 \end{aligned}\\ &\begin{aligned}&\textrm{Maka}\: \textrm{jumlah 20 suku pertama }\\ &\textrm{deret tersebut adalah}\\ &S_{n}=\displaystyle \frac{n}{2}\left ( 2a+(n-1)b \right )\\ &S_{20}=\displaystyle \frac{20}{2}\left ( 2.(8)+(20-1).(-3) \right )\\ &\: \: \quad=10\left ( 16-57 \right )\\ &\: \: \quad=10(-41)\\ &\: \: \quad=\color{red}-410\\ &\\ & \end{aligned} \end{array}$

DAFTAR PUSTAKA

1. Budhi, W.S. 2018. Bupena Matematika SMA/MA Kelas XI Kelompok Wajib. Jakarta: ERLANGGA.

DAFTAR PUSTAKA WEB

1. Thohir, A. https://ahmadthohir1089.wordpress.com/2016/01/11/insyaallah-44/

Latihan Soal 2 Persiapan PAS Gasal Matematika Wajib Kelas XI

 $\begin{array}{ll}\\ 11.&\textrm{Perhatikanlah pernyataan-pernyataan berikut}\\ &(1)\quad \displaystyle \sum_{i=1}^{5}(5i+2)=4\displaystyle \sum_{i=1}^{5}i+10\\ &(2)\quad \displaystyle \sum_{i=1}^{5}(5i^{2}-i)=5\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}i\\ &(3)\quad \displaystyle \sum_{i=1}^{5}(3i-4)=3\displaystyle \sum_{i=1}^{5}i^{2}-4\\ &(4)\quad \displaystyle \sum_{i=1}^{5}(i+7i^{2})=\displaystyle \sum_{i=1}^{5}i-7\sum_{i=1}^{5}i\\ &\textrm{Pernyataan yang tepat ditunjukkan oleh}....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&(1)\: \: \textrm{dan}\: \: (2)\\ \textrm{b}.&(1)\: \: \textrm{dan}\: \: (3)\\ \textrm{c}.&(1)\: \: \textrm{dan}\: \: (4)\\ \textrm{d}.&(2)\: \: \textrm{dan}\: \: (3)\\ \textrm{e}.&(2)\: \: \textrm{dan}\: \: (4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\begin{aligned}(1)\quad&\displaystyle \sum_{i=1}^{5}(5i+2)=4\displaystyle \sum_{i=1}^{5}i+\sum_{i=1}^{5}2\\ &=4\displaystyle \sum_{i=1}^{5}i+5\times 2\\ &=4\displaystyle \sum_{i=1}^{5}i+10\\ (2)\quad&\displaystyle \sum_{i=1}^{5}(5i^{2}-i)=5\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}i\\ (3)\quad&\displaystyle \sum_{i=1}^{5}(3i-4)=3\displaystyle \sum_{i=1}^{5}i^{2}-\sum_{i=1}^{5}4\\ &=3\displaystyle \sum_{i=1}^{5}i^{2}-5\times 4\\ &=3\displaystyle \sum_{i=1}^{5}i^{2}-20\\ (4)\quad&\displaystyle \sum_{i=1}^{5}(i+7i^{2})=\color{red}\displaystyle \sum_{i=1}^{5}i+7\sum_{i=1}^{5}i \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 12.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=1}^{4}i^{2}+\sum_{i=5}^{6}i^{2}\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 86\\ \color{red}\textrm{b}.&\displaystyle 91\\ \textrm{c}.&\displaystyle 95\\ \textrm{d}.&\displaystyle 101\\ \textrm{e}.&\displaystyle 105 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\begin{aligned}\displaystyle \sum_{i=1}^{4}i^{2}+\sum_{i=5}^{6}i^{2}&=\displaystyle \sum_{i=1}^{6}i^{2}\\ &=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+6^{2}\\ &=1+4+9+16+25+36\\ &=\color{red}91 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=2}^{5}\left ( 4i^{2}-2i \right )\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 144\\ \textrm{b}.&\displaystyle 148\\ \textrm{c}.&\displaystyle 154\\ \textrm{d}.&\displaystyle 164\\ \color{red}\textrm{e}.&\displaystyle 188 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\begin{aligned}&\displaystyle \sum_{i=2}^{5}\left ( 4i^{2}-2i \right )\\ &=\left ( 4.2^{2}-2.2 \right )+\left ( 4.3^{2}-2.3 \right )+\left ( 4.4^{2}-2.4 \right )+\left ( 4.5^{2}-2.5 \right )\\ &=12+30+56+90\\ &=\color{red}188 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 14.&\textrm{Bentuk}\: \: 11^{n}-1\: \: \textrm{dengan}\: \: n\: \: \textrm{bilangan asli}\\ &\textrm{akan habis dibagi oleh}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle 7\\ \textrm{b}.&\displaystyle 9\\ \color{red}\textrm{c}.&\displaystyle 10\\ \textrm{d}.&\displaystyle 11\\ \textrm{e}.&\displaystyle 13 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}\textrm{Bentuk}&\: \: 11^{n}-1\\ \textrm{untuk}&\: \: n=1\\ &=11^{1}-1\\ &=\color{red}10 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 15.&\textrm{Rumus yang tepat untuk pola}\: \: 12,13,14,15,...\\ &\textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle U_{n}=n+9\\ \textrm{b}.&\displaystyle U_{n}=n+10\\ \color{red}\textrm{c}.&\displaystyle U_{n}=n+11\\ \textrm{d}.&\displaystyle U_{n}=2n+10\\ \textrm{e}.&\displaystyle U_{n}=2n+11 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}\textrm{Bentuk}&\: \: 12,13,14,15,...\\ \textrm{untuk}&\: \: U_{n}=pn+q\\ 12&=p+q\\ 13&=2p+q\\ \textrm{akan}&\: \textrm{didapatkan}\\ &\begin{cases} p & =1 \\ q & =11 \end{cases}\\ \textrm{Sehing}&\textrm{ga}\\ U_{n}&=\color{red}n+11 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 16.&\textrm{Diketahui}\: \: 1+5+9+...+(4n-1)=2n^{2}-n\\ &\textrm{dengan}\: \: n\: \: \textrm{bilangan asli}.\: \textrm{Jika}\: \: m<k\: \: \textrm{dengan}\\ &m,k\: \: \textrm{bilangan asli juga},\: \textrm{maka}\\ &(4m-3)+(4m+1)+...+(4k-3)=....\\ &\begin{array}{llll}\\ \textrm{a}.&(k-m)(2k+2m-2)\\ \color{red}\textrm{b}.&(k-m+1)(2k+2m-3)\\ \textrm{c}.&(k-m+1)(2k-2m+1)\\ \textrm{d}.&(k-m+1)(2k^{2}+2m^{2}-3)\\ \textrm{e}.&(k-m)^{2}(2k-2m+4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\begin{aligned}&1+5+9+...+(4m-3)+(4m+1)+...+(4k-3)\\ &=\underset{2k^{2}-k}{\underbrace{1+5+...+(4k-3)}}-\underset{2(m-1)^{2}-(m-1)}{\underbrace{1+5+...+(4(m-1)-3)}}\\ &=2k^{2}-k-\left ( 2(m-1)^{2}-(m-1) \right )\\ &=2k^{2}-k-2(m-1)^{2}+(m-1)\\ &=2k^{2}-k-2\left ( m^{2}-2m+1 \right )+m-1\\ &=2k^{2}-k-2m^{2}+4m-2+m-1\\ &=2k^{2}-k-2m^{2}+5m-3\\ &=\color{red}(k-m+1)(2k+2m-3) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 17.&\textrm{Diketahui}\: \: 2^{1}+2^{2}+2^{3}+...+2^{n}=2^{n+1}-2\\ &\textrm{dengan}\: \: n\: \: \textrm{bilangan asli}.\: \textrm{Jika}\: \: k\: \: \textrm{bilangan asli},\\ &\textrm{maka}\: \: 2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}=....\\ &\begin{array}{llll}\\ \textrm{a}.&(k-m)(2k+2m-2)\\ \textrm{b}.&(k-m+1)(2k+2m-3)\\ \textrm{c}.&(k-m+1)(2k-2m+1)\\ \color{red}\textrm{d}.&(k-m+1)(2k^{2}+2m^{2}-3)\\ \textrm{e}.&(k-m)^{2}(2k-2m+4) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}&2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}\\ &=2^{1}+2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}-2^{1}\\ &=\underset{2^{k+1+1}-2}{\underbrace{2^{1}+2^{2}+2^{3}+2^{4}+...+2^{k}+2^{k+1}}}-2^{1}\\ &=2^{k+2}-2-2\\ &=2^{k+2}-4\\ &=2^{k}.2^{2}-4\\ &=2^{k}\times 4-4\\ &=4\left ( 2^{k}-1 \right ) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 18.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &2+5+10+17+...+\left ( n^{2}+1 \right )=\displaystyle \frac{1}{6}(n+1)\left ( 2n^{2}+n+6 \right )\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k,\: \: \textrm{maka}....\\ &\begin{array}{llll}\\ \color{red}\textrm{a}.&2+5+10+17+...+\left ( k^{2}+1 \right )\\ &=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{b}.&2+5+10+17+...+\left ( n^{2}+1 \right )\\ &=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{c}.&2+5+10+17+...+\left ( k^{2}+2 \right )\\ &=\displaystyle \frac{1}{6}(k+2)\left ( 2k^{2}+5k+9 \right )\\ \textrm{d}.&\left ( k^{2}+1 \right )=\displaystyle \frac{1}{6}(k+1)\left ( 2k^{2}+k+6 \right )\\ \textrm{e}.&\left ( n^{2}+2 \right )=\displaystyle \frac{1}{6}(n+1)\left ( 2n^{2}+5n+9 \right ) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{a}\\ &\begin{aligned}&\textrm{Cukup jelas}\\ &\textrm{Tinggal mensubstitusikan dari}\\ &\textrm{tiap}\: \: \color{red}n\: \: \color{black}\textrm{diganti}\: \: \color{red}k \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 19.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &12+17+22+...+\left ( 5n+7 \right )=\displaystyle \frac{1}{2}(n+1)(5n+14)\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k,\: \: \textrm{maka benar}\\ &\textrm{untuk}\: \: n=k+1.\: \textrm{Pernyataan ini dapat}\\ &\textrm{dinyatakan dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+14)\\ \textrm{b}.&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+19)\\ \textrm{c}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+1)(5k+19)\\ \textrm{d}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+2)(5k+14)\\ \color{red}\textrm{e}.&12+17+22+...+\left ( 5k+12 \right )=\displaystyle \frac{1}{2}(k+2)(5k+19) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\begin{aligned}&12+17+22+...+\left ( 5k+7 \right )=\displaystyle \frac{1}{2}(k+1)(5k+14)\\ &12+17+22+...+\left ( 5(k+1)+7 \right )\\ &\qquad\qquad\qquad\quad=\displaystyle \frac{1}{2}((k+1)+1)(5(k+1)+14)\\ &12+17+22+...+\left ( 5k+12 \right )=\color{red}\displaystyle \frac{1}{2}(k+2)(5k+19) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 20.&\textrm{Diketahui bahwa}\: \: S(n)\: \: \textrm{adalah formula dari}\\ &4+5+6+7+...+(n+3)<5n^{2}\\ &\textrm{Jika}\: \: S(n)\: \: \textrm{benar, untuk}\: \: n=k+1,\: \: \textrm{maka}\\ &\textrm{pernyataan ini dapat ditulis dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&4+5+6+...+(k+4)<5k^{2}\\ \textrm{b}.&4+5+6+...+(k+3)<5k^{2}\\ \textrm{c}.&4+5+6+...+(k+3)<5(k+1)^{2}\\ \color{red}\textrm{d}.&4+5+6+...+(k+4)<5(k^{2}+2k+1)\\ \textrm{e}.&4+5+6+...+(k+4)<5(k+1)(k-1) \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}&4+5+6+...+(n+3)<5n^{2}\\ &\textrm{Saat}\: \: n=k+1,\: \: \textrm{maka}\\ &4+5+6+...+((k+1)+3)<5(k+1)^{2}\\ &=4+5+6+...+(k+4)<\color{red}5\left ( k^{2}+2k+1 \right ) \end{aligned} \end{array}$.

Latihan Soal 1 Persiapan PAS Gasal Matematika Wajib Kelas XI

 $\begin{array}{ll}\\ 1.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=1}^{6}16i\: \: \textrm{adalah}....\\ &\begin{array}{llll}\\ \textrm{a}.&306\\ \textrm{b}.&314\\ \textrm{c}.&326\\ \color{red}\textrm{d}.&336\\ \textrm{e}.&402 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}\displaystyle \sum_{i=1}^{6}16i&=16.1+16.2+16.3+16.4+16.5+16.6\\ &=16+32+48+64+80+96\\ &=\color{red}336 \end{aligned}\end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Hasil dari}\: \: \displaystyle \sum_{i=2}^{9}i^{2}\: \: \textrm{adalah}....\\ &\begin{array}{llll}\\ \textrm{a}.&274\\ \textrm{b}.&278\\ \textrm{c}.&280\\ \color{red}\textrm{d}.&284\\ \textrm{e}.&286 \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}\displaystyle \sum_{i=2}^{9}i^{2}&=2^{2}+3^{2}+4^{2}+5^{2}+..+9^{2}\\ &=4+9+16+25+...+81\\ &=\color{red}284 \end{aligned}\end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Poa bilangan}\: \: 12,14,16,18,20,...,(2n+10).\\ &\textrm{Nilai suku ke-100 adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.&180\\ \textrm{b}.&194\\ \textrm{c}.&198\\ \textrm{d}.&208\\ \color{red}\textrm{e}.&210\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{e}\\ &\begin{aligned}U_{n}&=2n+10\\ U_{100}&=2\times 100+10\\ &=210 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui bahwa jika}\\ & 31+39+47+\cdots +8n+23=4n^{2}+27n\\ & \textrm{dengan}\: \: k,n\in \mathbb{N}\: \: \textrm{maka}\\ & 31+39+47+\cdots +8n+23+8k+31=....\\ &\begin{array}{lllllll}\\ \textrm{a}.&4k^{2}+27k\\ \textrm{b}.&4k^{2}+35k\\ \color{red}\textrm{c}.&4k^{2}+35k+31\\ \textrm{d}.&4k^{2}+35k+1\\ \textrm{e}.&4k^{2}+35k+54\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}&\underset{4k^{2}+27k}{\underbrace{31+39+47+\cdots +8k+23}}+8k+31\\ &=4k^{2}+27k+8k+31\\ &=\color{red}4k^{2}+35k+31 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 5.&\textrm{Dengan Induksi Matematika untuk}\: \: n\in \mathbb{N}\\ &\textrm{dapat dibuktikan bahwa}\: \: n(n+1)(n+2)\\ &\textrm{akan habis dibagi oleh}\\ &\begin{array}{lllllll}\\ \textrm{a}.&4\\ \textrm{b}.&5\\ \color{red}\textrm{c}.&6\\ \textrm{d}.&7\\ \textrm{e}.&8\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}P(n)&=n(n+1)(n+2)\\ P(1)&=1(1+1)(1+2)=\color{red}1.2.3\\ &\color{purple}\textrm{adalah bilangan yang habis dibagi 6} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 6.&\textrm{Dengan Induksi Matematika untuk}\: \: n\in \mathbb{N}\\ &\textrm{dapat dibuktikan juga bahwa}\: \: 7^{n}-2^{n}\\ &\textrm{akan habis dibagi oleh}\\ &\begin{array}{lllllll}\\ \textrm{a}.&2\\ \textrm{b}.&3\\ \textrm{c}.&4\\ \color{red}\textrm{d}.&5\\ \textrm{e}.&6\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}P(n)&=7^{n}-2^{n}\\ P(1)&=7^{1}-2^{1}\\ &=7-2=\color{red}5\\ &\textrm{adalah bilangan yang habis dibagi 5} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 7.&\textrm{Diketahui bahwa}\: \: P(n)\: \: \textrm{rumus dari}\\ & 3+6+9+\cdots +3n=\displaystyle \frac{3}{2}n(n+1)\\ &\textrm{maka langkah pertama dengan induksi matematika}\\ &\textrm{dalam pembuktian rumus tersebut adalah}....\\ &\begin{array}{lll}\\ \textrm{a}.&P(n)\: \: \textrm{benar untuk}\: \: n=-1\\ \color{red}\textrm{b}.&P(n)\: \: \textrm{benar untuk}\: \: n=1\\ \textrm{c}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan bulat}\\ \textrm{d}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan rasional}\\ \textrm{d}.&P(n)\: \: \textrm{benar untuk}\: \: n\: \: \textrm{bilangan real} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\begin{aligned}\textrm{Langkah}&\: \textrm{awal yang harus ditunjukkan adalah}\\ n=1&\: \: \textrm{atau}\: \: P(1)\: \: \textrm{harus benar, yaitu}:\\ P(1)&=3.1(\textit{ruas kiri})=\displaystyle \frac{3}{2}.1.(1+1)(\textit{ruas kanan})=\color{red}3 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 8.&\textrm{Bila kita hendak membuktikan}\: \: \displaystyle \sum_{i=1}^{n}=\displaystyle \frac{1}{2}n(n+1)\\ &\textrm{dengan induksi matematika}\\ &\textrm{maka untuk langkah}\: \: n=k+1\\ &\textrm{bentuk yang harus ditunjukkan adalah}...\\ &\begin{array}{lll}\\ \textrm{a}.&1+2+3+\cdots +n=\displaystyle \frac{1}{2}n(n+1)\\ \textrm{b}.&1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+1)\\ \textrm{c}.&1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+2)\\ \color{red}\textrm{d}.&1+2+3+\cdots +k+(k+1)=\displaystyle \frac{1}{2}(k+1)(k+2)\\ \textrm{e}.&1+2+3+\cdots +k+(k+1)=\displaystyle \frac{1}{2}(k+2)(k+3)\\ \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{d}\\ &\begin{aligned}P(n)&=1+2+3+\cdots +n=\displaystyle \frac{1}{2}n(n+1)\\ P(k)&=1+2+3+\cdots +k=\displaystyle \frac{1}{2}k(k+1)\\ P(k+1)&=1+2+3+\cdots +k+(k+1)\\ &=\underset{\displaystyle \frac{1}{2}k(k+1)}{\underbrace{1+2+3+\cdots +k}}+(k+1)\\ &=\displaystyle \frac{1}{2}k(k+1)+(k+1)=(k+1)\left ( \displaystyle \frac{1}{2}k+1 \right )\\ &=(k+1)\displaystyle \frac{1}{2}(k+2)\\ &=\color{red}\displaystyle \frac{1}{2}(k+1)(k+2) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 9.&\textrm{Jika}\: \: P(n)=\displaystyle \frac{n-1}{n+3},\: \textrm{maka}\: \: P(k+1)\\ & \textrm{dinyatakan dengan}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle \frac{k-1}{k+3}\\ \textrm{b}.&\displaystyle \frac{k-1}{k+4}\\ \color{red}\textrm{c}.&\displaystyle \frac{k}{k+4}\\ \textrm{d}.&\displaystyle \frac{k+1}{k+4}\\ \textrm{e}.&\displaystyle \frac{k+1}{k+5} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{c}\\ &\begin{aligned}P(n)=&\displaystyle \frac{n-1}{n+3}\\ P(k+1)&=\displaystyle \frac{k+1-1}{k+1+3}\\ &=\color{red}\displaystyle \frac{k}{k+4} \end{aligned}\end{array}$.

$\begin{array}{ll}\\ 10.&\textrm{Jika}\: \: P(n)=\displaystyle \frac{n^{2}+1}{4},\: \: \textrm{maka}\\ &\textrm{pernyataan untuk}\: \: P(k+1)\: \: \textrm{adalah}\: ....\\ &\begin{array}{llll}\\ \textrm{a}.&\displaystyle \frac{k^{2}+2k+1}{4}\\ \color{red}\textrm{b}.&\displaystyle \frac{k^{2}+2k+2}{4}\\ \textrm{c}.&\displaystyle \frac{k^{2}+2k+2}{5}\\ \textrm{d}.&\displaystyle \frac{k^{2}+2k+3}{5}\\ \textrm{e}.&\displaystyle \frac{k^{2}+2k+3}{4} \end{array}\\\\ &\textrm{Jawab}:\quad \color{red}\textbf{b}\\ &\begin{aligned}P(n)&=\displaystyle \frac{n^{2}+1}{4}\\ P(k+1)&=\displaystyle \frac{(k+1)^{2}+1}{4}\\ &=\color{red}\displaystyle \frac{k^{2}+2k+2}{4} \end{aligned} \end{array}$

Latihan Soal 11 Persiapan PAS Gasal Matematika Peminatan Kelas XI (Persamaan dan Rumus Jumlah dan Selisih Trigonometri)

$\begin{array}{ll}\\ 101.&\textrm{Nilai dari} \: \sin 1020^{\circ}=....\\ &\textrm{a}.\quad -1\\ &\textrm{b}.\quad \color{red}\displaystyle -\frac{1}{2}\sqrt{3}\\ &\textrm{c}.\quad \displaystyle -\frac{1}{2}\\ &\textrm{d}.\quad \displaystyle \frac{1}{2}\\ &\textrm{e}.\quad \displaystyle \frac{1}{2}\sqrt{3}\\\\ &\textrm{Jawab}:\qquad\color{red}\textbf{b}\\ &\begin{aligned}\sin 1020^{\circ}&=\sin \left ( 3\times 360^{\circ}-60^{\circ} \right )\\ &=\sin \left ( 0^{\circ}-60^{\circ} \right )\\ &=\sin \left ( -60^{\circ} \right )\\ &=-\sin 60^{\circ}\\ &=\color{red}-\displaystyle \frac{1}{2}\sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 102.&\textrm{Nilai dari} \: \cot (-1290)^{\circ}=....\\ &\textrm{a}.\quad \color{red}-\sqrt{3}\\ &\textrm{b}.\quad \displaystyle -\frac{1}{3}\sqrt{3}\\ &\textrm{c}.\quad \displaystyle \frac{1}{3}\sqrt{3}\\ &\textrm{d}.\quad \displaystyle -\frac{1}{2}\\ &\textrm{e}.\quad \displaystyle \frac{1}{2}\\ &\textrm{Jawab}:\qquad\color{red}\textrm{a}\\ &\begin{aligned}\cot (-1290)^{\circ}&=-\cot \left ( 3\times 360^{\circ}+210^{\circ} \right )\\ &=-\cot \left ( 0^{\circ}+210^{\circ} \right )\\ &=-\cot \left ( 210^{\circ} \right )\\ &=-\frac{1}{\tan 210^{\circ}}\\ &=-\frac{1}{\tan \left ( 180^{\circ}+30^{\circ} \right )}\\ &=-\frac{1}{\tan 30^{\circ}}\\ &=\color{red}-\displaystyle \sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 103.&\textrm{Nilai dari}\\ & \sin 240^{\circ}+\sin 225^{\circ}+\cos 315^{\circ}=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad -\sqrt{3}\qquad&&\textrm{d}.\quad \displaystyle \frac{1}{2}\sqrt{3}\\ \textrm{b}.\quad \color{red}\displaystyle -\frac{1}{2}\sqrt{3}&\qquad&\textrm{e}.\quad \displaystyle \frac{1}{3}\sqrt{3}\\ \textrm{c}.\quad \displaystyle -\frac{1}{2} \end{array}\\ &\textrm{Jawab}:\qquad\color{red}\textrm{b}\\ &\begin{aligned}&\sin 240^{\circ}+\sin 225^{\circ}+\cos 315^{\circ}\\ &=\sin \left ( 180^{\circ}+60^{\circ} \right )+\sin \left ( 180^{\circ}+45^{\circ} \right )+\cos \left ( 360^{\circ}-45^{\circ} \right )\\ &=-\sin 60^{\circ}+\left [ -\sin 45^{\circ} \right ]+\cos 45^{\circ}\\ &=\left ( -\frac{1}{2}\sqrt{3} \right )+\left ( -\frac{1}{2}\sqrt{2} \right )+\frac{1}{2}\sqrt{2}\\ &=\color{red}-\frac{1}{2}\sqrt{3} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 104.&\textrm{Nilai dari} \\ & \displaystyle \frac{\sin 30^{\circ}+\sin 150^{\circ}+\cos 330^{\circ}}{\tan 45^{\circ}+\cos 210^{\circ}}=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle \frac{1+\sqrt{3}}{1-\sqrt{3}}\\ \textrm{b}.\quad \displaystyle \frac{1-\sqrt{3}}{1+\sqrt{3}}\\ \textrm{c}.\quad \displaystyle \frac{2-\sqrt{3}}{2+\sqrt{3}}\\ \textrm{d}.\quad \color{red}\displaystyle \frac{2+\sqrt{3}}{2-\sqrt{3}}\\ \textrm{e}.\quad \displaystyle \frac{1+2\sqrt{3}}{1-2\sqrt{3}} \end{array}\\ &\textrm{Jawab}:\qquad\color{red}\textrm{d}\\ &\begin{aligned}&\displaystyle \frac{\sin 30^{\circ}+\sin 150^{\circ}+\cos 330^{\circ}}{\tan 45^{\circ}+\cos 210^{\circ}}\\ &=\displaystyle \frac{\sin 30^{\circ}+\sin \left ( 180^{\circ}-30^{\circ} \right )+\cos \left ( 360^{\circ}-30^{\circ} \right )}{\tan 45^{\circ}+\cos \left ( 180^{\circ}+30^{\circ} \right )}\\ &=\displaystyle \frac{\sin 30^{\circ}+\sin 30^{\circ}+\cos 30^{\circ}}{\tan 45^{\circ}-\cos 30^{\circ}}\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}+\frac{1}{2}+\frac{1}{2}\sqrt{3}}{1-\displaystyle \frac{1}{2}\sqrt{3}}\\ &=\displaystyle \frac{1+\displaystyle \frac{1}{2}\sqrt{3}}{1-\displaystyle \frac{1}{2}\sqrt{3}}\\ &=\color{red}\displaystyle \frac{2+\sqrt{3}}{2-\sqrt{3}} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 105.&\textrm{Nilai dari} \\ &\displaystyle \frac{\sin 270^{\circ}\times \cos 135^{\circ}\times \tan 135^{\circ}}{\sin 150^{\circ}\times \cos 225^{\circ}}=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad -2\qquad&&\textrm{d}.\quad 1\\ \textrm{b}.\quad \displaystyle -\frac{1}{2}&\textrm{c}.\quad \displaystyle \frac{1}{2}\qquad&\textrm{e}.\quad 2 \end{array}\\ &\textrm{Jawab}:\qquad\color{red}\textrm{e}\\ &\begin{aligned}&\displaystyle \frac{\sin 270^{\circ}\times \cos 135^{\circ}\times \tan 135^{\circ}}{\sin 150^{\circ}\times \cos 225^{\circ}}\\ &=\displaystyle \frac{\sin 270^{\circ}\times \cos \left ( 180^{\circ}-45^{\circ} \right )\times \tan \left ( 180^{\circ}-45^{\circ} \right )}{\sin \left ( 180^{\circ}-30^{\circ} \right )\times \cos \left ( 180^{\circ}+45^{\circ} \right )}\\ &=\displaystyle \frac{-1\times \left (-\cos 45^{\circ} \right )\times \left ( - \tan 45^{\circ}\right )}{\sin 30^{\circ}\times \left ( -\cos 45^{\circ} \right )}\\ &=\displaystyle \frac{-1\times \left ( -\displaystyle \frac{1}{2}\sqrt{2} \right )\times -1}{\displaystyle \frac{1}{2}\times \left ( -\frac{1}{2}\sqrt{2} \right )}\\ &=\displaystyle \frac{-\frac{1}{2}\sqrt{2}}{-\frac{1}{4}\sqrt{2}}\\ &=\color{red}\displaystyle 2\end{aligned} \end{array}$

$\begin{array}{ll}\\ 106.&\textrm{Perhatikanlah gambar kurva berikut ini}\end{array}$.

$\begin{array}{ll}\\ .\, \: \: \quad&\begin{array}{llllll}\\ \textrm{a}.&y=-2\cos 2x\\ \textrm{b}.&y=2\cos \displaystyle \frac{3}{2}x\\ \textrm{c}.&y=-2\cos \displaystyle \frac{3}{2}x\\ \textrm{d}.&y=2\sin \displaystyle \frac{3}{2}x\\ \textrm{e}.&y=-2\sin \displaystyle \frac{3}{2}x\\\\ &(\textbf{SIMAK UI 2009 Mat Das}) \end{array}\\ &\\ &\textrm{Jawab}:\quad\color{red}\textbf{c}\\ &\begin{aligned}&\textrm{Dari gambar tampak jelas bahwa}\\ &\textrm{grafik di atas atas adalah grafik}\: \textbf{fungsi cosinus}\\ &\textrm{dengan amplitudo 2 dan periodenya}\: :\: \displaystyle \frac{3}{2}\pi \\ &\textrm{Maka persamaan grafiknya adalah}:\\ &y=2\cos \displaystyle \frac{3}{2}\pi \\ &\textrm{Karena posisinya terbalik, maka}\\ &y=\color{red}-2\cos \displaystyle \frac{3}{2}\pi \\ \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 107.&\textrm{Nilai minimum jika}\\ & f(x)=\left ( 2004\cos 2005x-2006 \right )^{2}+2007\\ & \textrm{adalah}=....\\ &\begin{array}{llllll}\\ \textrm{a}.&2005\\ \textrm{b}.&2007\\ \textrm{c}.&\color{red}2011\\ \textrm{d}.&2013\\ \textrm{e}.&\textrm{tidak ada satupun jawaban dari a sampai d}\\\\ &(\textbf{NUS Mathematics A Level}) \end{array}\\ &\\ &\textrm{Jawab}:\quad\color{red}\textbf{c}\\ &\begin{aligned}&f(x)=\left ( 2004\cos 2005x-2006 \right )^{2}+2007\\ &\textrm{Supaya bernilai minimum, }\\ &\textrm{maka nilai}\quad \color{red}\cos 500x=1,\\ & \color{black}\textrm{ingat nilai}\: \: -1\leq \cos n\pi \leq 1\\ &\textrm{maka},\\ &f_{min}=\left ( 2004.1-2006 \right )^{2}+2007\\ &=(-2)^{2}+2007\\ &=4+2007\\ &=\color{red}2011 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 108.&\textrm{Penyelesaian persamaan}\\ & \cos ^{2}x-2\cos x=4\sin x-2\sin x\cos x\\ & \textrm{adalah}\, ....\\ &\begin{array}{llllll}\\ \textrm{a}.&\pi -\cot ^{-1}\left ( \displaystyle \frac{1}{2} \right )\\ \textrm{b}.&\pi +\tan ^{-1}\left ( \displaystyle \frac{1}{2} \right )\\ \textrm{c}.&\pi -\cot ^{-1}\left ( -1 \right )\\ \textrm{d}.&\color{red}\pi +\tan ^{-1}\left ( -\displaystyle \frac{1}{2} \right )\\ \textrm{e}.&\pi -\tan ^{-1}\left ( \displaystyle \frac{1}{4} \right ) \\ \end{array}\\ &\\ &\textrm{Jawab}:\quad\color{red}\textbf{d}\\ &\begin{aligned}&\textrm{Perhatikan bahwa},\\ &\cos ^{2}x-2\cos x=4\sin x-2\sin x\cos x\\ &\cos x\left ( \cos x-2 \right )=2\sin x\left ( 2-\cos x \right )\\ &\cos x\left ( \cos x-2 \right )=-2\sin x\left ( \cos x -2\right )\\ &\left (\cos x+2\sin x \right )\left ( \cos x-2 \right )=0\\ &\left (\cos x+2\sin x \right )=0\: \: \textrm{atau} \: \: \left ( \cos x-2 \right )=0\\ &2\sin x=-\cos x\: \: \textbf{(mm)}\: \: \textrm{atau}\: \: \cos x=2\: \: \textbf{(tm)}\\ &\textrm{maka}\\ &\displaystyle \frac{\sin x}{\cos x}=-\displaystyle \frac{1}{2}\: \: \Leftrightarrow \: \: \tan x=-\displaystyle \frac{1}{2}\\ &x=\color{red}\tan ^{-1}\left ( -\displaystyle \frac{1}{2} \right )+k.\pi ,\quad k\in \mathbb{Z} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 109.&\textrm{Jika diketahui bahwa}\\ & \sin \beta -\tan \beta -2\cos \beta +2=0\\ & \textrm{dengan}\: \: 0<\beta <\displaystyle \frac{\pi }{2},\\ &\textrm{maka himpunan harga}\: \: \sin \beta =....\\ &\begin{array}{llllll}\\ \textrm{a}.&\color{red}\left \{ \displaystyle \frac{2}{5}\sqrt{5} \right \}\\ \textrm{b}.&\left \{ 0 \right \}\\ \textrm{c}.&\left \{ \displaystyle \frac{2}{5}\sqrt{5},0 \right \}\\ \textrm{d}.&\left \{ \displaystyle \frac{1}{5}\sqrt{5} \right \}\\ \textrm{e}.&\left \{ \displaystyle \frac{1}{5}\sqrt{5},0 \right \}\\\\ &\textbf{(SIMAK UI 2009)} \end{array}\\ &\\ &\textrm{Jawab}:\quad\color{red}\textbf{a}\\ &\begin{aligned}&\sin \beta -\tan \beta -2\cos \beta +2=0\\ &\sin \beta -\displaystyle \frac{\sin \beta }{\cos \beta } -2\cos \beta +2=0\\ &\sin \beta \cos \beta -\sin \beta -2\cos^{2} \beta +2\cos \beta =0\\ &\sin \beta \left ( \cos \beta -1 \right )-2\cos \beta \left ( \cos \beta -1 \right )=0\\ &\left ( \sin \beta -2\cos \beta \right )\left ( \cos \beta -1 \right )=0\\ &\left ( \sin \beta -2\cos \beta \right )=0\: \textbf{(mm)}\\ &\qquad \textrm{atau}\quad \left ( \cos \beta -1 \right )=0\: \textbf{(tmm)}\\ &\textrm{maka},\\ &\left ( \sin \beta -2\cos \beta \right )=0\\ &\sin \beta =2\cos \beta\\ &\displaystyle \frac{\sin \beta }{\cos \beta }=2\\ &\tan \beta =2=\displaystyle \frac{2}{1},\qquad \textrm{buatlah ilustrasi} \\ &\textrm{dengan membuat segitiga siku-siku}.\\ &\textrm{Sehingga akan didapatkan nilai}\\ &\sin \beta =\color{red}\displaystyle \frac{2}{5}\sqrt{5} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 110.&\textrm{Diketahui bahwa}\\ &\sin \theta -\cos \theta =\displaystyle \frac{\sqrt{5}-\sqrt{3}}{2}\: \: \textrm{dan}\\ & \cos ^{3}\theta -\sin ^{3}\theta =\displaystyle \frac{1}{a}\left ( b\sqrt{5}-c\sqrt{3} \right ),\\ &\textrm{dengan}\: \: a,\: b,\: c\: \: \textrm{adalah bilangan asli, maka}\\ &(1) \quad b-c>0\\ &(2) \quad a-b=7\\ &(3)\quad a-3b+c=0\\ &(4)\quad a+b+c=12\\ &\begin{array}{llllll}\\ \textrm{a}.&(1),\: (2).\: \textrm{dan}\: (3)\: \textrm{benar}\\ \textrm{b}.&(1),\: \textrm{dan}\: (3)\: \textrm{benar}\\ \textrm{c}.&\color{red}(2),\: \textrm{dan}\: (4)\: \textrm{benar}\\ \textrm{d}.&\textrm{hanya}\: (4)\: \textrm{yang benar}\\ \textrm{e}.&\textrm{semuanya benar}\\\\ &(\textbf{SIMAK UI 2015 Mat IPA}) \end{array}\\ &\\ &\textrm{Jawab}:\quad\color{red}\textbf{c}\\ &\begin{aligned}&\sin \theta -\cos \theta =\displaystyle \frac{\sqrt{5}-\sqrt{3}}{2}\\ &\sin ^{2}\theta +\cos^{2}\theta -2\sin \theta \cos \theta =\displaystyle \frac{8-2\sqrt{5}}{4}\\ &1-2\sin \theta \cos \theta =\displaystyle \frac{8-2\sqrt{5}}{4}\\ &\sin \theta \cos \theta =\displaystyle \frac{\sqrt{5}-2}{4}\\ &\textrm{maka},\\ &\cos ^{3}\theta -\sin ^{3}\theta \\ &\qquad=\left ( \cos \theta -\sin \theta \right )\left ( \cos ^{2}\theta +\sin \theta \cos \theta +\sin ^{2}\theta \right )\\ &=\left ( \displaystyle \frac{\sqrt{3}-\sqrt{5}}{2} \right )\left ( 1+\displaystyle \frac{\sqrt{5}-2}{4} \right )\\ &=\displaystyle \frac{1}{8}\left ( \sqrt{3}-\sqrt{5} \right )\left ( 2+\sqrt{5} \right )\\ &=\displaystyle \frac{1}{8}\left ( 2\sqrt{3}+3\sqrt{5}-2\sqrt{5}-5\sqrt{3} \right )\\ &=\displaystyle \frac{1}{8}\left (\sqrt{5}-3\sqrt{3} \right )=\displaystyle \frac{1}{a}\left ( b\sqrt{5}-c\sqrt{3} \right ) \left\{\begin{matrix} a=8\\ b=1\\ c=3 \end{matrix}\right.\\ &\textrm{sehingga}\\ &a-b=8-1=\color{red}7\\ &a+b+c=8+1+3=\color{red}12 \end{aligned} \end{array}$

Latihan Soal 10 Persiapan PAS Gasal Matematika Peminatan Kelas XI (Persamaan dan Rumus Jumlah dan Selisih Trigonometri)

$\begin{array}{ll}\\ 91.&\textrm{Bentuk sederhana dari}\\ &\quad\quad 4\sin \left ( \displaystyle \frac{1}{4}\pi +x \right )\cos \left ( \displaystyle \frac{1}{4}\pi -x \right )\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \color{red}2+2\sin 2x &&&\textrm{d}.&2+2\sin x\\ \textrm{b}.&\displaystyle 2+\sin 2x&&&\textrm{e}.&2+\sin x\\ \textrm{c}.&\displaystyle 2\sin 2x \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&4\sin \left ( \displaystyle \frac{1}{4}\pi +x \right )\cos \left ( \displaystyle \frac{1}{4}\pi -x \right )\\ &=2\left ( \sin \left ( \displaystyle \frac{1}{2}\pi \right )+\sin (2x) \right )\\ &=2\left (1+\sin 2x \right )\\ &=2+2\sin 2x \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 92.&\textrm{Bentuk sederhana dari}\\ & 2\sin \left ( \displaystyle \frac{3}{4}\pi +x \right ).\cos \left ( \displaystyle \frac{\pi }{4}+x \right )=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}1-\sin 2x&&\textrm{d}.\quad \cos 2x\\\\ \textrm{b}.\quad 1+\sin 2x&\textrm{c}.\quad 1-\cos 2x&\textrm{e}.\quad -\cos 2x\end{array}\\\\ &\textbf{Jawab}:\: \: \color{red}\textbf{a}\\ &\begin{aligned}&2\sin \left ( \displaystyle \frac{3}{4}\pi +x \right ).\cos \left ( \displaystyle \frac{\pi }{4}+x \right )\\ &=2\sin \left ( 135^{\circ}+x \right ).\cos \left ( 45^{\circ}+x \right )\\ &=2\sin \left ( 90^{\circ}+45^{\circ}+x \right ).\cos \left ( 45^{\circ}+x \right )\\ &=2\cos \left ( 45^{\circ}+x \right ).\cos \left ( 45^{\circ}+x \right )\\ &=2\cos ^{2}\left ( 45^{\circ}+x \right )\\ &=2\left ( \cos 45^{\circ}\cos x-\sin 45^{\circ}\sin x \right )^{2}\\ &=2\left ( \frac{1}{2}\sqrt{2}.\cos x-\displaystyle \frac{1}{2}\sqrt{2}.\sin x \right )^{2}\\ &=\displaystyle \left ( \cos x-\sin x \right )^{2}\\ &=\cos ^{2}x+\sin ^{2}x-2\sin x\cos x\\ &=\color{red}1-\sin 2x \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 93.&\textrm{Bentuk sederhana dari}\\ & 2\cos \left ( x+\displaystyle \frac{\pi }{4} \right ). \cos \left ( \displaystyle \frac{3}{4}\pi -x \right )=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \cos (2x+\pi )&&\textrm{d}.\quad -\cos \left ( 2x-\displaystyle \frac{\pi }{2} \right )\\ \textrm{b}.\quad \cos \left ( 2x+\displaystyle \frac{\pi }{2} \right )&&\textrm{e}.\quad \color{red}\sin 2x-1\\ \textrm{c}.\quad \cos 2x \end{array}\\\\ &\textbf{Jawab}:\: \: \color{red}\textbf{e}\\ &\begin{aligned}&2\cos \left ( x+\displaystyle \frac{\pi }{4} \right ). \cos \left ( \displaystyle \frac{3}{4}\pi -x \right )\\ &=\cos \left ( x+\displaystyle \frac{\pi }{4}+\displaystyle \frac{3}{4}\pi -x \right )+\cos \left (x+\displaystyle \frac{\pi }{4} -\left ( \displaystyle \frac{3}{4}\pi -x \right ) \right )\\ &=\cos \pi +\cos \left ( 2x-\frac{2}{4}\pi \right )\\ &=-1+\cos \left ( \displaystyle \frac{1}{2}\pi -2x \right ),\\ &\quad\quad \color{blue}\textrm{ingat bahwa}\: \cos (-\alpha )=\cos \alpha \\ &=-1+\sin 2x\\ &=\color{red}\sin 2x-1 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 94.&\textrm{Nilai dari}\\ &\quad\quad \sqrt{3}\sin 80^{\circ}\sin 160^{\circ}\sin 320^{\circ}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle -\displaystyle \frac{3}{8} &&&\textrm{d}.&\displaystyle \color{red}\frac{3}{8}\\\\ \textrm{b}.&\displaystyle -\frac{1}{8}&&&\textrm{e}.&\displaystyle \frac{5}{8}\\ \textrm{c}.&\displaystyle \frac{1}{8} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\sqrt{3}\sin 80^{\circ}\sin 160^{\circ}\sin 320^{\circ}\\ &=\sqrt{3}\sin 80^{\circ}\sin 20^{\circ}\left (-\sin 40^{\circ} \right )\\ &=-\sqrt{3}\sin 80^{\circ}\sin 40^{\circ}\sin 20^{\circ}\\ &=-\sqrt{3}\sin 80^{\circ}\left ( -\displaystyle \frac{1}{2}\left ( \cos 60^{\circ}-\cos 20^{\circ} \right ) \right )\\ &=-\sqrt{3}\sin 80^{\circ}\left ( -\displaystyle \frac{1}{4}+\displaystyle \frac{\cos 20^{\circ}}{2} \right )\\ &=\displaystyle \frac{1}{4}\sqrt{3}\sin 80^{\circ}-\displaystyle \frac{1}{2}\sqrt{3}\sin 80^{\circ}\cos 20^{\circ}\\ &=\displaystyle \frac{1}{4}\sqrt{3}\sin 80^{\circ}-\displaystyle \frac{1}{4}\sqrt{3}\left ( \sin 100^{\circ}+\sin 60^{\circ} \right )\\ &=\displaystyle \frac{1}{4}\sqrt{3}\sin 80^{\circ}-\displaystyle \frac{1}{4}\sqrt{3}\left ( \sin 80^{\circ}+\displaystyle \frac{1}{2}\sqrt{3} \right )\\ &=\displaystyle \frac{1}{4}\sqrt{3}\sin 80^{\circ}-\displaystyle \frac{1}{4}\sqrt{3}\sin 80^{\circ}+\displaystyle \frac{1}{8}\sqrt{9}\\ &=\displaystyle \frac{3}{8} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 95.&\textrm{Nilai dari}\\ &\quad\quad \cos \displaystyle \frac{\pi }{7}\cos \frac{2\pi }{7}\cos \frac{4\pi }{7}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \color{red}-\displaystyle \frac{1}{8} &&&\textrm{d}.&\displaystyle \frac{1}{2}\\\\ \textrm{b}.&\displaystyle -\frac{1}{4}&\quad \textrm{c}.&0\quad &\textrm{e}.&\displaystyle \frac{1}{3} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textbf{Alternatif 1}\\ &\begin{aligned}&\cos \displaystyle \frac{\pi }{7}\cos \frac{2\pi }{7}\cos \frac{4\pi }{7}\times \displaystyle \frac{2\sin \displaystyle \frac{2\pi }{7}}{2\sin \displaystyle \frac{2\pi }{7}}\\ &=\left (\sin \displaystyle \frac{4\pi }{7}-\sin 0 \right )\frac{\displaystyle \cos \frac{\pi }{7}\cos \displaystyle \frac{4\pi }{7}}{2\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin \displaystyle \frac{4\pi }{7}\displaystyle \cos \frac{\pi }{7}\cos \displaystyle \frac{4\pi }{7}}{2\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\left ( \sin \displaystyle \frac{5\pi }{7}+\sin \displaystyle \frac{3\pi }{7} \right )\cos \displaystyle \frac{4\pi }{7}}{4\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin \displaystyle \frac{5\pi }{7}\cos \displaystyle \frac{4\pi }{7}+\sin \displaystyle \frac{3\pi }{7}\cos \displaystyle \frac{4\pi }{7}}{4\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin \displaystyle \frac{9\pi }{7}+\sin \displaystyle \frac{\pi }{7}+\sin \displaystyle \frac{7\pi }{7}+\sin \left (-\displaystyle \frac{\pi }{7} \right )}{8\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{-\sin \displaystyle \frac{2\pi }{7}+\sin \displaystyle \frac{\pi }{7}+0-\sin \displaystyle \frac{\pi }{7}}{8\sin \displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{-\sin \displaystyle \frac{2\pi }{7}}{8\sin \displaystyle \frac{2\pi }{7}}\\ &=-\displaystyle \frac{1}{8} \end{aligned}\\ &\textbf{Alternatif 2}\\ &\begin{aligned}&\cos \displaystyle \frac{\pi }{7}\cos \frac{2\pi }{7}\cos \frac{4\pi }{7}\\ &=\cos \displaystyle \frac{4\pi }{7}\cos \frac{2\pi }{7}\cos \frac{\pi }{7}\\ &=\displaystyle \frac{1}{2}\left ( \cos \displaystyle \frac{6\pi }{7}+\cos \displaystyle \frac{2\pi }{7} \right )\cos \displaystyle \frac{\pi }{7}\\ &=\displaystyle \frac{1}{2}\left ( \cos \left ( \pi -\displaystyle \frac{\pi }{7} \right )+\cos \displaystyle \frac{2\pi }{7} \right )\cos \displaystyle \frac{\pi }{7}\\ &=\displaystyle \frac{1}{2}\left ( -\cos \displaystyle \frac{\pi }{7}+\cos \displaystyle \frac{2\pi }{7} \right )\cos \displaystyle \frac{\pi }{7}\\ &= \displaystyle \frac{1}{2}\left (-\cos ^{2}\displaystyle \frac{\pi }{7}+\cos \displaystyle \frac{2\pi }{7}\cos \displaystyle \frac{\pi }{7} \right )\\ &=\displaystyle \frac{1}{4}\left ( -\cos \displaystyle \frac{2\pi }{7}-\cos 0+\cos \displaystyle \frac{3\pi }{7}+\cos \displaystyle \frac{\pi }{7} \right )\\ &=\displaystyle \frac{1}{4}\left ( -\cos 0+\color{red}\cos \displaystyle \frac{\pi }{7}-\cos \displaystyle \frac{2\pi }{7}+\cos \displaystyle \frac{3\pi }{7} \color{black}\right )\\ &=\displaystyle \frac{1}{4}\left ( -1+\color{red}\displaystyle \frac{1}{2}\color{black} \right )\\ &=\displaystyle \frac{1}{4}\times \left (-\frac{1}{2} \right )\\ &=-\displaystyle \frac{1}{8} \end{aligned} \end{array}$.

Berikut penjelasan untuk  $\cos \displaystyle \frac{\pi }{7}-\cos \displaystyle \frac{2\pi }{7}+\cos \displaystyle \frac{3\pi }{7}=\color{red}\displaystyle \frac{1}{2}$.

$\begin{aligned}&\cos \displaystyle \frac{\pi }{7}-\cos \displaystyle \frac{2\pi }{7}+\cos \displaystyle \frac{3\pi }{7}\\ &=\cos \displaystyle \frac{\pi }{7}-\cos \displaystyle \frac{2\pi }{7}+\cos \displaystyle \frac{3\pi }{7}\times \displaystyle \frac{\left (2\sin\displaystyle \frac{2\pi }{7} \right ) }{\left (2\sin\displaystyle \frac{2\pi }{7} \right )}\\ &=\displaystyle \frac{2\cos\displaystyle \frac{\pi }{7}\sin\displaystyle \frac{2\pi }{7}-2\cos\displaystyle \frac{2\pi }{7}\sin\displaystyle \frac{2\pi }{7}+2\cos\displaystyle \frac{3\pi }{7}\sin\displaystyle \frac{2\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\displaystyle \frac{3\pi }{7}-\sin\left (-\displaystyle \frac{\pi }{7} \right )-\left ( \sin\displaystyle \frac{4\pi }{7}-\sin\displaystyle \frac{0\pi }{7} \right )+\sin\displaystyle \frac{5\pi }{7}-\sin\displaystyle \frac{\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\displaystyle \frac{3\pi }{7}+\sin\displaystyle \frac{\pi }{7}-\sin\displaystyle \frac{4\pi }{7}+\sin\displaystyle \frac{5\pi }{7}-\sin\displaystyle \frac{\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\displaystyle \frac{3\pi }{7}-\sin\displaystyle \frac{4\pi }{7}+\sin\displaystyle \frac{5\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\left (\pi -\displaystyle \frac{4\pi }{7} \right )-\sin\displaystyle \frac{4\pi }{7}+\sin\left (\pi -\displaystyle \frac{2\pi }{7} \right )}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\displaystyle \frac{4\pi }{7}-\sin\displaystyle \frac{4\pi }{7}+\sin\displaystyle \frac{2\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{\sin\displaystyle \frac{2\pi }{7}}{2\sin\displaystyle \frac{2\pi }{7}}\\ &=\displaystyle \frac{1}{2}\qquad \blacksquare \end{aligned}$.

$\begin{array}{ll}\\ 96.&\textrm{Nilai dari}\\ &\quad\quad \sin \displaystyle \frac{\pi }{14}\sin \frac{3\pi }{14}\sin \frac{9\pi }{14}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \displaystyle \frac{1}{16} &&&\textrm{d}.&\displaystyle \frac{1}{2}\\\\ \textrm{b}.&\displaystyle \color{red}\frac{1}{8}&\quad \textrm{c}.&\displaystyle \frac{1}{4}\quad &\textrm{e}.&\displaystyle 1 \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}\textrm{Perhat}&\textrm{ikan bahwa}\\ \sin \displaystyle \displaystyle \frac{\pi }{14}&=\sin \left (\displaystyle \frac{7\pi }{14}-\frac{6\pi }{14} \right )=\sin \left ( \displaystyle \frac{1}{2}\pi -\frac{6\pi }{14} \right )\\ &=\cos \displaystyle \frac{6\pi }{14} \\ \sin \displaystyle \frac{3\pi }{14}&=...=\cos \displaystyle \frac{4\pi }{14}\\ \sin \displaystyle \frac{9\pi }{14}&=...=\sin \displaystyle \frac{5\pi }{14}=\cos \displaystyle \frac{2\pi }{14} \end{aligned}\\ &...\\ &\sin \displaystyle \frac{\pi }{14}\sin \frac{3\pi }{14}\sin \frac{9\pi }{14}\\ &=\cos \displaystyle \frac{6\pi }{14}\cos \displaystyle \frac{4\pi }{14}\cos \displaystyle \frac{2\pi }{14}\times \displaystyle \frac{2\sin \displaystyle \frac{2\pi }{14}}{2\sin \displaystyle \frac{2\pi }{14}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{6\pi }{14}\cos \displaystyle \frac{4\pi }{14}\sin \displaystyle \frac{4\pi }{14}}{2\sin \displaystyle \frac{2\pi }{14}}\\ &\textrm{silahkan dilanjutkan}\\ &...\\ &=\displaystyle \frac{1}{8} \end{array}$.

$\begin{array}{ll}\\ 97.&\textrm{Nilai dari}\\ & \cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{4\pi }{5}\cos \displaystyle \frac{8\pi }{5}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \color{red}-\displaystyle \frac{1}{16} &&&\textrm{d}.&\displaystyle \frac{1}{16}\\\\ \textrm{b}.&\displaystyle \frac{1}{8}&\quad \textrm{c}.&\displaystyle 0\quad &\textrm{e}.&\displaystyle \frac{1}{8} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{4\pi }{5}\cos \displaystyle \frac{8\pi }{5}\\ &=\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{4\pi }{5}\cos \left (\pi +\displaystyle \frac{3\pi }{5} \right )\\ &=\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{4\pi }{5}\left (-\cos \displaystyle \frac{3\pi }{5} \right )\\ &=-\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{4\pi }{5}\cos \displaystyle \frac{3\pi }{5}\\ &=-\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{3\pi }{5}\cos \displaystyle \frac{4\pi }{5}\\ &=-\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{3\pi }{5}\cos \displaystyle \frac{4\pi }{5}\times \displaystyle \frac{2\sin \displaystyle \frac{\pi }{5}}{2\sin \displaystyle \frac{\pi }{5}}\\ &=\frac{-\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{3\pi }{5}\left ( \sin \pi -\sin \displaystyle \frac{3\pi }{5} \right )}{2\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{\pi }{5}\cos \frac{2\pi }{5}\cos \frac{3\pi }{5} \sin \frac{3\pi }{5}}{2\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{\pi }{5}\cos \displaystyle \frac{3\pi }{5}\left ( \cos \displaystyle \frac{2\pi }{5}\sin \displaystyle \frac{3\pi }{5} \right )}{2\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{\pi }{5}\cos \displaystyle \frac{3\pi }{5}\left ( \sin \pi -\sin \left ( -\displaystyle \frac{\pi }{5} \right ) \right )}{4\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{\pi }{5}\cos \displaystyle \frac{3\pi }{5}\sin \displaystyle \frac{\pi }{5}}{4\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{3\pi }{5}\cos \displaystyle \frac{\pi }{5}\sin \displaystyle \frac{\pi }{5}}{4\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{3\pi }{5}\left (\cos \displaystyle \frac{\pi }{5}\sin \displaystyle \frac{\pi }{5} \right )}{4\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{3\pi }{5}\left (\sin \displaystyle \frac{2\pi }{5}-\sin 0 \right )}{8\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\cos \displaystyle \frac{3\pi }{5}\sin \displaystyle \frac{2\pi }{5}}{8\sin \displaystyle \frac{\pi }{5}}\\ &=\displaystyle \frac{\sin \pi -\sin \displaystyle \frac{\pi }{5}}{16\sin \displaystyle \frac{\pi }{5}}\\ &=-\displaystyle \frac{\sin \displaystyle \frac{\pi }{5}}{16\sin \displaystyle \frac{\pi }{5}}\\ &=\color{red}-\displaystyle \frac{1}{16} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 98.&\textrm{Nilai dari}\: \: \sin \displaystyle \frac{\pi }{24}.\sin \frac{5\pi }{24}.\sin \frac{7\pi }{24}.\sin \frac{11\pi }{24}\\ &\begin{array}{lll}\\ \textrm{a}.\quad \displaystyle \frac{5}{16}&&\textrm{d}.\quad \displaystyle \frac{2}{16}\\\\ \textrm{b}.\quad \displaystyle \frac{4}{16}&\textrm{c}.\quad \displaystyle \frac{3}{16}&\textrm{e}.\quad \color{red}\displaystyle \frac{1}{16} \end{array}\\\\ &\textbf{(Olimpiade Sains PORSEMA NU 2012)}\\\\ &\textbf{Jawab}:\: \: \color{red}\textbf{e}\\ &\begin{aligned}&\sin \displaystyle \frac{\pi }{24}.\sin \frac{5\pi }{24}.\sin \frac{7\pi }{24}.\sin \frac{11\pi }{24}\\ &=\displaystyle \frac{1}{4}\left ( 2\sin \displaystyle \frac{11\pi }{24}.\sin \frac{\pi }{24}.2\sin \frac{7\pi }{24}.\sin \frac{5\pi }{24} \right )\\ &=\displaystyle \frac{1}{4}\left [ \left ( \cos \left ( \frac{10\pi }{24} \right )-\cos \left ( \frac{12\pi }{24} \right ) \right )\times \left ( \cos \left ( \frac{2\pi }{24} \right )-\cos \left ( \frac{12\pi }{24} \right ) \right ) \right ]\\ &=\displaystyle \frac{1}{4}\left [ \left ( \cos 75^{\circ}-\cos 90^{\circ} \right )\times \left ( \cos 15^{\circ}-\cos 90^{\circ} \right ) \right ]\\ &=\displaystyle \frac{1}{4}\left [ \cos 75^{\circ}.\cos 15^{\circ} \right ]\\ &=\displaystyle \frac{1}{8}\left [ \cos 90^{\circ}+\cos 60^{\circ} \right ]\\ &=\displaystyle \frac{1}{8}\left ( 0+\frac{1}{2} \right )\\ &=\color{red}\displaystyle \frac{1}{16} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 99.&\textrm{Nilai dari}\\ & \qquad\qquad\sin 18^{\circ}\cos 36^{\circ}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \frac{1}{6} &&&\textrm{d}.&\displaystyle \frac{1}{3}\\\\ \textrm{b}.&\displaystyle \frac{1}{5}&\quad \textrm{c}.&\displaystyle \color{red}\displaystyle \frac{1}{4}\quad &\textrm{e}.&\displaystyle \frac{1}{2} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\sin 18^{\circ}\cos 36^{\circ}\\ &=\sin 18^{\circ}\cos 36^{\circ}\times \displaystyle \frac{2\cos 18^{\circ}}{2\cos 18^{\circ}}\\ &=\displaystyle \frac{\cos 36^{\circ}\left ( \sin 36^{\circ}+\sin 0^{\circ} \right )}{4\cos 18^{\circ}}\\ &=\displaystyle \frac{\cos 36^{\circ}\sin 36^{\circ}}{4\cos 18^{\circ}}\\ &=\displaystyle \frac{\sin 72^{\circ}}{4\cos 18^{\circ}}\\ &=\displaystyle \frac{\sin \left ( 90^{\circ}-18^{\circ} \right )}{4\cos 18^{\circ}}\\ &=\displaystyle \frac{\cos 18^{\circ}}{4\cos 18^{\circ}}\\ &=\color{red}\displaystyle \frac{1}{4} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 100.&\textrm{Nilai eksak dari}\: \: \sin 36^{\circ}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \displaystyle \frac{1}{4}\sqrt{10+2\sqrt{5}}&&&\textrm{d}.&\displaystyle \frac{\sqrt{5}-1}{4}\\ \textrm{b}.&\color{red}\displaystyle \frac{1}{4}\sqrt{10-2\sqrt{5}}&&\quad &\textrm{e}.&\displaystyle \frac{\sqrt{5}-1}{2}\\ \textrm{c}.&\displaystyle \displaystyle \frac{\sqrt{5}+1}{4} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\textrm{Perhatikanlah ilustrasi gambar berikut} \end{array}$.

$.\qquad\begin{aligned}&\textrm{Perhatikan bahwa}\: \: \color{red}\bigtriangleup ABC\: \: \color{black}\textrm{sama kaki}\\ &\textrm{dengan}\: \: AD=DC=CB=1,\: AC=x\\ &\textrm{Diketahui pula}\: \: CD\: \: \textrm{adalah garis bagi}\\ &\textrm{serta}\: \: ABC\: \: \textrm{sebangun}\: \: \bigtriangleup BCD\\ &\textrm{akibatnya}:\\ &\color{red}\textrm{perbandingan sisi yang bersesuaian}\\ &\color{red}\textrm{akan sama},\: \: \color{black}\textrm{maka}\\ &\displaystyle \frac{AB}{BC}=\displaystyle \frac{BC}{AB-AD}\\ &\Leftrightarrow \displaystyle \frac{x}{1}=\frac{1}{x-1}\\ &\Leftrightarrow x(x-1)=1\\ &\Leftrightarrow x^{2}-x-1=0\\ &\Leftrightarrow x=\displaystyle \frac{1\pm \sqrt{5}}{2}\\ &\textrm{akibatnya}\: \: AB=AC=\displaystyle \frac{1+\sqrt{5}}{2}\\ &\textrm{Selanjutnya gunakan}\: \: \color{blue}\textrm{aturan sinus}\\ &\displaystyle \frac{AB}{\sin \angle C}=\frac{BC}{\sin \angle A}\\ &\Leftrightarrow \displaystyle \frac{AB}{BC}=\frac{\sin \angle C}{\sin \angle A}\\ &\Leftrightarrow \displaystyle \frac{ \left (\displaystyle \frac{1+\sqrt{5} }{2} \right )}{1}=\frac{\sin 72^{\circ}}{\sin 36^{\circ}}\\ &\Leftrightarrow \displaystyle \frac{1+\sqrt{5}}{2}=\displaystyle \frac{2\sin 36^{\circ}\cos 36^{\circ}}{\sin 36^{\circ}}\\ &\Leftrightarrow \displaystyle \frac{1+\sqrt{5}}{2}=2\cos 36^{\circ}\\ &\Leftrightarrow \cos 36^{\circ}=\Leftrightarrow \displaystyle \frac{1+\sqrt{5}}{4}\\ &\textrm{Dari fakta di atas kita akan dengan}\\ &\textrm{mudah menentukan nilai sinusnya}\\ &\textrm{yaitu dengan menggunakan}\\ &\textrm{identitas trigonometri berikut}:\\ &\sin ^{2}36^{\circ}+\cos ^{2}36^{\circ}=1\\ &\Leftrightarrow \sin ^{2}36^{\circ}=1-\cos ^{2}36^{\circ}\\ &\Leftrightarrow \sin 36^{\circ}=\sqrt{1-\cos ^{2}36^{\circ}}\\ &\Leftrightarrow \: \: \quad\quad\quad =\sqrt{1-\left ( \displaystyle \frac{1+\sqrt{5}}{4} \right )^{2}}\\ &\Leftrightarrow \: \: \quad\quad\quad =\sqrt{1-\displaystyle \frac{6+2\sqrt{5}}{16}}\\ &\Leftrightarrow \: \: \quad\quad\quad =\sqrt{\displaystyle \frac{10-2\sqrt{5}}{16}}\\ &\Leftrightarrow \: \: \quad\quad\quad =\color{red}\displaystyle \frac{1}{4}\sqrt{10-2\sqrt{5}} \end{aligned}$.

 

Latihan Soal 9 Persiapan PAS Gasal Matematika Peminatan Kelas XI (Persamaan dan Rumus Jumlah dan Selisih Trigonometri)

 $\begin{array}{ll}\\ 81.&\textrm{Nilai}\: \: \cos \displaystyle \frac{5}{12}\pi -\cos \displaystyle \frac{1}{12}\pi \: \: \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&-\displaystyle \frac{1}{2}\sqrt{6}&&&\textrm{d}.&\displaystyle \frac{1}{2}\sqrt{2}\\\\ \textrm{b}.&-\displaystyle \frac{1}{2}\sqrt{3}&\textrm{c}.&\color{red}-\displaystyle \frac{1}{2}\sqrt{2}&\textrm{e}.&\displaystyle \frac{1}{2}\sqrt{6} \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\cos \displaystyle \frac{5}{12}\pi -\cos \displaystyle \frac{1}{12}\pi \\ &=-2\sin \left ( \displaystyle \frac{\displaystyle \frac{5}{12}\pi +\displaystyle \frac{1}{12}\pi }{2} \right )\sin \left ( \displaystyle \frac{\displaystyle \frac{5}{12}\pi -\displaystyle \frac{1}{12}\pi }{2} \right )\\ &=-2\sin \left (\displaystyle \frac{\displaystyle \frac{6}{12}\pi }{2} \right )\sin \left (\displaystyle \frac{\displaystyle \frac{4}{12}\pi }{2} \right ) \\ &=-2\sin \left (\displaystyle \frac{1 }{4}\pi \right )\sin \left (\displaystyle \frac{1 }{6}\pi \right ) \\ &=-2\left ( \displaystyle \frac{1}{2}\sqrt{2} \right )\left ( \displaystyle \frac{1}{2} \right )\\ &=\color{red}\displaystyle -\frac{1}{2}\sqrt{2} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 82.&\textrm{Bentuk}\: \: \sin \left ( 2x-\displaystyle \frac{3}{2}\pi \right )-\sin \left ( 4x+\displaystyle \frac{1}{2}\pi \right )\\ & \textrm{senilai dengan}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle -2\sin 3x.\sin x &&&\textrm{d}.&\color{red}\displaystyle 2\sin 3x.\sin x\\ \textrm{b}.&\displaystyle -2\cos 3x.\sin x&&&\textrm{e}.&\displaystyle 2\cos 3x.\sin x\\ \textrm{c}.&\displaystyle 2\sin 2\left ( x-\pi \right ) \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\sin \left ( 2x-\displaystyle \frac{3}{2}\pi \right )-\sin \left ( 4x+\displaystyle \frac{1}{2}\pi \right )\\ &=2\cos \left ( \displaystyle \frac{2x-\displaystyle \frac{3}{2}\pi+4x+\displaystyle \frac{1}{2}\pi}{2} \right )\\ &\qquad \times \sin \left ( \displaystyle \frac{2x-\displaystyle \frac{3}{2}\pi-\left (4x+\displaystyle \frac{1}{2}\pi \right )}{2} \right )\\ &=2\cos (3x-\displaystyle \frac{1}{2}\pi )\sin\left ( -x-\pi \right )\\ &=2\cos \left ( \displaystyle \frac{1}{2}\pi -3x \right )\left ( -\sin (\pi +x) \right )\\ &=2\left ( \sin 3x \right )\left ( -(-\sin x) \right )\\ &=2\sin 3x.\sin x \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 83.&\textrm{Nilai}\: \: \displaystyle \frac{\cos 75^{\circ}-\cos 15^{\circ}}{\sin 75^{\circ}-\sin 15^{\circ}}=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad \color{red}-1&&\textrm{d}.\quad \displaystyle \frac{1}{3}\sqrt{6}\\\\ \textrm{b}.\quad \displaystyle \frac{1}{2}\sqrt{2}&\textrm{c}.\quad 1&\textrm{e}.\quad \displaystyle \frac{1}{2}\sqrt{6} \end{array}\\\\ &\textbf{Jawab}:\: \: \color{red}\textbf{a}\\ &\begin{aligned}&\displaystyle \frac{\cos 75^{\circ}-\cos 15^{\circ}}{\sin 75^{\circ}-\sin 15^{\circ}}\\ &=\displaystyle \frac{-2\sin \displaystyle \frac{1}{2}\left ( 75^{\circ}+15^{\circ} \right )\sin \frac{1}{2}\left ( 75^{\circ}-15^{\circ} \right )}{2\cos \displaystyle \frac{1}{2}\left ( 75^{\circ}+15^{\circ} \right )\sin \frac{1}{2}\left ( 75^{\circ}-15^{\circ} \right )}\\ &=-\displaystyle \frac{2\sin 45^{\circ}\times \sin 30^{\circ}}{2\cos 45^{\circ}\times \sin 30^{\circ}}\\ &=-\tan 45^{\circ}\\ &=\color{red}-1 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 84.&\textrm{Bentuk}\: \: \displaystyle \frac{\cos 3x-\sin 6x-\cos 9x}{\sin 9x-\cos 6x-\sin 3x}\\ & \textrm{senilai dengan}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle -\tan 6x &&&\textrm{d}.&6\cot x\\ \textrm{b}.&\displaystyle -\cot 6x&&&\textrm{e}.&\displaystyle \color{red}\tan 6x\\ \textrm{c}.&\displaystyle 6\tan x \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \frac{\cos 3x-\sin 6x-\cos 9x}{\sin 9x-\cos 6x-\sin 3x}\\ &=\displaystyle \frac{\cos 3x-\cos 9x-\sin 6x}{\sin 9x-\sin 3x-\cos 6x}\\ &=\displaystyle \frac{-2\sin 6x\sin (-3x)-\sin 6x}{2\cos 6x\sin 3x-\cos 6x}\\ &=\displaystyle \frac{2\sin 6x\sin 3x-\sin 6x}{2\cos 6x\sin 3x-\cos 6x}\\ &=\displaystyle \frac{\sin 6x(2\sin 3x-1)}{\cos 6x(2\sin 3x-1)}\\ &=\tan 6x \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 85.&\textrm{Nilai dari}\\ &\displaystyle \frac{\sin x+\sin 3x+\sin 5x+\sin 7x}{\cos x+\cos 3x+\cos 5x+\cos 7x}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \tan 2x &&\textrm{d}.&\displaystyle \tan 8x\\ \textrm{b}.&\color{red}\displaystyle \tan 4x&\quad&\textrm{e}.&\displaystyle \tan 16x\\ \textrm{c}.&\displaystyle \displaystyle \tan 6x \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \frac{\sin x+\sin 3x+\sin 5x+\sin 7x}{\cos x+\cos 3x+\cos 5x+\cos 7x}\\ &=\displaystyle \frac{\sin 7x+\sin x+\sin 5x+\sin 3x}{\cos 7x+\cos x+\cos 5x+\cos 3x}\\ &=\displaystyle \frac{2\sin 4x\cos 3x+2\sin 4x\cos x}{2\cos 4x\cos 3x+2\cos 4x\cos x}\\ &=\displaystyle \frac{2\sin 4x\left ( \cos 3x+\cos x \right )}{2\cos 4x\left ( \cos 3x+\cos x \right )}\\ &=\tan 4x \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 86.&\textrm{Bentuk sederhana dari}\\ &\quad\quad \displaystyle \frac{\cos A+\sin A}{\cos A-\sin A}-\frac{\cos A-\sin A}{\cos A+\sin A}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle \tan A &&&\textrm{d}.&2\cos 2A\\ \textrm{b}.&\displaystyle 2\tan A&&&\textrm{e}.&\displaystyle \color{red}2\tan 2A\\ \textrm{c}.&\displaystyle 2\sin 2A \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \frac{\cos A+\sin A}{\cos A-\sin A}-\frac{\cos A-\sin A}{\cos A+\sin A}\\ &=\displaystyle \frac{(\cos A+\sin A)^{2}-(\cos A-\sin A)^{2}}{(\cos A-\sin A)(\cos A+\sin A)}\\ &=\displaystyle \frac{(\cos ^{2}A+2\cos A\sin A+\sin ^{2}A)-(\cos ^{2}A-2\cos A\sin A+\sin ^{2}A)}{\cos ^{2}A-\sin ^{2}A}\\ &=\displaystyle \frac{4\cos A\sin A}{\cos ^{2}A-\sin ^{2}A}\\ &=\displaystyle \frac{2\sin 2A}{\cos 2A}\\ &=2\tan 2A \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 87.&\textrm{Bentuk sederhana dari}\\ &\qquad\quad \displaystyle \frac{\cos 2x-\cos 2y}{\sin 2x+\sin 2y}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle -\sin (x-y) &&&\textrm{d}.&\cos (x-y)\\ \textrm{b}.&\displaystyle \color{red}-\tan (x-y)&&&\textrm{e}.&\displaystyle \tan (x-y)\\ \textrm{c}.&\displaystyle \sin (x+y) \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&\displaystyle \frac{\cos 2x-\cos 2y}{\sin 2x+\sin 2y}\\ &=\displaystyle \frac{-2\sin (x+y)\sin (x-y)}{2\sin (x+y)\cos (x-y)}\\ &=-\tan (x-y) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 88.&\textrm{Nilai dari}\: \: \cos 80^{\circ}+\cos 40^{\circ}-\cos 20^{\circ}=....\\ &\begin{array}{lll}\\ \textrm{a}.\quad 1&&\textrm{d}.\quad -\displaystyle \frac{1}{2}\\\\ \textrm{b}.\quad -1&\textrm{c}.\quad \displaystyle \frac{1}{2}&\textrm{e}.\quad \color{red}0 \end{array}\\\\ &\textbf{Jawab}:\: \: \color{red}\textbf{e}\\ &\begin{aligned}&\cos 80^{\circ}+\cos 40^{\circ}-\cos 20^{\circ}\\ &=2\cos \displaystyle \frac{1}{2}\left ( 80^{\circ}+40^{\circ} \right )\cos \displaystyle \frac{1}{2}\left ( 80^{\circ}-40^{\circ} \right )-\cos 20^{\circ}\\ &=2\cos 60^{\circ}\cos 20^{\circ}-\cos 20^{\circ}\\ &=2.\displaystyle \frac{1}{2}.\cos 20^{\circ}-\cos 20^{\circ}\\ &=\cos 20^{\circ}-\cos 20^{\circ}\\ &=\color{red}0 \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 89.&\textrm{Nilai dari}\\ &\quad\quad 8\cos 82,5^{\circ}\sin 37,5^{\circ}\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle 4(\sqrt{3}+\sqrt{2}) &&&\textrm{d}.&\color{red}2(\sqrt{3}-\sqrt{2})\\ \textrm{b}.&\displaystyle 4(\sqrt{3}-\sqrt{2})&&&\textrm{e}.&\displaystyle \sqrt{3}-\sqrt{2}\\ \textrm{c}.&\displaystyle 2(\sqrt{3}+\sqrt{2}) \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&8\cos 82,5^{\circ}\sin 37,5^{\circ}\\ &=4\times 2\cos 82,5^{\circ}\sin 37,5^{\circ}\\ &=4\times \left ( \sin (82,5^{\circ}+37,5^{\circ})-\sin (82,5^{\circ}-37,5^{\circ}) \right )\\ &=4\times \left (\sin 120^{\circ}-\sin 45^{\circ} \right )\\ &=4\times \left ( \sin \left ( 180^{\circ}-60^{\circ} \right )-\sin 45^{\circ} \right )\\ &=4\times \left ( \sin 60^{\circ}-\sin 45^{\circ} \right )\\ &=4\times \left ( \displaystyle \frac{1}{2}\sqrt{3}-\displaystyle \frac{1}{2}\sqrt{2} \right )\\ &=2\left ( \sqrt{3}-\sqrt{2} \right ) \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 90.&\textrm{Bentuk lain dari}\\ &\quad\quad -2\cos 5A.\cos 7A\\ & \textrm{adalah}\: ....\\ &\begin{array}{lllllll}\\ \textrm{a}.&\displaystyle -\cos 6A-\cos A &&&\\ \textrm{b}.&\displaystyle -\cos 6A+\cos A&&&\\ \textrm{c}.&\displaystyle \cos 12A-\cos 2A\\ \textrm{d}.&-\cos 12A+\cos 2A\\ \textrm{e}.&\color{red}\displaystyle -\cos 12A-\cos 2A \end{array}\\\\ &\color{blue}\textbf{Jawab}:\\ &\begin{aligned}&-2\cos 5A.\cos 7A\\ &=-\left ( 2\cos 5A.\cos 7A \right )\\ &=-\left ( \cos 12A+\cos (-2A) \right )\\ &=-\left ( \cos 12A+\cos 2A \right )\\ &=-\cos 12A-\cos 2A \\ \end{aligned} \end{array}$.