PAS MATEMATIKA BLOG

Ketaksamaan Muirhead

Ketaksamaan Muirhead

Diberikan $a=(a_{1},a_{2},a_{3},\cdots ,a_{n})$ dan $b=(b_{1},b_{2},b_{3},\cdots ,b_{n})$ yang merupakan barisan bilangan real, dengan barisan $a$ lebih utama dari barisan $b$ dan selanjutnya dituliskan dengan $a\succ b$ disebutkan demikian jika kedua barisan di atas memenuhi 3 kondisi berikut:

$\begin{aligned}1.\quad&a_{1}\geq a_{2}\geq \cdots \geq a_{n}\: \: \textrm{dan}\: \: b_{1}\geq b_{2}\geq \cdots \geq b_{n}\\ 2.\quad&a_{1}+a_{2}+\cdots +a_{n}=b_{1}+b_{2}+\cdots +b_{k}\\ 3.\quad&a_{1}+a_{2}+\cdots +a_{n}=b_{1}+b_{2}+\cdots +b_{k},\\ &\quad \textrm{untuk tiap}\: \: k,\: \: \textrm{dengan}\: :1\leq k\leq n\: \end{aligned}$.

Contoh:

$\begin{aligned}1.\quad&(4,0,0)\succ (3,1,0)\\ 2.\quad&(2,2,0)\succ (2,1,1)\\ 3.\quad&(2,0,0,0)\not{\succ }(1,1,0) \end{aligned}$.

Sebagai keterangan tambahan adalah:

Jika $(a)\succ (b)$, maka $\left [ a \right ]\geq \left [ b \right ]$. Kesamaan terjadi jika dan hanya jika barisan a dan b identik atau semua sama untuk nilai $x_{i}$.
Jika (a) barisan bilangan real positif, $(x_{n})\succ (y_{n})$, maka $\displaystyle \sum_{sym}^{.}a_{1}^{x_{1}}a_{2}^{x_{2}}a_{3}^{x_{3}}\cdots a_{n}^{x_{n}}\geq \displaystyle \sum_{sym}^{.}a_{1}^{y_{1}}a_{2}^{y_{2}}a_{3}^{y_{3}}\cdots a_{n}^{y_{n}}$. (untuk hal terkait symetri, silahkan klik link ini)

Lanjutan Materi Operasi Vektor di Ruang (Cross Product): Perkalian Silang Dua Vektor

$\color{blue}\textrm{C. Perkalian Silang Vektor (Pengayaan)}$.

Pada ruang dimensi tiga khususnya pada vektor akan berlaku perkalian silang (cross vektor) adalah perkalian antara dua vektor yang menghasilkan vektor tunggal. Misalkan diketahui $\vec{u}$ dan $\vec{v}$ adalah dua vektor sembarang dan keduanya membentuk sudut $\theta$, maka hasil kali kedua vektor tersebut adalah sebuah vektor baru dengan dinotasiakan sebagai $\vec{u}\times \vec{v}$. Tentunya sebagai syarat kedua vektor tersebut masing-masing tidak berupa vektor nol.

Jika $\vec{u}\times \vec{v}=\vec{c}$ , maka

$\begin{aligned}\vec{u}&\times \vec{v}=\vec{c}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{1} & y_{1} &z_{1} \\ x_{2} & y_{2} &z_{2} \end{vmatrix}\\ &=(y_{1}z_{2}-z_{1}y_{2})\vec{i}-(x_{1}z_{2}-z_{1}x_{2})\vec{j}+(x_{1}y_{2}-y_{1}x_{2})\vec{k} \end{aligned}$

Lalu kalau sudah demikian berapa besarnya? dan ke mana arahnya?

Besarnya adalah $\left | \vec{u}\times \vec{v} \right |=\left | \vec{u} \right |\left | \vec{v} \right |\sin \theta$ dan arahnya tegak lurus terhadap $\vec{u}$ dan $\vec{v}$.

Sebagai ilustrasi perhatikanlah gambar berikut untuk dua buah vektor sebagai misal $\vec{a}$ dan $\vec{b}$.

Jika putarannya dibalik, maka akan mendapatkan hasil sebagai mana ilustrasi berikut

Sehingga perlu diingat bahwa : $\vec{a}\times \vec{b}=-\vec{b}\times \vec{a}$.

Pada hasil kali silang dua vektor berlaku

tidak bersifat komutatif , karena $\vec{a}\times \vec{b}=-\vec{b}\times \vec{a}$.
distributif terhadap penjumlahan : $\vec{a}\times \left (\vec{b}+\vec{c} \right )=\vec{a}\times \vec{b}+\vec{a}\times \vec{c}$.
pada perkalian dengan skalar : $k\left (\vec{a}\times \vec{b} \right )=\left (k\vec{a} \right )\times \vec{b}=\vec{a}\times \left ( k\vec{b} \right )$.
berlaku untuk sembarang vektor : $\vec{a}\times \vec{a} =0$.
jika kedua vektor sejajar, maka hasil kalinya adalah = 0.
Nilai dari perkalian kedua vektor terbut adalah sama dengan hasil luas jajar genjang.
Nilai dari poin 6 jika dibagi 2 akan berupa hasil luas sebuah segitiga yang dibentuk oleh kedua vektor tersebut.
berlaku identitas Lagrange : $\left | \vec{a}\times \vec{b} \right |^{2}=\left | \vec{a} \right |^{2}.\left | \vec{b} \right |^{2}-\left ( \vec{a}\: \bullet \: \vec{b} \right )^{2}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui}\: \: \vec{a}=4\vec{i}+3\vec{j}\: \: \textrm{dan}\: \: \vec{b}=4\vec{i}-3\vec{k}\\ &\textrm{Tentukanlah hasil}\: \: \vec{a}\times \vec{b}\: \: \textrm{dan}\: \: \vec{b}\times \vec{a}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\vec{a}&\times \vec{b}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{1} & y_{1} &z_{1} \\ x_{2} & y_{2} &z_{2} \end{vmatrix}\\ &=(y_{1}z_{2}-z_{1}y_{2})\vec{i}-(x_{1}z_{2}-z_{1}x_{2})\vec{j}+(x_{1}y_{2}-y_{1}x_{2})\vec{k}\\ &=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ 4 & 3 &0 \\ 4 & 0 &-3 \end{vmatrix}\\ &=(-9-0)\vec{i}-(-12-0)\vec{j}+(0-12)\vec{k}\\ &=-9\vec{i}+12\vec{j}-12\vec{k} \end{aligned}\\ &\begin{aligned}\vec{b}&\times \vec{a}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{2} & y_{2} &z_{2} \\ x_{1} & y_{1} &z_{1} \end{vmatrix}\\ &=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ 4 & 0 &-3 \\ 4 & 3 &0 \end{vmatrix}\\ &=(0-(-9))\vec{i}-(0-(-12))\vec{j}+(12-0)\vec{k}\\ &=9\vec{i}-12\vec{j}+12\vec{k} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui}\: \: \vec{a}=6\vec{i}+2\vec{j}+10\vec{k}\: \: \textrm{dan}\: \: \vec{b}=4\vec{i}+\vec{j}+9\vec{k}\\ &\textrm{Tentukanlah hasil}\: \: \vec{a}\times \vec{b}\: \: \textrm{dan}\: \: \vec{b}\times \vec{a}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\vec{a}&\times \vec{b}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{1} & y_{1} &z_{1} \\ x_{2} & y_{2} &z_{2} \end{vmatrix}\\ &=(y_{1}z_{2}-z_{1}y_{2})\vec{i}-(x_{1}z_{2}-z_{1}x_{2})\vec{j}+(x_{1}y_{2}-y_{1}x_{2})\vec{k}\\ &=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ 6 & 2 &10 \\ 4 & 1 &9 \end{vmatrix}\\ &=(18-10)\vec{i}-(54-40)\vec{j}+(6-8)\vec{k}\\ &=8\vec{i}-14\vec{j}-2\vec{k} \end{aligned}\\ &\begin{aligned}\vec{b}&\times \vec{a}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{2} & y_{2} &z_{2} \\ x_{1} & y_{1} &z_{1} \end{vmatrix}\\ &=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ 4 & 1 &9 \\ 6 & 2 &10 \end{vmatrix}\\ &=(10-18)\vec{i}-(40-54)\vec{j}+(8-6)\vec{k}\\ &=-8\vec{i}+14\vec{j}+2\vec{k} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah luas segitiga}\: \: ABC\: \: \textrm{jika}\\ &\textrm{diketahui}\: \: A(2,1,-2),\: B(0,-1,0),\: \: \textrm{dan}\\ &C(-1,2,-1)\\\\ &\textbf{Jawab}:\\ &\textrm{Misalkan luas segitiga}\: \: \displaystyle \frac{1}{2}\left | \vec{p}\times \vec{q} \right |,\: \: \textrm{dengan}\\ &\begin{cases} \vec{p} & =\overline{AB}=\overline{OB}-\overline{OA}=\begin{pmatrix} 0\\ -1\\ 0 \end{pmatrix}-\begin{pmatrix} 2\\ 1\\ -2 \end{pmatrix}=\begin{pmatrix} -2\\ -2\\ 2 \end{pmatrix} \\ \vec{q} & =\overline{AC}=\overline{OC}-\overline{OA}=\begin{pmatrix} -1\\ 2\\ -1 \end{pmatrix}-\begin{pmatrix} 2\\ 1\\ -2 \end{pmatrix}=\begin{pmatrix} -3\\ 1\\ 1 \end{pmatrix} \end{cases}\\ &\begin{aligned}\vec{p}&\times \vec{q}=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ x_{1} & y_{1} &z_{1} \\ x_{2} & y_{2} &z_{2} \end{vmatrix}\\ &=(y_{1}z_{2}-z_{1}y_{2})\vec{i}-(x_{1}z_{2}-z_{1}x_{2})\vec{j}+(x_{1}y_{2}-y_{1}x_{2})\vec{k}\\ &=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ -2 & -2 &2 \\ -3 & 1 &1 \end{vmatrix}\\ &=(-2-2)\vec{i}-(-2-(-6))\vec{j}+(-2-6)\vec{k}\\ &=-4\vec{i}-4\vec{j}-8\vec{k}\\ &\textrm{Sehingga}\\ &\left | \vec{p}\times \vec{q} \right |=\sqrt{(-4)^{2}+(-4)^{2}+(-8)^{2}}\\ &\quad\qquad =\sqrt{16+16+64}=\sqrt{96}=4\sqrt{6}\\ &\textrm{Maka luas segi tiganya adalah}:\\ &\textrm{luas}\: \triangle ABC=\displaystyle \frac{1}{2}\left | \vec{p}\times \vec{q} \right |=\displaystyle \frac{1}{2}\left ( 4\sqrt{6} \right )=\color{red}2\sqrt{6} \end{aligned} \end{array}$

DAFTAR PUSTAKA

Yuana, R.A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan Matematika dan Ilmu Alam. Solo: PT. TIGA SERANGKAI PUSTAKA MANDIRI

Lanjutan Materi Operasi Vektor di Ruang (Dot Product)

$\begin{array}{ll}\\ 6.&\textrm{Diketahui}\: \: \overrightarrow{a}=\begin{pmatrix} -2\\ 1\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{b}=\begin{pmatrix} 4\\ -1\\ t \end{pmatrix},\\ & \textrm{jika}\: \: \overrightarrow{p}\: \: \textrm{tegak lurus}\: \: \overrightarrow{q},\: \: \textrm{maka tentukanlah}\\ &\textrm{nilai}\: \: t\: \: \textrm{adalah}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Karena}&\: \textrm{kedua vektor tersebut saling }\\ \textrm{tegak l}& \textrm{urus maka}\\ \overrightarrow{a}.\overrightarrow{b}&=0\\ \begin{pmatrix} -2\\ 1\\ 3 \end{pmatrix}&\begin{pmatrix} 4\\ -1\\ t \end{pmatrix}=0\\ (-2).4&+1.(-1)+3.t=0\\ -8-1&+3t=0\\ 3t&=9\\ t&=\color{red}3 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 7.&\textrm{Tentukanlah nilai}\: \: \overrightarrow{a}.\overrightarrow{b}\: \: \textrm{jika}\\ &\textrm{a}.\quad \left | \overrightarrow{a} \right |=4,\: \left | \overrightarrow{b} \right |=6,\: \: \angle \left ( \overrightarrow{a},\overrightarrow{b} \right )=60^{\circ}\\ &\textrm{b}.\quad \overrightarrow{a}=2\vec{i}+\vec{j}-5\vec{k}\: \: \textrm{dan}\: \: \overrightarrow{b}=2\vec{i}-3\vec{k}\\ &\textrm{c}.\quad \overrightarrow{a}=\begin{pmatrix} 0\\ -1\\ 3 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{b}=\begin{pmatrix} 4\\ -2\\ 1 \end{pmatrix}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad \overrightarrow{a}.\overrightarrow{b}&=\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |\cos \angle \left ( \overrightarrow{a},\overrightarrow{b} \right )\\ &=4.6.\cos 60^{\circ}\\ &=24.\left ( \displaystyle \frac{1}{2} \right )\\ &=12 \end{aligned}\\ &\textrm{b}.\quad \overrightarrow{a}.\overrightarrow{b}=2.2+1.0+(-5).(-3)=4+15=19\\ &\textrm{c}.\quad \overrightarrow{a}.\overrightarrow{b}=0.4+(-1).(-2)+3.1=0+2+3=5 \end{array}$

$\begin{array}{ll} 8.&\textrm{Diketahui}\: \: \left |\vec{a} \right |=10,\: \left | \vec{b} \right |=3\\ & \textrm{dan}\: \: \vec{a}\bullet \vec{b}=15\sqrt{3}\: .\: \textrm{Tentukan sudut}\\ &\textrm{yang dibentuk oleh}\: \: \vec{a}\: \: \textrm{dan}\: \: \vec{b}\\\\ &\textbf{Jawab}\\ &\textrm{Dari bentuk}\\ &\begin{aligned}\vec{a}\bullet \vec{b}&=\left | \vec{a} \right |\left | \vec{b} \right |\cos \theta \\ \textrm{dipe}&\textrm{roleh bentuk}\\ \cos \theta &=\displaystyle \frac{\vec{a}\bullet \vec{b}}{\left | \vec{a} \right |\left | \vec{b} \right |}\\ \cos \theta &=\displaystyle \frac{15\sqrt{3}}{10.3}=\frac{15}{30}\sqrt{3}=\frac{1}{2}\sqrt{3}\\ \cos \theta&=\cos 30^{\circ}\\ \theta &=\color{red}30^{\circ}\\ \textrm{Jadi}&\: \textrm{sudut antara keduanya adalah}\: \: \color{red}30^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 9.&\textrm{Tentukanlah besar sudut antara vektor}\\ &\overrightarrow{a}=\begin{pmatrix} -1\\ 1\\ 0\end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{b}=\begin{pmatrix} 1\\ -2\\ 2 \end{pmatrix}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\cos \theta &=\displaystyle \frac{\overrightarrow{a}.\overrightarrow{b}}{\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |}\\ &=\displaystyle \frac{\begin{pmatrix} -1\\ 1\\ 0 \end{pmatrix}\begin{pmatrix} 1\\ -2\\ 2 \end{pmatrix}}{\sqrt{(-1)^{2}+1^{2}}\sqrt{1^{2}+(-2)^{2}+2^{2}}}\\ &=\displaystyle \frac{-1-2+0}{\sqrt{2}\sqrt{9}}\\ &=-\displaystyle \frac{1}{\sqrt{2}}=-\displaystyle \frac{1}{2}\sqrt{2}\\ &=-\cos 45^{\circ}\\ &=\cos \left ( 180^{\circ}-45^{\circ} \right )\\ \cos \theta &=\cos 135^{\circ}\\ \therefore \: \theta &=\color{red}135^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 10.&\textrm{Diketahui bahwa}\: \: \left |\overrightarrow{a} \right |=\sqrt{6} ,\: \: (\overrightarrow{a}-\overrightarrow{b})(\overrightarrow{a}+\overrightarrow{b})=0\\ & \textrm{dan}\: \: \overrightarrow{a}(\overrightarrow{a}-\overrightarrow{b})=3.\: \textrm{Tentukanlah besar}\\ &\textrm{sudut antara}\: \: \overrightarrow{a}\: \: \textrm{dan}\: \: \overrightarrow{b}\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{Perhatikan}&\: \textrm{bahwa}\\ (\overrightarrow{a}-\overrightarrow{b})(\overrightarrow{a}+\overrightarrow{b})&=0\\ \left | \overrightarrow{a} \right |^{2}-\left | \overrightarrow{b} \right |^{2}&=0\\ \left | \overrightarrow{a} \right |^{2}&=\left | \overrightarrow{b} \right |^{2}\quad \Rightarrow \quad \left | \overrightarrow{a} \right |=\overrightarrow{b}=\sqrt{6}\\ \textrm{dan}\quad \overrightarrow{a}(\overrightarrow{a}-\overrightarrow{b})&=3\\ \left | \overrightarrow{a} \right |^{2}-\overrightarrow{a}\overrightarrow{b}&=3\\ 6-\overrightarrow{a}\overrightarrow{b}&=3\\ -\overrightarrow{a}\overrightarrow{b}&=3-6=-3\\ \overrightarrow{a}\overrightarrow{b}&=3\\ \left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |\cos \theta &=3\\ \cos \theta &=\displaystyle \frac{3}{\sqrt{6}\sqrt{6}}=\frac{3}{6}=\frac{1}{2}\\ \cos \theta &=\cos 60^{\circ}\\ \therefore \: \: \theta &=\color{red}60^{\circ} \end{aligned} \end{array}$

$\color{blue}\textrm{Berikut dua contoh untuk sudut tidak istimewa}$.

$\begin{array}{ll} 11.&\textrm{Diketahui}\: \: \vec{a} =\vec{i}+2\vec{j}+2\vec{k},\: \: \textrm{dan}\\ & \vec{b}=3\vec{i}+4\vec{j}\: .\: \textrm{Tentukan sudut}\\ &\textrm{yang dibentuk oleh}\: \: \vec{a}\: \: \textrm{dan}\: \: \vec{b}\\\\ &\textbf{Jawab}\\ &\begin{aligned}\textrm{Dik}&\textrm{etahui bahwa}\\ \triangleright \quad &\vec{a} =\vec{i}+2\vec{j}+2\vec{k}=\begin{pmatrix} 1\\ 2\\ 2 \end{pmatrix}\: \: \textrm{dan}\\ &\left | \vec{a} \right |=\sqrt{1^{2}+2^{2}+2^{2}}=\sqrt{9}=3\\ \triangleright \quad &\vec{b}=3\vec{i}+4\vec{j}=\begin{pmatrix} 3\\ 4\\ 0 \end{pmatrix}\: \: \textrm{dan}\\ &\left | \vec{b} \right |=\sqrt{3^{2}+4^{2}+0^{2}}=\sqrt{25}=5\\ \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned} \cos \theta &=\displaystyle \frac{\vec{a}\bullet \vec{b}}{\left | \vec{a} \right |\left | \vec{b} \right |}\\ \cos \theta &=\displaystyle \frac{\begin{pmatrix} 1\\ 2\\ 2 \end{pmatrix}\begin{pmatrix} 3\\ 4\\ 0 \end{pmatrix}}{3.5}=\frac{3+8+0}{15}=\frac{11}{15}\\ \cos \theta&=0,733\\ \theta &=\color{red}\arccos \left ( \displaystyle 0.733 \right )\\ &\quad \textrm{gunakan alat bantu tabel trigonometri}\\ &\quad \textrm{atau kalkulator scientific}\\ &=42,9^{\circ}\\ \textrm{Jadi}&\: \textrm{sudut antara keduanya adalah}\: \: 42,9^{\circ} \end{aligned} \end{array}$

$\begin{array}{ll} 12.&\textrm{Diketahui}\: \: \vec{p} =(1,2,2),\: \: \textrm{dan}\\ & \vec{q}=(3,-2,6)\: .\: \textrm{Tentukan sudut}\\ &\textrm{yang dibentuk oleh}\: \: \vec{p}\: \: \textrm{dan}\: \: \vec{q}\\\\ &\textbf{Jawab}\\ &\begin{aligned}\textrm{Dik}&\textrm{etahui bahwa}\\ \triangleright \quad &\vec{p} =(1,2,2)=\begin{pmatrix} 1\\ 2\\ 2 \end{pmatrix}\: \: \textrm{dan}\\ &\left | \vec{p} \right |=\sqrt{1^{2}+2^{2}+2^{2}}=\sqrt{9}=3\\ \triangleright \quad &\vec{q}=(3,-2,6)=\begin{pmatrix} 3\\ -2\\ 6 \end{pmatrix}\: \: \textrm{dan}\\ &\left | \vec{q} \right |=\sqrt{3^{2}+(-2)^{2}+6^{2}}=\sqrt{49}=7\\ \end{aligned}\\ &\textrm{Selanjutnya}\\ &\begin{aligned} \cos \theta &=\displaystyle \frac{\vec{p}\bullet \vec{q}}{\left | \vec{p} \right |\left | \vec{q} \right |}\\ \cos \theta &=\displaystyle \frac{\begin{pmatrix} 1\\ 2\\ 2 \end{pmatrix}\begin{pmatrix} 3\\ -2\\ 6 \end{pmatrix}}{3.7}=\frac{3-4+12}{21}=\frac{11}{21}\\ \cos \theta&=0,524\\ \theta &=\color{red}\arccos \left ( \displaystyle 0.524 \right )\\ &\quad \textrm{gunakan alat bantu tabel trigonometri}\\ &\quad \textrm{atau kalkulator scientific}\\ &=58,4^{\circ}\\ \textrm{Jadi}&\: \textrm{sudut antara keduanya adalah}\: \: 58,4^{\circ} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 13.&\textrm{Diketahui vektor}\: \: \overrightarrow{a}\: \: \textrm{dan}\: \: \overrightarrow{b}\: \: \textrm{memiliki }\\ &\textrm{panjang masing-masing adalah 2 dan 3}\\ &\textrm{serta}\: \: \angle \left ( \overrightarrow{a},\overrightarrow{b}\right )=60^{\circ}.\: \textrm{Carilah nilai}\\ &\textrm{a}.\quad \left | \overrightarrow{a}+\overrightarrow{b} \right |\\\\ &\textrm{b}.\quad \left | \overrightarrow{a}-\overrightarrow{b} \right |\\ &\textrm{b}\quad \textrm{besar sudut antara}\\ &\qquad \left ( \overrightarrow{a}+\overrightarrow{b} \right )\: \: \textrm{dan}\: \: \left ( \overrightarrow{a}-\overrightarrow{b} \right )\\\\ &\textbf{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&\left | \overrightarrow{a}+\overrightarrow{b} \right |^{2}\\ &=\left ( \overrightarrow{a}+\overrightarrow{b} \right )\left ( \overrightarrow{a}+\overrightarrow{b} \right )\\ &=\overrightarrow{a}\overrightarrow{a}+2\overrightarrow{a}\overrightarrow{b}+\overrightarrow{b}\overrightarrow{b}\\ &=\left | \overrightarrow{a} \right |^{2}\cos 0^{\circ}+2\left |\overrightarrow{a} \right |\left |\overrightarrow{b} \right |\cos 60^{\circ}+\left | \overrightarrow{b} \right |^{2}\cos 0^{\circ}\\ &=2^{2}.1+2.2.3.\displaystyle \frac{1}{2}+3^{2}.1\\ &=4+6+9=19\\ &\textrm{Jadi, nilainya adalah}\: \: \left | \overrightarrow{a}+\overrightarrow{b} \right |=\color{red}\sqrt{19} \end{aligned}\\ &\begin{aligned}\textrm{b}.\quad&\left | \overrightarrow{a}-\overrightarrow{b} \right |^{2}\\ &=\left ( \overrightarrow{a}-\overrightarrow{b} \right )\left ( \overrightarrow{a}-\overrightarrow{b} \right )\\ &=\overrightarrow{a}\overrightarrow{a}-2\overrightarrow{a}\overrightarrow{b}+\overrightarrow{b}\overrightarrow{b}\\ &=\left | \overrightarrow{a} \right |^{2}\cos 0^{\circ}-2\left |\overrightarrow{a} \right |\left |\overrightarrow{b} \right |\cos 60^{\circ}+\left | \overrightarrow{b} \right |^{2}\cos 0^{\circ}\\ &=2^{2}.1-2.2.3.\displaystyle \frac{1}{2}+3^{2}.1\\ &=4-6+9=7\\ &\textrm{Jadi, nilainya adalah}\: \: \left | \overrightarrow{a}-\overrightarrow{b} \right |=\color{red}\sqrt{7} \end{aligned}\\ &\begin{aligned}\textrm{c}.\quad \textrm{Untuk menentukan nilai}&\\ \cos \angle \left ( \overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}-\overrightarrow{b} \right )&=\displaystyle \frac{\left (\overrightarrow{a}+\overrightarrow{b} \right ).\left (\overrightarrow{a}-\overrightarrow{b} \right )}{\left | \overrightarrow{a}+\overrightarrow{b} \right |.\left | \overrightarrow{a}-\overrightarrow{b} \right |}\\ &=\displaystyle \frac{\overrightarrow{a}\overrightarrow{a}-\overrightarrow{a}\overrightarrow{b}+\overrightarrow{b}\overrightarrow{a}-\overrightarrow{b}\overrightarrow{b}}{\sqrt{19}.\sqrt{7}}\\ &=\displaystyle \frac{2^{2}-3^{2}}{\sqrt{133}}=-\frac{5}{\sqrt{133}}\\ \angle \left ( \overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}-\overrightarrow{b} \right )&=\color{red}\arccos \left ( -\frac{5}{\sqrt{133}} \right ) \end{aligned} \end{array}$

$\color{blue}\textrm{Berikut contoh untuk bentuk sudutnya}$.

$\begin{array}{ll} 14.&\textrm{Diketahui}\: \: \vec{p} =(x,3,2),\: \: \textrm{dan}\\ & \vec{q}=(2,-6,3)\: .\: \textrm{Tentukan nilai}\: \: x\\ &\textrm{agar kedua vektor}\\ &\textrm{a}\quad \textrm{membentuk sudut lancip}\\ &\textrm{b}\quad \textrm{membentuk sudut siku-siku}\\ &\textrm{c}\quad \textrm{membentuk sudut tumpul}\\ &\textrm{d}\quad \textrm{sama panjang}\\\\ &\textbf{Jawab}\\ &\begin{aligned}\textrm{Dik}&\textrm{etahui bahwa}\\ \triangleright \quad &\vec{p} =(x,3,2)=\begin{pmatrix} x\\ 3\\ 2 \end{pmatrix}\: \: \textrm{dan}\\ \triangleright \quad &\vec{q}=(2,-6,3)=\begin{pmatrix} 2\\ -6\\ 3 \end{pmatrix}\\ \end{aligned}\\ &\textrm{Selanjutnya}\\ &\vec{p}\bullet \vec{q}=\begin{pmatrix} x\\ 3\\ 2 \end{pmatrix}\begin{pmatrix} 2\\ -6\\ 3 \end{pmatrix}\\ &\quad =2x-18+6=2x-12\\ &\textrm{Selanjutnya}\\ &\begin{aligned} \textrm{a}\quad&\textbf{Syarat lancip},\: \textrm{yaitu}:\: \vec{p}\bullet \vec{q}>0\\ &2x-12>0\Leftrightarrow 2x>12\Leftrightarrow x>6\\ \textrm{b}\quad&\textbf{Syarat siku-siku},\: \textrm{yaitu}:\: \vec{p}\bullet \vec{q}=0\\ &2x-12=0\Leftrightarrow 2x=12\Leftrightarrow x=6\\ \textrm{c}\quad&\textbf{Syarat tumpul},\: \textrm{yaitu}:\: \vec{p}\bullet \vec{q}<0\\ &2x-12<0\Leftrightarrow 2x<12\Leftrightarrow x<6\\ \textrm{d}\quad&\textbf{Syarat panjang kedua vektor sama}\\ & \textrm{yaitu}:\: \left |\vec{p} \right |= \left |\vec{q} \right |,\: \textrm{maka}\\ &\begin{aligned}&\sqrt{x^{2}+3^{2}+2^{2}}=\sqrt{2^{2}+(-6)^{2}+3^{2}}\\ &x^{2}+9+4=4+36+9\\ &x^{2}=36\\ &x=\pm \sqrt{36}=\pm 6\\ &\textrm{Jadi},\: \color{red}x=-6\: \: \color{black}\textrm{atau}\: \: \color{red}x=6 \end{aligned} \end{aligned} \end{array}$

DAFTAR PUSTAKA

Johanes, Kastolan, Sulasim. 2006. Kompetensi Matematika Program IPA 3A SMA Kelas XII Semester Pertama. Jakarta: YUDHISTIRA.
Kanginan, M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas X Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri, Sucipto, E. 2003. Buku Pelajaran Matematika SMU untuk Kelas 3 Program IPA. Jakarta: ERLANGGA.
Yuana, R.A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan Matematika dan Ilmu Alam. Solo: PT. TIGA SERANGKAI PUSTAKA MANDIRI.

Metode Horner-Kino (Lanjutan Materi Operasi Polinom)

TAMBAHAN

Pembagian Horner - Kino

Perhatikanlah bagan berikut

Sebagai tambahan penjelasan dari bagan di atas adalah

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Dengan metode Horner, tentukanlah}\\ & \textrm{nilai suku banyak berikut ini}!\\ &\textrm{a})\quad 4x^{4}-7x^{3}+8x^{2}-2x+3\: \: \: \textrm{jika}\: \: x=2\\ &\textrm{b})\quad 2x^{5}+3x^{3}-x+1\: \: \: \textrm{jika}\: \: x=-3\\ &\textrm{c})\quad 2x^{3}+x^{2}-2x+3\: \: \: \textrm{jika}\: \: x=\displaystyle \frac{1}{3}\\\\ &\textrm{Jawab}:\\ &\textrm{Diketahui bahwa}\\ &f(x)=\color{red}4x^{4}-7x^{3}+8x^{2}-2x+3\\ &\textbf{Cara biasa (Substitusi)}\\ &\begin{aligned}f(2)&=4(2)^{4}-7(2)^{3}+8(2)^{2}-2(2)+3\\ &=64-56+32-4+3\\ &=39\\ \textrm{Seba}&\textrm{gai catatan bahwa}:\\ &\: \textrm{Polinom}\: \: f(x)\: \: \textrm{tersebut di atas }\\ &\textrm{jika dibagi}\: (x-2)\: \textrm{bersisa 39} \end{aligned}\\ &\textbf{Cara Horner}\\ & \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Hitunglah nilai}\: \: a,\: b,\: c,\: \: \textrm{dan}\: \: d,\: \: \textrm{jika}\\ &\textrm{a})\quad -3x+4\equiv a(x-7)-b(2x-3)\\ &\textrm{b})\quad a(x-1)^{2}-b(x+4)\equiv 2x^{2}-5x-7\\ &\textrm{c})\quad 3x^{2}+2x-5\equiv (ax+1)(x+b)-c(x+1)+2(ab-c)\\ &\textrm{d})\quad x^{4}-8x^{3}+15x-20\equiv x^{4}+ax^{3}+(a+b)x^{2}+(2b-c)x+d\\ &\textrm{e})\quad \displaystyle \frac{a}{x-1}+\frac{b}{x+3}\equiv \displaystyle \frac{8}{x^{2}+2x-3}\\ &\textrm{f})\quad \displaystyle \frac{a}{x-1}+\frac{b}{x-4}\equiv \displaystyle \frac{3}{x-1}+\frac{20}{x-4}+\frac{x+17}{x^{2}-5x+4}\\ &\textrm{g})\quad \displaystyle \frac{5x-4}{x^{2}-1}\equiv \displaystyle \frac{a}{x-1}+\frac{b}{x+1}-\frac{3}{x^{2}-1}\\ &\textrm{h})\quad \displaystyle \frac{2x^{2}+x+2}{x^{3}-1}\equiv \displaystyle \frac{a}{x-1}+\frac{bx+c}{x^{2}+x+1}\\ &\textrm{i})\quad \displaystyle \frac{3x^{2}+2x-5}{x^{2}+5x+6}\equiv \displaystyle \frac{a(x-3)}{x+3}+\frac{b(x-5)}{x+2}+\frac{4c}{(x+2)(x+3)}\\ &\textrm{j})\quad x^{3}+ax^{2}+bx+c=0\: \: \textrm{dengan akar-akar}\: \: x_{1}=x_{2}=-1\: \: \textrm{dan}\: \: x_{3}=-3\\ &\textrm{k})\quad x^{3}+ax^{2}+bx+c=0\: \: \textrm{dengan akar-akar}\: \: 1,\: 2,\: \: \textrm{dan}\: \: 3 \end{array}$

$.\: \qquad\begin{aligned}\color{blue}\textrm{Yang diba}&\color{blue}\textrm{has hanya no. 6 d}\\ x^{4}-8x^{3}+&15x-20\\ \equiv \color{red}x^{4}\color{black}+a\color{red}x^{3}&+(a+b)\color{red}x^{2}\color{black}+(2b-c)\color{red}x\color{black}+d\\ \textrm{koefisien}\: \: \color{red}x^{4}&:\: \: 1=1\\ \textrm{koefisien}\: \: \color{red}x^{3}&:\: \: -8=a,\: \: \textrm{maka}\: \: a=-8\\ \textrm{koefisien}\: \: \color{red}x^{2}&:\: \: 0=a+b,\: \: \textrm{maka}\: \: b=-a=-(-8)=8\\ \textrm{koefisien}\: \: \color{red}x^{1}&:\: \: 15=2b-c,\: \: \textrm{maka}\: \: c=2b-15=2(8)-15=1\\ \textrm{koefisien}\: \: \color{red}x^{0}&:\: \: -20=d,\: \: \textrm{maka}\: \: d=-20\\ \end{aligned}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil bagi dan sisanya}!\\ &\begin{array}{ll}\\ \textrm{a})\quad (3x^{3}-2x^{2}+x-4):(x-1)&\textrm{k})\quad (x^{7}+3x^{5}+1):(x^{2}-1)\\ \textrm{b})\quad (2x^{4}-3x^{3}+x^{2}-5x+3):(x-2)&\textrm{l})\quad (x^{4}-3x^{3}-5x^{2}+x-6):(x^{2}-x-2)\\ \textrm{c})\quad (3-x+4x^{2}-x^{3}):(x-3)&\textrm{m})\quad (2x^{4}-3x^{2}-x+2):(x^{2}-2x+1)\\ \textrm{d})\quad (x^{4}-x^{2}+11):(x+4)&\textrm{n})\quad (3x^{6}+4x^{4}-2x-1):(x-1)(x^{2}-4)\\ \textrm{e})\quad (x^{3}-10x+9):(x+5)&\textrm{o})\quad (x^{4}-4x^{3}+2x^{2}-x+1):(2x+1)(x^{2}-3x+2)\\ \textrm{f})\quad (2x^{3}-5x^{2}-11x+8):(3x+1)&\textrm{p})\quad (x^{7}-7x^{4}+3x):(x^{3}-4x)\\ \textrm{g})\quad (5x^{3}+11x^{2}+7x-4):(5x+1)&\textrm{q})\quad (2x^{3}+x^{2}-4x+5):(x^{2}+x+1)\\ \textrm{h})\quad (2x^{3}+5x^{2}-4x+5):(2x+3)&\textrm{r})\quad (2x^{4}+x^{3}-3x+6):(x^{2}+x+2)\\ \textrm{i})\quad (2x^{3}+7x^{2}-5x+4):(2x-1)&\textrm{s})\quad (x^{4}-3x^{2}+7x-4):(x^{2}-2x-1)\\ \textrm{j})\quad (6x^{3}-x^{2}+3):(2x-3)&\textrm{t})\quad (3x^{3}+4x-8):(3x^{2}+x+2) \end{array} \end{array}$

$.\qquad\begin{aligned}&\textrm{Untuk pembahasan no. 3 i} \end{aligned}$

$.\qquad\begin{aligned}&\begin{array}{|l|l|}\hline \textrm{Pembagi}&\begin{aligned}&\textrm{Sisa}\\ &s(x)=\displaystyle \frac{7}{2} \end{aligned}\\\hline \begin{aligned}&2x-1=2(x-\frac{1}{2}) \end{aligned}&\begin{aligned}&\textrm{Hasil bagi}\\ &\displaystyle \frac{h(x)}{2}=\frac{2x^{2}+8x-1}{2}=x^{2}+4x-\frac{1}{2}\ \end{aligned}\\\hline \end{array} \end{aligned}$

$.\qquad\begin{aligned}&\textrm{Dan untuk pembahasan no. 3 m} \end{aligned}$

$.\qquad\begin{array}{|l|l|}\hline \textrm{Pembagi}&\begin{aligned}&\textrm{Sisa}\\ &s_{2}(x-p)+s_{1}\\ &1(x-1)+0=x-1 \end{aligned}\\\hline \begin{aligned}(x-p)(x-q)&=(x-1)(x-1)\\ &=(x-1)^{2} \end{aligned}&\begin{aligned}&\textrm{Hasil bagi}\\ &2x^{2}+4x+3 \end{aligned}\\\hline \end{array}$

$.\qquad\begin{aligned}&\textrm{Coba bandingkan dengan cara Horner-Kino berikut} \end{aligned}$

$.\qquad\begin{cases} \textrm{Suku banyak}: & f(x)=2x^{4}-3x^{2}-x+2 \\ \textrm{Pembagai}: & p(x)=x^{2}-2x+1 \\ &: -1\: \: \textrm{dari}\: -\frac{1}{1},\: \: \textrm{sedang}\: \: 2=-\left ( \frac{-2}{1} \right )\\ \textrm{Hasil bagi}:&h(x)=2x^{2}+4x+3\\ \textrm{Sisa bagi}:&s(x)=x-1 \end{cases}$.

$.\qquad \textrm{Sehingga},\\\\ 2x^{4}-3x^{2}-x+2=\color{red}\left ( x^{2}-2x+1 \right )\left ( 2x^{2}+4x+3 \right )+x-1$

$\begin{array}{ll}\\ 4.&\textrm{Jika diketahui akar-akar persamaan}\: \: x^{2}+4x-5=0\\ &\textrm{juga akar-akar untuk persamaan}\: \: 2x^{3}+9x^{2}-6x-5=0,\\ &\textrm{maka akar ketiga untuk persamaan yang kedua adalah}\: ...\\\\ &\textrm{Jawab}:\\ \end{array}$

$.\qquad \begin{cases} \textrm{Suku banyak}: & f(x)=2x^{3}+9x^{2}-6x-5 \\ \textrm{Pembagai}: & p(x)=x^{2}+4x-5 \\ &: 5\: \: \textrm{dari}\: -\left (\frac{-5}{1} \right ),\: \: \textrm{sedang}\: \: -4=\left ( \frac{4}{1} \right )\\ \textrm{Hasil bagi}:&h(x)=2x+1\\ \textrm{Sisa bagi}:&s(x)=0 \end{cases}$

$.\qquad\begin{aligned}&\textrm{Sehingga}\\ &2x^{3}+9x^{2}-6x-5=\left ( x^{2}+4x-5 \right )\left ( 2x+1 \right )\\ &\textrm{Jadi, akar yang lain (yang ketiga) adalah}\\ & (2x+1)\Rightarrow x=\color{red}-\displaystyle \frac{1}{2} \end{aligned}$

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi dan sisanya}!\\ &\begin{array}{ll}\\ \textrm{a})\quad (x^{7}+3x^{5}+1):(x^{2}-1)\\ \textrm{b})\quad (x^{4}-3x^{3}-5x^{2}+x-6):(x^{2}-x-2)\\ \textrm{c})\quad (2x^{3}+x^{2}-4x+5):(x^{2}+x+1)\\ \textrm{d})\quad (2x^{4}+x^{3}-3x+6):(x^{2}+x+2)\\ \textrm{e})\quad (x^{4}-3x^{2}+7x-4):(x^{2}-2x-1)\\ \textrm{f})\quad (3x^{3}+4x-8):(3x^{2}+x+2) \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: a\: \: \textrm{dan}\: \: b\: \: \textrm{bilangan bulat yang menyebabkan}\\ & x^{2}-x-1\: \: \textrm{merupakan faktor dari}\: \: ax^{3}+bx^{2}+1,\\ &\textrm{maka harga}\: \: b\: \: \textrm{adalah}\: ....\\ &\begin{array}{llllll}\\ \textrm{a}.&-2&&&\textrm{d}.&1\\ \textrm{b}.&-1&\textrm{c}.&0&\textrm{e}.&2 \end{array}\\ &\qquad\qquad\qquad\quad\qquad\qquad\qquad (\textrm{AHSME 1988})\end{array}$.

$\color{blue}\textrm{Pembagian Istimewa}$

Aturan pembagian istimewa adalah

$\begin{aligned}1.\quad &\displaystyle \frac{x^{n}-a^{n}}{x-a}=x^{n-1}a^{0}+x^{n-2}a^{1}+\cdots +x^{1}a^{n-2}+x^{0}a^{n-1}\\ &\qquad =\displaystyle \sum_{k=1}^{n}x^{n-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}x^{n-k}a^{k-1}\\ 2.\quad&\displaystyle \frac{x^{2n}-a^{2n}}{x+a}=x^{2n-1}a^{0}-x^{2n-2}a^{1}+\cdots +x^{1}a^{2n-2}-x^{0}a^{2n-1}\\ &\qquad =\displaystyle \sum_{k=1}^{2n}(-1)^{k+1}x^{2n-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}(-1)^{k+1}x^{2n-k}a^{k-1}\\ 3.\quad&\displaystyle \frac{x^{2n+1}+a^{2n+1}}{x+a}=x^{2n}a^{0}-x^{2n-1}a^{1}+\cdots -x^{1}a^{2n-1}+x^{0}a^{2n}\\ &\qquad =\displaystyle \sum_{k=1}^{2n+1}(-1)^{k+1}x^{2n+1-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}(-1)^{k+1}x^{2n+1-k}a^{k-1} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi polinom}\\ &\textrm{untuk tiap pembagian istimewa berikut}\\ &\textrm{a}.\quad \left ( x^{3}-a^{3} \right ):(x-a)\\ &\textrm{b}.\quad \left ( x^{4}-a^{4} \right ):(x+a)\\ &\textrm{c}.\quad \left ( x^{5}+a^{5} \right ):(x+a)\\\\ &\textrm{Jawab}:\\ &\textrm{a}.\quad \displaystyle \frac{\left ( x^{3}-a^{3} \right )}{(x-a)}=x^{2}+xa+a^{2}\: \: ....(\textrm{rumus}\: 1)\\ &\textrm{b}.\quad \displaystyle \frac{\left ( x^{4}-a^{4} \right )}{(x+a)}=x^{3}-x^{2}a+xa^{2}-a^{3}\: \: ....(\textrm{rumus}\: 2)\\ &\textrm{c}.\quad \displaystyle \frac{\left ( x^{5}+a^{5} \right )}{(x+a)}=x^{4}-x^{3}a+x^{2}a^{2}-xa^{3}+a^{4}\: \: ....(\textrm{rumus}\: 3) \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil bagi polinom}\\ &\textrm{untuk tiap pembagian istimewa berikut}\\ &\textrm{a}.\quad \left ( m^{8}-n^{8} \right ):(m+n)\\ &\textrm{b}.\quad \left ( x^{10}-y^{10} \right ):(x+y)\\\\ &\textrm{Jawab}:\\ &\textrm{a}.\quad \displaystyle \frac{\left ( m^{8}-n^{8} \right )}{(m+n)}=m^{7}-m^{6}n+m^{5}n^{2}-\cdots +mn^{6}-n^{7}\\ &\textrm{b}.\quad \displaystyle \frac{\left ( x^{10}-y^{10} \right )}{(x+y)}=x^{9}-x^{8}y+x^{7}y^{2}-\cdots +xy^{8}-y^{9}\\ \end{array}$

Operasi Polinom

$\color{blue}\textrm{C. Operasi Pada Polinom}$

$\textbf{1. Kesamaan dua buah polinom}$

Dua buah polinom dikatakan sama jika keduanya memiliki pangkat/derajat sama dan koefisien-koefisien suku yang sejenis juga sama.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{aligned}1.\quad \textrm{Misalkan diketahui}\: \quad&\\\color{red}x^{4}+Ax^{3}-4x^{2}-10x+3&=\color{red}(x^{2}+2x+3)(x^{2}+Bx+1)\\ x^{4}+Ax^{3}-4x^{2}-10x+3&=x^{4}+(B+2)x^{3}+(2B+4)x^{2}\\ &+(3B+2)x+3\\ \textrm{Elemen yang bersesuaian}&\\ \textrm{untuk}\: \: x^{1}\: :\: \color{red}-10&=\color{red}3B+2\\ \textrm{maka}\: \: \: B& =4\\ \textrm{untuk}\: \: x^{3}\: :\: \color{red}A&=\color{red}B+2\\ A&=-2 \end{aligned}$.

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah nilai}\: \: m\: \: \textrm{dan}\: \: n,\: \textrm{jika diketahui}\\ &\displaystyle \color{red}\frac{m}{x+1}+\frac{n}{x-2}=\frac{3x+4}{x^{2}-x-2}\\\\ &\textbf{Jawab}:\\ &\textrm{Kalikan kedua ruas dengan}\\ &\color{red}x^{2}-x-2\: \: \color{black}\textrm{atau}\: \: \color{red}(x+1)(x-2)\\ &\textrm{maka}\\ &\color{red}3x+4=m(x-2)+n(x+1)\\ &\Leftrightarrow 3x+4=(m+n)x+(-2m+n)\\ &\textrm{Dari bentuk kesamaan di atas didapatkan}\\ &\color{red}m+n=3\\ &\color{red}-2m+n=4\\ &\textrm{Dengan eliminasi substitusi akan}\\ &\textrm{didapatkan nilai}\: \: m=-\displaystyle \frac{1}{3}\: \: \textrm{dan}\: \: n=\frac{10}{3} \end{array}$.

$\begin{array}{ll}\\ 3.&\textrm{Diketahui kesamaan dua polinom}\\ &\displaystyle \color{red}5x^{2}-2x+3=ax^{2}+(b+c)x+7(b-c)\\ &\textrm{Tentukan nilai}\: \: a+8b-6c\\\\ &\textbf{Jawab}:\\ &\textrm{Dari soal diketahui bahwa}\\ &\begin{cases} a &=5 \\ b+c &=-2 \\ 7(b-c) &=3 \end{cases}\\ &\textrm{maka}\\ &7b+7c=-14\\ &7b-7c=3\qquad +\\\hline &14b=-11\Rightarrow b=-11/14\\ &\textrm{dan}\\ &7b+7c=-14\\ &7b-7c=3\qquad -\\\hline &14c=-17\Rightarrow c=-17/14\\ &\textrm{maka nilai}\: \: a+8b-6c\\ &=\color{red}5+8\left ( \displaystyle \frac{-11}{14} \right )-6\left (-\displaystyle \frac{17}{14} \right )\\ &=\color{red}5+\displaystyle \frac{14}{14}\color{black}=\color{red}5+1\color{black}=\color{red}6 \end{array}$.

$\textbf{2. Penjumlahan}$

Dua polinom dapat dijumlahkan jika hanya jika suku-sukunya sejenis, jika tidak maka tidak bisa

$\textbf{3. Pengurangan}$

Pada operasi pengurangan juga juga berlaku seperti pada operasi penjumlahan, yaitu pengurangan hanya bisa terjadi pada suku-suku yang sejenis saja yang lainnya tidak dapat dilakukan.

$\textbf{4. Perkalian}$

Pada jenis operasi ini dilakukan seperti mengalikan biasa yaitu mengalikan semua suku-suku secara distribusi dari kedua polinom tersebut.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Diketahui 2 suku banyak berikut}\\ &\begin{cases} p(x) &=x^{3}+2x^{2}+x-1 \\ q(x) &=x^{4}+5x+2 \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{penjumlahan keduanya}\\ &\textrm{b}.\quad \textrm{pengurangan}\: \: p(x)\: \: \textrm{oleh}\: \: q(x)\\\\ &\textrm{Jawab}:\\ &\begin{array}{lllllllllll}\\ p(x)=&&x^{3}&+&2x^{2}&+&x&-&1&\\ q(x)=&x^{4}&&&&+&5x&+&2&(+)\\\hline &\color{red}x^{4}\: +&\color{red}x^{3}&+&\color{red}2x^{2}&+&\color{red}6x&+&\color{red}1& \end{array}\\ &\textrm{poin b Silahkan dicoba sebagai latihan} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil kali perkalian}\\ &\textrm{dari dua polinom berikut}\\ &\textrm{a}.\quad 3x(-5x^{2})\\ &\textrm{b}.\quad 2a(7a-3)\\ &\textrm{c}.\quad (x+2)(x-5)\\ &\textrm{d}.\quad (3t-2)(2t^{2}-5t+3)\\ &\textrm{e}.\quad (5a^{2}+2)(5a^{2}-2)\\ &\textrm{f}.\quad (x^{3}-2x)(x^{2}+3x-4)\\ &\textrm{g}.\quad (2a^{3}+1)(-a-3)^{2}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&3x(-5x^{2})=-3.5x^{1+2}=\color{red}-15x^{3}\\ \textrm{b}.\quad&2a(7a-3)=2.7a^{1+1}-2.3a=\color{red}14a^{2}-6a\\ &\color{blue}\textrm{Selanjutnya kita langsungkan saja}\\ \textrm{c}.\quad&(x+2)(x-5)=x^{2}+(2-5)x-2.5\\ &\qquad\qquad \qquad\: =\color{red}x^{2}-3x-10\\ \textrm{d}.\quad&(3t-2)(2t^{2}-5t+3)\\ &\qquad = 6t^{3}-15t^{2}+9t-4t^{2}+10t-6\\ &\qquad = \color{red}6t^{3}-19t^{2}+19t-6\\ \textrm{e}.\quad&(5a^{2}+2)(5a^{2}-2)\\ &\qquad = 25a^{4}-10x^{2}+10a^{2}-4\\ &\qquad =\color{red}25a^{4}-4\\ \textrm{f}.\quad&(x^{3}-2x)(x^{2}+3x-4)\\ &x^{5}+3x^{4}-4x^{3}-2x^{3}-6x^{2}+8x\\ &\qquad =\color{red}x^{5}+3x^{4}-6x^{3}-6x^{2}+8x\\ \textrm{g}.\quad&(2a^{2}+1)(-a-3)^{2}\\ &\qquad =(2a^{2}+1)(a^{2}+6a+9)\\ &\qquad =2a^{4}+12a^{3}+18a^{2}+a^{2}+6a+9\\ &\qquad =\color{red}2a^{4}+12a^{3}+19a^{2}+6a+9 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil dari perkalian}\\ &\textrm{dua polinom berikut}\\ &\textrm{a}.\quad \begin{cases} p(x) &=x^{2}-x-1 \\ q(x) &=x^{2}+x+1 \end{cases}\\\\ &\textrm{b}.\quad \begin{cases} p(x) &=x^{5}+3x^{3}-x-1 \\ q(x) &=x^{4}+2x+1 \end{cases}\\\\ &\textrm{c}.\quad \begin{cases} p(x) &=x^{6}+3x-6 \\ q(x) &=x^{3}-6x+3 \end{cases}\\\\ &\textrm{d}.\quad \begin{cases} p(x) &=x^{2020}-x \\ q(x) &=x^{2}+x-1 \end{cases}\\\\ &\textrm{e}.\quad \begin{cases} p(x) &=x^{2021}-1 \\ q(x) &=x^{2019}+1 \end{cases}\\\\ &\textrm{Jawab}:\\ &\textrm{Poin a sampai d silahkan dicoba}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Diketahui bahwa}\\ &\begin{cases} p(x) &=x^{2021}-1 \\ q(x) &=x^{2019}+1 \end{cases}\\ &\textrm{maka}\: \: p(x)\times q(x)\\ &=\left ( x^{2021}-1 \right )\times \left ( x^{2019}+1 \right )\\ &=x^{2021+2019}+1\times x^{2021}-1\times x2019-1\times 1\\ &=\color{red}x^{4040}+x^{2021}-x^{2019}-1 \end{aligned} \end{array}$

$\textbf{5. Pembagian}$

Perhatikanlah ilustrasi pembagian bersusun panjang berikut

Misalkan untuk pembagian $x^{3}+4x^{2}-2x+4$ oleh $x-1$ adalah sebagai berikut:

Selanjutnya dari caontoh di atas kita mendapatkan,

$\begin{aligned}x^{3}&+4x^{2}-2x+4\\ &=(x-1)(x^{2}+5x+3)+7 \end{aligned}$

Sehingga dari uraian di atas secara umum pembagian polinom dapat dinyatakan bahwa:

$\textrm{Polinomial}=\textrm{Pembagi}\times \textrm{Hasil bagi}+\textrm{Sisa}$

$\textbf{a. Pembagian bentuk}\: (x-h)$

$\textbf{b. Pembagian bentuk}\: (ax+b)$

$\textbf{c. Pembagian bentuk}\: (ax^{2}+bx+c)$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: x^{3}+4x^{2}-2x+4\: \: \textrm{oleh}\: \: x-1\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: 4x^{3}-8x^{2}-x+5\: \: \textrm{oleh}\: \: 2x-1\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: x^{4}-2x^{2}-13x-19\: \: \textrm{oleh}\: \: x^{2}-2x-3\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

Catatan hasil bagi adalah pada contoh no.1 s.d 3 adalah pada tiap pembahasan di tiap nomornya adalah terletak di bagian atas (berwarna biru) dan sisa pembagiannya adalah yang terletak di bagian paling bawah (berwarna merah).

DAFTAR PUSTAKA

Kanginan, M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri, B.K. 2017. Matematika Jilid 2 untuk SMA/MA Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.
Sukino. 2017. Matematika Jilid 2 untuk SMA/MA Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA

Polinom (Suku Banyak)

$\color{blue}\textrm{A. Pendahuluan}$

Polinom disebut juga suku banyak. Polinom atau suku banyak adalah suatu bentuk variabel yang berpangkat/berderajat.

Secara definisi suku banyak (polinomial) dalam $x$ berderajat $n$ adalah:

Suatu bentuk

$\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_{2}x^{2}+a_{1}x^{1}+a_{0}$

dengan $n$ bilangan cacah serta $a_{0},\: a_{1},\: a_{2},\: ...,\: a_{n}$ koefisien dari suku $x$ dan $a_{n}\neq 0$ dengan $a_{0}$ sebagai suku tetap (konstan)nya.

Selanjutnya perhatikanlah tabel berikut!

$\color{purple}\begin{array}{|l|l|}\hline \begin{aligned}a_{n}&\: \: \textrm{adalah koefisien dari} \: \: x^{n}\\ a_{n-1}&\: \: \textrm{adalah koefisien dari} \: \: x^{n-1}\\ a_{n-2}&\: \: \textrm{adalah koefisien dari} \: \: x^{n-2}\\ \vdots &\\ a_{2}&\: \: \textrm{adalah koefisien dari} \: \: x^{2}\\ a_{1}&\: \: \textrm{adalah koefisien dari} \: \: x^{1}\\ a_{0}&\: \: \textrm{adalah konstanta} \\ &(\textrm{suku tetap}) \end{aligned}&\begin{aligned}a_{n}\: &\: \neq 0\\ n:&\: \: \textrm{bilangan cacah},\\ :&\: \: \textrm{adalah derajat (pangkat)} \\ &\: \: \textrm{tertinggi dalam suku} \\ &\: \: \textrm{banyak tersebut}&\\ &\\ &\\ &\end{aligned}\\\hline \end{array}$

$\LARGE\colorbox{yellow}{CONTOH SOAL 1}$

$\begin{aligned}1.\quad&\textrm{Polinom}\: \: \color{red}2x^{3}-6x^{2}+2020\: \: \color{black}\textrm{dapat dinyatakan}\\ &\textrm{dengan}\: \: \: \color{blue}2x^{3}-6x^{2}+0x^{1}+2020x^{0}\\ &\textrm{Polinom tersebut memiliki suku tetap}\: \: 2020\\ 2.\quad&\textrm{Polinom}\: \: \color{red}5x^{4}-8x^{3}+6x-2021 \: \: \color{black}\textrm{dapat dinyatakan}\\ &\textrm{dengan}\: \: \: \color{blue}5x^{4}-8x^{3}+0x^{2}+6x^{1}-2021x^{0}\\ &\textrm{Polinom tersebut memiliki suku tetap}\: \: -2021\\ 3.\quad&\textrm{Polinom}\: \: \color{red}x^{4}-2x^{3}+3x^{2}-2\sqrt{x}+1 \: \: \color{black}\textrm{tidak dapat}\\ &\textrm{dinamakan polinom, sebab ada variabel dari}\: \: \: \color{blue}x\\ &\textrm{yang berderajat bukan bilangan cacah}\\ 4.\quad&\textrm{Sedangkan polinom}\: \: \color{red}5-x+(2-x)(1+x+x^{2})\\ &\textrm{adalah bentuk polinom, karena dapat dinayatakan}\\ &\textrm{dengan}\: \: \: \color{blue}-x^{3}+x^{2}+7 \end{aligned}$

$\color{blue}\textrm{B. Nilai Polinom}$

Polinom atau suku banyak yang berderajat $\color{red}n$ yang selanjutnya dinyatakan dengan

$f(x)=\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_{1}x^{1}+a_{0}$

Berkaitan dengan kebutuhan penentuan nilai ini, dapat ditentukan dengan dua cara:

$\textbf{a. Substitusi}$

$\begin{aligned}&\textrm{Nilai suku banyak}\: \: \color{red}f(x)\: \: \textrm{berderajat}\\ &n\: \: \textrm{saat}\: \: \color{red}x = k\: \: \color{black}\textrm{adalah}\: \: \color{blue}f(k).\\ &\textrm{Jika}\: \: f(k)=0\: \: \textrm{maka}\: \: x = k\: \: \textrm{akar dari}\: \: f(x),\\ &\textrm{dan}\: \: (x-k)\: \: \textrm{faktor dari}\: \: f(x)\\ &\end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL 2}$

Jika suatu polinom dinyatakan dengan $f(x)$, maka nilai polinom itu untuk $x=3$ adalah $f(3)$.

Misalkan diketahui

$\begin{aligned}1.\quad f(x)&=x^{3}-1\\ \textrm{mak}&\textrm{a}\\ f(1)&=1^{3}-1=1-1=0\\ f(3)&=3^{3}-1=27-1=26\\ f(-4)&=(-4)^{2}-1=-64-1=-65 \end{aligned}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui}\: \: h(x)=2x^{3}+5x^{2}-12x-6\\ &\textrm{Tentukanlah nilai untuk}\: \: h(-2),\: h(-1),\\ &h(0),\: h(1),\: \: \textrm{dan}\: \: h(2)\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{array}{|c|c|l|}\hline \color{red}x=k&\color{red}h(k)&\qquad\qquad\qquad\qquad\color{red}\textrm{Nilai}\\\hline x=-2&h(-2)&\begin{aligned}h(-2)&=2(-2)^{3}+5(-2)^{2}-12(-2)-6\\ &=-16+20+24-6\\ &=22 \end{aligned}\\\hline x=-1&h(-1)&\begin{aligned}h(-1)&=2(-1)^{3}+5(-1)^{2}-12(-1)-6\\ &=-2+5+12-6\\ &=9 \end{aligned}\\\hline x=0&h(0)&\begin{aligned}h(0)&=2(0)^{3}+5(0)^{2}-12(0)-6\\ &=-6 \end{aligned}\\\hline x=1&h(1)&\begin{aligned}h(1)&=2(1)^{3}+5(1)^{2}-12(1)-6\\ &=2+5-12-6\\ &=-11 \end{aligned}\\\hline x=2&h(2)&\begin{aligned}h(2)&=2(2)^{3}+5(2)^{2}-12(2)-6\\ &=16+20-24-6\\ &=6 \end{aligned}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Diketahui}\: \: p(x)=x-2019\\ &\textrm{dan}\: \: q(x)=x^{2019}+1.\: \textrm{Tentukanlah}\\ &\textrm{nilai untuk}\: \: p\left ( q(2) \right )\: \: \textrm{dan}\: \: q\left ( p(2) \right )\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Yang dibahas yang bagian}\: \: p\left ( q(2) \right )\\ &q(2)=2^{2019}+1,\: \textrm{maka nilai}\\ &\begin{aligned}p\left ( q(2) \right )&=\left ( 2^{2019}+1 \right )-2019\\ &=2^{2019}-2018 \end{aligned}\\\\ &\textrm{Untuk yang}\: \: q\left ( p(2) \right )\: \: \textrm{adalah}\\ &p(2)=\cdots , \: \textrm{maka nilai}\\ &\begin{aligned}q\left ( p(2) \right )&=\because \cdots ^{2019}+1\\ &=\cdots \end{aligned} \end{array}$

$\textbf{b. Horner/Sintetik}$

Nilai suatu polinom dapat ditentukan dengan pembagian sintesis Horner

Misalkan:

$\begin{aligned}f(x)&=\color{blue}ax^{3}+bx^{2}+cx+d\: \: \color{black}\textrm{saat akan dibagi}\\ &\color{red}x=h,\: \: \color{black}\textrm{maka pembagian Horner itu}:\\ & \end{aligned}$

Perhatikan bahwa proses ke bawah adalah berup proses penjumlahan.

Proses di atas akan sama saat kita mensubstitusikan $\color{red}x=h$ ke dalam $\color{red}f(x)$, yaitu:

$\begin{aligned}f(x)&=\color{blue}ax^{3}+bx^{2}+cx+d\: \: \textrm{saat}\\ &\color{red}x=h,\: \: \color{black}\textrm{maka}\\ f(\color{red}h\color{black})&=a\color{red}h^{3}\color{black}+b\color{red}h^{2}\color{black}+c\color{red}h\color{black}+d\\ &\\ &\textbf{Cukup JELAS bukan}? \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL 3}$

$\begin{array}{l}\\ \textrm{Tentukanlah nilai dari}\: \: f(4)\: \: \textrm{jika}\\ \textrm{diketahui}\: \: f(x)=x^{3}-x-5\\ \textrm{Jawab}:\\ \begin{aligned}(1).\quad&\textrm{Cara substitusi langsung}\\ &f(x)=x^{3}-x-5\\ &f(4)=\color{red}4^{3}-4-5\\ &\qquad=\color{red}64-9=\color{blue}55\\ (2).\quad&\textrm{Cara Horner}\\ &\textrm{Karena}\: \: f(x)=x^{3}-x-5\\ &\textrm{dan koefisiennya yang akan}\\ &\textrm{adalah}:\\ & a_{3}=1,\: a_{2}=0,\: a_{1}=-1,\: \&\: a_{0}=-5\\ &\textbf{maka bagan pembagian Hornernya}\\ &\begin{array}{ll|llllllllll}\\ &\color{red}x=4&1&\color{blue}0&\color{magenta}-1&-5&\\ &&&&&&\\ &&&\color{blue}4&\color{magenta}16&60&+\\\hline &&1&\color{blue}4&\color{magenta}15&55 \end{array} \end{aligned} \end{array}$

Contoh 8 Soal dan Pembahasan Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 36.&\textrm{Persamaan lingkaran yang menyinggung}\\ &\textrm{sumbu X serta melalui titik potong}\\ &\textrm{lingkaran}\: \: (x+1)^{2}+(y+2)^{2}=1\: \: \textrm{dan}\\ &x^{2}+y^{2}+3x+3y+4=0\: \: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-4x+2y+4=0\\ &\textrm{b}.\quad x^{2}+y^{2}-4x+2y-4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-4x-2y-4=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}+4x+2y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}+4x+2y-4=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=(x+1)^{2}+(y+2)^{2}=1\\ &\qquad \Leftrightarrow x^{2}+y^{2}+2x+4y+4=0\\ &\bullet \: L_{2}=x^{2}+y^{2}+3x+3y+4=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-x+y=0\Leftrightarrow y=x\\ &\color{blue}\textrm{Dengan cara coba-coba, maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}+2x+4y+4+p(-x+y)=0\\ &\color{blue}\textrm{Untuk}\: \: p=1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4+(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+x+5y+4=0\\ &\color{blue}\textrm{Untuk}\: \: p=-1\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-(-x+y)=0\\ &\Leftrightarrow x^{2}+y^{2}+3x+3y+4=0\\ &\color{blue}\textrm{Dan untuk}\: \: p=-2\\ &\Leftrightarrow x^{2}+y^{2}+2x+4y+4-2(-x+y)=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}+4x+2y+4=0 \end{aligned} \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya} \end{array}$

DAFTAR PUSTAKA

Kartini, Suprapto, Subandi, dan Setiadi, U. 2005. Matematika Program Studi Ilmu Alam Kelas XI untuk SMA dan MA. Klaten: INTAN PARIWARA.
Kanginan M., Nurdiansyah, H., Akhmad, G. 2016. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: YRAMA WIDYA.
Noormandiri. 2017. Matematika Jilid 2 untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SEWU
Sukino. 2017. Matematika Jilid 2 untuk Kelas SMA/MA Kelas XI Kelompok Peminatan dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Contoh 7 Soal dan Pembahasan Materi Hubungan Dua Lingkaran

$\begin{array}{ll}\\ 31.&\textrm{Persamaan lingkaran yang melalui titik}\\ &(0,0)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x-8y-11=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-6y-22=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-12x+10y=0\\ &\textrm{b}.\quad x^{2}+y^{2}+8x-10y=0\\ &\textrm{c}.\quad x^{2}+y^{2}-8x+12y=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-8x-10y=0\\ &\textrm{e}.\quad x^{2}+y^{2}+12x-8y=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x-8y-11=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-6y-22=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=-2x-2y+11=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (0,0), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x-8y-11 +p(-2x-2y+11)=0\\ &\Leftrightarrow 0^{2}+0^{2}-0-0-11+p(0+11)=0\\ &\Leftrightarrow p=\color{blue}1 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x-8y-11+(-2x-2y+11)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-10y=0 \end{aligned} \end{array}$.

Berikut ilustrasi gambarnya

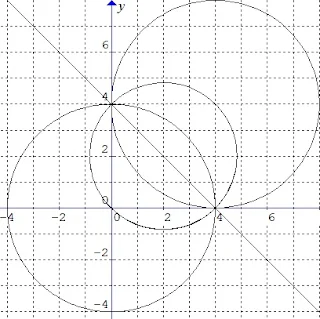
$\begin{array}{ll}\\ 32.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (8,4)\: \: \textrm{dan titik potong lingkaran}\: x^{2}+y^{2}=16\\ &\textrm{dan}\: \: x^{2}+y^{2}-4x-4y=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-8x-8y-16=0\\ &\textrm{b}.\quad x^{2}+y^{2}-8x+8y+16=0\\ &\textrm{c}.\quad \color{red}x^{2}+y^{2}-8x-8y+16=0\\ &\textrm{d}.\quad x^{2}+y^{2}+8x+8y-16=0\\ &\textrm{e}.\quad x^{2}+y^{2}+8x+8y+16=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-16=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-4x-4y=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=4x+4y-16=0\\ &\Leftrightarrow x+y=4\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (8,4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-16+p(x+y-4)=0\\ &\Leftrightarrow 8^{2}+4^{2}-16+p(8+4-4)=0\\ &\Leftrightarrow -8p=\color{blue}64\color{black}\Leftrightarrow p=\color{blue}-8 \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-16-8(x+y-4)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-8x-8y+16=0 \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnyanya} \end{array}$.

$\begin{array}{ll}\\ 33.&\textrm{Persamaan lingkaran yang melalui titik}\\ & (7,-4)\: \: \textrm{dan titik potong kedua lingkaran}\\ &x^{2}+y^{2}-6x+8y-27=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-26x+4y+121=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad x^{2}+y^{2}-36x-2y+121=0\\ &\textrm{b}.\quad x^{2}+y^{2}+24x-4y-222=0\\ &\textrm{c}.\quad 3x^{2}+3y^{2}-18x+2y-121=0\\ &\textrm{d}.\quad \color{red}x^{2}+y^{2}-36x+2y+195=0\\ &\textrm{e}.\quad x^{2}+y^{2}+24x+2y+195=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa}:\: \: L_{3}=L_{1}+p(L_{1}-L_{2})=0\\ &\textrm{dengan}\\ &\bullet \: L_{1}=x^{2}+y^{2}-6x+8y-27=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-26x+4y+121=0\\ &\textrm{Untuk}\: \: L_{1}-L_{2}=20x+4y-148=0\\ &\textrm{Karena}\: \: L_{3}\: \: \textrm{melalui}\: \: (7,-4), \: \textrm{maka}\\ &\begin{aligned}L_{3}&=L_{1}+p(L_{1}-L_{2})=0\\ &=x^{2}+y^{2}-6x+8y-27\\ &\qquad+p(20x+4y-148)=0\\ &\Leftrightarrow 7^{2}+(-4)^{2}-42-32-27\\ &\qquad+p(140-16-148)=0\\ &\Leftrightarrow -24p=\color{blue}36\color{black}\Leftrightarrow p=\color{blue}-\displaystyle \frac{3}{2} \end{aligned}\\ &\textrm{Sehingga}\\ &L_{3}=x^{2}+y^{2}-6x+8y-27\\ &\qquad-\displaystyle \frac{3}{2}(20x+4y-148)=0\\ &\Leftrightarrow L_{3}=\color{red}x^{2}+y^{2}-36x+2y+195=0 \end{aligned} \end{array}$.

Berikut ilustrasi gambarnya

Jika dimensi gambar diperkecil menjadi

$\begin{array}{ll}\\ 34.&\textrm{Persamaan lingkaran yang melalui perpotongan}\\&\textrm{lingkaran}\: \: x^{2}+y^{2}-12x+6y+20=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-16x-14y+64=0\: \: \textrm{serta pusatnya}\\ &\textrm{terletak pada garis}\: \: 8x-3y-19=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-20x-34y+108=0\\ &\textrm{b}.\quad x^{2}+y^{2}-16x+12y+96=0\\ &\textrm{c}.\quad x^{2}+y^{2}-12x+20y+88=0\\ &\textrm{d}.\quad x^{2}+y^{2}+16x-24y+108=0\\ &\textrm{e}.\quad x^{2}+y^{2}+22x-34y+96=0\\\\ &\textbf{Jawab}:\\ &\begin{aligned}&\textrm{Diketahui bahwa persamaan lingkaran}:\\ &\bullet \: L_{1}=x^{2}+y^{2}-12x+6y+20=0\\ &\bullet \: L_{2}=x^{2}+y^{2}-16x-14y+64=0\\ &\textrm{Persamaan tali busurnya (garis kuasa)}\\ &\textrm{adalah}:\\ &L_{1}(x,y)-L_{2}(x,y)\\ &=4x+20y-44=0\Leftrightarrow \color{blue}x=11-5y\\ &\textrm{Selanjutnya dengan substitusi }\\ &\begin{aligned}&x^{2}+y^{2}-12x+6y+20=0\\ &\Leftrightarrow (x-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (\color{blue}11-5y\color{black}-6)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow (y-5y)^{2}+(y+3)^{2}=25\\ &\Leftrightarrow 26y^2-44y+9=0 \end{aligned}\\ &\textrm{Sehingga dengan}\: \: \color{red}\textrm{memodifikasi}\\ &\begin{aligned}&26y^2-44y+9=0\\ &\Leftrightarrow 25y^2-44y+y^2+9=0\\ &\quad\textrm{arahkan ke bentuk kuadrat sempurna}\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+8=0\\ &\Leftrightarrow 25y^2-10y+1+y^2-34y+17^{2}-17^{2}+8=0\\ &\Leftrightarrow (5y-1)^{2}+(y-17)^{2}-281=0\\ &\quad \textrm{ingat bahwa ada tali busur}\: \: \color{blue}5y=11-x\\ &\Leftrightarrow (\color{blue}11-x\color{black}-1)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow (10-x)^{2}+(y-17)^{2}-281=0\\ &\Leftrightarrow x^{2}-20x+100+y^{2}-34y+289-281=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-20x-34y+108=0 \end{aligned} \end{aligned}\\ &\textbf{Berikut ilustrasi gambarnya} \end{array}$

$\begin{array}{ll}\\ 35.&\textrm{Persamaan lingkaran dengan titik pusat}\\ &\textrm{pada garis}\: \: x+2y-3=0\: \: \textrm{dan melalui}\\ &\textrm{titik potong dua lingkaran}\\ &x^{2}+y^{2}-2x-4y+1=0\: \: \textrm{dan}\\ &x^{2}+y^{2}-4x-2y+4=0\: \: \textrm{adalah}\: ....\\ &\textrm{a}.\quad \color{red}x^{2}+y^{2}-6x+7=0\\ &\textrm{b}.\quad x^{2}+y^{2}-3y+4=0\\ &\textrm{c}.\quad x^{2}+y^{2}-2x-2y+1=0\\ &\textrm{d}.\quad x^{2}+y^{2}-2x-4y+4=0\\ &\textrm{e}.\quad x^{2}+y^{2}-3x-2y+7=0\\\\ &\textbf{Jawab}:\\ &\color{blue}\textbf{Alternatif 1}\\ &\textrm{Gunakan cara pembahasan sebagaimana pada}\\ &\textrm{nomor-nomor sebelumnya}\\ &\color{blue}\textbf{Alternatif 2}\\ &\begin{aligned}&\textrm{Diketahui}\\ &L_{1}\equiv x^{2}+y^{2}-2x-4y+1=0,\: \: \textrm{dan}\\ &L_{2}\equiv x^{2}+y^{2}-4x-2y+4=0\\ &\textrm{Persamaan}\: \: \color{red}\textrm{tali busur}\: \color{black}\textrm{dari kedua}\\ &\textrm{lingkaran tersebut adalah}:\\ &\color{blue}L_{1}(x,y)- L_{2}(x,y)=0\\ &\Leftrightarrow x^{2}+y^{2}-2x-4y+1\\ &-(x^{2}+y^{2}-4x-2y+4)=0\\ &\Leftrightarrow 2x-2y-3=0\\ &\textrm{Selanjutnya perlu ditentukan juga}\\&\textrm{Persamaan}\: \: \color{red}\textrm{berkas lingkaran}\: \color{black}\textrm{melalui}\\ &\textrm{titik-titik potong kedua lingkaran}\\ &\textrm{di atas adalah}:\\ &L_{1}+\lambda L_{2}=0\\ &x^{2}+y^{2}-2x-4y+1\\ &\qquad+\lambda \left ( x^{2}+y^{2}-4x-2y+4 \right )=0\\ &\Leftrightarrow (1+\lambda )x^{2}+(1+\lambda )y^{2}-(2+4\lambda )x\\ &\qquad -(4+2\lambda )y+1+4\lambda =0\\ &\textrm{Saat}\: \: \lambda =-1,\: \textrm{maka persamaan berkas}\\ &\textrm{lingkarannya adalah}:\: 2x-2y-3=0\\ &\textrm{Hal ini hasilnya sama persis saat kita}\\ &\textrm{menentukan persamaan}\: \color{red}\textrm{tali busur}\: \color{black}\textrm{di atas}\\ &\textrm{Selanjutnya kita ambil}\\ &L_{2}-(L_{1}+\lambda L_{2})=0\\ &\Leftrightarrow x^{2}+y^{2}-4x-2y+4-(2x-2y-3)=0\\ &\Leftrightarrow \color{red}x^{2}+y^{2}-6x+7=0 \end{aligned} \end{array}$.

Gambar mula-mula

Lingkaran baru yang berpusat di (3,0)

Invers Fungsi Trigonometri, Koordinat Kartesius dan Koordinat Kutub

Lanjutan Materi Fungsi Trigonometri dan Grafiknya

F. 2 Garfik Fungsi Trigonometri

F. 2. 1 Grafik Fungsi Sinus

$\color{blue}\begin{array}{|c|c|c|c|c|c|c|c|c|c| }\hline \color{magenta}x&0&\frac{\pi }{6}&\frac{\pi }{4}&\frac{\pi }{3}&\frac{\pi }{2}&\frac{2\pi }{3}&\frac{3\pi }{4}&\frac{5\pi }{6}&\pi \\\hline \color{red}f(x)&0&\frac{1}{2}&\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{3}&1&\frac{1}{2}\sqrt{3}&\frac{1}{2}\sqrt{2}&\frac{1}{2}&0\\\hline \color{magenta}x&\frac{7\pi }{6}&\frac{5\pi }{4}&\frac{4\pi }{3}&\frac{3\pi }{2}&\frac{5\pi }{3}&\frac{7\pi }{4}&\frac{11\pi }{6}&2\pi & \\\hline \color{red}f(x)&-\frac{1}{2}&-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{3}&-1&-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\sqrt{2}&-\frac{1}{2}&0&\\\hline \end{array}$.

F. 2. 2 Grafik Fungsi Cosinus

$\color{blue}\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \color{black}x&0&\frac{\pi }{6}&\frac{\pi }{4}&\frac{\pi }{3}&\frac{\pi }{2}&\frac{2\pi }{3}&\frac{3\pi }{4}&\frac{5\pi }{6}&\pi \\\hline \color{red}f(x)&1&\frac{1}{2}\sqrt{3}&\frac{1}{2}\sqrt{2}&\frac{1}{2}&0&-\frac{1}{2}&-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{3}&-1\\\hline \color{black}x&\frac{7\pi }{6}&\frac{5\pi }{4}&\frac{4\pi }{3}&\frac{3\pi }{2}&\frac{5\pi }{3}&\frac{7\pi }{4}&\frac{11\pi }{6}&2\pi&\\\hline \color{red}f(x)&-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\sqrt{2}&-\frac{1}{2}&0&\frac{1}{2}&\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{3}&1&\\\hline \end{array}$.

F. 2. 3 Grafik Fungsi Tangen

$\color{blue}\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \color{black}x&0&\frac{\pi }{6}&\frac{\pi }{4}&\frac{\pi }{3}&\frac{\pi }{2}&\frac{2\pi }{3}&\frac{3\pi }{4}&\frac{5\pi }{6}&\pi \\\hline \color{red}f(x)&0&\frac{1}{3}\sqrt{3}&1&\sqrt{3}&\infty &-\sqrt{3}&-1&-\frac{1}{3}\sqrt{3}&0\\\hline \color{black}x&\frac{7\pi }{6}&\frac{5\pi }{4}&\frac{4\pi }{3}&\frac{3\pi }{2}&\frac{5\pi }{3}&\frac{7\pi }{4}&\frac{11\pi }{6}&2\pi&\\\hline \color{red}f(x)&\frac{1}{3}\sqrt{3}&1&\sqrt{3}&\infty &-\sqrt{3}&-1&-\frac{1}{3}\sqrt{3}&0&\\\hline \end{array}$.

Pada fungsi Tangen demikian juga nanti Cotangennya ada beberapa nilai fungsinya yang tidak terdefinisi. Dalam fungsi Tangen fungsi, nilai fungsi yang tidak terdefini terdapat pada saat nilai $x=\displaystyle \frac{\pi }{2}=90^{\circ}$ dan $x=\displaystyle \frac{3\pi }{2}=270^{\circ}$. Sehingga pada saat posisi nilai itu, maka dibuatlah garis bantu berupa garis putus-putus pada grafik yang dan ditampakkan berupa garis vertikal yang selanjutnya garis vertikal itu disebut sebagai asimtot.

F. 2. 4 Menggambar Grafik Fungsi Trigonometri

$\begin{aligned}&\textrm{untuk bentuk}\\ &f(x)=\begin{cases} y &=a\sin bx+c \\ y &=a\cos bx+c \\ y & =a\tan bx+c \end{cases}\\ &\begin{array}{|c|l|l|}\hline 1.&a&\textrm{Amplitudo}\\\hline 2.&b&\textrm{Periode}\\\hline 3.&c&\textrm{Geseran}\\\hline \end{array} \end{aligned}$.

$\LARGE\colorbox{yellow}{ CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Gambarlah grafik fungsi berikut} \\ &\textrm{jika}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{a}.\quad f(x)=-2\sin x\\ &\textrm{b}.\quad f(x)=3\cos x\\ &\textrm{c}.\quad f(x)=\displaystyle \frac{1}{2}\sin x\\ &\textrm{d}.\quad f(x)=4\cos x\\ &\textrm{e}.\quad f(x)=2\tan x\\\\&\color{blue}\textrm{Jawab}:\\&\begin{aligned}& \end{aligned} \end{array}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.1 a}\\ &y=f(x)=-2\sin x=a\sin bx+c\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |-2 \right |=2\\\hline 2.&b&\textrm{Periode}&\displaystyle \frac{2\pi }{b}=2\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.1 b}\\ &y=f(x)=3\cos x=a\cos bx+c\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |3 \right |=3\\\hline 2.&b&\textrm{Periode}&\displaystyle \frac{2\pi }{b}=2\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.1 c}\\ &y=f(x)=\displaystyle \frac{1}{2}\sin x=a\sin bx+c\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |\displaystyle \frac{1}{2} \right |=\displaystyle \frac{1}{2}\\\hline 2.&b&\textrm{Periode}&\displaystyle \frac{2\pi }{b}=2\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.1 d}\\ &y=f(x)=\displaystyle 4\cos x=a\cos bx+c\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |\displaystyle 4 \right |=\displaystyle 4\\\hline 2.&b&\textrm{Periode}&\displaystyle \frac{2\pi }{b}=2\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.1 e}\\ &y=f(x)=\displaystyle 2\tan x=a\tan bx+c\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |\displaystyle 2 \right |=\displaystyle 2\\\hline 2.&b&\textrm{Periode}&\displaystyle \frac{2\pi }{b}=2\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$\begin{array}{ll}\\ 2.&\textrm{Gambarlah grafik fungsi berikut} \\ &\textrm{jika}\: \: 0^{\circ}\leq x\leq 360^{\circ}\\ &\textrm{a}.\quad f(x)=\left |-2\sin x \right |\\ &\textrm{b}.\quad f(x)=\left |3\cos x \right |\\ &\textrm{c}.\quad f(x)=\left |\displaystyle \frac{1}{2}\sin x \right |\\ &\textrm{d}.\quad f(x)=\left |4\cos x \right |\\ &\textrm{e}.\quad f(x)=\left |2\tan x \right |\\\\&\color{blue}\textrm{Jawab}:\\&\begin{aligned}& \end{aligned} \end{array}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.2 a}\\ &y=f(x)=\left |-\displaystyle 2\sin x \right |=\left |a\sin bx+c \right |\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |\displaystyle 2 \right |=\displaystyle 2\\\hline 2.&b&\textrm{Periode}&\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$.\: \qquad\begin{aligned}&\color{blue}\textrm{No.2 b}\\ &y=f(x)=\left |\displaystyle 3\cos x \right |=\left |a\cos bx+c \right |\\ &\begin{array}{|c|l|l|l|}\hline 1.&a&\textrm{Amplitudo}&\left |\displaystyle 3 \right |=\displaystyle 3\\\hline 2.&b&\textrm{Periode}&\pi \Leftrightarrow b=1\\\hline 3.&c&\textrm{Geseran}&0\\\hline \end{array} \end{aligned}$.

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

Silahkan selesaikan soal yg belum dibahas

DAFTAR PUSTAKA

Yuana, R.A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Mata Pelajaran Wajib. Solo: TIGA SERANGKAI PUSTAKA MANDIRI.