PAS MATEMATIKA BLOG

Contoh Soal Vektor di Dimensi Dua (Matematika Peminatan Kelas X) Bagian 2

$\begin{array}{ll}\\ 4.&\color{blue}\textrm{Perhatikanlah ilustrasi gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Nyatakanlah vektor-vektor di atas dalam}\\ &\textrm{a}.\quad \textrm{vektor kolom}\\ &\textrm{b}.\quad \textrm{vektor baris}\\ &\textrm{c}.\quad \textrm{vektor basis}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Vektor di atas saat dinyatakan dengan}\\ &\begin{array}{|c|l|l|l|}\hline \textrm{No}&\quad\textrm{Kolom}&\qquad\textrm{Baris}&\qquad\textrm{Basis}\\\hline 1&\bar{a}=\begin{pmatrix} 2\\ 4 \end{pmatrix}&\bar{a}=\begin{pmatrix} 2, & 4 \end{pmatrix}&\bar{a}=2\bar{i}+4\bar{j}\\\hline 2&\bar{b}=\begin{pmatrix} 4\\ 2 \end{pmatrix}&\bar{b}=\begin{pmatrix} 4, & 2 \end{pmatrix}&\bar{b}=4\bar{i}+2\bar{j}\\\hline 3&\bar{c}=\begin{pmatrix} 5\\ 0 \end{pmatrix}&\bar{c}=\begin{pmatrix} 5, & 0 \end{pmatrix}&\bar{c}=5\bar{i}\\\hline 4&\bar{d}=\begin{pmatrix} -2\\ -4 \end{pmatrix}&\bar{d}=\begin{pmatrix} -2, & -4 \end{pmatrix}&\bar{d}=-2\bar{i}-4\bar{j}\\\hline 5&\bar{e}=\begin{pmatrix} 0\\ -4 \end{pmatrix}&\bar{e}=\begin{pmatrix} 0, & -4 \end{pmatrix}&\bar{e}=-4\bar{j}\\\hline 6&\bar{f}=\begin{pmatrix} 3\\ -3 \end{pmatrix}&\bar{f}=\begin{pmatrix} 3, & -3 \end{pmatrix}&\bar{f}=3\bar{i}-3\bar{j}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 5&\textrm{Tentukanlah panjang atau besar dari}\\ &\textrm{vektor-vektor berikut}\\ &\textrm{a}.\quad \bar{a}=\begin{pmatrix} -4\\ 3 \end{pmatrix}\quad\quad\quad \textrm{d}.\quad \bar{d}=\begin{pmatrix} 6, &-8 \end{pmatrix}\\ &\textrm{b}.\quad \bar{b}=\begin{pmatrix} 5\\ 0 \end{pmatrix}\qquad\quad\quad \textrm{e}.\quad \bar{e}=2\bar{i}+4\bar{j}\\ &\textrm{c}.\quad \bar{c}=\begin{pmatrix} 4, & -6 \end{pmatrix}\: \qquad \textrm{f}.\quad \bar{f}=-5\bar{i}+12\bar{j}\\\\ &\textrm{Jawab}:\\ &\color{blue}\textrm{Lambang panjang suatu vektor adalah}:\\ &\color{red}\left | \begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix} \right |=\sqrt{u_{1}^{2}+u_{2}^{2}},\: \: \color{black}\textrm{maka}\\ &\bullet \: \left | \bar{a} \right |=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5\\ &\bullet \: \left | \bar{b} \right |=\sqrt{5^{2}+0^{2}}=\sqrt{25}=5\\ &\bullet \: \left | \bar{c} \right |=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}=2\sqrt{13}\\ &\bullet \: \left | \bar{d} \right |=\sqrt{6^{2}+(-8)^{2}}=\sqrt{36+64}=\sqrt{100}=10\\ &\bullet \: \left | \bar{e} \right |=\sqrt{2^{2}+4^{2}}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\\ &\bullet \: \left | \bar{f} \right |=\sqrt{(-5)^{2}+12^{2}}=\sqrt{25+144}=\sqrt{169}=13 \end{array}$

$\begin{array}{ll}\\ 6&\textrm{Pada soal no.4 di atas dengan menggunakan}\\ &\textrm{aturan segitiga dan jajar genjang, gambarlah}\\ &\textrm{vektor-vektor berikut pada kertas berpertak}\\ &\textrm{a}.\quad \bar{a}+\bar{b}\qquad\qquad\qquad \textrm{d}.\quad \left ( \bar{a}+\bar{b} \right )+\bar{c}\\ &\textrm{b}.\quad \bar{b}+\bar{c}\, \qquad\qquad\qquad \textrm{e}.\quad 2\bar{a}+\bar{e}+2\bar{b}+3\bar{d}\\ &\textrm{c}.\quad \bar{a}+\left (\bar{b}+\bar{c} \right )\: \: \quad \qquad \textrm{f}.\quad 2\left ( \bar{a}+\bar{b}+\bar{c}+\bar{d}+\bar{e} \right )\\\\ &\textrm{Jawab}:\\ \end{array}$

Lanjutan Materi Vektor : Proyeksi Ortogonal Suatu Vektor

$\color{blue}\begin{aligned}\textrm{A}.\quad&\textrm{Panjang Proyeksi Ortogonal Suatu}\\ &\textrm{Vektor pada vektor lain} \end{aligned}$.

Perhatikanlah ilstrasi gambar yang dibentuk dari dua vektor berikut

Pada gambar di atas

$\begin{array}{|c|c|}\hline \triangle \textrm{OAC}&\angle \left ( \overrightarrow{a},\overrightarrow{b} \right )\\\hline \begin{aligned}\cos \theta &=\displaystyle \frac{\left | \overrightarrow{c} \right |}{\left | \overrightarrow{a} \right |}\\ \Leftrightarrow \left | \overrightarrow{c} \right |&=\left | \overrightarrow{a} \right |\cos \theta \: \: ........(1) \end{aligned}&\begin{aligned}\cos \theta &=\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |}\: \: ........(2) \end{aligned}\\\hline \end{array}$.

$\begin{aligned}\textrm{Dari}\: \: (1)\: \: &\textrm{dan} \: \: (2)\: \: \textrm{diperoleh}\\ \left | \overrightarrow{c} \right |&=\left | \overrightarrow{a} \right |\cos \theta \\ &=\left | \overrightarrow{a} \right |\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{a} \right |\left | \overrightarrow{b} \right |} \right )\\ &=\color{red}\left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right | \end{aligned}$

$\color{blue}\begin{aligned}\textrm{B}.\quad&\textrm{Proyeksi Ortogonal Suatu Vektor}\\ &\textrm{pada vektor lain} \end{aligned}$.

$\begin{array}{|c|}\hline {\textrm{Perhatikan pula misal}\: \: \hat{c}\: \: \textrm{adalah vektor satuan dari}\: \: \overrightarrow{c}\: \: \textrm{dan}\: \: \overrightarrow{b},}\\\hline \begin{aligned}\textrm{maka}\: \: \: \overrightarrow{c}&=\left | \overrightarrow{c} \right |\hat{c} \end{aligned}\qquad\qquad \textrm{dan}\qquad\qquad \begin{aligned}\overrightarrow{b}&=\left | \overrightarrow{b} \right |\hat{b}=\left | \overrightarrow{b} \right |\hat{c} \end{aligned}\\\hline {\begin{aligned}\textrm{Sehingga}&\: \: \textbf{proyeksi ortogonal vektor}\: \: \overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\: \: \textrm{adalah}:\\ \overrightarrow{c}&=\left | \overrightarrow{c} \right |\hat{b}\\ &=\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right )\left ( \displaystyle \frac{\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right )\\ &=\left (\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |^{2}} \right )\overrightarrow{b} \end{aligned}}\\\hline \end{array}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Diketahui vektor}\: \: \overrightarrow{a}=\begin{pmatrix} 3\\ 2 \end{pmatrix}\: \: \textrm{dan}\: \: \overrightarrow{b}=\begin{pmatrix} -2\\ 1 \end{pmatrix}.\\ & \textrm{Tentukanlah proyeksi ortogonal vektor}\\ &\overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\: \: \textrm{dan tentukanlah panjangnya} \\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{Misalkan}&\: \: \overrightarrow{c}\: \: \textrm{adalah vektor proyeksi yang dimaksud, }\\ &\textrm{maka}\\ \overrightarrow{c}&=\left ( \displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |^{2}} \right )\overrightarrow{b}\\ &=\displaystyle \frac{\begin{pmatrix} 3\\ 2 \end{pmatrix}.\begin{pmatrix} -2\\ 1 \end{pmatrix}}{(-2)^{2}+1^{2}}.\overrightarrow{b}=\frac{3.(-2)+2.1}{4+1}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=-\frac{4}{5}\begin{pmatrix} -2\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{8}{5}\\ -\frac{4}{5} \end{pmatrix}\quad \textbf{atau}\\ &=\color{red}\frac{8}{5}\bar{i}-\frac{4}{5}\bar{j} \end{aligned}\\ &\begin{aligned}\textrm{Dan panjang}\: \: &\textrm{vektor proyeksi yang dimaksud adalah}:\\ \left |\overrightarrow{c} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right |\\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ 2 \end{pmatrix}.\begin{pmatrix} -2\\ 1 \end{pmatrix}}{\sqrt{(-2)^{2}+1^{2}}} \right |=\left |\frac{3.(-2)+2.1}{\sqrt{4+1}} \right |\\ &=\left |-\frac{4}{\sqrt{5}} \right |\\ &=\displaystyle \frac{4}{\sqrt{5}}=\color{red}\frac{4}{5}\sqrt{5} \end{aligned} \end{array}$.

$\begin{array}{ll}\\ 2.&\textrm{Diketahui vektor}\: \: \overrightarrow{a}=3\bar{i}-2\bar{j}+2\bar{k}\: \: \textrm{dan}\: \: \overrightarrow{b}=2\bar{i}-2\bar{j}+\bar{k}\\ &\textrm{Tentukanlah panjang vektor proyeksi ortogonal}\\ &\textrm{a}.\quad \overrightarrow{a}\: \: \textrm{pada}\: \: \overrightarrow{b}\qquad\qquad\qquad \textrm{b}.\quad \overrightarrow{a}\: \: \textrm{pada}\: \: \left ( \overrightarrow{a}+\overrightarrow{b} \right ) \\\\ &\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad\textrm{Misal}&\textrm{kan}\: \: \overrightarrow{c}\: \: \textrm{adalah vektor proyeksi yang dimaksud,}\\ & \textrm{maka panjanynya}\\ \left |\overrightarrow{c} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\overrightarrow{b}}{\left | \overrightarrow{b} \right |} \right | \\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ -2\\ 2 \end{pmatrix}.\begin{pmatrix} 2\\ -2\\ 1 \end{pmatrix}}{\sqrt{2^{2}+(-2)^{2}+1^{2}}} \right |=\left |\frac{3.2+(-2).(-2)+2.1}{\sqrt{4+4+1}} \right |\\ &=\left | \displaystyle \frac{12}{3} \right |=\color{red}4 \end{aligned}\\ &\begin{aligned}\textrm{b}.\quad\textrm{Misal}&\textrm{kan}\: \: \overrightarrow{f}\: \: \textrm{adalah vektor proyeksi yang dimaksud,}\\ & \textrm{maka panjanynya}\\ \left |\overrightarrow{f} \right |&= \left |\displaystyle \frac{\overrightarrow{a}\left (\overrightarrow{a}+\overrightarrow{b} \right )}{\left |\overrightarrow{a}+ \overrightarrow{b} \right |} \right |\\ &=\left |\displaystyle \frac{\begin{pmatrix} 3\\ -2\\ 2 \end{pmatrix}.\begin{pmatrix} 3+2\\ -2+(-2)\\ 2+1 \end{pmatrix}}{\sqrt{(3+2)^{2}+(-2+(-2))^{2}+(2+1)^{2}}} \right |\\ &=\left |\frac{3.5+(-2).(-4)+2.3}{\sqrt{25+16+9}} \right |\\ &=\left |\frac{29}{\sqrt{50}} \right |\\ &=\displaystyle \frac{29}{5\sqrt{2}}=\color{red}\frac{29}{10}\sqrt{5} \end{aligned} \end{array}$

Lanjutan Materi Perkalian Skalar Dua Vektor Di Ruang Dimensi Dua (Matematika Peminatan Kelas X)

$\color{blue}\textrm{L. Operasi Perkalian Dua Buah Vektor}$

Perhatikanlah ilustrasi berikut

Bentuk perkalian dari ilustrasi dua vektor di atas dinotasikan dengan $\color{black}\bar{a}\bullet \bar{b}$. Dimisalkan sebuah vektor $\color{black}\bar{a}$ dan vektor $\color{black}\bar{b}$ membentuk sudut $\theta$ , maka perkalian skalar dua vektor didefinisikan dengan

$\color{black}\bar{a}\bullet \bar{b}=\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta ,\: \: \color{blue}\textrm{dengan}\: \: \color{black}0^{\circ}\leq \theta \leq 180^{\circ}$

Misalkan diberikan dua vektor

$\begin{aligned}&\bar{a}=\color{red}\begin{pmatrix} a_{1}\\ a_{2} \end{pmatrix}\: \: \color{black}\textrm{dan}\: \: \bar{b}=\color{blue}\begin{pmatrix} b_{1}\\ b_{2} \end{pmatrix}\\ &\textrm{Sesuai definisi, maka}\\ &\bar{a}\bullet \bar{b}=\color{red}\bar{a_{1}}\color{blue}\bar{b_{1}}\color{black}+\color{red}\bar{a_{2}}\color{blue}\bar{b_{2}} \end{aligned}$

Sebagai bukti diberikan uraian berikut

Perhatikanlah $\triangle \textbf{AOB}$ di atas, saat kita menentukan ruas garis AB yang terbentuk dari vektor posisi $\color{black}\bar{a}$ dan $\color{black}\bar{b}$ dengan sudut pengapitnya adalah $\theta$, maka kita dapat menggunakan aturan COSINUS, yaitu:

$\color{purple}\begin{aligned}\left | \overline{AB} \right |^{2}&=\left | \overline{OA} \right |^{2}+\left | \overline{OB} \right |^{2}-2\left | \overline{OA} \right |\left | \overline{OB} \right |\cos \theta \\ (b_{1}-a_{1})^{2}&+(b_{2}-a_{2})^{2}=a_{1}^{2}+a_{2}^{2}+b_{1}^{2}+b_{2}^{2}-2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta \\ -2a_{1}b_{1}-&2a_{2}b_{2}=-2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta \\ \displaystyle 2a_{1}b_{1}+&2a_{2}b_{2}=\displaystyle 2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta\\ &\textbf{Karena}\\ &\color{blue}\bar{a}\bullet \bar{b}=\displaystyle 2\left | \bar{a} \right |\left | \bar{b} \right |\cos \theta\\ \displaystyle 2a_{1}b_{1}+&2a_{2}b_{2}=\bar{a}\bullet \bar{b}\: \: \: \color{black}\blacksquare \end{aligned}$

Dan dari bentuk di atas kita juga akan mendapatkan bentuk:

$\cos \theta =\displaystyle \frac{\bar{a}\bullet \bar{b}}{\left | \bar{a} \right |\left | \bar{b} \right |}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Jika diketahui}\: \: \left | \bar{a} \right |=5,\: \: \textrm{dan}\: \: \left | \bar{b} \right |=8\\ &\textrm{dan kedua vektor itu membentuk sudut}\: \: 60^{\circ}\\ &\textrm{maka nilai}\: \: \bar{a}\bullet \bar{b}=....\\\\ &\textrm{Jawab}\\ &\begin{aligned}\bar{a}\bullet \bar{b}&=\left | \bar{a} \right |\left | \bar{b} \right |\cos \angle \left ( \bar{a},\bar{b} \right )\\ &=5.8.\cos 60^{\circ}\\ &=40\times \displaystyle \frac{1}{2}\\ &=20 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Jika diketahui vektor}\: \: \bar{a} =\begin{pmatrix} 15\\ -11 \end{pmatrix},\: \: \textrm{dan}\: \: \bar{b}=\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &\textrm{Tentukanlah nilai}\: \: \bar{a}\bullet \bar{b}\\\\ &\textrm{Jawab}\\ &\color{blue}\begin{aligned}\bar{a}\bullet \bar{b}&=\begin{pmatrix} 15\\ -11 \end{pmatrix}\begin{pmatrix} -2\\ 1 \end{pmatrix}\\ &=(15)(-2)+(-11)(1)\\ &=-30+(-11)\\ &=-30-11\\ &=-41 \end{aligned} \end{array}$

$\color{blue}\textrm{M. Perbandingan Vektor}$

Perhatikanlah ilustrasi gambar berikut!

Dari gambar tersebut di atas diketahui bahwa titik P dan Q dengan koordinat masing-masing adalah $(x_{1},y_{1})$ dan $(x_{1},y_{1})$, dan $\overrightarrow{PT}:\overrightarrow{TQ}=m:n$ , mak vektor posisi titik T adalah $\vec{t}=\displaystyle \frac{n\vec{p}+m\vec{q}}{m+n}$.

Berikut paparan buktinya

$\begin{aligned}\overrightarrow{PT}:\overrightarrow{TQ}&=m:n\\ \displaystyle \frac{\overrightarrow{PT}}{\overrightarrow{TQ}}&=\frac{m}{n}\\ \displaystyle \frac{\vec{t}-\vec{p}}{\vec{q}-\vec{t}}&=\frac{m}{n}\\ n\left ( \vec{t}-\vec{p} \right )&=m\left ( \vec{q}-\vec{t} \right )\\ n\vec{t}-n\vec{p}&=m\vec{q}-m\vec{t}\\ m\vec{t}+n\vec{t}&=m\vec{q}+n\vec{p}\\ \vec{t}\left ( m+n \right )&=n\vec{p}+m\vec{q}\\ \vec{t}&=\color{red}\displaystyle \frac{n\vec{p}+m\vec{q}}{m+n}\qquad\quad \color{black}\blacksquare \end{aligned}$.

$\LARGE\colorbox{yellow}{CONTOH SOAL}$.

$\begin{array}{ll}\\ 1.&\textrm{Perhatikanlah gambar pada soal No. 6 di atas. }\\ &\textrm{Jika titik T terletak pada}\: \overrightarrow{SP},\: \textrm{sehingga}\\&\: \: \overrightarrow{ST}:\overrightarrow{TP}=1:3,\: \textrm{maka}\\ &\textrm{a}.\quad \textrm{Tentukanlah koordinat titik T}\:\\ &\textrm{b}.\quad \textrm{Jika titik M terletak di tengah-tengah}\: \: \overrightarrow{SP},\\ &\qquad \textrm{tentukanlah koordinat titik M}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{array}{|l|l|}\hline \begin{aligned}\textrm{a}.\quad \vec{t}&=\displaystyle \frac{3\vec{s}+\vec{p}}{3+1}\\ &=\displaystyle \frac{3\begin{pmatrix} -3\\ 7 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix}}{3+1}\\ &=\displaystyle \frac{1}{4}\left ( \begin{pmatrix} -9\\ 21 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix} \right )\\ &=\displaystyle \frac{1}{4}\begin{pmatrix} -4\\ 24 \end{pmatrix}\\ &=\begin{pmatrix} -1\\ 6 \end{pmatrix}\\ \textrm{jadi}&\: \textrm{koordinat titik}\: \color{red}T(-1,6) \end{aligned}&\begin{aligned}\textrm{b}.\quad \vec{m}&=\displaystyle \frac{1}{2}\left ( \vec{s}+\vec{p} \right )\\ &=\displaystyle \frac{1}{2}\left ( \begin{pmatrix} -3\\ 7 \end{pmatrix}+\begin{pmatrix} 5\\ 3 \end{pmatrix} \right )\\ &=\displaystyle \frac{1}{2}\begin{pmatrix} 2\\ 10 \end{pmatrix}\\ &=\begin{pmatrix} 1\\ 5 \end{pmatrix}\\ \textrm{Jadi}&\: \textrm{koordinat titik}\: \color{red}M(1,5)\\ &\\ &\\ & \end{aligned}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui}\: \: \vec{u}=\begin{pmatrix} -8\\ 2 \end{pmatrix}\: \textrm{dan}\: \: \vec{v}=\begin{pmatrix} -4\\ m \end{pmatrix}.\\ &\textrm{Tentukan}\: \: m\: \: \textrm{jika}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\overrightarrow{u}&=k\vec{v}\\ &\quad (\textrm{vektor}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah})\\ \begin{pmatrix} -8\\ 2 \end{pmatrix}&=k\begin{pmatrix} -4\\ m \end{pmatrix}=\begin{pmatrix} -4k\\ mk \end{pmatrix}\\ -8&=-4m\: \: \Rightarrow \: \: m=\displaystyle \frac{-8}{-4}=2\\ \textrm{Jadi}\: &\: \color{red}m=2\\ \end{aligned} \end{array}$

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$.

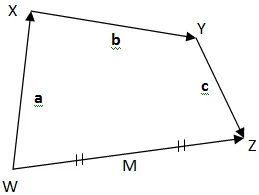
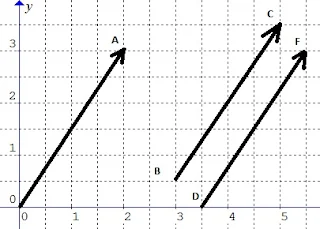
$\begin{array}{ll}\\ 1.&\textrm{Perhatikanlah gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad &\textrm{Nyatakan vektor-vektor pada gambar }\\ &\textrm{di atas ke dalam bentuk}\\ &\textrm{a}.\quad \textrm{Vektor kolom}\\ &\textrm{b}.\quad \textrm{Vektor baris}\\ &\textrm{c}.\quad \textrm{Vektor basis} \end{array}$

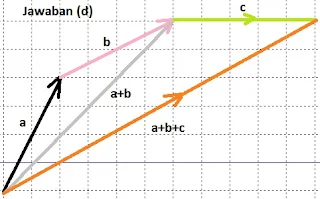
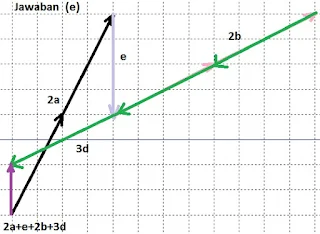
$\begin{array}{ll}\\ 2.&\textrm{Pada soal No. 1 di atas, gambarkanlah }\\ &\textrm{vektor-vektor berikut pada kertas berpetak}\\ &\textrm{a}.\quad \vec{a}+\vec{b}\\ &\textrm{b}.\quad \vec{b}+\vec{c}\\ &\textrm{c}.\quad \vec{c}+\vec{d}\\ &\textrm{d}.\quad (\vec{a}+\vec{b})+\vec{c}\\ &\textrm{e}.\quad \vec{b}+(\vec{c}+\vec{d})\\ &\textrm{f}.\quad (\vec{a}+\vec{b})+(\vec{c}+\vec{d})\\ &\textrm{g}.\quad (\vec{a}+\vec{b})-(\vec{c}+\vec{d})\\ &\textrm{h}.\quad \vec{a}+\vec{b}+\vec{c}+\vec{d}+\vec{e}+\vec{f}\\ &\textrm{i}.\quad \vec{a}-\vec{b}+\vec{c}-\vec{d}+\vec{e}-\vec{f}\end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar pada soal No. 6 di atas.}\\ &\textrm{Jika titik T terletak pada}\: \: \overrightarrow{SP},\: \textrm{sehingga}\\ &\overrightarrow{ST}:\overrightarrow{TP}=2:3,\: \textrm{maka}\\ &\textrm{a}.\quad \textrm{Tentukanlah koordinat titik T}\:\\ &\textrm{b}.\quad \textrm{Jika titik M terletak di tengah-tengah}\: \: \overrightarrow{SP},\\ &\qquad \textrm{tentukanlah koordinat titik M}\\ \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Diketahui}\: \: \vec{u}=\begin{pmatrix} 16\\ -2 \end{pmatrix}\: \textrm{dan}\: \: \vec{v}=\begin{pmatrix} -4\\ m \end{pmatrix}.\\ &\textrm{Tentukan}\: \: m\: \: \textrm{jika}\: \: \vec{u}\: \: \textrm{dan}\: \: \vec{v}\: \: \textrm{sejajar dan searah}\end{array}$

DAFTAR PUSTAKA

Kuntarti, Sulistiyono, & Kurnianingsih, S. 2005. Matematika untuk SMA dan MA Kelas XII Program Ilmu Alam. Jakarta: PT. Gelora Aksara Pratama.
Yuana, R. A., Indriyastuti. 2017. Perspektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan dan Ilmu Alam. Solo: PT TIGA SERANGKAI PUSTAKA MANDIRI.

Lanjutan Materi Polinom : Akar-Akar Persamaan Polinom

$\color{blue}\textbf{1. Pencarian akar-akar persamaan polinom}$

Persamaan suku banyak/polinom $a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0$ dengan $n>1\: \: \textrm{dan}\: \: a_{n}\neq 0$ paling sedikit memiliki sebuah akar riil atau imajiner. Pada bahasan ini untuk mendapatkan akar-akar rasional perlu dilakukan cara coba-coba. Misalkan $x=h$ kita pilih, selanjutnya tinggal kita buktikan bahwa apakah $x=h$ apakah akar polinom tersebut atau tidak, jika $f(h)=0$, maka $x=h$ adalah termasuk akar dari polinom tersebut, tetapi jika tidak atau $f(h) \neq 0$, maka $x=h$ bukan akar yang diinginkan.

Beberapa petunjuk agar $x=h$ terarah sebagai akar polinom

Misalkan $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}$ dengan $r$ adalah faktor dari $a_{0}$, dan $s$ adalah faktor dari $a_{n}$, maka akar-akar rasional jika ada adalah $x=h=\color{red}\displaystyle \frac{r}{s}$.
Jika pada langkah pertama di atas ditemukan sebuah akar rasional katakanlah $x=h_{1}$, maka tentukan hasil bagi $f(x)$ dengan $x=h_{1}$ ini. Misalkan hasil baginya adalah $h_{1}(x)$ atau $\color{blue}f(x)=(x-h_{1})h_{1}(x)$, maka langkah berikutnya carilah akar dari $h_{1}(x)$ ini. Dan jika didapatkan akar dari $h_{1}(x)$ adalah $x=h_{2}$, maka tentukanlah hasil bagi dari $h_{1}(x)$ oleh $x=h_{2}$, katakanlah hasilnya $h_{2}(x)$, maka $\color{blue}f(x)=(x-h_{1})(x-h_{2})h_{2}(x)$ demikian seterusnya.

$\color{blue}\textbf{2. Jumlah dan hasil kali akar-akar polinom}$

Untuk fungsi derajat 2 maka berlaku seperti menentukan rumus jumlah dan selisih pada persamaan kuadrat. Tetapi untuk polinom berderajat tiga $f(x)=ax^{3}+bx^{2}+cx+d$ saat $f(x)=0$, maka berlaku

$\begin{aligned}f(x)&=\color{red}ax^{3}+bx^{2}+cx+d\: \: \color{black}\textrm{dengan}\\ &x_{1},\: x_{2},\: x_{3}\: \: \textrm{adalah akar-akarnya, maka}\\ \bullet \: \: &x_{1}+x_{2}+x_{3}=-\displaystyle \frac{b}{a}\\ \bullet \: \: &x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3}=\displaystyle \frac{c}{a}\\ \bullet \: \: &x_{1}\times x_{2}\times x_{3}=-\displaystyle \frac{d}{a}\\ \end{aligned}$

$\begin{aligned}\textrm{Unt}&\textrm{uk yang berderajat empat}\\ f(x)&=\color{red}ax^{4}+bx^{3}+cx^{2}+dx+e\: \: \color{black}\textrm{saat}\: \: f(x)=0\\ &\textrm{dengan}\: \: \: x_{1},\: x_{2},\: x_{3},\: x_{4}\: \textrm{adalah akar-akarnya},\\ &\textrm{maka}\\ \bullet \: \: &x_{1}+x_{2}+x_{3}+x_{4}=-\displaystyle \frac{b}{a}\\ \bullet \: \: &x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{3}+...+x_{3}x_{4}=\displaystyle \frac{c}{a}\\ \bullet \: \: &x_{1} x_{2} x_{3}+x_{1} x_{2} x_{4}+x_{1}x_{3}x_{4}+x_{2} x_{3} x_{4}=-\displaystyle \frac{d}{a}\\ \bullet \: \: &x_{1} x_{2} x_{3}x_{4}=\displaystyle \frac{e}{a} \end{aligned}$

$\begin{aligned}&\color{blue}\textbf{Rumus Tambahan}\\ &\bullet \: \: \: x_{1}^{2}+x_{2}^{2}=\left ( x_{1}+x_{2} \right )^{2}-2x_{1}x_{2}\\ &\bullet \: \: \: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\\ &\qquad =\left ( x_{1}+x_{2}+x_{3} \right )^{2}-2\left ( x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3} \right )\\ &\bullet \: \: \: x_{1}^{3}+x_{2}^{3}+x_{3}^{3}\\ &\qquad =\left ( x_{1}+x_{2}+x_{3} \right )^{3}-3x_{1}x_{2}x_{3}\left ( x_{1}+x_{2}+x_{3} \right ) \end{aligned}$

$\begin{aligned}&\color{blue}\textbf{Teorema Vieta berkaitan polinom}\\ &\textrm{Persamaan polinom berderajat}\: \: n\\ &\color{red}a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0\\ &\textrm{dengan akar-akar}:\: \: \color{purple}x_{1},\: x_{2},\: x_{3},\: \cdots \: ,x_{n},\\ &\textrm{maka}:\\ &\bullet \quad x_{1}+x_{2}+x_{3}+\cdots +x_{n}=\color{blue}-\displaystyle \frac{a_{n-1}}{a_{n}}\\ &\bullet \quad x_{1}x_{2}+x_{1}x_{3}+\cdots +x_{2}x_{3}+\cdots +x_{n-1}x_{n}=\color{magenta}\displaystyle \frac{a_{n-2}}{a_{n}}\\ &\bullet \quad x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+\cdots +x_{n-2}x_{n-1}x_{n}=\color{blue}-\displaystyle \frac{a_{n-3}}{a_{n}}\\ &\qquad\qquad\qquad \vdots \\ &\bullet \quad x_{1}x_{2}x_{3}\cdots x_{n}=\color{magenta}(-1)^{n}.\displaystyle \frac{a_{0}}{a_{n}} \end{aligned}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Jika akar-akar dari polinom}\\ &x^{3}+2x^{2}-5x-6=0\: \: \textrm{adalah}\\ &x_{1},\: x_{2},\: \: \textrm{dan}\: \: x_{3},\: \textrm{tentukanlah nilai}\\ &\textrm{a}.\quad x_{1}+ x_{2}+ x_{3}\\ &\textrm{b}.\quad x_{1}x_{2}+ x_{1}x_{3}+ x_{2}x_{3}\\ &\textrm{c}.\quad x_{1}\times x_{2}\times x_{3}\\ &\textrm{d}.\quad x_{1}^{2}+ x_{2}^{2}+ x_{3}^{2}\\\\ &\textrm{Jawab}:\\ &\textrm{Diketahui bahwa}:\: \: \color{red}x^{3}+2x^{2}-5x-6=0\\ &\textrm{dengan koefisien-koefisien variabelnya}\\ & a_{3}=1,\: a_{2}=2,\: a_{1}=-5,\: \: \textrm{dan}\: \: a_{0}=-6\\ &\textrm{Menurut}\: \: \textbf{Teorema Vieta},\: \textrm{maka}\\ &\textrm{a}.\quad x_{1}+ x_{2}+ x_{3}=-\displaystyle \frac{a_{2}}{a_{3}}=-\frac{2}{1}=\color{red}-2\\ &\textrm{b}.\quad x_{1}x_{2}+ x_{1}x_{3}+ x_{2}x_{3}=\displaystyle \frac{a_{1}}{a_{3}}=\displaystyle \frac{-5}{1}=\color{red}-5\\ &\textrm{c}.\quad x_{1}\times x_{2}\times x_{3}=-\displaystyle \frac{a_{0}}{a_{3}}=-\displaystyle \frac{-6}{1}=\color{red}6\\ &\textrm{d}.\quad x_{1}^{2}+ x_{2}^{2}+ x_{3}^{2}\\ &\quad\quad =\left ( x_{1}+x_{2}+x_{3} \right )^{2}-2\left ( x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3} \right )\\ &\quad\quad =(-2)^{2}-2(-5)=4+10=\color{red}14 \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui polinom}\: \: x^{3}+3x-1=0\\ &\textrm{dengan akar-akar}\: \: \alpha ,\: \beta ,\: \textrm{dan}\: \: \gamma \\ &\textrm{tentukanlah nilai}\: \: \alpha^{3} +\beta^{3} + \gamma^{3} \\\\ &\textrm{Jawab}:\\ &\textrm{Pandang polinom}\: \: \color{red}x^{3}+3x-1=0\\ &\textrm{dengan}:\: a_{3}=1,\: a_{2}=0,\: a_{1}=3,\: a_{0}=-1\\ &\textrm{maka bentuk nilai dari akar-akarnya}\\ &\textrm{yaitu}:\\ &\bullet \quad \alpha ^{3}+3\alpha -1=0\: \: .......(1)\\ &\bullet \quad \beta ^{3}+3\beta -1=0\: \: .......(2)\\ &\bullet \quad \gamma ^{3}+3\gamma -1=0\: \: .......(3)\\ &\textrm{Ketika persamaan}\: \: (1)+(2)+(3)\: \: \textrm{maka}\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left (\alpha +\beta +\gamma \right ) -3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left ( \displaystyle \frac{a_{2}}{a_{3}} \right )-3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}+3\left ( 0 \right )-3=0\\ &\Leftrightarrow \: \alpha ^{3}+\beta ^{3}+\gamma ^{3}=\color{red}3 \end{array}$

Daftar Pustaka

Kartini, Suprapto, Subandi, Setiadi, U. 2005. Matematika Kelas XI untuk SMA dan MA Program Studi Ilmu Alam. Klaten: INTAN PARIWARA.
Nugroho, P. A., Gunarto, D. 2013. Big Bank Soal+Bahas Matematika SMA/MA Kelas 1, 2, 3. Jakarta: WAHYUMEDIA.
Sembiring, S., Zulkifli, M., Marsito, Rusdi, I. 2017. Matematika untuk Siswa SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT.
Sunardi, Waluyo, S., Sutrisno, Subagya. 2005. Matematika 2 untuk SMA Kelas XI IPA. Jakarta: BUMI AKSARA.
Sukino, S., Intan, T. S., Santiago, Y. E. 2015. Pena Emas Olimpiade Sains Nasional Matematika untuk SMP Seri Kinomatika 1: Seleksi Tingkat Sekolah dan Seleksi Tingkat Kabupaten\Kota. Bandung: YRAMA WIDYA.
Sukino. 2016. Matematika untuk SMA/MA Kelas XI Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta: ERLANGGA.

Lanjutan Materi Polinom : Teorema Sisa dan Teorema Faktor

$\textbf{1. Teorema Sisa}$

Sebelumnya telah diketahui bahwa jika suatu polinom $\textbf{f(x)}$ dibagi oleh $\textbf{g(x)}$ dengan hasil bagi $\textbf{h(x)}$ dan sisa pembagian berupa $\textbf{s(x)}$, maka kondisi tersebut dapat dituliskan dengan

$f(x)=g(x)\times h(x)+s(x)$

Selanjutnya apabila $\textbf{f(x)}$ berderajat $\color{blue}n$ dibagi oleh $\textbf{g(x)}$ berderajat $\color{blue}m$, maka hasil bagi $\textbf{h(x)}$ akan berderajat $\color{blue}n-m$ dan sisa pembagian maksimum berderajat $\color{blue}m-1$.

Perhatikan kembali contoh soal sebelumnya yaitu:

Dari paparan di atas apabila disederhanakan, maka:

$\begin{aligned}\textrm{Jika}\: &\textrm{polinomial}\: \: f(x)\: \: \textrm{dibagi oleh}\\ \textrm{a}.\quad&g(x)=(x-a),\: \: s(x)=\color{red}f(a)\\ \textrm{b}.\quad&g(x)=(x+a),\: \: s(x)=\color{red}f(-a)\\ \textrm{c}.\quad&g(x)=(ax-b),\: \: s(x)=\color{red}f\left ( \displaystyle \frac{b}{a} \right )\\ \textrm{d}.\quad&g(x)=(ax+b),\: \: s(x)=\color{red}f\left (- \displaystyle \frac{b}{a} \right )\\ \textrm{e}.\quad&g(x)=(x-a)(x-b)\\ &\quad s(x)=\displaystyle \frac{x-a}{b-a}\color{red}f(b)\color{black}+\frac{x-b}{a-b}\color{red}f(a)\\ \textrm{f}.\quad&g(x)=(x-a)(x-b)(x-c)\\ &\quad s(x)=\displaystyle \frac{(x-a)(x-b)}{(c-a)(c-b)}\color{red}f(c)\\ &\: \qquad +\displaystyle \frac{(x-a)(x-c)}{(b-a)(b-c)}\color{red}f(b)\\ &\: \qquad +\displaystyle \frac{(x-b)(x-c)}{(a-b)(a-c)}\color{red}f(a) \end{aligned}$

$\textbf{2. Teorema Faktor}$

Pada pembagian sebuah bilangan bahwa suatu bilangan dikatakan habis terbagi jika pembaginya adalah faktor dari bilangan tersebut. Sebagai misal 15 faktornya adalah: 1,3,5, dan 15. Dan pada bahasan materi tentang pemfaktoran pada persamaan kuadrat saat Anda duduk di kelas X sebagai misal $x^{2}+x-6$ akan habis terbagi oleh $x+3$ dan $x-2$. Demikian juga ketika $x^{2}+2x-8$ akan habis terbagi oleh $x+4$ dan $x-2$. Selanjutnya pembagi-pembagi tersebut kita namakan sebagai faktor dari yang dibagi tersebut.

Untuk selanjutnya toerema faktor dinyatakan:

Jika $(x-h)$ adalah faktor dari $f(x)$ jika dan hanya jika $f(h)=0$
Jika $(ax+h)$ merupakan faktor dari $f(x)$ jika dan hanya jika $f\left ( \displaystyle \frac{-h}{a} \right )=0$

Lanjutan Materi Operasi Polinom

$\color{blue}\textrm{C. Operasi Pada Polinom}$

$\textbf{1. Kesamaan dua buah polinom}$

Dua buah polinom dikatakan sama jika keduanya memiliki pangkat/derajat sama dan koefisien-koefisien suku yang sejenis juga sama.

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{aligned}x^{4}+Ax^{3}-4x^{2}-10x+3&=(x^{2}+2x+3)(x^{2}+Bx+1)\\ x^{4}+Ax^{3}-4x^{2}-10x+3&=x^{4}+(B+2)x^{3}+(2B+4)x^{2}\\ &+(3B+2)x+3\\ \textrm{Elemen yang bersesuaian}&\\ \textrm{untuk}\: \: x^{1}\: :\: \color{blue}-10&=3B+2\\ \textrm{maka}\: \: \: B& =4\\ \textrm{untuk}\: \: x^{3}\: :\: \color{blue}A&=B+2\\ A&=-2 \end{aligned}$

$\textbf{2. Penjumlahan}$

Dua polinom dapat dijumlahkan jika hanya jika suku-sukunya sejenis, jika tidak maka tidak bisa

$\textbf{3. Pengurangan}$

Pada operasi pengurangan juga juga berlaku seperti pada operasi penjumlahan, yaitu pengurangan hanya bisa terjadi pada suku-suku yang sejenis saja yang lainnya tidak dapat dilakukan.

$\textbf{4. Perkalian}$

Pada jenis operasi ini dilakukan seperti mengalikan biasa yaitu mengalikan semua suku-suku secara distribusi dari kedua polinom tersebut.

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Diketahui 2 suku banyak berikut}\\ &\begin{cases} p(x) &=x^{3}+2x^{2}+x-1 \\ q(x) &=x^{4}+5x+2 \end{cases}\\ &\textrm{Tentukanlah}\\ &\textrm{a}.\quad \textrm{penjumlahan keduanya}\\ &\textrm{b}.\quad \textrm{pengurangan}\: \: p(x)\: \: \textrm{oleh}\: \: q(x)\\\\ &\textrm{Jawab}:\\ &\begin{array}{lllllllllll}\\ p(x)=&&x^{3}&+&2x^{2}&+&x&-&1&\\ q(x)=&x^{4}&&&&+&5x&+&2&(+)\\\hline &\color{red}x^{4}\: +&\color{red}x^{3}&+&\color{red}2x^{2}&+&\color{red}6x&+&\color{red}1& \end{array}\\ &\textrm{poin b Silahkan dicoba sebagai latihan} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil kali perkalian}\\ &\textrm{dari dua polinom berikut}\\ &\textrm{a}.\quad 3x(-5x^{2})\\ &\textrm{b}.\quad 2a(7a-3)\\ &\textrm{c}.\quad (x+2)(x-5)\\ &\textrm{d}.\quad (3t-2)(2t^{2}-5t+3)\\ &\textrm{e}.\quad (5a^{2}+2)(5a^{2}-2)\\ &\textrm{f}.\quad (x^{3}-2x)(x^{2}+3x-4)\\ &\textrm{g}.\quad (2a^{3}+1)(-a-3)^{2}\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{aligned}\textrm{a}.\quad&3x(-5x^{2})=-3.5x^{1+2}=\color{red}-15x^{3}\\ \textrm{b}.\quad&2a(7a-3)=2.7a^{1+1}-2.3a=\color{red}14a^{2}-6a\\ &\color{blue}\textrm{Selanjutnya kita langsungkan saja}\\ \textrm{c}.\quad&(x+2)(x-5)=x^{2}+(2-5)x-2.5\\ &\qquad\qquad \qquad\: =\color{red}x^{2}-3x-10\\ \textrm{d}.\quad&(3t-2)(2t^{2}-5t+3)\\ &\qquad = 6t^{3}-15t^{2}+9t-4t^{2}+10t-6\\ &\qquad = \color{red}6t^{3}-19t^{2}+19t-6\\ \textrm{e}.\quad&(5a^{2}+2)(5a^{2}-2)\\ &\qquad = 25a^{4}-10x^{2}+10a^{2}-4\\ &\qquad =\color{red}25a^{4}-4\\ \textrm{f}.\quad&(x^{3}-2x)(x^{2}+3x-4)\\ &x^{5}+3x^{4}-4x^{3}-2x^{3}-6x^{2}+8x\\ &\qquad =\color{red}x^{5}+3x^{4}-6x^{3}-6x^{2}+8x\\ \textrm{g}.\quad&(2a^{2}+1)(-a-3)^{2}\\ &\qquad =(2a^{2}+1)(a^{2}+6a+9)\\ &\qquad =2a^{4}+12a^{3}+18a^{2}+a^{2}+6a+9\\ &\qquad =\color{red}2a^{4}+12a^{3}+19a^{2}+6a+9 \end{aligned} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil dari perkalian}\\ &\textrm{dua polinom berikut}\\ &\textrm{a}.\quad \begin{cases} p(x) &=x^{2}-x-1 \\ q(x) &=x^{2}+x+1 \end{cases}\\\\ &\textrm{b}.\quad \begin{cases} p(x) &=x^{5}+3x^{3}-x-1 \\ q(x) &=x^{4}+2x+1 \end{cases}\\\\ &\textrm{c}.\quad \begin{cases} p(x) &=x^{6}+3x-6 \\ q(x) &=x^{3}-6x+3 \end{cases}\\\\ &\textrm{d}.\quad \begin{cases} p(x) &=x^{2020}-x \\ q(x) &=x^{2}+x-1 \end{cases}\\\\ &\textrm{e}.\quad \begin{cases} p(x) &=x^{2021}-1 \\ q(x) &=x^{2019}+1 \end{cases}\\\\ &\textrm{Jawab}:\\ &\textrm{Poin a sampai d silahkan dicoba}\\ &\begin{aligned}\textrm{a}.\quad&\textrm{Diketahui bahwa}\\ &\begin{cases} p(x) &=x^{2021}-1 \\ q(x) &=x^{2019}+1 \end{cases}\\ &\textrm{maka}\: \: p(x)\times q(x)\\ &=\left ( x^{2021}-1 \right )\times \left ( x^{2019}+1 \right )\\ &=x^{2021+2019}+1\times x^{2021}-1\times x2019-1\times 1\\ &=\color{red}x^{4040}+x^{2021}-x^{2019}-1 \end{aligned} \end{array}$

$\textbf{5. Pembagian}$

Perhatikanlah ilustrasi pembagian bersusun panjang berikut

Misalkan untuk pembagian $x^{3}+4x^{2}-2x+4$ oleh $x-1$ adalah sebagai berikut:

Selanjutnya dari caontoh di atas kita mendapatkan,

$\begin{aligned}x^{3}&+4x^{2}-2x+4\\ &=(x-1)(x^{2}+5x+3)+7 \end{aligned}$

Sehingga dari uraian di atas secara umum pembagian polinom dapat dinyatakan bahwa:

$\textrm{Polinomial}=\textrm{Pembagi}\times \textrm{Hasil bagi}+\textrm{Sisa}$

$\textbf{a. Pembagian bentuk}\: (x-h)$

$\textbf{b. Pembagian bentuk}\: (ax+b)$

$\textbf{c. Pembagian bentuk}\: (ax^{2}+bx+c)$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: x^{3}+4x^{2}-2x+4\: \: \textrm{oleh}\: \: x-1\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: 4x^{3}-8x^{2}-x+5\: \: \textrm{oleh}\: \: 2x-1\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil bagi dan sisa pembagian}\\ &\textrm{jika}\: \: x^{4}-2x^{2}-13x-19\: \: \textrm{oleh}\: \: x^{2}-2x-3\\\\ &\color{blue}\textrm{Jawab}:\\ & \end{array}$

Catatan hasil bagi adalah pada contoh no.1 s.d 3 adalah pada tiap pembahasan di tiap nomornya adalah terletak di bagian atas (berwarna biru) dan sisa pembagiannya adalah yang terletak di bagian paling bawah (berwarna merah).

TAMBAHAN

Pembagian Horner - Kino

Perhatikanlah bagan berikut

Sebagai tambahan penjelasan dari bagan di atas adalah

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Dengan metode Horner, tentukanlah}\\ & \textrm{nilai suku banyak berikut ini}!\\ &\textrm{a})\quad 4x^{4}-7x^{3}+8x^{2}-2x+3\: \: \: \textrm{jika}\: \: x=2\\ &\textrm{b})\quad 2x^{5}+3x^{3}-x+1\: \: \: \textrm{jika}\: \: x=-3\\ &\textrm{c})\quad 2x^{3}+x^{2}-2x+3\: \: \: \textrm{jika}\: \: x=\displaystyle \frac{1}{3}\\\\ &\textrm{Jawab}:\\ &\textrm{Diketahui bahwa}\\ &f(x)=\color{red}4x^{4}-7x^{3}+8x^{2}-2x+3\\ &\textbf{Cara biasa (Substitusi)}\\ &\begin{aligned}f(2)&=4(2)^{4}-7(2)^{3}+8(2)^{2}-2(2)+3\\ &=64-56+32-4+3\\ &=39\\ \textrm{Seba}&\textrm{gai catatan bahwa}:\\ &\: \textrm{Polinom}\: \: f(x)\: \: \textrm{tersebut di atas }\\ &\textrm{jika dibagi}\: (x-2)\: \textrm{bersisa 39} \end{aligned}\\ &\textbf{Cara Horner}\\ & \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Hitunglah nilai}\: \: a,\: b,\: c,\: \: \textrm{dan}\: \: d,\: \: \textrm{jika}\\ &\textrm{a})\quad -3x+4\equiv a(x-7)-b(2x-3)\\ &\textrm{b})\quad a(x-1)^{2}-b(x+4)\equiv 2x^{2}-5x-7\\ &\textrm{c})\quad 3x^{2}+2x-5\equiv (ax+1)(x+b)-c(x+1)+2(ab-c)\\ &\textrm{d})\quad x^{4}-8x^{3}+15x-20\equiv x^{4}+ax^{3}+(a+b)x^{2}+(2b-c)x+d\\ &\textrm{e})\quad \displaystyle \frac{a}{x-1}+\frac{b}{x+3}\equiv \displaystyle \frac{8}{x^{2}+2x-3}\\ &\textrm{f})\quad \displaystyle \frac{a}{x-1}+\frac{b}{x-4}\equiv \displaystyle \frac{3}{x-1}+\frac{20}{x-4}+\frac{x+17}{x^{2}-5x+4}\\ &\textrm{g})\quad \displaystyle \frac{5x-4}{x^{2}-1}\equiv \displaystyle \frac{a}{x-1}+\frac{b}{x+1}-\frac{3}{x^{2}-1}\\ &\textrm{h})\quad \displaystyle \frac{2x^{2}+x+2}{x^{3}-1}\equiv \displaystyle \frac{a}{x-1}+\frac{bx+c}{x^{2}+x+1}\\ &\textrm{i})\quad \displaystyle \frac{3x^{2}+2x-5}{x^{2}+5x+6}\equiv \displaystyle \frac{a(x-3)}{x+3}+\frac{b(x-5)}{x+2}+\frac{4c}{(x+2)(x+3)}\\ &\textrm{j})\quad x^{3}+ax^{2}+bx+c=0\: \: \textrm{dengan akar-akar}\: \: x_{1}=x_{2}=-1\: \: \textrm{dan}\: \: x_{3}=-3\\ &\textrm{k})\quad x^{3}+ax^{2}+bx+c=0\: \: \textrm{dengan akar-akar}\: \: 1,\: 2,\: \: \textrm{dan}\: \: 3 \end{array}$

$.\: \qquad\begin{aligned}\color{blue}\textrm{Yang diba}&\color{blue}\textrm{has hanya no. 6 d}\\ x^{4}-8x^{3}+&15x-20\\ \equiv \color{red}x^{4}\color{black}+a\color{red}x^{3}&+(a+b)\color{red}x^{2}\color{black}+(2b-c)\color{red}x\color{black}+d\\ \textrm{koefisien}\: \: \color{red}x^{4}&:\: \: 1=1\\ \textrm{koefisien}\: \: \color{red}x^{3}&:\: \: -8=a,\: \: \textrm{maka}\: \: a=-8\\ \textrm{koefisien}\: \: \color{red}x^{2}&:\: \: 0=a+b,\: \: \textrm{maka}\: \: b=-a=-(-8)=8\\ \textrm{koefisien}\: \: \color{red}x^{1}&:\: \: 15=2b-c,\: \: \textrm{maka}\: \: c=2b-15=2(8)-15=1\\ \textrm{koefisien}\: \: \color{red}x^{0}&:\: \: -20=d,\: \: \textrm{maka}\: \: d=-20\\ \end{aligned}$

$\begin{array}{ll}\\ 3.&\textrm{Tentukanlah hasil bagi dan sisanya}!\\ &\begin{array}{ll}\\ \textrm{a})\quad (3x^{3}-2x^{2}+x-4):(x-1)&\textrm{k})\quad (x^{7}+3x^{5}+1):(x^{2}-1)\\ \textrm{b})\quad (2x^{4}-3x^{3}+x^{2}-5x+3):(x-2)&\textrm{l})\quad (x^{4}-3x^{3}-5x^{2}+x-6):(x^{2}-x-2)\\ \textrm{c})\quad (3-x+4x^{2}-x^{3}):(x-3)&\textrm{m})\quad (2x^{4}-3x^{2}-x+2):(x^{2}-2x+1)\\ \textrm{d})\quad (x^{4}-x^{2}+11):(x+4)&\textrm{n})\quad (3x^{6}+4x^{4}-2x-1):(x-1)(x^{2}-4)\\ \textrm{e})\quad (x^{3}-10x+9):(x+5)&\textrm{o})\quad (x^{4}-4x^{3}+2x^{2}-x+1):(2x+1)(x^{2}-3x+2)\\ \textrm{f})\quad (2x^{3}-5x^{2}-11x+8):(3x+1)&\textrm{p})\quad (x^{7}-7x^{4}+3x):(x^{3}-4x)\\ \textrm{g})\quad (5x^{3}+11x^{2}+7x-4):(5x+1)&\textrm{q})\quad (2x^{3}+x^{2}-4x+5):(x^{2}+x+1)\\ \textrm{h})\quad (2x^{3}+5x^{2}-4x+5):(2x+3)&\textrm{r})\quad (2x^{4}+x^{3}-3x+6):(x^{2}+x+2)\\ \textrm{i})\quad (2x^{3}+7x^{2}-5x+4):(2x-1)&\textrm{s})\quad (x^{4}-3x^{2}+7x-4):(x^{2}-2x-1)\\ \textrm{j})\quad (6x^{3}-x^{2}+3):(2x-3)&\textrm{t})\quad (3x^{3}+4x-8):(3x^{2}+x+2) \end{array} \end{array}$

$.\qquad\begin{aligned}&\textrm{Untuk pembahasan no. 3 i} \end{aligned}$

$.\qquad\begin{aligned}&\begin{array}{|l|l|}\hline \textrm{Pembagi}&\begin{aligned}&\textrm{Sisa}\\ &s(x)=\displaystyle \frac{7}{2} \end{aligned}\\\hline \begin{aligned}&2x-1=2(x-\frac{1}{2}) \end{aligned}&\begin{aligned}&\textrm{Hasil bagi}\\ &\displaystyle \frac{h(x)}{2}=\frac{2x^{2}+8x-1}{2}=x^{2}+4x-\frac{1}{2}\ \end{aligned}\\\hline \end{array} \end{aligned}$

$.\qquad\begin{aligned}&\textrm{Dan untuk pembahasan no. 3 m} \end{aligned}$

$.\qquad\begin{array}{|l|l|}\hline \textrm{Pembagi}&\begin{aligned}&\textrm{Sisa}\\ &s_{2}(x-p)+s_{1}\\ &1(x-1)+0=x-1 \end{aligned}\\\hline \begin{aligned}(x-p)(x-q)&=(x-1)(x-1)\\ &=(x-1)^{2} \end{aligned}&\begin{aligned}&\textrm{Hasil bagi}\\ &2x^{2}+4x+3 \end{aligned}\\\hline \end{array}$

$.\qquad\begin{aligned}&\textrm{Coba bandingkan dengan cara Horner-Kino berikut} \end{aligned}$

$.\qquad\begin{cases} \textrm{Suku banyak}: & f(x)=2x^{4}-3x^{2}-x+2 \\ \textrm{Pembagai}: & p(x)=x^{2}-2x+1 \\ &: -1\: \: \textrm{dari}\: -\frac{1}{1},\: \: \textrm{sedang}\: \: 2=-\left ( \frac{-2}{1} \right )\\ \textrm{Hasil bagi}:&h(x)=2x^{2}+4x+3\\ \textrm{Sisa bagi}:&s(x)=x-1 \end{cases}$.

$.\qquad \textrm{Sehingga},\\\\ 2x^{4}-3x^{2}-x+2=\color{red}\left ( x^{2}-2x+1 \right )\left ( 2x^{2}+4x+3 \right )+x-1$

$\begin{array}{ll}\\ 4.&\textrm{Jika diketahui akar-akar persamaan}\: \: x^{2}+4x-5=0\\ &\textrm{juga akar-akar untuk persamaan}\: \: 2x^{3}+9x^{2}-6x-5=0,\\ &\textrm{maka akar ketiga untuk persamaan yang kedua adalah}\: ...\\\\ &\textrm{Jawab}:\\ \end{array}$

$.\qquad \begin{cases} \textrm{Suku banyak}: & f(x)=2x^{3}+9x^{2}-6x-5 \\ \textrm{Pembagai}: & p(x)=x^{2}+4x-5 \\ &: 5\: \: \textrm{dari}\: -\left (\frac{-5}{1} \right ),\: \: \textrm{sedang}\: \: -4=\left ( \frac{4}{1} \right )\\ \textrm{Hasil bagi}:&h(x)=2x+1\\ \textrm{Sisa bagi}:&s(x)=0 \end{cases}$

$.\qquad\begin{aligned}&\textrm{Sehingga}\\ &2x^{3}+9x^{2}-6x-5=\left ( x^{2}+4x-5 \right )\left ( 2x+1 \right )\\ &\textrm{Jadi, akar yang lain (yang ketiga) adalah}\\ & (2x+1)\Rightarrow x=\color{red}-\displaystyle \frac{1}{2} \end{aligned}$

$\LARGE\colorbox{yellow}{LATIHAN SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi dan sisanya}!\\ &\begin{array}{ll}\\ \textrm{a})\quad (x^{7}+3x^{5}+1):(x^{2}-1)\\ \textrm{b})\quad (x^{4}-3x^{3}-5x^{2}+x-6):(x^{2}-x-2)\\ \textrm{c})\quad (2x^{3}+x^{2}-4x+5):(x^{2}+x+1)\\ \textrm{d})\quad (2x^{4}+x^{3}-3x+6):(x^{2}+x+2)\\ \textrm{e})\quad (x^{4}-3x^{2}+7x-4):(x^{2}-2x-1)\\ \textrm{f})\quad (3x^{3}+4x-8):(3x^{2}+x+2) \end{array} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: a\: \: \textrm{dan}\: \: b\: \: \textrm{bilangan bulat yang menyebabkan}\\ & x^{2}-x-1\: \: \textrm{merupakan faktor dari}\: \: ax^{3}+bx^{2}+1,\\ &\textrm{maka harga}\: \: b\: \: \textrm{adalah}\: ....\\ &\begin{array}{llllll}\\ \textrm{a}.&-2&&&\textrm{d}.&1\\ \textrm{b}.&-1&\textrm{c}.&0&\textrm{e}.&2 \end{array}\\ &\qquad\qquad\qquad\quad\qquad\qquad\qquad (\textrm{AHSME 1988})\end{array}$.

$\color{blue}\textrm{Pembagian Istimewa}$

Aturan pembagian istimewa adalah

$\begin{aligned}1.\quad &\displaystyle \frac{x^{n}-a^{n}}{x-a}=x^{n-1}a^{0}+x^{n-2}a^{1}+\cdots +x^{1}a^{n-2}+x^{0}a^{n-1}\\ &\qquad =\displaystyle \sum_{k=1}^{n}x^{n-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}x^{n-k}a^{k-1}\\ 2.\quad&\displaystyle \frac{x^{2n}-a^{2n}}{x+a}=x^{2n-1}a^{0}-x^{2n-2}a^{1}+\cdots +x^{1}a^{2n-2}-x^{0}a^{2n-1}\\ &\qquad =\displaystyle \sum_{k=1}^{2n}(-1)^{k+1}x^{2n-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}(-1)^{k+1}x^{2n-k}a^{k-1}\\ 3.\quad&\displaystyle \frac{x^{2n+1}+a^{2n+1}}{x+a}=x^{2n}a^{0}-x^{2n-1}a^{1}+\cdots -x^{1}a^{2n-1}+x^{0}a^{2n}\\ &\qquad =\displaystyle \sum_{k=1}^{2n+1}(-1)^{k+1}x^{2n+1-k}a^{k-1}\\ &\textrm{dengan suku ke}-k\: \: \textrm{hasil bagi}=\color{red}(-1)^{k+1}x^{2n+1-k}a^{k-1} \end{aligned}$

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah hasil bagi polinom}\\ &\textrm{untuk tiap pembagian istimewa berikut}\\ &\textrm{a}.\quad \left ( x^{3}-a^{3} \right ):(x-a)\\ &\textrm{b}.\quad \left ( x^{4}-a^{4} \right ):(x+a)\\ &\textrm{c}.\quad \left ( x^{5}+a^{5} \right ):(x+a)\\\\ &\textrm{Jawab}:\\ &\textrm{a}.\quad \displaystyle \frac{\left ( x^{3}-a^{3} \right )}{(x-a)}=x^{2}+xa+a^{2}\: \: ....(\textrm{rumus}\: 1)\\ &\textrm{b}.\quad \displaystyle \frac{\left ( x^{4}-a^{4} \right )}{(x+a)}=x^{3}-x^{2}a+xa^{2}-a^{3}\: \: ....(\textrm{rumus}\: 2)\\ &\textrm{c}.\quad \displaystyle \frac{\left ( x^{5}+a^{5} \right )}{(x+a)}=x^{4}-x^{3}a+x^{2}a^{2}-xa^{3}+a^{4}\: \: ....(\textrm{rumus}\: 3) \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah hasil bagi polinom}\\ &\textrm{untuk tiap pembagian istimewa berikut}\\ &\textrm{a}.\quad \left ( m^{8}-n^{8} \right ):(m+n)\\ &\textrm{b}.\quad \left ( x^{10}-y^{10} \right ):(x+y)\\\\ &\textrm{Jawab}:\\ &\textrm{a}.\quad \displaystyle \frac{\left ( m^{8}-n^{8} \right )}{(m+n)}=m^{7}-m^{6}n+m^{5}n^{2}-\cdots +mn^{6}-n^{7}\\ &\textrm{b}.\quad \displaystyle \frac{\left ( x^{10}-y^{10} \right )}{(x+y)}=x^{9}-x^{8}y+x^{7}y^{2}-\cdots +xy^{8}-y^{9}\\ \end{array}$

Lanjutan Materi Kaidah Pencacahan

$\color{blue}\textrm{B. Kaidah Pencacahan}$

Dalam kombinatorial kita harus melakukan perhitungan (counting) untuk mendapatkan semua kemungkinan dari pengaturan objekgar hasilnya didaptkan valid. Dua kaidah dasar yang digunakan dalam hal ini adalah adalah kaidah perkalian (rule of product) dan kaidah penjumlahan (rule of sum). Kedua kaidah tersebut nantinya akan selalu digunakan secara terpisah atau secara gabungan tergantung kondisi yang diinginkan dalam penentuan aturan pengisian tempat.

$\color{blue}\textrm{B. 1 Kaidah Perkalian}$

$\begin{cases} \color{red}\Rightarrow &\begin{array}{|c|}\hline \textrm{Kaidah Perkalian}\\\hline \begin{aligned}&\textrm{Jika percobaan 1 mendapat hasil}\: \: m,\\ & \textrm{percobaan 2 mendapatkan hasil}\: n,\\ & \textrm{maka jika percobaan 1 dan 2 dilakukan},\\ &\textrm{maka akan mendapatkan hasil} \: \: m \times n \\ &\textrm{kemungkinan} \end{aligned}\\\hline \end{array} \\\\\\ \color{blue}\Rightarrow &\begin{array}{|c|}\hline \textrm{Kaidah Penjumlah}\\\hline \begin{aligned}&\textrm{Jika percobaan 1 mendapat hasil}\: \: m,\\ & \textrm{percobaan 2 mendapatkan hasil}\: \: n,\\ & \textrm{maka jika hanya}\: \: \color{magenta}\textbf{satu percobaan}\: \: \color{black}\textrm{saja}\\ & \textrm{yang dilakukan (percobaan 1 atau percobaan 2)},\\ & \textrm{maka akan mendapatkan hasil}\: \: m + n\\ & \textrm{kemungkinan} \end{aligned}\\\hline \end{array} \end{cases}$

$\LARGE\colorbox{yellow}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Sekumpulan pelajar terdiri dari 5 anak putra}\\ & \textrm{dan 4 anak putri. Tentukanlah jumlah cara memilih}\\ & \textrm{satu orang wakil siswa dan satu orang wakil siswi}?\\\\ &\textrm{Jawab}:\\ &\textrm{ada 5 kemungkinan memilih seorang wakil siswa}\\ & \textrm{dan ada 4 kemungkinan memilih wakil siswi}.\\ & \textrm{Jika 2 orang wakil harus dipilih yang terdiri}\\ & \textrm{dari 1 siswa dan 1 siswi, maka jumlah}\\ & \textrm{kemungkinan perwakilan tersebut adalah yang}\\ & \textrm{dapat dipilih adalah 5 x 4 = 20 cara} \end{array}$

$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah ruang sampel dan banyaknya}\\ &\textrm{anggota untuk percobaan}\\ &\textrm{a}.\quad \textrm{melambungkan sebuah koin sebanyak 3 kali}\\ &\textrm{b}.\quad \textrm{melambungkan dua buah dadu sebanyak sekali}\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Jika S adalah ruang sampel dan n(S) adalah}\\ &\textrm{banyak anggota ruang sampel, maka}\\ &\textrm{a}.\quad \textrm{karena muka koin ada 2, maka n(S)}\\ &\qquad n(S)=2\times 2\times 2=2^{3}=8\\ &\textrm{b}.\quad \textrm{karena muka dadu ada 6, maka n(S)}\\ &\qquad n(S)=6\times 6=6^{2}=36\\ &\textrm{Dan berikut ilustrasi untuk seluruh ruang}\\ &\color{red}\textrm{sampelnya untuk kedua kasus di atas}\\ &\begin{array}{|c|c|}\hline \textrm{a}&\textrm{b}\\\hline \left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A&=AAA\\ \\ G&=AAG \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A&=AGA\\ \\ G&=AGG \end{matrix}\right. \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A\left\{\begin{matrix} A&=GAA\\ \\ G&=GAG \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A&=GGA\\ \\ G&=GGG \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. &\begin{array}{|c|c|c|c|c|c|c|}\hline \setminus&1&2&3&4&5&6\\\hline 1&(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\\hline 2&(2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\\hline 3&(3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)\\\hline 4&(4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6)\\\hline 5&(5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\\hline 6&(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)\\\hline \end{array} \\\hline \textrm{n}(\textrm{S})=8&\textrm{n}(\textrm{S})=36\\\hline \end{array} \end{array}$

Catatan :

Sebuah koin di lempar 3 kali sama dengan hasilnya untuk ruang sampel 3 buah koin dilempar sekali. Demikian juga sebuah dadu diundi 2 kali akan sama hasilnya dengan 2 buah dadi diundi sekali.

$\begin{array}{ll}\\ 3.&\textrm{Sekumpulan pelajar terdiri dari 5 anak putra dan}\\ & \textrm{4 anak putri. Tentukanlah jumlah cara memilih satu}\\ & \textrm{orang wakil pelajar tersebut(tidak masalah putra atau putri)}?\\\\ &\textrm{Jawab}:\\ &\textrm{ada 5 kemungkinan memilih seorang wakil siswa dan}\\ &\textrm{ada 4 kemungkinan memilih wakil siswi. Jika}\\ &\textrm{hanya 1 orang wakil yang harus dipilih}\\ & \textrm{(tidak peduli putra atau putri)},\\ & \textrm{maka banyak cara memilih adalah 5 + 4 = 9 cara} \end{array}$

$\begin{array}{ll}\\ 4.&\textrm{Sebuah bilangan dibentuk dari angka-angka}\\ & \textrm{1, 2, 3, 4, 5, 6, 7, 8, dan 9. Jika pengulangan} \\ &\textrm{tidak diperbolehkan, tentukan banyaknya bilangan}\\ &\textrm{a}.\quad \textrm{yang terdiri dari 1 angka dan kurang dari 5}\\ &\textrm{b}.\quad \textrm{yang terdiri dari 2 angka dan kurang dari 50}\\ &\textrm{c}.\quad \textrm{yang terdiri dari 3 angka dan kurang dari 500}\\ &\textrm{d}.\quad \textrm{yang terdiri dari 4 angka dan kurang dari 5000}\\ &\textrm{e}.\quad \textrm{yang terdiri dari 5 angka dan kurang dari 50000}\\ &\textrm{f}.\quad \textrm{yang terdiri dari 6 angka dan kurang dari 500000 dan habis dibagi 5}\\\\ &\textrm{Jawab}:\\ &\textrm{a}.\quad \textrm{jelas ada 4 angka yang memenuhi, yaitu: 1, 2, 3, dan 4}\\ &\textrm{b}.\quad \textrm{2 angka misalkan AB, posisi A dapat diisi dengan 4 cara dan posisi B dapat}\\ &\qquad \textrm{diisi dengan 8 cara, karena setelah diisikan ke A angka tinggal 8 buah dan}\\ &\qquad \textrm{semuanya memiliki kesempatan yang sama untuk diisikan ke B}.\\ &\qquad \textrm{sehingga AB dapat diisi dengan 4 x 8 = 32 cara}.\\ &\textrm{c}.\quad \textrm{3 angka misalkan ABC, posisi A dapat diisi dengan 4 cara, posisi B dapat}\\ &\qquad \textrm{diisi dengan 8 cara, dan posisi C dapat diisi dengan 7 cara}.\\ &\qquad \textrm{sehingga ABC dapat diisi dengan 4 x 8 x 7 = 224 cara}.\\ &\\ &\textrm{Untuk jawaban d, e, dan f silahkan dicoba sendiri sebagai latihan} \end{array}$

Aturan Pencacahan (Kelas XII Matematika Wajib)

$\color{blue}\textrm{A. Pendahuluan}$

$\color{blue}\textrm{A. 1 Kombinatorial}$

Dalam matematika ada cabang ilmu yang mengkhususkan mempelajari tentang pengaturan objek-objek. Cabang matematika ini selanjutnya dinamakan Kombinatorial. Hasil dari mempelajari bagian ini adalah diperoleh jumlah cara pengaturan objek-objek tertentu di dalam himpunannya.

Sebagai contoh nomor plat mobil di negara X terdiri atas 4 angka diikuti dengan 2 huruf. Angka pertama tidak boleh 0. Berapa banyak nomor plat mobil yang dapat dibuat?

Sebagai contoh yang lain sandi-lewat (password) sistem komputer panjangnya 6 sampai 8 karakter. Tiap karakter sendiri boleh berupa angka atau huruf, dengan huruf besar maupun huruf kecil tidak dibedakan. Berapa banyak sandi-lewat (password) yang dapat dibuat?

$\color{blue}\textrm{A. 2 Percobaan}$

Hasil dari Kombinatorial ini diperoleh dari percobaan(experiment). Percobaan dalam pengertian di sini adalah Proses yang berupa tindakan yang dapat diamati. Sebagai misal dalam percobaan melempar sebuah dadu, maka hasil yang mungkin adalah munculnya salah satu muka dadu yang enam, yaitu: 1,2,3,4,5, dan 6. Setiap kali kita melempar dapat dipastikan salah satu muka dadu akan muncul

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

$\begin{array}{ll}\\ 1.&\textrm{Pada saat melempar sebuah koin, maka akan}\\ &\textrm{didapatkan 2 kemungkinan, yaitu muka}\\ &\textrm{gambar (G) atau muka angka (A)}\\ 2.&\textrm{Ketika melempar dua koin sekaligus, maka }\\ &\textrm{akan didapatkan kemungkinan 4 muka koin}\\ &\textrm{4 kemungkinan itu yaitu: AA, AG, GA, dan GG}\\ 3.&\textrm{Selanjutnya saat kita melempar 3 koin sekaligus}\\ &\textrm{maka kita akan mendapatkan 8 kemungkinan}\\ &\textrm{muka koin, yaitu}:\\ &\textrm{AAA, AAG, AGA, AGG, GAA, GAG, GGA,}\\ &\textrm{dan GGG}\\ 4.&\textrm{Contoh yang lain saat kita melempar dua buah}\\ &\textrm{dadu, maka kita akan mendapatkan 36 kemungkinan}\\ &\textrm{muka dadu} \end{array}$

Untuk uraian contoh pada no.3 dan 4 disertakan tabel berikut

$\begin{array}{|c|c|}\hline \textrm{3}&\textrm{4}\\\hline \color{red}\left\{\begin{matrix} A\left\{\begin{matrix} A\left\{\begin{matrix} A&=AAA\\ \\ G&=AAG \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A&=AGA\\ \\ G&=AGG \end{matrix}\right. \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A\left\{\begin{matrix} A&=GAA\\ \\ G&=GAG \end{matrix}\right.\\ \\ G\left\{\begin{matrix} A&=GGA\\ \\ G&=GGG \end{matrix}\right. \end{matrix}\right. \end{matrix}\right. &\color{blue}\begin{array}{|c|c|c|c|c|c|c|}\hline \setminus&1&2&3&4&5&6\\\hline 1&(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\\hline 2&(2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\\hline 3&(3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)\\\hline 4&(4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6)\\\hline 5&(5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\\hline 6&(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)\\\hline \end{array} \\\hline \textrm{n}(\textrm{S})=8&\textrm{n}(\textrm{S})=36\\\hline \end{array}$

Sebagai catatan kemungkinan-kemungkinan yang muncul dalam setaip tindakan pada 4 contoh di atas selanjutnya akan disebut sebagai titik sampel.

DAFTAR PUSTAKA

Munir, R. 2012. Matematika Diskrit. Bandung: IMFORMATIKA.

Contoh Soal Vektor di Dimensi Dua (Matematika Peminatan Kelas X) Bagian 1

Perhatikanlah gambar berikut untuk menjawab soal no.1

$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: \overline{XW}=\textbf{a}\: ,\: \overline{XY}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{YZ}=\textbf{c}\\ &\textrm{Nyatakan dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{WY}\qquad\qquad\qquad \textrm{d}.\quad\overline{WZ}\\ &\textrm{b}. \quad\overline{XZ}\qquad\qquad\qquad \: \textrm{e}.\quad\overline{WM}\\ &\textrm{c}.\quad\overline{ZX}\qquad\qquad\qquad \: \: \textrm{f}.\quad\overline{MY}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{WY}&=\overline{WX}+\overline{XY}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{XZ}&=\overline{XY}+\overline{YZ}=\textbf{b}+\textbf{c}\\ \textrm{c}.\quad\overline{ZX}&=\overline{ZY}+\overline{YX}=-\textbf{c}+(-\textbf{b})=-\textbf{b}-\textbf{c}\\ &=-(\textbf{b}+\textbf{c})\\ &\textrm{atau}\\ \overline{ZX}&=-\overline{XZ}=-(\textbf{b}+\textbf{c})\\ \textrm{d}.\quad \overline{WZ}&=\overline{WX}+\overline{XY}+\overline{YZ}\\ &=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{e}.\quad \overline{WM}&=\displaystyle \frac{1}{2}\overline{WZ}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{MY}&=\overline{MZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\overline{WZ}+\overline{ZY}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )+(-\textbf{c})\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}+\textbf{c} \right )-\textbf{c}\\ &=\displaystyle \frac{1}{2}\left ( \textbf{a}+\textbf{b}-\textbf{c} \right )\end{aligned} \end{array}$

Perhatikanlah gambar berikut untuk menjawab soal no.2

$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: \overline{PQ}=\textbf{a}\: ,\: \overline{QR}=\textbf{b}\: ,\: \textrm{dan}\: \: \overline{RS}=\textbf{c}\\ &\textrm{dan titik}\: \: \textbf{E}\: \: \textrm{dan}\: \: \textbf{F}\: \: \textrm{adalah titik tegah}\\ &\overline{RS}\: \: \textrm{dan}\: \: \overline{QS},\\ &\textrm{nyatakanlah dalam vektor},\: \textbf{a},\: \textbf{b},\: \&\: \: \textbf{c}\\ &\textrm{untuk vektor-vektor berikut}\\ &\textrm{a}.\quad\overline{PR}\qquad\qquad\qquad \textrm{e}.\quad\overline{PF}\\ &\textrm{b}. \quad\overline{RP}\qquad\qquad\qquad \textrm{f}.\quad\overline{SF}\\ &\textrm{c}.\quad\overline{PS}\qquad\qquad\qquad \: \textrm{g}.\quad\overline{FR}\\ &\textrm{d}.\quad\overline{QE}\qquad\qquad\qquad \textrm{h}.\quad\overline{EF}\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}\textrm{a}.\quad\overline{PR}&=\overline{PQ}+\overline{QR}=\textbf{a}+\textbf{b}\\ \textrm{b}.\quad\overline{RP}&=\overline{RQ}+\overline{QP}=-\textbf{b}-\textbf{a}=-\left ( \textbf{a}+\textbf{b} \right )\\ \textrm{c}.\quad\overline{PS}&=\overline{PQ}+\overline{QR}+\overline{RS}=\textbf{a}+\textbf{b}+\textbf{c}\\ \textrm{d}.\quad \overline{QE}&=\overline{QR}+\overline{RE}=\overline{QR}+\displaystyle \frac{1}{2}\overline{RS}\\ &=\textbf{b}+\displaystyle \frac{1}{2}\textbf{c}\\ \textrm{e}.\quad \overline{PF}&=\overline{PQ}+\overline{QF}=\overline{PQ}+\displaystyle \frac{1}{2}\overline{QS}\\ &=\overline{PQ}+\displaystyle \frac{1}{2}\left ( \overline{QR}+\overline{RS} \right )\\ &=\displaystyle \frac{1}{2}\left ( 2\textbf{a}+\textbf{b}+\textbf{c} \right )\\ \textrm{f}.\quad \overline{SF}&=\displaystyle \frac{1}{2}\overline{SQ}=\displaystyle \frac{1}{2}\left (\overline{SR}+\overline{RQ} \right )=\displaystyle \frac{1}{2}\left ( -\textbf{c}+(-\textbf{b}) \right )\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )\\ \textrm{g}.\quad \overline{FR}&=\overline{FQ}+\overline{QR}=\displaystyle \frac{1}{2}\overline{SQ}+\overline{QR}\\ &=-\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right )+\textbf{b}=\displaystyle \frac{1}{2}\left ( \textbf{b}-\textbf{c} \right )\\ \textrm{h}.\quad \overline{EF}&=\overline{ES}+\overline{SF}=\displaystyle \frac{1}{2}\overline{RS}+\displaystyle \frac{1}{2}\overline{SQ}\\ &=\displaystyle \frac{1}{2}\textbf{c}+\left ( -\displaystyle \frac{1}{2}\left ( \textbf{b}+\textbf{c} \right ) \right )=-\displaystyle \frac{1}{2}\textbf{b} \end{aligned} \end{array}$

$\color{red}\begin{array}{ll}\\ 3.&\textrm{Perhatikanlah gambar berikut} \end{array}$

$\begin{array}{ll}\\ .\quad&\textrm{Jika pada titik P bekerja 3 buah gaya}\\ &\textrm{seperti pada gambar di bawah, lukislah}\\ &\textrm{vektor}\\ &\qquad\qquad \textbf{r}=\textbf{a}+\textbf{b}+\textbf{c}\\\\ &\textrm{Jawab}:\\ &\textrm{Dengan aturan poligon kita akan}\\ &\textrm{mendapatkan gambar berikut} \end{array}$

Polinom / Suku Banyak (Matematika Peminatan Kelas XI)

$\color{blue}\textrm{A. Pendahuluan}$

Polinom disebut juga suku banyak. Polinom atau suku banyak adalah suatu bentuk variabel yang berpangkat/berderajat.

Secara definisi suku banyak (polinomial) dalam $x$ berderajat $n$ adalah:

Suatu bentuk

$\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_{2}x^{2}+a_{1}x^{1}+a_{0}$

dengan $n$ bilangan cacah serta $a_{0},\: a_{1},\: a_{2},\: ...,\: a_{n}$ koefisien dari suku $x$ dan $a_{n}\neq 0$ dengan $a_{0}$ sebagai suku tetap (konstan)nya.

Selanjutnya perhatikanlah tabel berikut!

$\color{purple}\begin{array}{|l|l|}\hline \begin{aligned}a_{n}&\: \: \textrm{adalah koefisien dari} \: \: x^{n}\\ a_{n-1}&\: \: \textrm{adalah koefisien dari} \: \: x^{n-1}\\ a_{n-2}&\: \: \textrm{adalah koefisien dari} \: \: x^{n-2}\\ \vdots &\\ a_{2}&\: \: \textrm{adalah koefisien dari} \: \: x^{2}\\ a_{1}&\: \: \textrm{adalah koefisien dari} \: \: x^{1}\\ a_{0}&\: \: \textrm{adalah konstanta} \\ &(\textrm{suku tetap}) \end{aligned}&\begin{aligned}a_{n}\: &\: \neq 0\\ n:&\: \: \textrm{bilangan cacah},\\ :&\: \: \textrm{adalah derajat (pangkat)} \\ &\: \: \textrm{tertinggi dalam suku} \\ &\: \: \textrm{banyak tersebut}&\\ &\\ &\\ &\end{aligned}\\\hline \end{array}$

$\LARGE\colorbox{magenta}{CONTOH SOAL 1}$

$\begin{aligned}1.\quad&\textrm{Polinom}\: \: \color{red}2x^{3}-6x^{2}+2020\: \: \color{black}\textrm{dapat dinyatakan}\\ &\textrm{dengan}\: \: \: \color{blue}2x^{3}-6x^{2}+0x^{1}+2020x^{0}\\ &\textrm{Polinom tersebut memiliki suku tetap}\: \: 2020\\ 2.\quad&\textrm{Polinom}\: \: \color{red}5x^{4}-8x^{3}+6x-2021 \: \: \color{black}\textrm{dapat dinyatakan}\\ &\textrm{dengan}\: \: \: \color{blue}5x^{4}-8x^{3}+0x^{2}+6x^{1}-2021x^{0}\\ &\textrm{Polinom tersebut memiliki suku tetap}\: \: -2021\\ 3.\quad&\textrm{Polinom}\: \: \color{red}x^{4}-2x^{3}+3x^{2}-2\sqrt{x}+1 \: \: \color{black}\textrm{tidak dapat}\\ &\textrm{dinamakan polinom, sebab ada variabel dari}\: \: \: \color{blue}x\\ &\textrm{yang berderajat bukan bilangan cacah}\\ 4.\quad&\textrm{Sedangkan polinom}\: \: \color{red}5-x+(2-x)(1+x+x^{2})\\ &\textrm{adalah bentuk polinom, karena dapat dinayatakan}\\ &\textrm{dengan}\: \: \: \color{blue}-x^{3}+x^{2}+7 \end{aligned}$

$\color{blue}\textrm{B. Nilai Polinom}$

Polinom atau suku banyak yang berderajat $\color{red}n$ yang selanjutnya dinyatakan dengan

$f(x)=\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_{1}x^{1}+a_{0}$

Berkaitan dengan kebutuhan penentuan nilai ini, dapat ditentukan dengan dua cara:

$\textbf{a. Substitusi}$

$\begin{aligned}&\textrm{Nilai suku banyak}\: \: \color{red}f(x)\: \: \textrm{berderajat}\\ &n\: \: \textrm{saat}\: \: \color{red}x = k\: \: \color{black}\textrm{adalah}\: \: \color{blue}f(k).\\ &\textrm{Jika}\: \: f(k)=0\: \: \textrm{maka}\: \: x = k\: \: \textrm{akar dari}\: \: f(x),\\ &\textrm{dan}\: \: (x-k)\: \: \textrm{faktor dari}\: \: f(x)\\ &\end{aligned}$

$\LARGE\colorbox{magenta}{CONTOH SOAL 2}$

Jika suatu polinom dinyatakan dengan $f(x)$, maka nilai polinom itu untuk $x=3$ adalah $f(3)$.

Misalkan diketahui

$\begin{aligned}1.\quad f(x)&=x^{3}-1\\ \textrm{mak}&\textrm{a}\\ f(1)&=1^{3}-1=1-1=0\\ f(3)&=3^{3}-1=27-1=26\\ f(-4)&=(-4)^{2}-1=-64-1=-65 \end{aligned}$

$\begin{array}{ll}\\ 2.&\textrm{Diketahui}\: \: h(x)=2x^{3}+5x^{2}-12x-6\\ &\textrm{Tentukanlah nilai untuk}\: \: h(-2),\: h(-1),\\ &h(0),\: h(1),\: \: \textrm{dan}\: \: h(2)\\\\ &\color{blue}\textrm{Jawab}:\\ &\begin{array}{|c|c|l|}\hline \color{red}x=k&\color{red}h(k)&\qquad\qquad\qquad\qquad\color{red}\textrm{Nilai}\\\hline x=-2&h(-2)&\begin{aligned}h(-2)&=2(-2)^{3}+5(-2)^{2}-12(-2)-6\\ &=-16+20+24-6\\ &=22 \end{aligned}\\\hline x=-1&h(-1)&\begin{aligned}h(-1)&=2(-1)^{3}+5(-1)^{2}-12(-1)-6\\ &=-2+5+12-6\\ &=9 \end{aligned}\\\hline x=0&h(0)&\begin{aligned}h(0)&=2(0)^{3}+5(0)^{2}-12(0)-6\\ &=-6 \end{aligned}\\\hline x=1&h(1)&\begin{aligned}h(1)&=2(1)^{3}+5(1)^{2}-12(1)-6\\ &=2+5-12-6\\ &=-11 \end{aligned}\\\hline x=2&h(2)&\begin{aligned}h(2)&=2(2)^{3}+5(2)^{2}-12(2)-6\\ &=16+20-24-6\\ &=6 \end{aligned}\\\hline \end{array} \end{array}$

$\begin{array}{ll}\\ 3.&\textrm{Diketahui}\: \: p(x)=x-2019\\ &\textrm{dan}\: \: q(x)=x^{2019}+1.\: \textrm{Tentukanlah}\\ &\textrm{nilai untuk}\: \: p\left ( q(2) \right )\: \: \textrm{dan}\: \: q\left ( p(2) \right )\\\\ &\color{blue}\textrm{Jawab}:\\ &\textrm{Yang dibahas yang bagian}\: \: p\left ( q(2) \right )\\ &q(2)=2^{2019}+1,\: \textrm{maka nilai}\\ &\begin{aligned}p\left ( q(2) \right )&=\left ( 2^{2019}+1 \right )-2019\\ &=2^{2019}-2018 \end{aligned}\\\\ &\textrm{Untuk yang}\: \: q\left ( p(2) \right )\: \: \textrm{adalah}\\ &p(2)=\cdots , \: \textrm{maka nilai}\\ &\begin{aligned}q\left ( p(2) \right )&=\because \cdots ^{2019}+1\\ &=\cdots \end{aligned} \end{array}$

$\textbf{b. Horner/Sintetik}$

Nilai suatu polinom dapat ditentukan dengan pembagian sintesis Horner

Misalkan:

$\begin{aligned}f(x)&=\color{blue}ax^{3}+bx^{2}+cx+d\: \: \color{black}\textrm{saat akan dibagi}\\ &\color{red}x=h,\: \: \color{black}\textrm{maka pembagian Horner itu}:\\ & \end{aligned}$

Perhatikan bahwa proses ke bawah adalah berup proses penjumlahan.

Proses di atas akan sama saat kita mensubstitusikan $\color{red}x=h$ ke dalam $\color{red}f(x)$, yaitu:

$\begin{aligned}f(x)&=\color{blue}ax^{3}+bx^{2}+cx+d\: \: \textrm{saat}\\ &\color{red}x=h,\: \: \color{black}\textrm{maka}\\ f(\color{red}h\color{black})&=a\color{red}h^{3}\color{black}+b\color{red}h^{2}\color{black}+c\color{red}h\color{black}+d\\ &\\ &\textbf{Cukup JELAS bukan}? \end{aligned}$

$\LARGE\colorbox{magenta}{CONTOH SOAL 3}$

$\begin{array}{l}\\ \textrm{Tentukanlah nilai dari}\: \: f(4)\: \: \textrm{jika}\\ \textrm{diketahui}\: \: f(x)=x^{3}-x-5\\ \textrm{Jawab}:\\ \begin{aligned}(1).\quad&\textrm{Cara substitusi langsung}\\ &f(x)=x^{3}-x-5\\ &f(4)=\color{red}4^{3}-4-5\\ &\qquad=\color{red}64-9=\color{blue}55\\ (2).\quad&\textrm{Cara Horner}\\ &\textrm{Karena}\: \: f(x)=x^{3}-x-5\\ &\textrm{dan koefisiennya yang akan}\\ &\textrm{adalah}:\\ & a_{3}=1,\: a_{2}=0,\: a_{1}=-1,\: \&\: a_{0}=-5\\ &\textbf{maka bagan pembagian Hornernya}\\ &\begin{array}{ll|llllllllll}\\ &\color{red}x=4&1&\color{blue}0&\color{magenta}-1&-5&\\ &&&&&&\\ &&&\color{blue}4&\color{magenta}16&60&+\\\hline &&1&\color{blue}4&\color{magenta}15&55 \end{array} \end{aligned} \end{array}$

Lanjutan Materi Vektor Di Ruang Dimensi Dua (Matematika Peminatan Kelas X)

$\color{blue}\textrm{E. Modulus Vektor}$

Modulus suatu vektor adalah ukuran (panjang) suatu vektor. Dalam hal ini modulus suatu vektor adalah besar/panjang suatu vektor.

Lihat pada pembahasan sebelumnya tentang panjang vektor di $\color{red}\textrm{R}^{2}$ di sini.

Dalam menuliskan modulus/panjang vektor ini digunakan notasi $\left | \overline{a} \right |$ jika vektornya $\overline{a}$.

Bila $\color{red}\overline{a}=\begin{pmatrix} x_{1}\\ y_{1} \end{pmatrix},\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\sqrt{x_{1}^{2}+y_{1}^{2}}$

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

Perhatikanlah ilustrasi gambar berikut

Tentukanlah modulus/panjang vektor $\overline{u}$ ?

Jawab:

$\begin{aligned}&\textrm{Diketahui bahwa vektor}\: \: \color{red}\overline{u}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\\ &\textrm{maka modulus vektor}\: \: \overline{u}\\ &=\left | \overline{u} \right |\\ &=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=\sqrt{52}\\ &=\color{red}2\sqrt{13} \end{aligned}$

$\color{blue}\textrm{F. Vektor Posisi dan Vektor Bebas}$

Perhatikanlah ilustrasi berikut

Vektor yang titik pangkalnya berada di titik O(0,0), maka vektor tersebut dinamakan vektor posisi. Pada gambar di atas titik A rekatif terhadapa O(0,0), maka $\color{red}\overline{OA}$ disebut vektor posisi A terhadap titik O(0,0) dan vektor yang lainnya dinamakan vektor bebas. Pada gambar di atas $\color{red}\overline{BC}\: \&\: \overline{DF}$ adalah contoh vektor bebasnya.

$\color{blue}\textrm{G. Kesamaan Dua Vektor}$

Perhatikanlah dua vektor bebas pada gambar di atas, cukup jelas secara geometri tampak panjang vektor $\color{red}\overline{BC}\: \&\: \overline{DF}$ sama. Dan secara aljabar dapat ditunjukkan juga bahwa:

$\color{red}\overline{BC}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \&\: \color{red}\overline{DF}=\begin{pmatrix} 4\\ 6 \end{pmatrix}$

Secara definisi

$\overline{a}=\overline{b}\: \: \begin{cases} \bullet & \left | \overline{a} \right |=\left | \overline{b} \right | \\\\ \bullet & \textrm{arah}\: \: \overline{a}=\textrm{arah}\: \: \overline{b} \end{cases}$

$\color{blue}\textrm{H. Vektor Negatif}$

Perhatikanlah ilustrasi berikut

$\color{red}\overline{a}=\begin{pmatrix} 4\\ 6 \end{pmatrix}\: \color{black}\&\: \: \color{red}\overline{b}=\color{black}\begin{pmatrix} -4\\ -6 \end{pmatrix}=-\color{red}\begin{pmatrix} 4\\ 6 \end{pmatrix}$

Vektor $\color{red}-\: \overline{a}=\overline{b}$ memiliki ukuran yang sama dengan $\overline{a}$.

Selanjutnya vektor $\color{red}\overline{a}=-\: \overline{b}\: \: \color{black}\textrm{maka}\: \: \color{red}\left | \overline{a} \right |=\left | \overline{b} \right |$

$\color{blue}\textrm{I. Vektor Satuan}$

Perhatikanlah ilustrasi berikut

Jika diketahui $\color{red}\overline{a}\: \color{black}\&\: \: \color{red}\overline{b}$ seperti gambar di atas, maka

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{a} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}\textrm{adalah vektor satuan dari vektor}\: \: \: \color{red}\overline{b} \end{cases}$

Dan panjang dari vektor satuan ini adalah selalu satu satuan.

$\LARGE\colorbox{magenta}{CONTOH SOAL}$

Tentukanlah vektor satuan dari dua vektor pada gambar di atas?

Jawab:

$\begin{cases} \color{red}\displaystyle \frac{\overline{a}}{\left | \overline{a} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} -2\\ 5 \end{pmatrix}}{\sqrt{(-2)^{2}+5^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{29}}\begin{pmatrix} -2\\ 5 \end{pmatrix}=\displaystyle \frac{1}{29}\sqrt{29}\begin{pmatrix} -2\\ 5 \end{pmatrix} \\\\ \color{red}\displaystyle \frac{\overline{b}}{\left | \overline{b} \right |} & \color{black}=\displaystyle \frac{\begin{pmatrix} 6\\ 4 \end{pmatrix}}{\sqrt{6^{2}+4^{2}}}\\ &=\displaystyle \frac{1}{\sqrt{52}}\begin{pmatrix} 6\\ 4 \end{pmatrix}=\displaystyle \frac{1}{26}\sqrt{52}\begin{pmatrix} 6\\ 4 \end{pmatrix} \end{cases}$

$\color{blue}\textrm{J. Vektor Basis}$

Vektor satuan yang saling tegak lurus. Didalam ruang dimensi dua terdapat dua vektir basis., yaitu:

$\bar{i}=\color{red}\begin{pmatrix} 1\\ 0 \end{pmatrix}\: \: \color{black}\textrm{dan}\: \: \bar{j}=\color{blue}\begin{pmatrix} 0\\ 1 \end{pmatrix}$

$\begin{aligned}&\textrm{Misalkan vektor}\: \: \bar{u}=\color{red}\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}\\ &\textrm{dapat dinyatakan dalam kombinasi linear}\\ &\textrm{vektor basis}\: \: \bar{i}\: \: \textrm{dan}\: \: \bar{j}\: \: \textrm{di atas, yaitu}\\ &\bar{u}=\begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix}=u_{1}\begin{pmatrix} 1\\ 0 \end{pmatrix}+u_{2}\begin{pmatrix} 0\\ 1 \end{pmatrix}\\ &\textrm{maka akan menjadi}\\ &\bar{u}=u_{1}\bar{i}+u_{2}\bar{j}\\ &\textrm{SEBAGAI CONTOH}\\ &\overline{AB}=\begin{pmatrix} 5\\ 8 \end{pmatrix}\: \: \color{blue}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=5\bar{i}+8\bar{j}\\ &\textrm{Demikian juga jika}\\ &\overline{CD}=\begin{pmatrix} -3\\ -8 \end{pmatrix}\: \: \color{red}\textrm{dalam vektor basis menjadi}\\ &\overline{AB}=-3\bar{i}-8\bar{j}\\ \end{aligned}$

$\color{blue}\textrm{K. Vektor Nol}$

Jika vektor $\overline{a}=\overline{b}$ , maka $\overline{a}-\overline{b}=0$.

$\textbf{0}$ disebut sebagai vektor ol.

Sebagai tabahan penjelasan vektor $\textbf{0}$ tidak mempunyai besar dan arahnya tak tentu.