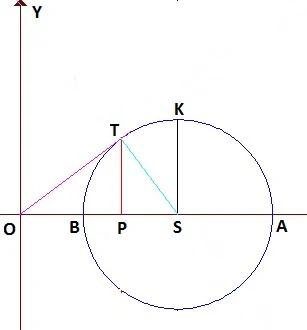
Perhatikanlah ilustrasi berikut
Dari gambar di atas, misalkan sebuah lingkaran yang berpusat di titik $S$ dengan titik $A$ dan $B$ pada lingkaran yang masih-masing memiliki koordinat $(a,0)$ dan $(b,0)$. Dari sani koordinat titik S adalah $\left ( \displaystyle \frac{a+b}{2},0 \right )$. Selain itu terdapat garis singgung lingkaran melalui sebuah titik di luar lingkaran tersebut sebagaimana ilustrasi gambar di atas yaitu titik $O(0,0)$.
$\begin{array}{|l|}\hline \begin{aligned}1.\quad TS&=BS=OS-OB=\left ( \displaystyle \frac{a+b}{2} \right )-b\\ &=\color{red}\displaystyle \displaystyle \frac{a-b}{2} \end{aligned}\\ \begin{aligned}2.\quad OT&=\sqrt{OS^{2}-TS^{2}}\\ &=\sqrt{\left ( \displaystyle \displaystyle \frac{a+b}{2} \right )^{2}-\left (\displaystyle \displaystyle \frac{a-b}{2} \right )^{2}}\\ &=\color{red}\sqrt{ab} \end{aligned}\\ \begin{aligned}3.\quad TP&=...\\ &\textrm{Kita gunakan luas}\: \: \triangle OTS\\ &OS\times TP=OT\times TS\\ &TP=\displaystyle \frac{OT\times TS}{OS}=\sqrt{ab}\left ( \displaystyle \frac{a-b}{a+b} \right )\\ &\begin{aligned}4.\quad OP&=\sqrt{OT^{2}-PT^{2}}\\ &=\sqrt{\left ( \sqrt{ab} \right )^{2}-\left ( \sqrt{ab} \right )^{2}\left (\displaystyle \displaystyle \frac{a-b}{a+b} \right )^{2}}\\ &=\sqrt{ab\left ( 1-\left (\displaystyle \frac{a-b}{a+} \right )^{2} \right )}\\ &=\sqrt{ab\left ( \frac{4ab}{(a+b)^{2}} \right )}\\ &=\color{red}\displaystyle \frac{2ab}{a+b} \end{aligned}\\ &\begin{aligned}5.\quad OK&=\sqrt{OS^{2}+SK^{2}}\\ &=\sqrt{\left ( \displaystyle \frac{a+b}{2} \right )^{2}+\left ( \displaystyle \frac{a-b}{2} \right )^{2}}\\ &=\color{red}\sqrt{\displaystyle \frac{a^{2}+b^{2}}{2}} \end{aligned} \end{aligned} \\\hline \end{array}$.
$\begin{array}{|c|}\hline \begin{aligned}&\left | OB \right |< \left | OP \right |< \left | OT \right |< \left | OS \right |< \left | OK \right |< \left | OA \right |\\ &\textrm{maka}\\ &\color{red}b\color{black}< \color{red}\displaystyle \frac{2ab}{a+b}\color{black}<\color{red} \sqrt{ab}\color{black}<\color{red} \displaystyle \frac{a+b}{2}\color{black}< \color{red}\sqrt{\displaystyle \frac{a^{2}+b^{2}}{2}}\color{black}< \color{red}b\\ &\textrm{Selanjutnya dapat dituliskan sebagai bentuk}\\ &\color{red}b\color{black}< \color{red}\displaystyle \frac{2}{\displaystyle \frac{1}{a}+\frac{1}{b}}\color{black}<\color{red} \sqrt{ab}\color{black}<\color{red} \displaystyle \frac{a+b}{2}\color{black}< \color{red}\sqrt{\displaystyle \frac{a^{2}+b^{2}}{2}}\color{black}< \color{red}b \end{aligned}\\\hline \end{array}$.
Bentuk akhir pada tabel terakhir di atas selanjutnya yang kita kenal dengan ketaksamaan HM-GM-AM-QM
$\begin{aligned}&\textrm{Misalkan diberikan}\: \: x_{1},x_{2},x_{3},\cdots ,x_{n}\\ & \textrm{bilangan real positif, maka hubungan }\\ &\textrm{ketaksamaan}\: \: \color{red}\textrm{QM-AM-GM-HM}\\ & \color{black}\textrm{dapat dituliskan}\\ &\begin{aligned}\bullet \quad&\textrm{QM}(x_{1},x_{2},x_{3},\cdots ,x_{n})=\sqrt{\displaystyle \frac{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+\cdots +x_{n}^{2}}{n}}\\ &Quadratic\: Mean\: (\textrm{rata-rata kuadrat})\\ \bullet \quad&\textrm{AM}(x_{1},x_{2},x_{3},\cdots ,x_{n})=\displaystyle \frac{x_{1}+x_{2}+x_{3}+\cdots +x_{n}}{n}\\ &Arithmetic\: Mean\: (\textrm{rata-rata aritmetika})\\ \bullet \quad&\textrm{GM}(x_{1},x_{2},x_{3},\cdots ,x_{n})=\sqrt[n]{x_{1}.x_{2}.x_{3}\cdots x_{n}}\\ &Geometric\: Mean\: (\textrm{rata-rata geometri})\\ \bullet \quad&\textrm{HM}(x_{1},x_{2},x_{3},\cdots ,x_{n})=\displaystyle \frac{n}{\displaystyle \frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}+\cdots +\frac{1}{x_{n}}}\\ &Harmonic\: Mean\: (\textrm{rata-rata harmoni}) \end{aligned} \end{aligned}$.
$\LARGE\colorbox{yellow}{CONTOH SOAL}$.
$\begin{array}{ll}\\ 1.&\textrm{Jika}\: \: a,b\: \: \textrm{bilangan real positif bahwa}\\ &(a+b)\left (\displaystyle \frac{1}{a} +\displaystyle \frac{1}{b} \right )\geq 4\\\\ &\textbf{Bukti}\\ &\color{blue}\textrm{Alternatif 1}\\ &\begin{aligned}&(a+b)\left (\displaystyle \frac{1}{a} +\displaystyle \frac{1}{b} \right )\\ &= 1+\displaystyle \frac{a}{b}+\frac{b}{a}+1\\ &= 2+\displaystyle \frac{a}{b}+\frac{b}{a}\\ &\textrm{Dengan}\: \: \textbf{AM-GM}\\ &\geq 2+2\sqrt{\displaystyle \frac{a}{b}\times \frac{b}{a}}\\ &\geq 2+2.1=4\qquad \blacksquare \end{aligned}\\ &\color{blue}\textrm{Alternatif 2}\\ &\begin{aligned}&(a+b)\left (\displaystyle \frac{1}{a} +\displaystyle \frac{1}{b} \right )\\ &\textrm{Dengan}\: \: \textbf{AM-GM}\\ &\geq 2\sqrt{ab}\times \displaystyle \frac{2}{\sqrt{ab}}=4\qquad \blacksquare \end{aligned} \end{array}$.
$\begin{array}{ll}\\ 2.&\textrm{Jika}\: \: a,b,c\: \: \textrm{bilangan real, tunjukkan}\\ &\textrm{bahwa}\: \: a^{2}+b^{2}+y^{2}\geq ab+ac+bc\\\\ &\textbf{Bukti}\\ &\textrm{Dengan ketaksamaan}\: \: \textbf{AM-GM}\\ &\textrm{pada bilangan}\: \: a,b,c\: \: \textrm{bilangan real}\\ &\textrm{kita akan peroleh}\\ &\begin{array}{ll} a^{2}+b^{2}\geq 2ab&\\ a^{2}+c^{2}\geq 2ac&\\ b^{2}+c^{2}\geq 2bc&+\\\hline 2(a^{2}+b^{2}+c^{2})&\geq 2ab+2ac+2bc\\ a^{2}+b^{2}+c^{2}&\geq ab+ac+bc\\ &\qquad\textbf{terbukti} \end{array} \end{array}$.
$\begin{array}{ll}\\ 3.&\textrm{Jika}\: \: a_{i}\geq 0\: ,\: i\in \left \{ 1,2,3,4 \right \}\\ &\textrm{tunjukkan bahwa}\\ &\displaystyle \frac{a_{1}+a_{2}+a_{3}+a_{4}}{4}\geq \sqrt[4]{a_{1}a_{2}a_{3}a_{4}}\\\\ &\textbf{Bukti}\\ &\displaystyle \frac{a_{1}+a_{2}+a_{3}+a_{4}}{4}=\displaystyle \frac{\displaystyle \frac{a_{1}+a_{2}}{2}+\frac{a_{3}+a_{4}}{2}}{2}\\ &\qquad\qquad\qquad\qquad \geq \displaystyle \frac{\sqrt{a_{1}a_{2}}+\sqrt{a_{3}a_{4}}}{2}\\ &\qquad\qquad\qquad\qquad \geq \sqrt{\sqrt{a_{1}a_{2}}.\sqrt{a_{3}a_{4}}}\\ &\qquad\qquad\qquad\qquad = \sqrt[4]{a_{1}a_{2}a_{3}a_{4}}\qquad \blacksquare \end{array}$.
DAFTAR PUSTAKA
- Bambang, S. 2012. Materi, Soal dan Penyelesaian Olimpiade Matematika Tingkat SMA/MA. Jakarta: BINA PRESTASI INSANI.
- Leo Bocek.----. Nerovnosti a Nerovnice. dalam : https://olympiada.karlin.mff.cuni.cz/prednasky/bocek1.pdf
Tidak ada komentar:
Posting Komentar
Informasi