MASALAH YANG MELIBATKAN TURUNAN PERTAMA FUNGSI TRIGONOMETRI
$\color{blue}\textrm{G. Nilai Stasioner}$
Jika fungsi $y=f(x)$ kontinu dan diferensiabel di $x=f'(a)=0$ , maka fungsi tersebut mempunyai nilai stasioner di $x=a$.
$\begin{array}{ll}\\ \textrm{a}.&\textrm{Suatu fungsi memiliki nilai stasioner}\\ &\textrm{adalah}\: \: f'(x)=0\: \: \textrm{untuk suatu nilai}\: \: x\\ \textrm{b}&\textrm{Jika fungsi}\: \: f(x)\: \: \textrm{mempunyai nilai}\: \: f(a)\\ &\textrm{di}\: \: x=a\: \: , \: \textrm{maka titik}\: \: \left ( a,f(a) \right )\: \: \textrm{adalah}\\ &\color{red}\textbf{titik stasioner} \end{array}$
Selanjutnya titik stasioner disebut juga dengan titik kritis atau titik ekstrim dan titik stasioner ini terbagi dalam 3 macam
- titik maksimum
- titik minimum, dan
- titik belok
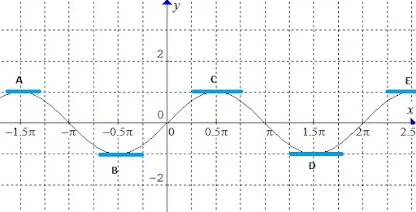
Sebagai ilustrasi pada fungsi trigonometri, perhatikanlah ilustrasi fungsi sinus berikut
$\begin{array}{l}\\ \underset{\begin{matrix} \Downarrow\\ \overbrace{\begin{matrix} \color{blue}\begin{aligned}&\textrm{Maksimum}\\ &\Downarrow\\ &\textrm{Nilai} \\ &\textrm{maksimum}\\ &=f(a)\\ &\textrm{titiknya}\\ &=(a,f(a))\\ &\textrm{atau}\\ &f''(x)<0\\ &\textrm{Pada contoh di atas}\\ &\textrm{Titik A,C,E}\\ & \end{aligned} & \color{red}\begin{aligned}&\textrm{Minimum}\\ &\Downarrow\\ &\textrm{Nilai} \\ &\textrm{minimum}\\ &=f(a)\\ &\textrm{titiknya}\\ &=(a,f(a))\\ &\textrm{atau}\\ &f''(x)>0\\ &\textrm{Pada contoh di atas}\\ &\textrm{Titik B,D}\\ & \end{aligned} & \begin{aligned}&\textrm{Belok}\\ &\Downarrow\\ &\textrm{Nilai} \\ &\textrm{belok}\\ &=f(a)\\ &\textrm{titiknya}\\ &=(a,f(a))\\ &\textrm{atau}\\ &f''(x)=0\\ &\textrm{Pada contoh di atas}\\ &\textrm{Titik}\: \: \left ( -\pi ,0 \right )\\ &\left ( 0^{\circ},0 \right ),\left ( \pi ,0 \right ),\left ( 2\pi ,0 \right ) \end{aligned} \end{matrix}} \end{matrix}}{\begin{matrix} \textrm{Stasioner}\\ f'(x)=0\: \: \textrm{saat}\: \: x=a \end{matrix}} \end{array}$
Sebagai catatan bahwa, nilai maksimum dan minimum yang telah di dapatkan sampai dengan memasukkan titik ujinya adalah sebenarnya titik maksimum atau minimum LOKAL dalam selang yang diberikan. Supaya menjadi nilai maksimum atau minimum mutlak, maka nilai-nilai dari nilai stasioner ini harus dibandingkan dengan nilai-nilai FUNGSI pada titik-titik ujung intervalnya yang diberikan tersebut.
$\LARGE\color{black}\fbox{CONTOH SOAL}$
$\begin{array}{ll}\\ 1.&\textrm{Tentukanlah semua titik stasioner}\\ &\textrm{berikut jenisnya dari fungsi}\\ &f(x)=\sin x+\cos x\: \: \textrm{dengan}\\ &0\leq x\leq 2\pi\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}&\textrm{Diketahui}\\ &f(x)=\sin x+\cos x\\ &f'(x)=\cos x-\sin x\\ &\textrm{Saat}\quad \color{black}f'(x)=0,\\ &\color{black}f'(x)=\cos x-\sin x=0 \: \: \cos x=\sin x\\ &\cos x=\cos \left ( \displaystyle \frac{\pi }{2}-x \right )\\ &\: \: \: \quad x=\pm \left ( \displaystyle \frac{\pi }{2}-x \right )+k.2\pi \\ &\: \: \: \quad \begin{cases} x+x &=\displaystyle \frac{\pi }{2}+k.2\pi ,\: \: \color{red}\textrm{atau} \\ x-x &=-\displaystyle \frac{\pi }{2}+k.2\pi \end{cases}\\ &\textrm{maka}\\ &\: \: \: \quad \begin{cases} x &=\displaystyle \frac{\pi }{4}+k.\pi ,\: \: \color{red}\textrm{atau} \\ 0&=-\displaystyle \frac{\pi }{2}+k.2\pi\: \: (\color{black}\textrm{tidak memenuhi}) \end{cases}\\ &\textrm{Sehingga ada dua absis yang memenuhi}\\ &\color{red}\textrm{sebagai titik STASIONER},\: \: \color{black}\textrm{yaitu}\\ &\color{black}x=\displaystyle \frac{\pi }{4}\: \: \textrm{dan}\: \: \quad x=\frac{5\pi }{4}\\ &\textrm{untuk}\: \: \: \color{black}x=\displaystyle \frac{\pi }{4}\\ &f\left ( \displaystyle \frac{\pi }{4} \right )=\sin \left ( \displaystyle \frac{\pi }{4} \right )-\cos \left (\displaystyle \frac{\pi }{4} \right )\\ &\qquad=\displaystyle \frac{1}{2}\sqrt{2}+\frac{1}{2}\sqrt{2}=\sqrt{2}\\ &\textrm{untuk}\: \: \: \color{black}x=\displaystyle \frac{5\pi }{4}\\ &f\left ( \displaystyle \frac{5\pi }{4} \right )=\sin \left ( \displaystyle \frac{5\pi }{4} \right )+\cos \left (\displaystyle \frac{5\pi }{4} \right )\\ &\qquad=-\displaystyle \frac{1}{2}\sqrt{2}-\frac{1}{2}\sqrt{2}=-\sqrt{2}\\ &\textrm{Jadi titik stasionernya}:\: \: \left ( \displaystyle \frac{\pi }{4},2 \right )\: \&\: \: \left ( \displaystyle \frac{5\pi }{4},-\sqrt{2} \right )\\ &\color{black}\textrm{Langkah berikutnya gunakanlah titik}\\ &\color{black}\textrm{uji di sekitar nilai stasioner yaitu}:\\ &\begin{array}{ccccccccc} &&&&&&&&\\\hline \color{red}0&&\displaystyle \frac{\pi }{4}&&\color{red}\pi &&\displaystyle \frac{5\pi }{4}&&\color{red}2\pi \end{array}\\ &\textrm{Selanjutnya}\\ &\textrm{Untuk}\: \: f'(x)=\cos x-\sin x\\ &x=0\Rightarrow f'(0)=\cos 0-\sin 0\\ &\quad=1+0=1>0\quad (\color{black}\textrm{positif})\\ &x=\pi \Rightarrow f'(\pi )=\cos \pi -\sin \pi \\ &\quad=-1+0=-1<0\quad (\color{red}\textrm{negatif})\\ &x=0\Rightarrow f'(2\pi )=\cos 2\pi -\sin 2\pi \\ &\quad=1+0=1>0\quad (\color{black}\textrm{positif})\\ &\begin{array}{|c|c|c|c|c|l|}\hline x&0&\displaystyle \frac{\pi }{4}&\pi &\displaystyle \frac{5\pi }{4}&2\pi \\\hline \color{black}f'(x)&+&0&-&0&+\\\hline &&--&&&\\ \color{red}\textrm{Garfik}&/&&\backslash&&/\\ &&&&\_\_\_\_&\\\hline \end{array}\\ &\textrm{Dari tabel di atas didapatkan}\\ &\begin{cases} \color{black}\left ( \displaystyle \frac{\pi }{4},\sqrt{2} \right ) & \color{red}\textrm{titik balik maksimum} \\ \color{black}\left ( \displaystyle \frac{5\pi }{4},-\sqrt{2} \right ) & \color{red}\textrm{titik balik minimum} \end{cases} \end{aligned} \end{array}$
$\begin{aligned}&\color{blue}\textrm{Sebagai CATATAN bahwa}:\\ &\textrm{Nilai ujung intervalnya adalah}:\\ &\begin{cases} x=0 & \Rightarrow f(0)=\sin 0+\cos 0=0+1=1 \\ &\color{red}\textrm{titiknya}\: \: \left ( 0,1 \right )\\ x=2\pi & \Rightarrow f(2\pi )=\sin 2\pi +\cos 2\pi =0+1=1\\ &\color{red}\textrm{dan titiknya}\: \: (2\pi ,1) \end{cases} \end{aligned}$
$\begin{array}{ll}\\ 2.&\textrm{Tentukanlah semua titik stasioner}\\ &\textrm{berikut jenisnya dari fungsi}\\ &f(x)=\sin 2x\: \: \textrm{dengan}\\ &0\leq x\leq 2\pi\\\\ &\textrm{Jawab}:\\ &\color{blue}\begin{aligned}&\textrm{Diketahui}\\ &f(x)=\sin 2x\\ &f'(x)=2\cos 2x\\ &\color{red}\textrm{Stasioner saat}\: \: f'(x)=0\\ &2\cos 2x=0\\ &\cos 2x=0\\ &\cos 2x=\cos \displaystyle \frac{\pi }{2}\\ &\qquad 2x=\pm \displaystyle \frac{\pi }{2}+k.2\pi\\ &\qquad x=\pm \displaystyle \frac{\pi }{4}+k.\pi \\ &\textrm{saat}\: \: k=0,\Rightarrow x=\displaystyle \frac{\pi }{4}\\ &\textrm{saat}\: \: k=1,\Rightarrow x=\displaystyle \frac{5\pi }{4}\: \: \textrm{dan}\: \: x=\displaystyle \frac{3\pi }{4}\\ &\textrm{saat}\: \: k=2,\Rightarrow x=\displaystyle \frac{7\pi }{4}\\ &\textrm{Nilai stasionernya dari absis di atas}:\\ &\bullet \quad f\left ( \displaystyle \frac{\pi }{4} \right )=\sin 2\left ( \displaystyle \frac{\pi }{4} \right )=1\\ &\bullet \quad f\left ( \displaystyle \frac{3\pi }{4} \right )=\sin 2\left ( \displaystyle \frac{3\pi }{4} \right )=-1\\ &\bullet \quad f\left ( \displaystyle \frac{5\pi }{4} \right )=\sin 2\left ( \displaystyle \frac{5\pi }{4} \right )=1\\ &\bullet \quad f\left ( \displaystyle \frac{7\pi }{4} \right )=\sin 2\left ( \displaystyle \frac{7\pi }{4} \right )=-1 \\ &\\ &\color{red}\textrm{SILAHKAN LANJUTKAN SENDIRI} \end{aligned} \end{array}$
Tidak ada komentar:
Posting Komentar
Informasi