KUMPULAN MATERI MATEMATIKA PEMINATAN untuk MA Kurtilas Revisi 2018

 A. Kelas X (Sepuluh)

A. 1 Fungsi Eksponensial dan Fungsi Logaritma

• materi eksponen 1, materi fungsi eksponen 2, lanjutan fungsi eksponen, lanjutan materi 2 fungsi ekponen, lanjutan materi 3 fungsi eksponen, Persamaan eksponen.
• contoh soal eksponen 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 , contoh 6 , contoh 7 , contoh 8 , contoh 9 , contoh 10 
• materi logaritma 
• materi logaritma lanjutan
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 , contoh 6
• materi logaritma lanjutan 2
• materi persamaan logaritma 1, persamaan 2, persamaan 3, persamaan 4, persamaan 5. aplikasi logaritma, pengayaan (operasi logaritma natural)
• contoh soal 7 , contoh 8 , contoh 9 , contoh 10, contoh 11, contoh 12, contoh 13.

A. 2 Vektor

• materi vektor, operasi vektor, vektor di dimensi dua, perkalian skalar dua vektor, proyeksi ortogonal suatu vektor, vektor dimensi tiga, lanjutan vektor dimensi tiga, operasi vektor berdimensi tiga, lanjutan 1 operasi vektor berdimensi tiga, lanjutan 2 operasi vektor berdimensi tiga, proyeksi orthogonal suatu vektor di dimensi tiga, 
• contoh soal 1, contoh 2, contoh 3, contoh 4, (urutan) contoh soal 5, contoh 6, contoh 7, contoh 8, contoh 9, contoh 10, contoh 11, contoh 12, contoh 13.

B. Kelas XI (Sebelas)

B. 1 Persamaan Trigonometri

• materi persamaan trigonometri, identitas trigonometri, menentukan nilai perbandingan trigonometri pada segitiga siku-siku, relasi sudut, persamaan trigonometri sederhana.
• lanjutan materi 1 , materi 2 , materi 3
• materi baru
• persamaan tigonometri: identitas trigonometri, menentukan nilai perbandingan trigonometri, sudut-sudut berelasi, persamaan trigonometri sederhana, persamaan bentuk a sin x + b cos x=c, grafik fungsi trigonometri, 
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 , contoh 6
• soal tengah semester gasal : contoh 1, contoh 2, contoh 3, contoh 4,

B. 2 Rumus Jumlah dan Selisih

• rumus jumlah dan selisih 1
• rumus jumlah dan selisih 2
• materi terbaru : rumus jumlah dan selisih dudut sinus, cosinus, tangen, rumus sudut rangkap/ganda, sudut paruh/tengahan, rumus perkalian sinus dan cosinus, rumus jumlah dan selisih sinus dan cosinus, 
• soal persiapan menghadapi semester gasal: contoh 1, contoh 2, contoh 3, contoh 4, contoh 5, contoh 6, contoh 7.

B. 3 Persamaan Lingkaran

• materi lingkaran, kedudukan titik terhadap lingkaran, kedudukan garis terhadap lingkaran, persamaan garis singgung lingkaran, atau Persamaan Garis singgung Lingkaran (Lengkap), Persamaan Garis Singgung dengan gradien m, Persamaan Garis Singgung melalui sebuah titik di luar lingkaran, hubungan dua lingkaran
• contoh soal 1, contoh  2, contoh 3, contoh 4. Contoh 5 (Hubungan Dua Lingkaran), Contoh 6, Contoh 7, Contoh 8

B. 4 Polinom

• materi pendahuluan, operasi polinom, metode Horner-Kino (materi lanjutan operasi polinom) teorema sisa dan teorema faktor, persamaan polinom
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5, contoh 6, contoh 7, contoh 8, contoh 9

C. Kelas XII (Duabelas)

C. 1 Limit Fungsi Trigonometri

• limit fungsi trigonometri (materi lama-perkenalan dengan limit fungsi aljabar), lanjutan materi lama, lanjutan rumus dasar limit trigonometri, 
• materi pendahuluan limit, menentukan nilai limit fungsi trigonometri, pembuktian teorema apit (identitas limit fungsi trigonometri), limit fungsi trigonometri di tak hingga,
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5,
• materi limit diketakhinggan.
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5,

C.2 Turunan Fungsi Trigonometri

• materi turunan fungsi trigonometri
• lanjutan materi 
• contoh soal  (bagaian 1)
• lanjutan materi 2 
• lanjutan materi 3
• lanjutan materi 4 (sifat-sifat turunan)
• lanjutan materi 5
• contoh soal 1 (bagain 2) , contoh 2 , contoh 3 contoh 4 , contoh 5
• lanjutan materi 6 (persamaan garis singgung kurva)-turunan pertama
• lanjutan materi 7 (fungsi naik dan fungsi turun)-turunan pertama
• lanjutan materi 8 (nilai stasioner)-turunan pertama
• lanjutan materi 9 (aplikasi nilai stasioner)-turunan pertama
• contoh 6 , contoh 7 , contoh 8 , contoh 9
• turunan kedua fungsi trigonometri (Fungsi naik dan fungsi turun, titik belok serta selang kecekungan)
• contoh 10 , contoh 11 , contoh 12 , contoh 13

C.3 Distribusi peluang binomial

• materi distribusi binomial, distribusi peluang diskrit, 
• contoh soal 1, contoh 2, 
• distribusi peluang kontinu, Binomial Newton,
• contoh soal 1, contoh 2, contoh 3,

C.4 Distribusi normal

• materi distribusi normal, lanjutan 1 materi, lanjutan 2 materi
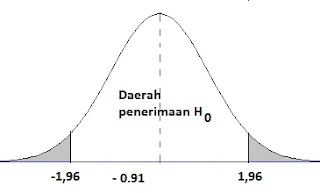
• materi distribusi student, penarikan kesimpulan (pengujian hipotesis)
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5, contoh 6

KUMPULAN MATERI MATEMATIKA WAJIB untuk MA Kurtilas Revisi 2018

 A. Kelas X (Sepuluh)

A. 1 Persamaan dan Pertidaksamaan Nilai Mutlak dari Bentuk Linear Satu Variabel

• materi persamaan nilai mutlak
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 
• materi pertidaksamaan nilai mutlak
• contoh soal 1 , contoh 2 , contoh 3 , 

A. 2 Pertidaksamaan Rasional dan Irasional Satu Variabel

• materi pertidaksamaan rasional dan irasional satu variabel
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , 

A. 3 Sistem Persamaan Linear Tiga Variabel

• materi sistem persamaan linear tiga variabel (SPLTV)
• lanjutan materi SPLTV
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 

A. 4 Sistem Pertidaksamaan Dua Variabel Linear-Linear

• materi sistem pertidaksamaan dua variabel linear-linear
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 

A. 5 Sistem Pertidaksamaan Dua Variabel Linear dan Kuadrat

• materi 1, materi 2, materi 3, 
• contoh Soal 1.

A. 6 Fungsi

• materi pendahuluan, domain-kodomain-range fungsi, 
• contoh soal 1, contoh 2, contoh 3, 

A. 7 Fungsi Komposisi dan Fungsi Invers

• materi fungsi komposisi dan fungsi invers
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5

A. 8 Rasio Trigonometri pada Segitiga Siku-Siku

• materi trigonometri awal
• perbandingan trigonometri pada segitiga siku-siku

A. 9 Rasio Trigonometri Sudut-Sudut diberbagai Kuadran

• koordinat kartesius, koordinat kutub serta sudut-sudut di berbagai kuadran

A. 10 Aturan Sinus dan Cosinus

• aturan sinus
• aturan cosinus (bagian 1), aturan cosinus (bagian 2)
• contoh soal

B. Kelas XI (Sebelas)

B. 1 Program Linear

• materi program linear
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 

B. 2 Matriks

• materi matriks 
• lanjutan materi 1
• lanjutan materi 2
• contoh soal 1 , contoh 2 , contoh 3 

B. 3 Determinan dan Invers Matriks Ordo 2x2

• materi determinan
• materi invers matriks ordo 2x2
• contoh soal 4 , contoh 5 , contoh 6 

B. 4 Transformasi Geometri

• materi
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5.

B. 5 Pola Bilangan dan Jumlah pada Barisan Aritmetika dan Geometri

• materi pola bilangan - induksi matematika
• pola bilangan dan barisan serta deret aritmetika
• pola bilangan dan barisan serta deret geometri 
• berikut contoh soal induksi matematika dan pola bilangan
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5
• materi barisan dan deret aritmetika (hitung)
• lanjutan materi barisan dan deret geometri (ukur)
• berikut contoh soalnya
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5, contoh 6, contoh 7.
• barisan dan deret aritmetika dan geometri sekaligus
• contoh soal selingan (diselipkan soal untuk kompetisi) yang terkait barisan dan deret: contoh 1, contoh 2, contoh 3, contoh 4.

B. 6 Limit Fungsi Aljabar

• materi
• contoh soal 1, contoh 2, 

B. 7 Turunan Fungsi Aljabar

• materi turunan fungsi aljabar
• bentuk umum turunan aljabar
• sifat turunan pertama dan aturan rantai
• aturan rantai pada turunan pertama dan kedua
• penggunaan turunan fungsi
• menyelesaikan masalah terkait keekstriman fungsi
• contoh soal 1, contoh 2, contoh 3, contoh 4

B. 8 Integral Tak Tentu Fungsi Aljabar

• materi pendahuluan
• teknik pengintegralan (dengan teknik substitusi)
• teknik pengintegralan (dengan integral parsial dan atau Tanzalin)
• penggunaan integral tak tentu
• contoh soal 1, contoh 2, contoh 3, contoh 4.

Tambahan/Pengayaan

Integral Tentu Fungsi Aljabar

• materi fungsi aljabar
• penggunaan inetgral tentu fungsi aljabar
• contoh soal 1, contoh 2, contoh 3, contoh 4, contoh 5, contoh 6, contoh 7, contoh 8.

C. Kelas XII (Dua Belas)

C. 1 Jarak dalm Ruang

• Geometri ruang
• Lanjutan materi 1, lanjutan materi 2, lanjutan materi 3, lanjutan materi 4, lanjutan materi 5.
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 

Statistika

• materi statistika, penyajian data dalam bentuk diagram.
• ukuran pemusatan data. ukuran letak data 1, ukuran letak data 2, ukuran letak data 3, interpolasi linear, ukuran penyebaran data 1, ukuran penyebaran data 2, koefisien variansi
• contoh soal 1 , contoh 2 , contoh 3 , contoh 4 , contoh 5 , contoh 6 , contoh 7 , contoh 8 , contoh 9 , contoh 10, contoh 11, contoh 12, contoh 13

C. 3 Aturan Pencacahan

• materi pendahuluan(kombinatorial dan percobaan), kaidah pencacahan(kaidah perkalian), faktorial-permutasi-kombinasi, 
• contoh soal 1 permutasi-kombinasi, contoh 2, contoh 3, 
• materi Binomial Newton (pengayaan), fungsi pembangkit untuk kombinasi (pengayaan), 
• contoh soal 1 (kaidah pencacahan), contoh 2, contoh 3,

C. 4 Peluang Kejadian Majmuk

• materi pendahuluan (percobaan, ruang sampel, dan kejadian), peluang kejadian tunggal dan frekuensi harapan, peluang kejadian majmuk (peluang komplemen, dua kejadian saling bebas, dua kejadian tidak saling bebas), kejadian saling lepas, kejadian tidak saling lepas, 
• contoh soal 1, contoh 2, contoh 3, 

Lanjutan Materi Polinom

Lanjutan Vektor di Ruang

Vektor di Ruang

 $\text{A. Vektor Di Ruang}$

Perhatikanlah ilustrasi gambar berikut

$\begin{array}{|cc|}\hline \text{Nama}& {\mathbf{\text{R}}}^3\\ \text{Vektor Satuan}& \text{Ruang (Bidang XYZ)}\\ {\hat{e}}_{\overline{a}}={\displaystyle \frac{\overline{a}}{\left|\overline{a}\right|}}& \{\begin{array}{ll}i=& \text{vektor satuan}\\ & \text{yang searah sumbu X}\\ j=& \text{Vektor satuan}\\ & \text{yang searah sumbu Y}\\ k=& \text{Vektor satuan}\\ & \text{searah sumbu Z}\end{array}\\ \text{Vektor nol}& \overrightarrow{O}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\\ \text{Vektor posisi}& \overrightarrow{OP}=\overrightarrow{p}=\left(\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right)=p_1\overline{i}+p_2\overline{j}+p_3\overline{j}\\ \text{Besar Vektor}& \overrightarrow{OP}=\sqrt{p_1^2+p_2^2+p_3^2}\\ \hline\end{array}$

$\text{B. Operasi Vektor}$

$\text{1. Sifat-Sifat Aljabar Vektor}$

$\begin{array}{|lll|}\hline 1.& \text{Komutatif penjumlahan}& \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\\ 2.& \text{Asosiatif penjumlahan}& (\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\\ 3.& \text{Elemen Identitas}& \overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}\\ 4.& \text{Invers Penjumlahan}& \overrightarrow{a}+(-\overrightarrow{a})=(-\overrightarrow{a})+\overrightarrow{a}=\overrightarrow{0}\\ 5.& \text{Perkalian dengan skalar}& k\left(l\overrightarrow{a}\right)=\left(kl\right)\overrightarrow{a}\\ & & k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}\\ & & k(\overrightarrow{a}-\overrightarrow{b})=k\overrightarrow{a}-k\overrightarrow{b}\\ 6.& \begin{array}{rl}& \text{Jika A, B, dan C segaris }\\ & \text{(Kolinear)}\end{array}& \{\begin{array}{l}\overrightarrow{AB}=k\overrightarrow{BC}\\ \overrightarrow{AC}=k\overrightarrow{AB}\\ dll\end{array}\\ \hline\end{array}$.

$\begin{array}{|cc|}\hline \text{Vektor}& \text{Contoh}\\ \overrightarrow{z}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}& \begin{array}{rl}& \text{diketahui}\overrightarrow{p}=\overrightarrow{i}-2\overrightarrow{j}+2\overrightarrow{k}\\ & \text{maka pangjang vektor}\overrightarrow{p}\text{adalah}\\ & \left|\overrightarrow{p}\right|=\sqrt{1^2+(-2{)}^2+2^2}\\ & =\sqrt{1+4+4}=\sqrt{9}=3\end{array}\\ & \begin{array}{rl}& \text{Vektor satuan dari}\overrightarrow{p}\text{adalah}\\ & {\overrightarrow{e}}_{\overrightarrow{p}}=\frac{\overrightarrow{p}}{\left|\overrightarrow{p}\right|}={\displaystyle \frac{\left(\begin{array}{c}1\\ -2\\ 2\end{array}\right)}{3}}\\ & ={\displaystyle \frac{1}{3}\left(\begin{array}{c}1\\ -2\\ 2\end{array}\right)={\displaystyle \left(\begin{array}{c}\frac{1}{3}\\ -\frac{2}{3}\\ \frac{2}{3}\end{array}\right)}}\end{array}\\ \hline\end{array}$.

$\text{CONTOH SOAL}$.

$\begin{array}{l}\\ 1.& \text{Diketahui vektor-vektor}\overrightarrow{a}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)\\ & \overrightarrow{b}=\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right),\text{dan}\overrightarrow{c}=\left(\begin{array}{c}7\\ 0\\ 4\end{array}\right),\\ & \text{tentukanlah hasil dari}\\ & \text{a}.\overrightarrow{a}+\overrightarrow{b}\\ & \text{b}.6\overrightarrow{a}+2\overrightarrow{b}\\ & \text{c}.2\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\\ & \text{d}.{\displaystyle \frac{1}{2}\overrightarrow{c}-\overrightarrow{a}+{\displaystyle \frac{3}{4}\overrightarrow{b}}}\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\text{a}& \overrightarrow{a}+\overrightarrow{b}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)+\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right)\\ & =\left(\begin{array}{c}2+(-3)\\ 1+(-5)\\ (-4)+2\end{array}\right)\\ & =\left(\begin{array}{c}2-3\\ 1-5\\ -4+2\end{array}\right)=\left(\begin{array}{c}-1\\ -4\\ -2\end{array}\right)\\ \text{b}.& 6\overrightarrow{a}+2\overrightarrow{b}=6\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)+2\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right)\\ & =\left(\begin{array}{c}18-6\\ 6-10\\ -24+4\end{array}\right)=\left(\begin{array}{c}12\\ -4\\ -20\end{array}\right)\\ \text{c}.& 2\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\\ & 2\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)-\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right)+\left(\begin{array}{c}7\\ 0\\ 4\end{array}\right)\\ & =\left(\begin{array}{c}4+3+7\\ 2+5+0\\ -8-2+4\end{array}\right)=\left(\begin{array}{c}17\\ 7\\ -6\end{array}\right)\\ \text{d}.& {\displaystyle \frac{1}{2}\overrightarrow{c}-\overrightarrow{a}+{\displaystyle \frac{3}{4}\overrightarrow{b}=\cdots }}\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Diketahui vektor-vektor}\overrightarrow{a}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)\\ & \text{tentukanlah}\left|\overrightarrow{a}\right|\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\left|\overrightarrow{a}\right|& =\sqrt{2^2+1^2+(-4{)}^2}\\ & =\sqrt{4+1+16}\\ & =\sqrt{21}\end{array}\end{array}$

$\text{2. Perkalian Skalar Dua Vektor}$

Konsep perkalian skalar dua buah vektor di ruang sama persis dengan konsep di bidang, yaitu:

$\overrightarrow{a}\cdot \overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|\cos \theta$.

Misalkan diketahui

$\begin{array}{rl}& \overrightarrow{a}=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right),\overrightarrow{b}=\left(\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right),\text{maka}\\ & \overrightarrow{a}\cdot \overrightarrow{b}=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)\cdot \left(\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right)\\ & =a_1{b}_1+a_2{b}_2+a_3{b}_3\end{array}$

$\text{CONTOH SOAL}$

$\begin{array}{l}\\ 1.& \text{Diketahui vektor-vektor}\overrightarrow{a}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)\\ & \overrightarrow{b}=\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right),\text{dan}\overrightarrow{c}=\left(\begin{array}{c}7\\ 0\\ 4\end{array}\right),\\ & \text{tentukanlah hasil dari}\\ & \text{a}.\overrightarrow{a}\cdot \overrightarrow{b}\\ & \text{b}.\overrightarrow{a}\cdot \overrightarrow{c}\\ & \text{c}.\overrightarrow{b}\cdot \overrightarrow{c}\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}\text{a}& \overrightarrow{a}\cdot \overrightarrow{b}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)\cdot \left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right)\\ & =(2)(-3)+(1)(-5)+(-4)(2)\\ & =-6-5-8=-19\\ \text{b}& \overrightarrow{a}\cdot \overrightarrow{c}=\left(\begin{array}{c}2\\ 1\\ -4\end{array}\right)\cdot \left(\begin{array}{c}7\\ 0\\ 4\end{array}\right)\\ & =(2)(7)+(1)(0)+(-4)(4)\\ & =14+0-16=-2\\ \text{c}& \overrightarrow{b}\cdot \overrightarrow{c}=\left(\begin{array}{c}-3\\ -5\\ 2\end{array}\right)\cdot \left(\begin{array}{c}7\\ 0\\ 4\end{array}\right)\\ & =(-3)(7)+(-5)(0)+(2)(4)\\ & =-21+0+8=-13\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Tentukanlah nilai}t\text{jika}\\ & \overrightarrow{p}=3\overline{i}+t\overline{j}+\overline{k}\text{dan}\overrightarrow{p}\cdot \overrightarrow{p}=13\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}& \overrightarrow{p}\cdot \overrightarrow{p}=13\\ & \overrightarrow{p}\cdot \overrightarrow{p}=\left|\overrightarrow{p}\right|\left|\overrightarrow{p}\right|\cos 0^{\circ }=13,\\ & \text{ingat bahwa}\mathrm{\angle }(\overrightarrow{p},\overrightarrow{p})=0^{\circ }\\ & \text{dan nilai}\cos 0^{\circ }=1,\\ & \text{maka}\\ & \overrightarrow{p}\cdot \overrightarrow{p}={\left|\overrightarrow{p}\right|}^2.1=13\iff {\left|\overrightarrow{p}\right|}^2=13\\ & \iff {\left(\sqrt{3^2+t^2+1^2}\right)}^2=13\\ & \iff 3^2+t^2+1^2=13\\ & \iff 9+t^2+1=13\\ & \iff t^2=13-9-1=10\\ & \iff t^2=3\\ & \iff t=\pm \sqrt{3}\end{array}\end{array}$

$\begin{array}{l}\\ 3.& \text{Diketahui}\overrightarrow{p}=\left(\begin{array}{c}-2\\ 1\\ 3\end{array}\right)\text{dan}\overrightarrow{q}=\left(\begin{array}{c}4\\ -1\\ t\end{array}\right)\\ & \text{Jika}\overrightarrow{p}\text{tegak lurus}\overrightarrow{q}\text{maka}\\ & \text{tentukanlah nilai}t\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}& \text{Diketahui bahwa}\\ & \overrightarrow{p}=\left(\begin{array}{c}-2\\ 1\\ 3\end{array}\right)\text{dan}\overrightarrow{q}=\left(\begin{array}{c}4\\ -1\\ t\end{array}\right)\\ & \text{dengan}\overrightarrow{p}\text{dan}\overrightarrow{q}\text{tegak lurus}\\ & \text{artinya}\mathrm{\angle }(\overrightarrow{p},\overrightarrow{q})={90}^{\circ }.\text{Sehingga}\\ & \text{nilai}\cos {90}^{\circ }=0\\ & \text{maka}\\ & \overrightarrow{p}\cdot \overrightarrow{q}=\left|\overrightarrow{p}\right|\left|\overrightarrow{q}\right|\cos \theta \\ & \overrightarrow{p}\cdot \overrightarrow{q}=\left|\overrightarrow{p}\right|\left|\overrightarrow{q}\right|\cdot 0=0\\ & \iff \left(\begin{array}{c}-2\\ 1\\ 3\end{array}\right)\cdot \left(\begin{array}{c}4\\ -1\\ t\end{array}\right)=0\\ & \iff (-2)(4)+(1)(-1)+(3)(t)=0\\ & \iff -8-1+3t=0\\ & \iff 3t=9\\ & \iff t=3\end{array}\end{array}$.

DAFTAR PUSTAKA

1. Yuana, R.A., Indriyastuti. 2017. Persektif Matematika untuk Kelas X SMA dan MA Kelompok Peminatan Matematika dan Ilmu Alam. Solo: PT TIGA SERANGKAI MANDIRI.

Polinom

 $\text{A. Pendahuluan}$

Polinom disebut juga suku banyak. Polinom atau suku banyak adalah suatu bentuk variabel yang berpangkat/berderajat.

Secara definisi suku banyak (polinomial) dalam  $x$  berderajat $n$ adalah:

Suatu bentuk

${\displaystyle a_n{x}^n+a_{n-1}{x}^{n-1}+a_{n-2}{x}^{n-2}+...+a_2{x}^2+a_1{x}^1+a_0}$

dengan  $n$  bilangan cacah serta  $a_0,a_1,a_2,...,a_n$  koefisien dari suku  $x$  dan  $a_n\ne 0$  dengan  $a_0$  sebagai suku tetap (konstan)nya.

Selanjutnya perhatikanlah tabel berikut!

$\begin{array}{|ll|}\hline \begin{array}{rl}{a}_n& \text{adalah koefisien dari}{x}^n\\ a_{n-1}& \text{adalah koefisien dari}{x}^{n-1}\\ a_{n-2}& \text{adalah koefisien dari}{x}^{n-2}\\ ⋮& \\ a_2& \text{adalah koefisien dari}{x}^2\\ a_1& \text{adalah koefisien dari}{x}^1\\ a_0& \text{adalah konstanta}\\ & (\text{suku tetap})\end{array}& \begin{array}{rl}{a}_n& \ne 0\\ n:& \text{bilangan cacah},\\ :& \text{adalah derajat (pangkat)}\\ & \text{tertinggi dalam suku}\\ & \text{banyak tersebut}& \\ & \\ & \\ & \end{array}\\ \hline\end{array}$

$\text{CONTOH SOAL 1}$

$\begin{array}{rl}1.& \text{Polinom}2x^3-6x^2+2020\text{dapat dinyatakan}\\ & \text{dengan}2x^3-6x^2+0x^1+2020x^0\\ & \text{Polinom tersebut memiliki suku tetap}2020\\ 2.& \text{Polinom}5x^4-8x^3+6x-2021\text{dapat dinyatakan}\\ & \text{dengan}5x^4-8x^3+0x^2+6x^1-2021x^0\\ & \text{Polinom tersebut memiliki suku tetap}-2021\\ 3.& \text{Polinom}{x}^4-2x^3+3x^2-2\sqrt{x}+1\text{tidak dapat}\\ & \text{dinamakan polinom, sebab ada variabel dari}x\\ & \text{yang berderajat bukan bilangan cacah}\\ 4.& \text{Sedangkan polinom}5-x+(2-x)(1+x+x^2)\\ & \text{adalah bentuk polinom, karena dapat dinayatakan}\\ & \text{dengan}-x^3+x^2+7\end{array}$

$\text{B. Nilai Polinom}$

Polinom atau suku banyak yang berderajat $n$ yang selanjutnya dinyatakan dengan 

$f(x)={\displaystyle a_n{x}^n+a_{n-1}{x}^{n-1}+a_{n-2}{x}^{n-2}+...+a_1{x}^1+a_0}$

Berkaitan dengan kebutuhan penentuan nilai ini, dapat ditentukan dengan dua cara:

$\mathbf{\text{a. Substitusi}}$

$\begin{array}{rl}& \text{Nilai suku banyak}f(x)\text{berderajat}\\ & n\text{saat}x=k\text{adalah}f(k).\\ & \text{Jika}f(k)=0\text{maka}x=k\text{akar dari}f(x),\\ & \text{dan}(x-k)\text{faktor dari}f(x)\\ & \end{array}$

$\text{CONTOH SOAL 2}$

Jika suatu polinom dinyatakan dengan  $f(x)$, maka nilai polinom itu untuk  $x=3$  adalah  $f(3)$.

Misalkan diketahui  

$\begin{array}{rl}1.f(x)& =x^3-1\\ \text{mak}& \text{a}\\ f(1)& =1^3-1=1-1=0\\ f(3)& =3^3-1=27-1=26\\ f(-4)& =(-4{)}^2-1=-64-1=-65\end{array}$

$\begin{array}{l}\\ 2.& \text{Diketahui}h(x)=2x^3+5x^2-12x-6\\ & \text{Tentukanlah nilai untuk}h(-2),h(-1),\\ & h(0),h(1),\text{dan}h(2)\\ \\ & \text{Jawab}:\\ & \begin{array}{|ccl|}\hline x=k& h(k)& \text{Nilai}\\ x=-2& h(-2)& \begin{array}{rl}h(-2)& =2(-2{)}^3+5(-2{)}^2-12(-2)-6\\ & =-16+20+24-6\\ & =22\end{array}\\ x=-1& h(-1)& \begin{array}{rl}h(-1)& =2(-1{)}^3+5(-1{)}^2-12(-1)-6\\ & =-2+5+12-6\\ & =9\end{array}\\ x=0& h(0)& \begin{array}{rl}h(0)& =2(0{)}^3+5(0{)}^2-12(0)-6\\ & =-6\end{array}\\ x=1& h(1)& \begin{array}{rl}h(1)& =2(1{)}^3+5(1{)}^2-12(1)-6\\ & =2+5-12-6\\ & =-11\end{array}\\ x=2& h(2)& \begin{array}{rl}h(2)& =2(2{)}^3+5(2{)}^2-12(2)-6\\ & =16+20-24-6\\ & =6\end{array}\\ \hline\end{array}\end{array}$

$\begin{array}{l}\\ 3.& \text{Diketahui}p(x)=x-2019\\ & \text{dan}q(x)=x^{2019}+1.\text{Tentukanlah}\\ & \text{nilai untuk}p(q(2))\text{dan}q(p(2))\\ \\ & \text{Jawab}:\\ & \text{Yang dibahas yang bagian}p(q(2))\\ & q(2)=2^{2019}+1,\text{maka nilai}\\ & \begin{array}{rl}p(q(2))& =(2^{2019}+1)-2019\\ & =2^{2019}-2018\end{array}\\ \\ & \text{Untuk yang}q(p(2))\text{adalah}\\ & p(2)=\cdots ,\text{maka nilai}\\ & \begin{array}{rl}q(p(2))& =\because {\cdots }^{2019}+1\\ & =\cdots \end{array}\end{array}$

$\mathbf{\text{b. Horner/Sintetik}}$

Nilai suatu polinom dapat ditentukan dengan pembagian sintesis Horner

Misalkan:

$\begin{array}{rl}f(x)& =a{x}^3+b{x}^2+cx+d\text{saat akan dibagi}\\ & x=h,\text{maka pembagian Horner itu}:\\ & \end{array}$

Perhatikan bahwa proses ke bawah adalah berup proses penjumlahan.

Proses di atas akan sama saat kita mensubstitusikan  $x=h$  ke dalam  $f(x)$, yaitu:

$\begin{array}{rl}f(x)& =a{x}^3+b{x}^2+cx+d\text{saat}\\ & x=h,\text{maka}\\ f(h)& =a{h}^3+b{h}^2+ch+d\\ & \\ & \mathbf{\text{Cukup JELAS bukan}}?\end{array}$

$\text{CONTOH SOAL 3}$

$\begin{array}{l}\\ \text{Tentukanlah nilai dari}f(4)\text{jika}\\ \text{diketahui}f(x)=x^3-x-5\\ \text{Jawab}:\\ \begin{array}{rl}(1).& \text{Cara substitusi langsung}\\ & f(x)=x^3-x-5\\ & f(4)=4^3-4-5\\ & =64-9=55\\ (2).& \text{Cara Horner}\\ & \text{Karena}f(x)=x^3-x-5\\ & \text{dan koefisiennya yang akan}\\ & \text{adalah}:\\ & a_3=1,a_2=0,a_1=-1,\mathrm{\&}{a}_0=-5\\ & \mathbf{\text{maka bagan pembagian Hornernya}}\\ & \begin{array}{l}\\ & x=4& 1& 0& -1& -5& \\ & & & & & & \\ & & & 4& 16& 60& +\\ & & 1& 4& 15& 55\end{array}\end{array}\end{array}$

Lanjutan Contoh Soal 6 Distribusi Normal

$\begin{array}{l}\\ 26.& \text{Untuk menguji hipotesis}\\ & \{\begin{array}{ll}{H}_0& :\mu =16\\ H_1& :\mu >16\end{array}\\ & \text{Jika dalam penelitian terhadap sampel}n=20\\ & \text{diperoleh}\bar{\text{x}}=16,9\text{dengan simpangan baku}\\ & \sqrt{2,3},\text{maka perhitungan nilai statistik ujinya}\\ & \text{adalah}....\\ & \text{a}.z=-2,65\\ & \text{b}.t=-2,65\\ & \text{c}.z=2,65\\ & \text{d}.t=2,65\\ & \text{e}.z=2,95\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{d}}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis (penelitian sampel)}}\\ & {\text{H}}_0:\mu =16\\ & {\text{H}}_0:\mu >16\\ & \text{dengan},n=20,\bar{\text{x}}=16,9,s=\sqrt{2,3}=1,52,\\ & \text{maka}\\ & \text{t}=\left({\displaystyle \frac{\bar{\text{x}}-\mu }{s}}\right)\sqrt{n}={\displaystyle \frac{16,9-16}{1,52}\sqrt{20}}\\ & =\left({\displaystyle \frac{0,9}{1,52}}\right)\times 4,472=2,65\end{array}\end{array}$.

$\begin{array}{l}\\ 27.& \text{Pada soal no.26 di atas, jika taraf nyata}\\ & 0,01,\text{maka kesimpulannya adalah}...\\ & \text{a}.H_0\text{ditolak}\\ & \text{b}.H_0\text{diterima}\\ & \text{c}.H_1\text{diterima}\\ & \text{d}.H_1\text{ditolak}\\ & \text{e}.\text{tidak dapat ditarik kesimpulan}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Kasus uji satu pihak}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis}}\\ & {\text{H}}_0:\mu =16\\ & {\text{H}}_0:\mu >16\\ & \text{dengan}\alpha =0,01=1\mathrm{\%}\Rightarrow t_{0,99}=2,54\\ & \text{Kriteria pengambilan keputusan}:\\ & \text{Tolak}{H}_0\text{jika}t\ge 2,54\end{array}\end{array}$.

$\begin{array}{l}\\ 28.& \text{Seorang petugas}customerservice\text{menyatakan}\\ & \text{bahwa di dealer A dapat mensevis rata-rata }\\ & \text{sebanyak}75\text{unit sepeda motor perhari}.\text{Untuk}\\ & \text{mengecek kebenaran pernyataan di atas diambil}\\ & \text{sampel beberapa hari secara random sebanyak }\\ & \text{20 hari. Dari penelitian ini diperoleh rata-rata}\\ & \text{78 unit dengan simpangan bakunya 5. Hasil}\\ & \text{perhitungan}{\text{z}}_0-\text{nya adalah}....\\ & \text{a}.2,35\\ & \text{b}.2,43\\ & \text{c}.2,55\\ & \text{d}.2,68\\ & \text{e}.2,75\\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{d}}\\ & \begin{array}{rl}& \text{Diketahui data dianggap berdistribusi}\\ & \text{normal baku}N(0,1)\text{dengan}\\ & \text{Rata-rata sampel}=\bar{\text{x}}=78\text{unit sepeda motor}\\ & \text{Rata-rata populasinya yang diuji}={\mu }_0=75\\ & \text{Simpangan bakunya}=\sigma =5\text{unit}\\ & \text{dengan banyak data sampel}=n=20\text{hari}\\ & \text{Penghitungan nilainya}z-\text{nya}\\ & ={\displaystyle \frac{\bar{\text{x}}-{\mu }_0}{{\displaystyle \frac{\sigma }{\sqrt{n}}}}}\\ & ={\displaystyle \frac{78-75}{{\displaystyle \frac{5}{\sqrt{20}}}}={\displaystyle \frac{3}{{\displaystyle \frac{5}{2\sqrt{5}}}}}}\\ & ={\displaystyle \frac{6}{\sqrt{5}}=\frac{6}{2,236}=2,683}\end{array}\end{array}$.

$\begin{array}{l}\\ 29.& \text{Tersiar kabar bahwa harga beras di pasar di}\\ & \text{wilayah B adalah}\text{Rp}8.000,00/\text{Kg dengan}\\ & \text{simpangan baku}\text{Rp}1.500,00.\text{Berdasar kabar}\\ & \text{tersebut dilakukan penelitian dengan mengambil}\\ & \text{sampel secara acak sebanyak}60\text{kios yang dan}\\ & \text{diperoleh rata-rata harga beras}\text{Rp}7.800,00/\text{Kg}\\ & \text{Jika penghitungan menggunakan tingkat}\\ & \text{signifikansi}5\mathrm{\%},\text{maka kesimpulan berikut }\\ & \text{yang tepat adalah}....\\ & \text{a}.\text{harga beras di pasar lebih dari}\text{Rp}7.800,00/\text{Kg}\\ & \text{b}.\text{harga beras di pasar lebih dari}\text{Rp}8.000,00/\text{Kg}\\ & \text{c}.\text{harga beras di pasar kurang dari}\text{Rp}0.000,00/\text{Kg}\\ & \text{d}.\text{harga beras di pasar}\text{Rp}7.800,00/\text{Kg}\\ & \text{e}.\text{harga beras di pasar}\text{Rp}8.000,00/\text{Kg}\\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{e}}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis}}\\ & \text{Rata-rata harga beras dipasar}\text{Rp}8.000,00/\text{Kg}\\ & {\text{H}}_0:\mu =8.000\\ & {\text{H}}_0:\mu \ne 8.000\\ & \underset{―}{\text{Daerah Kritis}}\\ & \text{Taraf nyata yang dipilih adalah}=\alpha =0,05=5\mathrm{\%}\\ & {\displaystyle \frac{\alpha }{2}=2,5\mathrm{\%}=0,025}\\ & {\text{z}}_{0,025}=1,96\\ & \text{maka daerah kritis/penolakannya adalah}\\ & \text{z}<-1,96\text{atau}\text{z}>1,96\end{array}\end{array}$.

$.\begin{array}{rl}& \underset{―}{\text{Nilai Satistik Uji}}\\ & \text{Dihitung dengan rumus}:\text{z}={\displaystyle \frac{\bar{\text{x}}-{\mu }_0}{{\displaystyle \frac{\sigma }{\sqrt{n}}}}}\\ & \text{z}={\displaystyle \frac{7.800-8.000}{{\displaystyle \frac{1.500}{\sqrt{60}}}}=-{\displaystyle \frac{200\sqrt{60}}{1.500}=-1,03}}\\ & \underset{―}{\text{Keputusan Uji}}\\ & \text{Karena nilai}-1,96<\text{z}<1,96,\\ & \text{maka}{\text{H}}_0\text{diterima}\\ & \underset{―}{\text{Kesimpulan}}\\ & \text{Rata-rata harga beras dipasar}\text{Rp}8.000,00/\text{Kg}\end{array}$ .

Lanjutan Contoh Soal 5 Distribusi Normal

$\begin{array}{l}\\ 21.& \text{Pada suatu kelas seorang guru matematika}\\ & \text{menyatakan bahwa nilai ulangan mapel }\\ & \text{yang diampunya tidak kurang dari}68\\ & \text{Untuk menentukan uji tersebut, maka guru}\\ & \text{yang bersangkutan memilih 10 anak secara}\\ & \text{acak untuk ditanyai nilai hasil ulangannya}\\ & \text{Hipotesis}{\text{H}}_0\text{dan}{\text{H}}_1\text{yang tepat dari kondisi}\\ & \text{kondisi di atas adalah}....\\ & \text{a}.\begin{array}{c}{\text{H}}_0:\mu =68\\ {\text{H}}_1:\mu \ne 68\end{array}\\ & \text{b}.\begin{array}{c}{\text{H}}_0:\mu =68\\ {\text{H}}_1:\mu >68\end{array}\\ & \text{c}.\begin{array}{c}{\text{H}}_0:\mu \ge 68\\ {\text{H}}_1:\mu <68\end{array}\\ & \text{d}.\begin{array}{c}{\text{H}}_0:\mu \le 68\\ {\text{H}}_1:\mu >q68\end{array}\\ & \text{e}.\begin{array}{c}{\text{H}}_0:\mu >68\\ {\text{H}}_1:\mu \ne 68\end{array}\\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{c}}\\ & \text{Cukup jelas}\\ & \text{Dan ini contoh uji satu pihak, yaitu kiri}\end{array}$.

$\begin{array}{l}\\ 22.& \text{Untuk menguji hipotesis}\\ & \{\begin{array}{ll}{H}_0& :\mu =800\\ H_1& :\mu \ne 800\end{array}\\ & \text{Jika dalam penelitian didapatkan}\bar{\text{x}}=795\\ & \text{dan}n=100\text{serta simpangan baku}\\ & \text{populasi}55,\text{maka perhitungan nilai}\\ & \text{statistik ujinya adalah}....\\ & \text{a}.z=-1,10\\ & \text{b}.z=-0,91\\ & \text{c}.t=-0,91\\ & \text{d}.t=0,91\\ & \text{e}.z=0,91\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis}}\\ & {\text{H}}_0:\mu =800\\ & {\text{H}}_0:\mu \ne 800\\ & \text{dengan},n=100,\bar{\text{x}}=795,\sigma =55,\text{maka}\\ & \text{z}=\left({\displaystyle \frac{\bar{\text{x}}-\mu }{\sigma }}\right)\sqrt{n}={\displaystyle \frac{795-800}{55}\sqrt{100}}\\ & =\left({\displaystyle \frac{-5}{55}}\right)\times 10=-0,91\end{array}\end{array}$.

$\begin{array}{l}\\ 23.& \text{Pada soal no.22 di atas, jika taraf nyata}\\ & 5\mathrm{\%},\text{maka kesimpulannya adalah}...\\ & \text{a}.H_0\text{ditolak}\\ & \text{b}.H_0\text{diterima}\\ & \text{c}.H_1\text{diterima}\\ & \text{d}.H_1\text{ditolak}\\ & \text{e}.\text{tidak dapat ditarik kesimpulan}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Kasus uji dua pihak}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis}}\\ & {\text{H}}_0:\mu =800\\ & {\text{H}}_0:\mu \ne 800\\ & \text{dengan}\alpha =5\mathrm{\%}=0,05\Rightarrow z_{\frac{1}{2}(1-0,05)}\\ & =z_{0,475}=1,96\end{array}\end{array}$.

$\begin{array}{l}\\ 24.& \text{Untuk menguji hipotesis}\\ & \{\begin{array}{ll}{H}_0& :\mu =20\\ H_1& :\mu <20\end{array}\\ & \text{Jika dalam penelitian terhadap sampel}n=21\\ & \text{diperoleh}\bar{\text{x}}=19,8\text{dengan simpangan baku}\\ & 0,4,\text{maka perhitungan nilai statistik ujinya}\\ & \text{adalah}....\\ & \text{a}.z=-2,29\\ & \text{b}.t=-2,29\\ & \text{c}.z=2,29\\ & \text{d}.t=2,29\\ & \text{e}.z=2,99\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis (penelitian sampel)}}\\ & {\text{H}}_0:\mu =20\\ & {\text{H}}_0:\mu <20\\ & \text{dengan},n=21,\bar{\text{x}}=19,8,s=0,4,\text{maka}\\ & \text{t}=\left({\displaystyle \frac{\bar{\text{x}}-\mu }{s}}\right)\sqrt{n}={\displaystyle \frac{19,8-20}{0,4}\sqrt{21}}\\ & =\left({\displaystyle \frac{-0,2}{0,4}}\right)\times 4,5828=-2,29\end{array}\end{array}$.

$\begin{array}{l}\\ 25.& \text{Pada soal no.24 di atas, jika taraf nyata}\\ & 0,01,\text{maka kesimpulannya adalah}...\\ & \text{a}.H_0\text{ditolak}\\ & \text{b}.H_0\text{diterima}\\ & \text{c}.H_1\text{diterima}\\ & \text{d}.H_1\text{ditolak}\\ & \text{e}.\text{tidak dapat ditarik kesimpulan}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Kasus uji satu pihak}\\ & \begin{array}{rl}& \underset{―}{\text{Hipotesis}}\\ & {\text{H}}_0:\mu =20\\ & {\text{H}}_0:\mu <20\\ & \text{dengan}\alpha =0,01=1\mathrm{\%}\Rightarrow t_{0,99}=2,53\\ & \text{Kriteria pengambilan keputusan}:\\ & \text{Tolak}{H}_0\text{jika}t\le -2,53\end{array}\end{array}$.

Lanjutan Contoh Soal 4 Distribusi Normal

$\begin{array}{l}\\ 16.& \text{Dalam pengujian hipotesis dapat terjadi kesalahan}\\ & \text{Jika kita menerima hipotesis yang seharusnya kita}\\ & \text{tolak. Kejadian ini merupakan kekeliruan, yaitu}....\\ & \text{a}.\text{kekeliruan tipe I}\\ & \text{b}.\text{kekeliruan tipe II}\\ & \text{c}.\text{kekeliruan tipe III}\\ & \text{d}.\text{kekeliruan sampling}\\ & \text{e}.\text{kekeliruan non sampling}\\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Cukup jelas}\end{array}$.

$\begin{array}{l}\\ 17.& \text{Pengertian dari taraf signifikansi}1\mathrm{\%}\text{adalah}....\\ & \text{a}.\text{sekitar}95\mathrm{\%}\text{kesimpulan benar telah diambil}\\ & \text{b}.\text{kurang lebih 5 dari 100 kesimpulan yang }\\ & \text{seharusnya hipotesisnya diterima kita tolak}\\ & \text{c}.\text{kurang lebih 1 dari 100 kesimpulan yang }\\ & \text{seharusnya hipotesisnya ditolak kita terima}\\ & \text{d}.\text{kurang lebih 1 dari 100 kesimpulan yang }\\ & \text{seharusnya hipotesisnya diterima kita tolak}\\ & \text{e}.\text{kurang lebih 5 dari 100 kesimpulan yang }\\ & \text{seharusnya hipotesisnya ditolak kita terima}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{d}}\\ & \text{Cukup jelas}\end{array}$.

$\begin{array}{l}\\ 18.& \text{Dalam pengujian hipotesis, penggunaan statistik}\\ & t\text{ketika penghitungan}....\\ & \text{a}.\text{simpsngsn baku saat sampel tidak diketahui}\\ & \text{b}.\text{rata-rata sampel tidak diketahui}\\ & \text{c}.\text{simpangan baku populasi tidak diketahui}\\ & \text{d}.\text{rata-rata populasi tidak diketahui}\\ & \text{e}.\text{simpangan baku populasi diketahui}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{c}}\\ & \text{Cukup jelas}\end{array}$.

$\begin{array}{l}\\ 19.& \text{Penggunaan kriteria pada uji pihak kiri jika}\\ & \text{diketahui}d\text{adalah nilai yang diperoleh dari}\\ & \text{daftar distribusi yang bersangkutan dengan}\\ & \text{peluang yang ditentukan oleh}\alpha \text{adalah}....\\ & \text{a}.\text{tolak}{H}_0\text{jika nilai statistik uji lebih dari}\\ & d,\text{dalam hal lainnya}{H}_0\text{diterima}\\ & \text{b}.\text{tolak}{H}_0\text{jika nilai statistik uji kurang dari}\\ & d,\text{dalam hal lainnya}{H}_0\text{diterima}\\ & \text{c}.\text{terima}{H}_0\text{jika nilai statistik uji kurang dari}\\ & d,\text{dalam hal lainnya}{H}_0\text{diterima}\\ & \text{d}.\text{terima}{H}_0\text{jika nilai statistik uji lebih dari}\\ & d,\text{dalam hal lainnya}{H}_0\text{ditolak}\\ & \text{e}.\text{terima}{H}_0\text{jika nilai statistik uji lebih dari}\\ & \text{atau sama dengan}d,\text{dalam hal lainnya}\\ & H_0\text{ditolak}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Cukup jelas}\end{array}$.

$\begin{array}{l}\\ 20.& \text{Hipotesis nol adalah}....\\ & \text{a}.\text{hipotesis yang nilai statistik ujinya}\\ & \text{bernilai nol}\\ & \text{b}.\text{hipotesis yang perumusannys mrngandung}\\ & \text{pengertian yang tidak memiliki perbedaan}\\ & \text{c}.\text{hipotesis yang perumusannya terkandung}\\ & \text{pengertian yang tidak sama}\\ & \text{d}.\text{hipotesis yang perumusannya mengandung}\\ & \text{pengertian lebih dari}\\ & \text{e}.\text{hipotesis yang perumusannya mengandung}\\ & \text{pengertian kurang dari}\\ \\ \\ & \mathbf{\text{Jawab}}:\mathbf{\text{b}}\\ & \text{Cukup jelas}\end{array}$.

Lanjutan Contoh Soal 3 Distribusi Normal

$\begin{array}{l}\\ 11.& \text{Perhatikan ilustrasi berikut}....\end{array}$.

$.\begin{array}{l}\\ & \text{Jika luas yang diarsir adalah 0,90 dan}n=21,\\ & \text{maka nilai}t\text{adalah}....\\ & \text{a}.1,32\\ & \text{b}.1,72\\ & \text{c}.2,08\\ & \text{d}.2,09\\ & \text{e}.2,53\\ \\ & \mathbf{\text{Jawab}}:\\ & \text{Luas arsiran (distribusi student) adalah}:\\ & =1-0,90=0,10,\text{karena luas kedua ujung}\\ & \text{sama, mulai dari}t\text{ke kanan}={\displaystyle \frac{0,10}{2}=0,05}\\ & \text{Sehingga luas dari}t\text{ke kiri}=1-0,05=0,95\\ & \text{Dari ini diketahui luas arsirannya}=p=0,95\\ & \text{Dengan}dk=n-1=21-1=20,\text{maka}\\ & t=\pm 1,72\end{array}$.

$\begin{array}{l}\\ 12.& \text{Misalkan luas dari}t\text{ke kiri}=0,05,\\ & \text{dengan}dk=15.\text{Nilai}t\text{adalah}....\\ & \text{a}.-1,76\\ & \text{b}.-1,75\\ & \text{c}.-1,74\\ & \text{d}.1,75\\ & \text{e}.1,76\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}& \text{Diketahui dari soal di atas}\\ & \text{dari}t\text{ke kiri}=0,05,\text{maka}\\ & \text{luas arsiran}=p=1-0,05=0,95\\ & t=-1,75(\text{lihat tabel})\end{array}\end{array}$.

$\begin{array}{l}\\ 13.& \text{Transformasi Z}-score\text{dikaitan dengan}\\ & \text{data dimaksudkan agar data}\\ & \text{terdistribusi secara}....\\ & \text{a}.\text{tak normal}\\ & \text{b}.\text{binomial}\\ & \text{c}.Chi-square\\ & \text{d}.\text{Poison}\\ & \text{e}.\text{normal}\\ \\ & \text{Jawab}:\\ & \begin{array}{rl}& \text{Cukup jelas}\end{array}\end{array}$.

$\begin{array}{l}\\ 14.& \text{Perhatikan ilustrasi berikut}....\end{array}$.

$.\begin{array}{l}\\ & \text{Jika kurva normal di atas memiliki simpangan}\\ & \text{bakunya}12,\text{maka luar daerah arsiran adalah}....\\ & \text{a}.0,4821\\ & \text{b}.0,4966\\ & \text{c}.0,4999\\ & \text{d}.0,5934\\ & \text{e}.0,6921\\ \\ & \mathbf{\text{Jawab}}:\\ & \text{Diketahui},\mu =60,\sigma =12,{\text{x}}_1=50,{\text{x}}_2=70\\ & \text{dengan nilai}z={\displaystyle \frac{\text{x}-\mu }{\sigma },\text{ maka}}\\ & \begin{array}{rl}{\text{z}}_1& ={\displaystyle \frac{{\text{x}}_1-\mu }{\sigma }=\frac{50-60}{12}=\frac{-10}{12}=-0.83}\\ {\text{z}}_2& ={\displaystyle \frac{{\text{x}}_2-\mu }{\sigma }=\frac{70-60}{12}=\frac{10}{12}=0.83}\end{array}\\ & \text{Luas}=P(-z\le Z\le z)=2\times P(0\le Z\le z)\\ & =2\times (0,2967)=0,5934\end{array}$.

$\begin{array}{l}\\ 15.& \text{Perhatikan ilustrasi berikut}....\end{array}$.

$.\begin{array}{l}\\ & \text{Jika kurva normal di atas memiliki simpangan}\\ & \text{bakunya}5,\text{maka luar daerah arsiran adalah}....\\ & \text{a}.0,1585\\ & \text{b}.0,1815\\ & \text{c}.0,3413\\ & \text{d}.0,8172\\ & \text{e}.0,8185\\ \\ & \mathbf{\text{Jawab}}:\\ & \text{Diketahui},\mu =40,\sigma =5,{\text{x}}_1=30,{\text{x}}_2=45\\ & \text{dengan nilai}z={\displaystyle \frac{\text{x}-\mu }{\sigma },\text{ maka}}\\ & \begin{array}{rl}{\text{z}}_1& ={\displaystyle \frac{{\text{x}}_1-\mu }{\sigma }=\frac{30-40}{5}=\frac{-10}{5}=-2}\\ {\text{z}}_2& ={\displaystyle \frac{{\text{x}}_2-\mu }{\sigma }=\frac{45-40}{5}=\frac{5}{5}=1}\end{array}\\ & \text{Luas}=P(z_1\le Z\le z_2)=P(0\le Z\le z_1)\\ & +P(0\le Z\le z_2)\\ & =P(0\le Z\le 2)+P(0\le Z\le 1)\\ & =0,3413+0,4772=0,8185\end{array}$.

Distribusi Student (Uji t)

Uji "t"

Dalam pengujian hipotesis kita mengenal 2 rumus pengujian yaitu rumus z (distribusi normal standar) dan rumus t (distribusi student). Rumus z digunakan manakala simpangan baku pada populasi diketahui, sedangkan rumus t digunakan ketika simpangan baku pada populasi tidak diketahui. Ketika simpangan baku setiap populasi jarang diketahui, maka biasanya alternatifnya adalah digunakan simpangan baku sampel dan selanjutnya digunakanlah uji t.

$\begin{array}{rl}t& ={\displaystyle \frac{\overline{\text{x}}-{\mu }_0}{\frac{s}{\sqrt{n}}}\text{atau}t={\displaystyle \frac{\overline{\text{x}}-{\mu }_0}{s}\sqrt{n}}}\\ & \text{Dimana}\\ & t=\text{nilai}t\text{yang dihitung}\\ & \overline{\text{x}}=\text{rata-rata sampel}\\ & \mu =\text{rata-rata populasi}\\ & \text{atau nilai yang dihipotesiskan}\\ & s=\text{simpangan baku sampel}\\ & n=\text{jumlah anggota sampel}\end{array}$.

Selanjutnya untuk perhitungan simpangan baku s digunakan rumus berikut

$\begin{array}{rl}s& =\sqrt{{\displaystyle \frac{\sum ({\text{x}}_i-\overline{\text{x}}{)}^2}{n-1}}}\\ & \text{Dimana}\\ & \overline{\text{x}}=\text{rata-rata sampel}\\ & n-1=\text{derajat kebebasan}\end{array}$.

Sebagai catatan dalam pemilihan statistik uji dan penghitungan statistik uji

• Jika ukuran sampel  $n\ge 30$, statistik uji yang digunakan adalah z (rumus z di atas), $Z\sim N(0,1)$.
• Jika ukuran sampel  $n<30$, statistik uji yang digunakan adalah t, dengan derajat kebebasan $dk=n-1$.

$\text{CONTOH SOAL}$.

$\begin{array}{l}\\ 1.& \text{Sebuah perusahaan X mengatakan bahwa}\\ & \text{performance pegawainya rata-rata nilai}\\ & \text{skornya adalah}8,5.\text{Untuk membuktikan}\\ & \text{pernyataan tersebut diambillah secara }\\ & \text{random 16 orang pegawai untuk dites dan}\\ & \text{hasilnya tersaji berikut}\\ & 7,88,28,47,88,99,18,57,7\\ & 8,57,99,17,89,28,98,88,3\\ & \text{Pada taraf}1\mathrm{\%},\text{apakah pernyataan}\\ & \text{perusahaan tersebut benar}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Misalkan rata-rata skor performance}\\ & \text{berdistribusi student}\\ & \mathbf{\text{Rumusan hipotesis}}{H}_0\text{dan}{H}_1\\ & H_0:\mu =8,5\\ & H_1:\mu \ne 8,5\\ & \mathbf{\text{Daerah kritis}}\\ & \text{Uji dua pihak/hipotesis dua arah dengan}\alpha =1\mathrm{\%}\\ & t_{1-\frac{1}{2}(0,01)}=t_{0,995}.\text{Dengan dk}=16-1=15\\ & \text{diperoleh nilai}t=2,95(\text{tabel distribusi student})\\ & \bullet \text{Terima}{H}_0,\text{jika}:-2,95<t<2,95\\ & \bullet \text{Tolak}{H}_0,\text{jika}:t<-2,95\text{atau}t>2,95\\ & \text{Berikut disajikan tabel}\mathbf{\text{distribusi student}}\\ & \begin{array}{|ccccc|}\hline dk& t_{0,995}& t_{0,99}& t_{0,975}& t_{0,95}\\ 1& 63,66& 31,82& 12,71& 6,31\\ 2& 9,92& 6,96& 4,3& 2,92\\ 3& 5,84& 4,54& 3,18& 2,35\\ 4& 4,6& 3,75& 2,78& 2,13\\ 5& 4,03& 3,36& 2,57& 2,02\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 15& 2,95& 2,60& 2,13& 1,75\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 99& \cdots & \cdots & 1,99& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 120& 2,62& 2,36& 1,98& 1,66\\ \mathrm{\infty }& 2,56& 2,33& 1,96& 1,645\\ \hline\end{array}\\ & \mathbf{\text{Nilai statistik uji}}\\ & \overline{x}={\displaystyle \frac{7,5+8,2+8,4+\cdots +8,8+8,3}{16},}\\ & =8,4125\\ & s=\sqrt{{\displaystyle \frac{(7,5-8,4125{)}^2+\cdots +(8,3-8,4125{)}^2}{16-1}}}\\ & =\sqrt{0,308}=0,555\\ & n=100,t={\displaystyle \frac{\overline{x}-{\mu }_0}{s}\sqrt{n}}\\ & \iff t={\displaystyle \frac{(8,4125-8,5)}{0,555}\sqrt{16}=-0,63}\\ & \mathbf{\text{Penentuan keputusan uji}}\\ & \text{Karena}:-2,95<-0,63<2,95,H_0\text{diterima}\\ & \mathbf{\text{Kesimpulan}}\\ & \text{Dengan taraf nyata 1}\mathrm{\%}\text{rata-rata skor}\\ & \text{performan pegawai adalah}8,5\end{array}\end{array}$.

$\begin{array}{l}\\ 2.& \text{Sebuah sampel acak 100 catatan kematian}\\ & \text{di negara A selama 1 tahun yang kemaren}\\ & \text{menunjukkan umur rata-rata 58,8 tahun}\\ & \text{dengan simpangan baku 7,8 tahun. Apakah}\\ & \text{hal itu menunjukkan bahwa harapan umur}\\ & \text{rata-rata sekarang minimal 60 tahun}?\\ & \text{Jelaskan pernyataan tersebut dengan tingkat}\\ & \text{signifikansi}5\mathrm{\%}\\ \\ & \mathbf{\text{Jawab}}:\\ & \begin{array}{rl}& \text{Misalkan umur rata-rata sekarang}\ge 60\text{tahun}\\ & \text{berdistribusi student}\\ & \mathbf{\text{Rumusan hipotesis}}{H}_0\text{dan}{H}_1\\ & H_0:\mu \ge 60\\ & H_1:\mu <60\\ & \mathbf{\text{Daerah kritis}}\\ & \text{Uji satu pihak/hipotesis pihak kiri dengan}\alpha =5\mathrm{\%}\\ & t_{1-(0,05)}=t_{0,995}.\text{Dengan dk}=100-1=99\\ & \text{diperoleh nilai}t=2,63(\text{tabel distribusi student})\\ & \bullet \text{Terima}{H}_0,\text{jika}:t>-2,63\\ & \bullet \text{Tolak}{H}_0,\text{jika}:t\le -2,63\\ & \mathbf{\text{Nilai statistik uji}}\\ & \mu =58,8,s=7,8\text{tahun}\\ & n=100,t={\displaystyle \frac{\overline{x}-{\mu }_0}{s}\sqrt{n}}\\ & \iff t={\displaystyle \frac{(58,8-60)}{7,8}\sqrt{100}=-1,54}\\ & \mathbf{\text{Penentuan keputusan uji}}\\ & \text{Karena}:t\le -1,54,H_0\text{diterima}\\ & \mathbf{\text{Kesimpulan}}\\ & \text{Dengan taraf nyata 5}\mathrm{\%}\text{umur rata-rata}\\ & \text{sekarang minimal}60\text{tahun}\end{array}\end{array}$.

DAFTAR PUSTAKA

1. Tasari, Aksin, N., Miyanto, Muklis. 2016. Matematika untuk SMA/MA Kelas XII Peminatan Matematika dan Ilmu-Ilmu Alam. Klaten: INTAN PARIWARA.
2. Sembiring, S., Zulkifli. M., Marsito, Rusdi. I. 2016. Matematika untuk Siswa SMA/MA Kelas XII Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Bandung: SRIKANDI EMPAT WIDYA UTAMA.
3. Sugiyono. 2013. Statistika untuk Penelitan. Bandung: ALFABETA